Egestion Versus Excretion: A Meta-Analysis Examining Nutrient Release Rates and Ratios across Freshwater Fauna
Abstract
1. Introduction
2. Methods
2.1. Literature Survey
2.2. Calculations
2.3. Statistical Analyses
3. Results
3.1. Literature Survey
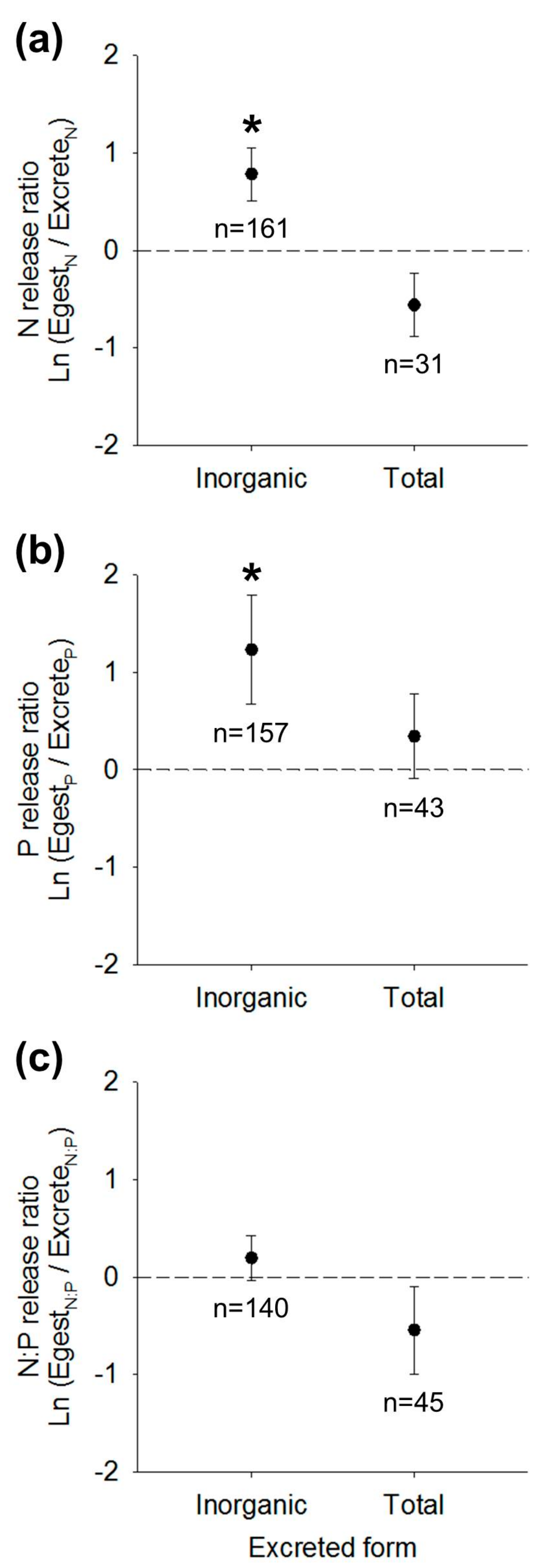
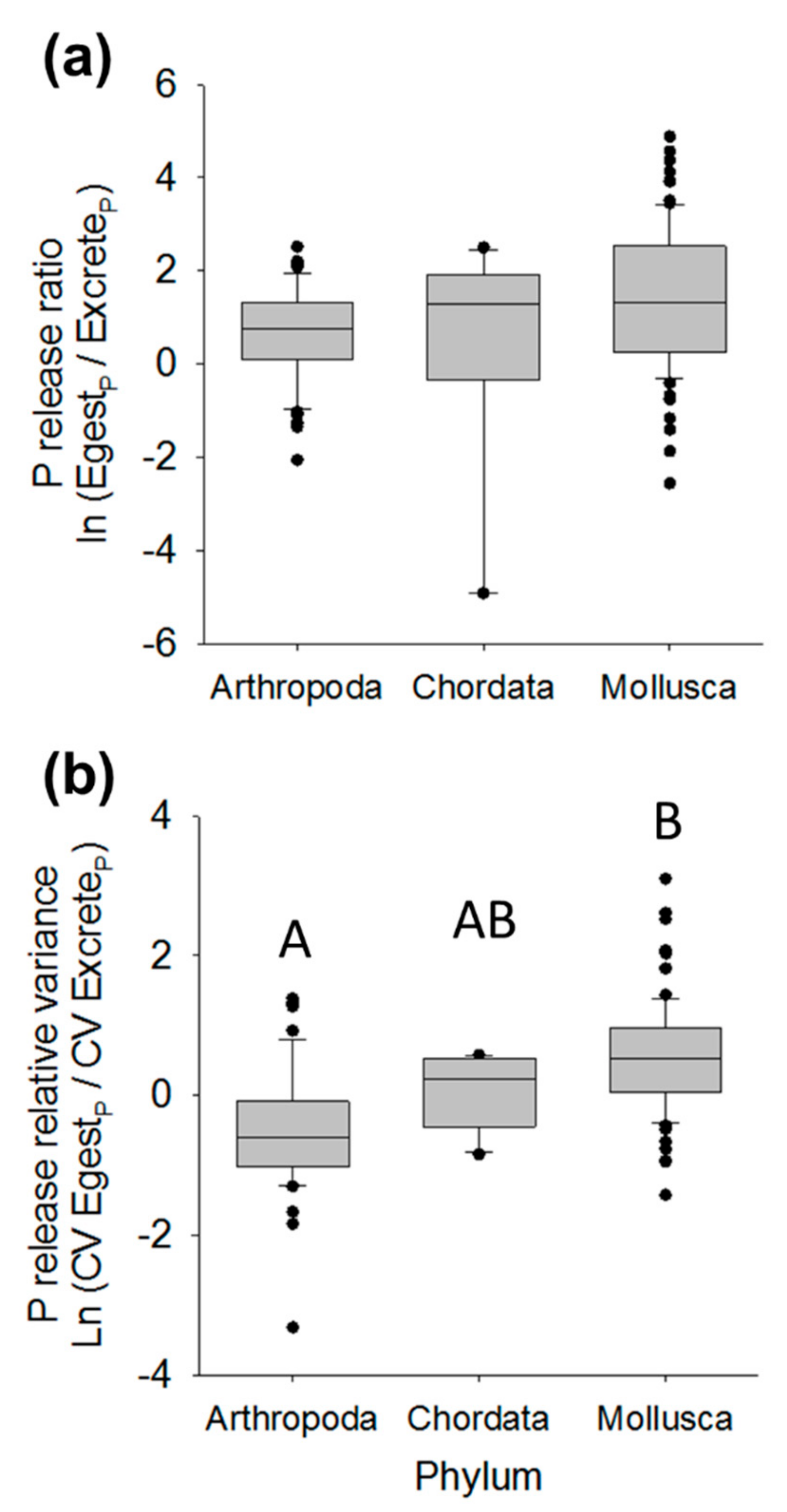
3.2. Nutrient Release Ratios
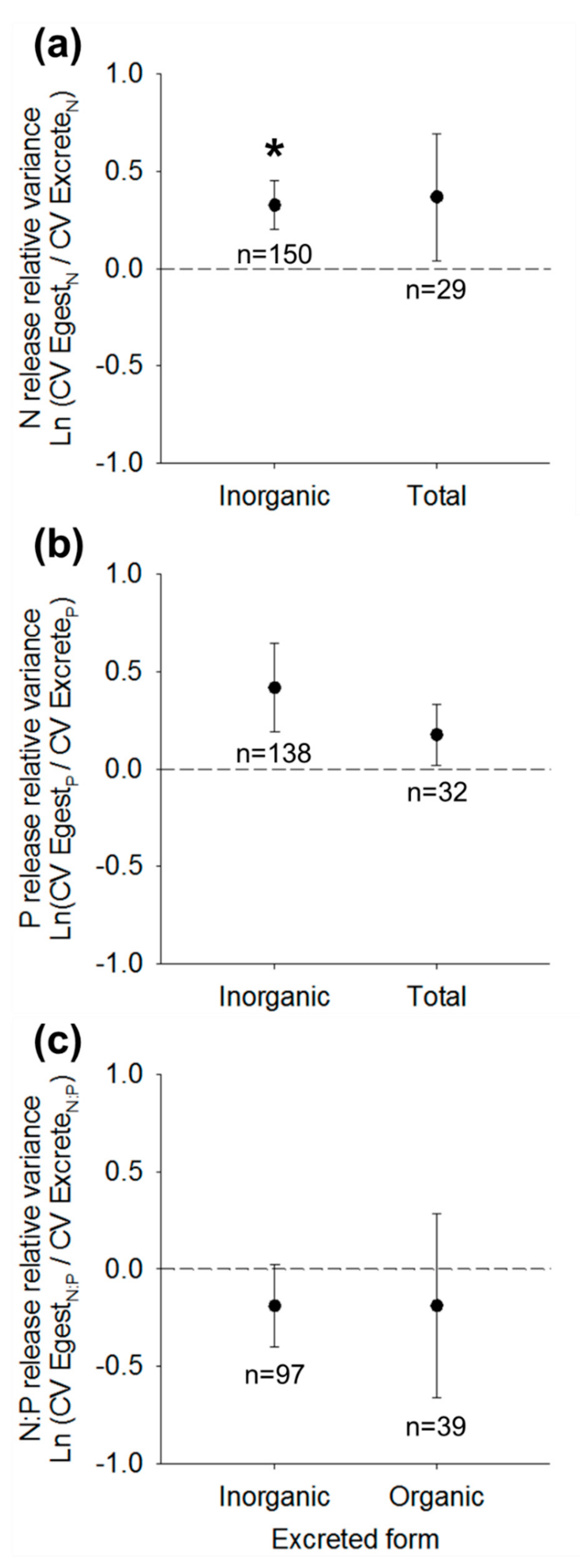
3.3. Nutrient Release Relative Variance
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vanni, M.J. Nutrient cycling by animals in freshwater ecosystems. Annu. Rev. Ecol. Syst. 2002, 33, 341–370. [Google Scholar] [CrossRef]
- Atkinson, C.L.; Capps, K.A.; Rugenski, A.T.; Vanni, M.J. Consumer-driven nutrient dynamics in freshwater ecosystems: From individuals to ecosystems. Biol. Rev. 2016, 92, 2003–2023. [Google Scholar] [CrossRef] [PubMed]
- Elser, J.J.; Urabe, J. The stoichiometry of consumer-driven nutrient recycling: Theory, observations, and consequences. Ecology 1999, 80, 735–751. [Google Scholar] [CrossRef]
- Sterner, R.W.; Elser, J.J. Ecological Stoichiometry: The Biology of Elements from Molecules to the Biosphere; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Evans-White, M.A.; Lamberti, G.A. Stoichiometry of consumer-driven nutrient recycling across nutrient regimes in streams. Ecol. Lett. 2006, 9, 1186–1197. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, C.L.; Vaughn, C.C.; Forshay, K.J.; Cooper, J.T. Aggregated filter-feeding consumers alter nutrient limitation: Consequences for ecosystem and community dynamics. Ecology 2013, 94, 1359–1369. [Google Scholar] [CrossRef]
- Atkinson, C.L.; Kelly, J.F.; Vaughn, C.C. Tracing consumer-derived nitrogen in riverine food webs. Ecosystems 2014, 17, 485–496. [Google Scholar] [CrossRef]
- McIntyre, P.B.; Flecker, A.S.; Vanni, M.J.; Hood, J.M.; Taylor, B.W.; Thomas, S.A. Fish distributions and nutrient cycling in streams: Can fish create biogeochemical hotspots? Ecology 2008, 89, 2335–2346. [Google Scholar] [CrossRef]
- Williamson, T.J.; Vanni, M.J.; González, M.J.; Renwick, W.H.; Bremigan, M.T.; Conroy, J.D. The importance of nutrient supply by fish excretion and watershed streams to a eutrophic lake varies with temporal scale over 19 years. Biogeochemistry 2018, 140, 233–253. [Google Scholar] [CrossRef]
- Griffiths, N.A.; Hill, W.R. Temporal variation in the importance of a dominant consumer to stream nutrient cycling. Ecosystems 2014, 17, 1169–1185. [Google Scholar] [CrossRef]
- Hopper, G.W.; Gido, K.B.; Vaughn, C.C.; Parr, T.B.; Popejoy, T.G.; Atkinson, C.L.; Gates, K.K. Biomass distribution of fishes and mussels mediates spatial and temporal heterogeneity in nutrient cycling in streams. Oecologia 2018, 188, 1133–1144. [Google Scholar] [CrossRef]
- Liess, A.; Haglund, A.L. Periphyton responds differentially to nutrients recycled in dissolved or faecal pellet form by the snail grazer Theodoxus fluviatilis. Freshw. Biol. 2007, 52, 1997–2008. [Google Scholar] [CrossRef]
- Halvorson, H.M.; Hall, D.J.; Evans-White, M.A. Long-term stoichiometry and fates highlight animal egestion as nutrient repackaging, not recycling, in aquatic ecosystems. Funct. Ecol. 2017, 31, 1802–1812. [Google Scholar] [CrossRef]
- Subalusky, A.L.; Dutton, C.L.; Rosi, E.J.; Post, D.M. Annual mass drownings of the Serengeti wildebeest migration influence nutrient cycling and storage in the Mara River. Proc. Natl. Acad. Sci. USA 2017, 114, 7647–7652. [Google Scholar] [CrossRef] [PubMed]
- Hood, J.M.; McNeely, C.; Finlay, J.C.; Sterner, R.W. Selective feeding determines patterns of nutrient release by stream invertebrates. Freshw. Sci. 2014, 33, 1093–1107. [Google Scholar] [CrossRef]
- Halvorson, H.M.; Fuller, C.; Entrekin, S.A.; Evans-White, M.A. Dietary influences on production, stoichiometry and decomposition of particulate wastes from shredders. Freshw. Biol. 2015, 60, 466–478. [Google Scholar] [CrossRef]
- Kohler, A.E.; Rugenski, A.; Taki, D. Stream food web response to a salmon carcass analogue addition in two central Idaho, U.S.A. streams. Freshw. Biol. 2008, 53, 446–460. [Google Scholar] [CrossRef]
- Wenger, S.J.; Subalusky, A.L.; Freeman, M.C. The missing dead: The lost role of animal remains in nutrient cycling in North American Rivers. Food Webs 2019, 18, e00106. [Google Scholar] [CrossRef]
- Zou, K.; Thébault, E.; Lacroix, G.; Barot, S. Interactions between the green and brown food web determine ecosystem functioning. Funct. Ecol. 2016, 30, 1454–1465. [Google Scholar] [CrossRef]
- Frost, P.C.; Evans-White, M.A.; Finkel, Z.V.; Jensen, T.C.; Matzek, V. Are you what you eat? Physiological constraints on organismal stoichiometry in an elementally imbalanced world. Oikos 2005, 109, 18–28. [Google Scholar] [CrossRef]
- Evans-White, M.A.; Halvorson, H.M. Comparing the ecological stoichiometry in green and brown food webs - A review and meta-analysis of freshwater food webs. Front. Microbiol. 2017, 8, 1184. [Google Scholar] [CrossRef]
- Anderson, T.R.; Hessen, D.O.; Elser, J.J.; Urabe, J. Metabolic stoichiometry and the fate of excess carbon and nutrients in consumers. Am. Nat. 2005, 165, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Clissold, F.J.; Tedder, B.J.; Conigrave, A.D.; Simpson, S.J. The gastrointestinal tract as a nutrient-balancing organ. Proc. R. Soc. B Biol. Sci. 2010, 277, 1751–1759. [Google Scholar] [CrossRef] [PubMed]
- Wagner, C.E.; McIntyre, P.B.; Buels, K.S.; Gilbert, D.M.; Michel, E. Diet predicts intestine length in Lake Tanganyika’s cichlid fishes. Funct. Ecol. 2009, 23, 1122–1131. [Google Scholar] [CrossRef]
- Liess, A.; Guo, J.; Lind, M.I.; Rowe, O. Cool tadpoles from Arctic environments waste fewer nutrients - high gross growth efficiencies lead to low consumer-mediated nutrient recycling in the North. J. Anim. Ecol. 2015, 84, 1744–1756. [Google Scholar] [CrossRef] [PubMed]
- Jochum, M.; Barnes, A.D.; Ott, D.; Lang, B.; Klarner, B.; Farajallah, A.; Scheu, S.; Brose, U. Decreasing stoichiometric resource quality drives compensatory feeding across trophic levels in tropical litter invertebrate communities. Am. Nat. 2017, 190, 131–143. [Google Scholar] [CrossRef]
- Iannino, A.; Vosshage, A.T.L.; Weitere, M.; Fink, P. High nutrient availability leads to weaker top-down control of stream periphyton: Compensatory feeding in Ancylus fluviatilis. Freshw. Biol. 2019, 64, 37–45. [Google Scholar] [CrossRef]
- Halvorson, H.M.; Fuller, C.L.; Entrekin, S.A.; Scott, J.T.; Evans-White, M.A. Detrital nutrient content and leaf species differentially affect growth and nutritional regulation of detritivores. Oikos 2018, 127, 1471–1481. [Google Scholar] [CrossRef]
- Allgeier, J.E.; Wenger, S.J.; Rosemond, A.D.; Schindler, D.E.; Layman, C.A. Metabolic theory and taxonomic identity predict nutrient recycling in a diverse food web. Proc. Natl. Acad. Sci. USA 2015, 112, E2640–E2647. [Google Scholar] [CrossRef]
- Vanni, M.J.; McIntyre, P.B. Predicting nutrient excretion of aquatic animals with metabolic ecology and ecological stoichiometry: A global synthesis. Ecology 2016, 97, 3460–3471. [Google Scholar] [CrossRef]
- Liess, A. Compensatory feeding and low nutrient assimilation efficiencies lead to high nutrient turnover in nitrogen-limited snails. Freshw. Sci. 2014, 33, 425–434. [Google Scholar] [CrossRef]
- Green, J.A.; Hardy, R.W.; Brannon, E.L. Effects of dietary phosphorus and lipid levels on utilization and excretion of phosphorus and nitrogen by rainbow trout (Oncorhynchus mykiss). 1. Laboratory-scale study. Aquac. Nutr. 2002, 8, 279–290. [Google Scholar] [CrossRef]
- Bureau, D.P.; Cho, C.Y. Phosphorus utilization by rainbow trout (Oncorhynchus mykiss): Estimation of phosphorus waste output. Aquaculture 1999, 179, 127–140. [Google Scholar] [CrossRef]
- André, E.R.; Hecky, R.E.; Duthie, H.C. Nitrogen and phosphorus regeneration by cichlids in the littoral zone of Lake Malawi, Africa. J. Great Lakes Res. 2003, 29, 190–201. [Google Scholar] [CrossRef]
- Atkinson, C.L.; Sansom, B.J.; Vaughn, C.C.; Forshay, K.J. Consumer aggregations drive nutrient dynamics and ecosystem metabolism in nutrient-limited systems. Ecosystems 2018, 21, 521–535. [Google Scholar] [CrossRef]
- Christian, A.D. Spatial and Temporal Analysis of Freshwater Mussel Assemblage Size Structure, Distribution, Trophic Status, and Nutrient Recycling in Low-Order Streams. Ph.D. Thesis, Miami University, Oxford, OH, USA, 2002. [Google Scholar]
- Christian, A.D.; Crump, B.G.; Berg, D.J. Nutrient release and ecological stoichiometry of freshwater mussels (Mollusca:Unionidae) in 2 small, regionally distinct streams. J. N. Am. Benthol. Soc. 2008, 27, 440–450. [Google Scholar] [CrossRef]
- Cyr, H.; Collier, K.J.; Clearwater, S.J.; Hicks, B.J.; Stewart, S.D. Feeding and nutrient excretion of the New Zealand freshwater mussel Echyridella menziesii (Hyriidae, Unionida): Implications for nearshore nutrient budgets in lakes and reservoirs. Aquat. Sci. 2017, 79, 557–571. [Google Scholar] [CrossRef]
- Greene, R. The Effect of Non-Native and Native Anuran Tadpoles on Aquatic Ecosystem Processes. Master’s Thesis, Arizona State University, Tempe, AZ, USA, 2015. [Google Scholar]
- Hall, R.O.H., Jr.; Tank, J.L.; Dybdahl, M.F. Exotic snails dominate nitrogen and carbon cycling in a highly productive stream. Front. Ecol. Environ. 2003, 1, 407–411. [Google Scholar] [CrossRef]
- Halvorson, H.M.; Sperfeld, E.; Evans-White, M.A. Quantity and quality limit detritivore growth: Mechanisms revealed by ecological stoichiometry and co-limitation theory. Ecology 2017, 98, 2995–3002. [Google Scholar] [CrossRef]
- Hoellein, T.J.; Zarnoch, C.B.; Bruesewitz, D.A.; DeMartini, J. Contributions of freshwater mussels (Unionidae) to nutrient cycling in an urban river: Filtration, recycling, storage, and removal. Biogeochemistry 2017, 135, 307–324. [Google Scholar] [CrossRef]
- Mas-Martí, E.; Romaní, A.M.; Muñoz, I. Consequences of warming and resource quality on the stoichiometry and nutrient cycling of a stream shredder. PLoS ONE 2015, 10, e0118520. [Google Scholar] [CrossRef]
- McLeay, S.M.; Smith, L.L.; Atkinson, C.L. The stoichiometry of larval anuran development in natural wetlands. J. Freshw. Ecol. 2019, 34, 497–512. [Google Scholar] [CrossRef]
- McLeay, S.M. The Role of Larval Anurans as Consumers in Ecosystem Processes within Geographically Isolated Wetlands in the Southeastern United States. Master’s Thesis, University of Alabama, Tuscaloosa, AL, USA, 2017. [Google Scholar]
- Mosley, C.; Bootsma, H. Phosphorus recycling by profunda quagga mussels (Dreissena rostriformis bugensis) in Lake Michigan. J. Great Lakes Res. 2015, 41, 38–48. [Google Scholar] [CrossRef]
- Norlin, L.; Byström, P.; Karlsson, J.; Johansson, M.; Liess, A. Climate change will alter amphibian-mediated nutrient pathways: Evidence from Rana temporaria tadpoles in experimental ponds. Freshw. Biol. 2016, 61, 472–485. [Google Scholar] [CrossRef]
- Ozersky, T.; Evans, D.O.; Ginn, B.K. Invasive mussels modify the cycling, storage and distribution of nutrients and carbon in a large lake. Freshw. Biol. 2015, 60, 827–843. [Google Scholar] [CrossRef]
- Subalusky, A.L.; Dutton, C.L.; Rosi-Marshall, E.J.; Post, D.M. The hippopotamus conveyor belt: Vectors of carbon and nutrients from terrestrial grasslands to aquatic systems in sub-Saharan Africa. Freshw. Biol. 2015, 60, 512–525. [Google Scholar] [CrossRef]
- Vanderploeg, H.A.; Sarnelle, O.; Liebig, J.R.; Morehead, N.R.; Robinson, S.D.; Johengen, T.H.; Horst, G.P. Seston quality drives feeding, stoichiometry and excretion of zebra mussels. Freshw. Biol. 2017, 62, 664–680. [Google Scholar] [CrossRef]
- Villanueva, V.D.; Albariño, R.; Canhoto, C. Detritivores feeding on poor quality food are more sensitive to increased temperatures. Hydrobiologia 2011, 678, 155–165. [Google Scholar] [CrossRef]
- Williamson, F.; Ozersky, T. Lake characteristics, population properties and invasion history determine impact of invasive bivalves on lake nutrient dynamics. Ecosystems 2019, in press. [Google Scholar] [CrossRef]
- Williamson, F. Role of Invasive Dreissenid Mussles in the Biogeochemical Cycling of Carbon, Nitrogen, and Phosphorus in Minnesota Lakes. Master’s Thesis, University of Minnesota, Minneapolis, MN, USA, 2017. [Google Scholar]
- Hillebrand, H.; Borer, E.T.; Bracken, M.E.S.; Cardinale, B.J.; Cebrian, J.; Cleland, E.E.; Elser, J.J.; Gruner, D.S.; Harpole, W.S.; Ngai, J.T.; et al. Herbivore metabolism and stoichiometry each constrain herbivore at different organizational scales across ecosystems. Ecol. Lett. 2009, 12, 516–527. [Google Scholar] [CrossRef]
- Bracken, M.E.S. Stoichiometric mismatch between consumers and resources mediates the growth of rocky intertidal suspension feeders. Front. Microbiol. 2017, 8, 1297. [Google Scholar] [CrossRef]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Package lme4: Linear Mixed Effects Models Using ‘Eigen’ and S4. R Package Version 1.1-21. 2019. Available online: https://cran.r-project.org/web/packages/lme4/index.html (accessed on 23 June 2019).
- Burnham, K.P.; Anderson, D.R.; Huyvaert, K.P. AIC model selection and multimodel inference in behavioral ecology: Some background, observations, and comparisons. Behav. Ecol. Sociobiol. 2011, 65, 23–35. [Google Scholar] [CrossRef]
- Bartón, B. PAckage MuMIn: Multi-Model Inference. R Package Version 1.43.6. 2019. Available online: https://cran.r-project.org/web/packages/MuMIn/index.html (accessed on 23 June 2019).
- R Core Team. R: A language and Environment for Statistical Computer; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: http://www.R-project.org/ (accessed on 23 June 2019).
- Alexiades, A.V.; Flecker, A.S.; Kraft, C.E. Nonnative fish stocking alters stream ecosystem nutrient dynamics. Ecol. Appl. 2017, 27, 956–965. [Google Scholar] [CrossRef] [PubMed]
- Parr, T.B.; Capps, K.A.; Inamdar, S.P.; Metcalf, K.A. Animal-mediated organic matter transformation: Aquatic insects as a source of microbially bioavailable organic nutrients and energy. Funct. Ecol. 2019, 33, 524–535. [Google Scholar] [CrossRef]
- Karasov, W.H.; Diamond, J.M. Interplay between physiology and ecology in digestion. Bioscience 1988, 38, 602–611. [Google Scholar] [CrossRef]
- Kozlovsky, D.G. A critical evaluation of the trophic level concept. I. Ecological efficiencies. Ecology 1968, 49, 48–60. [Google Scholar] [CrossRef]
- Joyce, P.; Wotton, R.S. Shredder fecal pellets as stores of allochthonous organic matter in streams. J. N. Am. Benthol. Soc. 2008, 27, 521–528. [Google Scholar] [CrossRef]
- Atkinson, C.L.; Allen, D.C.; Davis, L.; Nickerson, Z.L. Incorporating ecogeomorphic feedbacks to better understand resiliency in streams: A review and directions forward. Geomorphology 2018, 305, 123–140. [Google Scholar] [CrossRef]
- Vaughn, C.C.; Hoellein, T.J. Bivalve impacts in freshwater and marine ecosystems. Annu. Rev. Ecol. Evol. Syst. 2018, 49, 183–208. [Google Scholar] [CrossRef]
- Wotton, R.S.; Malmqvist, B. Feces in aquatic ecosystems. Bioscience 2001, 51, 537–544. [Google Scholar] [CrossRef]
- Joyce, P.; Warren, L.L.; Wotton, R.S. Faecal pellets in streams: Their binding, breakdown and utilization. Freshw. Biol. 2007, 52, 1868–1880. [Google Scholar] [CrossRef]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Toward a metabolic theory of ecology. Ecology 2004, 85, 1771–1789. [Google Scholar] [CrossRef]
- Elser, J.J.; Acharya, K.; Kyle, M.; Cotner, J.; Makino, W.; Markow, T.; Watts, T.; Hobbie, S.; Fagan, W.; Schade, J.; et al. Growth rate-stoichiometry couplings in diverse biota. Ecol. Lett. 2003, 6, 936–943. [Google Scholar] [CrossRef]
- Hood, J.M.; Sterner, R.W. Carbon and phosphorus linkages in Daphnia growth are determined by growth rate, not species or diet. Funct. Ecol. 2014, 28, 1156–1165. [Google Scholar] [CrossRef]
- Halvorson, H.M.; Fuller, C.L.; Entrekin, S.A.; Scott, J.T.; Evans-White, M.A. Interspecific homeostatic regulation and growth across aquatic invertebrate detritivores: A test of ecological stoichiometry theory. Oecologia 2019, 190, 229–242. [Google Scholar] [CrossRef] [PubMed]
- Back, J.A.; King, R.S. Sex and size matter: Ontogenetic patterns of nutrient content of aquatic insects. Freshw. Sci. 2013, 32, 837–848. [Google Scholar] [CrossRef]
- El-Sabaawi, R.W.; Travis, J.; Zandonà, E.; McIntyre, P.B.; Reznick, D.N.; Flecker, A. Intraspecific variability modulates interspecific variability in animal organismal stoichiometry. Ecol. Evol. 2014, 4, 1505–1515. [Google Scholar] [CrossRef]
- Jeyasingh, P.D.; Cothran, R.D.; Tobler, M. Testing the ecological consequences of evolutionary change using elements. Ecol. Evol. 2014, 4, 528–538. [Google Scholar] [CrossRef]
- Moody, E.K.; Carson, E.W.; Corman, J.R.; Espinosa-Pérez, H.; Ramos, J.; Sabo, J.L.; Elser, J.J. Consumption explains intraspecific variation in nutrient recycling stoichiometry in a desert fish. Ecology 2018, 99, 1552–1561. [Google Scholar] [CrossRef]
- Des Roches, S.; Post, D.M.; Turley, N.E.; Bailey, J.K.; Hendry, A.P.; Kinnison, M.T.; Schweitzer, J.A.; Palkovacs, E.P. The ecological importance of intraspecific variation. Nat. Ecol. Evol. 2018, 2, 57–64. [Google Scholar] [CrossRef]
- Whiles, M.R.; Huryn, A.D.; Taylor, B.W.; Reeve, J.D. Influence of handling stress and fasting on estimates of ammonium excretion by tadpoles and fish: Recommendations for designing excretion experiments. Limnol. Oceanogr. Methods 2009, 7, 1–7. [Google Scholar] [CrossRef]
- Oliveira-Cunha, P.; Capps, K.A.; Neres-Lima, V.; Lourenço-Amorim, C.; Tromboni, F.; Moulton, T.P.; Zandonà, E. Effects of incubation conditions on nutrient mineralisation rates in fish and shrimp. Freshw. Biol. 2018, 63, 1107–1117. [Google Scholar] [CrossRef]
- Subalusky, A.L.; Post, D.M. Context dependency of animal resource subsidies. Biol. Rev. 2019, 94, 517–538. [Google Scholar] [CrossRef] [PubMed]
- Ramamonjisoa, N.; Natuhara, Y. Contrasting effects of functionally distinct tadpole species on nutrient cycling and litter breakdown in a tropical rainforest stream. Freshw. Biol. 2018, 63, 202–213. [Google Scholar] [CrossRef]
| Source Study | Setting | Location | Phyla | # Species | # Study Populations |
|---|---|---|---|---|---|
| Andre et al. 2003 [34] | Field | Lake Malawi, Africa | Chordata | 5 | 5 |
| Atkinson et al. 2018 [35]; Atkinson et al. unpub. | Field | Oklahoma, USA | Mollusca | 6 | 15 |
| Atkinson et al. unpub. | Field | Alabama, USA | Mollusca | 10 | 28 |
| Christian 2002 [36]; Christian et al. 2008 [37] | Field | Arkansas and Ohio, USA | Mollusca | 4 | 27 |
| Cyr et al. 2017 [38] | Field | New Zealand | Mollusca | 1 | 5 |
| Greene 2015 [39] | Field | Arizona, USA | Chordata | 2 | 2 |
| Hall et al. 2003 [40] | Field | Wyoming, USA | Mollusca | 1 | 1 |
| Halvorson et al. 2015 [16] | Lab | Arkansas, USA | Arthropoda | 2 | 14 |
| Halvorson et al. 2017 [41] | Lab | Arkansas, USA | Arthropoda | 1 | 3 |
| Halvorson et al. unpub. | Field | Arkansas, USA | Arthropoda | 7 | 10 |
| Halvorson et al. unpub. | Lab | Arkansas, USA | Arthropoda | 2 | 8 |
| Hoellein et al. 2017 [42] | Field | Illinois, USA | Mollusca | 2 | 2 |
| Hood et al. 2014 [15] | Lab and Field | California and Minnesota, USA | Arthropoda | 3 | 21 |
| Liess 2014 [31] | Lab | Sweden | Mollusca | 2 | 2 |
| Liess et al. 2015 [25] | Lab | Sweden | Chordata | 1 | 8 |
| Mas-Marti et al. 2015 [43] | Lab | Spain | Arthropoda | 1 | 4 |
| McLeay et al. 2019 [44]; McLeay 2017 [45] | Field | Georgia, USA | Chordata | 1 | 17 |
| Mosley and Bootsma 2015 [46] | Field | Lake Michigan, USA | Mollusca | 1 | 15 |
| Norlin et al. 2016 [47] | Field | Sweden | Chordata | 1 | 4 |
| Ozersky et al. 2015 [48] | Field | Ontario, Canada | Mollusca | 2 | 6 |
| Subalusky et al. 2015 [49] | Lab | Milwaukee Zoo, USA | Chordata | 1 | 1 |
| Vanderploeg et al. 2017 [50] | Field | Lake Erie, USA | Mollusca | 1 | 1 |
| Villanueva et al. 2011 [51] | Lab | Portugal | Arthropoda | 1 | 6 |
| Williamson and Ozersky in press [52]; Williamson 2017 [53] | Field | Minnesota, USA | Mollusca | 1 | 10 |
| Response | Model Structure | AIC | Chi-Square | p-Value | R-Squared |
|---|---|---|---|---|---|
| N release ratio | 1|Source Study + 1|Family | 591.2 | 0.03 | ||
| Log Dry Mass + 1|Source Study + 1|Family | 592.4 | 0.82 | 0.365 | 0.03 | |
| Phylum + 1|Source Study + 1|Family | 594.6 | 0.00 | 1.000 | 0.03 | |
| Log Dry Mass + Phylum + 1|Source Study + 1|Family | 595.7 | 0.85 | 0.356 | 0.03 | |
| P release ratio | 1|Source Study + 1|Family | 1672.0 | <0.01 | ||
| Log Dry Mass + 1|Source Study + 1|Family | 549.6 | 1124.4 | <0.001 | 0.24 | |
| Phylum + 1|Source Study + 1|Family | 1668.2 | 0.00 | 1.000 | <0.01 | |
| Log Dry Mass + Phylum + 1|Source Study + 1|Family | 546.9 | 1123.3 | <0.001 | 0.22 | |
| N:P release ratio | 1|Source Study + 1|Family | 425.1 | 0.06 | ||
| Log Dry Mass + 1|Source Study + 1|Family | 428.4 | 0.00 | 1.000 | 0.06 | |
| Phylum + 1|Source Study + 1|Family | 428.1 | 2.3 | 0.131 | 0.07 | |
| Log Dry Mass + Phylum + 1|Source Study + 1|Family | 431.2 | 0.00 | 1.000 | 0.07 |
| Response | Model Structure | AIC | Chi-Square | p-Value | R-Squared |
|---|---|---|---|---|---|
| N release relative variance | 1|Family | 348.9 | 0.03 | ||
| Log Dry Mass + 1|Family | 350.5 | 0.5 | 0.496 | 0.03 | |
| Phylum + 1|Family | 354.9 | 0.0 | 1.000 | 0.03 | |
| Log Dry Mass + Phylum + 1|Family | 357.5 | 0.0 | 1.000 | 0.04 | |
| P release relative variance | 1|Family | 337.0 | 0.06 | ||
| Log Dry Mass + 1|Family | 334.8 | 4.2 | 0.040 | 0.12 | |
| Phylum + 1|Family | 338.8 | 0.0 | 1.000 | 0.06 | |
| Log Dry Mass + Phylum + 1|Family | 333.7 | 7.1 | 0.008 | 0.10 | |
| N:P release relative variance | 1|Family | 255.6 | 0.05 | ||
| Log Dry Mass + 1|Family | 259.4 | 0.0 | 1.000 | 0.05 | |
| Phylum + 1|Family | 258.9 | 2.5 | 0.117 | 0.05 | |
| Log Dry Mass + Phylum + 1|Family | 262.6 | 0.0 | 1.000 | 0.05 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halvorson, H.M.; Atkinson, C.L. Egestion Versus Excretion: A Meta-Analysis Examining Nutrient Release Rates and Ratios across Freshwater Fauna. Diversity 2019, 11, 189. https://doi.org/10.3390/d11100189
Halvorson HM, Atkinson CL. Egestion Versus Excretion: A Meta-Analysis Examining Nutrient Release Rates and Ratios across Freshwater Fauna. Diversity. 2019; 11(10):189. https://doi.org/10.3390/d11100189
Chicago/Turabian StyleHalvorson, Halvor M., and Carla L. Atkinson. 2019. "Egestion Versus Excretion: A Meta-Analysis Examining Nutrient Release Rates and Ratios across Freshwater Fauna" Diversity 11, no. 10: 189. https://doi.org/10.3390/d11100189
APA StyleHalvorson, H. M., & Atkinson, C. L. (2019). Egestion Versus Excretion: A Meta-Analysis Examining Nutrient Release Rates and Ratios across Freshwater Fauna. Diversity, 11(10), 189. https://doi.org/10.3390/d11100189





