Age-Independent Adult Mortality in a Long-Lived Herb
Abstract
1. Introduction
- Does the predicted mortality trajectory support the existence of demographic senescence?
- What is the life expectancy at different ages, as projected by the best-fitting mortality trajectory?
- Is there evidence of trade-offs between survival, reproduction and growth?
- How does plant shrinkage influence survival?
2. Materials and Methods
2.1. Study Plants
2.2. Study Sites
2.3. Data Collection and Calculation
2.4. Analysis and Modelling
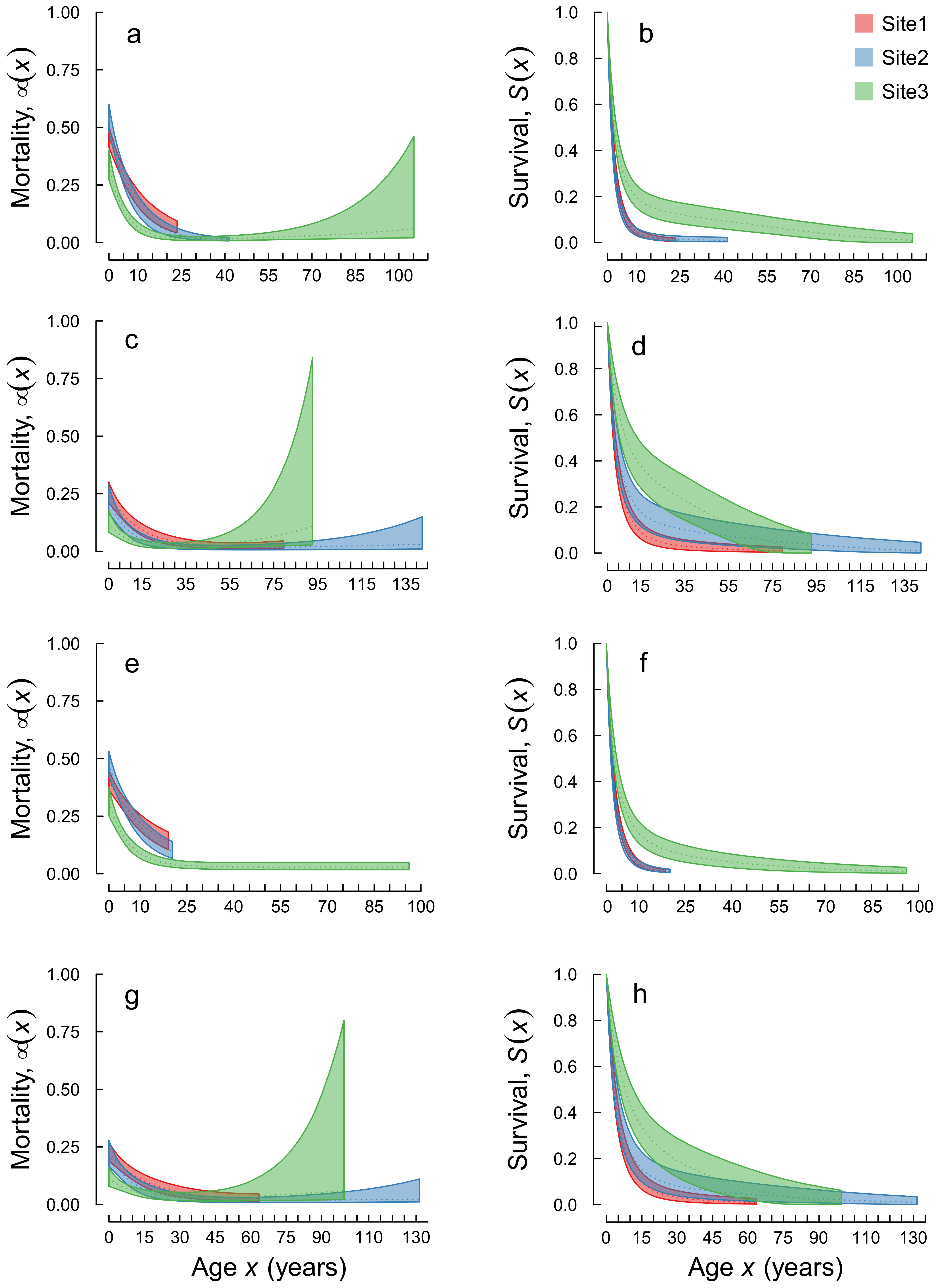
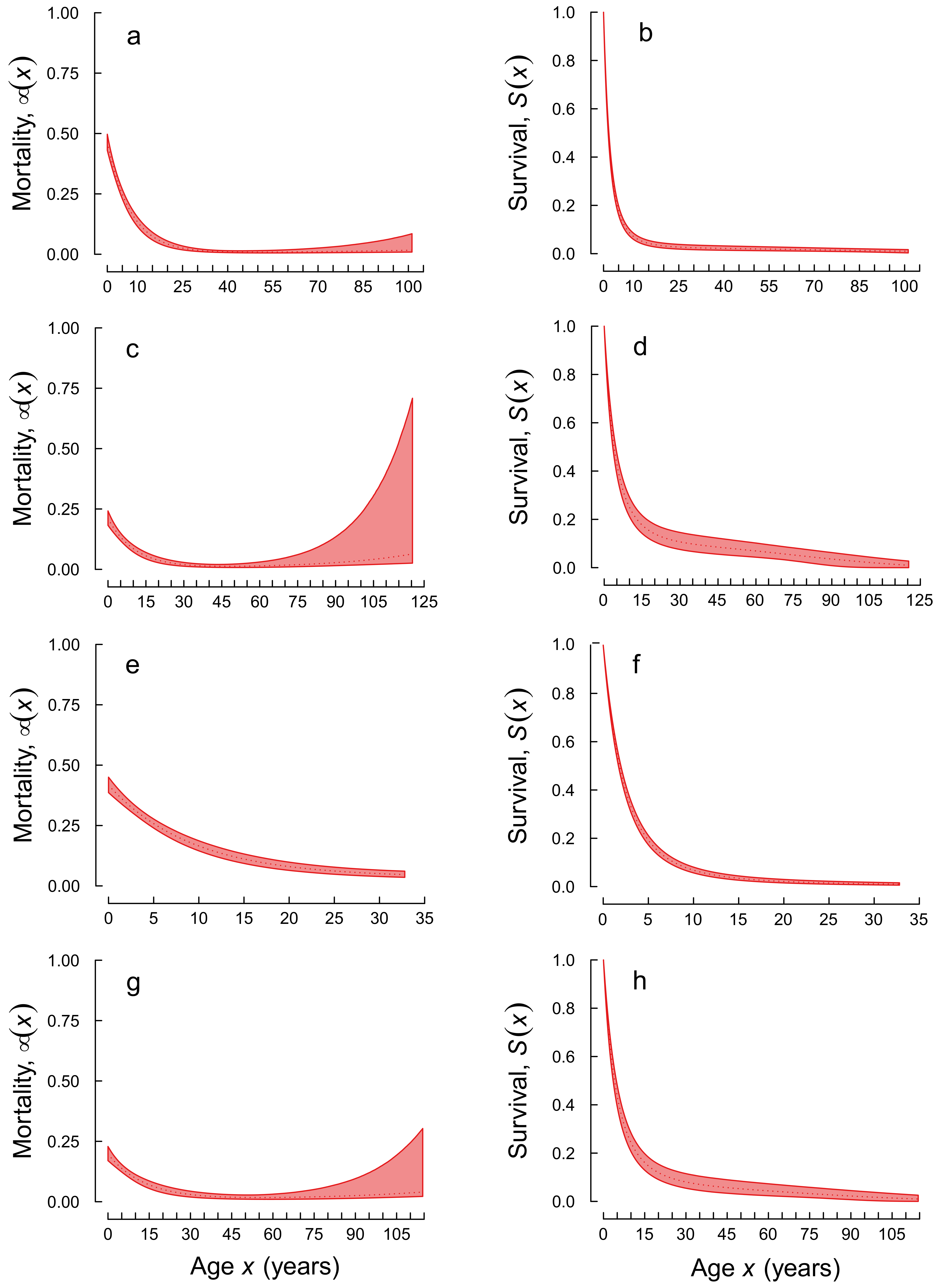
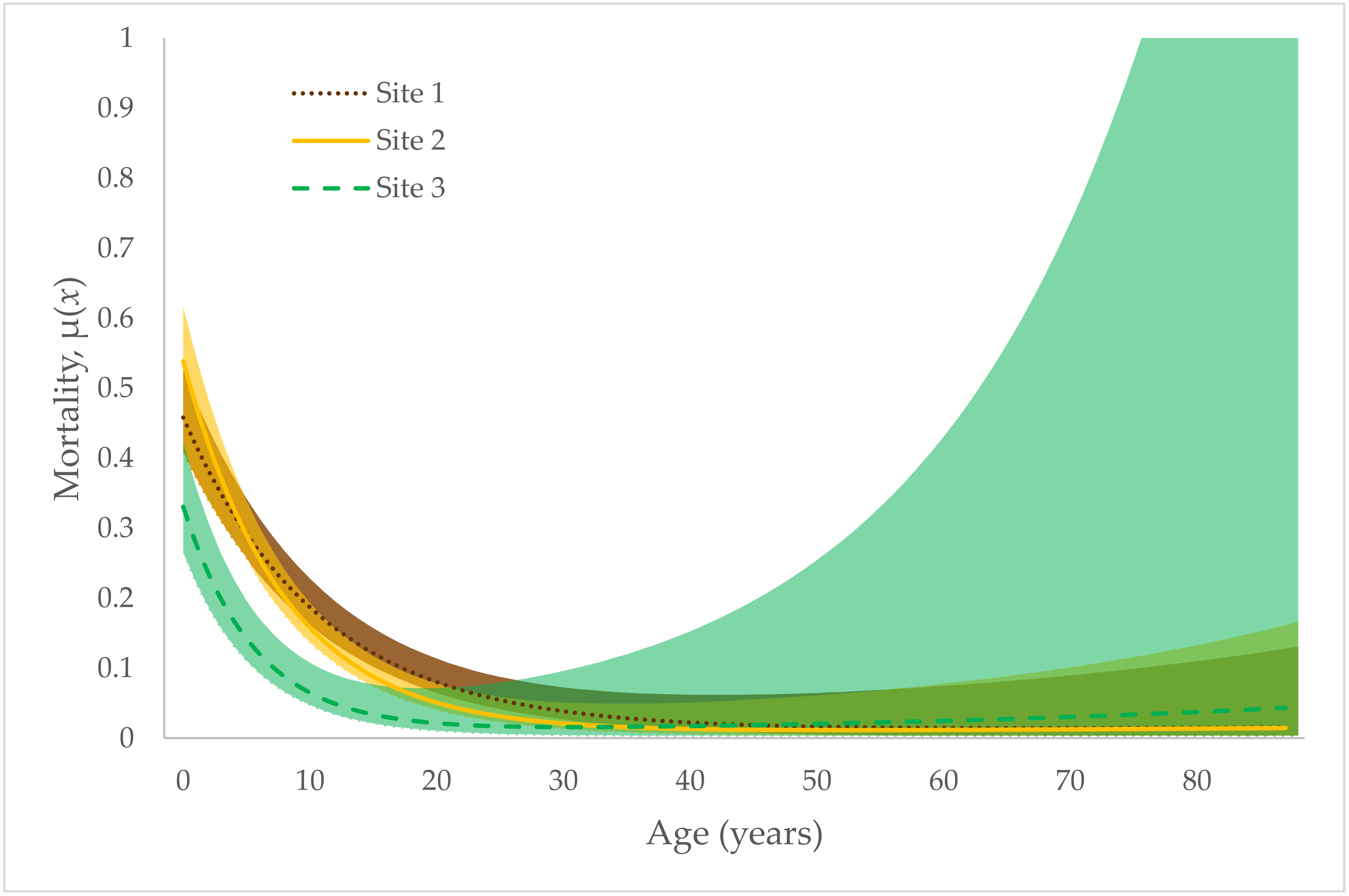
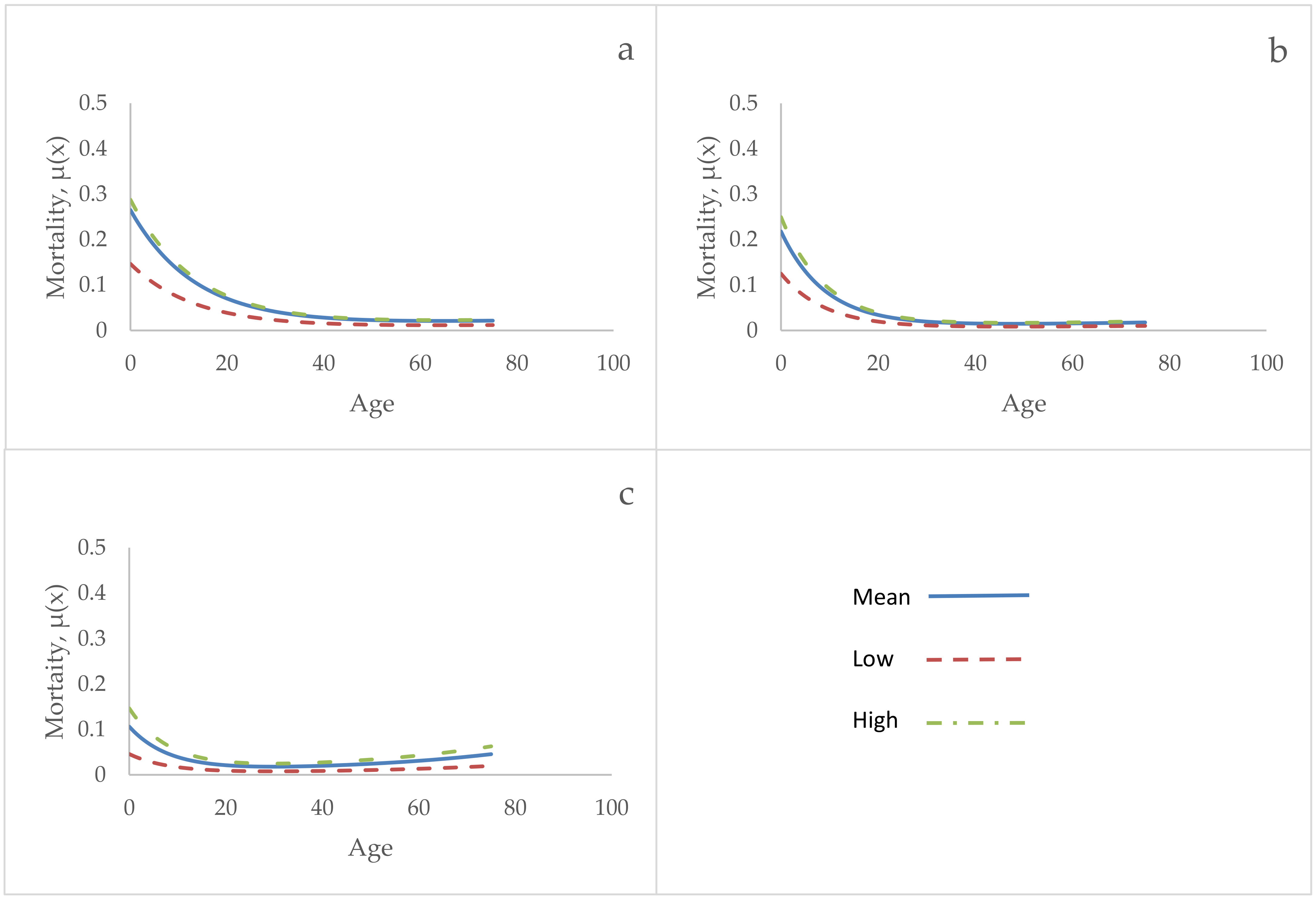
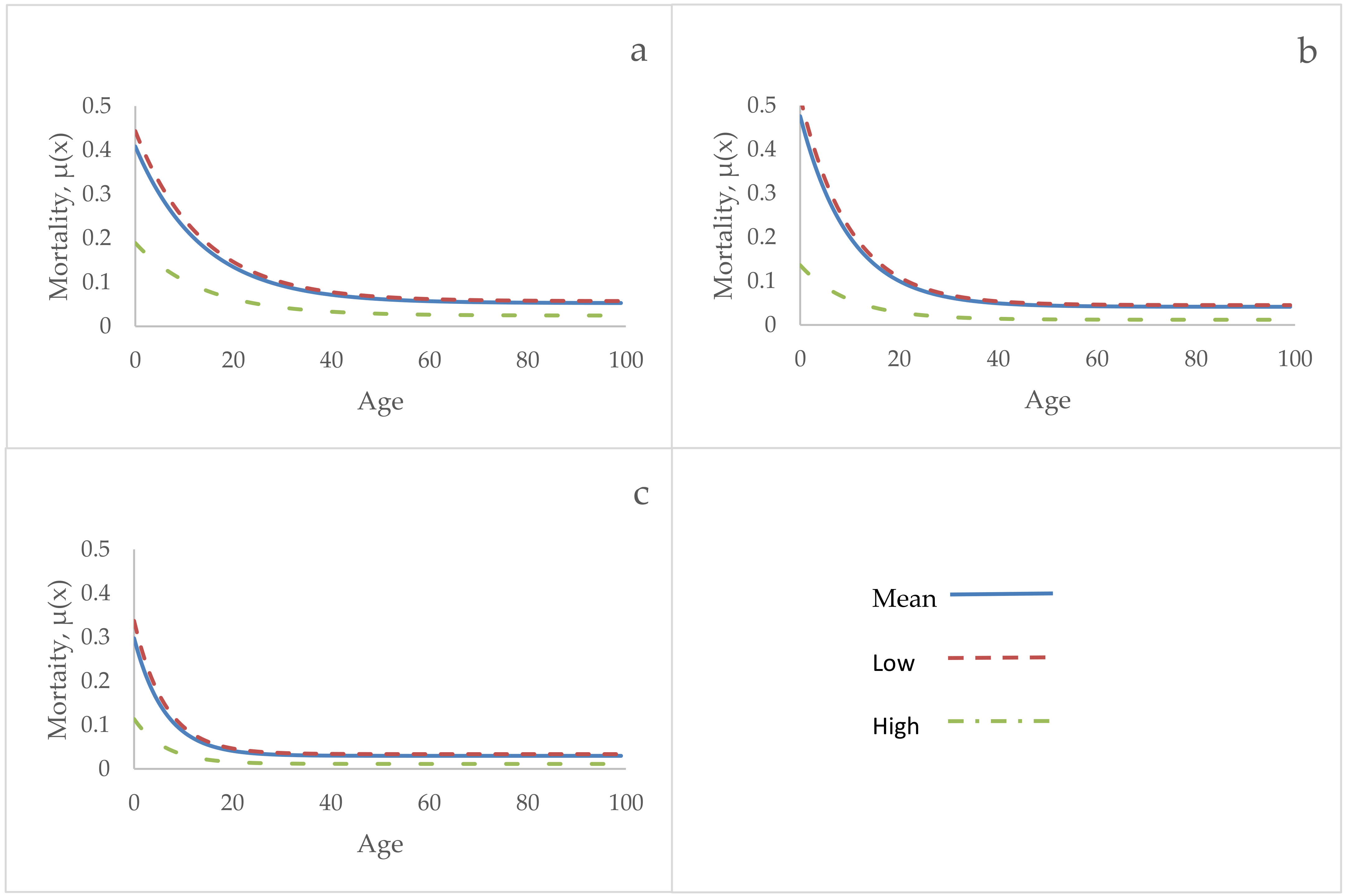
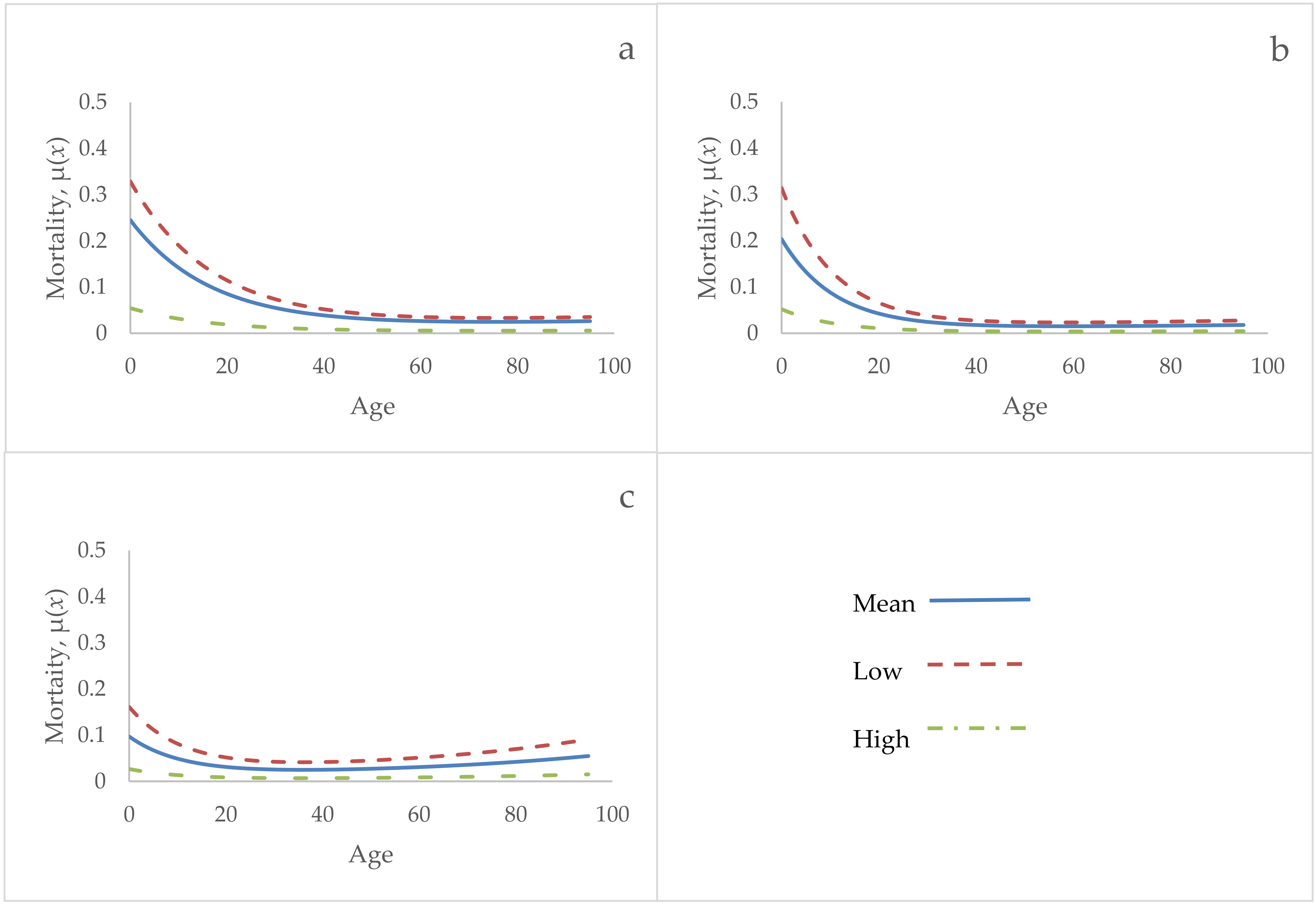
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Pico, F.X.; Retana, J. Age-specific, density-dependent and environment-based mortality of a short-lived perennial herb. Plant. Biol. 2008, 10, 374–381. [Google Scholar] [CrossRef]
- Roach, D.A.; Ridley, C.E.; Dudycha, J.L. Longitudinal analysis of Plantago: Age by environment interactions reveal aging. Ecology 2009, 90, 1427–1433. [Google Scholar] [CrossRef] [PubMed]
- Dahlgren, J.P.; Colchero, F.; Jones, O.R.; Øien, D.; Moen, A.; Sletvold, N. Actuarial senescence in a long-lived orchid challenge our current understanding of ageing. Proc. Biol. Sci. 2016, 283, 20161217. [Google Scholar] [CrossRef] [PubMed]
- Quarles, B.M.; Roach, D.A. Ageing in an herbaceous plant: Increases in mortality and decreases in physiology and seed mass. J. Ecol. 2019, 107, 1409–1418. [Google Scholar] [CrossRef]
- Harper, J.L.; White, J. The Demography of Plants. Annu. Rev. Ecol. Syst. 1974, 5, 419–463. [Google Scholar] [CrossRef]
- Rose, R.J.; Clarke, R.T.; Chapman, S.B. Individual variation and the effects of weather, age and flowering history on survival and flowering of the long-lived perennial Gentiana pneumonanthe. Ecography 1998, 21, 317–326. [Google Scholar] [CrossRef]
- Fair, J.; Lauenroth, W.; Coffin, D. Demography of Bouteloua gracilis in a mixed prairie: Analysis of genets and individuals. J. Ecol. 1999, 87, 233–243. [Google Scholar] [CrossRef]
- Hutchings, M.J. The population biology of the early spider orchid Ophrys sphegodes Mill: III. Demography over three decades. J. Ecol. 2010, 98, 867–878. [Google Scholar] [CrossRef]
- Dahlgren, J.; Roach, D.A. Demographic Senescence in Herbaceous Plants. In The Evolution of Senescence in the Tree of Life; Shefferson, R.P., Jones, O.R., Salguero-Gómez, R., Eds.; Cambridge University Press: Cambridge, UK, 2017; pp. 303–319. [Google Scholar]
- Cochran, M.E.; Ellner, S. Simple methods for calculating age-based life history parameters for stage- structured populations. Ecol. Monogr. 1992, 62, 345–364. [Google Scholar] [CrossRef]
- Menges, E.S. Population viability analyses in plants: Challenges and opportunities. Trends Ecol. Evol. 2000, 15, 51–56. [Google Scholar] [CrossRef]
- Ehrlén, J.; Lehtilä, K. How perennial are perennial plants? Oikos 2002, 98, 308–322. [Google Scholar] [CrossRef]
- Fenner, M. Seedlings. New Phytol. 1987, 106, 35–47. [Google Scholar] [CrossRef]
- Lauenroth, W.K.; Adler, P.B. Demography of perennial grassland plants: Survival, life expectancy and life span. J. Ecol. 2008, 96, 1023–1032. [Google Scholar] [CrossRef]
- Chu, C.; Havstad, K.M.; Kaplan, N.; Lauenroth, W.K.; McClaran, M.P.; Peters, D.P.; Vermeire, L.T.; Adler, P.B. Life form influences survivorship for 109 herbaceous perennials from six semi-arid ecosystems. J. Veg. Sci. 2014, 25, 947–954. [Google Scholar] [CrossRef]
- Obeso, J.R. The costs of reproduction in plants. New Phytol. 2002, 155, 320–348. [Google Scholar] [CrossRef]
- Bigler, C.; Veblen, T.T. Increased early growth rates decrease longevities of conifers in subalpine forests. Oikos 2009, 118, 1130–1138. [Google Scholar] [CrossRef]
- Seiwa, K. Trade-offs Between Seedling Growth and Survival in Deciduous Broadleaved Trees in a Temperate Forest. Ann. Bot. 2007, 99, 537–544. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, B.; Wright, S.J.; Muller-Landau, H.C.; Kitajima, K.; Hernandez, A. Life history trade-offs in tropical trees and lianas. Ecology 2006, 87, 1281–1288. [Google Scholar] [CrossRef]
- Negreiros, D.; Fernandes, G.W.; Efremova, A.A.; Stradic, S.; Neves, A.C.O. Growth-survival trade-off in shrub saplings from Neotropical mountain grasslands. S. Afr. J. Bot. 2016, 106, 17–22. [Google Scholar] [CrossRef]
- Kunstler, G.; Falster, D.; Coomes, D.A.; Hui, F.; Kooyman, R.M.; Laughlin, D.C.; Poorter, L.; Vanderwel, M.; Vieilledent, G.; Joseph Wright, S.J.; et al. Plant functional traits have globally consistent effects on competition. Nature 2016, 529, 204–207. [Google Scholar] [CrossRef]
- Silvertown, J.; Franco, M.; Perez-Ishiwara, R. Evolution of senescence in iteroparous perennial plants. Evol. Ecol. Res. 2001, 3, 393–412. [Google Scholar]
- Ehlers, B.; Olesen, J.M. Flower production in relation to individual plant age and leaf production among different patches of Corydalis intermedia. Plant. Ecol. 2004, 174, 71–78. [Google Scholar] [CrossRef]
- Tuomi, J.; Crone, E.E.; Gremer, J.R.; Jäkäläniemi, A.; Lesica, P.; Pedersen, B.; Ramula, S. Prolonged dormancy interacts with senescence for two perennial herbs. J. Ecol. 2013, 101, 566–576. [Google Scholar] [CrossRef]
- Shefferson, R.P.; Roach, D.A. Longitudinal analysis in Plantago: Strength of selection and reverse-age reveal age-indeterminate senescence. J. Ecol. 2013, 101, 577–584. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.; Day, T.; Fletcher, Q.; Rowe, L. The shaping of senescence in the wild. Trends Ecol. Evol. 2006, 21, 458–463. [Google Scholar] [CrossRef]
- Martin, J.G.; Festa-Bianchet, M. Age-independent and age-dependent decreases in reproduction of females. Ecol. Lett. 2011, 14, 576–581. [Google Scholar] [CrossRef]
- Koenig, W.D.; Knops, J.M.H.; Carmen, W.J.; Pesendorfer, M.B. Testing the terminal investment hypothesis in California oaks. Am. Nat. 2017, 189, 564–569. [Google Scholar] [CrossRef]
- Horvitz, C.C.; Schemske, D.W. Spatiotemporal variation in demographic transitions of a tropical understory herb: Projection matrix analysis. Ecol. Monogr. 1995, 65, 155–192. [Google Scholar] [CrossRef]
- Morris, W.F.; Doak, D.F. Life history of the long-lived gynodioecious cushion plant, Silene acaulis (Caryophyllaceae), inferred from size-based population projection matrices. Am. J. Bot. 1998, 85, 784–793. [Google Scholar] [CrossRef] [PubMed]
- Colchero, F.; Jones, O.R.; Rebke, M. BaSTA: An R package for Bayesian estimation of age-specific survival from incomplete mark-recapture/recovery data with covariates. Methods Ecol. Evol. 2012, 3, 466–470. [Google Scholar] [CrossRef]
- Record, S.; Kobe, R.K.; Vriesendorp, C.F.; Finley, A.O. Seedling survival responses to conspecific density, soil nutrients, and irradiance vary with age in a tropical forest. Ecology 2016, 97, 2406–2415. [Google Scholar] [CrossRef]
- Přívětivý, T.; Adama, D.; Vrška, T. Decay dynamics of Abies alba and Picea abies deadwood in relation to environmental conditions. For. Ecol. Manag. 2018, 427, 250–259. [Google Scholar] [CrossRef]
- Johansson, B.G.; Petersson, J.; Ingmansson, G. Gotlands Flora Band 2; SBF-förlag: Uppsala, Sweden, 2016. [Google Scholar]
- Lindell, T. Breeding systems and crossing experiments in Anemone patens and in the Anemone pulsatilla group (Ranunculaceae). Nord. J. Bot. 1998, 18, 549–561. [Google Scholar] [CrossRef]
- Lindell, T. Åtgärdsprogram för Nipsippa och Gotlandssippa 2006–2010; Rapport 5672; Naturvårdsverket: Stockholm, Sweden, 2007; pp. 9–19. [Google Scholar]
- Lindell, T. Pulsatilla. In Flora Nordica; Jonsell, B., Ed.; The Bergius Foundation: Stockholm, Sweden, 2001; Volume 2, pp. 305–310. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 12 September 2019).
- Colchero, F.; Jones, O.; Rebke, M. Package ‘BaSTA’. Available online: https://CRAN.R-project.org/package=BaSTA (accessed on 12 September 2019).
- Makeham, W.M. On the law of mortality. J. Inst. Actuar. 1867, 13, 325–358. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; van der Linde, A. Bayesian measures of model complexity and fit. J. R. Statist. Soc. B 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Edelfeldt, S.; Bengtsson, K.; Dahlgren, J.P. Demographic Senescence and Effects on Population Dynamics of a Perennial Plant. Ecology in Press. Available online: https://esajournals.onlinelibrary.wiley.com/doi/abs/10.1002/ecy.2742 (accessed on 12 September 2019).
- Ferrer, M.M.; Montaña, C.; Franco, M. Habitat-specific demography, source-sink dynamics, and the niche of a common shrub in a heterogeneous and fluctuating environment. Ecography 2015, 38, 930–938. [Google Scholar] [CrossRef]
- Flores-Torres, A.; Montaña, C.; Franco, M. Coexistence and the niche in a nurse–cactus interaction: Is cyclic dynamics justified? J. Ecol. 2019, 107, 407–417. [Google Scholar] [CrossRef]
- Metcalf, C.J.E.; Rees, M.; Alexander, J.M.; Rose, K. Growth-survival trade-offs and allometries in rosette-forming perennials. Funct. Ecol. 2006, 20, 217–225. [Google Scholar] [CrossRef]
- Sletvold, N.; Ågren, J. Nonlinear costs of reproduction in a long-lived plant. J. Ecol. 2015, 130, 1205–1213. [Google Scholar] [CrossRef]
- Pfister, C.A. Patterns of variance in stage-structured populations: Evolutionary predictions and ecological implications. Proc. Natl. Acad. Sci. USA 1998, 95, 213–218. [Google Scholar] [CrossRef]
- Morris, W.F.; Doak, D.F. Buffering of life histories against environmental stochasticity: Accounting for a spurious correlation between the variabilities of vital rates and their contributions to fitness. Am. Nat. 2004, 163, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Garcia, M.B.; Picó, F.X.; Ehrlén, J. Life span correlates with population dynamics in perennial herbaceous plants. Am. J. Bot. 2008, 95, 258–262. [Google Scholar] [CrossRef] [PubMed]
- Villellas, J.; Garcia, M.B. Life-history trade-offs vary with resource availability across the geographic range of a widespread plant 2018. Plant Biol. 2018, 20, 483–489. [Google Scholar]
- Salguero-Gómez, R.; Casper, B.B. Keeping plant shrinkage in the demographic loop. J. Ecol. 2010, 98, 312–323. [Google Scholar] [CrossRef]
- Salguero-Gómez, R.; Siewert, W.; Casper, B.B.; Tielbörger, K. A demographic approach to study effects of climate change in desert plants. Philos. Trans. R. Soc. 2012, 367, 3100–3114. [Google Scholar] [CrossRef] [PubMed]
- Martínková, M.; Šmilauer, P.; Mihulka, S.; Latzel, V.; Klimešová, J. The effect of injury on whole-plant senescence: An experiment with two root-sprouting Barbarea species. Ann. Bot. 2016, 117, 667–679. [Google Scholar] [CrossRef]
- Harper, J.L. Population Biology of Plants; Academic Press: New York, NY, USA, 1977; pp. 195–196, 600–604. [Google Scholar]
| Basic Model | Growth | Reproductive Output | Shrinkage | ||||
|---|---|---|---|---|---|---|---|
| Model | DIC | Model | DIC | Model | DIC | Model | DIC |
| GO bathtub | 13,251 | GO bathtub | 6399 | GO Makeham | 13,040 | GO bathtub | 6443 |
| LO bathtub | 13,344 | WE Makeham | 6453 | GO bathtub | 13,051 | WE Makeham | 6452 |
| LO Makeham | 13,505 | EX simple | 6471 | LO bathtub | 13,140 | WE simple | 6453 |
| LO simple | 13,508 | WE simple | 6531 | LO Makeham | 13,320 | EX simple | 6476 |
| GO simple | 13,631 | LO bathtub | 6547 | LO simple | 13,348 | GO simple | 6514 |
| WE simple | 13,775 | LO Makeham | 6554 | GO simple | 13,476 | WE bathtub | 6535 |
| WE Makeham | 13,778 | LO simple | 6569 | WE Makeham | 13,615 | GO Makeham | 6579 |
| EX simple | 13,988 | GO simple | 6577 | WE simple | 13,616 | ||
| GO Makeham | 6604 | EX simple | 13,819 | ||||
| Model Covariate | Optimal Model | Min Age | DIC | Covariate Mortality Coefficient | Site 1 | Site 2 | Site 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e0 | e10 | e30 | e0 | e10 | e30 | e0 | e10 | e30 | |||||
| Basic model | GO bathtub | 0 | 13,251 | - | 2.8 † | 27.1 | 31.5 | 3.2 † | 49.5 | 50.5 | 11.0 † | 49.6 | 32.7 |
| Basic model | EX simple | 10 | 12,360 | - | - | 31.5 | 28.9 | - | 40.8 | 50.3 | - | 55.3 | 44.1 |
| Growth | GO bathtub | 0 | 6399 | 0.118 * | 4.6 | 23.6 | 22.3 | 8.3 | 41.2 | 31.1 | 24.3 | 48.2 | 29.8 |
| Growth | EX simple | 10 | 6226 | −0.098 * | - | 39.1 | 28.6 | - | 60.2 | 62.5 | - | 63.9 | 50.1 |
| Reproductive output | GO Makeham | 0 | 13,040 | −2.080 * | 2.7 † | 18.3 | 14.3 | 2.8 † | 52.9 | 46.9 | 12.5 † | 59.9 | 47.7 |
| Reproductive output | EX simple | 10 | 12,373 | −0.620 * | - | 29.3 | 37.3 | - | 47.4 | 49.7 | - | 53.3 | 41.8 |
| Shrinkage | GO bathtub | 0 | 6443 | −1.798 * | 4.9 | 28.9 | 32.0 | 9.6 | 55.2 | 50.1 | 22.9 | 51.2 | 34.5 |
| Shrinkage | EX simple | 10 | 6285 | −0.194 | - | 35.1 | 26.3 | - | 45.4 | 52.5 | - | 57.9 | 44.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edelfeldt, S.; Lindell, T.; Dahlgren, J.P. Age-Independent Adult Mortality in a Long-Lived Herb. Diversity 2019, 11, 187. https://doi.org/10.3390/d11100187
Edelfeldt S, Lindell T, Dahlgren JP. Age-Independent Adult Mortality in a Long-Lived Herb. Diversity. 2019; 11(10):187. https://doi.org/10.3390/d11100187
Chicago/Turabian StyleEdelfeldt, Stina, Torbjörn Lindell, and Johan P. Dahlgren. 2019. "Age-Independent Adult Mortality in a Long-Lived Herb" Diversity 11, no. 10: 187. https://doi.org/10.3390/d11100187
APA StyleEdelfeldt, S., Lindell, T., & Dahlgren, J. P. (2019). Age-Independent Adult Mortality in a Long-Lived Herb. Diversity, 11(10), 187. https://doi.org/10.3390/d11100187





