Abstract
A simple, fast and cost-effective three-step synthesis of 1-methyl-8-phenyl-1,3-diazaspiro[4.5]decane-2,4-dione has been developed. The reactions described herein proceed readily, with high yields and no further purification. Therefore, the proposed method, with an overall yield of 60%, offers a facile pathway to the synthesis of N-1 monosubstituted spiro carbocyclic imidazolidine-2,4-diones (hydantoins), which constitute a privileged class of heterocyclic scaffolds with pharmacological interest.
1. Introduction
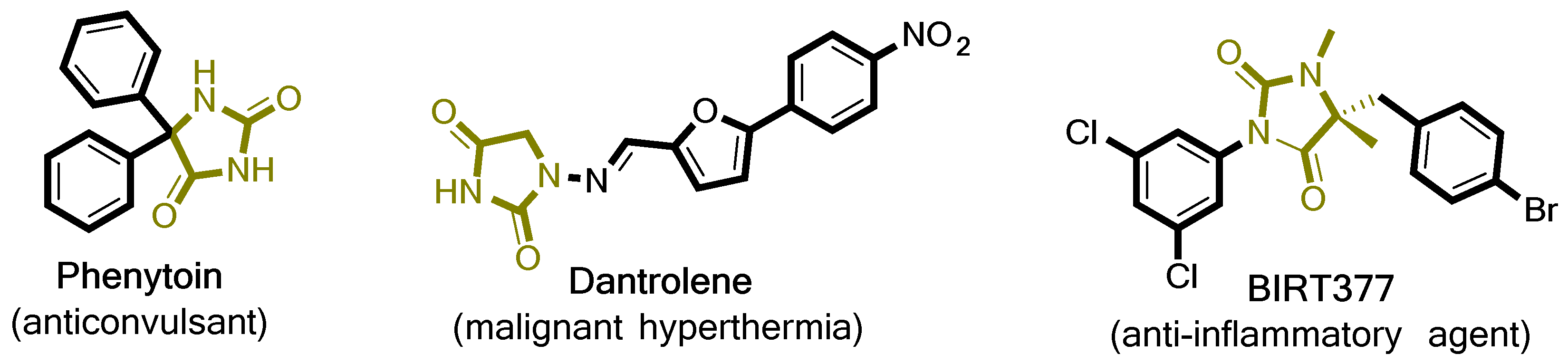
Hydantoins, or imidazolidine-2,4-diones, is a class of compounds first isolated as a product from allantoin hydrogenolysis in 1861 from the Nobel laureate Adolph von Baeyer. Since then, hydantoin derivatives have become increasingly important, with various applications across chemical and pharmaceutical industries. Although, the hydantoin ring itself possesses no biological activity, 5- and especially 5,5-substituted derivatives have a documented, wide range of therapeutic applications [1]. The most noticeable drugs in this class of compounds showcase anticonvulsant [2], antidiabetic [3], anticancer [4], antiarrhythmic [5] and anti-inflammatory [6] activity. For example, Figure 1 depicts three well-known hydantoins with medicinal applications. Phenytoin exhibits a regulatory effect on the central nervous system (CNS) and has been applied successfully to ameliorating epilepsy symptoms for more than 70 years now and as a treatment of neuropathic pain [7]. More recently, Dantrolene (Figure 1), has been used in the clinical treatment of malignant hyperthermia through the inhibition of abnormal Ca2+ release at the sarcoplasmic reticulum and physiological Ca2+ release from skeletal muscles [8], whilst another compound known as BIRT377 (Figure 1) demonstrates potent anti-inflammatory activity as an antagonist of lymphocyte function-associated antigen-1 (LFA-1) [9]. Therefore, hydantoins are catching the attention of both the medicinal and organic chemistry spectrums based on their facilitated, privileged pharmacological profile [10].
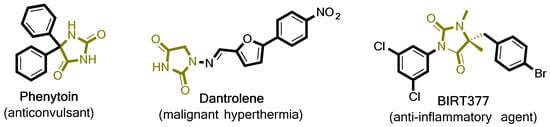
Figure 1.
Chemical structures of hydantoin-containing compounds with important biological activity.
Our medicinal chemistry lab has an active research interest in the development of such molecules incorporating bulky lipophilic carbocyclic rings into the spiro hydantoin core structure. These specific analogs are highly functionalized ‘building blocks’, with significant antiviral and trypanocidal activity, suitable for further synthetic transformations [11].
The introduction of substituents at the N-3 position of the hydantoin ring may be accomplished easily using alkyl halides in an alkaline solution. However, the synthesis of N-1 monosubstituted hydantoins cannot be achieved through direct alkylation unless the N-3 nitrogen is protected. The specified reactivity is explained due to the more activated N-3 position with the two neighboring activating carbonyl groups. In this paper, we report a simple, fast and effective 3-steps synthesis of 1-methyl-8-phenyl-1,3-diazaspiro[4.5]decane-2,4-dione (4). This synthetic route affords pure products in very good yields (overall yield of 60%) that can be used without further purifications. Therefore, the proposed facile and cost-effective method can be generally applied for the synthesis of N-1 monosubstituted spiro carbocyclic hydantoins that are building blocks of high interest to medicinal chemists.
2. Results
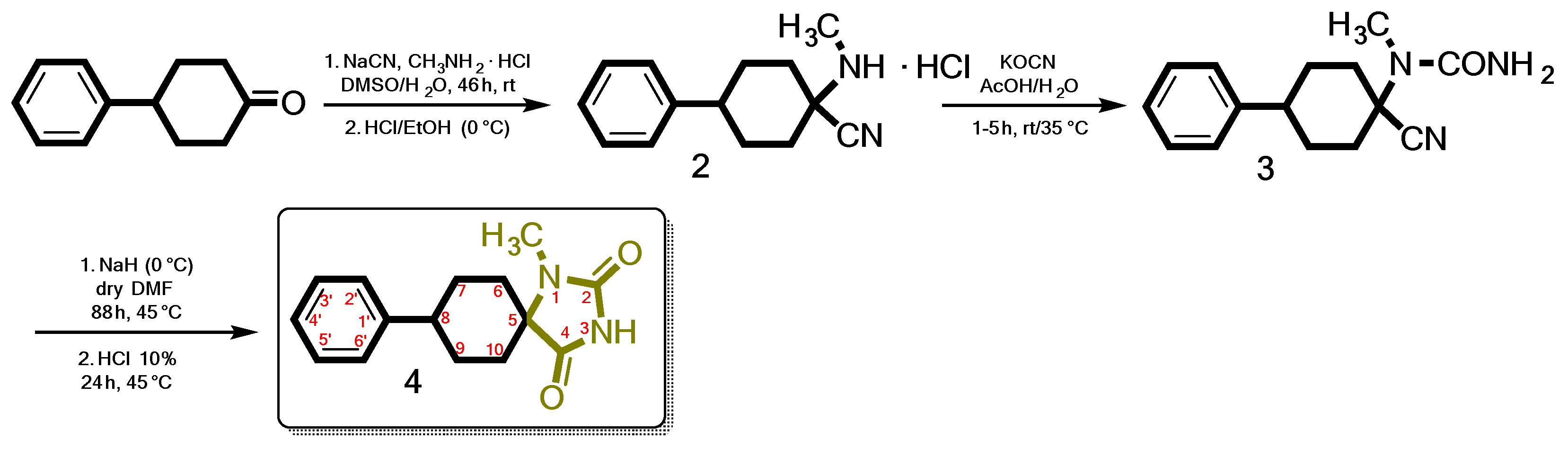
The target compound (4), is obtained by following the synthetic procedure shown in Scheme 1. The key intermediate α-amino nitrile hydrochloride (2) was obtained by a Strecker reaction of the bulky commercially available 4-phenylcyclohexan-1-one with NaCN and methylamine hydrochloride in a mixture of DMSO/H2O. After workup, the resulting dry Et2O solution of the free amino nitrile was treated with saturated ethanolic hydrochloric acid solution under ice cooling. 1-(Methylamino)-4-phenylcyclohexane-1-carbonitrile hydrochloride (2) was then treated with potassium cyanate (KOCN) in the presence of acetic acid and water to yield the corresponding ureido derivative (3). Cyclization of the latter with sodium hydride (60% NaH in mineral oil) in dry DMF and subsequent acid hydrolysis led to the target 1-methyl-8-phenyl-1,3-diazaspiro[4.5]decane-2,4-dione (4).
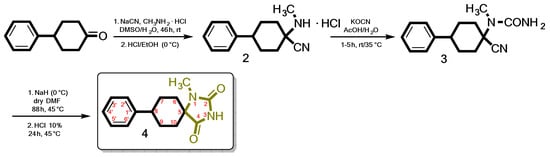
Scheme 1.
The proposed facile and cost-effective method applied for the synthesis of N-1 monosubstituted spiro carbocyclic hydantoins.
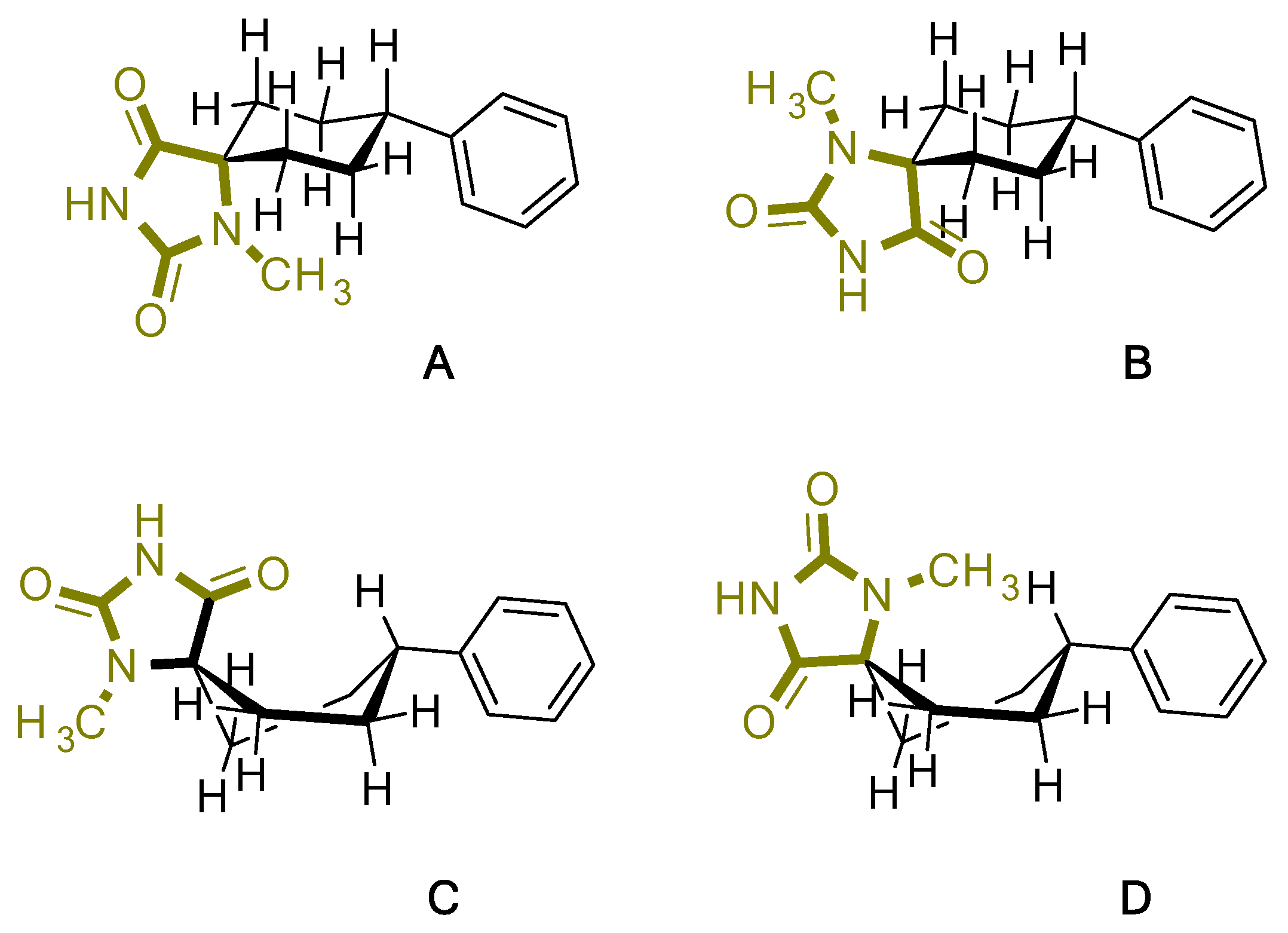
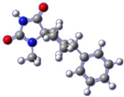
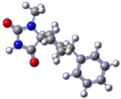
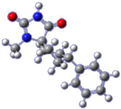
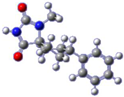
For the target compound (4), a structure optimization step took place in order to determine its energy minima conformation. Starting from the selection of the cyclohexane, two more stable conformations (i.e., chair and twisted boat) [12], we drew the possible four more favorable structures that underwent the ab initio calculation (Figure 2). Although the twisted boat conformation of cyclohexane bears a 23.01 kJ/mol higher energy, it was nonetheless included in our experiments. Additionally, in all of the structures, the phenyl ring always occupies always the equatorial position since the axial position would introduce additional hindering effects on the respective conformations, resulting in even higher energies. Based on our calculations (Table 1), the energy minima for compound (4) resulted in being the conformation B (0 kJ/mol), while on ascending order the rest follow with the second being conformation A (9.43 kJ/mol), third being conformation C (26.08 kJ/mol) and fourth being conformation D (30.83 kJ/mol). Additional information upon all minimized conformers regarding bond lengths, angles and dihedrals can be found on Supplementary Tables S1–S4.
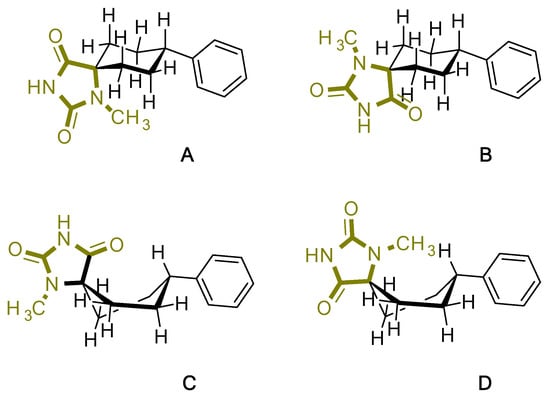
Figure 2.
Chemical structure representation of compound (4) conformations (A–D).

Table 1.
DFT summary of the calculated 4 conformations A–D.
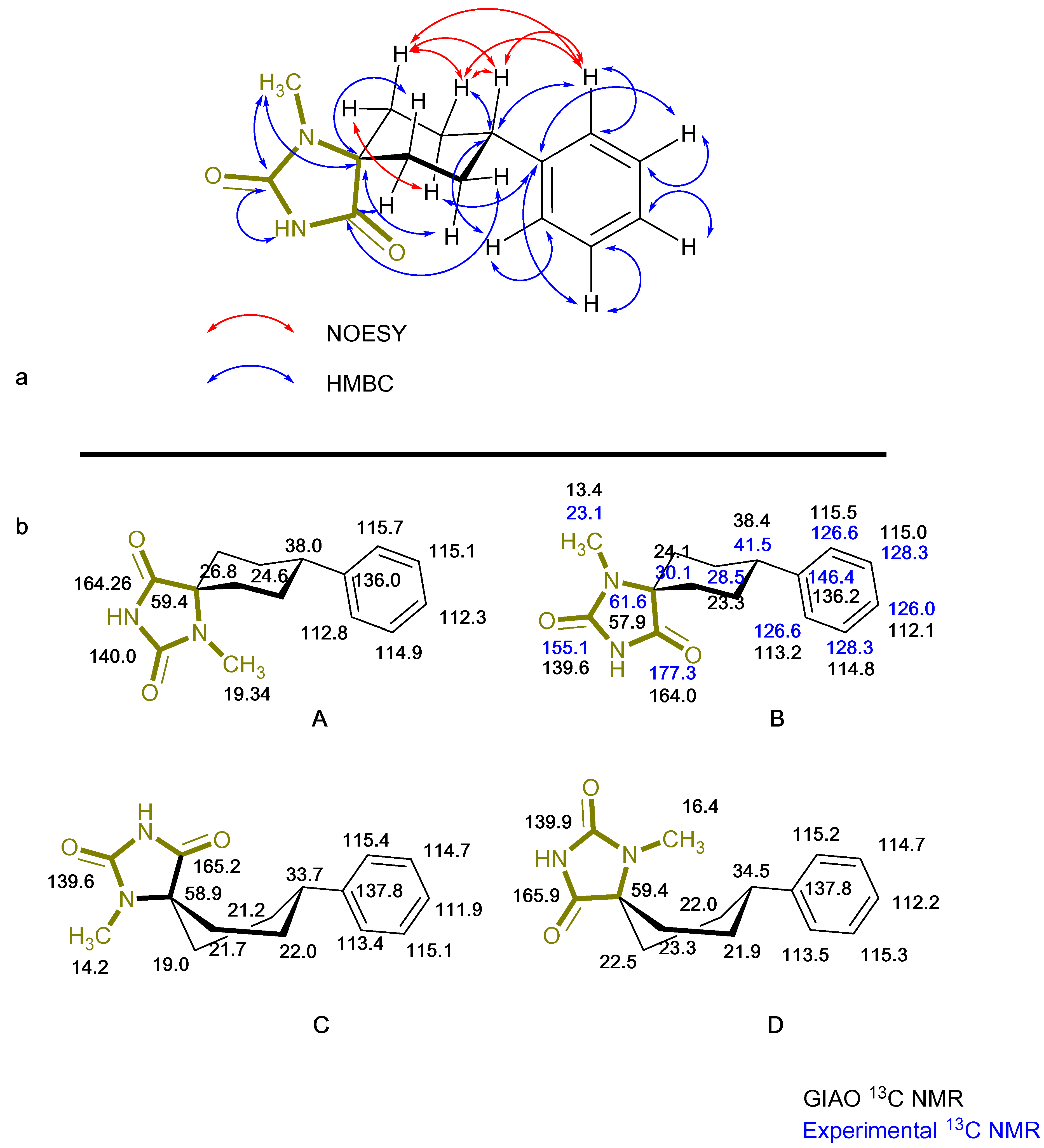
Based on the NMR of compound (4), provided on the supporting information, stereochemistry as determined from the data for the 3D structure with HMBC and NOESY (Figure 3a), correlations verify that the experimentally obtained structure matches the calculated energy minima conformation B. On the contrary Gauge-Independent Atomic Orbital (GIAO), theoretical calculations predicted similar signals for conformations A–D (Figure 3b) when referred to the hydantoin and the phenyl rings, respectively. For the cyclohexane ring conformations, A and B represent a more relatively true estimation, with two signals for carbons C7,9 and C6,10.

Figure 3.
(a) Representation of experimental NMR data for (4) with HMBC correlations illustrated as blue two-way bent arrows and NOESY illustrated as red two-way bent arrows. (b) GIAO predicted 13C NMR chemical shifts of all conformers with black writing and experimental shifts for the assigned conformer B in a blue color.
3. Materials and Methods
3.1. Chemistry
Materials, apparatuses and techniques for the experimental part are as follows. Melting points were determined using a Büchi capillary apparatus and are uncorrected. NMR experiments were performed to elucidate the structure and determine the purity of the newly synthesized compounds. 1H NMR and 2D NMR spectra (COSY, HSQC-DEPT, HMBC) were recorded on a Bruker Ultrashield™ Plus Avance III 600 spectrometer (150.9 MHz, 13C NMR). Chemical shifts δ (delta) are reported in parts per million (ppm) downfield from the NMR solvent, with the tetramethylsilane or solvent (DMSO-d6) as internal standard. Data processing including Fourier transformation, baseline correction, phasing, peak peaking and integrations were performed using MestReNova software v.12.0.0. Splitting patterns are designated as follows: s, singlet; d, doublet; t, triplet; dd, doublet of doublets; td, triplet of doublets; m, multiplet; complex m, complex multiplet. Coupling constants (J) are expressed in units of Hertz (Hz). The spectra were recorded at 293 K (20 °C) unless otherwise specified. The solvent used to obtain the spectra was deuterated DMSO, DMSO-d6 (quin, 2.50 ppm, 1H NMR; septet, 39.52 ppm, 13C NMR). IR spectra were recorded on a Perkin Elmer Spectrum BX FT-IR FTIR Spectrophotometer. Analytical thin-layer chromatography (TLC) was used to monitor the progress of the reactions, as well as to authenticate the compounds. TLCs were conducted on and precoated with normal-phase silica gel, aluminum sheets (Silica gel 60 F254, Merck) (layer thickness 0.2 mm), precoated with reverse-phase silica gel, aluminum sheets (Silica gel 60 RP-18 F254s, Merck) and precoated aluminum oxide plates (TLC Aluminium oxide 60 F254, neutral). Developed plates were examined under a UV light source, at wavelengths of 254 nm or after being stained by iodine vapors. The Retention factor (Rf) of the newly synthesized compounds, which equals to the distance migrated over the total distance covered by the solvent, was also measured on the chromatoplates. Elemental analyses (C, H, N) were performed by the Service Central de Microanalyse at CNRS (Paris, France), and were within ±0.4% of the theoretical values. Elemental analysis results for the tested compounds correspond to ˃95% purity. The HRMS spectra were acquired in the negative ionization mode, employing a QTOF-MS (Maxis Impact, Bruker Daltonics, Bremen, Germany) using a resolving power of 40,000. The commercial reagents were purchased from Alfa Aesar, Sigma-Aldrich and Merck, and were used without further purification. Solvent abbreviations: ACN, acetonitrile; AcOEt, ethyl acetate; Et2O, diethyl ether; EtOH, ethanol; MeOH, methanol.
3.2. Computational
Density Functional Theory (DFT) calculations are as follows. All in silico calculations were carried out on a typical desktop PC running a Windows 10 64-bit operating system (Intel i7 3.4 GHz CPU processors, RAM 32 GB), in gas phase unless otherwise specified, using the G09W [13] software package. The hybrid DFT method with Becke’s [14] three-parameter functional and the nonlocal correlation provided by the Lee, Yang and Parr expression (B3LYP) [15] was used for optimization, employing the 6−31+G(d,p) basis set [16,17]. Single-point calculations of all structures were also carried out using the same basis set [16,17], following the optimized-geometries step. NMR shielding tensors computed with the GIAO method [18,19,20,21,22] on default parameters for degeneracy tolerance (0.05) in DMSO solvent, including spin–spin coupling constants [23,24,25,26,27].
3.3. Synthesis
1-(Methylamino)-4-phenylcyclohexane-1-carbonitrile hydrochloride (2): To a stirred suspension of sodium cyanide (843 mg, 17.2 mmol) and methylamine hydrochloride (1.16 g, 17.2 mmol) in 12 mL of DMSO/H2O 9:1 (v/v), a solution of 4-phenylcyclohexanone (3.0 g, 17.2 mmol) in DMSO (24 mL) was added in one portion. The reaction mixture was stirred for 46 h at rt, poured into 130 mL of ice–water mixture and extracted with AcOEt (3 × 60 mL). The combined organic phases were washed with brine (2 × 60 mL), dried with anh. Na2SO4 and the solvent was evaporated under reduced pressure. The residue was dissolved in Et2O (80 mL) and treated dropwise with an ethanolic solution saturated with gaseous hydrochloric acid to pH ~2 under ice bath. The precipitate formed was filtered off in vacuo, washed with small portions of dry Et2O and dried over P2O5 to afford the title compound 2 as a white crystalline solid (3.55 g, 80%). This intermediate was used for the next reaction without further purification.
1-(1-Cyano-4-phenylcyclohexyl)-1-methylurea (3): To a stirred solution of the carbonitrile 2 (3.1 g, 12.4 mmol) in 20 mL acetic acid, a solution of potassium cyanate (2.01 g, 24.8 mmol) in 3 mL H2O was added. After stirring for 1 h at 35 °C, the reaction mixture was poured into 70 mL H2O and extracted with CHCl3 (3 × 50 mL). The combined organic layers were washed with H2O (3 × 50 mL) and brine (2 × 50 mL), dried with anh. Na2SO4 and the solvents were evaporated to dryness under reduced pressure to afford the title compound 3 as a white solid (2.97 g, 93%). This intermediate was used for the next reaction without further purification.
1-Methyl-8-phenyl-1,3-diazaspiro[4.5]decane-2,4-dione (4): A stirred solution of 3 (2.9 g, 11.3 mmol) in 40 mL dry DMF was cooled in an ice bath and sodium hydride (353 mg, 14.7 mmol, 60% dispersion in mineral oil) was added portion-wise. After 4 d of stirring at 45 °C under Argon, the mixture was treated with a solution of HCl 10% (96 mL) and stirring was continued for 24 h at 45 °C. After this time, the reaction mixture was poured into 400 mL of ice–water mixture and extracted with CHCl3 (4 × 200 mL). The combined organic extracts were washed with H2O (3 × 250 mL) and brine (2 × 250 mL), dried with anh. Na2SO4 and the solvent was evaporated in vacuo. The remaining solid was treated with Et2O and n-pentane to give the desired compound 4 as a pale yellow crystalline product. (2.44 g, 79%); Rf = 0.34 (CH2Cl2/AcOEt 5:1); mp 211–214 °C (AcOEt/dry Et2O-n-pentane).
1H NMR (600 MHz, DMSO-d6) δ 1.70-1.75 (m, 4H, H6, H7, H9, H10), 1.93 (td, 2H, J = 12.8, 4.3 Hz, H6, H10), 2.18 (qd, 2H, J = 13.1, 3.9 Hz, H7, H9), 2.57 (tt, 1H, J = 12.5, 3.5 Hz, H8), 2.73 (s, 3H, CH3), 7.19 (m, 1H, H4’), 7.24 (m, 2H, H2’, H6’), 7.30 (t, 2H, J = 7.6 Hz, H3’, H5’), 10.73 (s, 1H, H3) ppm.
13C NMR (150 MHz, DMSO-d6) δ 23.1 (CH3), 28.5 (C7, C9), 30.1 (C6, C10), 41.5 (C8), 61.6 (C5), 126.0 (C4’), 126.6 (C2’, C6’), 128.3 (C3’, C5’), 146.4 (C1’), 155.1 (C2=O), 177.3 (C4=O) ppm.
IR (mull) ν 3143.9 (>N-H)amide, 2923.6 (C-H)sp2, 2856.1 (C-H)sp3, 2723.2 (C-H)sp3, 1764.6 (C=O)amide, 1707.5 (C=O)amide, 1459.5 (C=C)Ar, 1406.5 (C=C)Ar, 1376.8 (C-H)methyl, 1141.0 (C-N)methyl, 1118.9 (C-N)spiro, 1067.3 (>CH2) cm−1.
Anal. Calcd for C15H18N2O2: C, 69.74; H, 7.02; N, 10.84. Found: C, 69.90; H, 7.30; N, 10.50. HRMS m/z calc. for C15H18N2O2 [M − H]+ 257.1285, obtained 257.1287.
4. Conclusions
1-Methyl-8-phenyl-1,3-diazaspiro[4.5]decane-2,4-dione (4) was obtained through a facile and cost-effective method that offers a general route for the synthesis of N-1 monosubstituted spiro carbocyclic hydantoins, which are heterocyclic scaffolds of great interest to the pharmaceutical industry. The reactions were executed under mild (rt to 45 °C) and sustainable (intermediates can be used without further purifications) conditions. The structure of compound (4) was determined using 1H NMR, 13C NMR, HSQC, HMBC, elemental analysis, FT-IR and HRMS, while stereochemistry was elucidated from the data for the 3D structure obtained by HMBC, NOESY and DFT energy minima/GIAO calculations.
Supplementary Materials
The following are available online, NMR spectra of (4) in DMSO-d6 (600 MHz) (1H, 13C, COSY, HSQC-DEPT, HMBC, NOESY) p. S3, NMR spectra of (4) in CDCl3 (400 MHz) (1H, 13C, COSY, HSQC-DEPT, HMBC) p.S9, HRMS Spectra of (4), p. S14, FT-IR Spectra of (4), p. S16, Table S1: Conformation A properties p. S17, Table S2: Conformation B properties p. S20, Table S3: Conformation C properties p. S23, Table S4: Conformation D properties p. S26.
Author Contributions
V.P.: investigation; S.K.: DFT calculations, data curation, writing—original draft preparation and editing; E.G.: editing; G.Z.: conceptualization, methodology, data curation, writing—original draft preparation and editing, supervision and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
G.Z. would like to thank ‘Empirikion Foundation’ for financial support. V.P. would like to thank the State Scholarships Foundation of Greece for providing her a Ph.D. fellowship (MIS-5000432, NSRF 2014–2020).
Data Availability Statement
Not applicable.
Acknowledgments
We thank Evangelos Gikas (Laboratory of Analytical Chemistry, Department of Chemistry, National and Kapodistrian University of Athens) for performing the HRMS spectra and Dimitra Benaki (Division of Pharmaceutical Chemistry, Department of Pharmacy, School of Health Sciences, National and Kapodistrian University of Athens) for performing the NMR experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cho, S.H.; Kim, S.-H.; Shin, D. Recent applications of hydantoin and thiohydantoin in medicinal chemistry. Eur. J. Med. Chem. 2019, 164, 517–545. [Google Scholar] [CrossRef] [PubMed]
- Trišović, N.; Valentić, N.; Ušćumlić, G. Solvent effects on the structure-property relationship of anticonvulsant hydantoin derivatives: A solvatochromic analysis. Chem. Cent. J. 2011, 5, 62. [Google Scholar] [CrossRef]
- Iqbal, Z.; Ali, S.; Iqbal, J.; Abbas, Q.; Qureshi, I.Z.; Hameed, S. Dual action spirobicycloimidazolidine-2,4-diones: Antidiabetic agents and inhibitors of aldose reductase-an enzyme involved in diabetic complications. Bioorg. Med. Chem. Lett. 2013, 23, 488–491. [Google Scholar] [CrossRef]
- Zhang, M.; Liang, Y.R.; Li, H.; Liu, M.M.; Wang, Y. Design, synthesis, and biological evaluation of hydantoin bridged analogues of combretastatin A-4 as potential anticancer agents. Bioorg. Med. Chem. 2017, 25, 6623–6634. [Google Scholar] [CrossRef]
- Czopek, A.; Byrtus, H.; Zagórska, A.; Siwek, A.; Kazek, G.; Bednarski, M.; Sapa, J.; Pawłowski, M. Design, synthesis, anticonvulsant, and antiarrhythmic properties of novel N-Mannich base and amide derivatives of β-tetralinohydantoin. Pharmacol. Rep. 2016, 68, 886–893. [Google Scholar] [CrossRef]
- Wang, Z.D.; Sheikh, S.O.; Zhang, Y. A Simple Synthesis of 2-Thiohydantoins. Molecules 2006, 11, 739–750. [Google Scholar] [CrossRef]
- Kopsky, D.J.; Keppel Hesselink, J.M. Phenytoin Cream for the Treatment of Neuropathic Pain: Case Series. Pharmaceuticals 2018, 11, 53. [Google Scholar] [CrossRef]
- Hosoya, T.; Aoyama, H.; Ikemoto, T.; Hiramatsu, T.; Kihara, Y.; Endo, M.; Suzuki, M. Dantrolene analogues revisited: General synthesis and specific functions capable of discriminating two kinds of Ca2+ release from sarcoplasmic reticulum of mouse skeletal muscle. Bioorg. Med. Chem. 2003, 11, 663–673. [Google Scholar] [CrossRef]
- Last-Barney, K.; Davidson, W.; Cardozo, M.; Frye, L.L.; Grygon, C.A.; Hopkins, J.L.; Jeanfavre, D.D.; Pav, S.; Stevenson, J.M.; Tong, L.; et al. Binding Site Elucidation of Hydantoin-Based Antagonists of LFA-1 Using Multidisciplinary Technologies: Evidence for the Allosteric Inhibition of a Protein−Protein Interaction. J. Am. Chem. Soc. 2001, 123, 5643–5650. [Google Scholar] [CrossRef]
- Giannakopoulou, E.; Pardali, V.; Skrettas, I.; Zoidis, G. Transesterification instead of N-Alkylation: An Intriguing Reaction. ChemistrySelect 2019, 4, 3195–3198. [Google Scholar] [CrossRef]
- Giannakopoulou, E.; Pardali, V.; Frakolaki, E.; Siozos, V.; Myrianthopoulos, V.; Mikros, E.; Taylor, M.C.; Kelly, J.M.; Vassilaki, N.; Zoidis, G. Scaffold hybridization strategy towards potent hydroxamate-based inhibitors of Flaviviridae viruses and Trypanosoma species. Med. Chem. Commun. 2019, 10, 991–1006. [Google Scholar] [CrossRef]
- Dragojlovic, V. Conformational analysis of cycloalkanes. ChemTexts 2015, 1, 1–30. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z=11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 2002, 112, 8251–8260. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- McWeeny, R. Perturbation Theory for the Fock-Dirac Density Matrix. Phys. Rev. 1962, 126, 1028–1034. [Google Scholar] [CrossRef]
- London, F. Théorie quantique des courants interatomiques dans les combinaisons aromatiques. J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- Deng, W.; Cheeseman, J.R.; Frisch, M.J. Calculation of Nuclear Spin-Spin Coupling Constants of Molecules with First and Second Row Atoms in Study of Basis Set Dependence. J. Chem. Theory Comput. 2006, 2, 1028–1037. [Google Scholar] [CrossRef]
- Peralta, J.E.; Scuseria, G.E.; Cheeseman, J.R.; Frisch, M.J. Basis set dependence of NMR spin–spin couplings in density functional theory calculations: First row and hydrogen atoms. Chem. Phys. Lett. 2003, 375, 452–458. [Google Scholar] [CrossRef]
- Barone, V.; Peralta, J.E.; Contreras, R.H.; Snyder, J.P. DFT Calculation of NMR JFF Spin−Spin Coupling Constants in Fluorinated Pyridines. J. Phys. Chem. A 2002, 106, 5607–5612. [Google Scholar] [CrossRef]
- Helgaker, T.; Watson, M.; Handy, N.C. Analytical calculation of nuclear magnetic resonance indirect spin–spin coupling constants at the generalized gradient approximation and hybrid levels of density-functional theory. J. Chem. Phys. 2000, 113, 9402–9409. [Google Scholar] [CrossRef]
- Sychrovský, V.R.; Gräfenstein, J.; Cremer, D. Nuclear magnetic resonance spin–spin coupling constants from coupled perturbed density functional theory. J. Chem. Phys. 2000, 113, 3530–3547. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).