Remarks on Muscle Contraction Mechanism
Abstract
:1. Introduction
2. Difficulty in the power stroke model
2.1 A thermodynamic relationship
2.2 Inconsistency in the power-stroke model
3. Basic ideas in the new model
3.1 X-ray diffraction studies suggest constant r
3.2 Traveling distance of myosin heads along actin filament during one ATP hydrolysis cycle in shortening muscle
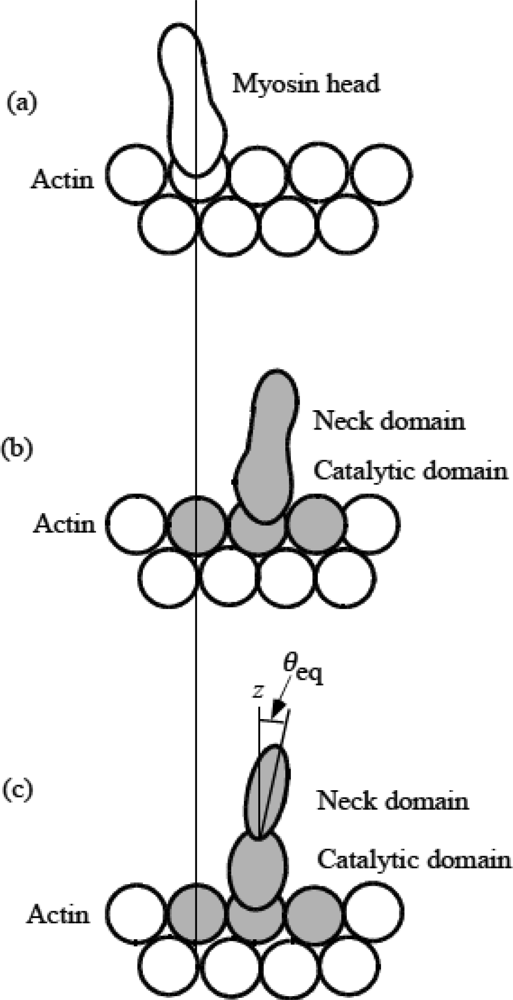
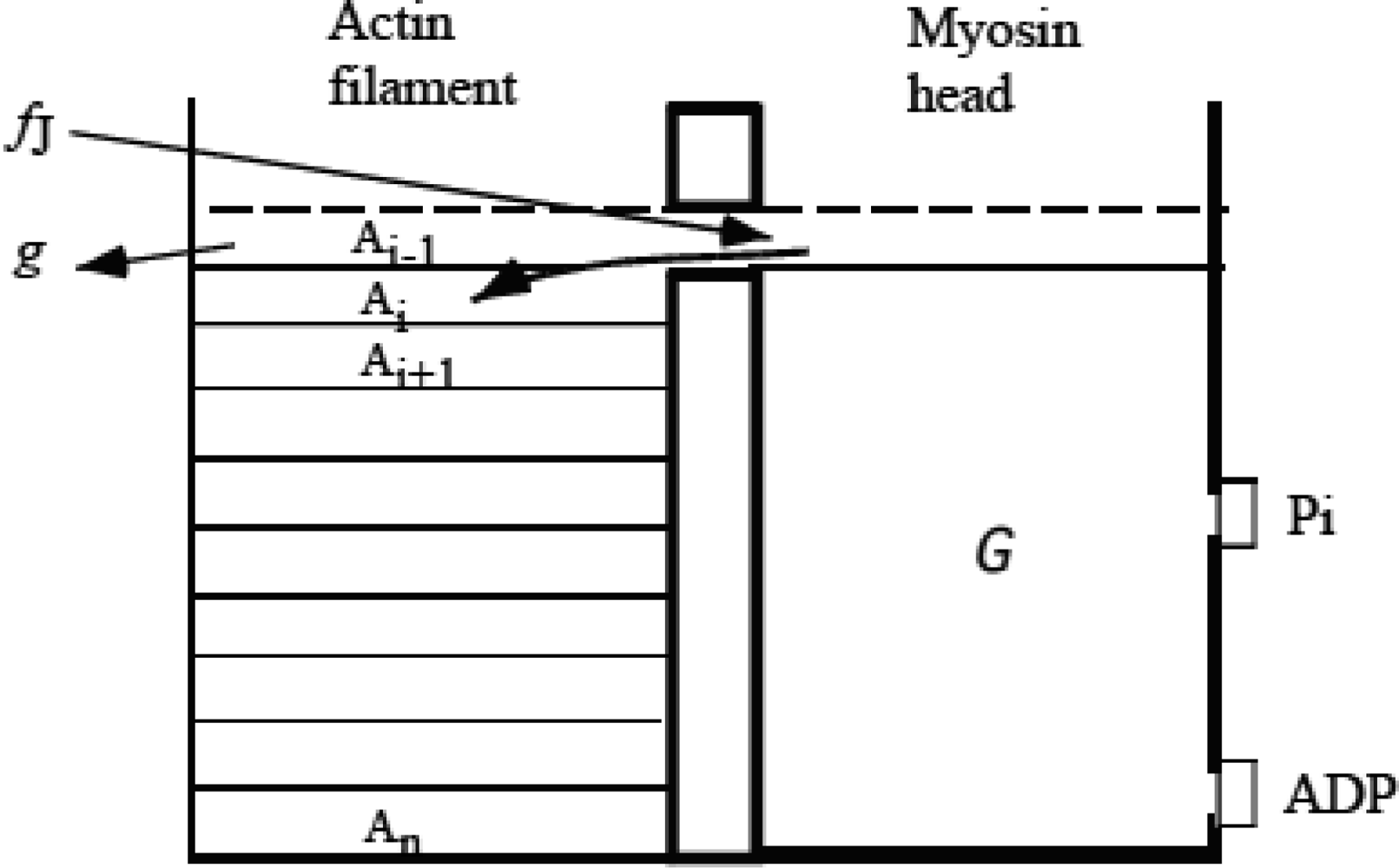
3.3 Formation of molecular complex of myosin head and actin molecules
3.4 Elastic deformation and force production of crossbridge
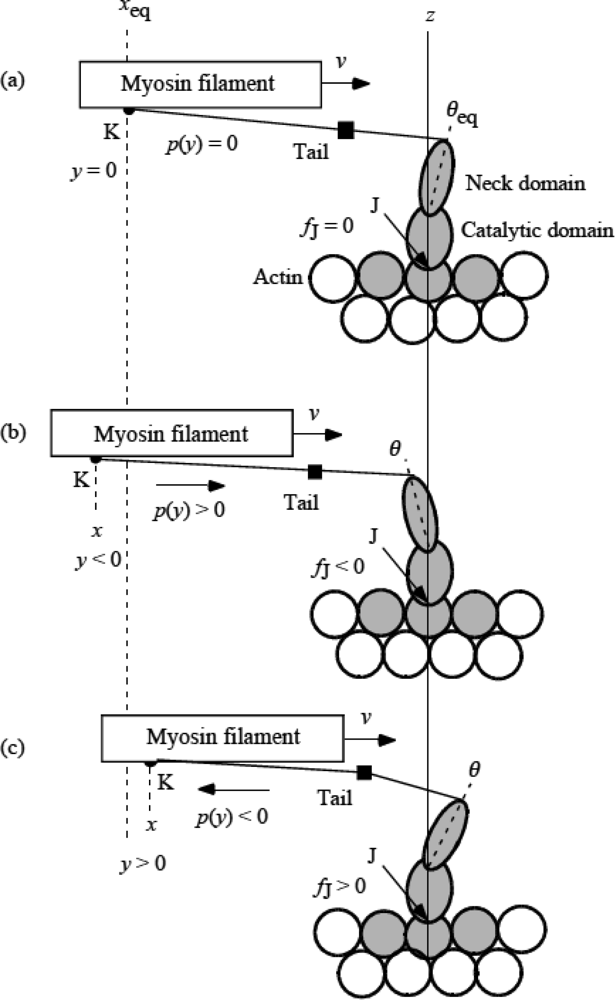
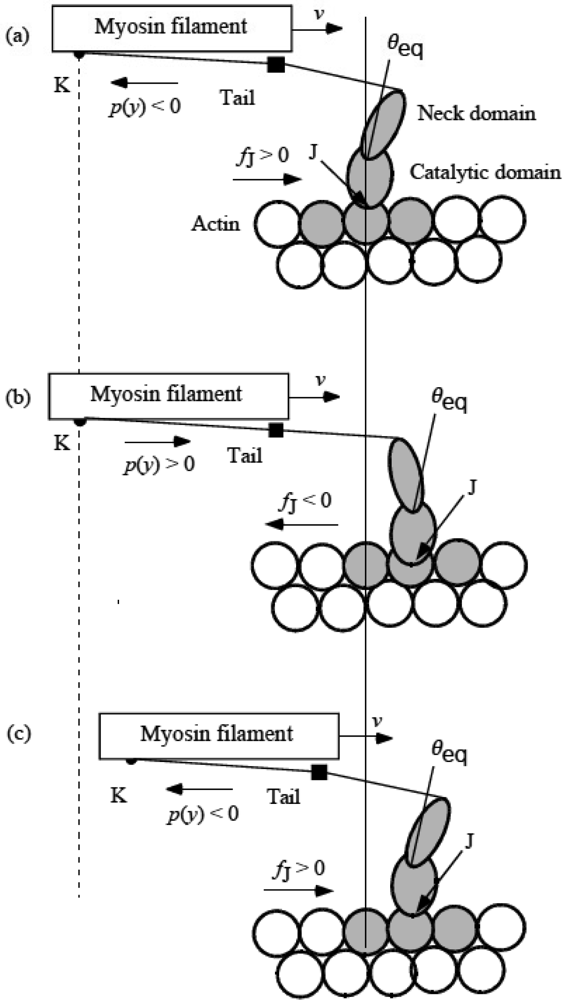
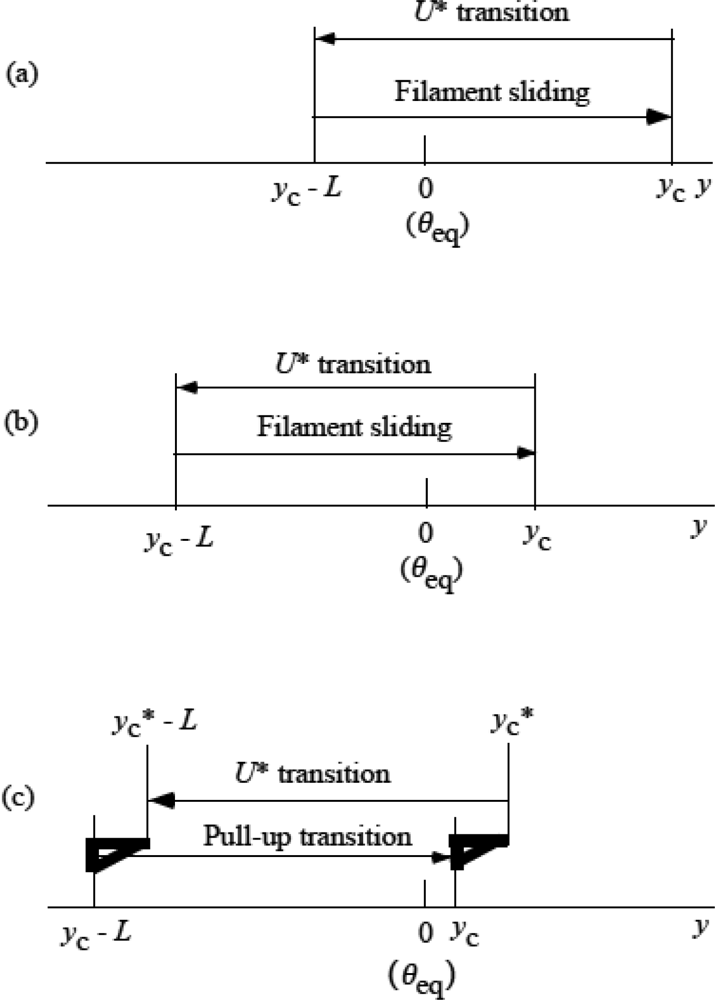
3.5 Step motion of myosin head along actin filament
3.6 Cycles of force generation and the isometric tension
3.7 Cooperativity of myosin heads, and energy flow and chemical reactions associated with force production
3.8 Role of thermal fluctuation
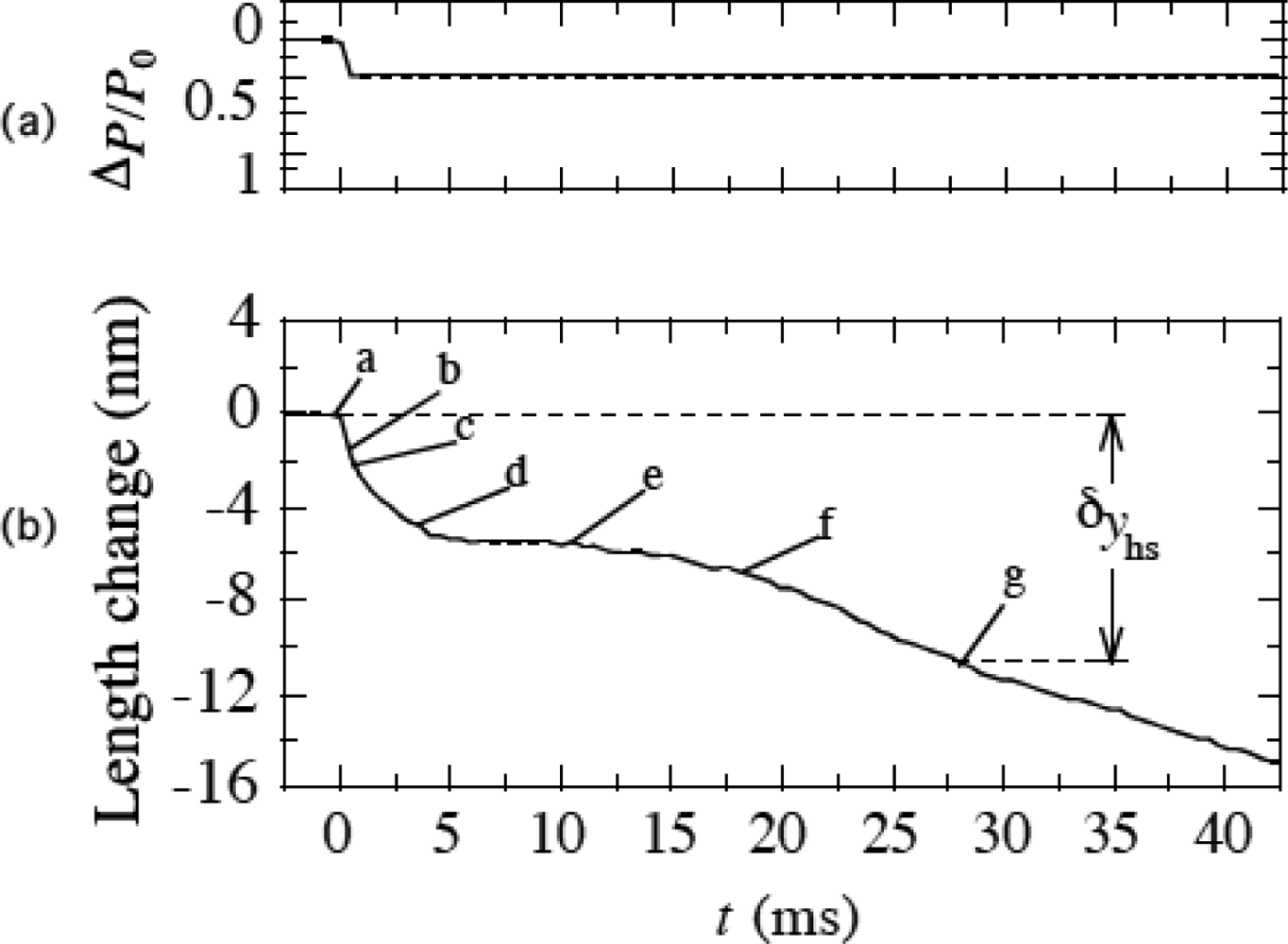
3.9 Isometric tension transient
3.10 Isotonic velocity transient
4. Quantitative explanation of experimental data
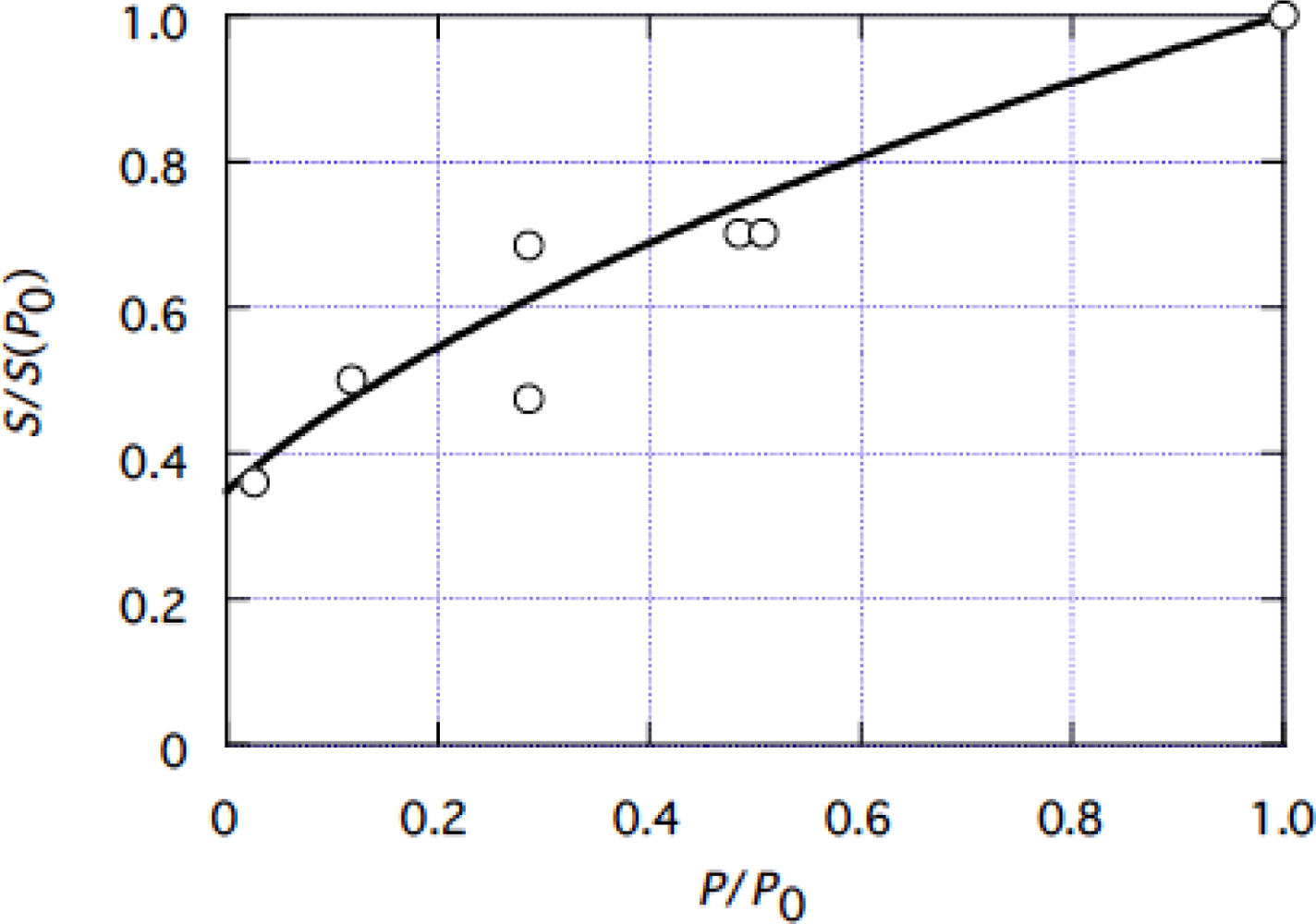
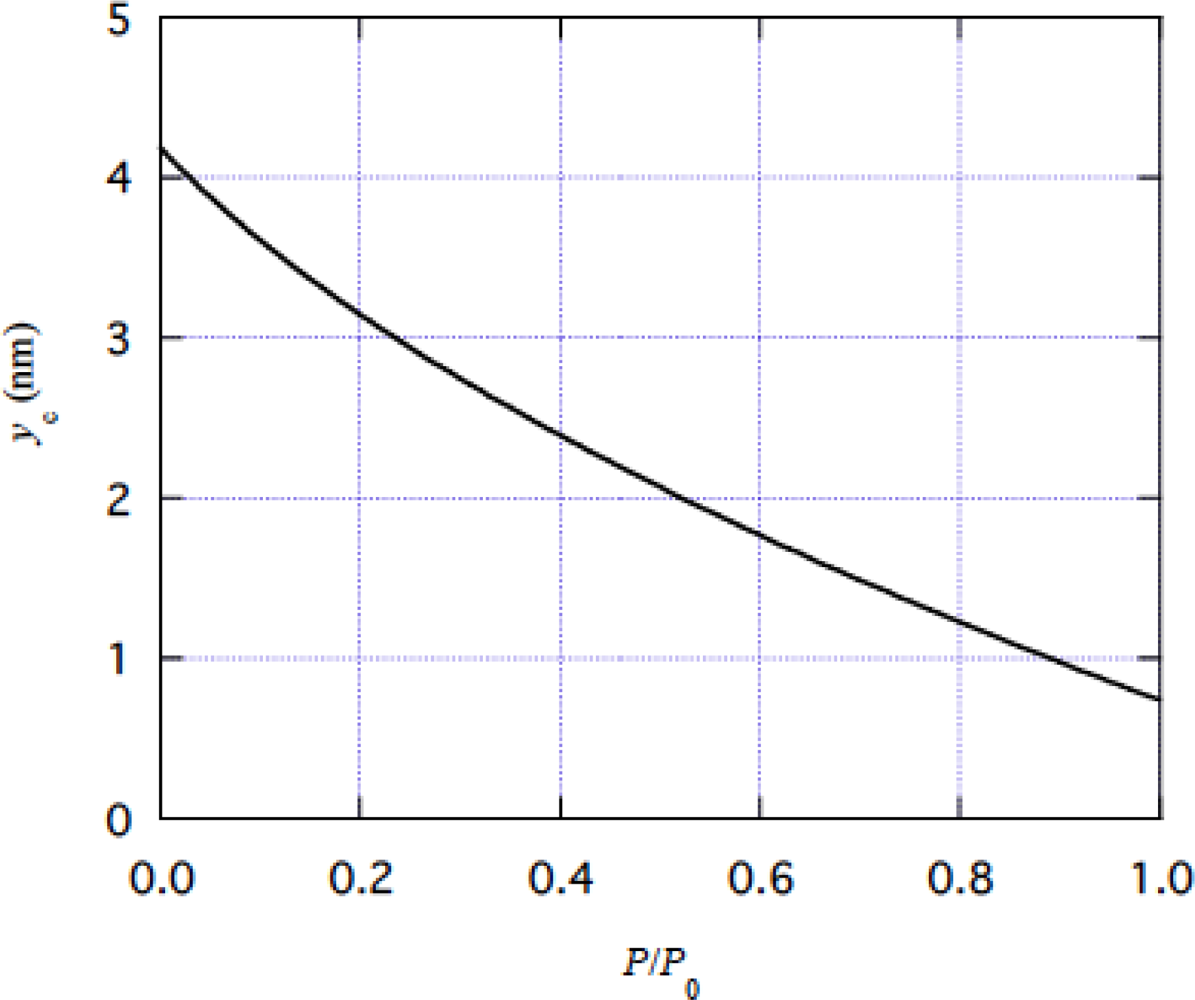
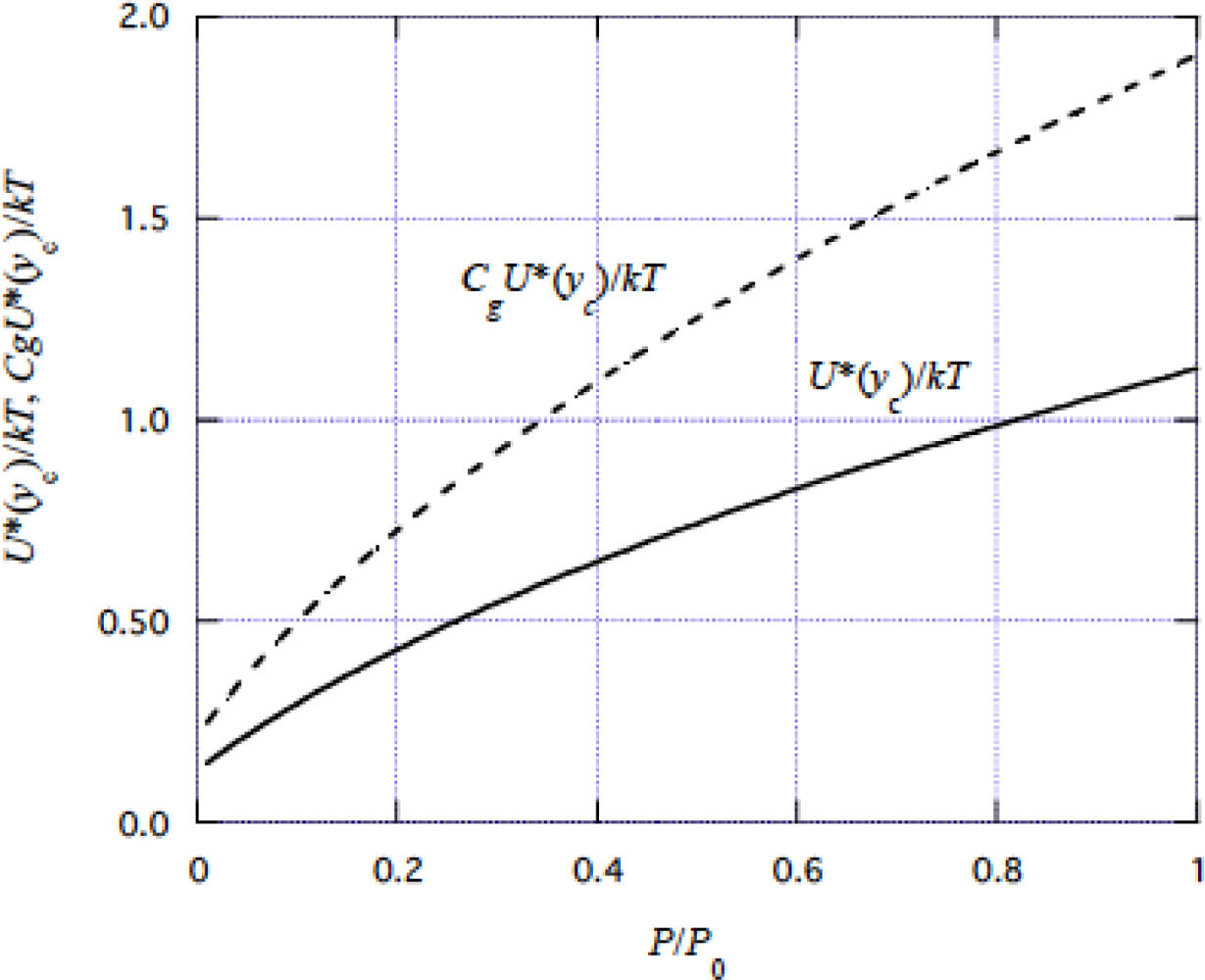
4.1 Tension dependence of muscle stiffness
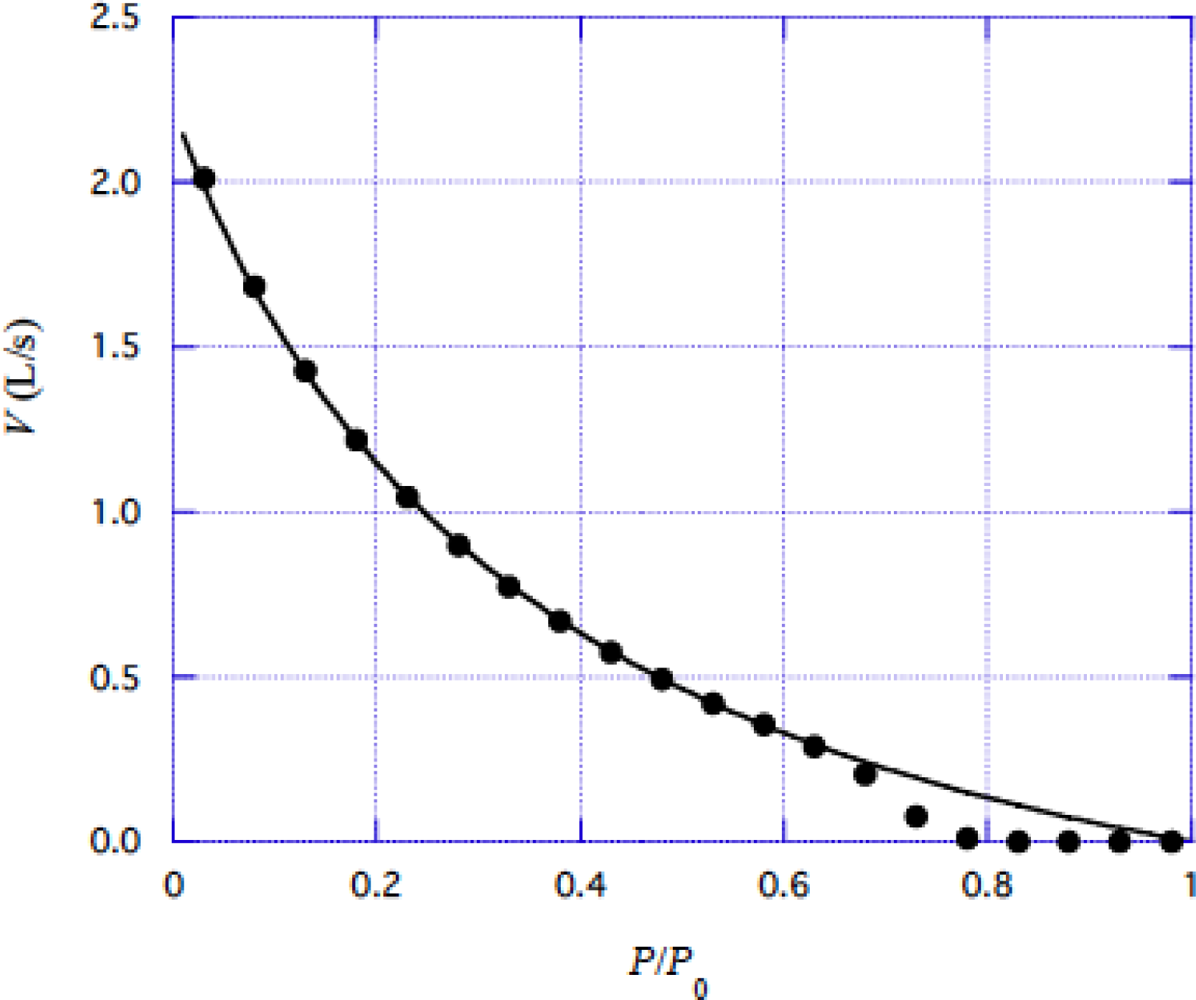
4.2 Force-velocity relation
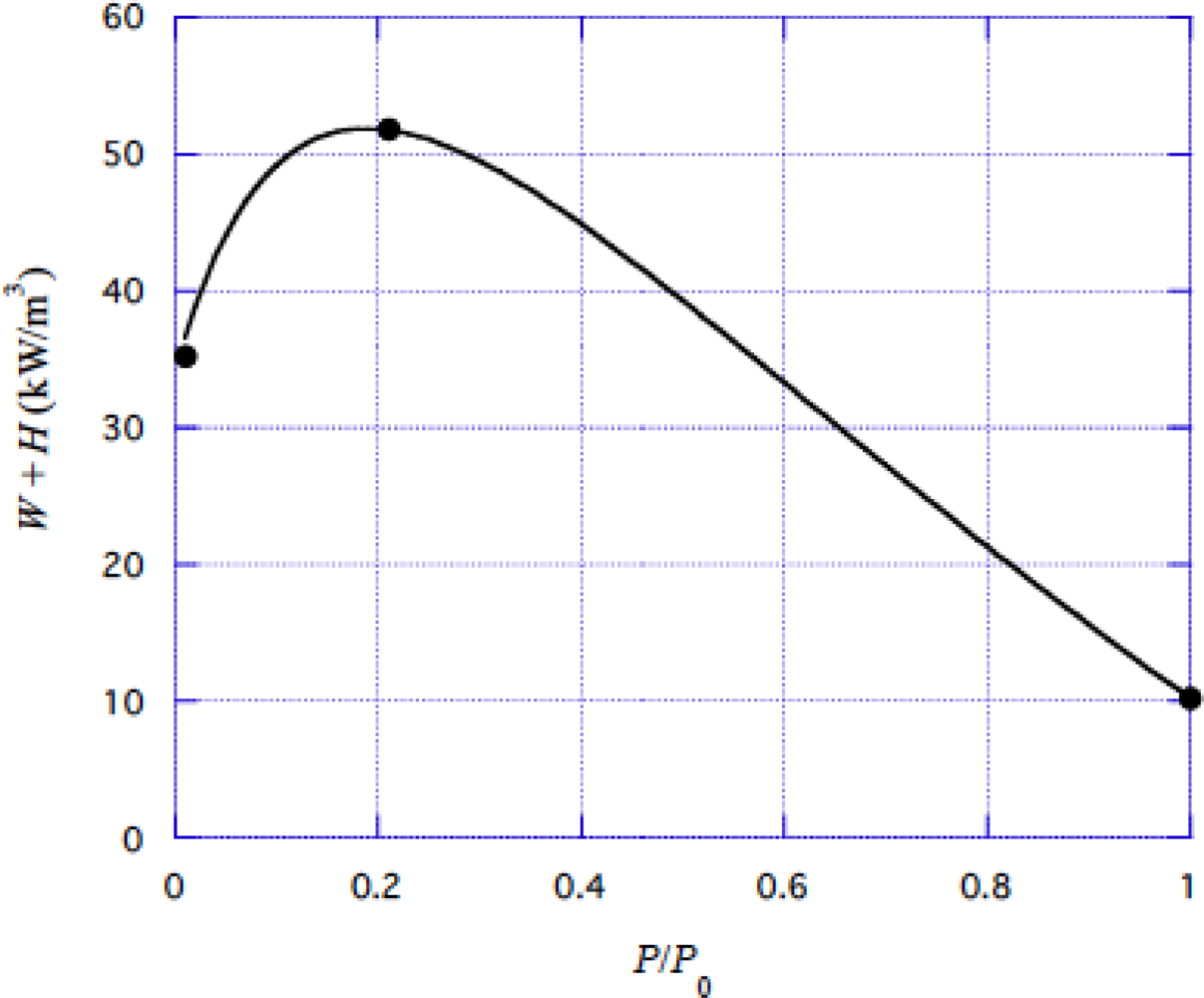
4.3 Energy liberation rate
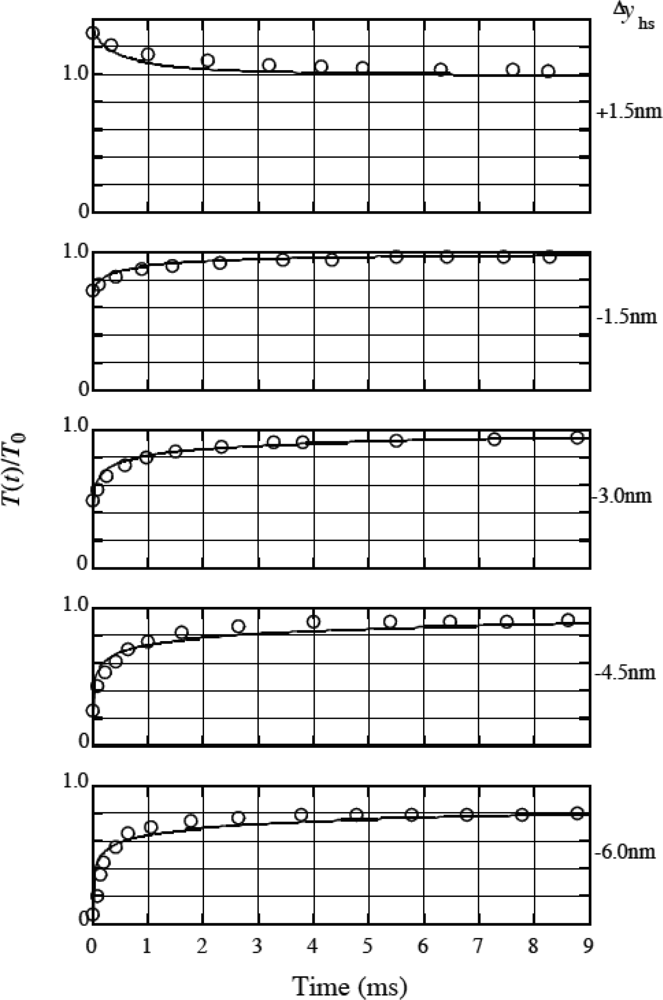
4. 4 Isometric tension transient
4. 5 Isotonic Velocity Transient
5. Additional comments
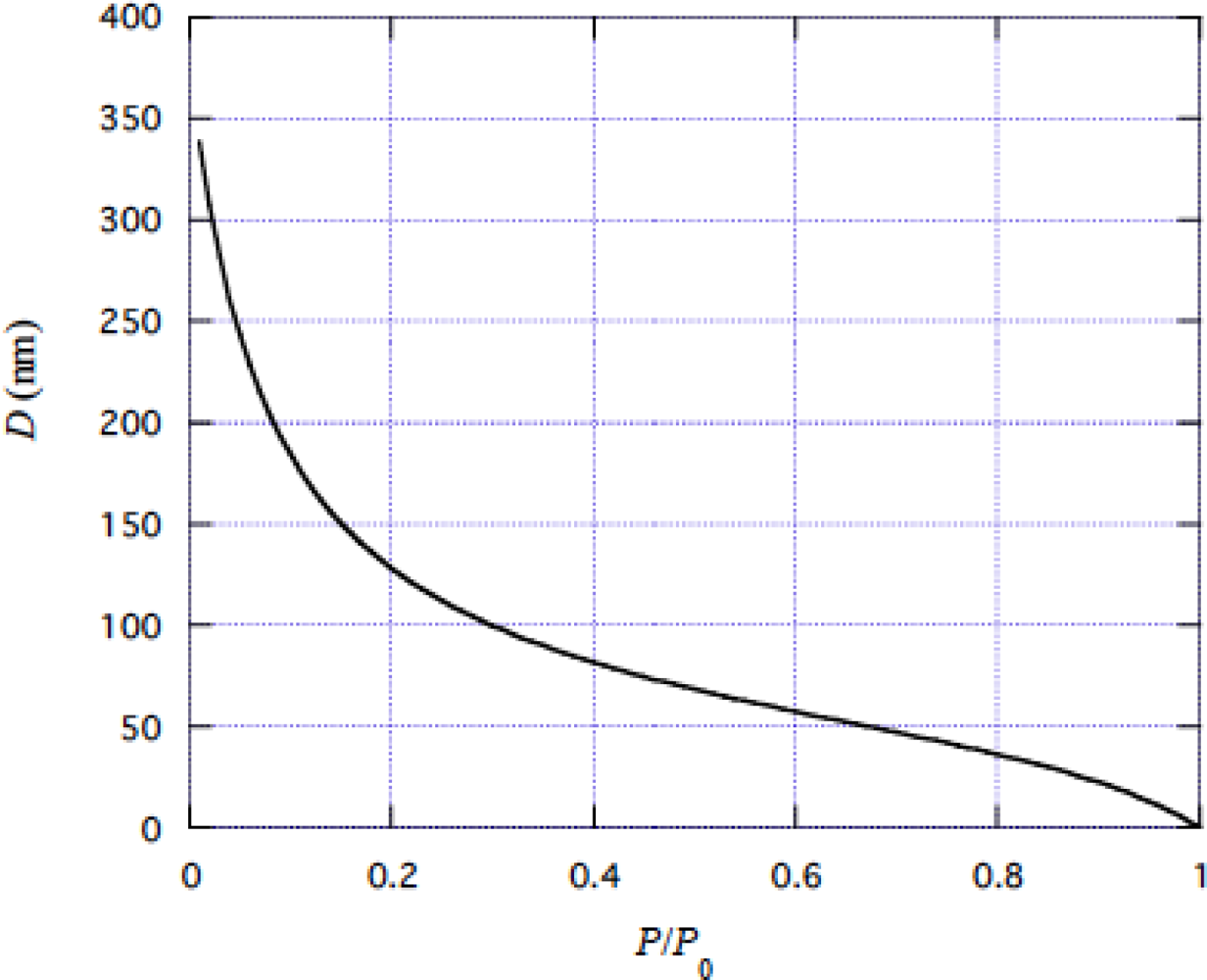
5.1 On the large values of D/r
5.2 On the two-headed structure of myosin molecule
5.3 On cytoplasmic streaming in Characean algae
6. Summary
Acknowledgments
Appendix
Fundamental Parameter Values
| kT | 3.77×10−21 J at 0°C |
| L | period of actin strand projection onto the filament axis: 5.46 nm |
| N | number of myosin heads in 1 m 3, calculated with Nhs and s: :1.68×1023 m−3 |
| Nhs | number of myosin heads in a volume with a base of 1 m2 and a thickness of half the sarcomere length : 1.76×1017 m−2 [49] |
| P0 | isometric tension : 4.1×105 N/m2 [31] |
| p0 | |
| r | ratio of the number of myosin heads simultaneously in the attached state to the number of all the heads: 0.41 (Eq. 3-1-1) |
| s | sarcomere length: 2.10 μm [31] |
| Vmax | |
| vmax | velocity of filament sliding under no load in muscle at 1.8°C: 2.36 μm/s [31] |
| yc(0) | critical y at free shortening : 4.2 nm (Eq. 4-1-11) |
| yc0 | critical y at the isometric tension : 0.73 nm (Eq. 4-1-12) |
| εATP | energy liberated by the hydrolysis of one ATP molecule: 8.0×10−20 J/molecule [50], 21kT at 0°C |
| κf | stiffness of crossbridge when the myosin head exertes positive force on a myosin filament: 2.80×10−3 N/m = 2.80 pN/nm (Eq. 4-1-13) |
| κb | stiffness of crossbridge when the myosin head exerts negative force on a myosin filament: 0.26×10−3 N/m = 0.26 pN/nm (Eq. 4-1-14) |
References
- Huxley, AF. Muscle structure and theories of contraction. Progr. Biophys. Biophys. Chem. 1957, 7, 255–318. [Google Scholar]
- Huxley, HE. The mechanism of muscular contraction. Science 1969, 164, 1356–1366. [Google Scholar]
- Huxley, AF; Simmons, RM. Proposed mechanism of force generation in striated muscle. Nature 1971, 233, 533–538. [Google Scholar]
- Huxley, AF. Mechanics and models of the myosin motor. Phil. Trans. R. Soc. Lond. B 2000, 355, 433–440. [Google Scholar]
- Mitsui, T; Chiba, H. Proposed modification of the Huxley-Simmons model for myosin head motion along an actin filament. J. Theor. Biol. 1996, 182, 147–159. [Google Scholar]
- Mitsui, T; Kumagai, S; Chiba, H; Yoshimura, H; Ohshima, H. Induced potential model for musculat contraction mechanism, including two attached states of myosin head. J. Theor. Biol. 1998, 192, 35–41. [Google Scholar]
- Mitsui, T. Induced potential model of muscular contraction mechanism and myosin molecular structure. Adv. Biophys. 1999, 36, 107–158. [Google Scholar]
- Mitsui, T; Tatsuzaki, I; Nakamura, E. An introduction to the physics of ferroelectrics; Gordon & Breach: New York, NY, USA, 1976. [Google Scholar]
- Geeves, MA; Holmes, KC. The molecular mechanism of muscular contraction. Advance in Protein Chemistry 2005, 71, 161–193. [Google Scholar]
- Ford, LE; Huxley, AF; Simmons, RM. Tension transients during steady shortening of frog muscle fibres. J. Physiol. 1985, 361, 131–150. [Google Scholar]
- Ishijima, A; Harada, Y; Kojima, H; Funatsu, T; Higuchi, H; Yanagida, T. Single-molecule analysis of the actomyosin motor using nano-manipulation. Biochem. Biophys. Res. Comm. 1994, 199, 1057–1063. [Google Scholar]
- Matsubara, I; Yagi, N; Hashizume, H. Use of an X-ray television for diffraction of the frog striated muscle. Nature 1975, 255, 728–729. [Google Scholar]
- Yagi, N; Takemori, S; Watanabe, M. An X-ray diffraction study of frog skeletal muscle during shortening near the maximum velocity. J. Mol. Biol. 1993, 231, 668–677. [Google Scholar]
- Podolsky, RJ; Onge, SSt; Yu, L; Lymn, RW. X-ray diffraction of actively shortening muscle. Proc. Natl. Acad. Sci. USA 1976, 73, 813–817. [Google Scholar]
- Huxley, HE. Time resolved X-ray diffraction studies in muscle. In Crossbridge Mechanism in Muscle Contraction; Sugi, H, Pollack, GH, Eds.; University of Tokyo Press: Tokyo, Japan, 1979; pp. 391–405. [Google Scholar]
- Huxley, HE; Kress, M. Crossbridge behaviour during muscle contraction. J. Musc. Res. Cell Motility 1985, 6, 153–161. [Google Scholar]
- Molloy, JE; Burns, JE; Kendrick-Jones, J; Tregear, RT; White, DCS. Movement and force produced by a single myosin head. Nature 1995, 378, 209–212. [Google Scholar]
- Kitamura, K; Tokunaga, M; Hikikoshi-Iwane, A; Yanagida, T. A single myosin head moves along an actin filament with regular steps of 5.3 nanometres. Nature 1999, 397, 129–134. [Google Scholar]
- Ramsey, RW; Street, SF. The isometric length-tension diagram of isolated skeletal muscle fibers of the frog. J. Cell. Comp. Physiol. 1940, 15, 11–34. [Google Scholar]
- Andreeva, AL; Andreev, OA; Borejdo, J. Structure of the 265-kilodalton complex formed upon EDC cross-linking of subfragment 1 to F-actin. Biochem. 1993, 32, 13956–13960. [Google Scholar]
- Xiao, M; Andreev, OA; Borejdo, J. Rigor crossbridges bind to two actin monomers in thin filaments of rabbit psoas muscle. J. Mol. Biol. 1995, 248, 294–307. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 6th Ed. ed; John Wiley & Sons: New York, NY, USA, 1986; pp. 281–286. [Google Scholar]
- Rayment, I; Rypniewski, WR; Schmidt-Bäse, K; Smith, R; Tomchick, DR; Benning, MM; Winkelmann, DA; Wesenberg, G; Holden, HH. Three-dimensional structure o myosin subfragment-1: a molecular motor. Science 1993, 261, 50–58. [Google Scholar]
- Rayment, I; Holden, HM; Whittaker, M; Yohn, CB; Lorenz, M; Holmes, KC; Milligan, RA. Structure of the actin-myosin complex and its implications for muscle contraction. Science 1993, 261, 58–65. [Google Scholar]
- Burgess, SA; Walker, ML; White, HD; Trinick, J. Extensibility within myosin heads revealed by negative strain and single-particle analysis. J. Cell Biol. 1997, 139, 675–681. [Google Scholar]
- Wakabayashi, K; Yagi, N. Muscle contraction: challenges for synchrotron radiation. J. Synchrotron Rad. 1999, 6, 875–890. [Google Scholar]
- Mandelson, RA; Morales, MF; Botts, J. Segmental flexibility of the S-1 moiety of myosin. Biochem. 1973, 12, 2250–2255. [Google Scholar]
- Elliott, A; Offer, G. Shape and flexibility of the myosin molecule. J. Mol.Biol. 1978, 123, 505–519. [Google Scholar]
- Walker, M; Knight, P; Trinick, J. Negative staining of myosin molecules. J. Mol. Biol. 1985, 184, 535–542. [Google Scholar]
- Eyring, H. Viscosity, plasticity, and diffusion as examples of absolute reaction rate. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar]
- Edman, KAP. Double-hyperbolic force-velocity relation in frog muscle fibres. J. Physiol. 1988, 404, 301–321. [Google Scholar]
- Lymn, RW; Taylor, EW. Mechanism of adenosin triphosphate hydrolysis by actomyosin. Biochemistry 1971, 10, 4617–4624. [Google Scholar]
- Ford, LE; Huxley, AF; Simmons, RM. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J. Physiol. 1977, 269, 441–515. [Google Scholar]
- Podolsky, RJ. Kinetics of molecular contraction: the approach to steady state. Nature 1960, 188, 666–668. [Google Scholar]
- Civan, MM; Podolsky, RJ. Contraction kinetics of striated muscle fibres following quick changes in load. J. Physiol. 1966, 184, 511–534. [Google Scholar]
- Huxley, AF. Muscular contraction. J. Physiol. 1974, 243, 1–43. [Google Scholar]
- Huxley, HE; Steward, A; Sosa, H; Irving, T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 1994, 67, 2411–2421. [Google Scholar]
- Wakabayashi, K; Sugimoto, Y; Tanaka, H; Ueno, Y; Takazawa, Y; Amemiya, Y. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 1994, 67, 2422–2435. [Google Scholar]
- Irving, M. Give in the filament. Nature 1995, 374, 14–15. [Google Scholar]
- Homsher, E; Irving, M; Yamada, T. The effect of shortening on energy liberation and high energy phosphate hydrolysis in frog skeletal muscle. In Contractile Mechanism in Muscle; Pollack, GH, Sugi, H, Eds.; Plenum Press: New York, NY, USA, 1984; pp. 865–876. [Google Scholar]
- Hill, AV. The effect of load on the heat of shortening muscle. Proc. Roy. Soc. B 1964, 159, 297–318. [Google Scholar]
- Yanagida, T; Arata, T; Oosawa, F. Sliding distance of actin filamentinduced by a myosin crossbridge during one ATP hydrolysis cycle. Nature 1985, 316, 366–369. [Google Scholar]
- Harada, Y; Sakurada, K; Aoki, T; Thomas, DD; Yanagida, T. Mechanochemical coupling in actomyosin energy transduction studied by in vitro movment assay. J. Mol. Biol. 1990, 216, 49–68. [Google Scholar]
- Mitsui, T. A supplement to the theory of muscle contraction. Bussei-Kenkyu 2002, 78, 603–611. (in Japanese). [Google Scholar]
- Nothnagel, EA; Webb, WW. Hydrodynamic models of viscous coupling between motile myosin and endoplasm in Characean algae. J. Cell Biol. 1982, 94, 444–454. [Google Scholar]
- Rivolta, MN; Urrutia, R; Kachar, B. A soluble motor from the alga Nitella supports fast movement of actin filament in vitro. Biochim. Biophys. Acta 1995, 1232, 1–4. [Google Scholar]
- Higashi-Fujime, S; Ishikawa, R; Iwasawa, H; Kagami, O; Kurimoto, E; Kohama, K; Hozumi, T. The fastest actin-based motor protein from the green algae, Chara, and its distinct mode of interaction with actin. FEBS Lett. 1995, 375, 151–154. [Google Scholar]
- Mitsui, T; Ohshima, H. Proposed model for the flagellar rotary motor. Colloid and Surfaces B: Biointerfaces 2005, 46, 32–44. [Google Scholar]
- Mitsui, T; Ohshima, H. A self-induced translation model of myosin head motion in contracting muscle I. Foece-velocity relation and energy liberation. J. Musc. Res. Cell Motility 1988, 9, 248–260. [Google Scholar]
- Woledge, RC; Curtin, NA; Homsher, E. Chapter 4 Heaat production and chemical change. Energetic Aspects of Muscle Contraction 1985. [Google Scholar]
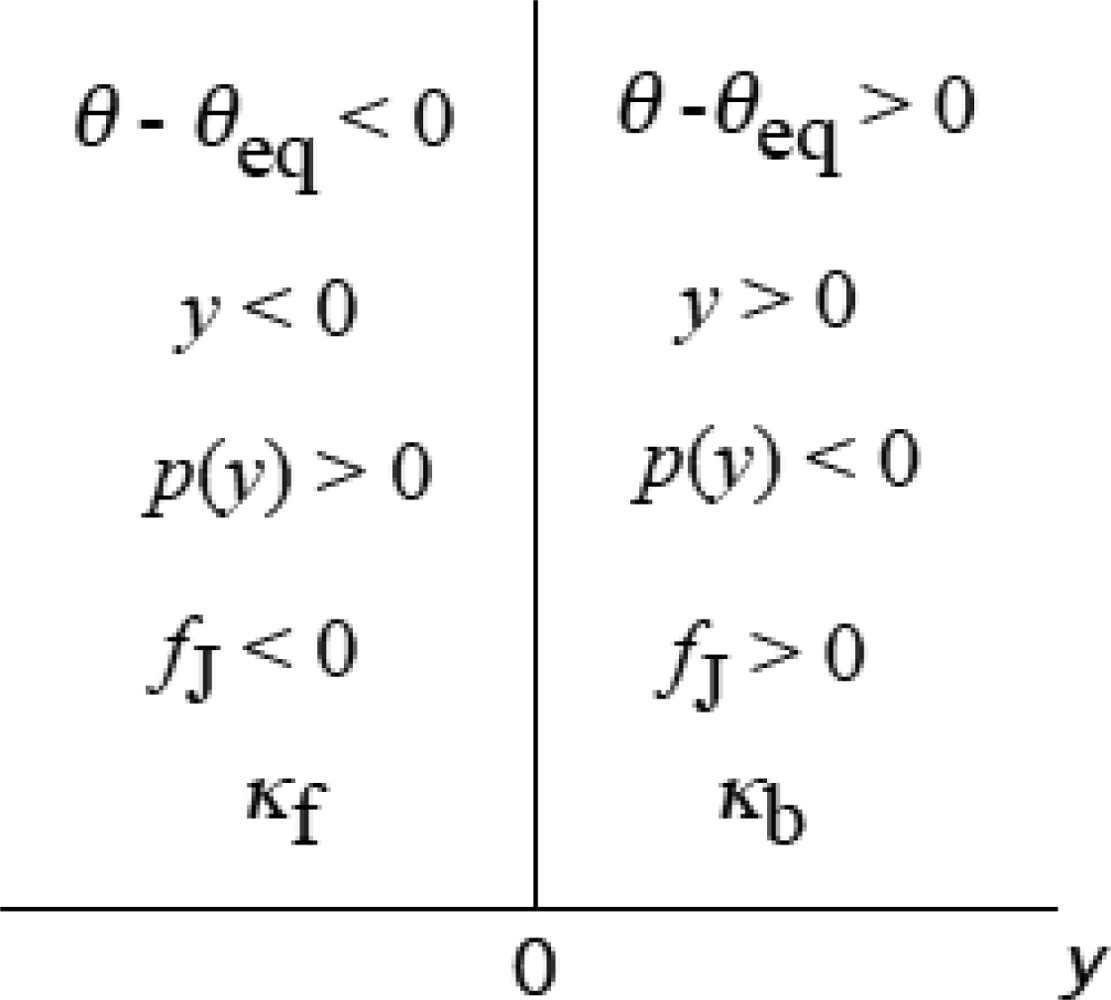
Share and Cite
Mitsui, T.; Ohshima, H. Remarks on Muscle Contraction Mechanism. Int. J. Mol. Sci. 2008, 9, 872-904. https://doi.org/10.3390/ijms9050872
Mitsui T, Ohshima H. Remarks on Muscle Contraction Mechanism. International Journal of Molecular Sciences. 2008; 9(5):872-904. https://doi.org/10.3390/ijms9050872
Chicago/Turabian StyleMitsui, Toshio, and Hiroyuki Ohshima. 2008. "Remarks on Muscle Contraction Mechanism" International Journal of Molecular Sciences 9, no. 5: 872-904. https://doi.org/10.3390/ijms9050872
APA StyleMitsui, T., & Ohshima, H. (2008). Remarks on Muscle Contraction Mechanism. International Journal of Molecular Sciences, 9(5), 872-904. https://doi.org/10.3390/ijms9050872