Circular RNA-Drug Association Prediction Based on Multi-Scale Convolutional Neural Networks and Adversarial Autoencoders
Abstract
1. Introduction
2. Results and Discussion
2.1. Experiment Settings and Evaluation Metrics
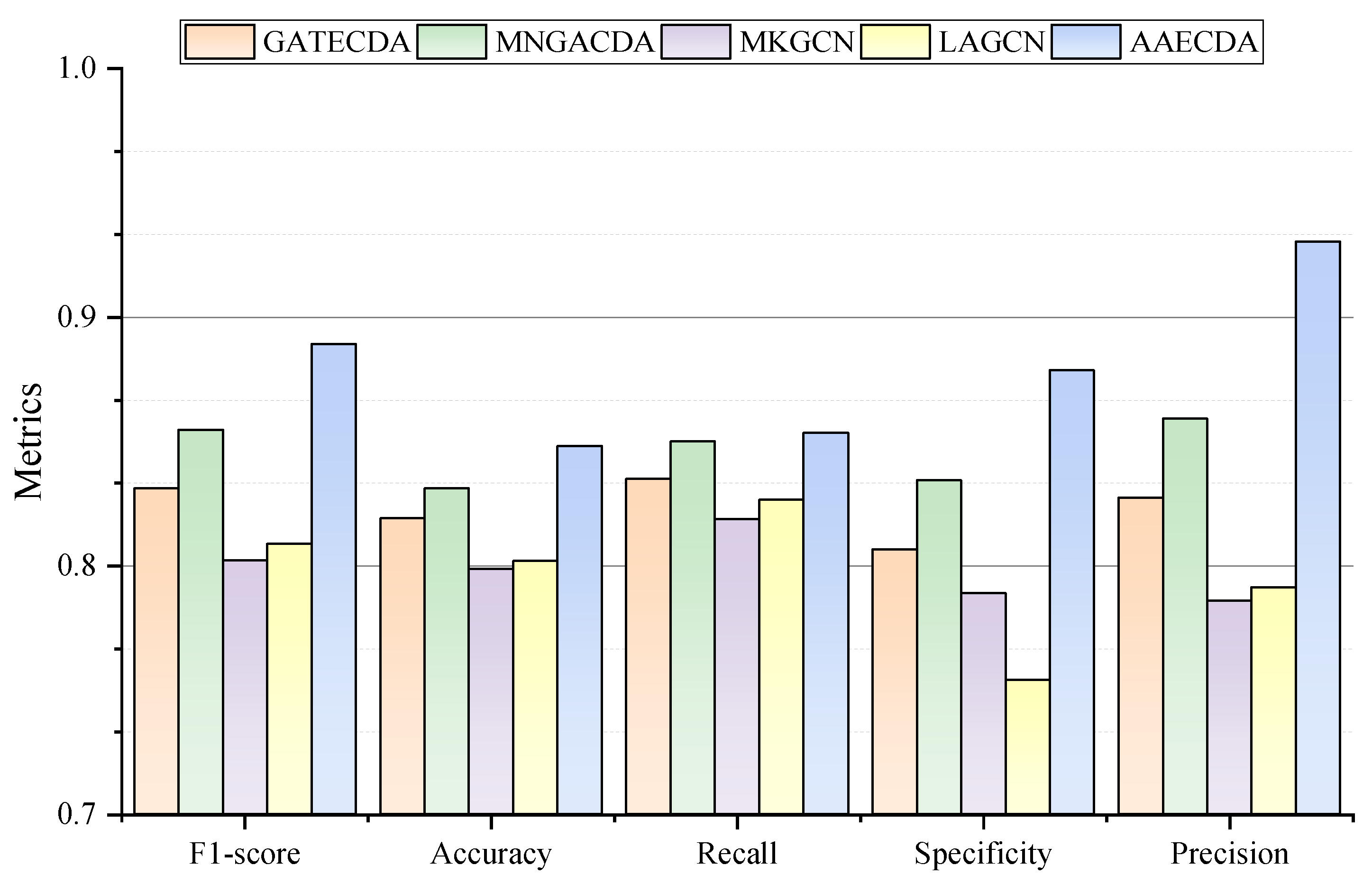
2.2. Performance Comparison with Other Methods Under 5-CV and 10-CV Experiments
- GATECDA: This computational model employs a graph attention autoencoder and DNN to predict associations between circRNAs and drugs.
- MNGACDA: This model utilizes a node-level attention-based graph autoencoder to extract feature representations and employs an inner-product decoder to predict associations.
- MNCLCDA: This model applies a random walk with a restart method to preprocess the similarity network and capture features, followed by using a mixed-neighborhood graph convolutional network to acquire node neighborhood information.
- MKGCN: This method predicts microbe-drug associations by integrating multiple data sources and applying dual Laplacian regularized fewest squares on multiple kernel matrices.
- LAGCN: The model constructs a heterogeneous network, applies graph convolution to obtain the weights of each layer’s embedding, and then predicts disease-drug associations.
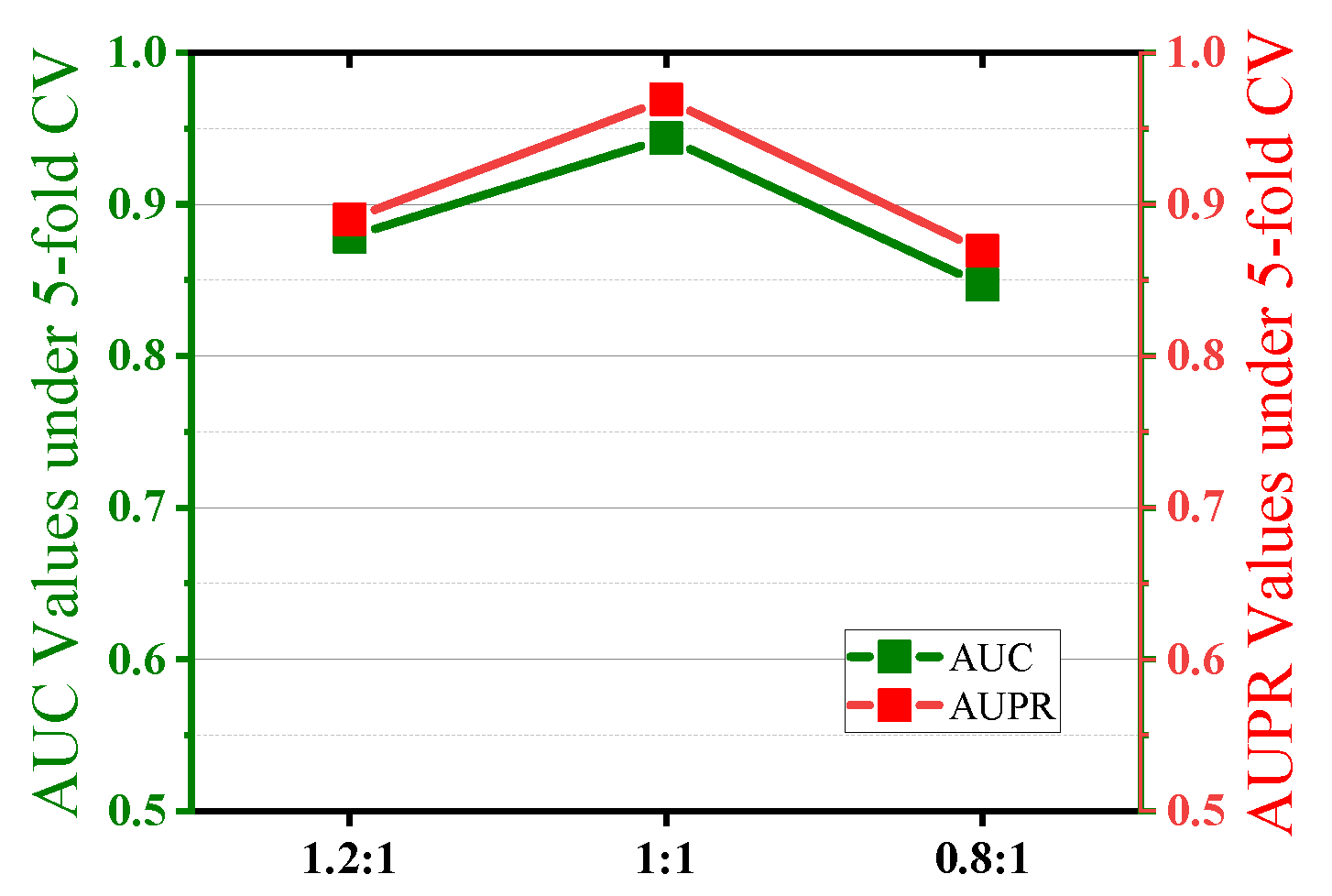
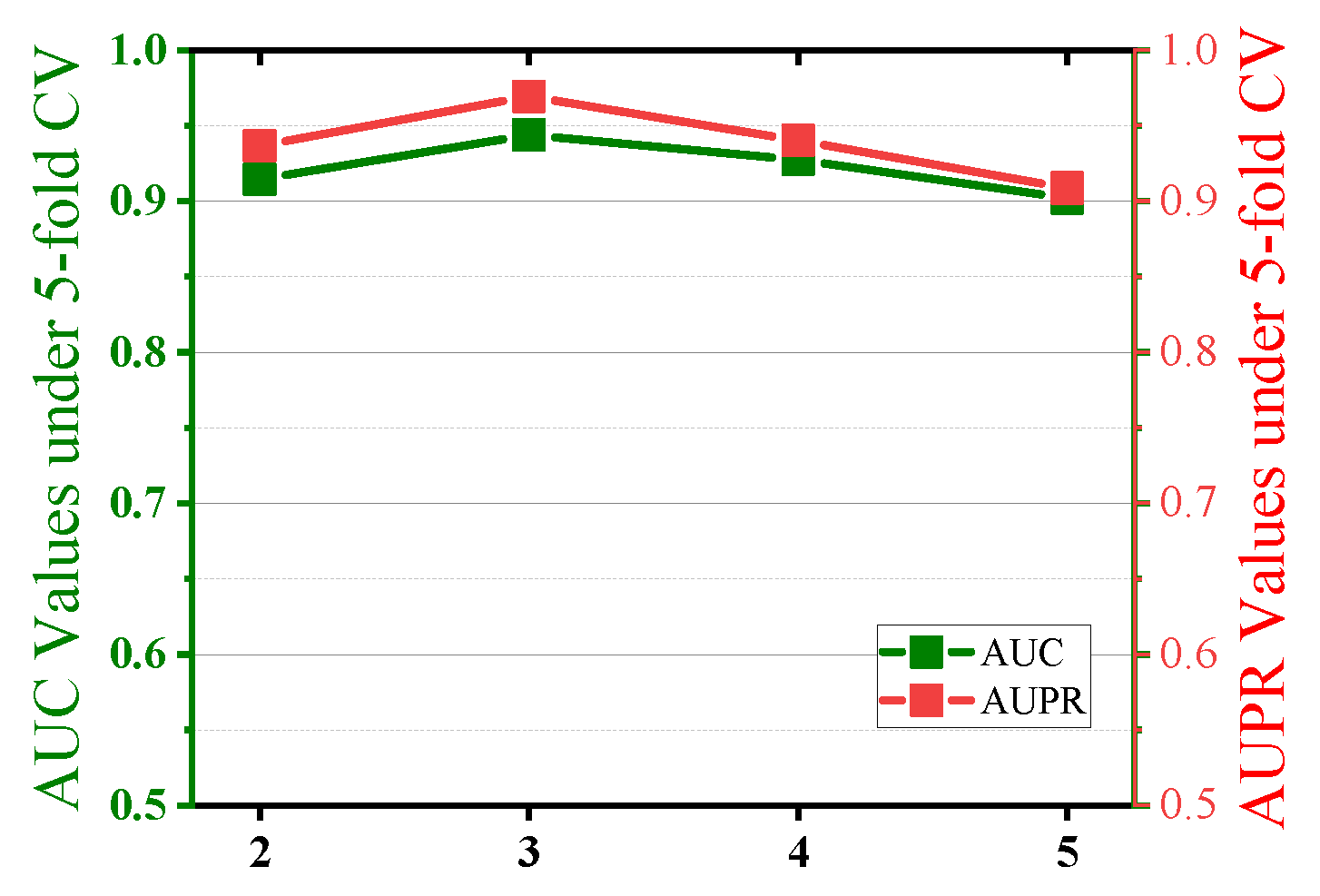
2.3. Parameter Sensitivity Analysis
2.4. Ablation Experiments
- AAECDA_no_encoder removes the encoder, and the original input data are processed directly by the discriminator without encoding. This is equivalent to using the raw input data for adversarial training without compressed representations.
- AAECDA_no_discriminator degrades the AAE into a regular autoencoder, where the model structure contains only the encoder and decoder without adversarial training. This design evaluates the importance of the discriminator in guiding the AAE to learn the latent space distribution.
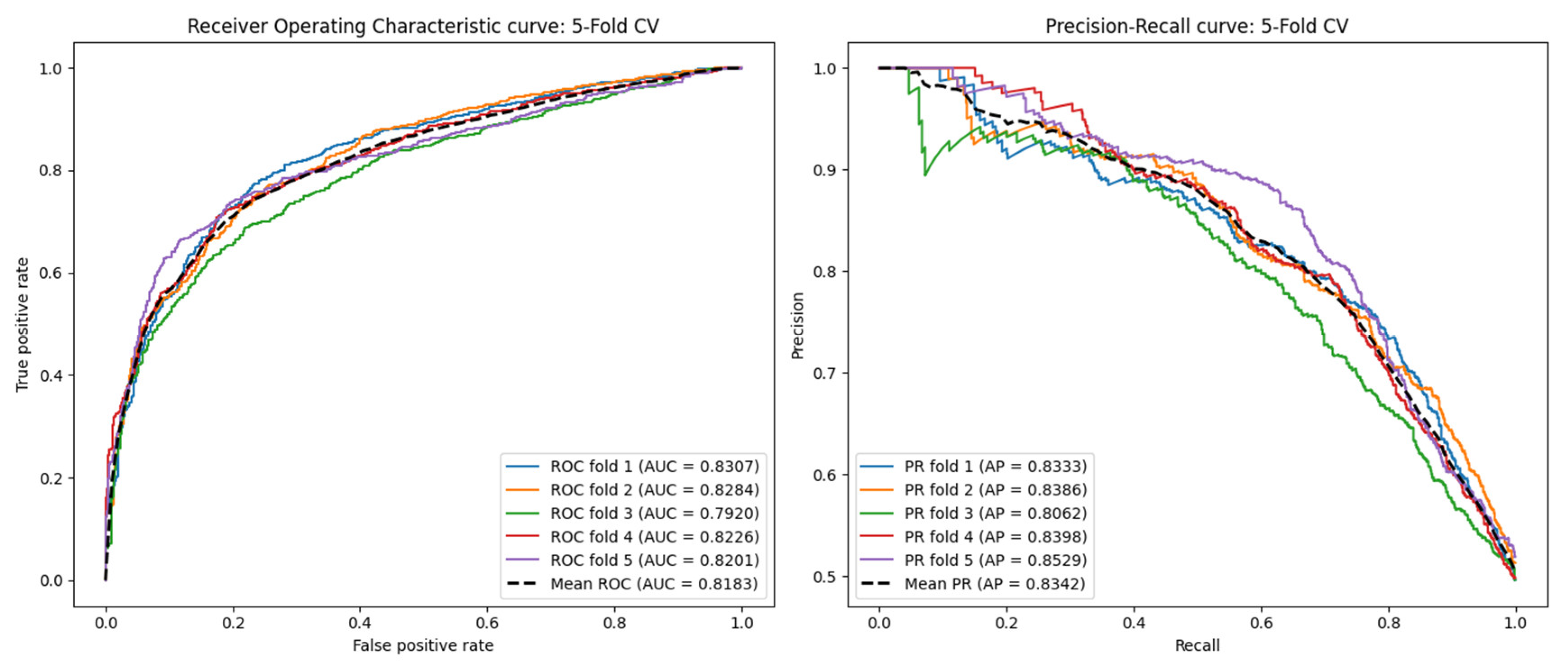
2.5. Performance Under the Blind Test Set
2.6. Case Studies
3. Materials and Methods
3.1. Dataset
3.2. Construction of the Similarity Network
3.2.1. Sequence Similarity of Host Genes of circRNAs
3.2.2. Structural Similarity of Drugs
3.2.3. Gaussian Interaction Profile Kernel Similarity of circRNAs and Drugs
3.2.4. Similarity Fusion
3.2.5. Multi-Scale Convolutional Neural Network
3.3. AAECDA
- (1)
- Construction of similarity networks, as well as the sensitivity association network.
- (2)
- Extraction of integrated circRNA and drug features using the MSCNN.
- (3)
- Extraction of the latent representations of circRNA and drugs using the AAE.
- (4)
- Inputting the extracted latent representations into the DNN to predict the circRNA-drug association score.
3.3.1. Adversarial Autoencoder
3.3.2. Association Prediction Based on Deep Neural Networks
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, L.; Shamsuzzama; Haque, R.; Baghel, T.; Nazir, A. Circular RNAs: The Emerging Class of Non-coding RNAs and Their Potential Role in Human Neurodegenerative Diseases. Mol. Neurobiol. 2017, 54, 7224–7234. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Zhong, Y.; Wang, X.; Shen, J.; An, W. Advances in Circular RNA and Its Applications. Int. J. Med. Sci. 2022, 19, 975–985. [Google Scholar] [CrossRef] [PubMed]
- Syvänen, A.C. Accessing genetic variation: Genotyping single nucleotide polymorphisms. Nat. Rev. Genet. 2001, 2, 930–942. [Google Scholar] [CrossRef] [PubMed]
- Stoll, L.; Rodríguez-Trejo, A.; Guay, C.; Brozzi, F.; Bayazit, M.B.; Gattesco, S.; Menoud, V.; Sobel, J.; Marques, A.C.; Venø, M.T.; et al. A circular RNA generated from an intron of the insulin gene controls insulin secretion. Nat. Commun. 2020, 11, 5611. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.-G.; Awan, F.M.; Du, W.W.; Zeng, Y.; Lyu, J.; Wu, D.; Gupta, S.; Yang, W.; Yang, B.B. The Circular RNA Interacts with STAT3, Increasing Its Nuclear Translocation and Wound Repair by Modulating Dnmt3a and miR-17 Function. Mol. Ther. 2017, 25, 2062–2074. [Google Scholar] [CrossRef]
- Salzman, J.; Gawad, C.; Wang, P.L.; Lacayo, N.; Brown, P.O. Circular RNAs Are the Predominant Transcript Isoform from Hundreds of Human Genes in Diverse Cell Types. PLoS ONE 2012, 7, e30733. [Google Scholar] [CrossRef]
- Jeck, W.R.; Sorrentino, J.A.; Wang, K.; Slevin, M.K.; Burd, C.E.; Liu, J.; Marzluff, W.F.; Sharpless, N.E. Circular RNAs are abundant, conserved, and associated with ALU repeats. RNA 2013, 19, 426. [Google Scholar] [CrossRef]
- Guo, Y.; Lei, X.; Liu, L.; Pan, Y. circ2CBA: Prediction of circRNA-RBP binding sites combining deep learning and attention mechanism. Front. Comput. Sci. 2022, 17, 175904. Available online: https://link.springer.com/article/10.1007/s11704-022-2151-0 (accessed on 14 September 2024). [CrossRef]
- Deng, L.; Liu, Z.; Qian, Y.; Zhang, J. Predicting circRNA-drug sensitivity associations via graph attention auto-encoder. BMC Bioinform. 2022, 23, 160. [Google Scholar] [CrossRef]
- Yang, B.; Chen, H. Predicting circRNA-drug sensitivity associations by learning multimodal networks using graph auto-encoders and attention mechanism. Brief. Bioinform. 2023, 24, bbac596. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Liang, C.; Luo, J. DeepWalk-aware graph attention networks with CNN for circRNA-drug sensitivity association identification. Brief. Funct. Genom. 2023, 23, 418–428. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Lei, X. Predicting circRNA-disease associations based on autoencoder and graph embedding—ScienceDirect. Inf. Sci. 2021, 571, 323–336. Available online: https://www.sciencedirect.com/science/article/pii/S0020025521004084 (accessed on 14 September 2024). [CrossRef]
- Lei, X.; Tie, J.; Pan, Y. Inferring Metabolite-Disease Association Using Graph Convolutional Networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 19, 688–698. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Lei, X.; Pan, Y. Prioritizing CircRNA-disease Associations with Convolutional Neural Network Based on Multiple Similarity Feature Fusion. Front. Genet. 2020, 11, 540751. [Google Scholar] [CrossRef]
- Yang, J.; Lei, X.; Pan, Y. Predicting circRNA-disease Associations by Using Multi-Biomolecular Networks Based on Variational Graph Auto-Encoder with Attention Mechanism. Chin. J. Electron. 2024, 33, 1526–1537. [Google Scholar] [CrossRef]
- Lei, X.; Chen, Y.; Pan, Y. Multi-source Data with Laplacian Eigenmaps and Denoising Autoencoder for Predicting Microbe-disease Association via Convolutional Neural Network. J. Comput. Sci. Technol. 2024. [Google Scholar] [CrossRef]
- Guo, Y.; Lei, X.; Pan, Y. An Encoding-Decoding Framework Based on CNN for circRNA-RBP Binding Sites Prediction. Chin. J. Electron. 2024, 33, 256–263. [Google Scholar] [CrossRef]
- Liu, Z.; Dai, Q.; Yu, X.; Duan, X.; Wang, C. Predicting circRNA-drug resistance associations based on a multimodal graph representation learning framework. IEEE J. Biomed. Health Inform. 2023. Available online: https://webofscience.clarivate.cn/wos/alldb/summary/f9308609-b5af-4a7c-bea0-26f1cc0a0375-01063c258d/relevance/1 (accessed on 6 September 2024).
- Lu, S.; Liang, Y.; Li, L.; Liao, S.; Zou, Y.; Yang, C.; Ouyang, D. Inferring circRNA-drug sensitivity associations via dual hierarchical attention networks and multiple kernel fusion. BMC Genom. 2023, 24, 796. [Google Scholar] [CrossRef]
- Li, G.; Zeng, F.; Luo, J.; Liang, C.; Xiao, Q. MNCLCDA: Predicting circRNA-drug sensitivity associations by using mixed neighbourhood information and contrastive learning. BMC Med. Inform. Decis. Mak. 2023, 23, 291. [Google Scholar] [CrossRef]
- Yu, Z.; Huang, F.; Zhao, X.; Xiao, W.; Zhang, W. Predicting drug-disease associations through layer attention graph convolutional network. Brief. Bioinform. 2021, 22, bbaa243. [Google Scholar] [CrossRef]
- Yang, H.; Ding, Y.; Tang, J.; Guo, F. Inferring human microbe-drug associations via multiple kernel fusion on graph neural network. Knowl.-Based Syst. 2022, 238, 107888. [Google Scholar] [CrossRef]
- Yang, W.; Soares, J.; Greninger, P.; Edelman, E.J.; Lightfoot, H.; Forbes, S.; Bindal, N.; Beare, D.; Smith, J.A.; Thompson, I.R.; et al. Genomics of Drug Sensitivity in Cancer (GDSC): A resource for therapeutic biomarker discovery in cancer cells. Nucleic Acids Res. 2013, 41, D955–D961. [Google Scholar] [CrossRef] [PubMed]
- Rees, M.G.; Seashore-Ludlow, B.; Cheah, J.H.; Adams, D.J.; Price, E.V.; Gill, S.; Javaid, S.; E Coletti, M.; Jones, V.L.; E Bodycombe, N.; et al. Correlating chemical sensitivity and basal gene expression reveals mechanism of action. Nat. Chem. Biol. 2016, 12, 109–116. [Google Scholar] [CrossRef]
- Gonzalez, R.D.; Small, G.W.; Green, A.J.; Akhtari, F.S.; Havener, T.M.; Quintanilha, J.C.F.; Cipriani, A.B.; Reif, D.M.; McLeod, H.L.; Motsinger-Reif, A.A.; et al. RYK Gene Expression Associated with Drug Response Variation of Temozolomide and Clinical Outcomes in Glioma Patients. Pharmaceuticals 2023, 16, 726. [Google Scholar] [CrossRef] [PubMed]
- El Charif, O.; Mapes, B.; Trendowski, M.R.; Wheeler, H.E.; Wing, C.; Dinh, P.C.; Frisina, R.D.; Feldman, D.R.; Hamilton, R.J.; Vaughn, D.J.; et al. Clinical and Genome-wide Analysis of Cisplatin-induced Tinnitus Implicates Novel Ototoxic Mechanisms. Clin. Cancer Res. 2019, 25, 4104–4116. [Google Scholar] [CrossRef]
- Ruan, H.; Xiang, Y.; Ko, J.; Li, S.; Jing, Y.; Zhu, X.; Ye, Y.; Zhang, Z.; Mills, T.; Feng, J.; et al. Comprehensive characterization of circular RNAs in ∼ 1000 human cancer cell lines. Genome Med. 2019, 11, 55. [Google Scholar] [CrossRef]
- Rangwala, S.H.; Kuznetsov, A.; Ananiev, V.; Asztalos, A.; Borodin, E.; Evgeniev, V.; Joukov, V.; Lotov, V.; Pannu, R.; Rudnev, D.; et al. Accessing NCBI data using the NCBI Sequence Viewer and Genome Data Viewer (GDV). Genome Res. 2021, 31, 159–169. [Google Scholar] [CrossRef]
- Wang, Y.; Bryant, S.H.; Cheng, T.; Wang, J.; Gindulyte, A.; Shoemaker, B.A.; Thiessen, P.A.; He, S.; Zhang, J. PubChem BioAssay: 2017 update. Nucleic Acids Res. 2017, 45, D955–D963. [Google Scholar] [CrossRef]
- Saowapa, K.; Kaneko, H.; Fujiwara, E. Systematic binary deletion/insertion error correcting codes capable of correcting random bit errors. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2000, E83A, 2699–2705. [Google Scholar]
- Landrum, G. RDKit: Open-source cheminformatics from machine learning to chemical registration. Abstr. Pap. Am. Chem. Soc. 2019, 258. [Google Scholar] [CrossRef]
- Shen, L.; Liu, F.; Huang, L.; Liu, G.; Zhou, L.; Peng, L. VDA-RWLRLS: An anti-SARS-CoV-2 drug prioritizing framework combining an unbalanced bi-random walk and Laplacian regularized least squares. Comput. Biol. Med. 2022, 140, 105119. [Google Scholar] [CrossRef] [PubMed]
- Niu, M.; Zou, Q.; Wang, C. GMNN2CD: Identification of circRNA-disease associations based on variational inference and graph Markov neural networks. Bioinformatics 2022, 38, 2246–2253. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, J.; Nie, R.; You, Z.-H.; Bao, W. A graph auto-encoder model for miRNA-disease associations prediction. Brief. Bioinform. 2021, 22, bbaa240. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lei, X.; Fang, Z.; Pan, Y. CircRNA-Disease Associations Prediction Based on Metapath2vec++ and Matrix Factorization. Big Data Min. Anal. 2020, 3, 280–291. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, X.; Wei, M.; Li, Z. A comprehensive review of graph convolutional networks: Approaches and applications. Electron. Res. Arch. 2023, 31, 4185–4215. [Google Scholar] [CrossRef]
- Jang, K.; Hong, S.; Kim, M.; Na, J.; Moon, I. Adversarial Autoencoder Based Feature Learning for Fault Detection in Industrial Processes. IEEE Trans. Ind. Inform. 2022, 18, 827–834. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]




| GATECDA | MNGACDA | MKGCN | LAGCN | AAECDA | |
|---|---|---|---|---|---|
| AUC | 0.8846 | 0.9139 | 0.8664 | 0.8642 | 0.9438 |
| AUPR | 0.8928 | 0.9209 | 0.8662 | 0.8738 | 0.9553 |
| F1_SCORE | 0.8279 | 0.8489 | 0.8023 | 0.8084 | 0.8305 |
| ACCURACY | 0.8190 | 0.8310 | 0.7985 | 0.8019 | 0.8480 |
| RECALL | 0.8348 | 0.8498 | 0.8186 | 0.8265 | 0.8534 |
| SPECIFICITY | 0.8065 | 0.8343 | 0.7889 | 0.7539 | 0.8785 |
| PRECISION | 0.8273 | 0.8590 | 0.7857 | 0.7912 | 0.9302 |
| GATECDA | MNGACDA | MKGCN | LAGCN | AAECDA | |
|---|---|---|---|---|---|
| AUC | 0.8918 | 0.9182 | 0.8683 | 0.8710 | 0.9464 |
| AUPR | 0.9015 | 0.9249 | 0.8769 | 0.8818 | 0.9570 |
| F1_SCORE | 0.8267 | 0.8373 | 0.8047 | 0.8133 | 0.8410 |
| ACCURACY | 0.8271 | 0.8427 | 0.8026 | 0.8076 | 0.8407 |
| RECALL | 0.8312 | 0.8536 | 0.8173 | 0.8312 | 0.8437 |
| SPECIFICITY | 0.8135 | 0.8323 | 0.7973 | 0.7486 | 0.8881 |
| PRECISION | 0.8225 | 0.8517 | 0.7937 | 0.7956 | 0.9383 |
| Variant | AUC | AUPR | F1_SCORE | ACCURACY | RECALL | SPECIFICITY | PRECISION |
|---|---|---|---|---|---|---|---|
| AAECDAnoEncoder | 0.6889 | 0.7106 | 0.7205 | 0.7022 | 0.7864 | 0.6975 | 0.7764 |
| AAECDAnoDiscriminator | 0.8346 | 0.8531 | 0.8014 | 0.8012 | 0.8248 | 0.7967 | 0.8083 |
| AAECDAnoMSCN | 0.8901 | 0.9022 | 0.8095 | 0.8237 | 0.8533 | 0.7991 | 0.8238 |
| AAECDA | 0.9438 | 0.9553 | 0.8305 | 0.8480 | 0.8534 | 0.8785 | 0.9302 |
| GATECDA | MNGACDA | AAECDA | |
|---|---|---|---|
| AUC | 0.7760 | 0.7947 | 0.8183 |
| AUPR | 0.7821 | 0.8013 | 0.8342 |
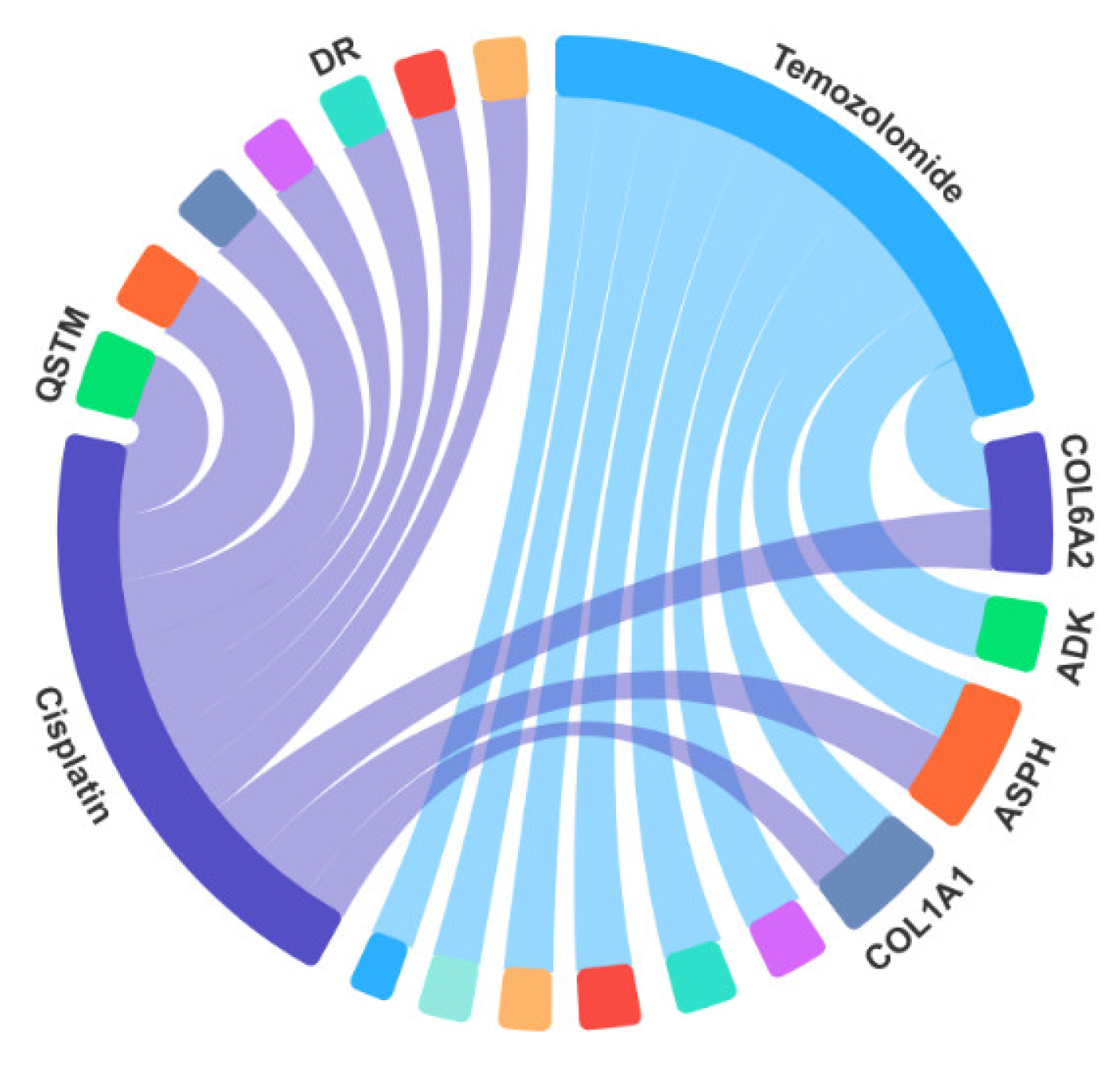
| Drug | Rank | circRNA | Evidence |
|---|---|---|---|
 Temozolomide | 1 | COL6A2 | CTPR |
| 2 | ADK | CTPR | |
| 3 | ASPH | CTPR | |
| 4 | COL1A1 | CTPR | |
| 5 | EFEMP1 | CTPR | |
| 6 | RPN1 | NA | |
| 7 | MYH9 | CTPR | |
| 8 | ADGRG1 | CTPR | |
| 9 | COPG1 | CTPR | |
| 10 | KATNB1 | NA |
| Drug | Rank | circRNA | Evidence |
 Cisplatin | 1 | SQSTM1 | CTPR |
| 2 | CALR | CTPR | |
| 3 | ASPH | CTPR | |
| 4 | COL6A2 | CTPR | |
| 5 | LTBP1 | CTPR | |
| 6 | VIM | CTPR | |
| 7 | WDR5 | CTPR | |
| 8 | MYADM | CTPR | |
| 9 | POLR2A | NA | |
| 10 | COL1A1 | CTPR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lei, X.; Chen, Y.; Guo, L.; Wu, F.-X. Circular RNA-Drug Association Prediction Based on Multi-Scale Convolutional Neural Networks and Adversarial Autoencoders. Int. J. Mol. Sci. 2025, 26, 1509. https://doi.org/10.3390/ijms26041509
Wang Y, Lei X, Chen Y, Guo L, Wu F-X. Circular RNA-Drug Association Prediction Based on Multi-Scale Convolutional Neural Networks and Adversarial Autoencoders. International Journal of Molecular Sciences. 2025; 26(4):1509. https://doi.org/10.3390/ijms26041509
Chicago/Turabian StyleWang, Yao, Xiujuan Lei, Yuli Chen, Ling Guo, and Fang-Xiang Wu. 2025. "Circular RNA-Drug Association Prediction Based on Multi-Scale Convolutional Neural Networks and Adversarial Autoencoders" International Journal of Molecular Sciences 26, no. 4: 1509. https://doi.org/10.3390/ijms26041509
APA StyleWang, Y., Lei, X., Chen, Y., Guo, L., & Wu, F.-X. (2025). Circular RNA-Drug Association Prediction Based on Multi-Scale Convolutional Neural Networks and Adversarial Autoencoders. International Journal of Molecular Sciences, 26(4), 1509. https://doi.org/10.3390/ijms26041509






