Expected Mitochondrial Haplotype Richness in Remaining Populations of the Critically Endangered European Mink Mustela lutreola and Its Conservation Implications
Abstract
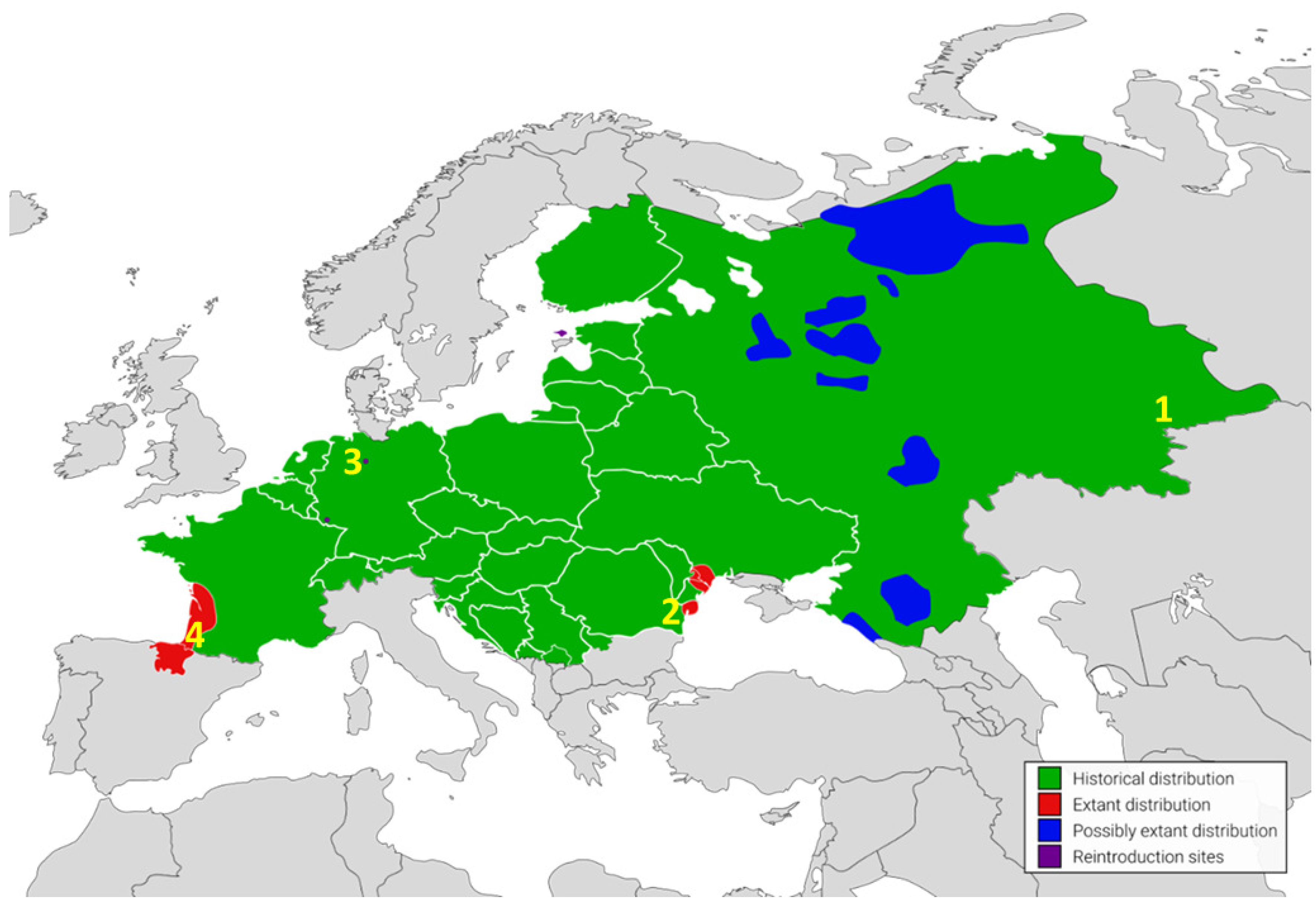
1. Introduction
2. Results
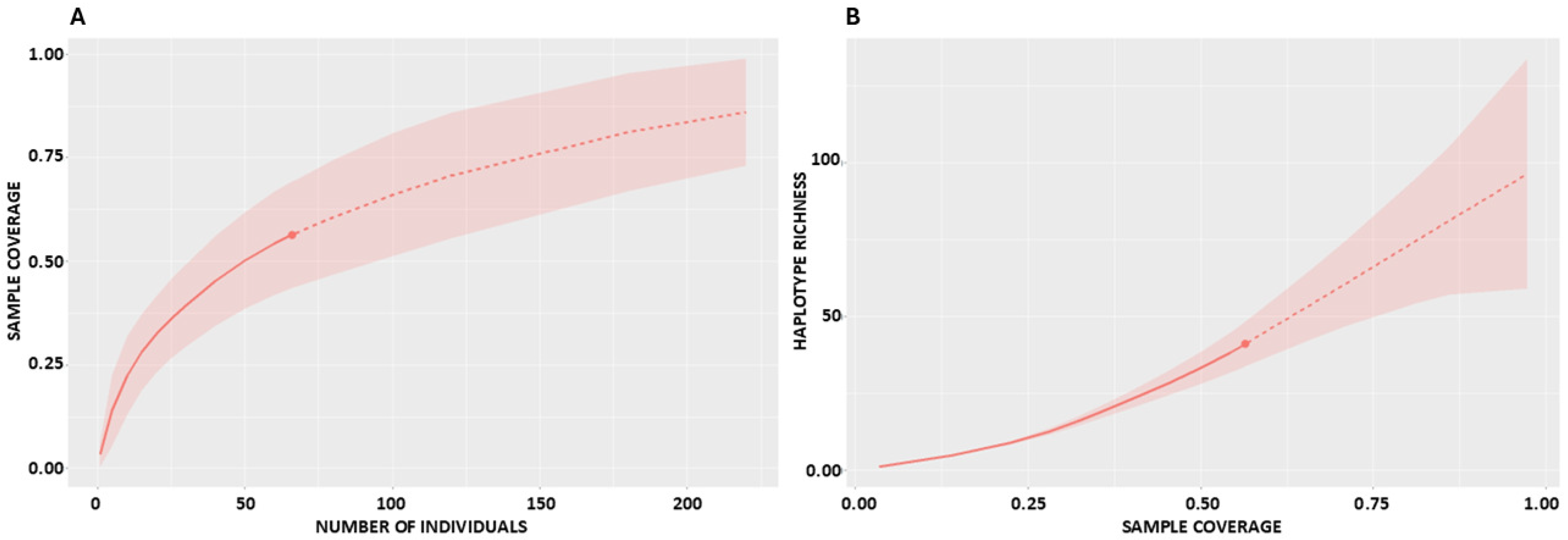
2.1. Observed and Estimated Haplotype Richness
2.2. Sampling Completeness and Coverage
2.3. Required Sample Sizes
3. Discussion
4. Materials and Methods
4.1. Sampling and Sequencing
4.2. Observed Richness and Frequency Spectrum
4.3. Diversity Estimators
4.4. Sample Coverage
4.5. Rarefaction and Extrapolation
4.6. Sample Size Requirements
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allendorf, F.W.; Luikart, G.; Aitken, S.N. Conservation and the Genetics of Populations, 2nd ed.; Wiley-Blackwell: Oxford, UK, 2010. [Google Scholar]
- Frankham, R. Genetics and extinction. Biol. Conserv. 2005, 126, 131–140. [Google Scholar] [CrossRef]
- Lindblom, L. Sample size and haplotype richness in population samples of the lichen-forming ascomycete Xanthoria parietina. Lichenologist 2009, 41, 529–535. [Google Scholar] [CrossRef]
- Cabria, M.T.; Gonzalez, E.G.; Gomez-Moliner, B.J.; Michaux, J.R.; Skumatov, D.; Kranz, A.; Fournier, P.; Palazon, S.; Zardoya, R. Patterns of genetic variation in the endangered European mink (Mustela lutreola L., 1761). BMC Evol. Biol. 2015, 15, 141. [Google Scholar] [CrossRef] [PubMed]
- Skorupski, J.; Michaux, J.; Śmietana, P. A Meta-Analytical Investigation of the Gap between Measured and Predicted Inter-Population Genetic Diversity in Species of High Conservation Concern—The Case of the Critically Endangered European Mink Mustela lutreola L., 1761. Genes 2021, 12, 1555. [Google Scholar] [CrossRef] [PubMed]
- Chao, A.; Jost, L. Coverage-based rarefaction and extrapolation: Standardizing samples by completeness rather than size. Ecology 2012, 93, 2533–2547. [Google Scholar] [CrossRef] [PubMed]
- Chao, A.; Gotelli, N.J.; Hsieh, T.C.; Sander, E.L.; Ma, K.H.; Colwell, R.K.; Ellison, A.M. Rarefaction and extrapolation with Hill numbers: A framework for sampling and estimation in species diversity studies. Ecol. Monogr. 2014, 84, 45–67. [Google Scholar] [CrossRef]
- Põdra, M.; Harrington, L.A.; Díez-León, M.; Maran, T. Mustela lutreola (Europe assessment) (Amended Version of 2025 Assessment). The IUCN Red List of Threatened Species. 2025, p. e.T14018A283655511. Available online: https://www.iucnredlist.org/species/14018/283655511 (accessed on 20 August 2025).
- Skorupski, J.; Seebass, C.; Festl, W.; Kiseleva, N.; Śmietana, P.; Marinov, M. To mix, or not to mix?: Mitogenomic insights for risk assessment of an interpopulation translocations of the critically endangered European mink. Conserv. Sci. Pract. 2025, 7, e13291. [Google Scholar] [CrossRef]
- Skorupski, J. Fifty Years of Research on European Mink Mustela lutreola L., 1761 Genetics: Where Are We Now in Studies on One of the Most Endangered Mammals? Genes 2020, 11, 1332. [Google Scholar] [CrossRef]
- Avise, J.C. Phylogeography: The History and Formation of Species; Harvard University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Michaux, J.; Libois, R.; Davison, A.; Chevret, P.; Rosoux, R. Is the western population of the European mink, (Mustela lutreola), a distinct Management Unit for conservation? Biol. Conserv. 2004, 15, 357–367. [Google Scholar] [CrossRef]
- Knaus, B.J.; Cronn, R.; Liston, A.; Pilgrim, K.; Schwartz, M.K. Mitochondrial genome sequences illuminate maternal lineages of conservation concern in a rare carnivore. BMC Ecol. 2011, 11, 10. [Google Scholar] [CrossRef]
- Ki, J.-S.; Hwang, D.-S.; Park, T.-J.; Han, S.-H.; Lee, J.-S. A comparative analysis of the complete mitochondrial genome of the Eurasian otter Lutra lutra (Carnivora; Mustelidae). Mol. Biol. Rep. 2010, 37, 1943–1955. [Google Scholar] [CrossRef]
- Etherington, G.J.; Ciezarek, A.; Shaw, R.; Michaux, J.; Croose, E.; Haerty, W.; Di Palma, F. Extensive genome introgression between domestic ferret and European polecat during population recovery in Great Britain. J. Hered. 2022, 113, 500–515. [Google Scholar] [CrossRef]
- Fisher, R.A.; Corbet, A.S.; Williams, C.B. The relation between the number of species and the number of individuals in a random sample of an animal population. J. Anim. Ecol. 1943, 12, 42–58. [Google Scholar] [CrossRef]
- Burnham, K.P.; Overton, W.S. Estimation of the size of a closed population when capture probabilities vary among animals. Biometrika 1978, 65, 625–633. [Google Scholar] [CrossRef]
- Smith, E.P.; van Belle, G. Nonparametric estimation of species richness. Biometrics 1984, 40, 119–129. [Google Scholar] [CrossRef]
- Chao, A.; Lee, S.M. Estimating the number of classes via sample coverage. J. Am. Stat. Assoc. 1992, 87, 210–217. [Google Scholar] [CrossRef]
- Chiu, C.-H.; Wang, Y.T.; Walther, B.A.; Chao, A. An improved nonparametric lower bound of species richness via a modified Good–Turing frequency formula. Biometrics 2014, 70, 671–682. [Google Scholar] [CrossRef] [PubMed]
- Bunge, J.; FitzPatrick, M. Estimating the number of species: A review. J. Am. Stat. Assoc. 1993, 88, 364–373. [Google Scholar] [CrossRef]
- Chao, A. Nonparametric estimation of the number of classes in a population. Scand. J. Stat. 1984, 11, 265–270. [Google Scholar]
- Chao, A. Estimating the population size for capture-recapture data with unequal catchability. Biometrics 1987, 43, 783–791. [Google Scholar] [CrossRef]
- Good, I.J. The population frequencies of species and the estimation of population parameters. Biometrika 1953, 40, 237–264. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Zar, J.H. Biostatistical Analysis, 5th ed.; Prentice-Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Chao, A.; Bunge, J. Estimating the Number of Species in a Stochastic Abundance Model. Biometrics 2002, 58, 531–539. [Google Scholar] [CrossRef]
- Soberón M, J.; Llorente B, J. The Use of Species Accumulation Functions for the Prediction of Species Richness. Conserv. Biol. 1993, 7, 480–488. [Google Scholar] [CrossRef]
- Magurran, A.E. Measuring Biological Diversity; Blackwell Publishing: Oxford, UK, 2004. [Google Scholar]
- Wang, J.-P.Z.; Lindsay, B.G. A penalized nonparametric maximum likelihood approach to species richness estimation. J. Am. Stat. Assoc. 2005, 100, 942–959. [Google Scholar] [CrossRef]
- Hill, M.O. Diversity and evenness: A unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Pledger, S.; Pollock, K.H.; Norris, J.L. Open capture–recapture models with heterogeneity: I. Cormack–Jolly–Seber model. Biometrics 2003, 59, 786–794. [Google Scholar] [CrossRef]
- Link, W.A.; Barker, R.J. Bayesian Inference: With Ecological Applications; Academic Press: London, UK, 2009. [Google Scholar]
- Hsieh, T.C.; Ma, K.H.; Chao, A. iNEXT: An R package for interpolation and extrapolation of species diversity (Hill numbers). Methods Ecol. Evol. 2016, 7, 1451–1456. [Google Scholar] [CrossRef]
- Hilbe, J.M. Negative Binomial Regression, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Colwell, R.K.; Chao, A.; Gotelli, N.J.; Lin, S.Y.; Mao, C.X.; Chazdon, R.L.; Longino, J.T. Models and estimators linking individual-based and sample-based rarefaction, extrapolation and comparison of assemblages. J. Plant Ecol. 2012, 5, 3–21. [Google Scholar] [CrossRef]
- Chao, A.; Chiu, C.-H. Species Richness: Estimation and Comparison. In Wiley StatsRef: Statistics Reference Online; Balakrishnan, N., Colton, T., Everitt, B., Piegorsch, W., Ruggeri, F., Teugels, J.L., Eds.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Petit, R.J.; El Mousadik, A.; Pons, O. Identifying populations for conservation on the basis of genetic markers. Conserv. Biol. 1998, 12, 844–855. [Google Scholar] [CrossRef]
- Michaux, J.; Hardy, O.; Justy, F.; Fournier, P.; Kranz, A.; Cabria, M.; Davison, A.; Rosoux, R.; Libois, R. Conservation genetics and population history of the threatened European mink Mustela lutreola, with an emphasis on the West European population. Mol. Ecol. 2005, 14, 2373–2388. [Google Scholar] [CrossRef]
- Maran, T.; Põdra, M.; Harrington, L.A.; Macdonald, D.W. European Mink: Restoration Attempts for a Species on the Brink of Extinction. In Biology and Conservation of Musteloids; Macdonald, D.W., Newman, C., Harrington, L.A., Eds.; Oxford University Press: Oxford, UK, 2017; pp. 287–307. [Google Scholar]
- Hoban, S.; Arntzen, J.A.; Bruford, M.W.; Godoy, J.A.; Rus Hoelzel, A.; Segelbacher, G.; Vilà, C.; Bertorelle, G. Comparative evaluation of potential indicators and temporal sampling protocols for monitoring genetic erosion. Evol. Appl. 2014, 7, 984–998. [Google Scholar] [CrossRef]
- Skorupski, J.; Brandes, F.; Seebass, C.; Festl, W.; Śmietana, P.; Balacco, J.; Jain, N.; Tilley, T.; Abueg, L.; Wood, J.; et al. Prioritizing Endangered Species in Genome Sequencing: Conservation Genomics in Action with the First Platinum-Standard Reference-Quality Genome of the Critically Endangered European Mink Mustela lutreola L., 1761. Int. J. Mol. Sci. 2023, 24, 14816. [Google Scholar] [CrossRef]
- Chenna, R.; Sugawara, H.; Koike, T.; Lopez, R.; Gibson, T.J.; Higgins, D.G.; Thompson, J.D. Multiple sequence alignment with the Clustal series of programs. Nucleic Acids Res. 2003, 31, 3497–3500. [Google Scholar] [CrossRef]
- Skorupski, J. Characterisation of the Complete Mitochondrial Genome of Critically Endangered Mustela lutreola (Carnivora: Mustelidae) and Its Phylogenetic and Conservation Implications. Genes 2022, 13, 125. [Google Scholar] [CrossRef] [PubMed]
- Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009; Available online: https://www.python.org/ (accessed on 2 November 2024).
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference (SciPy 2010), Austin, TX, USA, 28 June–3 July 2010; pp. 51–56. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272, Erratum in Nat. Methods 2020, 17, 352. https://doi.org/10.1038/s41592-020-0772-5. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury Press: Pacific Grove, CA, USA, 2002. [Google Scholar]
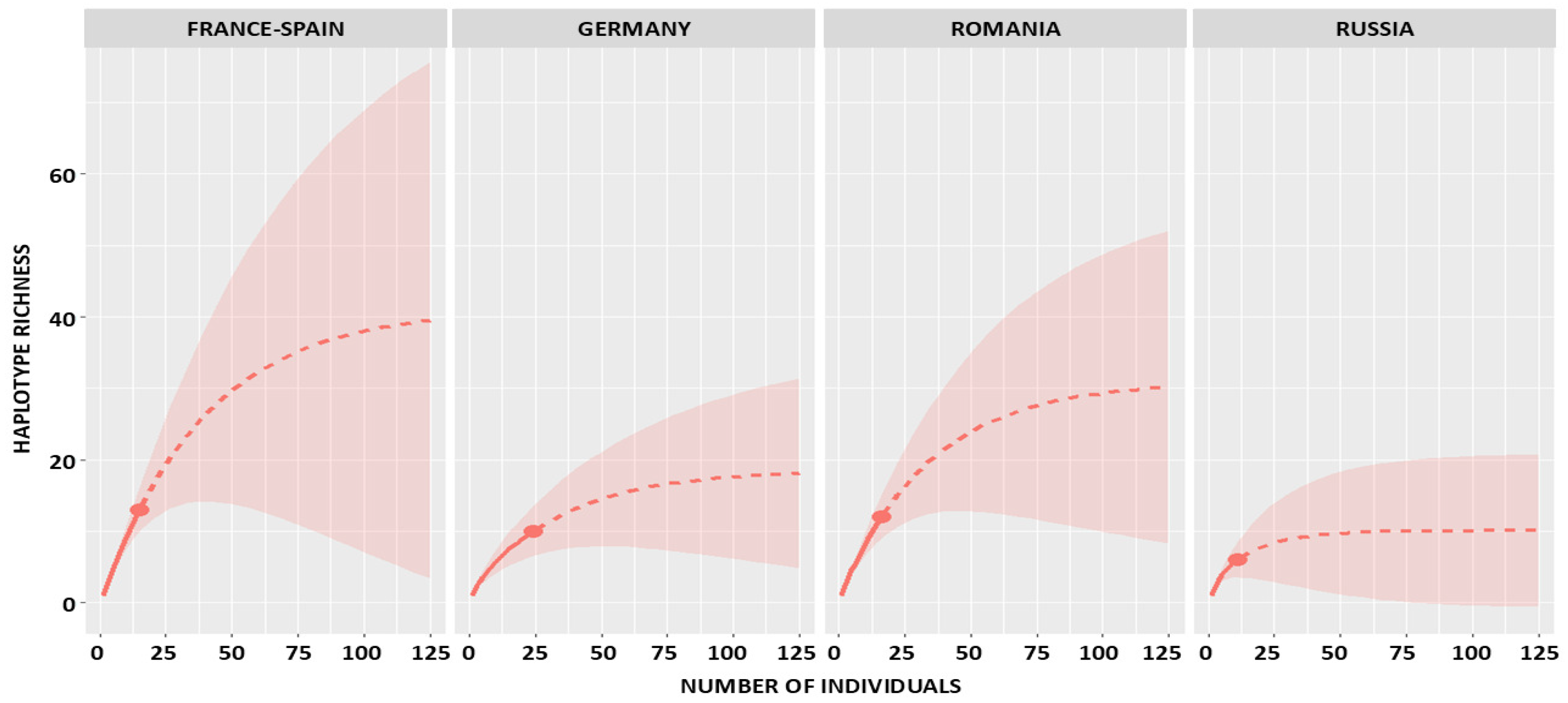

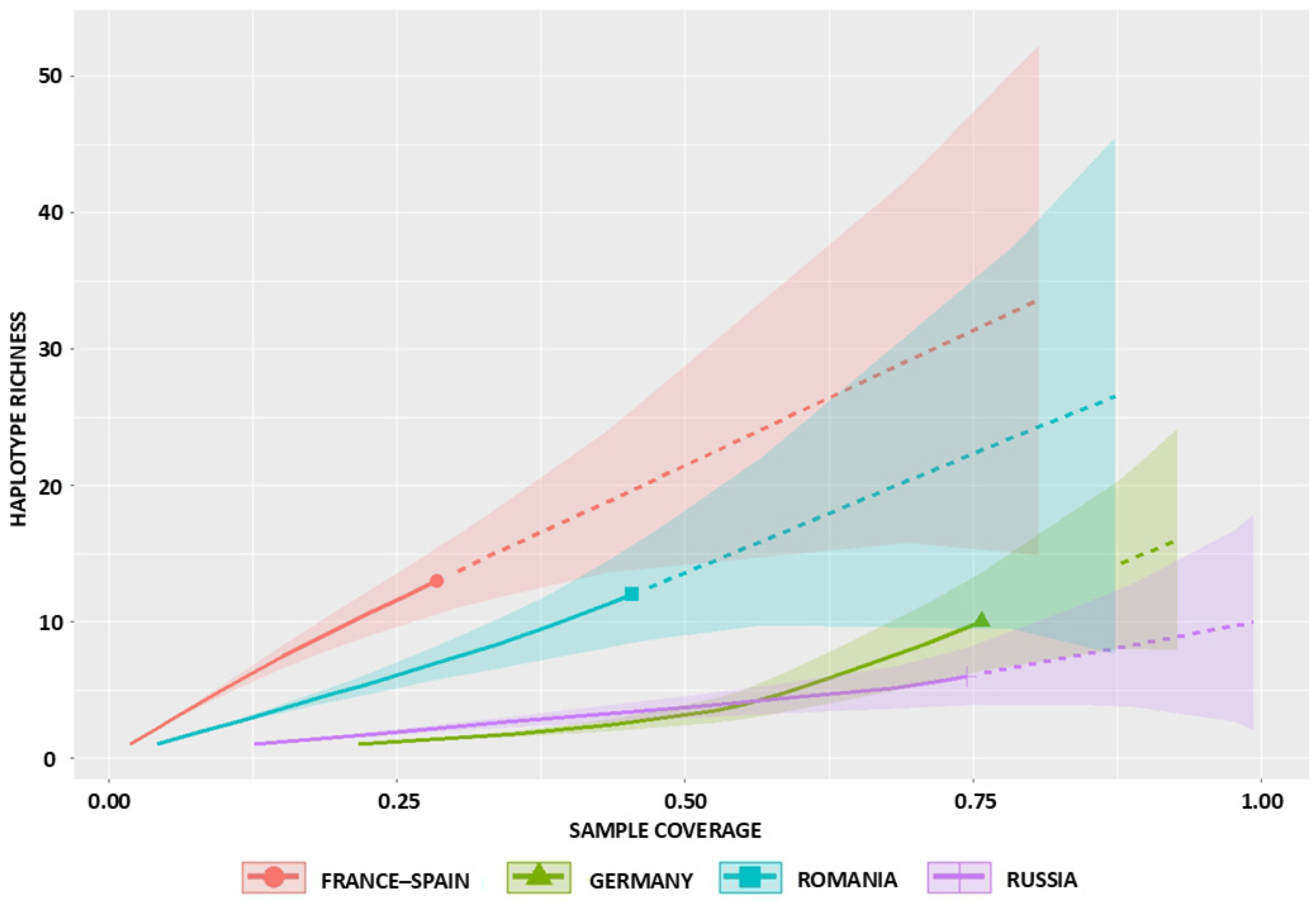
| Population | n | ho | hr | ha | nr | f1 | f2 | iNEXT (CI0.95) | ACE (CI0.95) | Jackknife1 (CI0.95) | Bootstrap (CI0.95) | Fisher’s α (CI0.95) | SC (CI0.95) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Russia | 11 | 6 | 6 | 0 | 11 | 3 | 1 | 10.09 (6.45–43.40) | 8.46 (6.20–12.8) | 8.73 (6.10–10.50) | 7.22 (6.00–8.40) | 5.40 (3.10–8.20) | 0.74 (0.64–1.00) |
| Romania | 16 | 12 | 12 | 0 | 16 | 9 | 2 | 30.98 (15.72–108.90) | 30.37 (21.00–42.30) | 20.44 (16.50–24.30) | 15.48 (13.50–17.60) | 21.81 (15.50–30.20) | 0.45 (0.31–0.66) |
| Germany | 24 | 10 | 9 | 1 | 13 | 6 | 2 | 18.63 (11.45–61.17) | 18.51 (14.20–24.60) | 15.75 (13.50–18.60) | 12.45 (11.00–14.30) | 6.44 (4.40–9.10) | 0.76 (0.58–0.93) |
| France-Spain | 15 | 13 | 13 | 0 | 15 | 11 | 2 | 41.23 (18.88–148.66) | 48.75 (33.20–68.80) | 23.27 (19.00–27.50) | 17.14 (15.20–19.30) | 46.48 (31.50–67.20) | 0.29 (0.18–0.39) |
| TOTAL | 66 | 41 | 40 | 1 | 55 | 29 | 7 | 100.16 (62.75–201.90) | 90.68 (65.70–126.80) | 69.56 (56.40–84.70) | 52.69 (46.10–60.00) | 46.22 (33.40–64.10) | 0.56 (0.47–0.65) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skorupski, J.; Śmietana, P.; Seebass, C.; Festl, W.; Vasile, A.; Kiseleva, N.; Brandes, F.; Marinov, M. Expected Mitochondrial Haplotype Richness in Remaining Populations of the Critically Endangered European Mink Mustela lutreola and Its Conservation Implications. Int. J. Mol. Sci. 2025, 26, 9935. https://doi.org/10.3390/ijms26209935
Skorupski J, Śmietana P, Seebass C, Festl W, Vasile A, Kiseleva N, Brandes F, Marinov M. Expected Mitochondrial Haplotype Richness in Remaining Populations of the Critically Endangered European Mink Mustela lutreola and Its Conservation Implications. International Journal of Molecular Sciences. 2025; 26(20):9935. https://doi.org/10.3390/ijms26209935
Chicago/Turabian StyleSkorupski, Jakub, Przemysław Śmietana, Christian Seebass, Wolfgang Festl, Alexe Vasile, Natalia Kiseleva, Florian Brandes, and Mihai Marinov. 2025. "Expected Mitochondrial Haplotype Richness in Remaining Populations of the Critically Endangered European Mink Mustela lutreola and Its Conservation Implications" International Journal of Molecular Sciences 26, no. 20: 9935. https://doi.org/10.3390/ijms26209935
APA StyleSkorupski, J., Śmietana, P., Seebass, C., Festl, W., Vasile, A., Kiseleva, N., Brandes, F., & Marinov, M. (2025). Expected Mitochondrial Haplotype Richness in Remaining Populations of the Critically Endangered European Mink Mustela lutreola and Its Conservation Implications. International Journal of Molecular Sciences, 26(20), 9935. https://doi.org/10.3390/ijms26209935









