Resonant Oscillations of Ion-Stabilized Nanobubbles in Water as a Possible Source of Electromagnetic Radiation in the Gigahertz Range
Abstract
1. Introduction
- the state and probable role of nanobubbles, which are defects in the hydrogen-bond network and contain atmospheric gases, including carbon dioxide, the hydration of which produces bicarbonate ions;
- the nature and concentration of the sources of electromagnetic radiation depending on the vibrational treatment; and
- the ability of aqueous solutions to emit electromagnetic radiation upon shaking.
2. Results
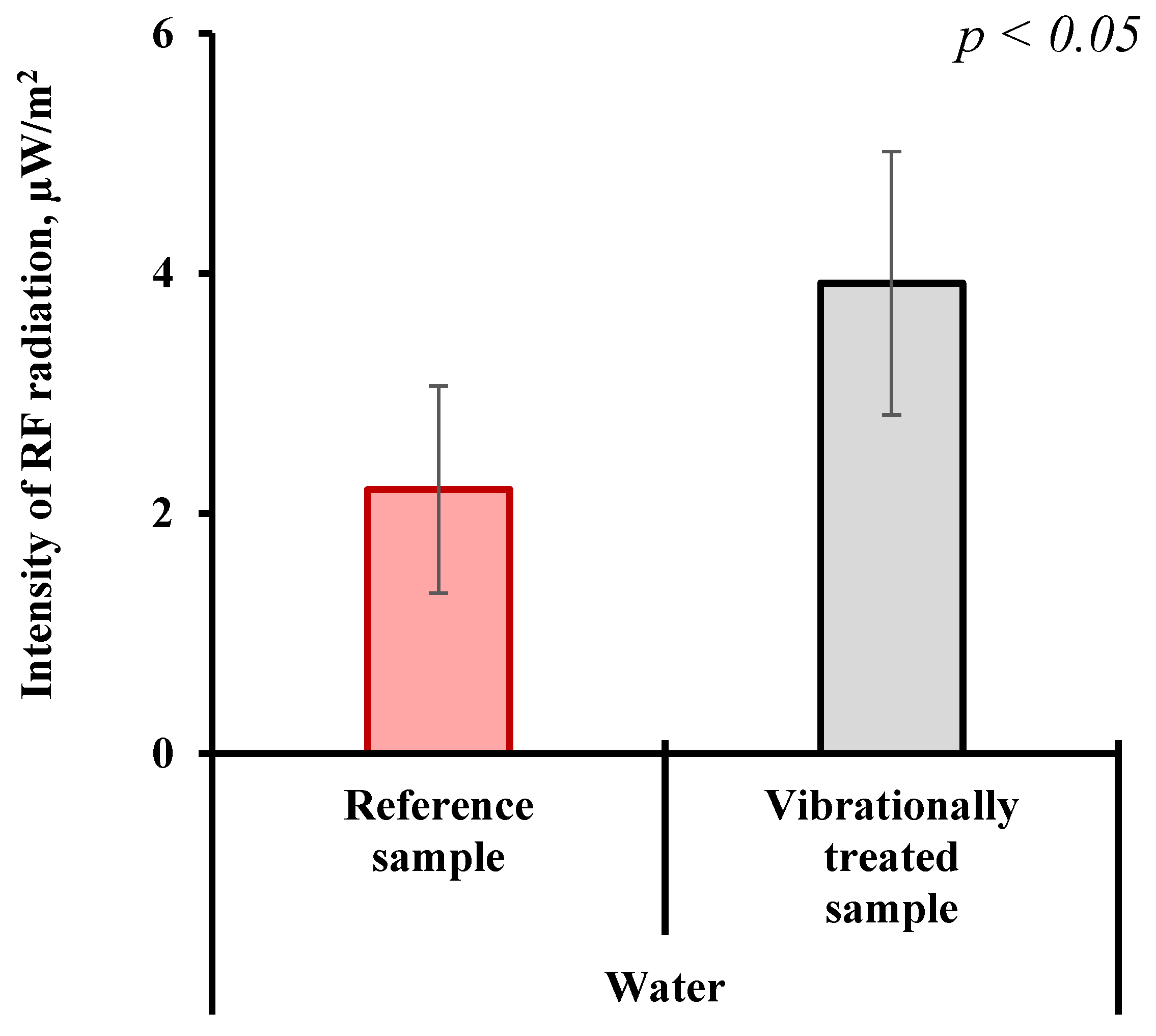
2.1. Experimental Results
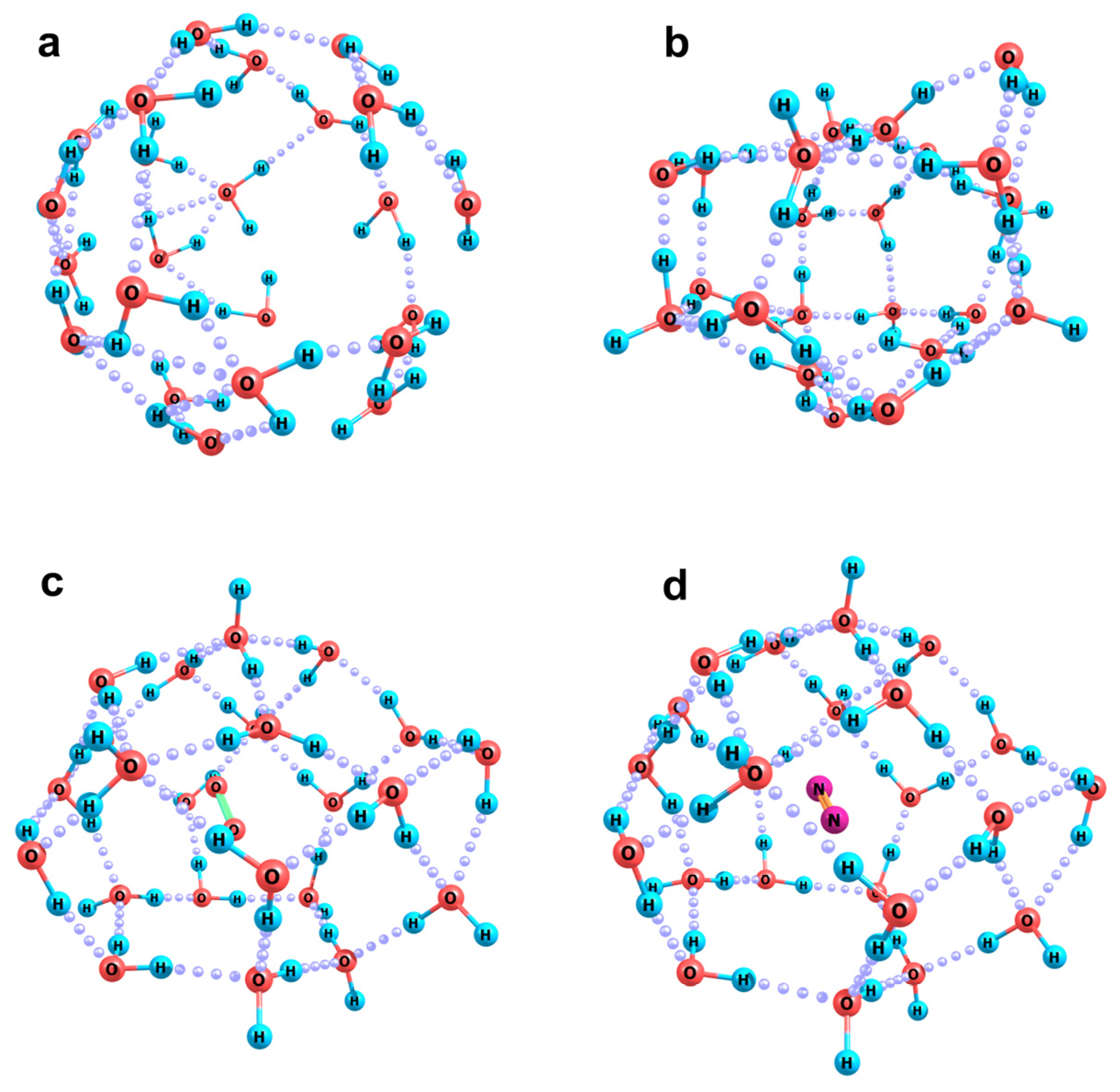
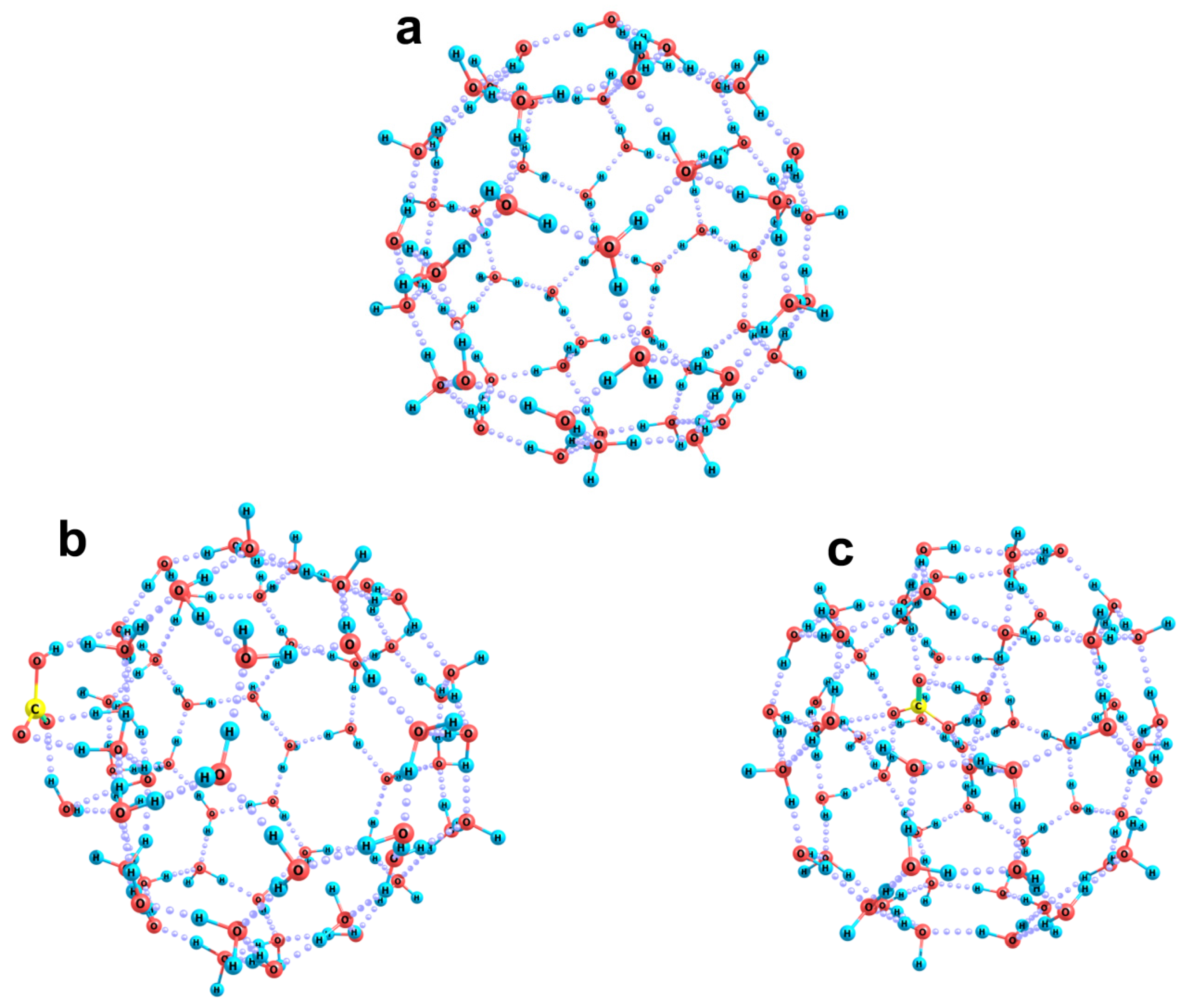
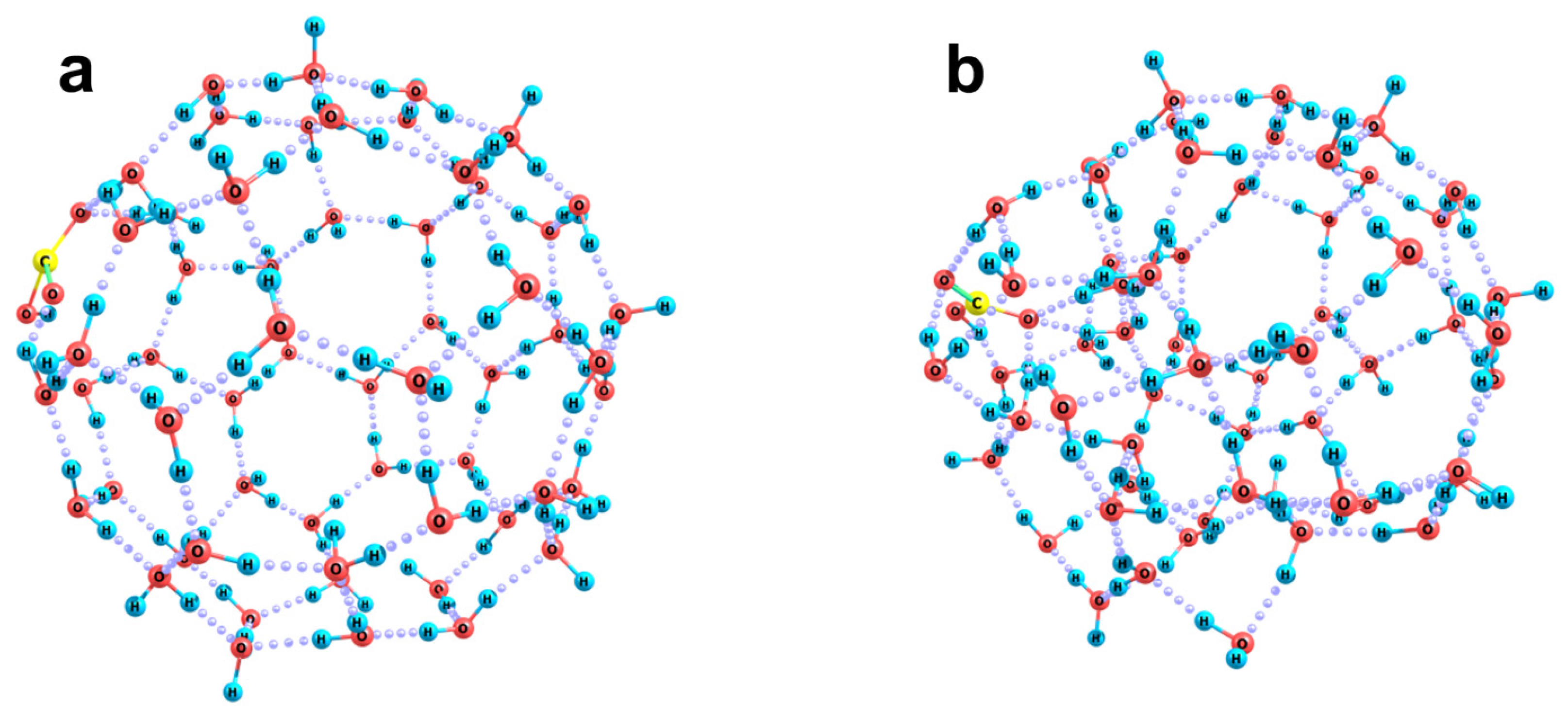
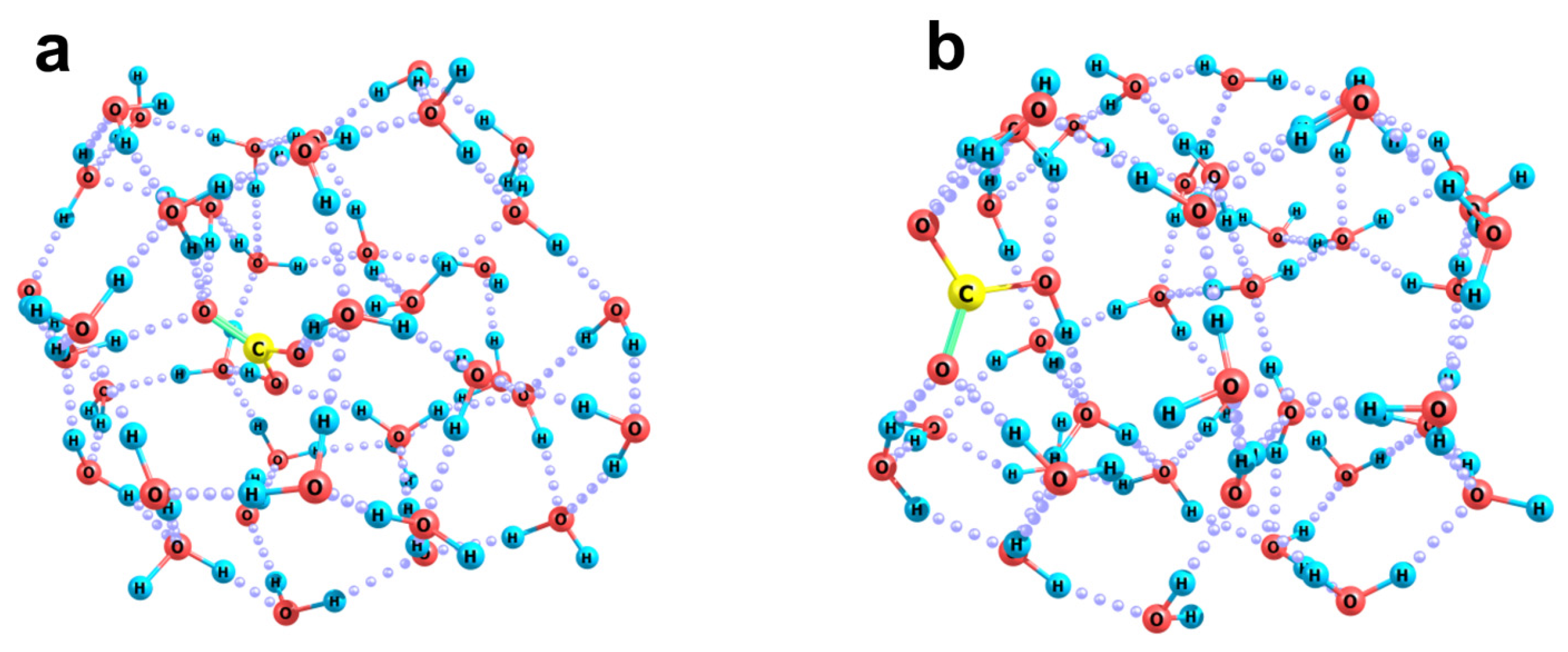
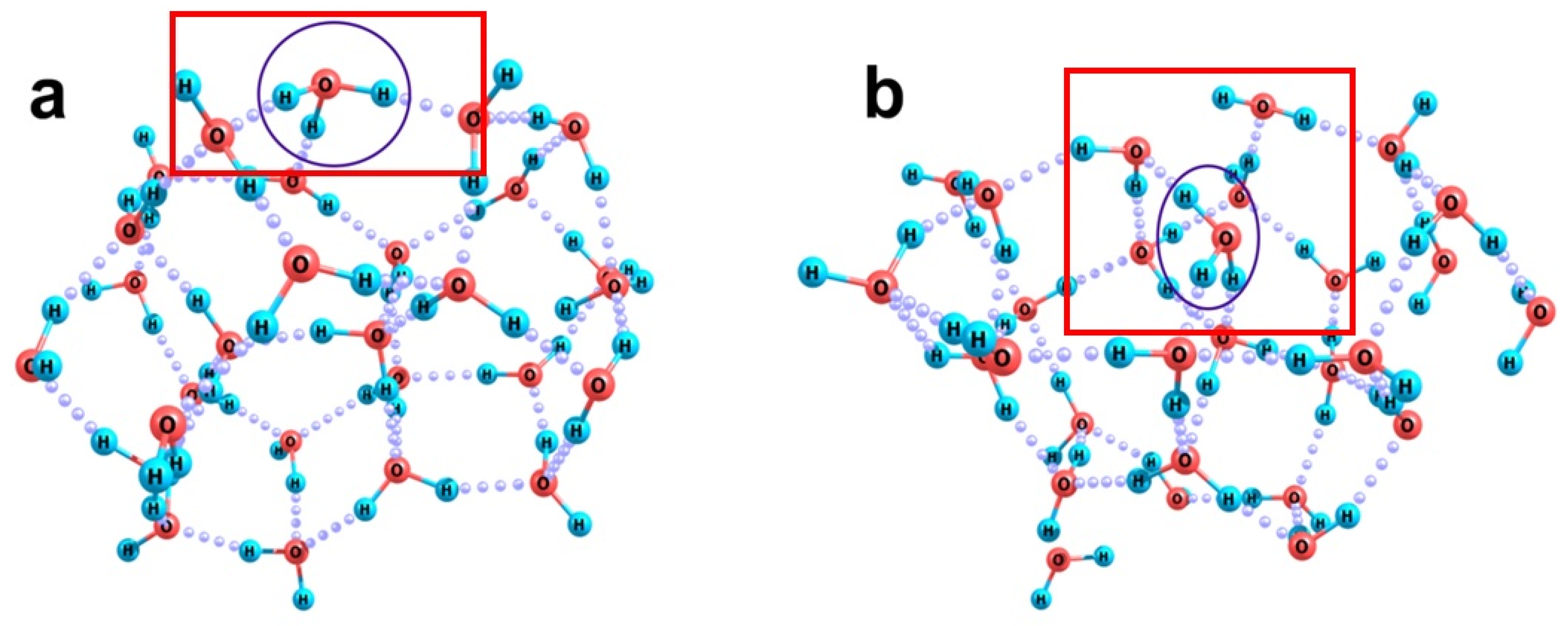
2.2. Quantum Chemical Modeling: The State of Hydronium and Bicarbonate Ions in the Nanobubble Shells
| (H2O)23 | O2(H2O)23 | N2(H2O)23 | |
| Surface area, Å2 | 551 | 597 | 601 |
| Volume, Å3 | 383 | 407 | 410 |
3. Discussion
3.1. Stability of Nanobubbles: Bubbles Stabilized by Ions
3.2. Possible Electromagnetic Radiation of Bubble Compound Species
3.2.1. Model 1: Oscillations Promoted by a Periodic External Force
3.2.2. Model 2: Oscillations Caused by Thermal Motion of Particles in the Environment
4. Materials and Methods
4.1. Sample Preparation
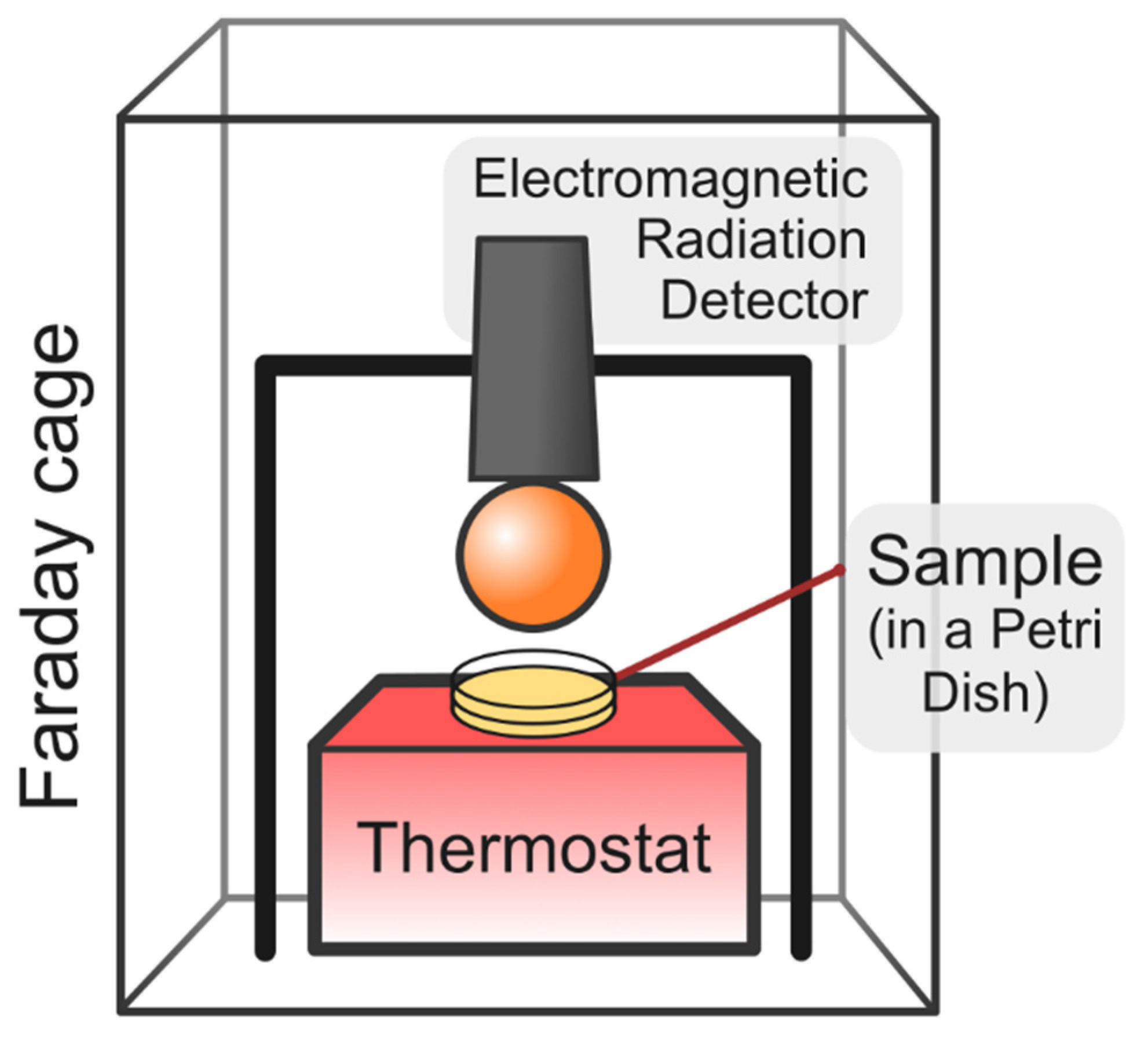
4.2. Dynamic Light Scattering Measurements of the Volume Number Density of Nanobubbles and Water Radiometry
4.3. Quantum-Chemical Simulations of Ionic Clusters Within the Surface Layers of Water Molecules
4.4. Experimental Data Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vladimirov, Y.A.; Proskurnina, E.V. Free Radicals and Cell Chemiluminescence. Biochem. Mosc. 2009, 74, 1545–1566. [Google Scholar] [CrossRef] [PubMed]
- Gudkov, S.V.; Bruskov, V.I.; Astashev, M.E.; Chernikov, A.V.; Yaguzhinsky, L.S.; Zakharov, S.D. Oxygen-Dependent Auto-Oscillations of Water Luminescence Triggered by the 1264 Nm Radiation. J. Phys. Chem. B 2011, 115, 7693–7698. [Google Scholar] [CrossRef] [PubMed]
- Pospíšil, P.; Prasad, A.; Rác, M. Role of Reactive Oxygen Species in Ultra-Weak Photon Emission in Biological Systems. J. Photochem. Photobiol. B Biol. 2014, 139, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Gudkov, S.; Astashev, M.; Bruskov, V.; Kozlov, V.; Zakharov, S.; Bunkin, N. Self-Oscillating Water Chemiluminescence Modes and Reactive Oxygen Species Generation Induced by Laser Irradiation; Effect of the Exclusion Zone Created by Nafion. Entropy 2014, 16, 6166–6185. [Google Scholar] [CrossRef] [PubMed]
- Lee, J. Perspectives on Bioluminescence Mechanisms. Photochem. Photobiol. 2017, 93, 389–404. [Google Scholar] [CrossRef] [PubMed]
- Vacher, M.; Fdez Galván, I.; Ding, B.-W.; Schramm, S.; Berraud-Pache, R.; Naumov, P.; Ferré, N.; Liu, Y.-J.; Navizet, I.; Roca-Sanjuán, D.; et al. Chemi-and Bioluminescence of Cyclic Peroxides. Chem. Rev. 2018, 118, 6927–6974. [Google Scholar] [CrossRef] [PubMed]
- Cifra, M.; Fields, J.Z.; Farhadi, A. Electromagnetic Cellular Interactions. Prog. Biophys. Mol. Biol. 2011, 105, 223–246. [Google Scholar] [CrossRef] [PubMed]
- Harvey, E.N. A History of Luminescence from the Earliest Times Until 1900; American Philosophical Society: Philadelphia, PA, USA, 1957. [Google Scholar]
- Volodyaev, I.; Beloussov, L.V. Revisiting the Mitogenetic Effect of Ultra-Weak Photon Emission. Front. Physiol. 2015, 6, 241. [Google Scholar] [CrossRef] [PubMed]
- Gurwitsch, A.G. Die Natur Des Spezifischen Erregers Der Zellteilung. Arch. Mikrosk. Anat. Entwicklungsmechanik 1923, 100, 11–40. [Google Scholar] [CrossRef]
- Frank, G.M.; Gurwitsch, A. Zur Frage der Identität mitogenetischer und ultravioletter Strahlen. Wilhelm Roux’Archiv Entwicklungsmechanik Org. 1927, 109, 451–454. [Google Scholar] [CrossRef] [PubMed]
- Popp, F.A.; Chang, J.J.; Herzog, A.; Yan, Z.; Yan, Y. Evidence of Non-Classical (Squeezed) Light in Biological Systems. Phys. Lett. A 2002, 293, 98–102. [Google Scholar] [CrossRef]
- Bajpai, R.P. Coherent Nature of the Radiation Emitted in Delayed Luminescence of Leaves. J. Theor. Biol. 1999, 198, 287–299. [Google Scholar] [CrossRef] [PubMed]
- Astashev, M.E.; Serov, D.A.; Sarimov, R.M.; Gudkov, S.V. Influence of the Vibration Impact Mode on the Spontaneous Chemiluminescence of Aqueous Protein Solutions. Phys. Wave Phen. 2023, 31, 189–199. [Google Scholar] [CrossRef]
- Montagnier, L.; Del Giudice, E.; Aïssa, J.; Lavallee, C.; Motschwiller, S.; Capolupo, A.; Polcari, A.; Romano, P.; Tedeschi, A.; Vitiello, G. Transduction of DNA Information through Water and Electromagnetic Waves. Electromagn. Biol. Med. 2015, 34, 106–112. [Google Scholar] [CrossRef] [PubMed]
- Petrova, A.; Tarasov, S.; Gorbunov, E.; Stepanov, G.; Fartushnaya, O.; Zubkov, E.; Molodtsova, I.; Boriskin, V.; Zatykina, A.; Smirnov, A.; et al. Phenomenon of Post-Vibration Interactions. Symmetry 2024, 16, 958. [Google Scholar] [CrossRef]
- Adams, M.H. Surface Inactivation of Bacterial Viruses and of Proteins. Substantia 2023, 7, 67–78. [Google Scholar] [CrossRef]
- Novikov, V.V.; Yablokova, E.V.; Shaev, I.A.; Novikova, N.I.; Fesenko, E.E. A Decrease in the Background Production of Reactive Oxygen Species by Neutrophils after the Action of Hypomagnetic Field Is Not Accompanied by a Violation of Their Chemiluminescent Response to Respiratory Burst Activators. Biophysics 2023, 68, 978–983. [Google Scholar] [CrossRef]
- Shaev, I.A.; Novikov, V.V.; Yablokova, E.V.; Fesenko, E.E. A Brief Review of the Current State of Research on the Biological Effects of Weak Magnetic Fields. Biophysics 2022, 67, 245–251. [Google Scholar] [CrossRef]
- Ninham, B.W.; Bunkin, N.; Battye, M. The Endothelial Surface Layer-Glycocalyx-Universal Nano-Infrastructure Is Fundamental to Physiology, Cell Traffic and a Complementary Neural Network. Adv. Colloid Interface Sci. 2025, 338, 103401. [Google Scholar] [CrossRef] [PubMed]
- Craig, V.S.J.; Ninham, B.W.; Pashley, R.M. The Effect of Electrolytes on Bubble Coalescence in Water. J. Phys. Chem. 1993, 97, 10192–10197. [Google Scholar] [CrossRef]
- Nafi, A.W.; Taseidifar, M.; Pashley, R.M.; Ninham, B.W. The Effect of Amino Acids on Bubble Coalescence in Aqueous Solution. J. Mol. Liq. 2023, 369, 120963. [Google Scholar] [CrossRef]
- Henry, C.L.; Craig, V.S.J. Inhibition of Bubble Coalescence by Osmolytes: Sucrose, Other Sugars, and Urea. Langmuir 2009, 25, 11406–11412. [Google Scholar] [CrossRef] [PubMed]
- Ninham, B.W.; Lo Nostro, P. Unexpected Properties of Degassed Solutions. J. Phys. Chem. B 2020, 124, 7872–7878. [Google Scholar] [CrossRef] [PubMed]
- Ninham, B.W.; Pashley, R.M.; Nostro, P.L. Surface Forces: Changing Concepts and Complexity with Dissolved Gas, Bubbles, Salt and Heat. Curr. Opin. Colloid Interface Sci. 2017, 27, 25–32. [Google Scholar] [CrossRef]
- Strasberg, M. Onset of Ultrasonic Cavitation in Tap Water. J. Acoust. Soc. Am. 1959, 31, 163–176. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-1-107-64476-2. [Google Scholar]
- Azevedo, A.; Etchepare, R.; Calgaroto, S.; Rubio, J. Aqueous Dispersions of Nanobubbles: Generation, Properties and Features. Miner. Eng. 2016, 94, 29–37. [Google Scholar] [CrossRef]
- Kaye, G.W.C.; Laby, T.H. Tables of Physical and Chemical Constants, and Some Mathematical Functions. Nature 1921, 107, 264. [Google Scholar] [CrossRef]
- Kimura, T.; Yamazaki, Y. Effects of CO2 Concentration and Electric Current on the Ionic Conductivity of Anion Exchange Membranes for Fuel Cells. Electrochemistry 2011, 79, 94–97. [Google Scholar] [CrossRef]
- Garrido Sanchis, A.; Ninham, B.; Taseidifar, M.; Pashley, R. Reusing CO2 for the Sustainable Development of Several New Technologies. J. Environ. Chem. Eng. 2025, 13, 115683. [Google Scholar] [CrossRef]
- Yan, X.; Delgado, M.; Aubry, J.; Gribelin, O.; Stocco, A.; Boisson-Da Cruz, F.; Bernard, J.; Ganachaud, F. Central Role of Bicarbonate Anions in Charging Water/Hydrophobic Interfaces. J. Phys. Chem. Lett. 2018, 9, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Bunkin, N.F.; Shkirin, A.V.; Ignatiev, P.S.; Chaikov, L.L.; Burkhanov, I.S.; Starosvetskij, A.V. Nanobubble Clusters of Dissolved Gas in Aqueous Solutions of Electrolyte. I. Experimental proof. J. Chem. Phys. 2012, 137, 054706. [Google Scholar] [CrossRef] [PubMed]
- Bunkin, N.F.; Shkirin, A.V.; Suyazov, N.V.; Babenko, V.A.; Sychev, A.A.; Penkov, N.V.; Belosludtsev, K.N.; Gudkov, S.V. Formation and Dynamics of Ion-Stabilized Gas Nanobubble Phase in the Bulk of Aqueous NaCl Solutions. J. Phys. Chem. B 2016, 120, 1291–1303. [Google Scholar] [CrossRef] [PubMed]
- Lyashchenko, A.K.; Efimov, A.Y.; Dunyashev, V.S. Radiation of Aqueous Solutions of Non-Electrolytes in the Millimeter Range of the Spectrum and Their Dielectric Properties. Russ. J. Phys. Chem. 2021, 95, 713–716. [Google Scholar] [CrossRef]
- Lyashchenko, A.K.; Karataeva, I.M.; Kozmin, A.S.; Betskii, O.V. Radio Brightness Contrasts and Radiation of Aqueous Salt Solutions in the Millimeter Spectral Range. Dokl. Phys. Chem. 2015, 462, 127–130. [Google Scholar] [CrossRef]
- Epstein, P.S.; Plesset, M.S. On the Stability of Gas Bubbles in Liquid-Gas Solutions. J. Chem. Phys. 1950, 18, 1505–1509. [Google Scholar] [CrossRef]
- Ljunggren, S.; Eriksson, J.C. The Lifetime of a Colloid-Sized Gas Bubble in Water and the Cause of the Hydrophobic Attraction. Colloids Surf. A Physicochem. Eng. Asp. 1997, 129–130, 151–155. [Google Scholar] [CrossRef]
- Yakovlev, E.V.; Kryuchkov, N.P.; Gorbunov, E.A.; Zotov, A.K.; Ovcharov, P.V.; Yurchenko, S.O. The Influence of Salt Concentration on the Dissolution of Microbubbles in Bulk Aqueous Electrolyte Solutions. J. Chem. Phys. 2024, 161, 144704. [Google Scholar] [CrossRef] [PubMed]
- Alheshibri, M.; Qian, J.; Jehannin, M.; Craig, V.S.J. A History of Nanobubbles. Langmuir 2016, 32, 11086–11100. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Wang, S.; Zhang, L.; Hu, J. Generation and Stability of Bulk Nanobubbles: A Review and Perspective. Curr. Opin. Colloid Interface Sci. 2021, 53, 101439. [Google Scholar] [CrossRef]
- Nirmalkar, N.; Pacek, A.W.; Barigou, M. On the Existence and Stability of Bulk Nanobubbles. Langmuir 2018, 34, 10964–10973. [Google Scholar] [CrossRef] [PubMed]
- Tan, B.H.; An, H.; Ohl, C.-D. How Bulk Nanobubbles Might Survive. Phys. Rev. Lett. 2020, 124, 134503. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhou, L.; Gao, Y. Can Bulk Nanobubbles Be Stabilized by Electrostatic Interaction? Phys. Chem. Chem. Phys. 2021, 23, 16501–16505. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Wu, W.; Sun, W.; Wang, B. Understanding the Stabilization of a Bulk Nanobubble: A Molecular Dynamics Analysis. Langmuir 2021, 37, 11281–11291. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lohse, D. Minimum Current for Detachment of Electrolytic Bubbles. J. Fluid. Mech. 2023, 975, R3. [Google Scholar] [CrossRef]
- Parsons, D.F.; Ninham, B.W. Surface Charge Reversal and Hydration Forces Explained by Ionic Dispersion Forces and Surface Hydration. Colloids Surf. A Physicochem. Eng. Asp. 2011, 383, 2–9. [Google Scholar] [CrossRef]
- Ninham, B.W.; Duignan, T.T.; Parsons, D.F. Approaches to Hydration, Old and New: Insights through Hofmeister Effects. Curr. Opin. Colloid Interface Sci. 2011, 16, 612–617. [Google Scholar] [CrossRef]
- Duignan, T.T.; Parsons, D.F.; Ninham, B.W. Ion Interactions with the Air–Water Interface Using a Continuum Solvent Model. J. Phys. Chem. B 2014, 118, 8700–8710. [Google Scholar] [CrossRef] [PubMed]
- Duignan, T.T.; Parsons, D.F.; Ninham, B.W. Collins’s Rule, Hofmeister Effects and Ionic Dispersion Interactions. Chem. Phys. Lett. 2014, 608, 55–59. [Google Scholar] [CrossRef]
- Yurchenko, S.O.; Shkirin, A.V.; Ninham, B.W.; Sychev, A.A.; Babenko, V.A.; Penkov, N.V.; Kryuchkov, N.P.; Bunkin, N.F. Ion-Specific and Thermal Effects in the Stabilization of the Gas Nanobubble Phase in Bulk Aqueous Electrolyte Solutions. Langmuir 2016, 32, 11245–11255. [Google Scholar] [CrossRef] [PubMed]
- Kelsall, G.H.; Tang, S.; Yurdakul, S.; Smith, A.L. Electrophoretic Behaviour of Bubbles in Aqueous Electrolytes. J. Chem. Soc. Faraday Trans. 1996, 92, 3887–3893. [Google Scholar] [CrossRef]
- Mucha, M.; Frigato, T.; Levering, L.M.; Allen, H.C.; Tobias, D.J.; Dang, L.X.; Jungwirth, P. Unified Molecular Picture of the Surfaces of Aqueous Acid, Base, and Salt Solutions. J. Phys. Chem. B 2005, 109, 7617–7623. [Google Scholar] [CrossRef] [PubMed]
- Bunkin, N.F.; Bunkin, F.V. Bubston Structure of Water and Electrolyte Aqueous Solutions. Physics-Uspekhi 2016, 59, 846–865. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Babenko, V.A.; Sychev, A.A. Nonlinear Light Scattering Spectra in Water: Dependence on the Content of Dissolved Gas and Effects of Non-stationarity. J. Raman Spectrosc. 2022, 53, 1070–1080. [Google Scholar] [CrossRef]
- Babenko, V.A.; Bunkin, N.F.; Sychev, A.A. Role of Gas Nanobubbles in Nonlinear Hyper-Raman Scattering of Light in Water. J. Opt. Soc. Am. B 2020, 37, 2805. [Google Scholar] [CrossRef]
- Parmar, R.; Majumder, S.K. Microbubble Generation and Microbubble-Aided Transport Process Intensification—A State-of-the-Art Report. Chem. Eng. Process. Process Intensif. 2013, 64, 79–97. [Google Scholar] [CrossRef]
- Terasaka, K.; Hirabayashi, A.; Nishino, T.; Fujioka, S.; Kobayashi, D. Development of Microbubble Aerator for Waste Water Treatment Using Aerobic Activated Sludge. Chem. Eng. Sci. 2011, 66, 3172–3179. [Google Scholar] [CrossRef]
- Ulatowski, K.; Sobieszuk, P.; Mróz, A.; Ciach, T. Stability of Nanobubbles Generated in Water Using Porous Membrane System. Chem. Eng. Process.-Process Intensif. 2019, 136, 62–71. [Google Scholar] [CrossRef]
- Hu, L.; Xia, Z. Application of Ozone Micro-Nano-Bubbles to Groundwater Remediation. J. Hazard. Mater. 2018, 342, 446–453. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Hu, L.; Xia, Z. Impact of Groundwater Salinity on Bioremediation Enhanced by Micro-Nano Bubbles. Materials 2013, 6, 3676–3687. [Google Scholar] [CrossRef] [PubMed]
- Pourkarimi, Z.; Rezai, B.; Noaparast, M. Effective Parameters on Generation of Nanobubbles by Cavitation Method for Froth Flotation Applications. Physicochem. Probl. Miner. Process. 2017, 53, 920–942. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Shkirin, A.V.; Penkov, N.V.; Goltayev, M.V.; Ignatiev, P.S.; Gudkov, S.V.; Izmailov, A.Y. Effect of Gas Type and Its Pressure on Nanobubble Generation. Front. Chem. 2021, 9, 630074. [Google Scholar] [CrossRef] [PubMed]
- Bunkin, N.F.; Shkirin, A.V.; Ninham, B.W.; Chirikov, S.N.; Chaikov, L.L.; Penkov, N.V.; Kozlov, V.A.; Gudkov, S.V. Shaking-Induced Aggregation and Flotation in Immunoglobulin Dispersions: Differences between Water and Water–Ethanol Mixtures. ACS Omega 2020, 5, 14689–14701. [Google Scholar] [CrossRef] [PubMed]
- Stern, O. The Theory of the Electrolytic Double-Layer. Z. Elektrochem. 1924, 30, 1014–1020. [Google Scholar]
- Landau, L.D.; Lifšic, E.M.; Pitaevskij, L.P.; Sykes, J.B.; Kearsley, M.J. Statistical Physics. In Course of Theoretical Physics, 3rd ed.; Pergamon press: Oxford, UK, 1980; ISBN 978-0-08-023039-9. [Google Scholar]
- Ball, P.; Ben-Jacob, E. Water as the Fabric of Life. Eur. Phys. J. Spec. Top. 2014, 223, 849–852. [Google Scholar] [CrossRef]
- Hongray, T.; Ashok, B.; Balakrishnan, J. Effect of Charge on the Dynamics of an Acoustically Forced Bubble. Nonlinearity 2014, 27, 1157–1179. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Lobeyev, A.V.; Lyakhov, G.A.; Ninham, B.W. Mechanism of Low-Threshold Hypersonic Cavitation Stimulated by Broadband Laser Pump. Phys. Rev. E 1999, 60, 1681–1690. [Google Scholar] [CrossRef] [PubMed]
- Beard, K.V. Cloud and Precipitation Physics Research 1983–1986. Rev. Geophys. 1987, 25, 357–370. [Google Scholar] [CrossRef]
- Grigor’ev, A.I.; Kolbneva, N.Y.; Shiryaeva, S.O. Radiation of Electromagnetic Waves of an Oscillating Charged Drop. Surf. Engin. Appl. Electrochem. 2015, 51, 530–539. [Google Scholar] [CrossRef]
- Lord Rayleigh, F.R.S. XX. On the Equilibrium of Liquid Conducting Masses Charged with Electricity. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1882, 14, 184–186. [Google Scholar] [CrossRef]
- Hendricks, C.D.; Schneider, J.M. Stability of a Conducting Droplet under the Influence of Surface Tension and Electrostatic Forces. Am. J. Phys. 1963, 31, 450–453. [Google Scholar] [CrossRef]
- Tonks, L. A Theory of Liquid Surface Rupture by a Uniform Electric Field. Phys. Rev. 1935, 48, 562–568. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Shkirin, A.V.; Penkov, N.V.; Chirikov, S.N.; Ignatiev, P.S.; Kozlov, V.A. The Physical Nature of Mesoscopic Inhomogeneities in Highly Diluted Aqueous Suspensions of Protein Particles. Phys. Wave Phenom. 2019, 27, 102–112. [Google Scholar] [CrossRef]
- Chikramane, P.S.; Kalita, D.; Suresh, A.K.; Kane, S.G.; Bellare, J.R. Why Extreme Dilutions Reach Non-Zero Asymptotes: A Nanoparticulate Hypothesis Based on Froth Flotation. Langmuir 2012, 28, 15864–15875. [Google Scholar] [CrossRef] [PubMed]
- Berne, B.J.; Pecora, R. Dynamic Light Scaterring: With Applications to Chemistry, Biology and Physics, 2nd ed.; with corrections and new pref; Dover Publications: Mineola, NY, USA, 2000; ISBN 978-0-486-41155-2. [Google Scholar]
- Chu, B. Laser Light Scattering: Basic Principles and Practice; Elsevier Science: Oxford, UK, 1974; ISBN 978-0-12-174550-9. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theoret. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Novakovskaya, Y.V. Flexibility and Regularity of the Hydration Structures of Ions by an Example of Na+: Nonempirical Insight. J. Phys. Chem. A 2022, 126, 8434–8448. [Google Scholar] [CrossRef] [PubMed]
- Granovsky, A.A. Firefly V.8.2.0. Available online: http://classic.chem.msu.su/gran/firefly/index.html. (accessed on 22 November 2019).
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Chemcraft—Graphical Software for Visualization of Quantum Chemistry Computations, Version 1.8. Available online: http://www.chemcraftprog.com (accessed on 3 July 2024).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bunkin, N.F.; Novakovskaya, Y.V.; Gerasimov, R.Y.; Ninham, B.W.; Tarasov, S.A.; Rodionova, N.N.; Stepanov, G.O. Resonant Oscillations of Ion-Stabilized Nanobubbles in Water as a Possible Source of Electromagnetic Radiation in the Gigahertz Range. Int. J. Mol. Sci. 2025, 26, 6811. https://doi.org/10.3390/ijms26146811
Bunkin NF, Novakovskaya YV, Gerasimov RY, Ninham BW, Tarasov SA, Rodionova NN, Stepanov GO. Resonant Oscillations of Ion-Stabilized Nanobubbles in Water as a Possible Source of Electromagnetic Radiation in the Gigahertz Range. International Journal of Molecular Sciences. 2025; 26(14):6811. https://doi.org/10.3390/ijms26146811
Chicago/Turabian StyleBunkin, Nikolai F., Yulia V. Novakovskaya, Rostislav Y. Gerasimov, Barry W. Ninham, Sergey A. Tarasov, Natalia N. Rodionova, and German O. Stepanov. 2025. "Resonant Oscillations of Ion-Stabilized Nanobubbles in Water as a Possible Source of Electromagnetic Radiation in the Gigahertz Range" International Journal of Molecular Sciences 26, no. 14: 6811. https://doi.org/10.3390/ijms26146811
APA StyleBunkin, N. F., Novakovskaya, Y. V., Gerasimov, R. Y., Ninham, B. W., Tarasov, S. A., Rodionova, N. N., & Stepanov, G. O. (2025). Resonant Oscillations of Ion-Stabilized Nanobubbles in Water as a Possible Source of Electromagnetic Radiation in the Gigahertz Range. International Journal of Molecular Sciences, 26(14), 6811. https://doi.org/10.3390/ijms26146811






