Cryo-EM Map Anisotropy Can Be Attenuated by Map Post-Processing and a New Method for Its Estimation
Abstract
1. Introduction
2. Results and Discussion
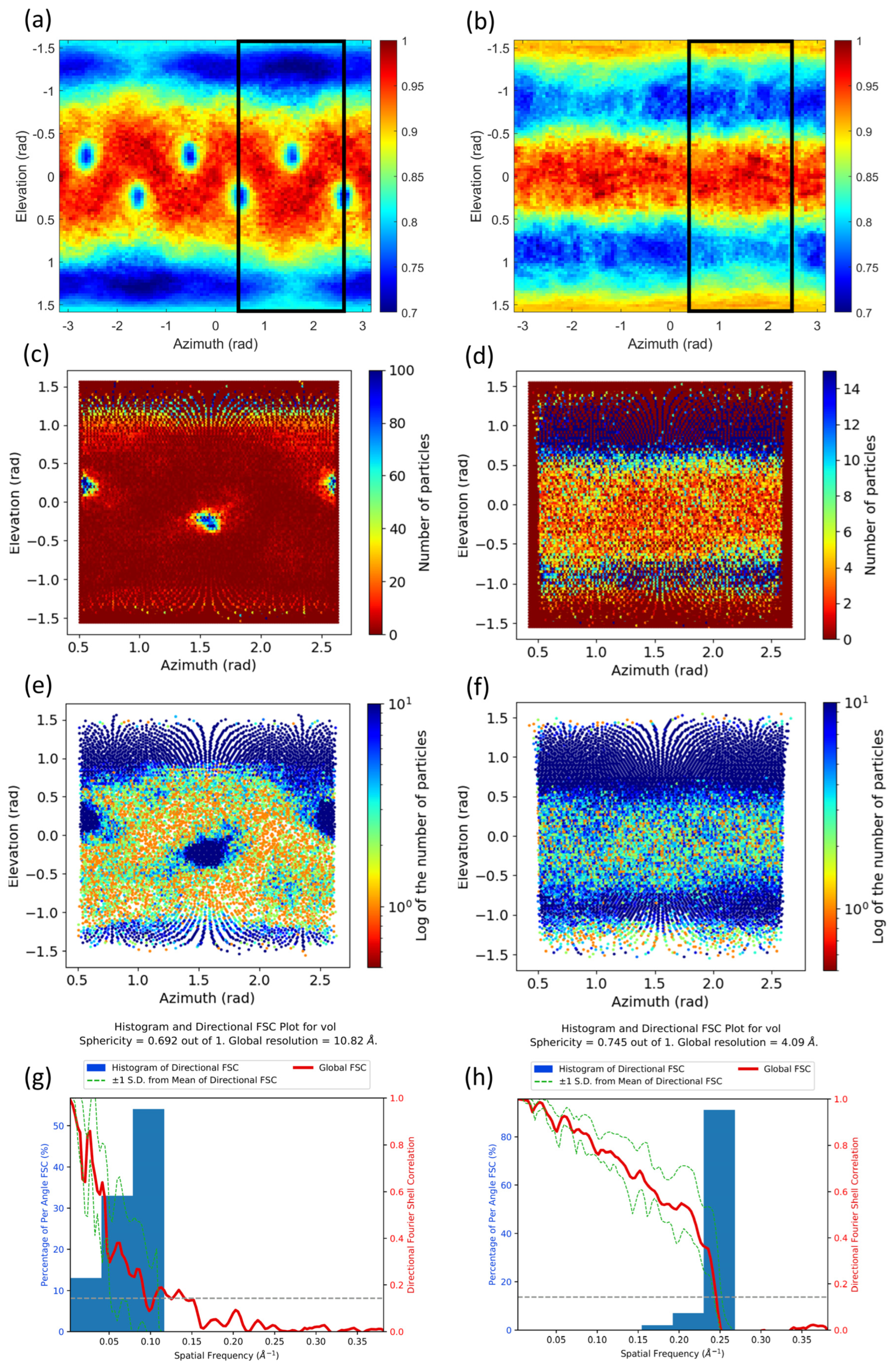
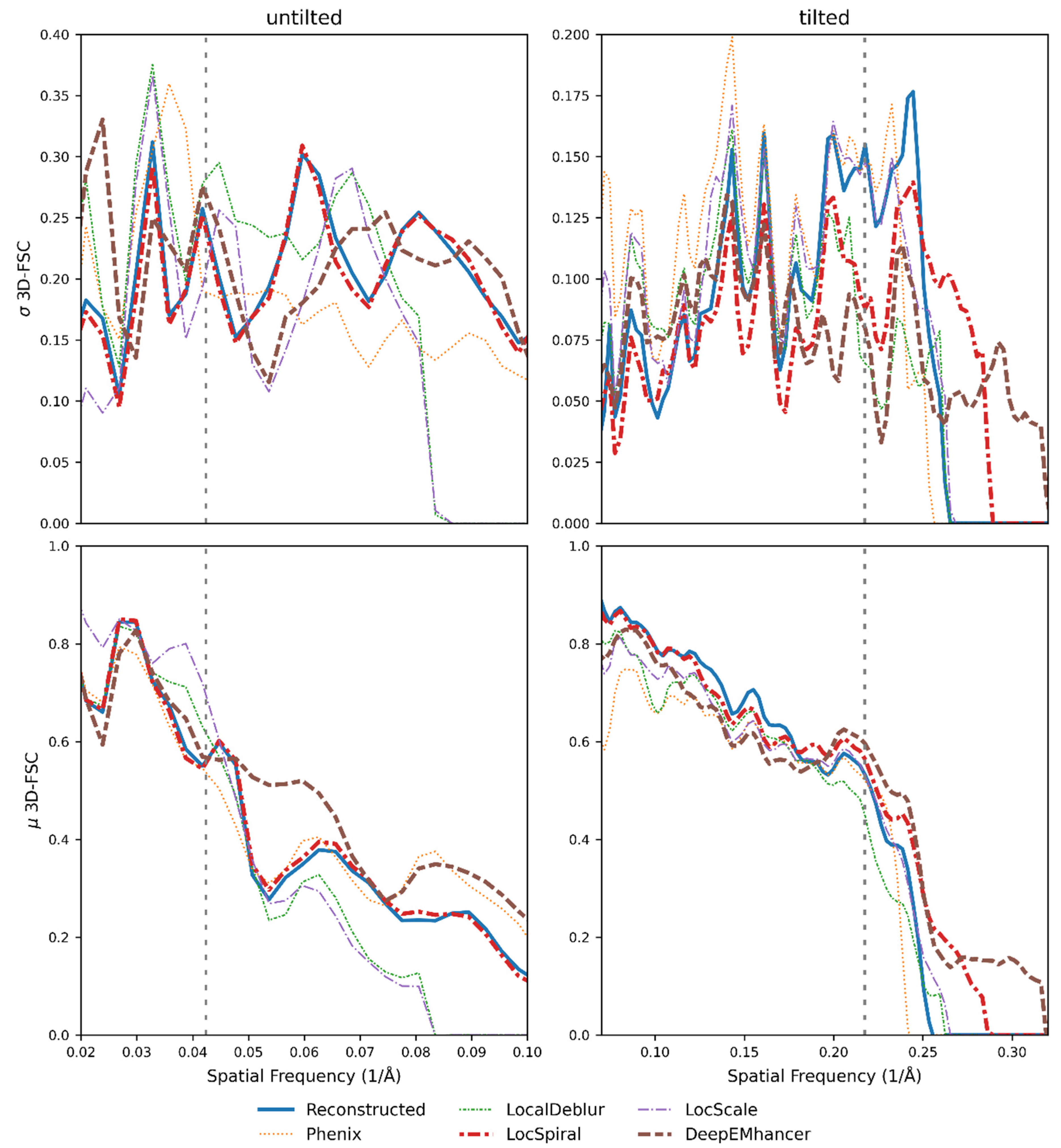
2.1. Common Map Anisotropy Metrics Are Affected by the Shape of the Specimen
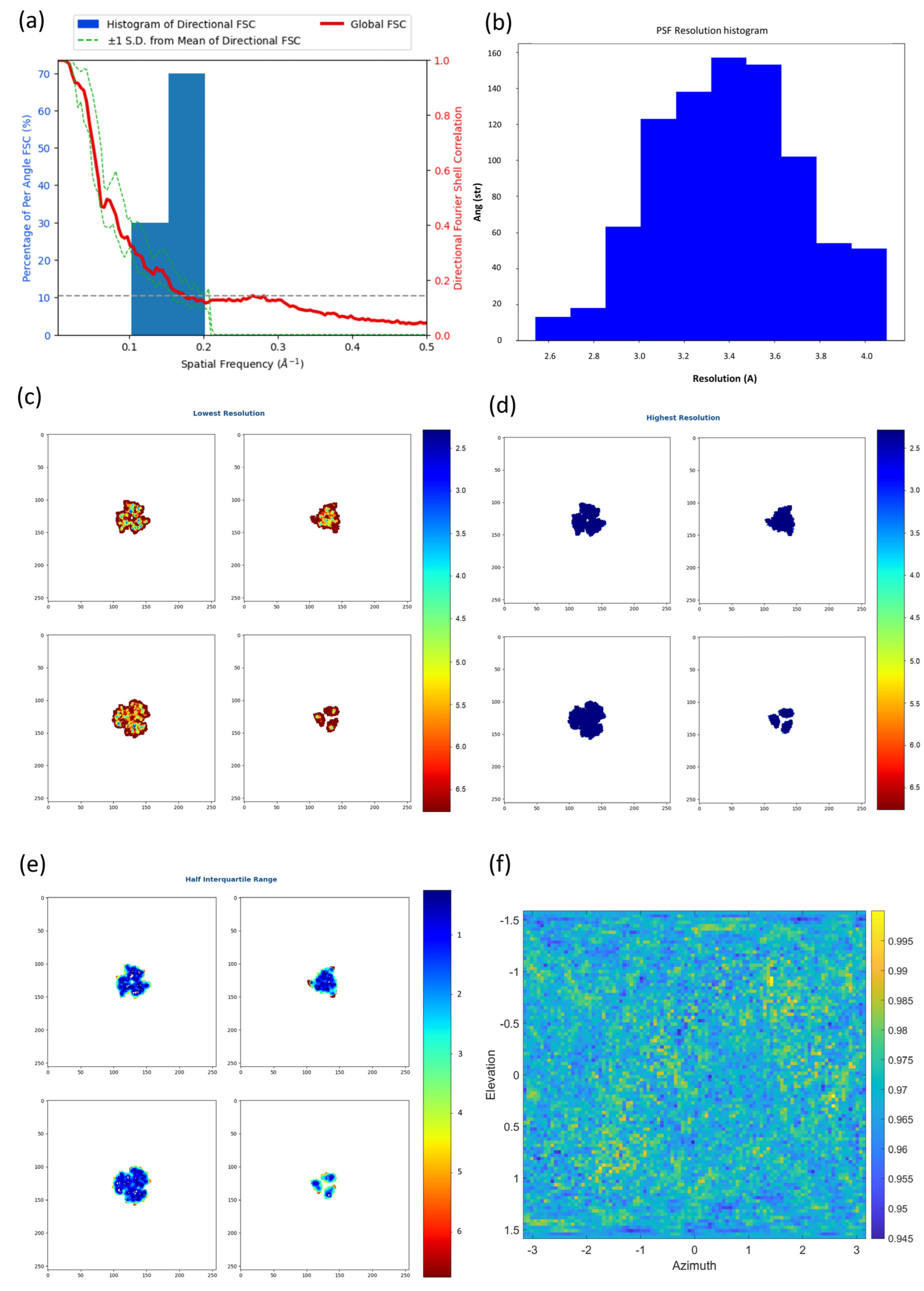
2.2. New Anisotropy Method Results
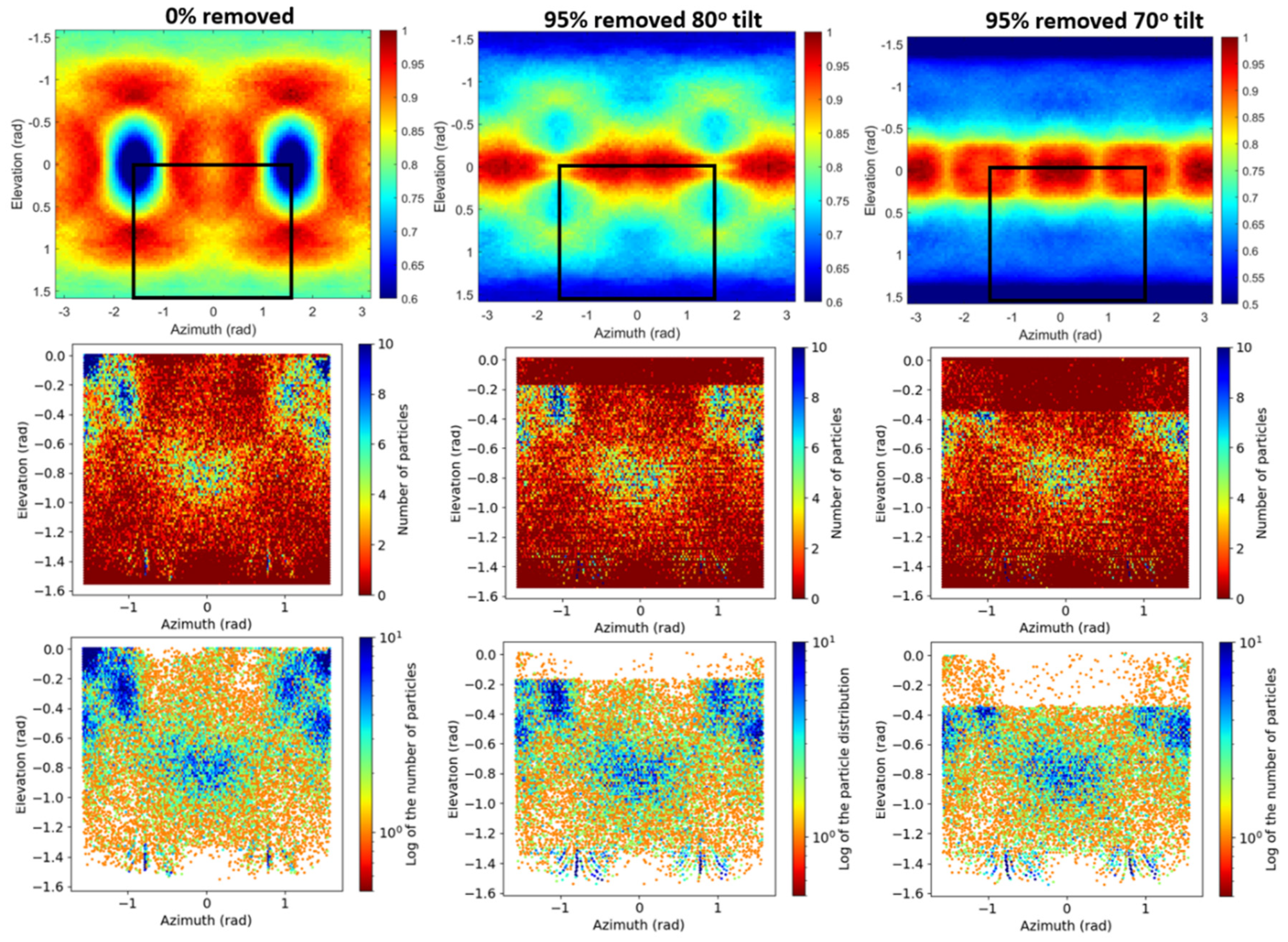
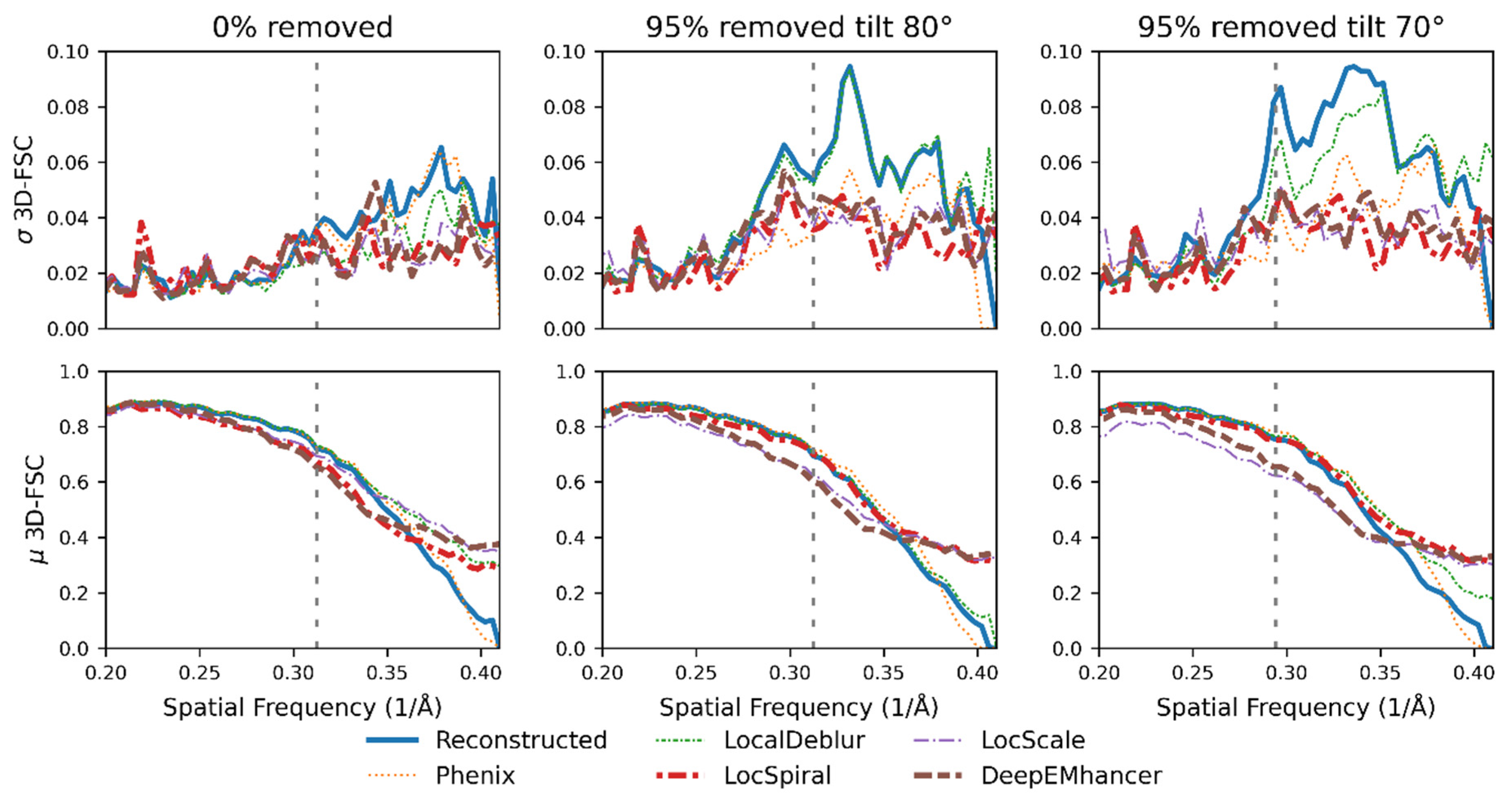
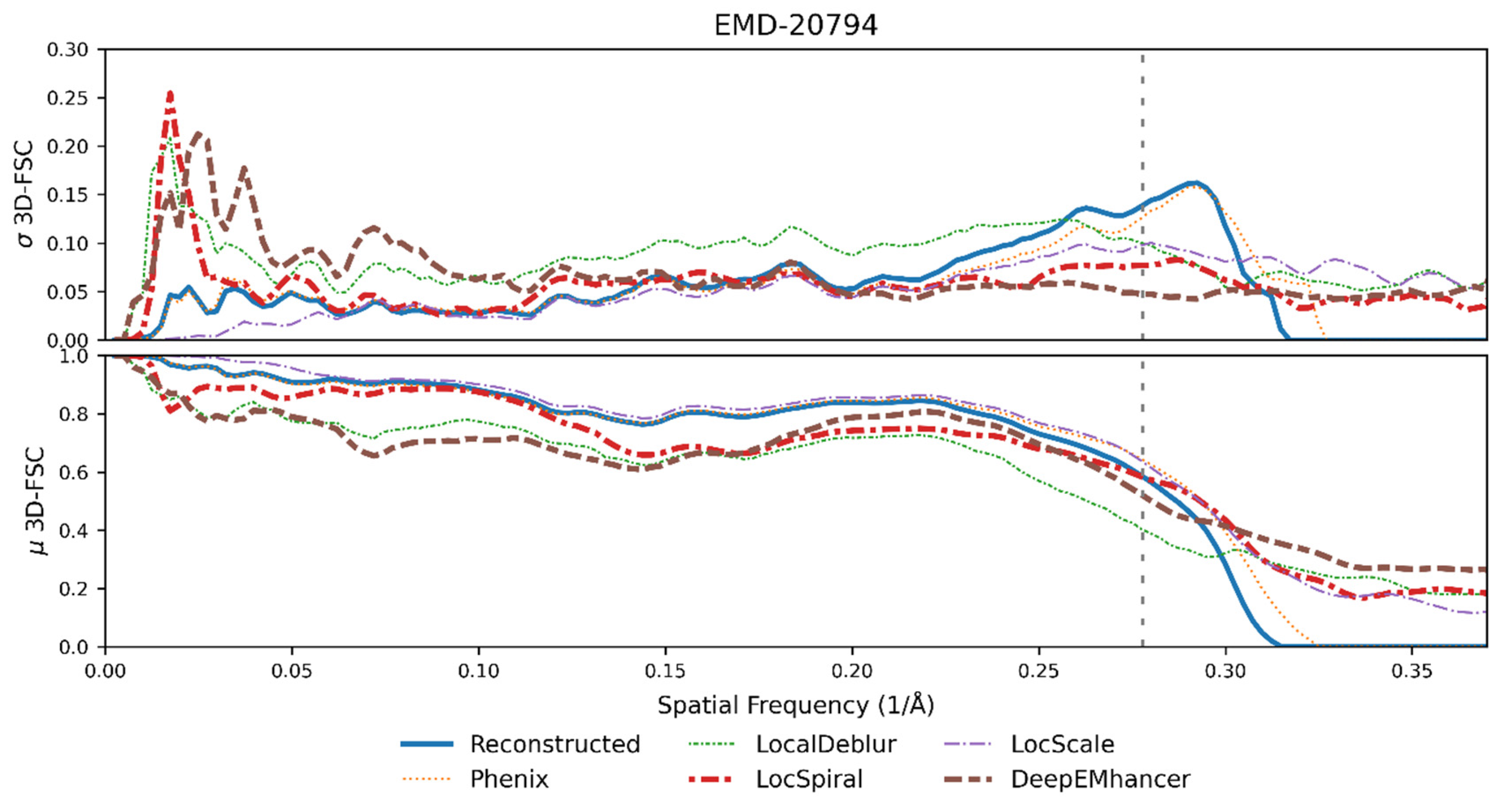
2.3. Nonlinear Post-Processing Methods Can Attenuate Map Anisotropy
3. Materials and Methods
3.1. Datasets
3.1.1. Artificial Anisotropy
3.1.2. Experimental Maps
3.2. FSC-3D Calculation
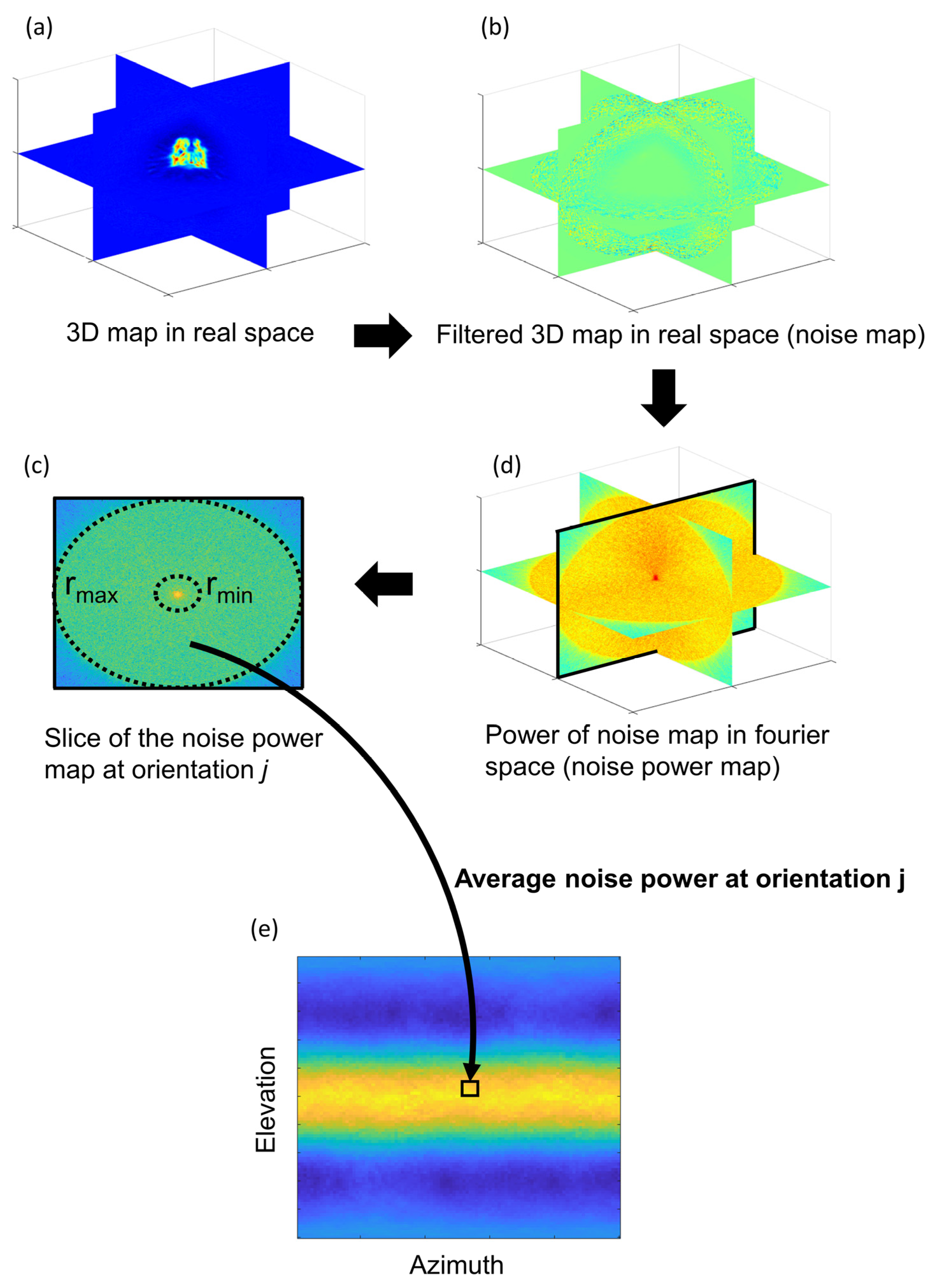
3.3. New Anisotropy Method
3.4. Map Post-Processing
3.5. Map Visualisation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kühlbrandt, W. The Resolution Revolution. Science 2014, 343, 1443–1444. [Google Scholar] [CrossRef]
- D’Imprima, E.; Kühlbrandt, W. Current Limitations to High-Resolution Structure Determination by Single-Particle CryoEM. Q. Rev. Biophys. 2021, 54, e4. [Google Scholar] [CrossRef]
- Naydenova, K.; Russo, C.J. Measuring the Effects of Particle Orientation to Improve the Efficiency of Electron Cryomicroscopy. Nat. Commun. 2017, 8, 629. [Google Scholar] [CrossRef]
- Noble, A.J.; Dandey, V.P.; Wei, H.; Brasch, J.; Chase, J.; Acharya, P.; Tan, Y.Z.; Zhang, Z.; Kim, L.Y.; Scapin, G.; et al. Routine Single Particle CryoEM Sample and Grid Characterization by Tomography. eLife 2018, 7, e34257. [Google Scholar] [CrossRef]
- Chua, E.Y.D.; Mendez, J.H.; Rapp, M.; Ilca, S.L.; Tan, Y.Z.; Maruthi, K.; Kuang, H.; Zimanyi, C.M.; Cheng, A.; Eng, E.T.; et al. Better, Faster, Cheaper: Recent Advances in Cryo–Electron Microscopy. Annu. Rev. Biochem. 2022, 91, 1–32. [Google Scholar] [CrossRef]
- Tan, Y.Z.; Baldwin, P.R.; Davis, J.H.; Williamson, J.R.; Potter, C.S.; Carragher, B.; Lyumkis, D. Addressing Preferred Specimen Orientation in Single-Particle Cryo-EMthrough Tilting. Nat. Methods 2017, 14, 793–796. [Google Scholar] [CrossRef]
- Sorzano, C.O.S.; Semchonok, D.; Lin, S.C.; Lo, Y.C.; Vilas, J.L.; Jiménez-Moreno, A.; Gragera, M.; Vacca, S.; Maluenda, D.; Martínez, M.; et al. Algorithmic Robustness to Preferred Orientations in Single Particle Analysis by CryoEM. J. Struct. Biol. 2021, 213, 107695. [Google Scholar] [CrossRef]
- Vilas, J.L.; Tagare, H.D.; Vargas, J.; Carazo, J.M.; Sorzano, C.O.S. Measuring Local-Directional Resolution and Local Anisotropy in Cryo-EM Maps. Nat. Commun. 2020, 11, 55. [Google Scholar] [CrossRef]
- Vilas, J.; Tagare, H.D. Three New Measures of Anisotropy of Cryo-EM Maps Three New Measures of Anisotropy of Cryo-EM Maps. Nat. Methods 2023, 20, 1021–1024. [Google Scholar] [CrossRef]
- Glaeser, R.M.; Han, B.-G. Opinion: Hazards Faced by Macromolecules When Confined to Thin Aqueous Films. Biophys. Rep. 2017, 3, 1–7. [Google Scholar] [CrossRef]
- Russo, C.J.; Passmore, L.A. Controlling Protein Adsorption on Graphene for Cryo-EM Using Low-Energy Hydrogen Plasmas. Nat. Methods 2014, 11, 649–652. [Google Scholar] [CrossRef]
- Han, B.G.; Walton, R.W.; Song, A.; Hwu, P.; Stubbs, M.T.; Yannone, S.M.; Arbeláez, P.; Dong, M.; Glaeser, R.M. Electron Microscopy of Biotinylated Protein Complexes Bound to Streptavidin Monolayer Crystals. J. Struct. Biol. 2012, 180, 249–253. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Y.; Yu, Z.; Li, S.; Feng, S.; Cheng, Y.; Agard, D.A. General and Robust Covalently Linked Graphene Oxide Affinity Grids for High-Resolution Cryo-EM. Proc. Natl. Acad. Sci. USA 2020, 117, 24269–24273. [Google Scholar] [CrossRef]
- Noble, A.J.; Wei, H.; Dandey, V.P.; Zhang, Z.; Tan, Y.Z.; Potter, C.S.; Carragher, B. Reducing Effects of Particle Adsorption to the Air–Water Interface in Cryo-EM. Nat. Methods 2018, 15, 793–795. [Google Scholar] [CrossRef]
- Terwilliger, T.C.; Sobolev, O.V.; Afonine, P.V.; Adams, P.D. Automated Map Sharpening by Maximization of Detail and Connectivity. Acta Crystallogr. D Struct. Biol. 2018, 74, 545–559. [Google Scholar] [CrossRef]
- Peter, M.F.; Ruland, J.A.; Depping, P.; Schneberger, N.; Severi, E.; Moecking, J.; Gatterdam, K.; Tindall, S.; Durand, A.; Heinz, V.; et al. Structural and Mechanistic Analysis of a Tripartite ATP-Independent Periplasmic TRAP Transporter. Nat. Commun. 2022, 13, 4471. [Google Scholar] [CrossRef]
- Melo, A.A.; Sprink, T.; Noel, J.K.; Vázquez-Sarandeses, E.; van Hoorn, C.; Mohd, S.; Loerke, J.; Spahn, C.M.T.; Daumke, O. Cryo-Electron Tomography Reveals Structural Insights into the Membrane Remodeling Mode of Dynamin-like EHD Filaments. Nat. Commun. 2022, 13, 7641. [Google Scholar] [CrossRef]
- Rosenthal, P.B.; Henderson, R. Optimal Determination of Particle Orientation, Absolute Hand, and Contrast Loss in Single-Particle Electron Cryomicroscopy. J. Mol. Biol. 2003, 333, 721–745. [Google Scholar] [CrossRef]
- Scheres, S.H.W. RELION: Implementation of a Bayesian Approach to Cryo-EM Structure Determination. J. Struct. Biol. 2012, 180, 519–530. [Google Scholar] [CrossRef]
- Zivanov, J.; Nakane, T.; Forsberg, B.O.; Kimanius, D.; Hagen, W.J.H.; Lindahl, E.; Scheres, S.H.W. New Tools for Automated High-Resolution Cryo-EM Structure Determination in RELION-3. eLife 2018, 7, e42166. [Google Scholar] [CrossRef]
- Sanchez-Garcia, R.; Gomez-Blanco, J.; Cuervo, A.; Carazo, J.M.; Sorzano, C.O.S.; Vargas, J. DeepEMhancer: A Deep Learning Solution for Cryo-EM Volume Post-Processing. Commun. Biol. 2021, 4, 874. [Google Scholar] [CrossRef] [PubMed]
- Jakobi, A.J.; Wilmanns, M.; Sachse, C. Model-Based Local Density Sharpening of Cryo-EM Maps. eLife 2017, 6, e27131. [Google Scholar] [CrossRef] [PubMed]
- Bharadwaj, A.; Jakobi, A.J. Electron Scattering Properties of Biological Macromolecules and Their Use for Cryo-EM Map Sharpening. Faraday Discuss. 2022, 240, 168–183. [Google Scholar] [CrossRef] [PubMed]
- Kaur, S.; Gomez-Blanco, J.; Khalifa, A.A.Z.; Adinarayanan, S.; Sanchez-Garcia, R.; Wrapp, D.; McLellan, J.S.; Bui, K.H.; Vargas, J. Local Computational Methods to Improve the Interpretability and Analysis of Cryo-EM Maps. Nat. Commun. 2021, 12, 1240. [Google Scholar] [CrossRef]
- Ramírez-Aportela, E.; Vilas, J.L.; Glukhova, A.; Melero, R.; Conesa, P.; Martínez, M.; Maluenda, D.; Mota, J.; Jiménez, A.; Vargas, J.; et al. Automatic Local Resolution-Based Sharpening of Cryo-EM Maps. Bioinformatics 2020, 36, 765–772. [Google Scholar] [CrossRef] [PubMed]
- Bartesaghi, A.; Merk, A.; Banerjee, S.; Matthies, D.; Wu, X.; Milne, J.L.S.; Subramaniam, S. 2.2 Å Resolution Cryo-EM Structure of β-Galactosidase in Complex with a Cell-Permeant Inhibitor. Science 2015, 348, 1147–1151. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.G.; Cormier, A.; Ito, S.; Seed, R.I.; Bondesson, A.J.; Lou, J.; Marks, J.D.; Baron, J.L.; Cheng, Y.; Nishimura, S.L. Cryo-EM Reveals Integrin-Mediated TGF-β Activation without Release from Latent TGF-β. Cell 2020, 180, 490–501.e16. [Google Scholar] [CrossRef]
- Clarke, O.B. @OliBClarke, Twitter. 2020. Available online: https://twitter.com/OliBClarke/status/1301985078231232512 (accessed on 24 March 2024).
- Fan, H.; Wang, B.; Zhang, Y.; Zhu, Y.; Song, B.; Xu, H.; Zhai, Y.; Qiao, M.; Sun, F. A cryo-electron microscopy support film formed by 2D crystals of hydrophobin HFBI. Nat. Commun. 2021, 12, 7257. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Peng, L.; Baldwin, P.R.; Mann, D.S.; Jiang, W.; Rees, I.; Ludtke, S.J. EMAN2: An Extensible Image Processing Suite for Electron Microscopy. J. Struct. Biol. 2007, 157, 38–46. [Google Scholar] [CrossRef]
- Punjani, A.; Rubinstein, J.L.; Fleet, D.J.; Brubaker, M.A. CryoSPARC: Algorithms for Rapid Unsupervised Cryo-EM Structure Determination. Nat. Methods 2017, 14, 290–296. [Google Scholar] [CrossRef]
- Pipe, J.G.; Menon, P. Sampling Density Compensation in MRI: Rationale and an Iterative Numerical Solution. Magn. Reson. Med. 1999, 41, 179–186. [Google Scholar] [CrossRef]
- Střelák, D.; Sorzano, C.Ó.S.; Carazo, J.M.; Filipovič, J. A GPU Acceleration of 3-D Fourier Reconstruction in Cryo-EM. Int. J. High Perform. Comput. Appl. 2019, 33, 948–959. [Google Scholar] [CrossRef]
- Vargas, J.; Gómez-Pedrero, J.A.; Quiroga, J.A.; Quiroga, J.A.; Alonso, J.; Alonso, J. Enhancement of Cryo-EM Maps by a Multiscale Tubular Filter. Opt. Express 2022, 30, 4515–4527. [Google Scholar] [CrossRef] [PubMed]
- Terwilliger, T.C.; Ludtke, S.J.; Read, R.J.; Adams, P.D.; Afonine, P.V. Improvement of Cryo-EM Maps by Density Modification. Nat. Methods 2020, 17, 923–927. [Google Scholar] [CrossRef] [PubMed]
- Penczek, P.A.; Grassucci, R.A.; Frank, J. The Ribosome at Improved Resolution: New Techniques for Merging and Orientation Refinement in 3D Cryo-Electron Microscopy of Biological Particles. Ultramicroscopy 1994, 53, 251–270. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Briggs, J.A.G. Cryo-Electron Tomography and Subtomogram Averaging. Methods Enzymol. 2016, 579, 329–367. [Google Scholar] [CrossRef] [PubMed]
- Vilas, J.L.; Gómez-Blanco, J.; Conesa, P.; Melero, R.; Miguel de la Rosa-Trevín, J.; Otón, J.; Cuenca, J.; Marabini, R.; Carazo, J.M.; Vargas, J.; et al. MonoRes: Automatic and Accurate Estimation of Local Resolution for Electron Microscopy Maps. Structure 2018, 26, 337–344.e4. [Google Scholar] [CrossRef] [PubMed]
- Goddard, T.D.; Huang, C.C.; Meng, E.C.; Pettersen, E.F.; Couch, G.S.; Morris, J.H.; Ferrin, T.E. UCSF ChimeraX: Meeting Modern Challenges in Visualization and Analysis. Protein Sci. 2018, 27, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Meng, E.C.; Couch, G.S.; Croll, T.I.; Morris, J.H.; Ferrin, T.E. UCSF ChimeraX: Structure Visualization for Researchers, Educators, and Developers. Protein Sci. 2021, 30, 70–82. [Google Scholar] [CrossRef]
- Croll, T.I. ISOLDE: A Physically Realistic Environment for Model Building into Low-Resolution Electron-Density Maps. Acta Crystallogr. D Struct. Biol. 2018, 74, 519–530. [Google Scholar] [CrossRef]
- Iudin, A.; Korir, P.K.; Somasundharam, S.; Weyand, S.; Cattavitello, C.; Fonseca, N.; Salih, O.; Kleywegt, G.J.; Patwardhan, A. EMPIAR: The Electron Microscopy Public Image Archive. Nucleic Acids Res. 2023, 51, D1503–D1511. [Google Scholar] [CrossRef] [PubMed]
- Trabuco, L.G.; Villa, E.; Schreiner, E.; Harrison, C.B.; Schulten, K. Molecular Dynamics Flexible Fitting: A Practical Guide to Combine Cryo-Electron Microscopy and X-ray Crystallography. Methods 2009, 49, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-T.; Hu, J.; Zhou, Z.H. Resolving the Preferred Orientation Problem in CryoEM Reconstruction with Self-Supervised Deep Learning. Microsc. Microanal. 2023, 29, 1918–1919. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez-Garcia, R.; Gaullier, G.; Cuadra-Troncoso, J.M.; Vargas, J. Cryo-EM Map Anisotropy Can Be Attenuated by Map Post-Processing and a New Method for Its Estimation. Int. J. Mol. Sci. 2024, 25, 3959. https://doi.org/10.3390/ijms25073959
Sanchez-Garcia R, Gaullier G, Cuadra-Troncoso JM, Vargas J. Cryo-EM Map Anisotropy Can Be Attenuated by Map Post-Processing and a New Method for Its Estimation. International Journal of Molecular Sciences. 2024; 25(7):3959. https://doi.org/10.3390/ijms25073959
Chicago/Turabian StyleSanchez-Garcia, Ruben, Guillaume Gaullier, Jose Manuel Cuadra-Troncoso, and Javier Vargas. 2024. "Cryo-EM Map Anisotropy Can Be Attenuated by Map Post-Processing and a New Method for Its Estimation" International Journal of Molecular Sciences 25, no. 7: 3959. https://doi.org/10.3390/ijms25073959
APA StyleSanchez-Garcia, R., Gaullier, G., Cuadra-Troncoso, J. M., & Vargas, J. (2024). Cryo-EM Map Anisotropy Can Be Attenuated by Map Post-Processing and a New Method for Its Estimation. International Journal of Molecular Sciences, 25(7), 3959. https://doi.org/10.3390/ijms25073959






