Computational Models of Claudin Assembly in Tight Junctions and Strand Properties
Abstract
1. Introduction
2. Cldn-15: From Crystal Structure to Computational Model
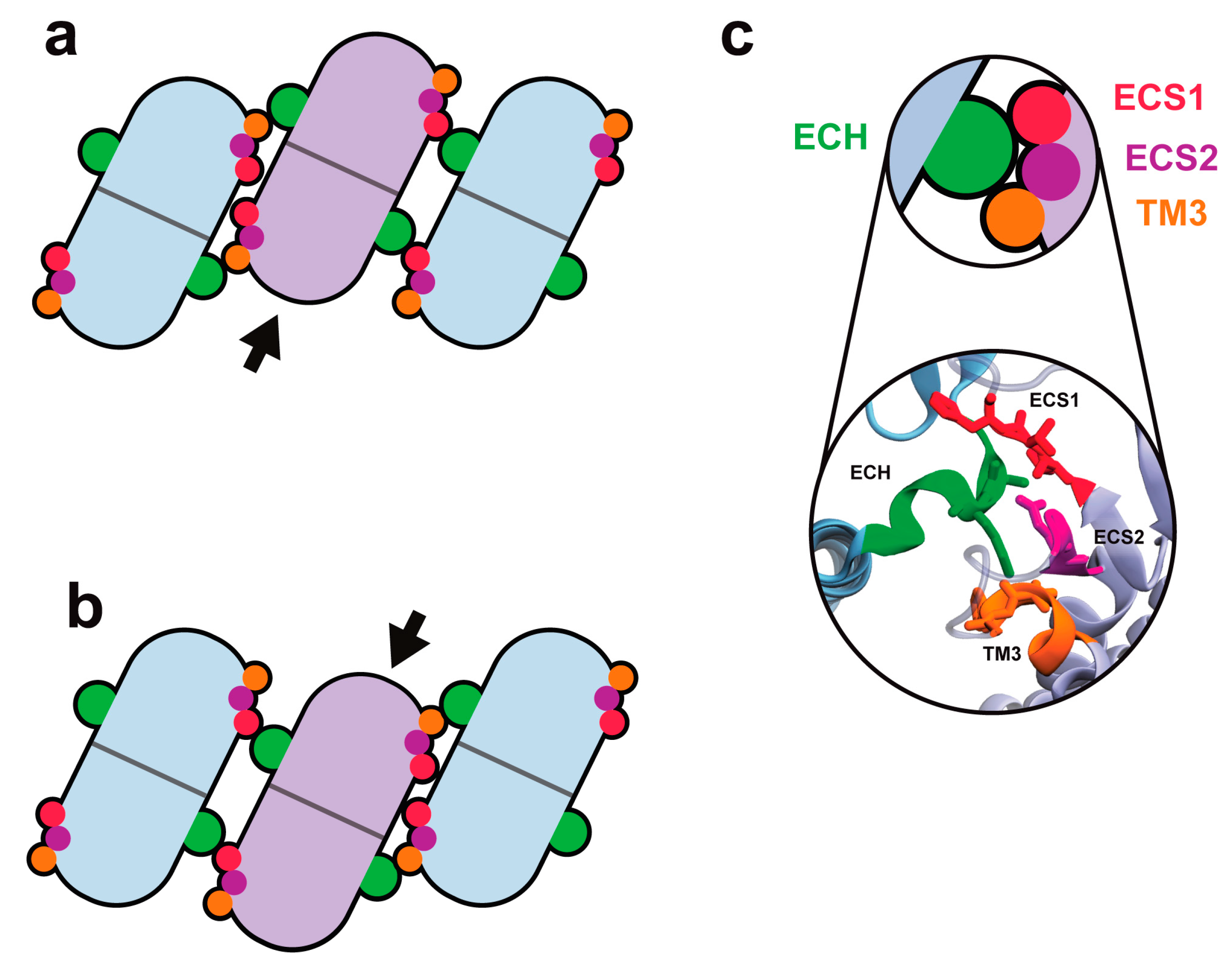
3. Multiple Cldn–Cldn cis Interfaces
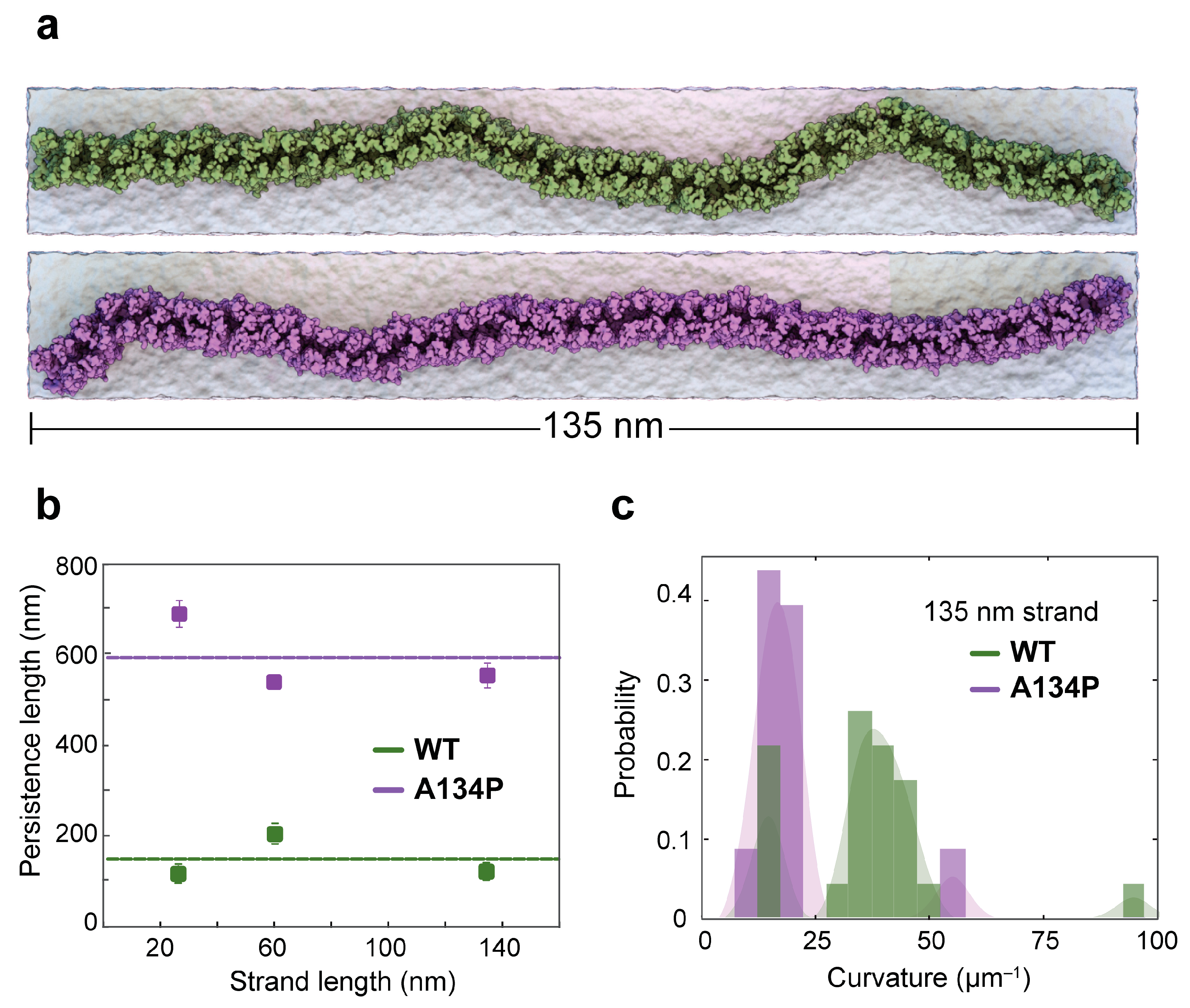
4. A Mechanism for Lateral Flexibility at cis Interfaces
5. Evaluation of Computational Methods and Models
5.1. Protein–Protein Docking
5.2. All-Atom Molecular Dynamics Simulation
5.3. Coarse-Grained Molecular Dynamics Simulations
5.4. Hybrid-Resolution Molecular Dynamics Simulations
5.5. Additional Limitations
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Cldn | claudin |
| MD | molecular dynamics |
| CG | coarse grained |
| TJ | tight junction |
| TM | transmembrane |
| ECS | extracellular segment |
| ECH | extracellular helix |
References
- Claude, P.; Goodenough, D.A. Fracture Faces of Zonulae Occludentes from “Tight” and “Leaky” Epithelia. J. Cell Biol. 1973, 58, 390–400. [Google Scholar] [CrossRef]
- Farquhar, M.G.; Palade, G.E. Junctional Complexes in Various Epithelia. J. Cell Biol. 1963, 17, 375–412. [Google Scholar] [CrossRef] [PubMed]
- Staehelin, L.A. Structure and Function of Intercellular Junctions. Int. Rev. Cytol. 1974, 39, 191–283. [Google Scholar] [PubMed]
- Tsukita, S.; Furuse, M.; Itoh, M. Multifunctional Strands in Tight Junctions. Nat. Rev. Mol. Cell Biol. 2001, 2, 285–293. [Google Scholar] [CrossRef]
- Blasig, I.E.; Winkler†, L.; Lassowski, B.; Mueller, S.L.; Zuleger, N.; Krause, E.; Krause, G.; Gast, K.; Kolbe, M.; Piontek, J. On the Self-Association Potential of Transmembrane Tight Junction Proteins. Cell. Mol. Life Sci. CMLS 2006, 63, 505–514. [Google Scholar] [CrossRef]
- Krause, G. Structure and Function of Claudins. Biochim. Biophys. Acta 2008, 1778, 631–645. [Google Scholar] [CrossRef] [PubMed]
- Van Itallie, C.M.; Rogan, S.; Yu, A.; Vidal, L.S.; Holmes, J.; Anderson, J.M. Two Splice Variants of Claudin-10 in the Kidney Create Paracellular Pores with Different Ion Selectivities. Am. J. Physiol.-Ren. Physiol. 2006, 291, F1288–F1299. [Google Scholar] [CrossRef] [PubMed]
- Mineta, K.; Yamamoto, Y.; Yamazaki, Y.; Tanaka, H.; Tada, Y.; Saito, K.; Tamura, A.; Igarashi, M.; Endo, T.; Takeuchi, K.; et al. Predicted Expansion of the Claudin Multigene Family. FEBS Lett. 2011, 585, 606–612. [Google Scholar] [CrossRef] [PubMed]
- Gunzel, D.; Yu, A.S. Claudins and the Modulation of Tight Junction Permeability. Physiol. Rev. 2013, 93, 525–569. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Tokumasu, R.; Kimura, H.; Tsukita, S. Role of Claudin Species–Specific Dynamics in Reconstitution and Remodeling of the Zonula Occludens. Mol. Biol. Cell 2011, 22, 1495–1504. [Google Scholar] [CrossRef]
- Tamura, A.; Tsukita, S. Paracellular Barrier and Channel Functions of TJ Claudins in Organizing Biological Systems: Advances in the Field of Barriology Revealed in Knockout Mice. Semin. Cell Dev. Biol. 2014, 36, 177–185. [Google Scholar] [CrossRef]
- Milatz, S.; Piontek, J.; Hempel, C.; Meoli, L.; Grohe, C.; Fromm, A.; Lee, I.-F.M.; El-Athman, R.; Günzel, D. Tight Junction Strand Formation by Claudin-10 Isoforms and Claudin-10a/-10b Chimeras. Ann. N. Y. Acad. Sci. 2017, 1405, 102–115. [Google Scholar] [CrossRef]
- Tao, D.; Guan, B.; Li, H.; Zhou, C. Expression Patterns of Claudins in Cancer. Heliyon 2023, 9, e21338. [Google Scholar] [CrossRef]
- Li, J. Dysregulated Expression of Claudins in Cancer (Review). Oncol. Lett. 2021, 22, 1–11. [Google Scholar] [CrossRef]
- Nakamura, S.; Irie, K.; Tanaka, H.; Nishikawa, K.; Suzuki, H.; Saitoh, Y.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Morphologic Determinant of Tight Junctions Revealed by Claudin-3 Structures. Nat. Commun. 2019, 10, 816. [Google Scholar] [CrossRef]
- Lynn, K.S.; Peterson, R.J.; Koval, M. Ruffles and Spikes: Control of Tight Junction Morphology and Permeability by Claudins. Biochim. Biophys. Acta BBA—Biomembr. 2020, 1862, 183339. [Google Scholar] [CrossRef]
- Furuse, M.; Sasaki, H.; Tsukita, S. Manner of Interaction of Heterogeneous Claudin Species within and between Tight Junction Strands. J. Cell Biol. 1999, 147, 891–903. [Google Scholar] [CrossRef]
- Tanaka, H.; Yamamoto, Y.; Kashihara, H.; Yamazaki, Y.; Tani, K.; Fujiyoshi, Y.; Mineta, K.; Takeuchi, K.; Tamura, A.; Tsukita, S. Claudin-21 Has a Paracellular Channel Role at Tight Junctions. Mol. Cell. Biol. 2016, 36, 954–964. [Google Scholar] [CrossRef] [PubMed]
- Jan, R.; Carolin, P.; Fränze, V.; Tarek, S.; Jonas, P.; Dorothee, G.; Hartwig, W.; Gerd, K.; Jörg, P. Claudin-3 and Claudin-5 Protein Folding and Assembly into the Tight Junction Are Controlled by Non-Conserved Residues in the Transmembrane 3 (TM3) and Extracellular Loop 2 (ECL2) Segments. J. Biol. Chem. 2014, 289, 7641–7653. [Google Scholar]
- Milatz, S.; Krug, S.M.; Rosenthal, R.; Günzel, D.; Müller, D.; Schulzke, J.-D.; Amasheh, S.; Fromm, M. Claudin-3 Acts as a Sealing Component of the Tight Junction for Ions of Either Charge and Uncharged Solutes. Biochim. Biophys. Acta 2010, 1798, 2048–2057. [Google Scholar] [CrossRef] [PubMed]
- Tamura, A. Loss of Claudin-15, but Not Claudin-2, Causes Na+ Deficiency and Glucose Malabsorption in Mouse Small Intestine. Gastroenterology 2011, 140, 913–923. [Google Scholar] [CrossRef]
- Amasheh, S.; Meiri, N.; Gitter, A.H.; Schöneberg, T.; Mankertz, J.; Schulzke, J.D.; Fromm, M. Claudin-2 Expression Induces Cation-Selective Channels in Tight Junctions of Epithelial Cells. J. Cell Sci. 2002, 115, 4969–4976. [Google Scholar] [CrossRef] [PubMed]
- Alexandre, M.D.; Lu, Q.; Chen, Y.-H. Overexpression of Claudin-7 Decreases the Paracellular Cl− Conductance and Increases the Paracellular Na+ Conductance in LLC-PK1 Cells. J. Cell Sci. 2005, 118, 2683–2693. [Google Scholar] [CrossRef] [PubMed]
- Gonschior, H.; Schmied, C.; Van der Veen, R.E.; Eichhorst, J.; Himmerkus, N.; Piontek, J.; Günzel, D.; Bleich, M.; Furuse, M.; Haucke, V.; et al. Nanoscale Segregation of Channel and Barrier Claudins Enables Paracellular Ion Flux. Nat. Commun. 2022, 13, 4985. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Weber, C.R.; Turner, J.R. The Tight Junction Protein Complex Undergoes Rapid and Continuous Molecular Remodeling at Steady State. J. Cell Biol. 2008, 181, 683–695. [Google Scholar] [CrossRef] [PubMed]
- Higashi, T.; Arnold, T.R.; Stephenson, R.E.; Dinshaw, K.M.; Miller, A.L. Maintenance of the Epithelial Barrier and Remodeling of Cell-Cell Junctions during Cytokinesis. Curr. Biol. CB 2016, 26, 1829–1842. [Google Scholar] [CrossRef] [PubMed]
- Citi, S. The Mechanobiology of Tight Junctions. Biophys. Rev. 2019, 11, 783–793. [Google Scholar] [CrossRef] [PubMed]
- Varadarajan, S.; Stephenson, R.E.; Miller, A.L. Multiscale Dynamics of Tight Junction Remodeling. J. Cell Sci. 2019, 132, jcs229286. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, H.; Nishizawa, T.; Tani, K.; Tamazaki, Y.; Tamura, A.; Ishitani, R.; Dohmae, N.; Tsukita, S.; Nureki, O.; Fujiyoshi, Y. Crystal Structure of a Claudin Provides Insight into the Architecture of Tight Junctions. Science 2014, 18, 304–307. [Google Scholar] [CrossRef]
- Suzuki, H.; Tani, K.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Model for the Architecture of Claudin-Based Paracellular Ion Channels through Tight Junctions. J. Mol. Biol. 2015, 427, 291–297. [Google Scholar] [CrossRef]
- Krause, G.; Protze, J.; Piontek, J. Assembly and Function of Claudins: Structure-Function Relationships Based on Homology Models and Crystal Structures. Semin. Cell Dev. Biol. 2015, 42, 3–12. [Google Scholar] [CrossRef]
- Van Itallie, C.M.; Anderson, J.M. Claudin Interactions in and out of the Tight Junction. Tissue Barriers 2013, 1, 25247. [Google Scholar] [CrossRef]
- Samanta, P.; Yitang, W.; Shadi, F.; Jinjing, Z.; Ye, L.; Le, S.; Christopher, W.; Fatemeh, K.-A. Molecular Determination of Claudin-15 Organization and Channel Selectivity. J. Gen. Physiol. 2018, 150, 949–968. [Google Scholar] [CrossRef]
- Alberini, G.; Benfenati, F.; Maragliano, L. A Refined Model of Claudin-15 Tight Junction Paracellular Architecture by Molecular Dynamics Simulations. PLoS ONE 2017, 12, e0184190. [Google Scholar] [CrossRef]
- Alberini, G.; Benfenati, F.; Maragliano, L. Molecular Dynamics Simulations of Ion Selectivity in a Claudin-15 Paracellular Channel. J. Phys. Chem. B 2018, 122, 10783–10792. [Google Scholar] [CrossRef]
- Fuladi, S.; Jannat, R.-W.; Shen, L.; Weber, C.R.; Khalili-Araghi, F. Computational Modeling of Claudin Structure and Function. Int. J. Mol. Sci. 2020, 21, 742. [Google Scholar] [CrossRef] [PubMed]
- McGuinness, S.; Li, P.; Li, Y.; Fuladi, S.; Konar, S.; Sajjadi, S.; Sidahmed, M.; Li, Y.; Shen, L.; Araghi, F.K.; et al. Molecular Dynamics Analyses of CLDN15 Pore Size and Charge Selectivity. bioRxiv 2023. [Google Scholar] [CrossRef]
- Nagarajan, S.K.; Klein, S.; Fadakar, B.S.; Piontek, J. Claudin-10b Cation Channels in Tight Junction Strands: Octameric-Interlocked Pore Barrels Constitute Paracellular Channels with Low Water Permeability. Comput. Struct. Biotechnol. J. 2023, 21, 1711–1727. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J. Multiple Claudin-Claudin Cis Interfaces Are Required for Tight Junction Strand Formation and Inherent Flexibility. Commun. Biol. 2018, 1, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Christina, M.V.I.; Amber Jean, T.; James, M.A. Visualizing the Dynamic Coupling of Claudin Strands to the Actin Cytoskeleton through ZO-1. Mol. Biol. Cell 2017, 28, 524–534. [Google Scholar]
- Sasaki, H.; Matsui, C.; Furuse, K.; Mimori-Kiyosue, Y.; Furuse, M.; Tsukita, S. Dynamic Behavior of Paired Claudin Strands within Apposing Plasma Membranes. Proc. Natl. Acad. Sci. USA 2003, 100, 3971–3976. [Google Scholar] [CrossRef]
- Irudayanathan, F.J. Molecular Architecture of the Blood Brain Barrier Tight Junction Proteins–A Synergistic Computational and In Vitro Approach. J. Phys. Chem. B 2016, 120, 77–88. [Google Scholar] [CrossRef]
- Irudayanathan, F.J. Architecture of the Paracellular Channels Formed by Claudins of the Blood-Brain Barrier Tight Junctions. Ann. N. Y. Acad. Sci. 2017, 1405, 131–146. [Google Scholar] [CrossRef]
- Rajagopal, N.; Nangia, S. Unique Structural Features of Claudin-5 and Claudin-15 Lead to Functionally Distinct Tight Junction Strand Architecture. Ann. N. Y. Acad. Sci. 2022, 1517, 225–233. [Google Scholar] [CrossRef]
- Berselli, A.; Alberini, G.; Benfenati, F.; Maragliano, L. Computational Assessment of Different Structural Models for Claudin-5 Complexes in Blood–Brain Barrier Tight Junctions. ACS Chem. Neurosci. 2022, 13, 2140–2153. [Google Scholar] [CrossRef]
- Irudayanathan, F.J.; Wang, X.; Wang, N.; Willsey, S.R.; Seddon, I.A.; Nangia, S. Self-Assembly Simulations of Classic Claudins-Insights into the Pore Structure, Selectivity, and Higher Order Complexes. J. Phys. Chem. B 2018, 122, 7463–7474. [Google Scholar] [CrossRef] [PubMed]
- Berselli, A.; Alberini, G.; Benfenati, F.; Maragliano, L. Computational Study of Ion Permeation through Claudin-4 Paracellular Channels. Ann. N. Y. Acad. Sci. 2022, 1516, 162–174. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, Y.; Poirier, K.; Boddaert, N.; Hubert, L.; Aubart, M.; Kaminska, A.; Alison, M.; Desguerre, I.; Munnich, A.; Campbell, M. Recurrent de Novo Mutations in CLDN5 Induce an Anion-Selective Blood–Brain Barrier and Alternating Hemiplegia. Brain 2022, 145, 3374–3382. [Google Scholar] [CrossRef]
- Berselli, A.; Alberini, G.; Benfenati, F.; Maragliano, L. The Impact of Pathogenic and Artificial Mutations on Claudin-5 Selectivity from Molecular Dynamics Simulations. Comput. Struct. Biotechnol. J. 2023, 21, 2640–2653. [Google Scholar] [CrossRef] [PubMed]
- Hempel, C.; Protze, J.; Altun, E.; Riebe, B.; Piontek, A.; Fromm, A.; Lee, I.M.; Saleh, T.; Günzel, D.; Krause, G.; et al. Assembly of Tight Junction Strands: Claudin-10b and Claudin-3 Form Homo-Tetrameric Building Blocks That Polymerise in a Channel-Independent Manner. J. Mol. Biol. 2020, 432, 2405–2427. [Google Scholar] [CrossRef]
- Raya-Sandino, A.; Lozada-Soto, K.M.; Rajagopal, N.; Garcia-Hernandez, V.; Luissint, A.-C.; Brazil, J.C.; Cui, G.; Koval, M.; Parkos, C.A.; Nangia, S.; et al. Claudin-23 Reshapes Epithelial Tight Junction Architecture to Regulate Barrier Function. Nat. Commun. 2023, 14, 6214. [Google Scholar] [CrossRef] [PubMed]
- Fuladi, S.; McGuinness, S.; Shen, L.; Weber, C.R.; Khalili-Araghi, F. Molecular Mechanism of Claudin-15 Strand Flexibility: A Computational Study. J. Gen. Physiol. 2022, 154, e202213116. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Schulten, K. Further Optimization of a Hybrid United-Atom and Coarse-Grained Force Field for Folding Simulations: Improved Backbone Hydration and Interactions between Charged Side Chains. J. Chem. Theory Comput. 2012, 8, 4413–4424. [Google Scholar] [CrossRef][Green Version]
- Han, W.; Wan, C.-K.; Jiang, F.; Wu, Y.-D. PACE Force Field for Protein Simulations. 1. Full Parameterization of Version 1 and Verification. J. Chem. Theory Comput. 2010, 6, 3373–3389. [Google Scholar] [CrossRef]
- Wan, C.-K.; Han, W.; Wu, Y.-D. Parameterization of PACE Force Field for Membrane Environment and Simulation of Helical Peptides and Helix–Helix Association. J. Chem. Theory Comput. 2012, 8, 300–313. [Google Scholar] [CrossRef]
- Fuladi, S.; McGuinness, S.; Khalili-Araghi, F. Role of TM3 in Claudin-15 Strand Flexibility: A Molecular Dynamics Study. Front. Mol. Biosci. 2022, 9, 964877. [Google Scholar] [CrossRef]
- Janin, J. Protein–Protein Docking Tested in Blind Predictions: The CAPRI Experiment. Mol. Biosyst. 2010, 6, 2351–2362. [Google Scholar] [CrossRef]
- Llanos, M.A.; Gantner, M.E.; Rodriguez, S.; Alberca, L.N.; Bellera, C.L.; Talevi, A.; Gavernet, L. Strengths and Weaknesses of Docking Simulations in the SARS-CoV-2 Era: The Main Protease (Mpro) Case Study. J. Chem. Inf. Model. 2021, 61, 3758–3770. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingólfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational Modeling of Realistic Cell Membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef]
- Feig, M.; Nawrocki, G.; Yu, I.; Wang, P.-H.; Sugita, Y. Challenges and Opportunities in Connecting Simulations with Experiments via Molecular Dynamics of Cellular Environments. J. Phys. Conf. Ser. 2018, 1036, 012010. [Google Scholar] [CrossRef]
- Rizo, J.; Sari, L.; Qi, Y.; Im, W.; Lin, M.M. All-Atom Molecular Dynamics Simulations of Synaptotagmin-SNARE-Complexin Complexes Bridging a Vesicle and a Flat Lipid Bilayer. eLife 2022, 11, e76356. [Google Scholar] [CrossRef]
- Milles, L.F.; Schulten, K.; Gaub, H.E.; Bernardi, R.C. Molecular Mechanism of Extreme Mechanostability in a Pathogen Adhesin. Science 2018, 359, 1527–1533. [Google Scholar] [CrossRef]
- Jiang, W.; Del Rosario, J.S.; Botello-Smith, W.; Zhao, S.; Lin, Y.; Zhang, H.; Lacroix, J.; Rohacs, T.; Luo, Y.L. Crowding-Induced Opening of the Mechanosensitive Piezo1 Channel in Silico. Commun. Biol. 2021, 4, 1–14. [Google Scholar] [CrossRef]
- Gumbart, J.; Khalili-Araghi, F.; Sotomayor, M.; Roux, B. Constant Electric Field Simulations of the Membrane Potential Illustrated with Simple Systems. Biochim. Biophys. Acta BBA—Biomembr. 2012, 1818, 294–302. [Google Scholar] [CrossRef]
- Aksimentiev, A.; Schulten, K. Imaging α-Hemolysin with Molecular Dynamics: Ionic Conductance, Osmotic Permeability, and the Electrostatic Potential Map. Biophys. J. 2005, 88, 3745–3761. [Google Scholar] [CrossRef]
- Sotomayor, M.; Vásquez, V.; Perozo, E.; Schulten, K. Ion Conduction through MscS as Determined by Electrophysiology and Simulation. Biophys. J. 2007, 92, 886–902. [Google Scholar] [CrossRef] [PubMed]
- Khalili-Araghi, F.; Tajkhorshid, E.; Schulten, K. Dynamics of K+ Ion Conduction through Kv1.2. Biophys. J. 2006, 91, L72–L74. [Google Scholar] [CrossRef]
- Khalili-Araghi, F.; Tajkhorshid, E.; Roux, B.; Schulten, K. Molecular Dynamics Investigation of the ω-Current in the Kv1.2 Voltage Sensor Domains. Biophys. J. 2012, 102, 258–267. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jensen, M.Ø.; Borhani, D.W.; Lindorff-Larsen, K.; Maragakis, P.; Jogini, V.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Principles of Conduction and Hydrophobic Gating in K+ Channels. Proc. Natl. Acad. Sci. USA 2010, 107, 5833–5838. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.Ø.; Jogini, V.; Eastwood, M.P.; Shaw, D.E. Atomic-Level Simulation of Current–Voltage Relationships in Single-File Ion Channels. J. Gen. Physiol. 2013, 141, 619–632. [Google Scholar] [CrossRef]
- Jiang, W.; Lacroix, J.; Luo, Y.L. Importance of Molecular Dynamics Equilibrium Protocol on Protein-Lipid Interaction near Channel Pore. Biophys. Rep. 2022, 2, 100080. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, M.; Lyubchenko, Y.L. Hybrid Resolution Molecular Dynamics Simulations of Amyloid Proteins Interacting with Membranes. Methods San Diego Calif. 2022, 197, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Davidson, W.S.; Jonas, A.; Clayton, D.F.; George, J.M. Stabilization of α-Synuclein Secondary Structure upon Binding to Synthetic Membranes *. J. Biol. Chem. 1998, 273, 9443–9449. [Google Scholar] [CrossRef] [PubMed]
- Nusrat, A.; Parkos, C.A.; Verkade, P.; Foley, C.S.; Liang, T.W.; Innis-Whitehouse, W.; Eastburn, K.K.; Madara, J.L. Tight Junctions Are Membrane Microdomains. J. Cell Sci. 2000, 113, 1771–1781. [Google Scholar] [CrossRef] [PubMed]
- Shigetomi, K.; Ono, Y.; Matsuzawa, K.; Ikenouchi, J. Cholesterol-Rich Domain Formation Mediated by ZO Proteins Is Essential for Tight Junction Formation. Proc. Natl. Acad. Sci. USA 2023, 120, e2217561120. [Google Scholar] [CrossRef]
- Shigetomi, K.; Ono, Y.; Inai, T.; Ikenouchi, J. Adherens Junctions Influence Tight Junction Formation via Changes in Membrane Lipid Composition. J. Cell Biol. 2018, 217, 2373–2381. [Google Scholar] [CrossRef]
- Van Itallie, C.M.; Gambling, T.M.; Carson, J.L.; Anderson, J.M. Palmitoylation of Claudins Is Required for Efficient Tight-Junction Localization. J. Cell Sci. 2005, 118, 1427–1436. [Google Scholar] [CrossRef]
- Heiler, S.; Mu, W.; Zöller, M.; Thuma, F. The Importance of Claudin-7 Palmitoylation on Membrane Subdomain Localization and Metastasis-Promoting Activities. Cell Commun. Signal. 2015, 13, 29. [Google Scholar] [CrossRef]
- Rajagopal, N.; Irudayanathan, F.J.; Nangia, S. Palmitoylation of Claudin-5 Proteins Influences Their Lipid Domain Affinity and Tight Junction Assembly at the Blood–Brain Barrier Interface. J. Phys. Chem. B 2019, 123, 983–993. [Google Scholar] [CrossRef] [PubMed]
- Rodenburg, R.N.P.; Snijder, J.; van de Waterbeemd, M.; Schouten, A.; Granneman, J.; Heck, A.J.R.; Gros, P. Stochastic Palmitoylation of Accessible Cysteines in Membrane Proteins Revealed by Native Mass Spectrometry. Nat. Commun. 2017, 8, 1280. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McGuinness, S.; Sajjadi, S.; Weber, C.R.; Khalili-Araghi, F. Computational Models of Claudin Assembly in Tight Junctions and Strand Properties. Int. J. Mol. Sci. 2024, 25, 3364. https://doi.org/10.3390/ijms25063364
McGuinness S, Sajjadi S, Weber CR, Khalili-Araghi F. Computational Models of Claudin Assembly in Tight Junctions and Strand Properties. International Journal of Molecular Sciences. 2024; 25(6):3364. https://doi.org/10.3390/ijms25063364
Chicago/Turabian StyleMcGuinness, Sarah, Samaneh Sajjadi, Christopher R. Weber, and Fatemeh Khalili-Araghi. 2024. "Computational Models of Claudin Assembly in Tight Junctions and Strand Properties" International Journal of Molecular Sciences 25, no. 6: 3364. https://doi.org/10.3390/ijms25063364
APA StyleMcGuinness, S., Sajjadi, S., Weber, C. R., & Khalili-Araghi, F. (2024). Computational Models of Claudin Assembly in Tight Junctions and Strand Properties. International Journal of Molecular Sciences, 25(6), 3364. https://doi.org/10.3390/ijms25063364





