High Correlation Between Li+ Solvation Energy and Li+ Ionic Conductivity in Lithium Metal Battery Electrolytes
Abstract
1. Introduction
2. Results and Discussion
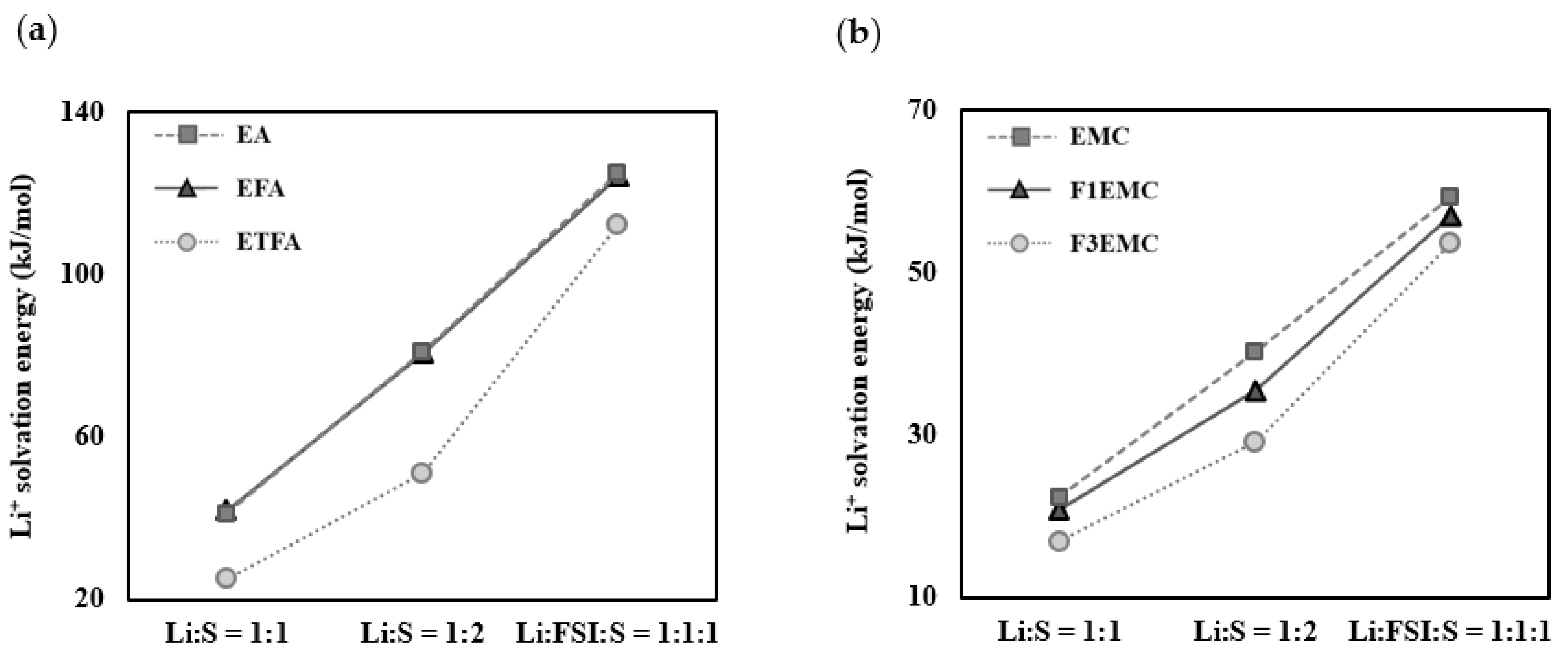
2.1. Li+ Solvation Energies According to the Solvation Sheath Compositions
2.2. Linear Regression Analysis of the Correlation Between Li+ Solvation Energies and Ionic Conductivities
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Bao, Z.; Cui, Y.; Dufek, E.J.; Goodenough, J.B.; Khalifah, P.; Li, Q.; Liaw, B.Y.; Liu, P.; Manthiram, A.; et al. Pathways for practical high-energy long-cycling lithium metal batteries. Nat. Energy 2019, 4, 180–186. [Google Scholar] [CrossRef]
- Hobold, G.M.; Lopez, J.; Guo, R.; Minafra, N.; Banerjee, A.; Meng, Y.S.; Shao-Horn, Y.; Gallant, B.M. Moving beyond 99.9% Coulombic Efficiency for Lithium Anodes in Liquid Electrolytes. Nat. Energy 2021, 6, 951–960. [Google Scholar] [CrossRef]
- Angarita-Gomez, S.; Balbuena, P.B. Understanding Solid Electrolyte Interphase Nucleation and Growth on Lithium Metal Surfaces. Batteries 2021, 7, 73. [Google Scholar] [CrossRef]
- Qin, Z.; Wu, B.; Danilov, D.L.; Eichel, R.A.; Notten, P.H. Dual-Salts Electrolyte with Fluoroethylene Carbonate Additive for High-Voltage Li-Metal Batteries. Batteries 2023, 9, 477. [Google Scholar] [CrossRef]
- Shi, P.; Wang, X.; Cheng, X.; Jiang, Y. Progress on Designing Artificial Solid Electrolyte Interphases for Dendrite-Free Sodium Metal Anodes. Batteries 2023, 9, 345. [Google Scholar] [CrossRef]
- Dessantis, D.; Di Prima, P.; Versaci, D.; Amici, J.; Francia, C.; Bodoardo, S.; Santarelli, M. Aging of a Lithium-Metal/LFP Cell: Predictive Model and Experimental Validation. Batteries 2023, 9, 146. [Google Scholar] [CrossRef]
- Ishfaq, H.A.; Cruz Cardona, C.; Tchernychova, E.; Johansson, P.; Dominko, R.; Drvarič Talian, S. Enhanced Performance of Lithium Metal Batteries via Cyclic Fluorinated Ether-Based Electrolytes. Energy Storage Mater. 2024, 69, 103375. [Google Scholar] [CrossRef]
- Zhang, Y.; Viswanathan, V. Design Rules for Selecting Fluorinated Linear Organic Solvents for Li Metal Batteries. J. Phys. Chem. Lett. 2021, 12, 5821–5828. [Google Scholar] [CrossRef]
- Perez-Beltran, S.; Kuai, D.; Balbuena, P.B. SEI Formation and Lithium-Ion Electrodeposition Dynamics in Lithium Metal Batteries via First-Principles Kinetic Monte Carlo Modeling. ACS Energy Lett. 2024, 9, 5268–5278. [Google Scholar] [CrossRef]
- Quilty, C.D.; Marin Bernardez, E.J.; Nicoll, A.; Hossain, M.J.; Kingan, A.; Arnot, D.J.; Mohamed, H.A.; O’Connor, C.L.; Tong, X.; Jaye, C.; et al. Lithium-Ion Battery Functionality over Broad Operating Conditions via Local High-Concentration Fluorinated Ester Electrolytes. RSC Appl. Interfaces 2024, 1, 1077–1092. [Google Scholar] [CrossRef]
- Dalmijn, J.; Teunissen, P.; Verhoeven, P.; Weijers, J. Emission Inventory of PFASs and Other Fluorinated Organic Substances for the Fluoropolymer Production Industry in Europe. Environ. Sci. Process. Impacts 2023, 26, 269–287. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Chang, J.; Wang, L.; Li, J.; Wang, C.; Wang, R.; Shi, G.; Yu, K.; Huang, W.; Zheng, H.; et al. A monofluoride ether-based electrolyte solution for fast-charging and low-temperature non-aqueous lithium metal batteries. Nat. Commun. 2023, 14, 1081. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Dong, S.; Gao, Y.; Lee, P.K.; Tian, Y.; Meng, Y.; Hu, X.; Zhao, X.; Li, B.; Zhou, D.; et al. Difluoroester solvent toward fast-rate anion-intercalation lithium metal batteries under extreme conditions. Nat. Commun. 2024, 15, 5408. [Google Scholar] [CrossRef] [PubMed]
- Ruan, D.; Tan, L.; Chen, S.; Fan, J.; Nian, Q.; Chen, L.; Wang, Z.; Ren, X. Solvent versus Anion Chemistry: Unveiling the Structure-Dependent Reactivity in Tailoring Electrochemical Interphases for Lithium-Metal Batteries. J. Am. Chem. Soc. Au 2023, 3, 953–963. [Google Scholar] [CrossRef]
- Yu, Z.; Rudnicki, P.E.; Zhang, Z.; Huang, H.; Celik, S.T.; Oyakhire, Y.; Chen, X.; Kong, S.C.; Kim, X.; Xiao, H.; et al. Rational solvent molecule tuning for high-performance lithium metal battery electrolytes. Nat. Energy 2022, 7, 94–106. [Google Scholar] [CrossRef]
- Mo, Y.; Liu, G.; Yin, Y.; Tao, M.; Chen, J.; Peng, Y.; Wang, Y.; Yang, Y.; Wang, C.; Dong, X.; et al. Fluorinated Solvent Molecule Tuning Enables Fast-Charging and Low-Temperature Lithium-Ion Batteries. Adv. Energy Mater. 2023, 13, 2301285. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, W.; Chen, Y.; Mondonico, L.; Xiao, X.; Zheng, Y.; Liu, F.; Hung, S.T.; Cui, Y.; Bao, Z. Tuning Fluorination of Linear Carbonate for Lithium-Ion Batteries. J. Electrochem. Soc. 2022, 169, 40555. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, T.; Mensi, M.; Choi, J.W.; Coskun, A. Electrolyte Engineering via Ether Solvent Fluorination for Developing Stable Non-Aqueous Lithium Metal Batteries. Nat. Commun. 2023, 14, 299. [Google Scholar] [CrossRef]
- Xu, J.; Koverga, V.; Phan, A.; Min Li, A.; Zhang, N.; Baek, M.; Jayawardana, C.; Lucht, B.L.; Ngo, A.T.; Wang, C. Revealing the Anion–Solvent Interaction for Ultralow Temperature Lithium Metal Batteries. Adv. Mater. 2024, 36, 2306462. [Google Scholar] [CrossRef]
- Li, C.; Xu, H.; Ni, L.; Qin, B.; Ma, Y.; Jiang, H.; Xu, G.; Zhao, J.; Cui, G. Nonaqueous Liquid Electrolytes for Sodium-Ion Batteries: Fundamentals, Progress and Perspectives. Adv. Energy Mater. 2023, 13, 2301758. [Google Scholar] [CrossRef]
- Kawaji, J.; Unemoto, A.; Seki, E.; Hirooka, M.; Ikeshoji, T.; Ueno, K.; Dokko, K.; Watanabe, M.; Okumura, T. Local Lithium-Ion Transport of a Ternary Sulfolane-Lithium Bis(trifluoromethanesulfonyl)amide-Carbonate Electrolyte: Experimental and First-Principles Molecular Dynamics Analysis toward Quasi-Solid-State Lithium-Ion Battery. J. Electrochem. Soc. 2022, 169, 20534. [Google Scholar] [CrossRef]
- Li, Z.; Borodin, O.; Smith, G.D.; Bedrov, D. Effect of organic solvents on Li+ ion solvation and transport in ionic liquid electrolytes: A molecular dynamics simulation study. J. Phys. Chem. B 2015, 119, 3085–3096. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, T.C.; Barros, L.M.S.; Anchieta, C.G.; Nepel, T.C.M.; Júlio, J.P.O.; Dias, L.G.; Filho, R.M.; Doubek, G.; Da Silva, J.L.F. Tuning aprotic solvent properties with long alkyl chain ionic liquid for lithium-based electrolytes. J. Mater. Chem. A 2022, 10, 11684–11701. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Abbotto, A.; Streitwieser, A.; Schleyer, P.V.R. Ab initio and semiempirical study of the effect of ethereal solvent on aggregation of a lithium enolate. J. Am. Chem. Soc. 1997, 119, 11255–11268. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1998, 37, 785. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Kim, Y.M.; Park, B.K.; Kang, S.; Yang, S.J.; Choi, S.H.; Yoo, D.J.; Kim, K.J. Bespoke dual-layered interface enabled by cyclic ether in localized high-concentration electrolytes for lithium metal batteries. Adv. Funct. Mater. 2024, 169, 2408365. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, W.; Liu, S.; Cao, Q.; Yan, S.; Liu, H.; Hou, W.; Zhou, P.; Song, X.; Ou, Y.; et al. Tuning the Li+ solvation structure by a “bulky coordinating” strategy enables nonflammable electrolyte for ultrahigh voltage lithium metal batteries. ACS Nano 2023, 17, 9586–9599. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Tang, M.; Dong, S.; Wang, J.; Cheng, L.; Zhu, Q.; Li, Y.; Yang, X.; Guo, L.; Wang, H. Low-temperature anode-free potassium metal batteries. Nat. Commun. 2023, 14, 6006. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Ding, Y.; Wang, Y.; Li, H.; Shang, J.; Cao, Y.; Wang, H. Bulk bismuth anodes for wide-temperature sodium-ion batteries enabled by electrolyte chemistry modulation. J. Colloid Interface Sci. 2024, 657, 502–510. [Google Scholar] [CrossRef] [PubMed]
- Evshchik, E.Y.; Kalinovskaya, I.V.; Yachmenyov, V.A.; Shapranova, O.V.; Kovalenko, L.M.; Fomina, L.A.; Tikhomirova, V.A. Determining the Oxidation Stability of Electrolytes for Lithium-Ion Batteries Using Quantum Chemistry and Molecular Dynamics. Electrochem 2024, 5, 107–123. [Google Scholar] [CrossRef]
- Dobrovolsky, Y.A.; Ilyina, M.G.; Evshchik, E.Y.; Khamitov, E.M.; Chernyak, A.V.; Shikhovtseva, A.V.; Melnikova, T.I.; Bushkova, O.V.; Borisevich, S.S. QC and MD Modelling for Predicting the Electrochemical Stability Window of Electrolytes: New Estimating Algorithm. Batteries 2022, 8, 292. [Google Scholar] [CrossRef]
- Galimzyanov, R.R.; Stakhanova, S.V.; Krechetov, I.S.; Kalashnik, A.T.; Astakhov, M.V.; Lisitsin, A.V.; Rychagov, A.Y.; Galimzyanov, T.R.; Tabarov, F.S. Electrolyte mixture based on acetonitrile and ethyl acetate for a wide temperature range performance of supercapacitors. J. Power Sources 2021, 495, 229442. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0: New Vistas in Localized and Delocalized Chemical Bonding Theory. J. Comput. Chem. 2019, 40, 2234–2241. [Google Scholar] [CrossRef]
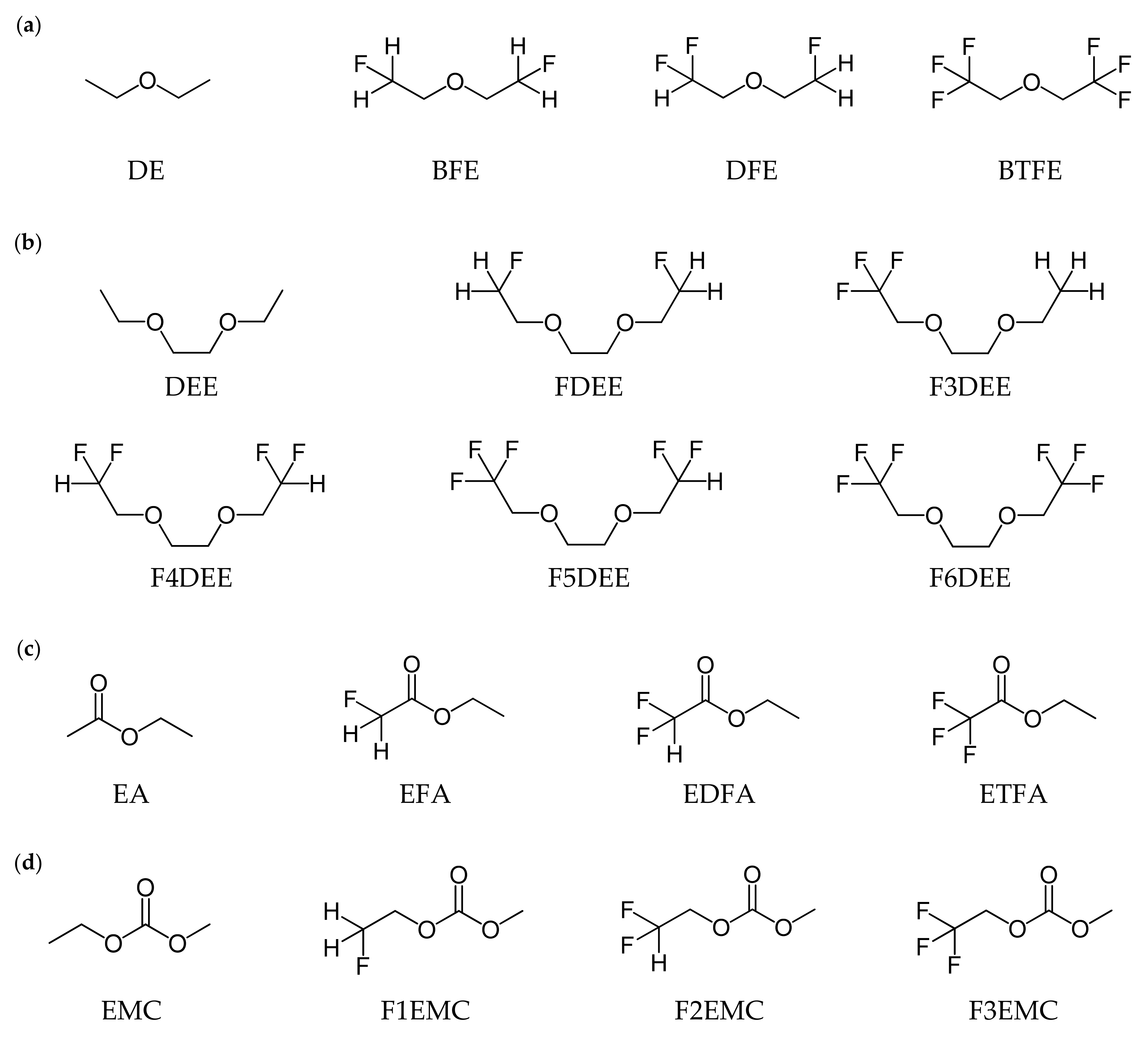
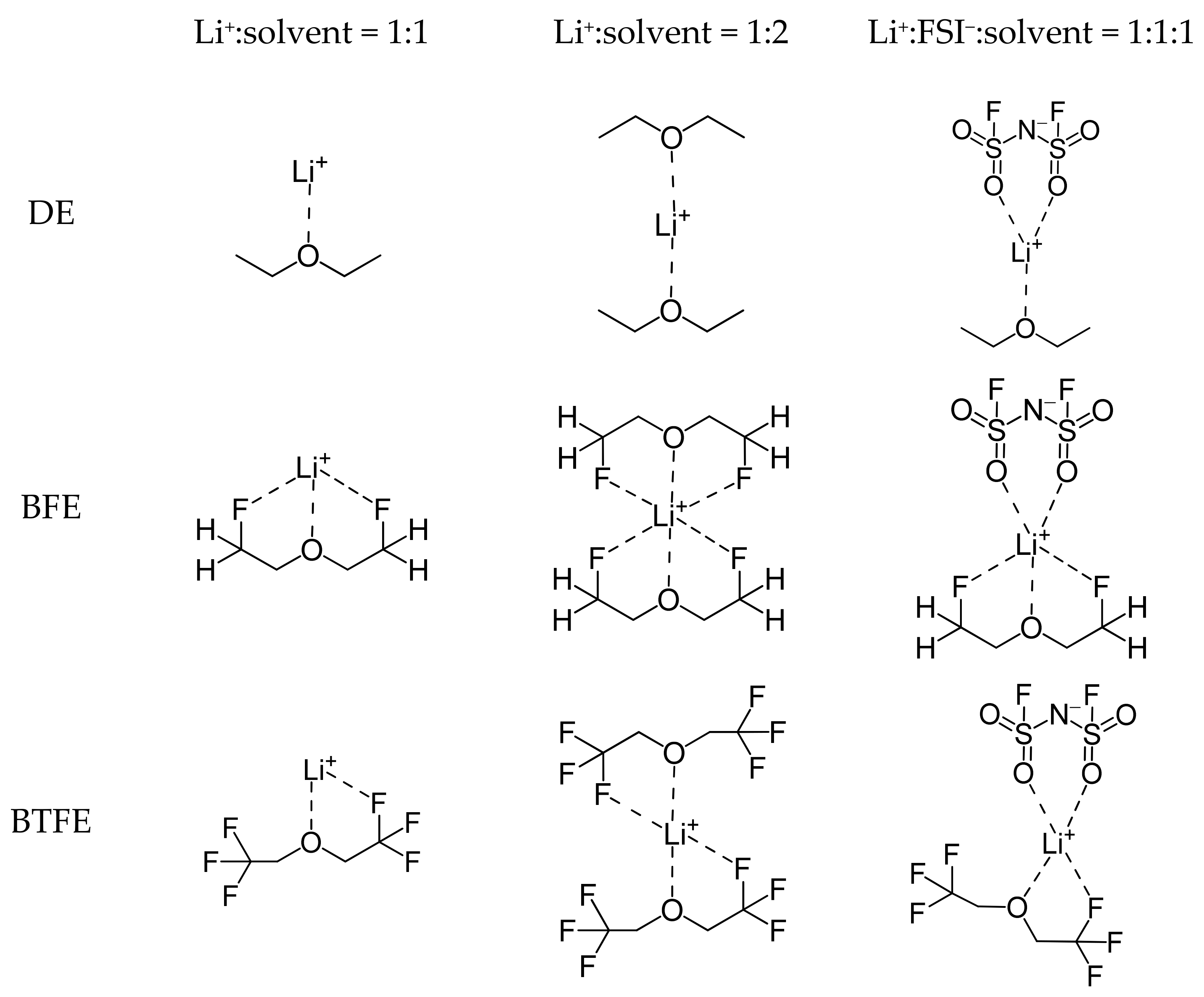
| Molecule | Li+ Solvation Energy | Ionic Conductivity | ||
|---|---|---|---|---|
| Li+:Solvent = 1:1 | Li+:Solvent = 1:2 | Li+:FSI−:Solvent = 1:1:1 | Experiment (Reference) | |
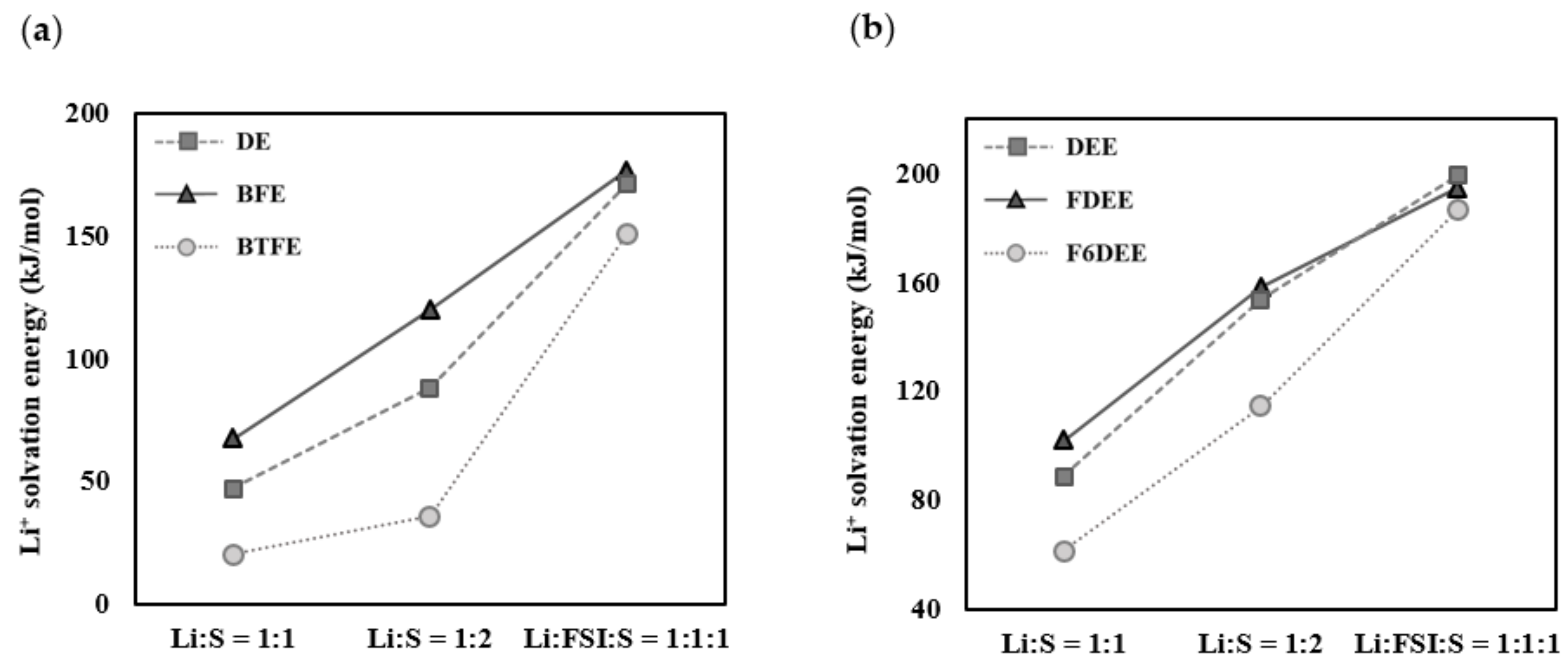
| DE | 47.3 | 88.1 | 171.4 | 1.0 a |
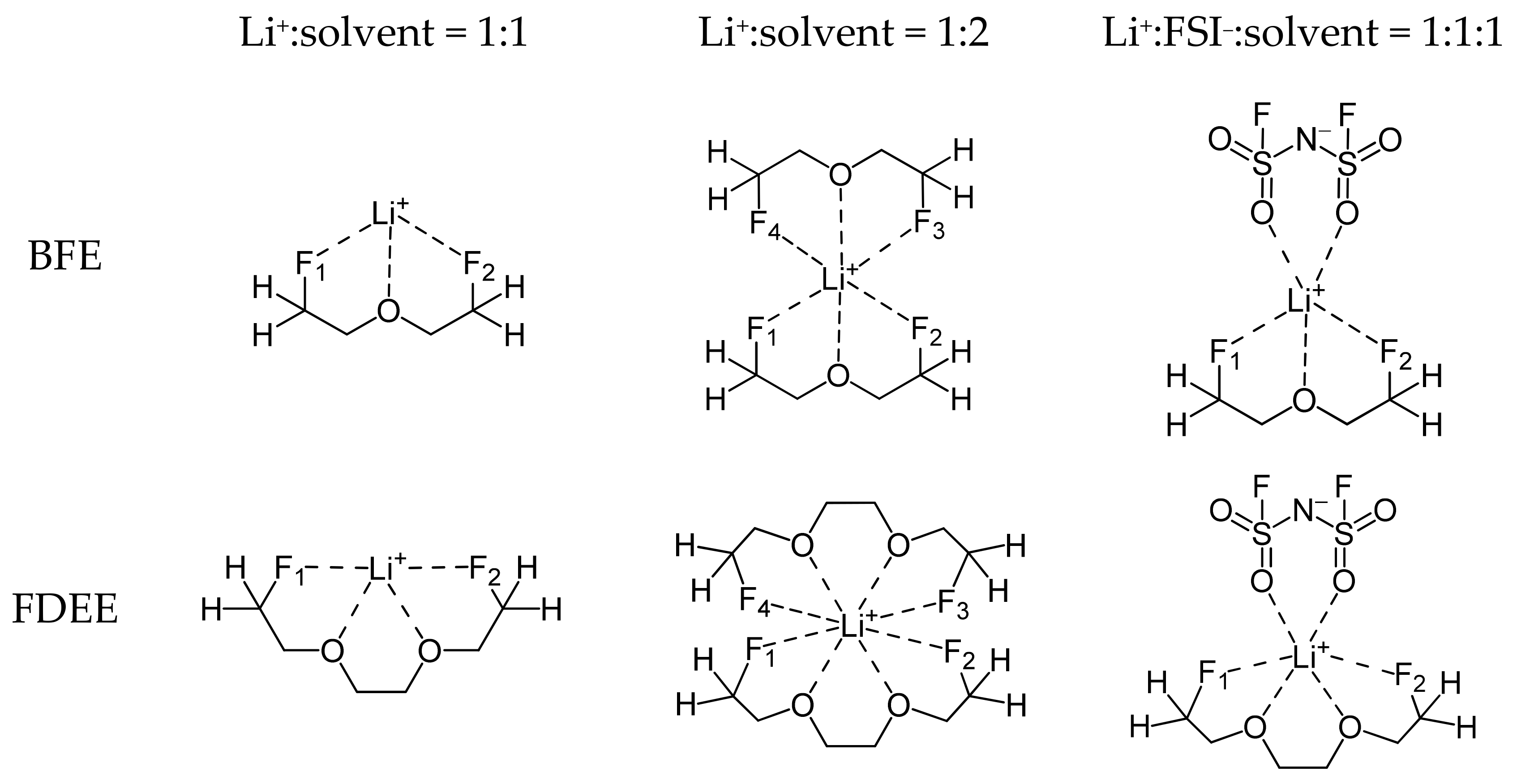
| BFE | 67.4 | 120.2 | 176.6 | 7.4 a |
| BTFE | 20.4 | 35.9 | 150.9 | – |
| DEE | 88.8 | 153.9 | 199.3 | 7.2 b |
| FDEE | 102.0 | 158.7 | 194.7 | 3.2 b |
| F6DEE | 61.6 | 114.7 | 186.8 | – |
| Molecule | Li+−F Bond Length | ||
|---|---|---|---|
| Li+:Solvent = 1:1 | Li+:Solvent = 1:2 | Li+:FSI−:Solvent = 1:1:1 | |
| BFE | |||
| Li+–F1 | 2.08 | 2.12 | 2.11 |
| Li+–F2 | 2.15 | 2.17 | 2.13 |
| Li+–F3 | 2.11 | ||
| Li+–F4 | 2.15 | ||
| FDEE | |||
| Li+–F1 | 2.08 | 2.94 | 2.78 |
| Li+–F2 | 2.08 | 3.16 | 2.70 |
| Li+–F3 | 3.12 | ||
| Li+–F4 | 3.14 | ||
| Molecule | Li+ Solvation Energy | Ionic Conductivity | ||
|---|---|---|---|---|
| Li+:Solvent = 1:1 | Li+:Solvent = 1:2 | Li+:FSI−:Solvent = 1:1:1 | Experiment (Reference) | |
| EA | 41.2 | 81.0 | 125.1 | 11.2 a |
| EFA | 41.8 | 80.6 | 124.0 | 8.9 a |
| ETFA | 25.0 | 51.0 | 112.3 | 4.2 a |
| EMC | 22.5 | 40.4 | 59.5 | 0.54 b |
| F1EMC | 20.7 | 35.5 | 57.1 | 0.52 b |
| F3EMC | 17.1 | 29.3 | 53.8 | 0.42 b |
| Molecule | Li+ Solvation Energy | Ionic Conductivity | ||
|---|---|---|---|---|
| Li+:Solvent = 1:1 | Li+:Solvent = 1:2 | Li+:FSI−:Solvent = 1:1:1 | Experiment (Reference) | |
| DE | 47.3 | 88.1 | 171.4 | 1.0 a |
| BFE | 67.4 | 120.2 | 176.6 | 7.4 a |
| DFE | 56.9 | 98.5 | 172.4 | 2.6 a |
| DEE | 88.8 | 153.9 | 199.3 | 11.0 b |
| F3DEE | 73.2 | 130.5 | 191.1 | 6.2 b |
| F4DEE | 76.5 | 119.4 | 187.2 | 4.8 b |
| F5DEE | 67.6 | 123.4 | 187.8 | 5.0 b |
| F6DEE | 61.6 | 114.7 | 186.8 | 4.5 b |
| EA | 41.2 | 81.0 | 125.1 | 11.2 c |
| EFA | 41.8 | 80.6 | 124.0 | 8.9 c |
| EDFA | 32.6 | 65.6 | 117.7 | 7.9 c |
| ETFA | 25.0 | 51.0 | 112.3 | 4.2 c |
| EMC | 22.5 | 40.4 | 59.5 | 0.54 d |
| F1EMC | 20.7 | 35.5 | 57.1 | 0.52 d |
| F2EMC | 18.0 | 33.1 | 55.9 | 0.50 d |
| F3EMC | 17.1 | 29.3 | 53.8 | 0.42 d |
| Group | Correlation Coefficient (R2) | |||
|---|---|---|---|---|
| Li+:Solvent = 1:1 | Li+:Solvent = 1:2 | Li+:FSI−:Solvent = 1:1:1 | Li+:Solvent = 1:1 (Reference) | |
| A | 0.968 | 0.997 | 0.998 | 0.986 a |
| B | 0.871 | 0.986 | 0.996 | 0.278 b |
| C | 0.921 | 0.940 | 0.950 | 0.763 c |
| D | 0.863 | 0.918 | 0.931 | 0.698 d |
| Average correlation coefficient | ||||
| A−D | 0.906 | 0.960 | 0.969 | 0.681 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Han, Y.-K. High Correlation Between Li+ Solvation Energy and Li+ Ionic Conductivity in Lithium Metal Battery Electrolytes. Int. J. Mol. Sci. 2024, 25, 13268. https://doi.org/10.3390/ijms252413268
Choi J, Han Y-K. High Correlation Between Li+ Solvation Energy and Li+ Ionic Conductivity in Lithium Metal Battery Electrolytes. International Journal of Molecular Sciences. 2024; 25(24):13268. https://doi.org/10.3390/ijms252413268
Chicago/Turabian StyleChoi, Jihoon, and Young-Kyu Han. 2024. "High Correlation Between Li+ Solvation Energy and Li+ Ionic Conductivity in Lithium Metal Battery Electrolytes" International Journal of Molecular Sciences 25, no. 24: 13268. https://doi.org/10.3390/ijms252413268
APA StyleChoi, J., & Han, Y.-K. (2024). High Correlation Between Li+ Solvation Energy and Li+ Ionic Conductivity in Lithium Metal Battery Electrolytes. International Journal of Molecular Sciences, 25(24), 13268. https://doi.org/10.3390/ijms252413268







