Quelling the Geometry Factor Effect in Quantum Chemical Calculations of 13C NMR Chemical Shifts with the Aid of the pecG-n (n = 1, 2) Basis Sets
Abstract
1. Introduction
2. Results and Discussion
2.1. The PEC Method and the pecG-n (n = 1, 2) Basis Sets
2.2. Theoretical Analysis of the pecG-n (n = 1, 2) Basis Sets
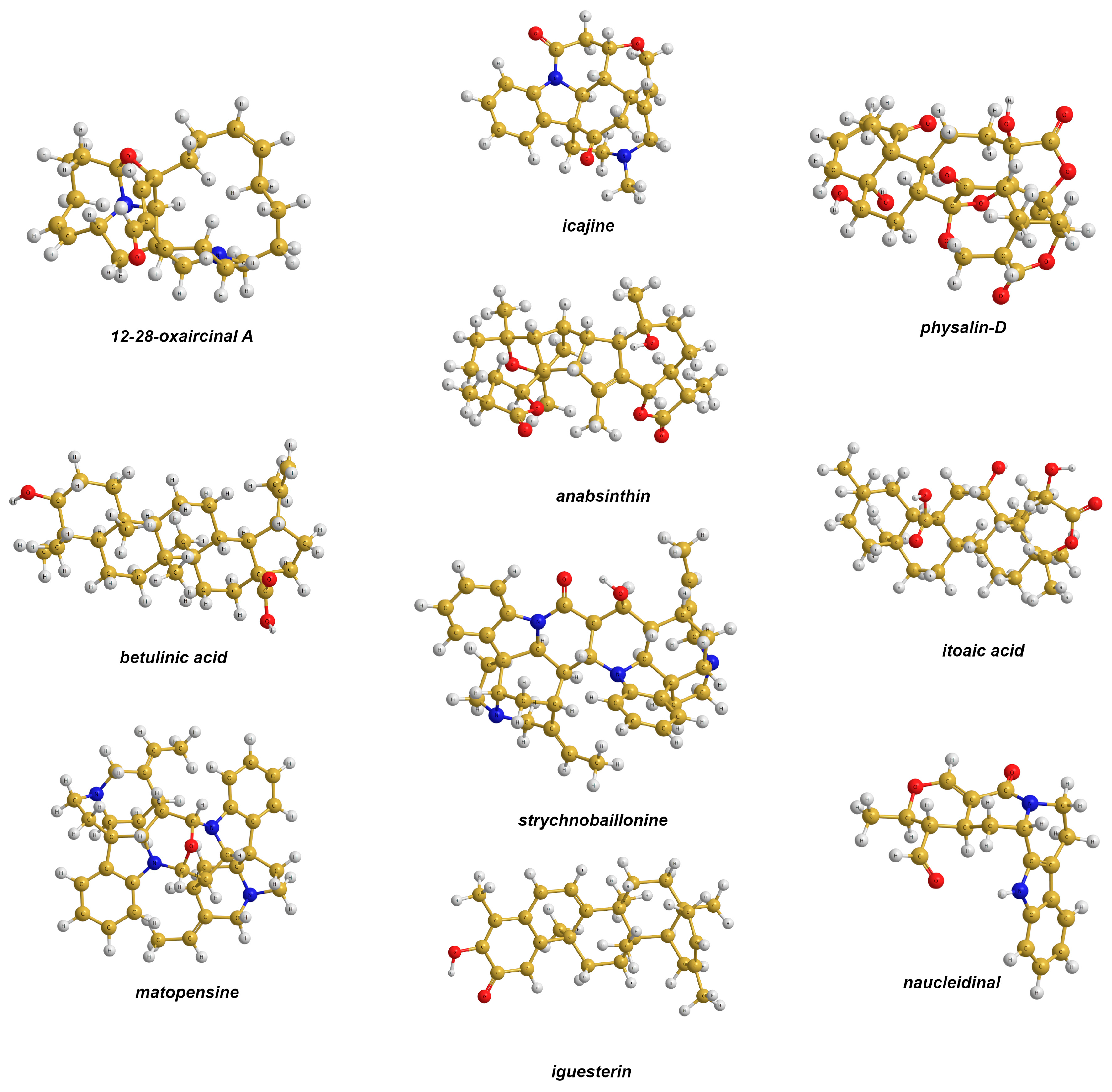
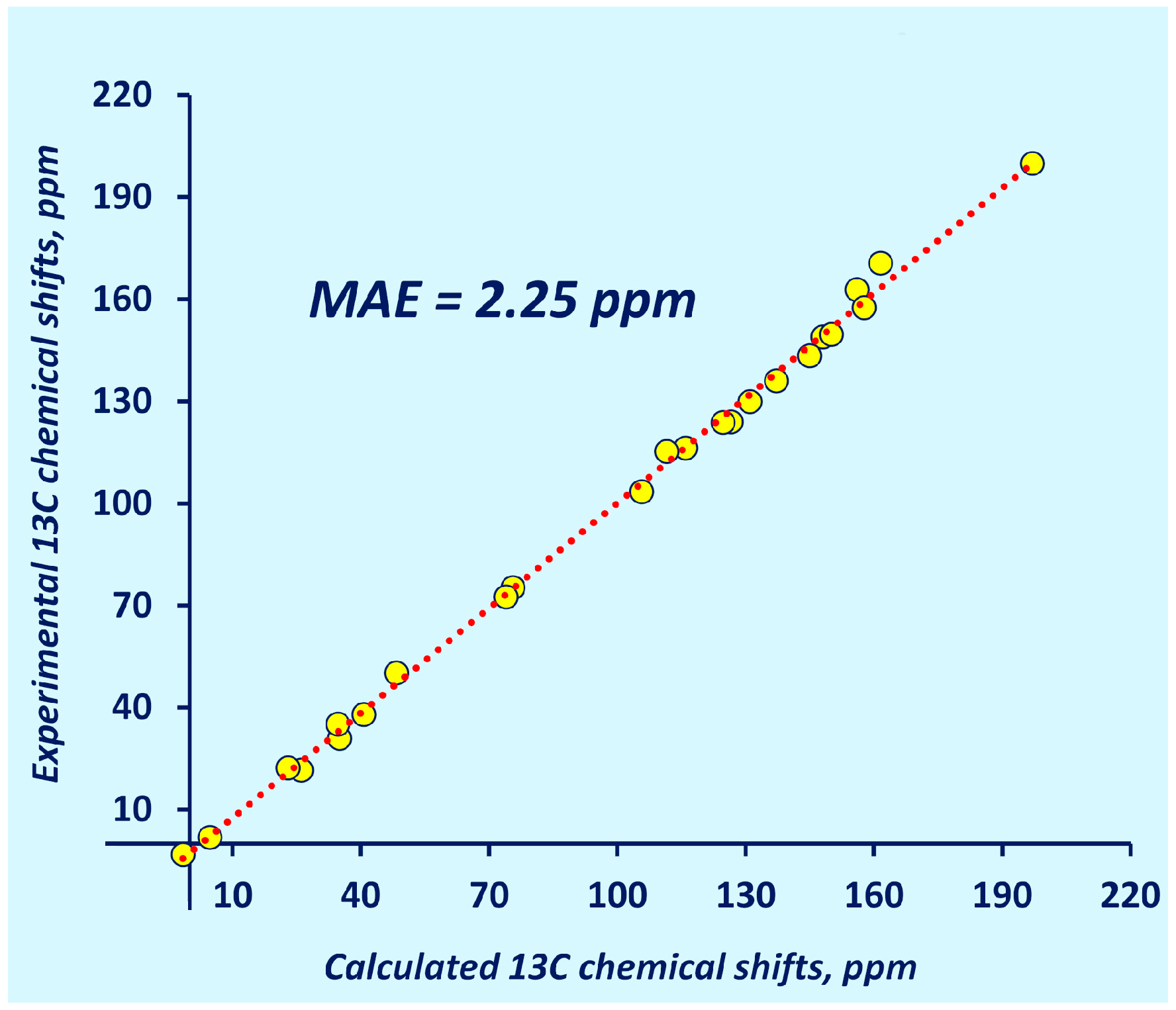
2.3. Analysis of the Performance of the pecG-n (n = 1, 2) Basis Sets Based on a Comparison of the Theoretical Data with Experimental Data
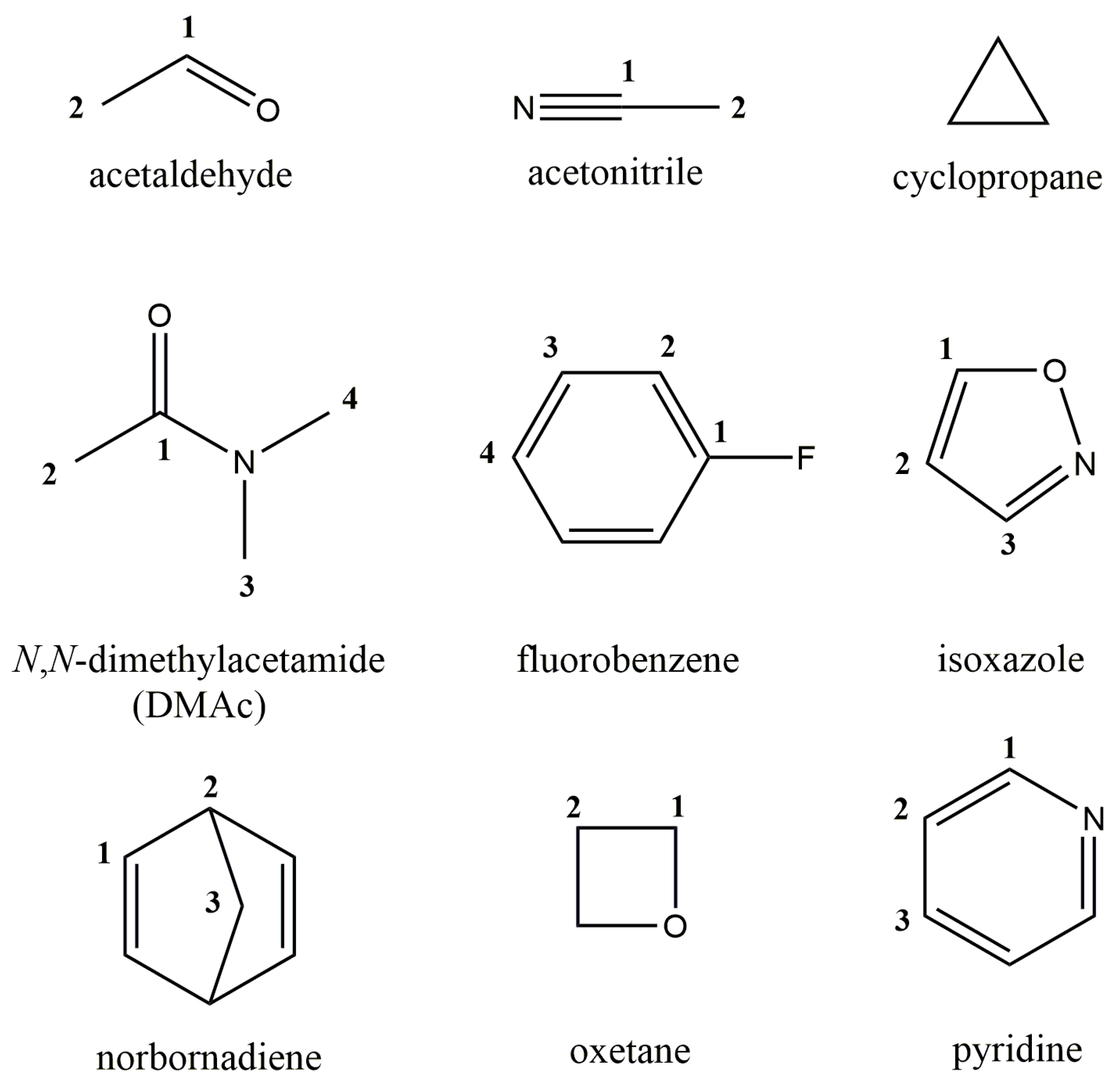
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Z.; Bi, T.; Jiang, H.; Liu, H. Review on NMR as a tool to analyse natural products extract directly: Molecular structure elucidation and biological activity analysis. Phytochem. Anal. 2024, 35, 5–16. [Google Scholar] [CrossRef] [PubMed]
- Semenov, V.A.; Krivdin, L.B. Computational NMR of natural products. Russ. Chem. Rev. 2022, 91, RCR5027. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational 1H and 13C NMR in structural and stereochemical studies. Magn. Reson. Chem. 2022, 60, 733–828. [Google Scholar] [CrossRef] [PubMed]
- Helgaker, T.; Jaszuński, M.; Ruud, K. Ab Initio Methods for the Calculation of NMR Shielding and Indirect Spin−Spin Coupling Constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef] [PubMed]
- Rusakova, I.L. Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances. Magnetochemistry 2022, 8, 50. [Google Scholar] [CrossRef]
- Rablen, P.R.; Pearlman, S.A.; Finkbiner, J. A comparison of density functional methods for the estimation of proton chemical shifts with chemical accuracy. J. Phys. Chem. A 1999, 103, 7357–7363. [Google Scholar] [CrossRef]
- Toušek, J.; Dostál, J.; Marek, R. Theoretical and experimental NMR chemical shifts of norsanguinarine and norchelerythrine. J. Mol. Struct. 2004, 689, 115–120. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Quin, L.D. A study of NMR chemical shielding in 5-coordinate phosphorus compounds (phosphoranes). Tetrahedron 2005, 61, 12343–12349. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Yan, Y. Systematic investigation on the geometric dependence of the calculated nuclear magnetic shielding constants. J. Comput. Chem. 2008, 29, 1798–1807. [Google Scholar] [CrossRef]
- Nguyen, T.T. 1H/13C chemical shift calculations for biaryls: DFT approaches to geometry optimization. R. Soc. Open Sci. 2021, 8, 210954. [Google Scholar] [CrossRef]
- Kondrashova, S.A.; Polyancev, F.M.; Ganushevich, Y.S.; Latypov, S.K. DFT approach for predicting 13C NMR shifts of atoms directly coordinated to nickel. Organometallics 2021, 40, 1614–1625. [Google Scholar] [CrossRef]
- Wu, H.; Hemmingsen, L.; Sauer, S.P.A. On the geometry dependence of the nuclear magnetic resonance chemical shift of mercury in thiolate complexes: A relativistic density functional theory study. Magn. Reson. Chem. 2024, 62, 648–669. [Google Scholar] [CrossRef] [PubMed]
- Helgaker, T.; Gauss, J.; Jørgensen, P.; Olsen, J. The prediction of molecular equilibrium structures by the standard electronic wave functions. J. Chem. Phys. 1997, 106, 6430–6440. [Google Scholar] [CrossRef]
- Temelso, B.; Valeev, E.F.; Sherrill, C.D. A Comparison of One-Particle Basis Set Completeness, Higher-Order Electron Correlation, Relativistic Effects, and Adiabatic Corrections for Spectroscopic Constants of BH, CH+, and NH+. J. Phys. Chem. A 2004, 108, 3068–3075. [Google Scholar] [CrossRef]
- Heckert, M.; Kállay, M.; Tew, D.P.; Klopper, W.; Gauss, J. Basis-set extrapolation techniques for the accurate calculation of molecular equilibrium geometries using coupled-cluster theory. J. Chem. Phys. 2006, 125, 044108. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Nikurashina, Y.A.; Rusakova, I.L. On the utmost importance of the geometry factor of accuracy in the quantum chemical calculations of 31P NMR chemical shifts: New efficient pecG-n (n = 1, 2) basis sets for the geometry optimization procedure. J. Chem. Phys. 2024, 160, 084109. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakova, I.L. An efficient method for generating propertyenergy consistent basis sets. New pecJ-n (n = 1, 2) basis sets for high-quality calculations of indirect nuclear spin–spin coupling constants involving 1H, 13C, 15N, and 19F nuclei. Phys. Chem. Chem. Phys. 2021, 23, 14925–14939. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakova, I.L. Getaway from the Geometry Factor Error in the Molecular Property Calculations: Efficient pecG-n (n = 1, 2) Basis Sets for the Geometry Optimization of Molecules Containing Light p Elements. J. Chem. Theory Comput. 2024, 20, 6661–6673. [Google Scholar] [CrossRef]
- Bartlett, R.J. Many-Body Perturbation Theory and Coupled Cluster Theory for Electron Correlation in Molecules. Annu. Rev. Phys. Chem. 1981, 32, 359–401. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Janssen, C.L.; Schaefer, H.F., III. An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations. J. Chem. Phys. 1988, 89, 7382–7387. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Gordon, M.S.; Binkley, J.S.; Pople, J.A.; Pietro, W.J.; Hehre, W.J. Self-consistent molecular-orbital methods. 22. Small split-valence basis sets for second-row elements. J. Am. Chem. Soc. 1982, 104, 2797–2803. [Google Scholar] [CrossRef]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Rao, K.V.; Donia, M.S.; Peng, J.; Garcia-Palomero, E.; Alonso, D.; Martinez, A.; Medina, M.; Franzblau, S.G.; Tekwani, B.L.; Khan, S.I.; et al. Manzamine B and E and Ircinal a Related Alkaloids from an Indonesian Acanthostrongylophora Sponge and Their Activity against Infectious, Tropical Parasitic, and Alzheimer’s Diseases. J. Nat. Prod. 2006, 69, 1034–1040. [Google Scholar] [CrossRef]
- Tchinda, A.T.; Tamze, V.; Ngono, A.R.N.; Ayimele, G.A.; Cao, M.; Angenot, L.; Frèdèrich, M. Alkaloids from the stem bark of Strychnos icaja. Phytochem. Lett. 2012, 5, 108–113. [Google Scholar] [CrossRef]
- Frèdèrich, M.; Choi, Y.H.; Angenot, L.; Harnischfeger, G.; Lefeber, A.W.M.; Verpoorte, R. Metabolomic analysis of Strychnos nux-vomica, Strychnos icaja and Strychnos ignatii extracts by 1H nuclear magnetic resonance spectrometry and multivariate analysis techniques. Phytochemistry 2004, 65, 1993–2001. [Google Scholar] [CrossRef]
- Januário, A.H.; Filho, E.R.; Pietro, R.C.L.R.; Kashima, S.; Sato, D.N.; França, S.C. Antimycobacterial physalins from Physalis angulata L. (Solanaceae). Phytother. Res. 2002, 16, 445–448. [Google Scholar] [CrossRef]
- Chudzik, M.; Korzonek-Szlacheta, I.; Król, W. Triterpenes as Potentially Cytotoxic Compounds. Molecules 2015, 20, 1610–1625. [Google Scholar] [CrossRef]
- Liu, J.H.; Tang, J.; Zhu, Z.F.; Chen, L. Design, synthesis, and anti-tumor activity of novel betulinic acid derivatives. J. Asian Nat. Prod. Res. 2014, 16, 34–42. [Google Scholar] [CrossRef]
- Boryczka, S.; Bębenek, E.; Wietrzyk, J.; Kempińska, K.; Jastrzębska, M.; Kusz, J.; Nowak, M. Synthesis, structure and cytotoxic activity of new acetylenic derivatives of betulin. Molecules 2013, 18, 4526–4543. [Google Scholar] [CrossRef] [PubMed]
- Urban, M.; VLK, M.; Dzubak, P.; Hajduch, M.; Sarek, J. Cytotoxic heterocyclic triterpenoids derived from betulin and betulinic acid. Bioorg. Med. Chem. 2012, 20, 3666–3674. [Google Scholar] [CrossRef] [PubMed]
- Baratto, L.C.; Porsani, M.V.; Pimentel, I.C.; Pereira Netto, A.B.; Paschke, R.; Oliveira, B.H. Preparation of betulinic acid derivatives by chemical and biotransformation methods and detrmination of cytotoxicity against selected cancer cell lines. Eur. J. Med. Chem. 2013, 68, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Aberham, A.; Cicek, S.S.; Schneider, P.; Stuppner, H. Analysis of Sesquiterpene Lactones, Lignans, and Flavonoids in Wormwood (Artemisia absinthium L.) Using High-Performance Liquid Chromatography (HPLC)-Mass Spectrometry, Reversed Phase HPLC, and HPLC-Solid Phase Extraction-Nuclear Magnetic Resonance. J. Agric. Food Chem. 2010, 58, 10817–10823. [Google Scholar] [CrossRef]
- Chai, X.-Y.; Xu, Z.-R.; Bai, C.-C.; Zhou, F.-R.; Tu, P.-F. A new seco-friedelolactone acid from the bark and twigs of Itoa orientalis. Fitoterapia 2009, 80, 408–410. [Google Scholar] [CrossRef]
- Frédérich, M.; Jacquier, M.-J.; Thépenier, P.; De Mol, P.; Tits, M.; Philippe, G.; Delaude, C.; Angenot, L.; Zèches-Hanrot, M. Antiplasmodial Activity of Alkaloids from Various Strychnos Species. J. Nat. Prod. 2002, 65, 1381–1386. [Google Scholar] [CrossRef]
- Tchinda, A.T.; Jansen, O.; Nyemb, J.-N.; Tits, M.; Dive, G.; Angenot, L.; Frédérich, M. Strychnobaillonine, an Unsymmetrical Bisindole Alkaloid with an Unprecedented Skeleton from Strychnos icaja Roots. J. Nat. Prod. 2014, 77, 1078–1082. [Google Scholar] [CrossRef]
- González, A.G.; Francisco, C.G.; Freire, R.; Hernández, R.; Salazar, J.A.; Suárez, E. Iguesterin, a new quinonoid triterpene from Catha cassinoides. Phytochemistry 1975, 14, 1067–1070. [Google Scholar] [CrossRef]
- Sneden, A.T. Isoiguesterin, A New Antileukemic Bisnortriterpene from Salacia madagascariensis. J. Nat. Prod. 1981, 44, 503–507. [Google Scholar] [CrossRef]
- Sichaem, J.; Worawalai, W.; Tip-pyang, S. Chemical constituents from the roots of nauclea orientalis. Chem. Natur. Comp. 2012, 48, 827–830. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Kiohara, V.O.; Carvalho, E.F.V.; Paschoal, C.W.A.; Machado, F.B.C.; Roberto-Neto, O. DFT and CCSD(T) electronic properties and structures of aluminum clusters: Alnx (n = 1–9, x = 0, ±1). Chem. Phys. Lett. 2013, 568–569, 42–48. [Google Scholar] [CrossRef]
- Walker, M.; Harvey, A.J.A.; Sen, A.; Dessent, C.E.H. Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions. Phys. Chem. A 2013, 117, 12590–12600. [Google Scholar] [CrossRef] [PubMed]
- Gauss, J.; Stanton, J.F. Perturbative treatment of triple excitations in coupled-cluster calculations of nuclear magnetic shielding constants. J. Chem. Phys. 1996, 104, 2574–2583. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Wilson, P.J.; Bradley, T.J.; Tozer, D.J. Hybrid exchange-correlation functional determined from thermochemical data and ab initio potentials. J. Chem. Phys. 2001, 115, 9233–9242. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakova, I.L. New pecS-n (n = 1, 2) basis sets for quantum chemical calculations of the NMR chemical shifts of H, C, N, and O nuclei. J. Chem. Phys. 2022, 156, 244112. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Rusakova, I.L. New efficient pecS-n (n = 1, 2) basis sets for quantum chemical calculations of 31P NMR chemical shifts. Phys. Chem. Chem. Phys. 2023, 25, 18728–18741. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Semenov, V.A.; Rusakova, I.L. On the Efficiency of the Density Functional Theory (DFT)-Based Computational Protocol for 1H and 13C Nuclear Magnetic Resonance (NMR) Chemical Shifts of Natural Products: Studying the Accuracy of the pecS-n (n = 1, 2) Basis Sets. Int. J. Mol. Sci. 2023, 24, 14623. [Google Scholar] [CrossRef]
- Teale, A.M.; Lutnæs, O.B.; Helgaker, T.; Tozer, D.J.; Gauss, J. Benchmarking density-functional theory calculations of NMR shielding constants and spin–rotation constants using accurate coupled-cluster calculations. J. Chem. Phys. 2013, 138, 024111. [Google Scholar] [CrossRef]
- Brzyska, A.; Borowski, P.; Woliński, K. Solvent effects on the nitrogen NMR chemical shifts in 1-methylazoles—A theoretical study. New J. Chem. 2015, 39, 9627–9640. [Google Scholar] [CrossRef]
- Hoffmann, F.; Li, D.-W.; Sebastiani, D.; Brüschweiler, R. Improved Quantum Chemical NMR Chemical Shift Prediction of Metabolites in Aqueous Solution Toward the Validation of Unknowns. J. Phys. Chem A 2017, 121, 3071–3078. [Google Scholar] [CrossRef] [PubMed]
- Chirchir, K.D.; Cheplogoi, K.P.; Omolo, O.J.; Langat, K.M. Chemical constituents of Solanum mauense (Solanaceae) and Dovyalis abyssinica (Salicaceae). Int. J. Biol. Chem. Sci. 2018, 12, 999–1007. [Google Scholar] [CrossRef]
- Verpoorte, R.; van Beek, T.A.; Riegman, R.L.M.; Hylands, P.J.; Bisset, N.G. Carbon-13 NMR spectroscopy of some Strychnos alkaloids: Part 2. Org. Magn. Reson. 1984, 22, 345–348. [Google Scholar] [CrossRef]
- Massiot, G.; Massoussa, B.; Thepenier, P.; Jaquier, M.-J.; le Men-Olivier, L.; Delaude, C. Structure of matopensine, a novel dimeric indole alkaloid from Strychnos species. Heterocycles 1983, 20, 2339–2342. [Google Scholar] [CrossRef]
- Massiot, G.; Massoussa, B.; Jacquier, M.-J.; Thépénier, P.; Le Men-Olivier, L.; Delaude, C.; Verpoorte, R. Alkaloids from roots of strychnos matopensis. Phytochemistry 1988, 27, 3293–3304. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; Cabral de Menezes, S.M.; Goodfellow, R.; Granger, P. NMR Nomenclature: Nuclear Spin Properties and Conventions for Chemical Shifts: IUPAC Recommendations 2001. Solid State Nucl. Magn. Reson. 2002, 22, 458–483. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; Cabral De Menezes, S.M.; Granger, P.; Hoffman, R.E.; Zilm, K.W. Further Conventions for NMR Shielding and Chemical Shifts (IUPAC Recommendations 2008). Magn. Reson. Chem. 2008, 46, 582–598. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Cohen, R.D.; Wood, J.S.; Lam, Y.-H.; Buevich, A.V.; Sherer, E.C.; Reibarkh, M.; Williamson, R.T.; Martin, G.E. DELTA50: A Highly Accurate Database of Experimental 1H and 13C NMR Chemical Shifts Applied to DFT Benchmarking. Molecules 2023, 28, 2449. [Google Scholar] [CrossRef]
- Jensen, F. Basis Set Convergence of Nuclear Magnetic Shielding Constants Calculated by Density Functional Methods. J. Chem. Theory Comput. 2008, 4, 719–727. [Google Scholar] [CrossRef]
- Newberry, R.W.; Raines, R.T. The n→π* Interaction. Acc. Chem. Res. 2017, 50, 1838–1846. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, J.; Schuster, D.I. The Anomalous Reactivity of Fluorobenzene in Electrophilic Aromatic Substitution and Related Phenomena. J. Chem. Educ. 2003, 80, 6–679. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Cheng, L.; Harding, M.E.; Matthews, D.A.; Szalay, P.G. CFOUR. A Quantum Chemical Program Package. Available online: https://cfour.uni-mainz.de/cfour/ (accessed on 1 September 2024).
- Irkutsk Supercomputer Center of SB RAS. Irkutsk: ISDCT SB RAS. Available online: https://hpc.icc.ru (accessed on 8 September 2024).
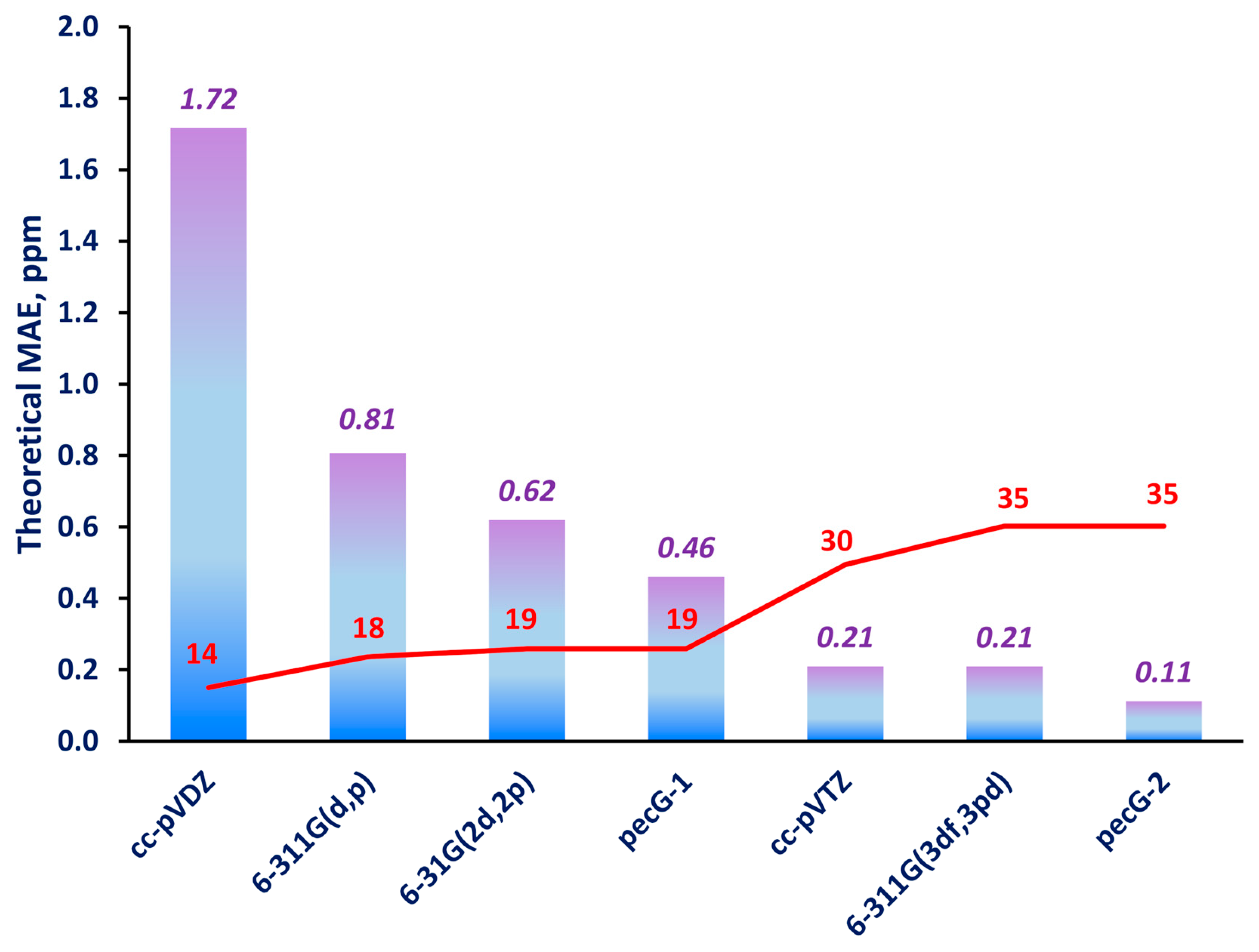

| Basis Set | Element | Contracted Composition | Number of Contracted Basis Functions |
|---|---|---|---|
| Rusakov’s pecG-n series | |||
| pecG-1 | H | [2s2p] | 8 |
| B-F | [3s2p2d] | 19 | |
| pecG-2 | H | [3s3p1d] | 17 |
| B-F | [4s3p3d1f] | 35 | |
| Dunning’s cc-pVXZ series | |||
| cc-pVDZ | H | [2s1p] | 5 |
| B-F | [3s2p1d] | 14 | |
| cc-pVTZ | H | [3s2p1d] | 14 |
| B-F | [4s3p2d1f] | 30 | |
| cc-pVQZ | H | [4s3p2d1f] | 30 |
| B-F | [5s4p3d2f1g] | 55 | |
| Pople-style K-LMNG(x,y) series | |||
| 6-311G(d,p) | H | [3s1p] | 6 |
| B-F | [4s3p1d] | 18 | |
| 6-31G(2d,2p) | H | [2s2p] | 8 |
| B-F | [3s2p2d] | 19 | |
| 6-311G(3df,3pd) | H | [3s3p1d] | 17 |
| B-F | [4s3p3d1f] | 35 | |
| Molecule | No. of Carbon Atoms 1 | 6-311G(d,p) | 6-31G(2d,2p) | 6-311G(3df,3pd) | pecG-1 | pecG-2 | Exp. 2 |
|---|---|---|---|---|---|---|---|
| Acetaldehyde | 1 | 196.19 | 197.17 | 196.25 | 196.37 | 196.97 | 199.97 |
| 2 | 34.92 | 34.70 | 35.09 | 34.90 | 35.02 | 30.99 | |
| Acetonitrile | 1 | 4.95 | 4.84 | 4.85 | 4.61 | 4.65 | 1.91 |
| 2 | 115.07 | 115.73 | 115.57 | 115.91 | 115.93 | 116.33 | |
| Cyclopropane | −1.61 | −1.66 | −1.37 | −1.63 | −1.57 | −3.15 | |
| DMAc | 1 | 160.74 | 161.03 | 161.06 | 160.69 | 161.50 | 170.66 |
| 2 | 25.58 | 25.25 | 26.12 | 25.34 | 26.10 | 21.58 | |
| 3 | 40.35 | 39.75 | 40.60 | 39.86 | 40.61 | 38.05 | |
| 4 | 34.32 | 33.74 | 34.61 | 33.88 | 34.60 | 35.20 | |
| Fluorobenzene | 1 | 155.98 | 156.06 | 155.61 | 156.09 | 155.93 | 162.86 |
| 2 | 111.85 | 111.65 | 111.51 | 111.72 | 111.49 | 115.32 | |
| 3 | 131.15 | 130.89 | 131.09 | 131.00 | 130.94 | 129.96 | |
| 4 | 127.11 | 126.88 | 126.52 | 126.89 | 126.55 | 123.98 | |
| Isoxazole | 1 | 158.00 | 158.72 | 157.55 | 158.28 | 157.62 | 157.64 |
| 2 | 106.04 | 105.96 | 105.78 | 105.95 | 105.65 | 103.47 | |
| 3 | 148.72 | 149.18 | 148.16 | 148.83 | 147.96 | 149.02 | |
| Norbornadiene | 1 | 145.04 | 145.27 | 145.17 | 145.05 | 144.97 | 143.43 |
| 2 | 48.28 | 48.27 | 48.29 | 48.63 | 48.27 | 50.26 | |
| 3 | 74.67 | 74.19 | 75.34 | 75.13 | 75.50 | 75.32 | |
| Oxetane | 1 | 73.80 | 74.05 | 73.96 | 73.87 | 73.94 | 72.55 |
| 2 | 23.41 | 23.09 | 23.46 | 23.41 | 22.91 | 22.35 | |
| Pyridine | 1 | 150.18 | 150.07 | 149.91 | 150.29 | 149.98 | 149.74 |
| 2 | 125.15 | 124.97 | 124.99 | 124.95 | 124.69 | 123.78 | |
| 3 | 137.53 | 137.41 | 137.21 | 137.33 | 137.11 | 136.09 | |
| α | 196.12 | 196.82 | 197.81 | 197.18 | 198.54 | ||
| MAE | 2.43 | 2.34 | 2.39 | 2.31 | 2.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusakov, Y.Y.; Semenov, V.A.; Rusakova, I.L. Quelling the Geometry Factor Effect in Quantum Chemical Calculations of 13C NMR Chemical Shifts with the Aid of the pecG-n (n = 1, 2) Basis Sets. Int. J. Mol. Sci. 2024, 25, 10588. https://doi.org/10.3390/ijms251910588
Rusakov YY, Semenov VA, Rusakova IL. Quelling the Geometry Factor Effect in Quantum Chemical Calculations of 13C NMR Chemical Shifts with the Aid of the pecG-n (n = 1, 2) Basis Sets. International Journal of Molecular Sciences. 2024; 25(19):10588. https://doi.org/10.3390/ijms251910588
Chicago/Turabian StyleRusakov, Yuriy Yu., Valentin A. Semenov, and Irina L. Rusakova. 2024. "Quelling the Geometry Factor Effect in Quantum Chemical Calculations of 13C NMR Chemical Shifts with the Aid of the pecG-n (n = 1, 2) Basis Sets" International Journal of Molecular Sciences 25, no. 19: 10588. https://doi.org/10.3390/ijms251910588
APA StyleRusakov, Y. Y., Semenov, V. A., & Rusakova, I. L. (2024). Quelling the Geometry Factor Effect in Quantum Chemical Calculations of 13C NMR Chemical Shifts with the Aid of the pecG-n (n = 1, 2) Basis Sets. International Journal of Molecular Sciences, 25(19), 10588. https://doi.org/10.3390/ijms251910588








