The Impact of Non-Pathogenic Bacteria on the Spread of Virulence and Resistance Genes
Abstract
1. Introduction
- (i)
- People that have not used antibiotics for a long time have a lower diversity of drug-resistance genes in their microbiomes;
- (ii)
- The diversity of resistance genes in a person’s microbiome increases when that person takes an antibiotic;
- (iii)
- Antibiotic overuse increases the diversity of resistance genes in human microbiomes;
- (iv)
- The co-location of virulence and resistance genes in bacterial genomes explains the positive correlation between the resistance and virulence genes’ diversities in microbiomes observed over human microbiomes.
2. The Fate of Commensal Bacteria
2.1. Brief Review of the R0, the Basic Reproductive Number
2.2. The Human Network of Physical Contacts
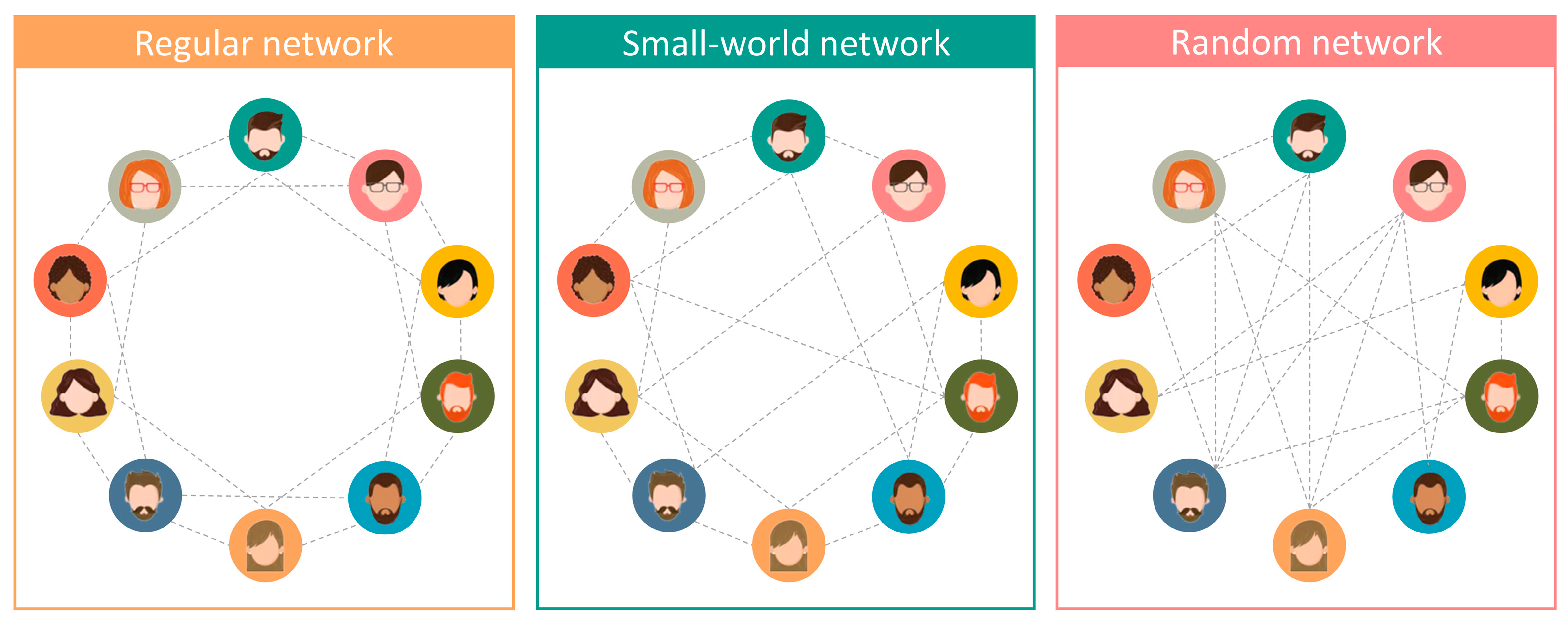
2.2.1. Brief Review of Small-World Networks
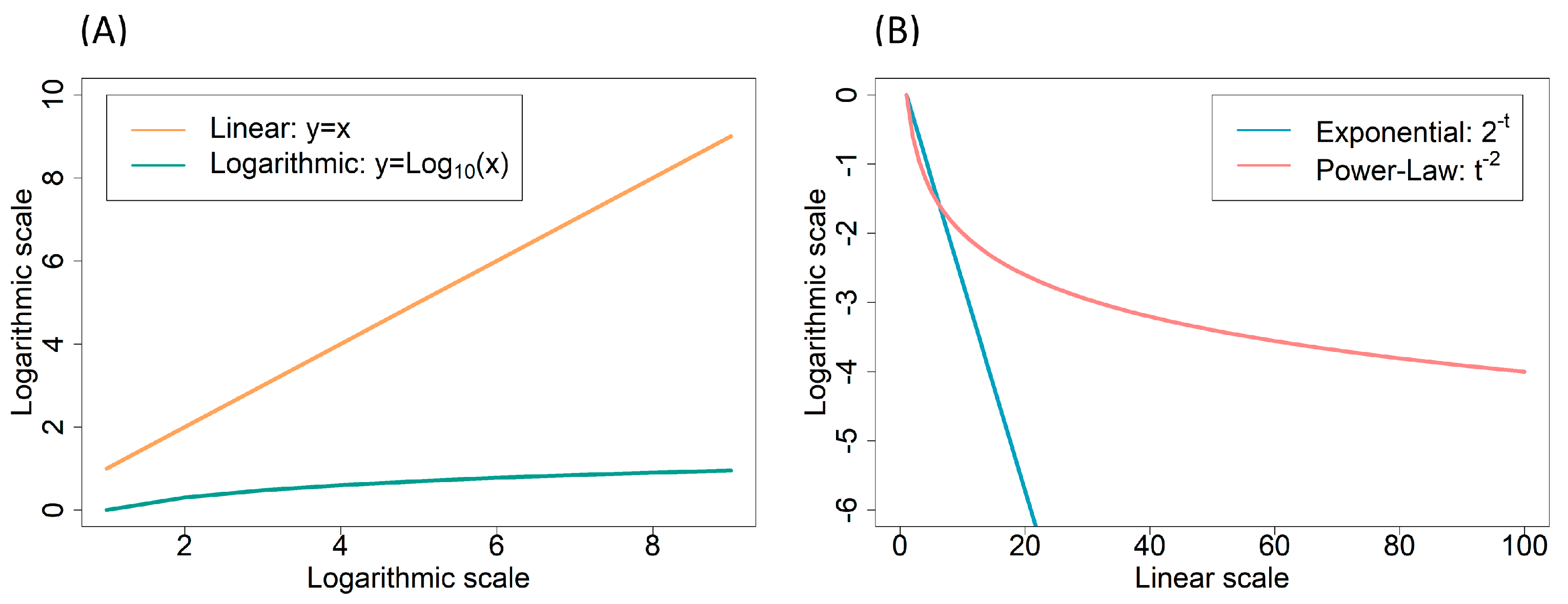
2.2.2. Power-Laws and Scale-Free Networks
2.3. Selection and Weak Counter-Selection of Virulence and Resistance Genes
2.4. The Diversity of Virulence and Resistance Genes across Microbiomes
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saint-Exupery, A.D. The Little Prince; Farshore Picture Books: London, UK, 2017; ISBN 978-1-4052-8819-4. [Google Scholar]
- Murray, C.J.; Ikuta, K.S.; Sharara, F.; Swetschinski, L.; Aguilar, G.R.; Gray, A.; Han, C.; Bisignano, C.; Rao, P.; Wool, E.; et al. Global burden of bacterial antimicrobial resistance in 2019: A systematic analysis. Lancet 2022, 399, 629–655. [Google Scholar] [CrossRef] [PubMed]
- WHO. Antimicrobial Resistance: Global Report on Surveillance; WHO: Geneva, Switzerland, 2014.
- WHO. WHO Report on Surveillance of Antibiotic Consumption: 2016–2018 Early Implementation; WHO: Geneva, Switzerland, 2018.
- Salyers, A.A.; Gupta, A.; Wang, Y. Human intestinal bacteria as reservoirs for antibiotic resistance genes. Trends Microbiol. 2004, 12, 412–416. [Google Scholar] [CrossRef] [PubMed]
- Rolain, J.-M. Food and human gut as reservoirs of transferable antibiotic resistance encoding genes. Front. Microbiol. 2013, 4, 173. [Google Scholar] [CrossRef] [PubMed]
- Dionisio, F.; Matic, I.; Radman, M.; Rodrigues, O.R.; Taddei, F. Plasmids Spread Very Fast in Heterogeneous Bacterial Com-munities. Genetics 2002, 162, 1525–1532. [Google Scholar] [CrossRef] [PubMed]
- Bailey, J.; Pinyon, J.; Anantham, S.; Hall, R.M. Commensal Escherichia coli of healthy humans: A reservoir for antibiotic-resistance determinants. J. Med. Microbiol. 2010, 59, 1331–1339. [Google Scholar] [CrossRef]
- Sommer, M.O.A.; Dantas, G.; Church, G.M. Functional Characterization of the Antibiotic Resistance Reservoir in the Human Microflora. Science 2009, 325, 1128–1131. [Google Scholar] [CrossRef]
- Smillie, C.S.; Smith, M.B.; Friedman, J.; Cordero, O.X.; David, L.A.; Alm, E.J. Ecology drives a global network of gene exchange connecting the human microbiome. Nature 2011, 480, 241–244. [Google Scholar] [CrossRef]
- Balasubramanian, D.; López-Pérez, M.; Grant, T.-A.; Ogbunugafor, C.B.; Almagro-Moreno, S. Molecular mechanisms and drivers of pathogen emergence. Trends Microbiol. 2022, 30, 898–911. [Google Scholar] [CrossRef]
- Goytia, M.; Thompson, S.; Jordan, S.; King, K. Antimicrobial Resistance Profiles of Human Commensal Neisseria Species. Antibiotics 2021, 10, 538. [Google Scholar] [CrossRef]
- Arnold, B.J.; Huang, I.-T.; Hanage, W.P. Horizontal gene transfer and adaptive evolution in bacteria. Nat. Rev. Genet. 2021, 20, 206–218. [Google Scholar] [CrossRef]
- Baquero, F.; Martínez, J.L.; Lanza, V.F.; Rodríguez-Beltrán, J.; Galán, J.C.; Millán, A.S.; Cantón, R.; Coque, T.M. Evolutionary Pathways and Trajectories in Antibiotic Resistance. Clin. Microbiol. Rev. 2021, 34, e0005019. [Google Scholar] [CrossRef] [PubMed]
- Heintz-Buschart, A.; Wilmes, P. Human Gut Microbiome: Function Matters. Trends Microbiol. 2018, 26, 563–574. [Google Scholar] [CrossRef] [PubMed]
- Sender, R.; Fuchs, S.; Milo, R. Revised Estimates for the Number of Human and Bacteria Cells in the Body. PLoS Biol. 2016, 14, e1002533. [Google Scholar] [CrossRef] [PubMed]
- Ursell, L.K.; Metcalf, J.L.; Parfrey, L.W.; Knight, R. Defining the human microbiome. Nutr. Rev. 2012, 70, S38–S44. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK; New York, NY, USA, 1992; ISBN 978-0-19-854040-3. [Google Scholar]
- Frank, S.A. Models of Parasite Virulence. Q. Rev. Biol. 1996, 71, 37–78. [Google Scholar] [CrossRef]
- Zeng, X.; Lin, J. Factors influencing horizontal gene transfer in the intestine. Anim. Health Res. Rev. 2017, 18, 153–159. [Google Scholar] [CrossRef]
- McInnes, R.S.; McCallum, G.E.; Lamberte, L.E.; van Schaik, W. Horizontal transfer of antibiotic resistance genes in the human gut microbiome. Curr. Opin. Microbiol. 2020, 53, 35–43. [Google Scholar] [CrossRef]
- Brito, I.L. Examining horizontal gene transfer in microbial communities. Nat. Rev. Microbiol. 2021, 19, 442–453. [Google Scholar] [CrossRef]
- Johnston, C.; Martin, B.; Fichant, G.; Polard, P.; Claverys, J.-P. Bacterial transformation: Distribution, shared mechanisms and divergent control. Nat. Rev. Microbiol. 2014, 12, 181–196. [Google Scholar] [CrossRef]
- Smillie, C.; Garcillán-Barcia, M.P.; Francia, M.V.; Rocha, E.P.C.; de la Cruz, F. Mobility of Plasmids. Microbiol. Mol. Biol. Rev. 2010, 74, 434–452. [Google Scholar] [CrossRef]
- Sessions, S.K. Genome Size. In Brenner’s Encyclopedia of Genetics, 2nd ed.; Maloy, S., Hughes, K., Eds.; Elsevier: London, UK, 2013; Volume 3, pp. 144–151. ISBN 978-0-08-096156-9. [Google Scholar]
- McGowan, J.E.; Tenover, F.C. Confronting bacterial resistance in healthcare settings: A crucial role for microbiologists. Nat. Rev. Genet. 2004, 2, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.P.J.; Wood, A.J.; Harrison, E.; Brockhurst, M.A. Source–sink plasmid transfer dynamics maintain gene mobility in soil bacterial communities. Proc. Natl. Acad. Sci. USA 2016, 113, 8260–8265. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Combadão, J.; Campos, P.R.A.; Dionisio, F.; Gordo, I. Small-world networks decrease the speed of Muller’s ratchet. Genet. Res. 2007, 89, 7–18. [Google Scholar] [CrossRef]
- Campos, P.R.A.; Combadão, J.; Dionisio, F.; Gordo, I. Muller’s ratchet in random graphs and scale-free networks. Phys. Rev. E 2006, 74, 42901. [Google Scholar] [CrossRef]
- Liljeros, F.; Edling, C.R.; Amaral, L.A.N.; Stanley, H.E.; Åberg, Y. The web of human sexual contacts. Nature 2001, 411, 907–908. [Google Scholar] [CrossRef]
- Liljeros, F.; Edling, C.R.; Stanley, H.E.; Åberg, Y.; Amaral, L.A.N. Sexual contacts and epidemic thresholds. Nature 2003, 423, 606. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Scala, A.; Barthélémy, M.; Stanley, H.E. Classes of small-world networks. Proc. Natl. Acad. Sci. USA 2000, 97, 11149–11152. [Google Scholar] [CrossRef]
- Newman, M.E.J. Spread of epidemic disease on networks. Phys. Rev. E 2002, 66, 16128. [Google Scholar] [CrossRef]
- Drake, J.W. A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. USA 1991, 88, 7160–7164. [Google Scholar] [CrossRef]
- Drake, J.W. The Distribution of Rates of Spontaneous Mutation over Viruses, Prokaryotes, and Eukaryotes. Ann. N. Y. Acad. Sci. 1999, 870, 100–107. [Google Scholar] [CrossRef] [PubMed]
- Sung, W.; Ackerman, M.S.; Miller, S.F.; Doak, T.G.; Lynch, M. Drift-barrier hypothesis and mutation-rate evolution. Proc. Natl. Acad. Sci. USA 2012, 109, 18488–18492. [Google Scholar] [CrossRef] [PubMed]
- Şimşek, E.; Kim, M. Power-law tail in lag time distribution underlies bacterial persistence. Proc. Natl. Acad. Sci. USA 2019, 116, 17635–17640. [Google Scholar] [CrossRef] [PubMed]
- Rebelo, J.S.; Domingues, C.P.F.; Monteiro, F.; Nogueira, T.; Dionisio, F. Bacterial persistence is essential for susceptible cell survival in indirect resistance, mainly for lower cell densities. PLoS ONE 2021, 16, e0246500. [Google Scholar] [CrossRef] [PubMed]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic Spreading in Scale-Free Networks. Phys. Rev. Lett. 2001, 86, 3200–3203. [Google Scholar] [CrossRef]
- Boguñá, M.; Pastor-Satorras, R.; Vespignani, A. Absence of Epidemic Threshold in Scale-Free Networks with Connectivity Correlations. Phys. Rev. Lett. 2003, 90, 28701. [Google Scholar] [CrossRef]
- Schlosser, F.; Maier, B.F.; Jack, O.; Hinrichs, D.; Zachariae, A.; Brockmann, D. COVID-19 lockdown induces disease-mitigating structural changes in mobility networks. Proc. Natl. Acad. Sci. USA 2020, 117, 32883–32890. [Google Scholar] [CrossRef]
- Klemm, P.; Schembri, M.A. Bacterial adhesins: Function and structure. Int. J. Med. Microbiol. 2000, 290, 27–35. [Google Scholar] [CrossRef]
- Modi, R.I.; Adams, J. Coevolution in bacterial-plasmid populations. Evolution 1991, 45, 656–667. [Google Scholar] [CrossRef] [PubMed]
- Levin, B.R.; Lipsitch, M.; Perrot, V.; Schrag, S.; Antia, R.; Simonsen, L.; Walker, N.M.; Stewart, F.M. The Population Genetics of Antibiotic Resistance. Clin. Infect. Dis. 1997, 24, S9–S16. [Google Scholar] [CrossRef] [PubMed]
- Schrag, S.J.; Perrot, V.; Levin, B.R. Adaptation to the fitness costs of antibiotic resistance in Escherichia coli. Proc. R. Soc. B Biol. Sci. 1997, 264, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Björkman, J.; Nagaev, I.; Berg, O.G.; Hughes, D.; Andersson, D.I. Effects of Environment on Compensatory Mutations to Ameliorate Costs of Antibiotic Resistance. Science 2000, 287, 1479–1482. [Google Scholar] [CrossRef]
- Dahlberg, C.; Chao, L. Amelioration of the Cost of Conjugative Plasmid Carriage in Eschericha coli K12. Genetics 2003, 165, 1641–1649. [Google Scholar] [CrossRef]
- Maisnier-Patin, S.; Andersson, D.I. Adaptation to the deleterious effects of antimicrobial drug resistance mutations by compensatory evolution. Res. Microbiol. 2004, 155, 360–369. [Google Scholar] [CrossRef]
- Dionisio, F.; Conceição, I.; Marques, A.C.; Fernandes, L.; Gordo, I. The evolution of a conjugative plasmid and its ability to increase bacterial fitness. Biol. Lett. 2005, 1, 250–252. [Google Scholar] [CrossRef]
- Nilsson, A.I.; Zorzet, A.; Kanth, A.; Dahlström, S.; Berg, O.G.; Andersson, D.I. Reducing the fitness cost of antibiotic resistance by amplification of initiator tRNA genes. Proc. Natl. Acad. Sci. USA 2006, 103, 6976–6981. [Google Scholar] [CrossRef]
- Hall, J.P.J.; Wright, R.C.T.; Guymer, D.; Harrison, E.; Brockhurst, M.A. Extremely fast amelioration of plasmid fitness costs by multiple functionally diverse pathways. Microbiology 2020, 166, 56–62. [Google Scholar] [CrossRef]
- Sørensen, M.E.S.; Wood, A.J.; Cameron, D.D.; Brockhurst, M.A. Rapid compensatory evolution can rescue low fitness symbioses following partner switching. Curr. Biol. 2021, 31, 3721–3728.e4. [Google Scholar] [CrossRef]
- Brockhurst, M.A.; Harrison, E. Ecological and evolutionary solutions to the plasmid paradox. Trends Microbiol. 2022, 30, 534–543. [Google Scholar] [CrossRef] [PubMed]
- Trindade, S.; Sousa, A.; Xavier, K.B.; Dionisio, F.; Ferreira, M.G.; Gordo, I. Positive Epistasis Drives the Acquisition of Multi-drug Resistance. PLoS Genet. 2009, 5, e1000578. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.F.; Mendonça, S.C.M.; Carvalho, L.M.; Reis, A.M.; Gordo, I.; Trindade, S.; Dionisio, F. Pervasive Sign Epistasis between Conjugative Plasmids and Drug-Resistance Chromosomal Mutations. PLoS Genet. 2011, 7, e1002181. [Google Scholar] [CrossRef] [PubMed]
- Millan, A.S.; Heilbron, K.; MacLean, R.C. Positive epistasis between co-infecting plasmids promotes plasmid survival in bacterial populations. ISME J. 2014, 8, 601–612. [Google Scholar] [CrossRef] [PubMed]
- Gama, J.A.; Zilhão, R.; Dionisio, F. Co-resident plasmids travel together. Plasmid 2017, 93, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Gama, J.A.; Zilhão, R.; Dionisio, F. Multiple plasmid interference—Pledging allegiance to my enemy’s enemy. Plasmid 2017, 93, 17–23. [Google Scholar] [CrossRef]
- Gama, J.A.; Zilhão, R.; Dionisio, F. Conjugation efficiency depends on intra and intercellular interactions between distinct plasmids: Plasmids promote the immigration of other plasmids but repress co-colonizing plasmids. Plasmid 2017, 93, 6–16. [Google Scholar] [CrossRef] [PubMed]
- Gama, J.A.; Fredheim, E.G.A.; Cléon, F.; Reis, A.M.; Zilhão, R.; Dionisio, F. Dominance between Plasmids Determines the Extent of Biofilm Formation. Front. Microbiol. 2020, 11, 2070. [Google Scholar] [CrossRef]
- Gama, J.A.; Zilhão, R.; Dionisio, F. Plasmid Interactions Can Improve Plasmid Persistence in Bacterial Populations. Front. Microbiol. 2020, 11, 2033. [Google Scholar] [CrossRef]
- Zwanzig, M.; Harrison, E.; Brockhurst, M.A.; Hall, J.P.J.; Berendonk, T.U.; Berger, U. Mobile Compensatory Mutations Promote Plasmid Survival. mSystems 2019, 4, e00186-18. [Google Scholar] [CrossRef]
- Valle, A.A.-D.; León-Sampedro, R.; Rodríguez-Beltrán, J.; DelaFuente, J.; Hernández-García, M.; Ruiz-Garbajosa, P.; Cantón, R.; Peña-Miller, R.; Millán, A.S. Variability of plasmid fitness effects contributes to plasmid persistence in bacterial communities. Nat. Commun. 2021, 12, 2653. [Google Scholar] [CrossRef] [PubMed]
- Dionisio, F.; Nogueira, T.; Carvalho, L.M.; Mendes-Soares, H.; Mendonça, S.C.; Domingues, I.; Moreira, B.; Reis, A.M. What Maintains Plasmids among Bacteria. In Horizontal Gene Transfer in Microorganisms; Caister Academic Press: Norwich, UK, 2012; pp. 131–154. [Google Scholar]
- Domingues, C.P.F.; Rebelo, J.S.; Monteiro, F.; Nogueira, T.; Dionisio, F. Harmful behaviour through plasmid transfer: A successful evolutionary strategy of bacteria harbouring conjugative plasmids. Philos. Trans. R. Soc. B Biol. Sci. 2022, 377, 20200473. [Google Scholar] [CrossRef] [PubMed]
- Ghigo, J.-M. Natural conjugative plasmids induce bacterial biofilm development. Nature 2001, 412, 442–445. [Google Scholar] [CrossRef] [PubMed]
- Reisner, A.; Höller, B.M.; Molin, S.; Zechner, E.L. Synergistic Effects in Mixed Escherichia coli Biofilms: Conjugative Plasmid Transfer Drives Biofilm Expansion. J. Bacteriol. 2006, 188, 3582–3588. [Google Scholar] [CrossRef]
- Davies, J.; Davies, D. Origins and Evolution of Antibiotic Resistance. Microbiol. Mol. Biol. Rev. 2010, 74, 417–433. [Google Scholar] [CrossRef]
- Escudeiro, P.; Pothier, J.; Dionisio, F.; Nogueira, T. Antibiotic Resistance Gene Diversity and Virulence Gene Diversity Are Correlated in Human Gut and Environmental Microbiomes. mSphere 2019, 4, e00135-19. [Google Scholar] [CrossRef]
- Beceiro, A.; Tomás, M.; Bou, G. Antimicrobial Resistance and Virulence: A Successful or Deleterious Association in the Bacterial World? Clin. Microbiol. Rev. 2013, 26, 185–230. [Google Scholar] [CrossRef]
- Deng, Y.; Xu, L.; Liu, S.; Wang, Q.; Guo, Z.; Chen, C.; Feng, J. What drives changes in the virulence and antibiotic resistance of Vibrio harveyi in the South China Sea? J. Fish Dis. 2020, 43, 853–862. [Google Scholar] [CrossRef]
- Pan, Y.; Zeng, J.; Li, L.; Yang, J.; Tang, Z.; Xiong, W.; Li, Y.; Chen, S.; Zeng, Z. Coexistence of Antibiotic Resistance Genes and Virulence Factors Deciphered by Large-Scale Complete Genome Analysis. mSystems 2020, 5, e00821-19. [Google Scholar] [CrossRef]
- Canteón, R. Antibiotic resistance genes from the environment: A perspective through newly identified antibiotic resistance mechanisms in the clinical setting. Clin. Microbiol. Infect. 2009, 15, 20–25. [Google Scholar] [CrossRef]
- Martinez, J.L. The role of natural environments in the evolution of resistance traits in pathogenic bacteria. Proc. R. Soc. B Biol. Sci. 2009, 276, 2521–2530. [Google Scholar] [CrossRef] [PubMed]
- Allen, H.K.; Donato, J.; Wang, H.H.; Cloud-Hansen, K.A.; Davies, J.; Handelsman, J. Call of the wild: Antibiotic resistance genes in natural environments. Nat. Rev. Microbiol. 2010, 8, 251–259. [Google Scholar] [CrossRef] [PubMed]
- Castanon, J.I.R. History of the Use of Antibiotic as Growth Promoters in European Poultry Feeds. Poult. Sci. 2007, 86, 2466–2471. [Google Scholar] [CrossRef]
- Darmancier, H.; Domingues, C.P.F.; Rebelo, J.S.; Amaro, A.; Dionísio, F.; Pothier, J.; Serra, O.; Nogueira, T. Are Virulence and Antibiotic Resistance Genes Linked? A Comprehensive Analysis of Bacterial Chromosomes and Plasmids. Antibiotics 2022, 11, 706. [Google Scholar] [CrossRef] [PubMed]
- Cho, I.; Blaser, M.J. The human microbiome: At the interface of health and disease. Nat. Rev. Genet. 2012, 13, 260–270. [Google Scholar] [CrossRef]
- Domingues, C.P.F.; Rebelo, J.S.; Pothier, J.; Monteiro, F.; Nogueira, T.; Dionisio, F. The Perfect Condition for the Rising of Superbugs: Person-to-Person Contact and Antibiotic Use Are the Key Factors Responsible for the Positive Correlation between Antibiotic Resistance Gene Diversity and Virulence Gene Diversity in Human Metagenomes. Antibiotics 2021, 10, 605. [Google Scholar] [CrossRef] [PubMed]
- Valentino, V.; Sequino, G.; Cobo-Díaz, J.F.; Álvarez-Ordóñez, A.; De Filippis, F.; Ercolini, D. Evidence of virulence and antibiotic resistance genes from the microbiome mapping in minimally processed vegetables producing facilities. Food Res. Int. 2022, 162, 112202. [Google Scholar] [CrossRef] [PubMed]
- Carr, W.; Kurbatova, E.; Starks, A.; Goswami, N.; Allen, L.; Winston, C. Interim Guidance: 4-Month Rifapentine-Moxifloxacin Regimen for the Treatment of Drug-Susceptible Pulmonary Tuberculosis—United States. MMWR. Morb. Mortal. Wkly. Rep. 2022, 71, 285–289. [Google Scholar] [CrossRef]
- Chambers, H.F.; DeLeo, F.R. Waves of resistance: Staphylococcus aureus in the antibiotic era. Nat. Rev. Microbiol. 2009, 7, 629–641. [Google Scholar] [CrossRef]
- Smith, H.W.; Halls, S. Observations on infective drug resistance in Britain. Br. Med. J. 1966, 1, 266–269. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dionisio, F.; Domingues, C.P.F.; Rebelo, J.S.; Monteiro, F.; Nogueira, T. The Impact of Non-Pathogenic Bacteria on the Spread of Virulence and Resistance Genes. Int. J. Mol. Sci. 2023, 24, 1967. https://doi.org/10.3390/ijms24031967
Dionisio F, Domingues CPF, Rebelo JS, Monteiro F, Nogueira T. The Impact of Non-Pathogenic Bacteria on the Spread of Virulence and Resistance Genes. International Journal of Molecular Sciences. 2023; 24(3):1967. https://doi.org/10.3390/ijms24031967
Chicago/Turabian StyleDionisio, Francisco, Célia P. F. Domingues, João S. Rebelo, Francisca Monteiro, and Teresa Nogueira. 2023. "The Impact of Non-Pathogenic Bacteria on the Spread of Virulence and Resistance Genes" International Journal of Molecular Sciences 24, no. 3: 1967. https://doi.org/10.3390/ijms24031967
APA StyleDionisio, F., Domingues, C. P. F., Rebelo, J. S., Monteiro, F., & Nogueira, T. (2023). The Impact of Non-Pathogenic Bacteria on the Spread of Virulence and Resistance Genes. International Journal of Molecular Sciences, 24(3), 1967. https://doi.org/10.3390/ijms24031967





