Lanthanide Contraction in LnF3 (Ln = Ce-Lu) and Its Chemical and Structural Consequences: Part 2: Specialized Empirical System of R3+ (R = Y, La, and 14 Ln) and F1− Ionic Radii for RF3 Series
Abstract
:1. Introduction
2. Results and Discussion
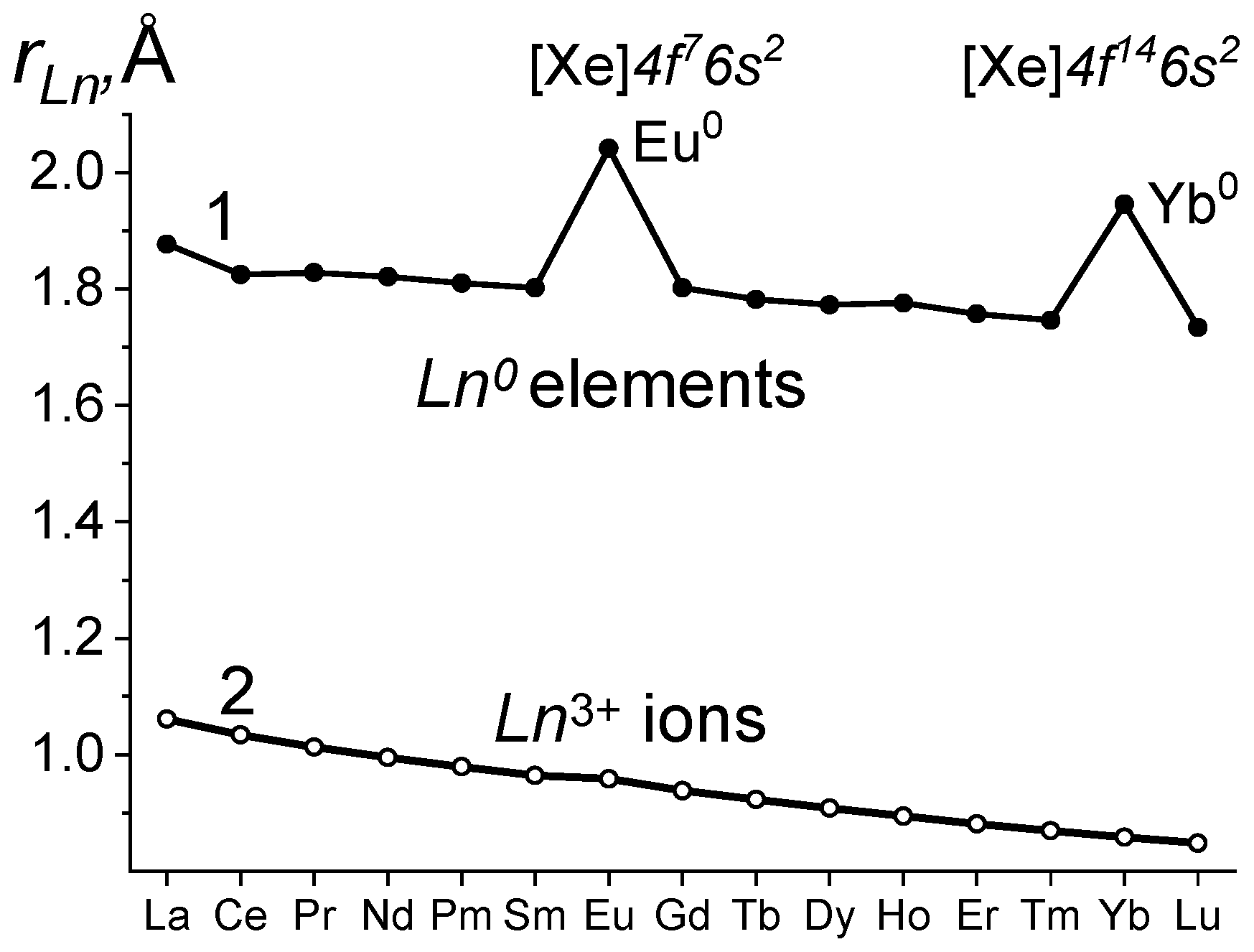
2.1. Lanthanide Contraction of Ln0 Elements and Ln3+ Ions
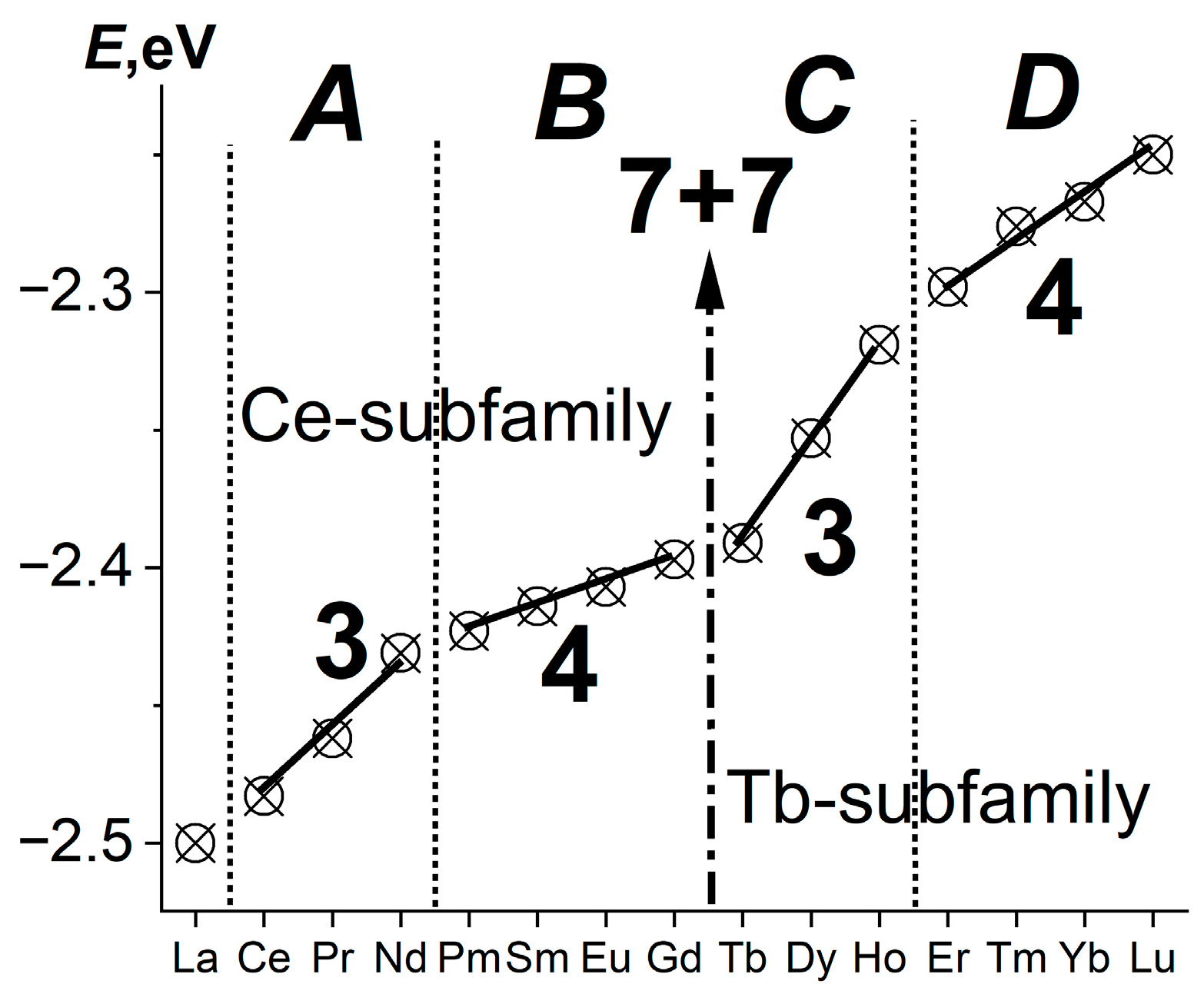
2.2. LC in Large Arrays of Ln Compounds and the Variability of the Ln3+ Radii
2.3. Advantages of the (La,Ln)F3 Series for Precise Study of LC and Obtaining r+ and r−
2.4. Lande’s Empirical Approach to Determining the Radius of an Anion
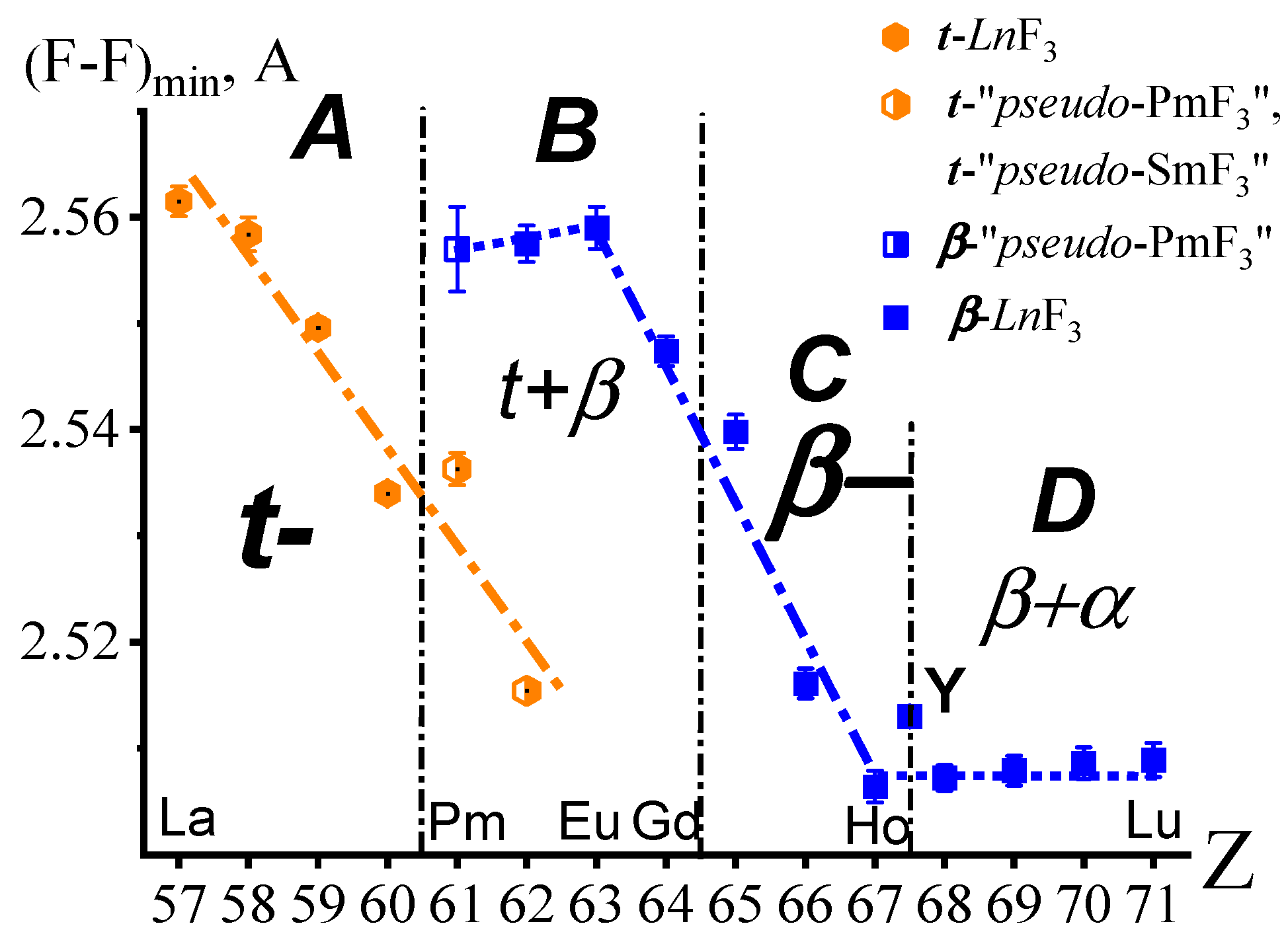
2.5. Determination of r− from the (F-F)min Dependency on Z in the (La,Ln)F3 Series
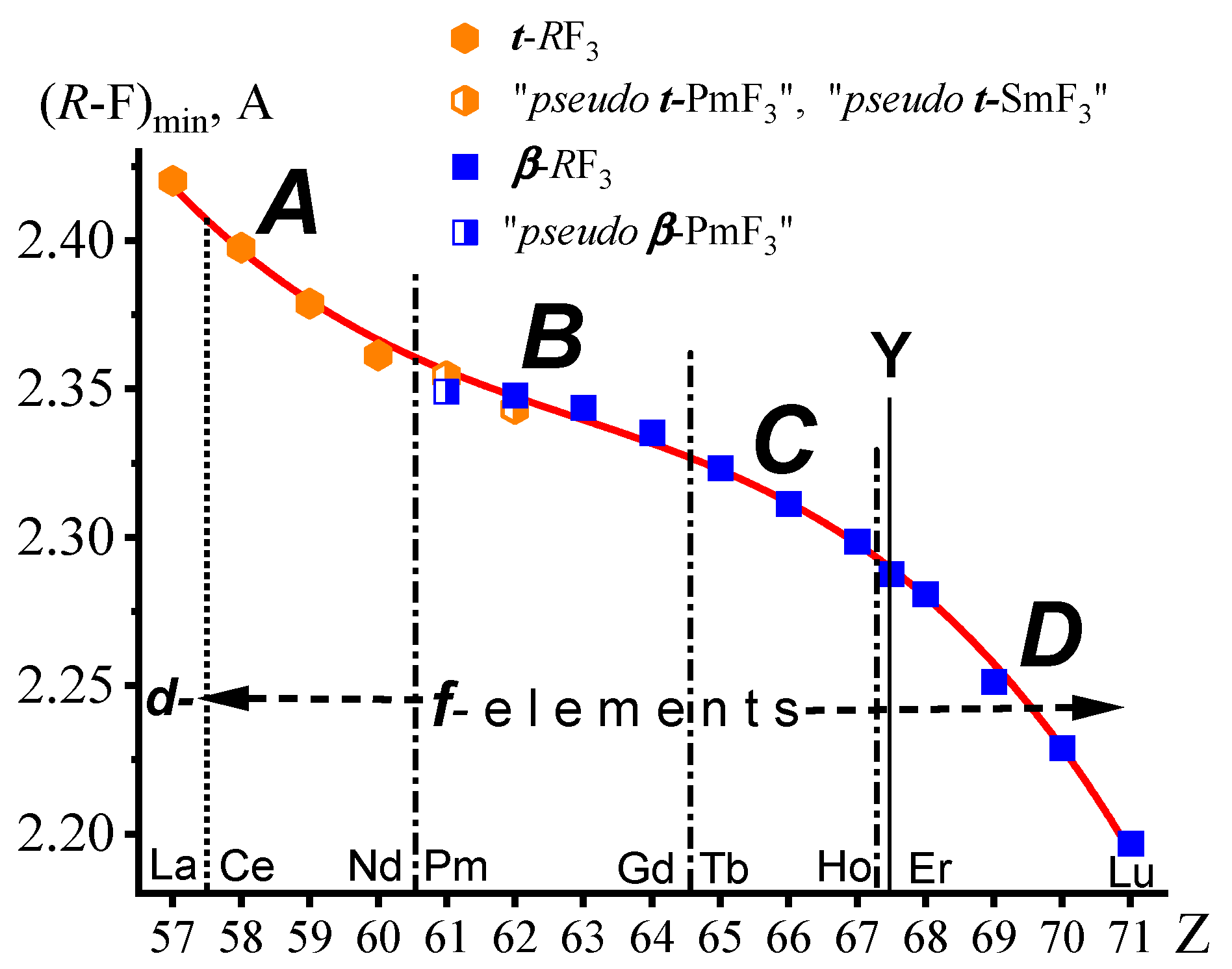
2.6. The Shortest (R-F)min Distances in (La,Ln)F3
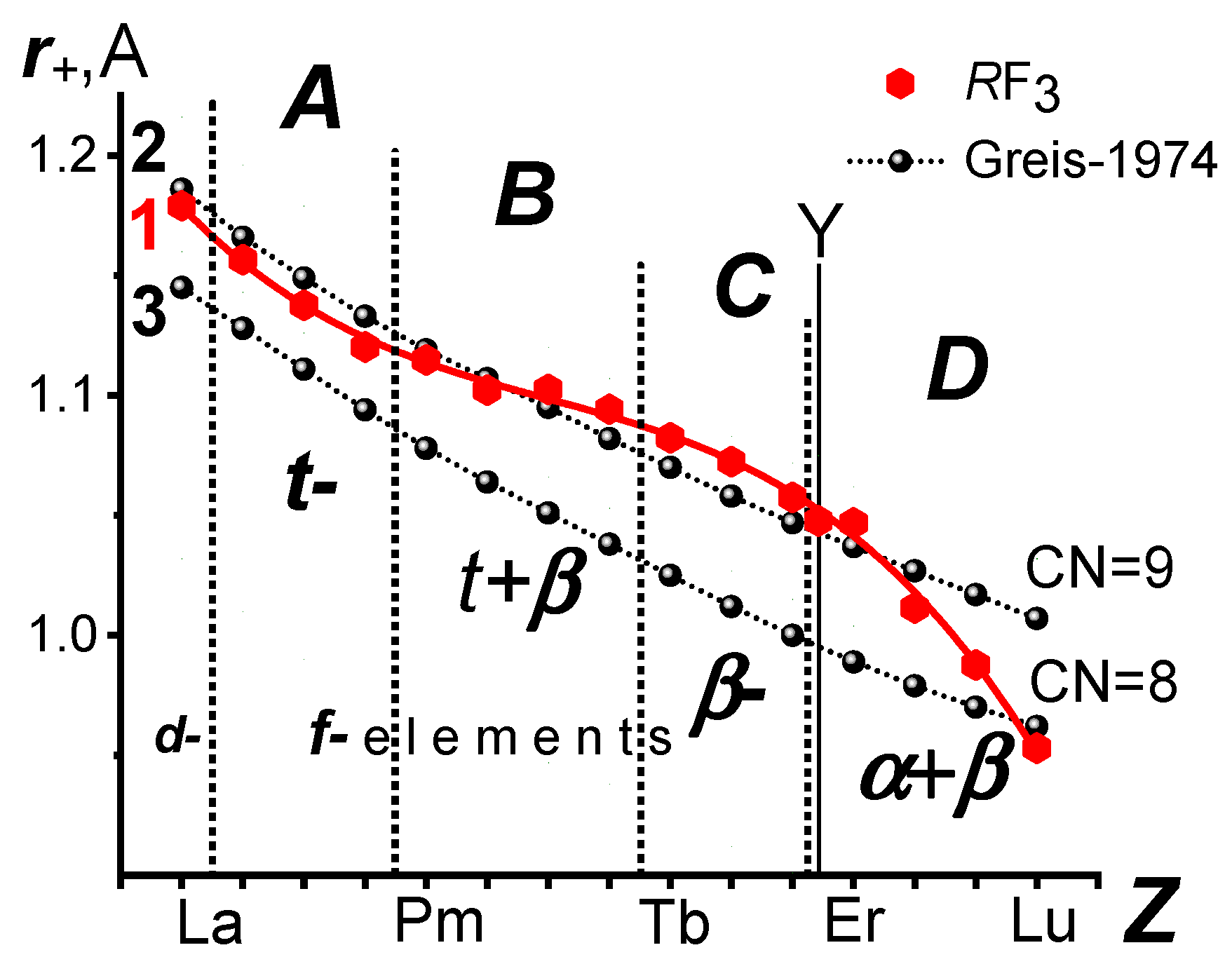
2.7. Calculation of the Sres-zd Emp SIR of R3+ (R = Y, La, and 14 Ln) and F1− for (R,Ln)F3
2.8. Comparison of r+ in the Spec-zd Emp SIR with r+ in SIR [28]
2.9. Application of the Spec-zd Emp SIR for RF3 and RF3-R’F3 Systems
2.10. Prospects for the Expansion of the Spes-zd Emp SIR for (R,Ln)F3 to Ionic Inorganic Fluorides
3. Methods and Materials
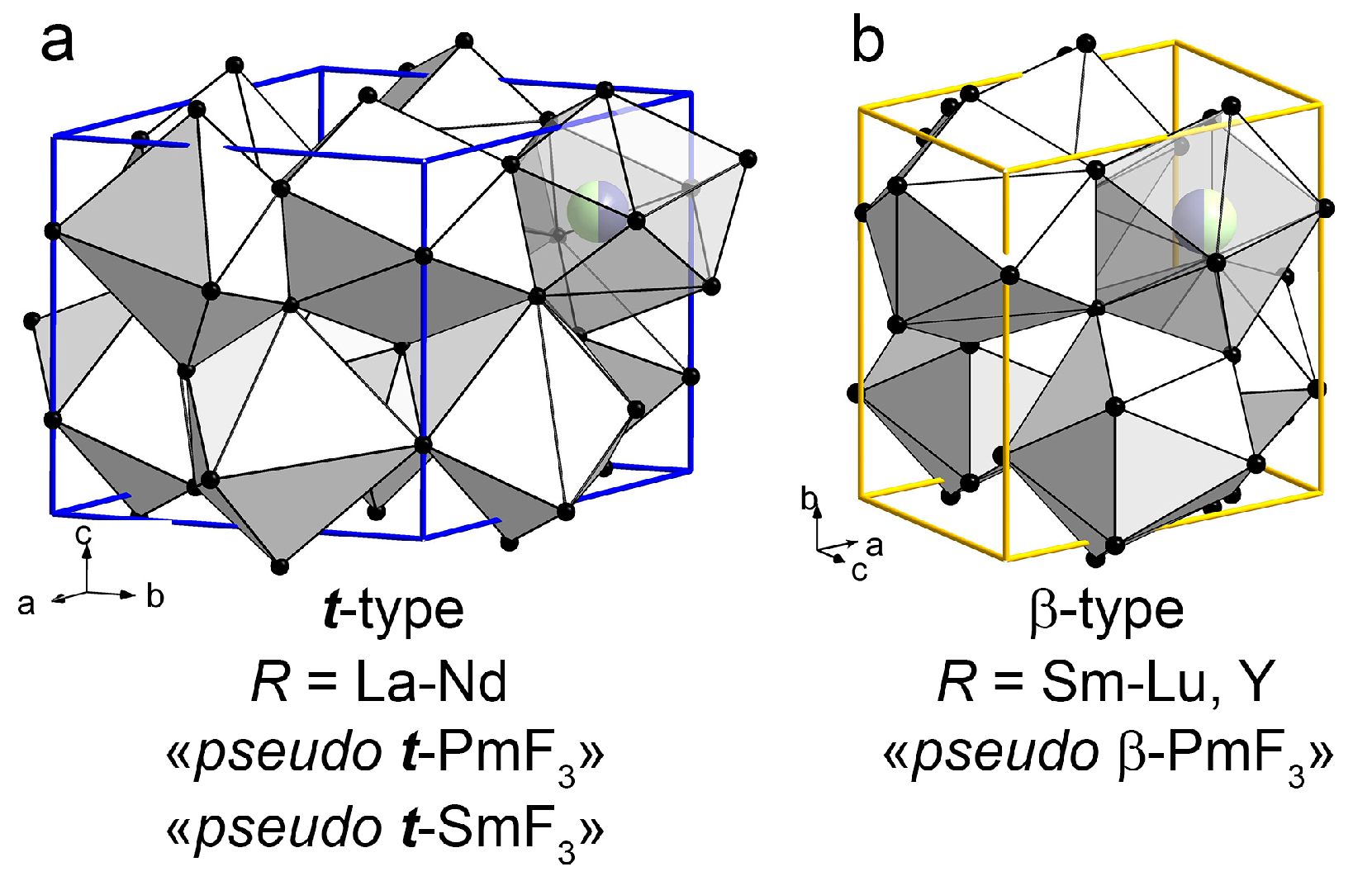
3.1. Obtaining t-RF3 (R = La–Nd), “pseudo t-SmF3”, and β-LnF3 (Ln = Sm-Dy) for Structural Studies
3.2. X-ray Diffraction Study of t-RF3 (R = La–Nd), “pseudo t-SmF3”, and β-LnF3 (Ln = Sm-Dy) Crystals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sobolev, B.P.; Sulyanova, E.A. Lanthanide Contraction in LnF3 (Ln = Ce-Lu) and its Chemical and Structural Consequences: Part 1: Location of YF3 in the LnF3 Series According to its Chemical and Structural Characteristics. Int. J. Mol. Sci. 2023, 24, 17013. [Google Scholar] [CrossRef]
- Komissarova, L.N. Inorganic and Analytical Chemistry of Scandium; URSS Editorial: Moscow, Russia, 2001; 512p. (In Russian) [Google Scholar]
- Spedding, F.H.; Henderson, D.C. High-Temperature Heat Contents and Related Thermodynamic Functions of Seven Trifluorides of the Rare Earths: Y, La, Pr, Nd, Gd, Ho, and Lu. J. Chem. Phys. 1971, 54, 2476–2483. [Google Scholar] [CrossRef]
- Spedding, F.H.; Beaudry, B.J.; Henderson, D.C.; Moorman, J. High-temperature enthalpies and related thermodynamic functions of the trifluorides of Sc, Ce, Sm, Eu, Gd, Tb, Dy, Er, Tm, and Yb. J. Chem. Phys. 1974, 60, 1578–1588. [Google Scholar] [CrossRef]
- Spedding, F.H.; Daane, A.H. The Rare Earths; Willey: New York, NY, USA, 1961; 641p. [Google Scholar]
- Mansmann, M. Die Kristallstruktur von Lanthantrifluorid. Z. Krist. 1965, 122, 375–398. [Google Scholar] [CrossRef]
- Greis, O.; Bevan, D.J.M. Electron diffraction from LaF3 single crystals. J. Solid State Chem. 1978, 24, 113–114. [Google Scholar] [CrossRef]
- Greis, O.; Cader, M.S.R. Polymorphism of high purity rare earth trifluorides. Thermochim. Acta. 1985, 87, 145–150. [Google Scholar] [CrossRef]
- Zalkin, A.; Templeton, D.H. The crystal structures of YF3 and related compounds. J. Amer. Chem. Soc. 1953, 75, 2453–2458. [Google Scholar] [CrossRef]
- Sulyanova, E.A.; Sobolev, B.P.; Svetogorov, R.D.; Kulikova, E.S. Promethium Trifluoride: Polymorphism and the Structure of Modifications on the Model Crystal 61(Ce0.5Gd0.5)F3. Part II. In situ X-ray diffraction study of t- and β-“pseudo 61PmF3” crystal structures near the temperature of polymorphic transformation. CrystEngComm 2023, 25, 4238–4246. [Google Scholar] [CrossRef]
- Goldschmidt, V.M.; Barth, T.; Lunde, G.; Zachariasen, W. Geochemische Verteilungsgesetze Der Elemente. Part V. Isomorphie Und Polymorphie Der Sesquioxyde. Die Lanthaniden-Kontraktion Und Ihre Konsequenzen; Jacob Dybwad, Kristiania: Oslo, Norway, 1926; Volume 7, pp. 1–117. [Google Scholar]
- Garashina, L.S.; Sobolev, B.P.; Alexandrov, V.B.; Vishniakov, Y.S. Crystal chemistry of rare earth trifluorides. Crystallogr. Rep. 1980, 25, 171–175. [Google Scholar]
- Shannon, R.D.; Prewitt, C.T. Effective ionic radii in oxides and fluorides. Acta Cryst. 1969, B25, 925–946. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Sobolev, B.P. The yttrium, lanthanum, and lanthanide trifluorides: Internal periodicity of phase transitions. Crystallogr. Rep. 2019, 64, 713–723. [Google Scholar] [CrossRef]
- Lang, P.F.; Smith, B.C. Ionization Energies of Lanthanides. J. Chem. Ed. 2010, 87, 875–881. [Google Scholar] [CrossRef]
- Bandurkin, G.A.; Dzhurinskii, B.F.; Tananaev, I.V. Features of Crystal Chemistry of RE Compounds; Nauka: Moscow, Russia, 1984; 230p. (In Russian) [Google Scholar]
- Bandurkin, G.A. On the irregular property changes of rare-earth elements. Geochemistry 1964, 1, 3–15. (In Russian) [Google Scholar]
- Bandurkin, G.A. Relation between structural and catalyst properties of RE compounds. Izvestiya AN SSSR Neorgan. Mater. 1965, 1, 1569–1572. (In Russian) [Google Scholar]
- Bandurkin, G.A.; Dzhurinskii, B.F. Regularities in structural properties of RE compounds due to the atomic structure. Doklady AN SSSR 1966, 168, 1315–1318. (In Russian) [Google Scholar]
- Batsanov, S.S.; Batsanov, A.S. Introduction to Structural Chemistry; Springer: Derderecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2012; 542p. [Google Scholar] [CrossRef]
- Lande, A. Uber die Grosse der Atome. Z. Physik. 1920, 1, 191–197. [Google Scholar] [CrossRef]
- Tantardini, C.; Oganov, A.R. Thermochemical electronegativities of the elements. Nat. Commun. 2021, 12, 2087. [Google Scholar] [CrossRef]
- Lobanov, N.N.; Venskovsky, N.U. Choosing systems of ionic radii for crystal-chemical laws in lanthanide oxobromotungstates. Russ. J. Inorg. Chem. 2008, 53, 890–896. [Google Scholar] [CrossRef]
- Takenaka, K. Progress of Research in Negative Thermal Expansion Materials: Paradigm Shift in the Control of Thermal Expansion. Front. Chem. 2018, 6, 267. [Google Scholar] [CrossRef]
- Shi, N.; Song, Y.; Xing, X.; Chen, J. Negative thermal expansion in framework structure materials. Coord. Chem. Rev. 2021, 449, 214204. [Google Scholar] [CrossRef]
- Liang, E.; Sun, Q.; Yuan, H.; Wang, J.; Zeng, G.; Gao, Q. Negative thermal expansion: Mechanisms and materials. Front. Phys. 2021, 16, 53302. [Google Scholar] [CrossRef]
- Greis, O.; Petzel, T. Ein Beitrag zur Strukturchemie eder Seltenerd-Trifluoride. Z. Anorgan. Allgem. Chem. 1974, 403, 1–22. [Google Scholar] [CrossRef]
- Greis, O.; Haschke, J.M. Rare Earth Fluorides. In Handbook on the Physics and Chemistry of Rare Earths; Gscheidner, K.A., Eyring, L.R., Eds.; Elsevier (North Holland Publishing Co.): Amsterdam, The Netherlands, 1982; Volume 5, pp. 387–460. [Google Scholar]
- Glavin, G.G.; Karpov, Y.A. Oxygen determination in metallic RE and their fluorides. Zavod. Lab. 1964, 30, 306–308. (In Russian) [Google Scholar]
- Barishnikov, N.V.; Karpov, Y.A.; Guschina, T.I. Oxygen sources in RE fluorides. Izvestiya AN SSSR Neorgan. Mater. 1968, 4, 532–536. (In Russian) [Google Scholar]
- Glavin, G.G.; Karpov, Y.A.; Olzhataev, B.A. Oxygen determination in Y, Sr, Ca and Li fluorides by isotope dilution method. Zavod. Lab. 1969, 35, 172–175. (In Russian) [Google Scholar]
- Kudryavtseva, O.V.; Garashina, L.S.; Rivkina, K.K.; Sobolev, B.P. The solubility of LnF3 in LaF3. Sov. Phys. Crystallog. 1974, 18, 531. [Google Scholar]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system Jana2006: General features. Z. Kristallogr. 2014, 229, 345. [Google Scholar] [CrossRef]
- Becker, P.J.; Coppens, P. Extinction within the limit of validity of the Darwin transfer equations. I. General formalism for primary and secondary extinction and their applications to spherical crystals. Acta Cryst. A 1974, 30, 129–147. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. The Analytical Expression of the Results of the Theory of Space-Groups; Carnegie Institution of Washington: Washington, DC, USA, 1922; 180p. [Google Scholar]
| RF3 | (F-F)min, Å | (R-F)min, Å |
|---|---|---|
| t-LaF3 | 2.5615(14) | 2.4201(4) |
| t-CeF3 | 2.5584(16) | 2.3976(4) |
| t-PrF3 | 2.5496(9) | 2.3787(3) |
| t-NdF3 | 2.5340(8) | 2.3613(3) |
| “pseudo t-PmF3” | 2.5363(15) | 2.3542(3) |
| “pseudo β-PmF3” | 2.557(4) | 2.349(4) |
| “pseudo t-SmF3” | 2.5154(18) | 2.3432(4) |
| β-SmF3 | 2.5575(17) | 2.3478(12) |
| β-EuF3 | 2.559(2) | 2.3437(17) |
| β-GdF3 | 2.5474(14) | 2.3353(10) |
| β-TbF3 | 2.5398(16) | 2.3234(10) |
| β-DyF3 | 2.5161(14) | 2.3113(17) |
| β-HoF3 | 2.5064(15) | 2.2986(14) |
| β-ErF3 | 2.5072(12) | 2.2809(13) |
| β-TmF3 | 2.5079(14) | 2.2513(15) |
| β-YbF3 | 2.5086(15) | 2.2290(12) |
| β-LuF3 | 2.5089(16) | 2.1969(17) |
| β-YF3 | 2.5130(9) | 2.2877(11) |
| R3+ | Struct. Type | r+, Å | R3+ | Struct. Type | r+, Å |
|---|---|---|---|---|---|
| La | t- | 1.1671(16) | Gd | β- | 1.0823(16) |
| Ce | 1.1446(16) | Tb | 1.0704(16) | ||
| Pr | 1.1257(16) | Dy | 1.0583(17) | ||
| Nd | 1.1083(16) | Ho | 1.0456(16) | ||
| “pseudo t-Pm” | 1.1012(16) | Er | 1.0279(16) | ||
| “pseudo β-Pm” | β- | 1.096(4) | Tm | 0.9983(16) | |
| “pseudo t-Sm” | t- | 1.0902(18) | Yb | 0.9760(16) | |
| Sm | β- | 1.0948(17) | Lu | 0.9439(17) | |
| Eu | 1.0907(17) | Y | 1.0347(16) |
| RF3 | t-LaF3 | t-CeF3 | t-PrF3 | t-NdF3 | “pseudo t-SmF3” |
|---|---|---|---|---|---|
| ICSD ID | 2253935 | 2253989 | 2253990 | 2254005 | 2267804 |
| Crystal system | Trigonal | ||||
| Sp.gr., Z | P-3c1, z = 6 | ||||
| a (Å) | 7.1859(2) | 7.1296(3) | 7.0780(2) | 7.0298(3) | 6.9626(7) |
| c (Å) | 7.3543(2) | 7.2867(4) | 7.2392(3) | 7.1988(3) | 7.1317(8) |
| V (Å 3) | 328.88(2) | 320.77(3) | 314.08(2) | 308.09(3) | 299.41(7) |
| Vform | 54.812 | 53.462 | 52.347 | 51.348 | 49.901 |
| Dx (g·cm−3) | 5.9347 | 6.1225 | 6.2778 | 6.5077 | 6.8980 |
| μ (mm−1) | 10.167 | 11.154 | 12.194 | 13.288 | 15.535 |
| Tmin, Tmax | 0.2007, 0.2909 | 0.1806, 0.2707 | 0.1824, 0.2723 | 0.1345, 0.2306 | 0.0856, 0.1845 |
| Shape, color | colorless | colorless | light green | lilac | light yellow |
| Diameter (mm) | 0.22 | 0.22 | 0.20 | 0.22 | 0.115 |
| Wavelength (Å) | 0.56087 | ||||
| Θ range (deg) | 2.58–75.85 | 2.6–72.77 | 2.62–72.85 | 2.64–72.8 | 2.67–72.83 |
| Refl. collected | 34,709 | 33,176 | 32,968 | 32,720 | 31,459 |
| Refl. unique/Rint | 4760/4.11 | 4438/4.20 | 4358/4.21 | 4267/4.76 | 3947 |
| Refin. method | Full matrix least squares on F | ||||
| Param/Restrains | 22/0 | 22/0 | 22/0 | 22/0 | 35/0 |
| R/wR, % | 2.06/3.60 | 1.71/4.03 | 1.79/3.25 | 1.73/2.85 | 2.01/3.15 |
| Δρmin/Δρmax, Å−3 | −2.07/2.39 | −2.30/1.19 | −3.28/2.16 | −1.58/2.23 | −2.71/1.17 |
| GOF | 1.22 | 1.51 | 1.14 | 1.03 | 0.97 |
| Twins’ fractions | 0.645(3)/ 0.355(3) | 0.929(3)/ 0.071(3) | 0.0398(18)/ 0.9602(18) | 0.0190(17)/ 0.9810(17) | - |
| LnF3 | β-SmF3 | β-EuF3 | β-GdF3 | β-TbF3 | β-DyF3 |
|---|---|---|---|---|---|
| ICSD ID | 2254295 | 2254410 | 2254301 | 2254298 | 2254299 |
| Crystal system | orthorhombic | ||||
| Sp.gr., Z | Pnma, 4 | ||||
| a (Å) | 6.6964(8) | 6.6228(4) | 6.5733(4) | 6.5093(3) | 6.4561(3) |
| b (Å) | 7.0713(5) | 7.0181(5) | 6.9856(4) | 6.9458(3) | 6.9066(4) |
| c (Å) | 4.3855(9) | 4.3956(3) | 4.3898(2) | 4.3875(2) | 4.3797(2) |
| V (Å 3) | 207.66(5) | 204.31(2) | 201.573(19) | 198.369(15) | 195.290(17) |
| Vform | 51.916 | 51.076 | 50.393 | 49.592 | 48.822 |
| Dx (g·cm−3) | 6.6323 | 6.7933 | 7.0597 | 7.2298 | 7.4654 |
| μ (mm−1) | 14.953 | 16.128 | 17.469 | 18.860 | 20.345 |
| Tmin, Tmax | 0.724, 1.469 empirical | 0.614, 1.646 empirical | 0.1173, 0.215 | 0.0816, 0.1804 | 0.0816, 0.1804 |
| Shape, color | light yellow | light rose | colorless | colorless | colorless |
| Sample size, max/mid/min (mm) | 0.191/ 0.133/ 0.042 | 0.268/ 0.163/ 0.121 | 0.18, diameter | 0.20, diameter | 0.20, diameter |
| Wavelength (Å) | 0.56087 | ||||
| Θ range (deg) | 4.32–75.14 | 4.32–74.71 | 4.33–72.83 | 4.34–72.79 | 4.35–72.82 |
| Refl. collected | 172,260 | 163,839 | 21,098 | 21,136 | 20,682 |
| Refl. unique/Rint | 4527/4.50 | 4472/6.05 | 3876/4.52 | 3595/4.96 | 3700/4.96 |
| Refin. method | Full matrix least squares on F | ||||
| Param/Restrains | 23/0 | 38/0 | 23/0 | 23/0 | 23/0 |
| R/wR, % | 2.11/3.92 | 3.28/4.95 | 2.32/3.74 | 2.36/3.57 | 2.45/3.78 |
| Δρmin/Δρmax, Å−3 | −2.60/1.98 | −3.62/4.17 | −3.59/4.02 | −2.57/4.39 | −4.17/4.68 |
| GOF | 0.85 | 1.04 | 1.49 | 1.48 | 1.46 |
| RF3 | Ion | W.p. | s.o.f. | x/a | y/b | z/c | Ueq |
|---|---|---|---|---|---|---|---|
| t-LaF3 | La | 6f | 1 | 0.339998(8) | 0 | 1/4 | 0.006504(11) |
| F(1) | 12g | 1 | 0.3653(2) | 0.0526(2) | 0.58164(13) | 0.0160(4) | |
| F(2) | 4d | 1 | 1/3 | 2/3 | 0.1845(3) | 0.0128(2) | |
| F(3) | 2a | 1 | 0 | 0 | 1/4 | 0.0261(8) | |
| t-CeF3 | Ce | 6f | 1 | 0.340509(9) | 0 | 1/4 | 0.006236(12) |
| F(1) | 12g | 1 | 0.3672(3) | 0.0552(2) | 0.58078(15) | 0.0150(3) | |
| F(2) | 4d | 1 | 1/3 | 2/3 | 0.1857(3) | 0.0115(2) | |
| F(3) | 2a | 1 | 0 | 0 | 1/4 | 0.0222(7) | |
| t-PrF3 | Pr | 6f | 1 | 0.341071(8) | 0 | 1/4 | 0.006086(10) |
| F(1) | 12g | 1 | 0.3678(2) | 0.05667(18) | 0.58057(8) | 0.0141(2) | |
| F(2) | 4d | 1 | 1/3 | 2/3 | 0.1855(2) | 0.01157(15) | |
| F(3) | 2a | 1 | 0 | 0 | 1/4 | 0.0208(6) | |
| t-NdF3 | Nd | 6f | 1 | 0.341508(7) | 0 | 1/4 | 0.006144(10) |
| F(1) | 12g | 1 | 0.36866(16) | 0.05757(14) | 0.58086(8) | 0.0134(2) | |
| F(2) | 4d | 1 | 1/3 | 2/3 | 0.18539(18) | 0.01138(14) | |
| F(3) | 2a | 1 | 0 | 0 | 1/4 | 0.0200(5) | |
| “pseudo t-SmF3” | Sm | 6f | 0.995 | 0.34030(2) | 0 | 1/4 | 0.00772(5) |
| La | 6f | 0.005 | |||||
| F(1) | 12g | 1 | 0.3691(3) | 0.0580(3) | 0.58021(16) | 0.0187(4) | |
| F(2) | 4d | 1 | 1/3 | 2/3 | 0.1846(3) | 0.0137(2) | |
| F(3) | 2a | 1 | 0 | 0 | 1/4 | 0.0285(8) | |
| β-SmF3 | Sm | 4c | 1 | 0.366109(13) | 1/4 | 0.062105(18) | 0.005419(10) |
| F(1) | 4c | 1 | 0.5195(3) | 1/4 | 0.5778(4) | 0.0109(2) | |
| F(2) | 8b | 1 | 0.16446(18) | 0.06374(17) | 0.3932(3) | 0.01010(14) | |
| β-EuF3 | Eu | 4c | 1 | 0.36668(3) | 1/4 | 0.06272(6) | 0.00649(5) |
| F(1) | 4c | 1 | 0.5199(4) | 1/4 | 0.5802(6) | 0.0127(4) | |
| F(2) | 8b | 1 | 0.1652(2) | 0.0645(2) | 0.3897(4) | 0.0108(2) | |
| β-GdF3 | Gd | 4c | 1 | 0.367519(9) | 1/4 | 0.063353(13) | 0.005183(10) |
| F(1) | 4c | 1 | 0.5190(2) | 1/4 | 0.5806(3) | 0.00944(15) | |
| F(2) | 8b | 1 | 0.16517(14) | 0.06404(14) | 0.3878(3) | 0.00937(10) | |
| β-TbF3 | Tb | 4c | 1 | 0.367331(9) | 1/4 | 0.061873(13) | 0.005439(10) |
| F(1) | 4c | 1 | 0.5213(3) | 1/4 | 0.5841(3) | 0.01023(16) | |
| F(2) | 8b | 1 | 0.16517(18) | 0.06421(12) | 0.3842(2) | 0.00948(10) | |
| β-DyF3 | Dy | 4c | 1 | 0.367890(9) | 1/4 | 0.062002(16) | 0.005198(11) |
| F(1) | 4c | 1 | 0.5220(3) | 1/4 | 0.5857(4) | 0.0104(2) | |
| F(2) | 8b | 1 | 0.16413(14) | 0.06354(14) | 0.3819(3) | 0.00888(11) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobolev, B.P.; Sulyanova, E.A. Lanthanide Contraction in LnF3 (Ln = Ce-Lu) and Its Chemical and Structural Consequences: Part 2: Specialized Empirical System of R3+ (R = Y, La, and 14 Ln) and F1− Ionic Radii for RF3 Series. Int. J. Mol. Sci. 2023, 24, 17080. https://doi.org/10.3390/ijms242317080
Sobolev BP, Sulyanova EA. Lanthanide Contraction in LnF3 (Ln = Ce-Lu) and Its Chemical and Structural Consequences: Part 2: Specialized Empirical System of R3+ (R = Y, La, and 14 Ln) and F1− Ionic Radii for RF3 Series. International Journal of Molecular Sciences. 2023; 24(23):17080. https://doi.org/10.3390/ijms242317080
Chicago/Turabian StyleSobolev, Boris P., and Elena A. Sulyanova. 2023. "Lanthanide Contraction in LnF3 (Ln = Ce-Lu) and Its Chemical and Structural Consequences: Part 2: Specialized Empirical System of R3+ (R = Y, La, and 14 Ln) and F1− Ionic Radii for RF3 Series" International Journal of Molecular Sciences 24, no. 23: 17080. https://doi.org/10.3390/ijms242317080
APA StyleSobolev, B. P., & Sulyanova, E. A. (2023). Lanthanide Contraction in LnF3 (Ln = Ce-Lu) and Its Chemical and Structural Consequences: Part 2: Specialized Empirical System of R3+ (R = Y, La, and 14 Ln) and F1− Ionic Radii for RF3 Series. International Journal of Molecular Sciences, 24(23), 17080. https://doi.org/10.3390/ijms242317080






