Effects of Sequence Composition, Patterning and Hydrodynamics on the Conformation and Dynamics of Intrinsically Disordered Proteins
Abstract
1. Introduction
2. Results
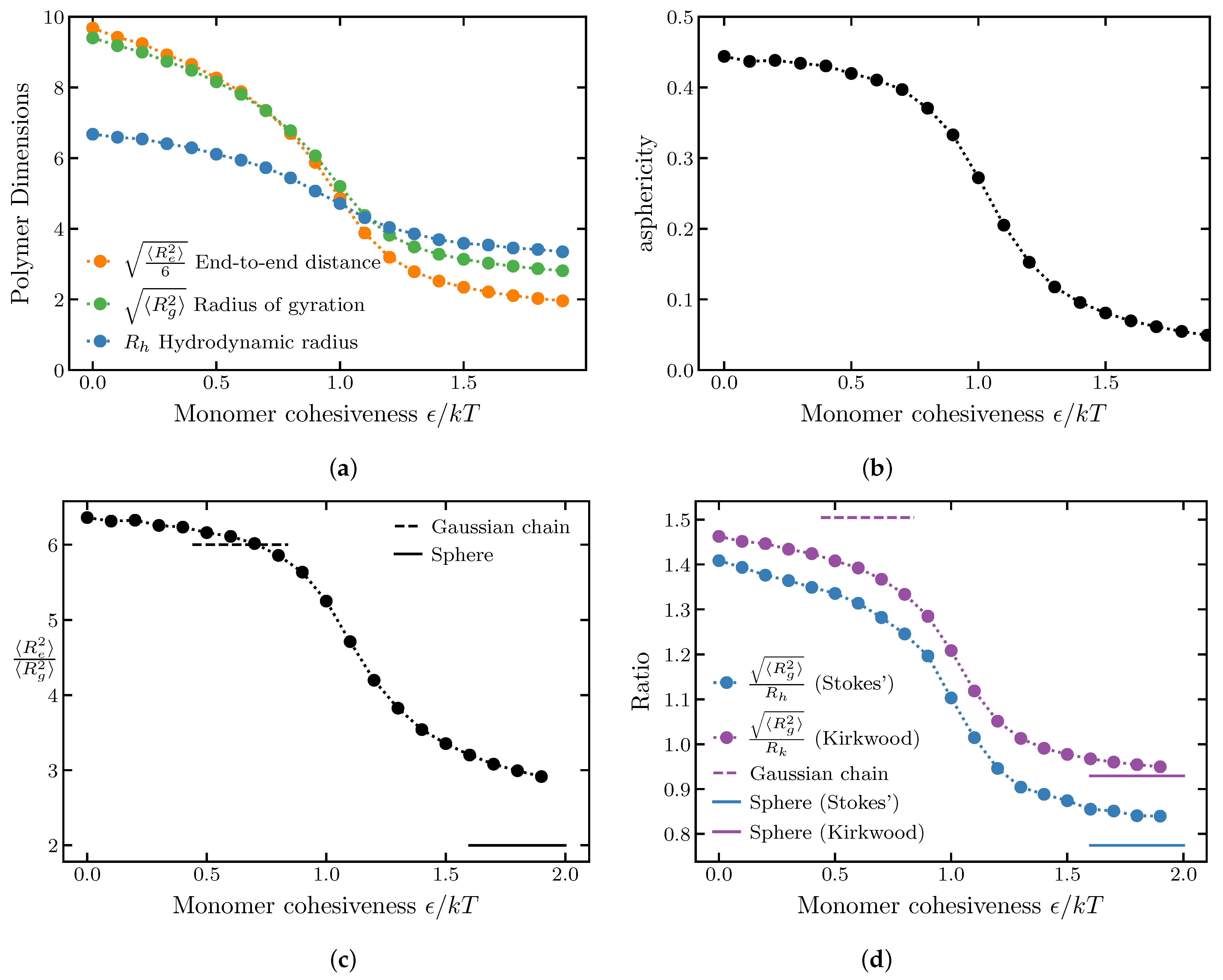
2.1. Effects of Sequence and Interactions on the Chain Dimensions
2.1.1. Effects of Internal Cohesiveness on the Chain Dimensions: Averaged Homopolymer Models
2.1.2. Chain Ensemble Asphericity
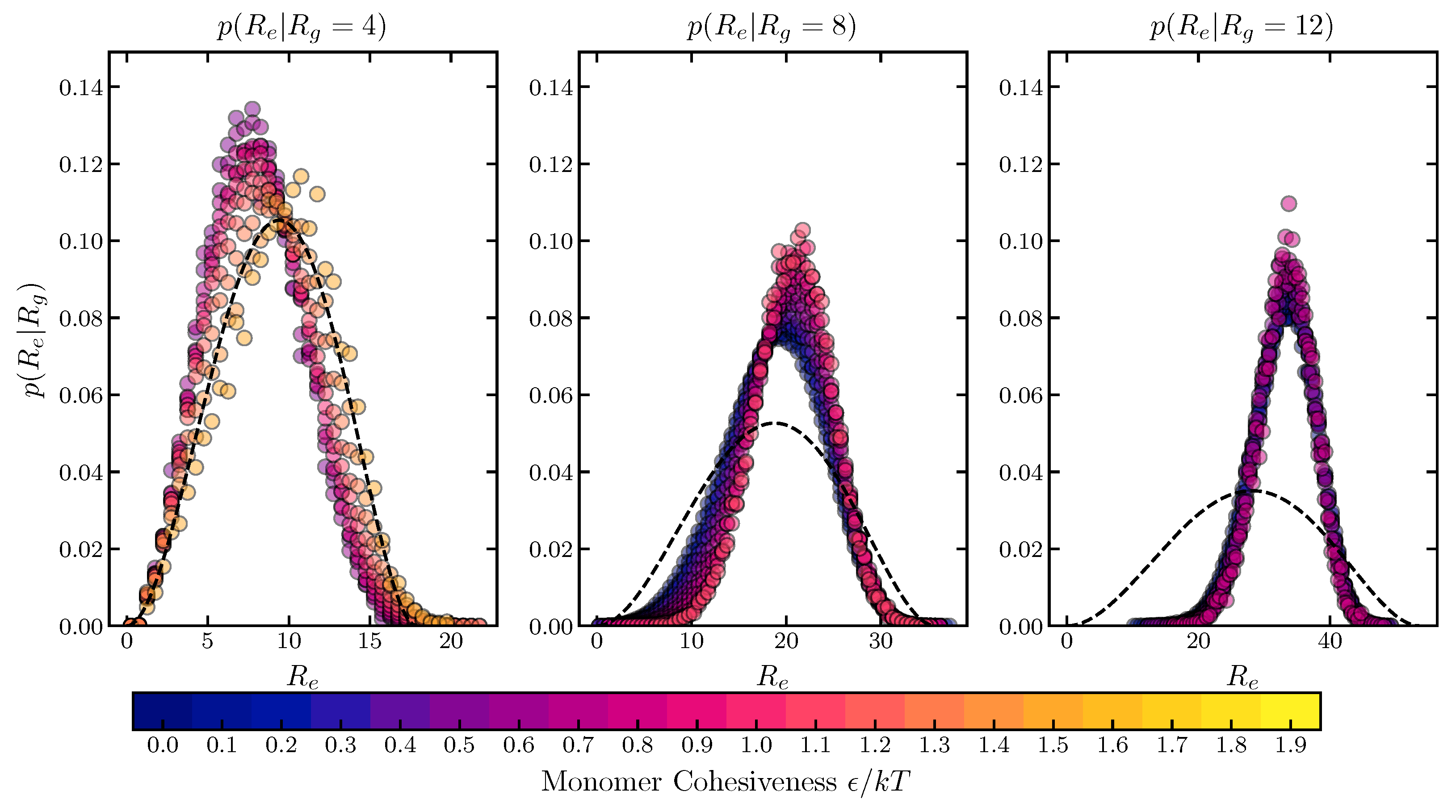
2.1.3. Conditional Sub-Ensemble Distributions
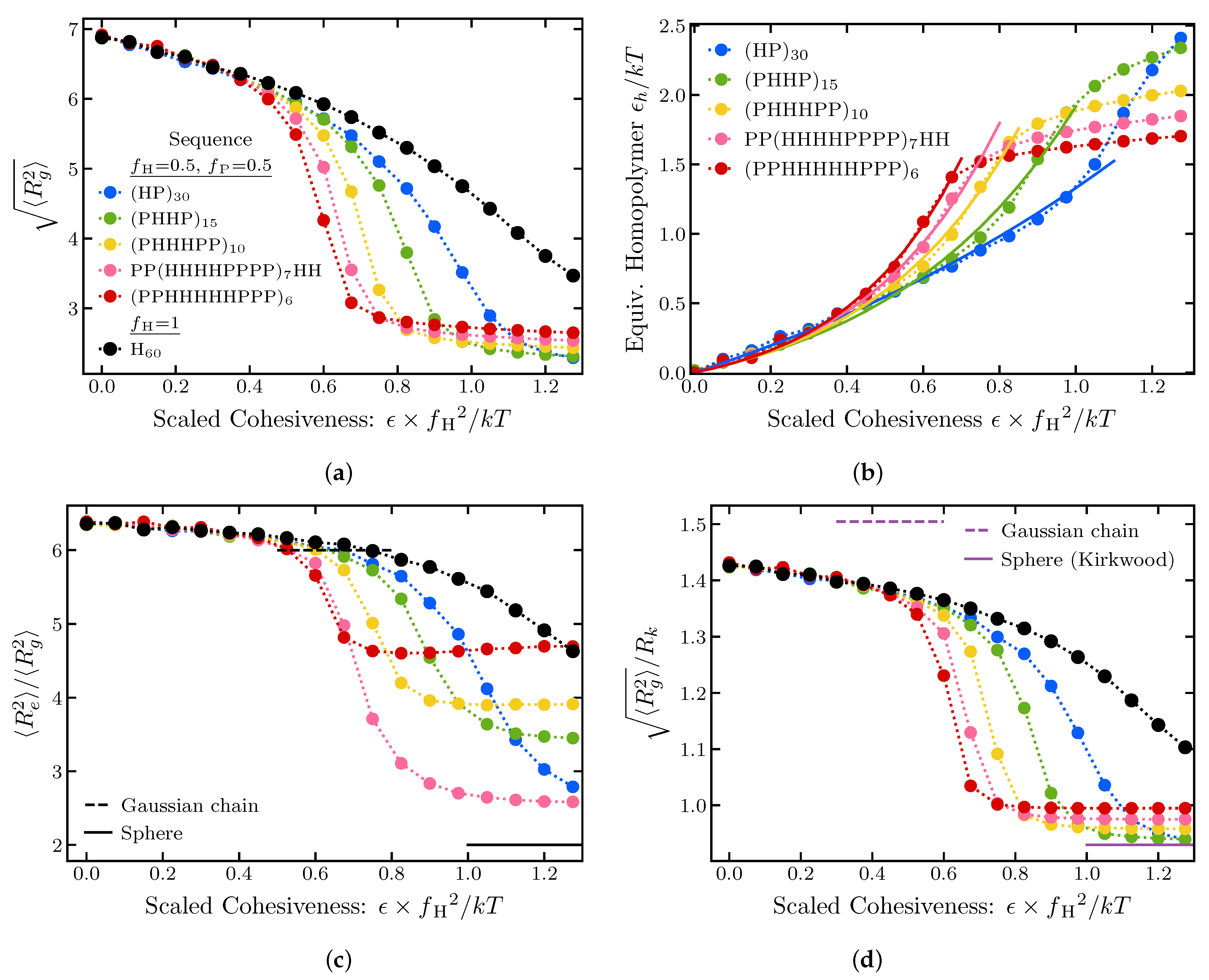
2.1.4. Effects of Sequence Composition and Patterning
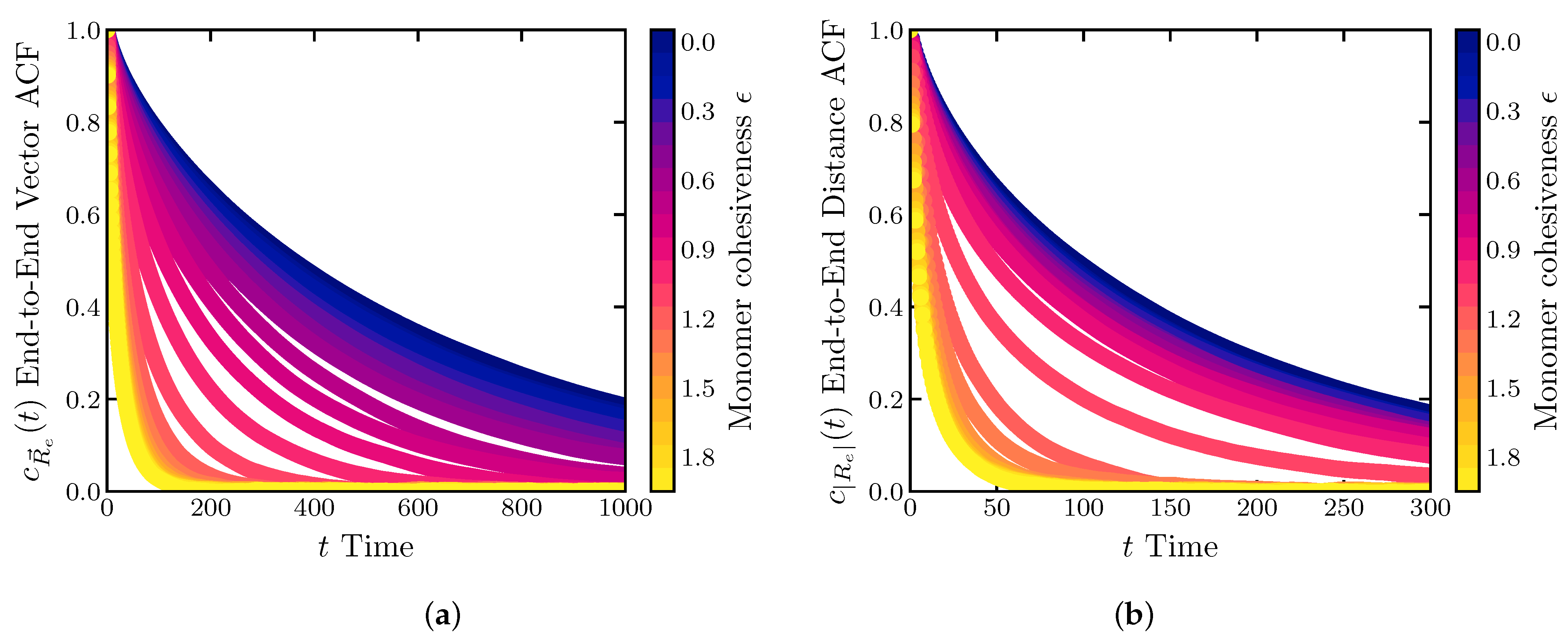
2.2. Dynamics of IDP Conformational Reconfiguration
3. Discussion and Experimental Implications
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uversky, V.N. Intrinsically disordered proteins from A to Z. Int. J. Biochem. Cell Biol. 2011, 43, 1090–1103. [Google Scholar] [CrossRef]
- Habchi, J.; Tompa, P.; Longhi, S.; Uversky, V.N. Introducing protein intrinsic disorder. Chem. Rev. 2014, 114, 6561–6588. [Google Scholar] [CrossRef] [PubMed]
- Dunker, A.K.; Oldfield, C.J.; Meng, J.; Romero, P.; Yang, J.Y.; Chen, J.W.; Vacic, V.; Obradovic, Z.; Uversky, V.N. The unfoldomics decade: An update on intrinsically disordered proteins. BMC Genom. 2008, 9, S1. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P. Intrinsically disordered proteins: A 10-year recap. Trends Biochem. Sci. 2012, 37, 509–516. [Google Scholar] [CrossRef]
- Hoogenboom, B.W.; Hough, L.E.; Lemke, E.A.; Lim, R.Y.; Onck, P.R.; Zilman, A. Physics of the nuclear pore complex: Theory, modeling and experiment. Phys. Rep. 2021, 921, 1–53. [Google Scholar] [CrossRef]
- Rajasekaran, N.; Kaiser, C.M. Co-Translational Folding of Multi-Domain Proteins. Front. Mol. Biosci. 2022, 9, 869027. [Google Scholar] [CrossRef]
- Dyla, M.; Kjaergaard, M. Intrinsically disordered linkers control tethered kinases via effective concentration. Proc. Natl. Acad. Sci. USA 2020, 117, 21413–21419. [Google Scholar] [CrossRef]
- Sørensen, C.S.; Kjaergaard, M. Effective concentrations enforced by intrinsically disordered linkers are governed by polymer physics. Proc. Natl. Acad. Sci. USA 2019, 116, 23124–23131. [Google Scholar] [CrossRef]
- Davey, N.E.; Van Roey, K.; Weatheritt, R.J.; Toedt, G.; Uyar, B.; Altenberg, B.; Budd, A.; Diella, F.; Dinkel, H.; Gibson, T.J. Attributes of short linear motifs. Mol. BioSyst. 2012, 8, 268–281. [Google Scholar] [CrossRef]
- Brodsky, S.; Jana, T.; Mittelman, K.; Chapal, M.; Kumar, D.K.; Carmi, M.; Barkai, N. Intrinsically disordered regions direct transcription factor in vivo binding specificity. Mol. Cell 2020, 79, 459–471. [Google Scholar] [CrossRef] [PubMed]
- Burger, V.M.; Gurry, T.; Stultz, C.M. Intrinsically disordered proteins: Where computation meets experiment. Polymers 2014, 6, 2684–2719. [Google Scholar] [CrossRef]
- Van Der Lee, R.; Buljan, M.; Lang, B.; Weatheritt, R.J.; Daughdrill, G.W.; Dunker, A.K.; Fuxreiter, M.; Gough, J.; Gsponer, J.; Jones, D.T.; et al. Classification of intrinsically disordered regions and proteins. Chem. Rev. 2014, 114, 6589–6631. [Google Scholar] [CrossRef] [PubMed]
- Schuler, B.; Soranno, A.; Hofmann, H.; Nettels, D. Single-Molecule FRET Spectroscopy and the Polymer Physics of Unfolded and Intrinsically Disordered Proteins. Annu. Rev. Biophys. 2016, 45, 207–231. [Google Scholar] [CrossRef] [PubMed]
- Bright, J.N.; Woolf, T.B.; Hoh, J.H. Predicting properties of intrinsically unstructured proteins. Prog. Biophys. Mol. Biol. 2001, 76, 131–173. [Google Scholar] [CrossRef]
- Ghavami, A.; Veenhoff, L.M.; van der Giessen, E.; Onck, P.R. Probing the disordered domain of the nuclear pore complex through coarse-grained molecular dynamics simulations. Biophys. J. 2014, 107, 1393–1402. [Google Scholar] [CrossRef]
- Tagliazucchi, M.; Peleg, O.; Kröger, M.; Rabin, Y.; Szleifer, I. Effect of charge, hydrophobicity, and sequence of nucleoporins on the translocation of model particles through the nuclear pore complex. Proc. Natl. Acad. Sci. USA 2013, 110, 3363–3368. [Google Scholar] [CrossRef]
- Ghavami, A.; Van der Giessen, E.; Onck, P.R. Towards a Coarse-Grained Model for Unfolded Proteins. In Computer Models in Biomechanics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–10. [Google Scholar]
- Vovk, A.; Gu, C.; Opferman, M.G.; Kapinos, L.E.; Lim, R.Y.; Coalson, R.D.; Jasnow, D.; Zilman, A. Simple biophysics underpins collective conformations of the intrinsically disordered proteins of the nuclear pore complex. eLife 2016, 5, e10785. [Google Scholar] [CrossRef]
- Zheng, T.; Zilman, A. Self-regulation of the nuclear pore complex enables clogging-free crowded transport. bioRxiv 2022. [Google Scholar] [CrossRef]
- Yamada, J.; Phillips, J.L.; Patel, S.; Goldfien, G.; Calestagne-Morelli, A.; Huang, H.; Reza, R.; Acheson, J.; Krishnan, V.V.; Newsam, S.; et al. A Bimodal Distribution of Two Distinct Categories of Intrinsically Disordered Structures with Separate Functions in FG Nucleoporins. Mol. Cell. Proteom. 2010, 9, 2205–2224. [Google Scholar] [CrossRef]
- Weathers, E.A.; Paulaitis, M.E.; Woolf, T.B.; Hoh, J.H. Reduced amino acid alphabet is sufficient to accurately recognize intrinsically disordered protein. FEBS Lett. 2004, 576, 348–352. [Google Scholar] [CrossRef]
- He, B.; Wang, K.; Liu, Y.; Xue, B.; Uversky, V.N.; Dunker, A.K. Predicting intrinsic disorder in proteins: An overview. Cell Res. 2009, 19, 929–949. [Google Scholar] [CrossRef]
- Mao, A.H.; Lyle, N.; Pappu, R.V. Describing sequence-ensemble relationships for intrinsically disordered proteins. Biochem. J. 2013, 449, 307–318. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. A decade and a half of protein intrinsic disorder: Biology still waits for physics. Protein Sci. 2013, 22, 693–724. [Google Scholar] [CrossRef]
- Das, R.K.; Ruff, K.M.; Pappu, R.V. Relating sequence encoded information to form and function of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2015, 32, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Holehouse, A.S.; Pappu, R.V. Collapse Transitions of Proteins and the Interplay Among Backbone, Sidechain, and Solvent Interactions. Annu. Rev. Biophys. 2018, 47, 19–39. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Tompa, P.; Pappu, R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. [Google Scholar] [CrossRef]
- Zahn, R.; Osmanović, D.; Ehret, S.; Callis, C.A.; Frey, S.; Stewart, M.; You, C.; Görlich, D.; Hoogenboom, B.W.; Richter, R.P. A physical model describing the interaction of nuclear transport receptors with FG nucleoporin domain assemblies. eLife 2016, 5, e14119. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Wotton-under-Edge, UK, 1998. [Google Scholar]
- Hofmann, H.; Soranno, A.; Borgia, A.; Gast, K.; Nettels, D.; Schuler, B. Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy. Biophys. Comput. Biol. 2012, 109, 16155–16160. [Google Scholar] [CrossRef]
- Muller-Spath, S.; Soranno, A.; Hirschfeld, V.; Hofmann, H.; Ruegger, S.; Reymond, L.; Nettels, D.; Schuler, B. Charge interactions can dominate the dimensions of intrinsically disordered proteins. Biophys. Comput. Biol. 2010, 107, 14609–14614. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Unusual biophysics of intrinsically disordered proteins. J. Books 2013, 1834, 932–951. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar] [CrossRef]
- Wu, C.; Wang, X. Globule-to-Coil Transition of a Single Homopolymer Chain in Solution. Phys. Rev. Lett. 1998, 80, 4092–4094. [Google Scholar] [CrossRef]
- Marsh, J.A.; Forman-Kay, J.D. Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J. 2010, 98, 2383–2390. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.; Vovk, A.; Zheng, T.; Coalson, R.D.; Zilman, A. The Role of Cohesiveness in the Permeability of the Spatial Assemblies of FG Nucleoporins. Biophys. J. 2019, 116, 1204–1215. [Google Scholar] [CrossRef] [PubMed]
- Simon, J.R.; Carroll, N.J.; Rubinstein, M.; Chilkoti, A.; López, G.P. Programming molecular self-assembly of intrinsically disordered proteins containing sequences of low complexity. Nat. Chem. 2017, 9, 509. [Google Scholar] [CrossRef]
- Davis, L.K.; Šarić, A.A.; Hoogenboom, B.W.; Zilman, A. Physical modelling of multivalent interactions in the nuclear pore complex. Biophys. J. 2021, 9, 1565–1577. [Google Scholar] [CrossRef]
- Yoo, T.Y.; Meisburger, S.P.; Hinshaw, J.; Pollack, L.; Haran, G.; Sosnick, T.R.; Plaxco, K. Small-angle X-ray scattering and single-molecule FRET spectroscopy produce highly divergent views of the low-denaturant unfolded state. J. Mol. Biol. 2012, 418, 226–236. [Google Scholar] [CrossRef]
- Watkins, H.M.; Simon, A.J.; Sosnick, T.R.; Lipman, E.A.; Hjelm, R.P.; Plaxco, K.W. Random coil negative control reproduces the discrepancy between scattering and FRET measurements of denatured protein dimensions. Proc. Natl. Acad. Sci. USA 2015, 112, 6631–6636. [Google Scholar] [CrossRef]
- Borgia, A.; Zheng, W.; Buholzer, K.; Borgia, M.B.; Schüler, A.; Hofmann, H.; Soranno, A.; Nettels, D.; Gast, K.; Grishaev, A.; et al. Consistent View of Polypeptide Chain Expansion in Chemical Denaturants from Multiple Experimental Methods. J. Am. Chem. Soc. 2016, 138, 11714–11726. [Google Scholar] [CrossRef]
- Zheng, W.; Borgia, A.; Buholzer, K.; Grishaev, A.; Schuler, B.; Best, R.B. Probing the Action of Chemical Denaturant on an Intrinsically Disordered Protein by Simulation and Experiment. J. Am. Chem. Soc. 2016, 138, 11702–11713. [Google Scholar] [CrossRef]
- Fuertes, G.; Banterle, N.; Ruff, K.M.; Chowdhury, A.; Mercadante, D.; Koehler, C.; Kachala, M.; Estrada Girona, G.; Milles, S.; Mishra, A.; et al. Decoupling of size and shape fluctuations in heteropolymeric sequences reconciles discrepancies in SAXS vs. FRET measurements. Proc. Natl. Acad. Sci. USA 2017, 114, 201704692. [Google Scholar] [CrossRef]
- Zerze, G.H.; Best, R.B.; Mittal, J. Modest influence of FRET chromophores on the properties of unfolded proteins. Biophys. J. 2014, 107, 1654–1660. [Google Scholar] [CrossRef] [PubMed]
- Riback, J.A.; Bowman, M.A.; Zmyslowski, A.M.; Plaxco, K.W.; Clark, P.L.; Sosnick, T.R. Commonly-used FRET fluorophores promote collapse of an otherwise disordered protein. Proc. Natl. Acad. Sci. USA 2019, 116, 8889–8894. [Google Scholar] [CrossRef]
- Theillet, F.X.; Kalmar, L.; Tompa, P.; Han, K.H.; Selenko, P.; Dunker, A.K.; Daughdrill, G.W.; Uversky, V.N. The alphabet of intrinsic disorder I. Act like a Pro: On the abundance and roles of proline residues in intrinsically disordered proteins. Intrinsically Disord. Proteins 2013, 1, e24360-1. [Google Scholar] [CrossRef] [PubMed]
- Oldfield, C.J.; Dunker, A.K. Intrinsically Disordered Proteins and Intrinsically Disordered Protein Regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef]
- Uversky, V.N. Paradoxes and wonders of intrinsic disorder: Complexity of simplicity. Intrinsically Disord. Proteins 2016, 4, e1135015. [Google Scholar] [CrossRef]
- Das, R.K.; Pappu, R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA 2013, 110, 13392–13397. [Google Scholar] [CrossRef]
- Martin, E.W.; Holehouse, A.S.; Grace, C.R.; Hughes, A.; Pappu, R.V.; Mittag, T. Sequence Determinants of the Conformational Properties of an Intrinsically Disordered Protein Prior to and upon Multisite Phosphorylation. J. Am. Chem. Soc. 2016, 138, 15323–15335. [Google Scholar] [CrossRef] [PubMed]
- Ginell, G.M.; Holehouse, A.S. An Introduction to the Stickers-and-Spacers Framework as Applied to Biomolecular Condensates. In Phase-Separated Biomolecular Condensates; Springer: Berlin/Heidelberg, Germany, 2023; pp. 95–116. [Google Scholar]
- Mittag, T.; Pappu, R.V. A conceptual framework for understanding phase separation and addressing open questions and challenges. Mol. Cell 2022, 82, 2201–2214. [Google Scholar] [CrossRef]
- Huang, K.; Tagliazucchi, M.; Park, S.H.; Rabin, Y.; Szleifer, I. Nanocompartmentalization of the Nuclear Pore Lumen. Biophys. J. 2019, 118, 219–231. [Google Scholar] [CrossRef]
- Peyro, M.; Soheilypour, M.; Ghavami, A.; Mofrad, M.R.K. Nucleoporin’s Like Charge Regions Are Major Regulators of FG Coverage and Dynamics Inside the Nuclear Pore Complex. PLoS ONE 2015, 10, e0143745. [Google Scholar] [CrossRef]
- Popken, P.; Ghavami, A.; Onck, P.R.; Poolman, B.; Veenhoff, L.M. Size-dependent leak of soluble and membrane proteins through the yeast nuclear pore complex. Mol. Biol. Cell 2015, 26, 1386–1394. [Google Scholar] [CrossRef] [PubMed]
- Soranno, A.; Buchli, B.; Nettels, D.; Cheng, R.R.; Müller-Späth, S.; Pfeil, S.H.; Hoffmann, A.; Lipman, E.A.; Makarov, D.E.; Schuler, B. Quantifying internal friction in unfolded and intrinsically disordered proteins with single-molecule spectroscopy. Proc. Natl. Acad. Sci. USA 2012, 109, 17800–17806. [Google Scholar] [CrossRef] [PubMed]
- Echeverria, I.; Makarov, D.E.; Papoian, G.A. Concerted dihedral rotations give rise to internal friction in unfolded proteins. J. Am. Chem. Soc. 2014, 136, 8708–8713. [Google Scholar] [CrossRef] [PubMed]
- De Sancho, D.; Sirur, A.; Best, R.B. Molecular origins of internal friction effects on protein-folding rates. Nat. Commun. 2014, 5, 4307. [Google Scholar] [CrossRef] [PubMed]
- Rauscher, S.; Pomes, R. Molecular simulations of protein disorder. Biochem. Cell Biol. 2010, 88, 269–290. [Google Scholar] [CrossRef] [PubMed]
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; De Groot, B.L.; Grubmüller, H. Structural ensembles of intrinsically disordered proteins depend strongly on force field: A comparison to experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. [Google Scholar] [CrossRef]
- Mercadante, D.; Wagner, J.A.; Aramburu, I.V.; Lemke, E.A.; Gräter, F. Sampling Long-versus Short-Range Interactions Defines the Ability of Force Fields to Reproduce the Dynamics of Intrinsically Disordered Proteins. J. Chem. Theory Comput. 2017, 13, 3964–3974. [Google Scholar] [CrossRef]
- Chong, S.H.; Chatterjee, P.; Ham, S. Computer Simulations of Intrinsically Disordered Proteins. Annu. Rev. Phys. Chem. 2017, 68, 117–134. [Google Scholar] [CrossRef]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef]
- Ashbaugh, H.S.; Hatch, H.W. Natively unfolded protein stability as a coil-to-globule transition in charge/hydropathy space. J. Am. Chem. Soc. 2008, 130, 9536–9542. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Gomes, G.N.; Gradinaru, C.C.; Chan, H.S. An Adequate Account of Excluded Volume Is Necessary to Infer Compactness and Asphericity of Disordered Proteins by Forster Resonance Energy Transfer. J. Phys. Chem. B 2015, 119, 15191–15202. [Google Scholar] [CrossRef]
- Ananth, A.N.; Mishra, A.; Frey, S.; Dwarkasing, A.; Versloot, R.; van der Giessen, E.; Görlich, D.; Onck, P.; Dekker, C. Spatial structure of disordered proteins dictates conductance and selectivity in nuclear pore complex mimics. eLife 2018, 7, e31510. [Google Scholar] [CrossRef] [PubMed]
- Fragasso, A.; De Vries, H.W.; Andersson, J.; Van Der Sluis, E.O.; Van Der Giessen, E.; Dahlin, A.; Onck, P.R.; Dekker, C. A designer FG-Nup that reconstitutes the selective transport barrier of the nuclear pore complex. Nat. Commun. 2021, 12, 2010. [Google Scholar] [CrossRef]
- Davis, L.K.; Ford, I.J.; Šarić, A.; Hoogenboom, B.W. Intrinsically disordered nuclear pore proteins show ideal-polymer morphologies and dynamics. Phys. Rev. E 2020, 101, 022420. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Forman-Kay, J.D.; Chan, H.S. Theories for Sequence-Dependent Phase Behaviors of Biomolecular Condensates. Biochemistry 2018, 57, 2499–2508. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Forman-Kay, J.D.; Chan, H.S. Sequence-Specific Polyampholyte Phase Separation in Membraneless Organelles. Phys. Rev. Lett. 2016, 117, 178101. [Google Scholar] [CrossRef] [PubMed]
- Frey, S.; Gorlich, D. A saturated FG-repeat hydrogel can reproduce the permeability properties of nuclear pore complexes. Cell 2007, 130, 512–523. [Google Scholar] [CrossRef]
- Schmidt, H.B.; Görlich, D. Nup98 FG domains from diverse species spontaneously phase-separate into particles with nuclear pore-like permselectivity. eLife 2015, 4, e04251. [Google Scholar] [CrossRef]
- Schmidt, H.B.; Görlich, D. Transport Selectivity of Nuclear Pores, Phase Separation, and Membraneless Organelles. Trends Biochem. Sci. 2016, 41, 46–61. [Google Scholar] [CrossRef] [PubMed]
- Gomes, G.N.; Gradinaru, C.C. Insights into the conformations and dynamics of intrinsically disordered proteins using single-molecule fluorescence. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2017, 1865, 1696–1706. [Google Scholar] [CrossRef] [PubMed]
- Steinhauser, M.O. A molecular dynamics study on universal properties of polymer chains in different solvent qualities. Part I. A review of linear chain properties. J. Chem. Phys. 2015, 122, 94901. [Google Scholar] [CrossRef] [PubMed]
- Benhamou, M.; Mahoux, G. Long polymers in good solvent: ϵ-expansion of the ratio of the radius of gyration to the end to end distance. J. Phys. Lett. 1985, 46, 689–693. [Google Scholar] [CrossRef]
- Chen, M.; Lin, K.Y. Universal amplitude ratios for three-dimensional self-avoiding walks. J. Phys. A Math. General 2002, 35, 1501. [Google Scholar] [CrossRef]
- Parry, M.; Fischbach, E. Probability distribution of distance in a uniform ellipsoid: Theory and applications to physics. J. Math. Phys. 2000, 41, 2417–2433. [Google Scholar] [CrossRef]
- Dünweg, B.; Reith, D.; Steinhauser, M.; Kremer, K. Corrections to scaling in the hydrodynamic properties of dilute polymer solutions. J. Chem. Phys. 2002, 117, 914–924. [Google Scholar] [CrossRef]
- Ziv, G.; Haran, G. Protein folding, protein collapse, and Tanford’s transfer model: Lessons from single-molecule FRET. J. Am. Chem. Soc. 2009, 131, 2942–2947. [Google Scholar] [CrossRef]
- Sanchez, I.C. Phase Transition Behavior of the Isolated Polymer Chain. Macromolecules 1979, 12, 980–988. [Google Scholar] [CrossRef]
- Dill, K.A. Theory for the folding and stability of globular proteins. Biochemistry 1985, 24, 1501–1509. [Google Scholar] [CrossRef]
- Zamyatnin, A. Protein volume in solution. Prog. Biophys. Mol. Biol. 1972, 24, 107–123. [Google Scholar] [CrossRef] [PubMed]
- Levitt, M. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol. 1976, 104, 59–107. [Google Scholar] [CrossRef]
- Sawle, L.; Ghosh, K. A theoretical method to compute sequence dependent configurational properties in charged polymers and proteins. J. Chem. Phys. 2015, 143, 085101. [Google Scholar] [CrossRef] [PubMed]
- Vovk, A. Coarse Grained Modeling of Intrinsically Disordered Protein Structures and Dynamics. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2019. [Google Scholar]
- Vitalis, A.; Pappu, R.V. ABSINTH: A new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2019, 30, 673–699. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Chan, H.S. Phase Separation and Single-Chain Compactness of Charged Disordered Proteins Are Strongly Correlated. Biophys. J. 2019, 112, 2043–2046. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Nettels, D.; Gopich, I.V.; Hoffmann, A.; Schuler, B. Ultrafast dynamics of protein collapse from single-molecule photon statistics. Proc. Natl. Acad. Sci. USA 2017, 104, 2655–2660. [Google Scholar] [CrossRef]
- Portman, J.J. Non-Gaussian dynamics from a simulation of a short peptide: Loop closure rates and effective diffusion coefficients. J. Chem. Phys. 2013, 118, 2381–2391. [Google Scholar] [CrossRef]
- Cheng, R.R.; Hawk, A.T.; Makarov, D.E. Exploring the role of internal friction in the dynamics of unfolded proteins using simple polymer models. J. Chem. Phys. 2013, 138, 74112. [Google Scholar] [CrossRef]
- Soranno, A.; Zosel, F.; Hofmann, H. Internal friction in an intrinsically disordered protein - Comparing Rouse-like models with experiments. J. Chem. Phys. 2013, 148, 123326. [Google Scholar] [CrossRef]
- Nettels, D.; Hoffmann, A.; Schuler, B. Unfolded protein and peptide dynamics investigated with single-molecule FRET and correlation spectroscopy from picoseconds to seconds. J. Phys. Chem. B 2008, 112, 6137–6146. [Google Scholar] [CrossRef]
- Schuler, B. Perspective: Chain dynamics of unfolded and intrinsically disordered proteins from nanosecond fluorescence correlation spectroscopy combined with single-molecule FRET. J. Chem. Phys. 2018, 149, 20901. [Google Scholar] [CrossRef] [PubMed]
- Calandrini, V.; Pellegrini, E.; Calligari, P.; Hinsen, K.; Kneller, G. nMoldyn—Interfacing spectroscopic experiments, molecular dynamics simulations and models for time correlation functions. Ecole th´ematique de la Soci´et´e Fran¸caise de la Neutronique 2011, 12, 201–232. [Google Scholar] [CrossRef]
- Liu, B.; Dünweg, B. Translational diffusion of polymer chains with excluded volume and hydrodynamic interactions by Brownian dynamics simulation. J. Chem. Phys. 2003, 118, 5057. [Google Scholar] [CrossRef]
- Pham, T.T.; Bajaj, M.; Prakash, J.R. Brownian dynamics simulation of polymer collapse in a poor solvent: Influence of implicit hydrodynamic interactions. Soft Matter 2008, 4, 1196–1207. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez Schmidt, R.; Hernández Cifre, J.G.; García de la Torre, J. Translational diffusion coefficients of macromolecules. Eur. Phys. J. E Soft Matter 2012, 35, 9806. [Google Scholar] [CrossRef]
- Opferman, M.G.; Coalson, R.D.; Jasnow, D.; Zilman, A. Morphological control of grafted polymer films via attraction to small nanoparticle inclusions. Phys. Rev. E 2012, 86, 031806. [Google Scholar] [CrossRef]
- Opferman, M.G.; Coalson, R.D.; Jasnow, D.; Zilman, A. Morphology of polymer brushes infiltrated by attractive nanoinclusions of various sizes. Langmuir 2013, 29, 8584–8591. [Google Scholar] [CrossRef]
- Stirnemann, G.; Giganti, D.; Fernandez, J.M.; Berne, B.J. Elasticity, structure, and relaxation of extended proteins under force. Proc. Natl. Acad. Sci. USA 2013, 110, 3847–3852. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Yamakawa, H. Transport Properties of Polymer Chains in Dilute Solution: Hydrodynamic Interaction. J. Chem. Phys. 1970, 53, 436. [Google Scholar] [CrossRef]
- Zuk, P.J.; Wajnryb, E.; Mizerski, K.A.; Szymczak, P. Rotne-Prager-Yamakawa approximation for different-sized particles in application to macromolecular bead models. J. Fluid Mech. 2014, 741, 5. [Google Scholar] [CrossRef]
- Slater, G.W.; Holm, C.; Chubynsky, M.V.; de Haan, H.W.; Dubé, A.; Grass, K.; Hickey, O.A.; Kingsburry, C.; Sean, D.; Shendruk, T.N.; et al. Modeling the separation of macromolecules: A review of current computer simulation methods. Electrophoresis 2009, 30, 792–818. [Google Scholar] [CrossRef] [PubMed]
- Szymczak, P.; Cieplak, M. Hydrodynamic effects in proteins. J. Phys. Condens. Matter 2011, 23, 33102–33114. [Google Scholar] [CrossRef]
- Kirkwood, G.; Riseman, J. The intrinsic viscosities and diffusion constants of flexible macro- molecules in solution. J. Chem. Phys. 1948, 16, 565–573. [Google Scholar] [CrossRef]
- Schmidt, R.R.; Cifre, J.G.; De La Torre, J.G. Comparison of Brownian dynamics algorithms with hydrodynamic interaction. J. Chem. Phys. 2011, 135, 84116. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: Cambridge, MA, USA, 2002; p. 638. [Google Scholar]
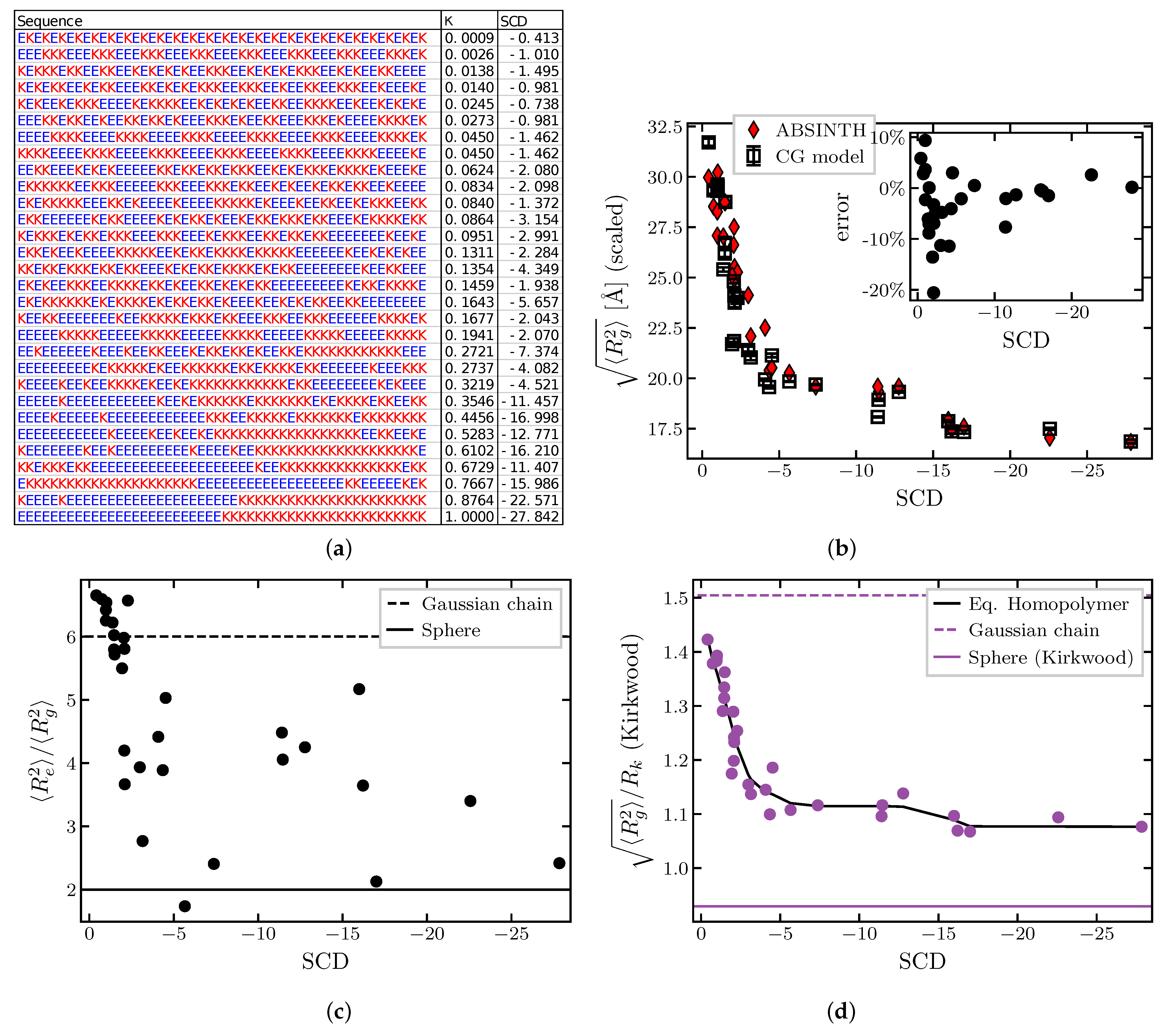


| Sequence | SCD |
|---|---|
| (HP | −0.410 |
| (PHHP | −0.537 |
| (PHHHPP | −0.778 |
| PP(HHHHPPPPHH | −1.002 |
| (PPHHHHHPPP | −1.319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vovk, A.; Zilman, A. Effects of Sequence Composition, Patterning and Hydrodynamics on the Conformation and Dynamics of Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2023, 24, 1444. https://doi.org/10.3390/ijms24021444
Vovk A, Zilman A. Effects of Sequence Composition, Patterning and Hydrodynamics on the Conformation and Dynamics of Intrinsically Disordered Proteins. International Journal of Molecular Sciences. 2023; 24(2):1444. https://doi.org/10.3390/ijms24021444
Chicago/Turabian StyleVovk, Andrei, and Anton Zilman. 2023. "Effects of Sequence Composition, Patterning and Hydrodynamics on the Conformation and Dynamics of Intrinsically Disordered Proteins" International Journal of Molecular Sciences 24, no. 2: 1444. https://doi.org/10.3390/ijms24021444
APA StyleVovk, A., & Zilman, A. (2023). Effects of Sequence Composition, Patterning and Hydrodynamics on the Conformation and Dynamics of Intrinsically Disordered Proteins. International Journal of Molecular Sciences, 24(2), 1444. https://doi.org/10.3390/ijms24021444




