Optical Differentiation of Brain Tumors Based on Raman Spectroscopy and Cluster Analysis Methods
Abstract
:1. Introduction
2. Results
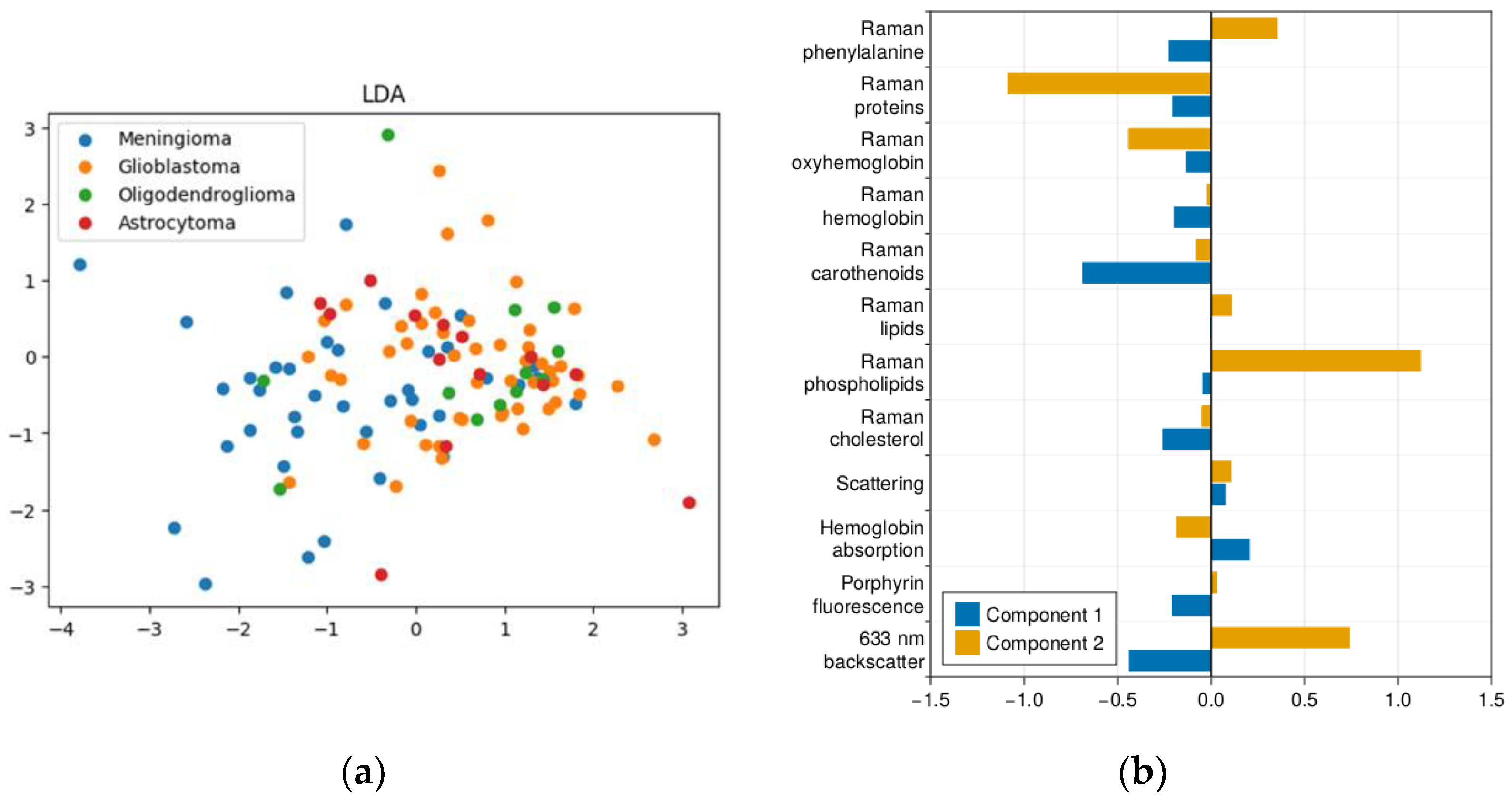
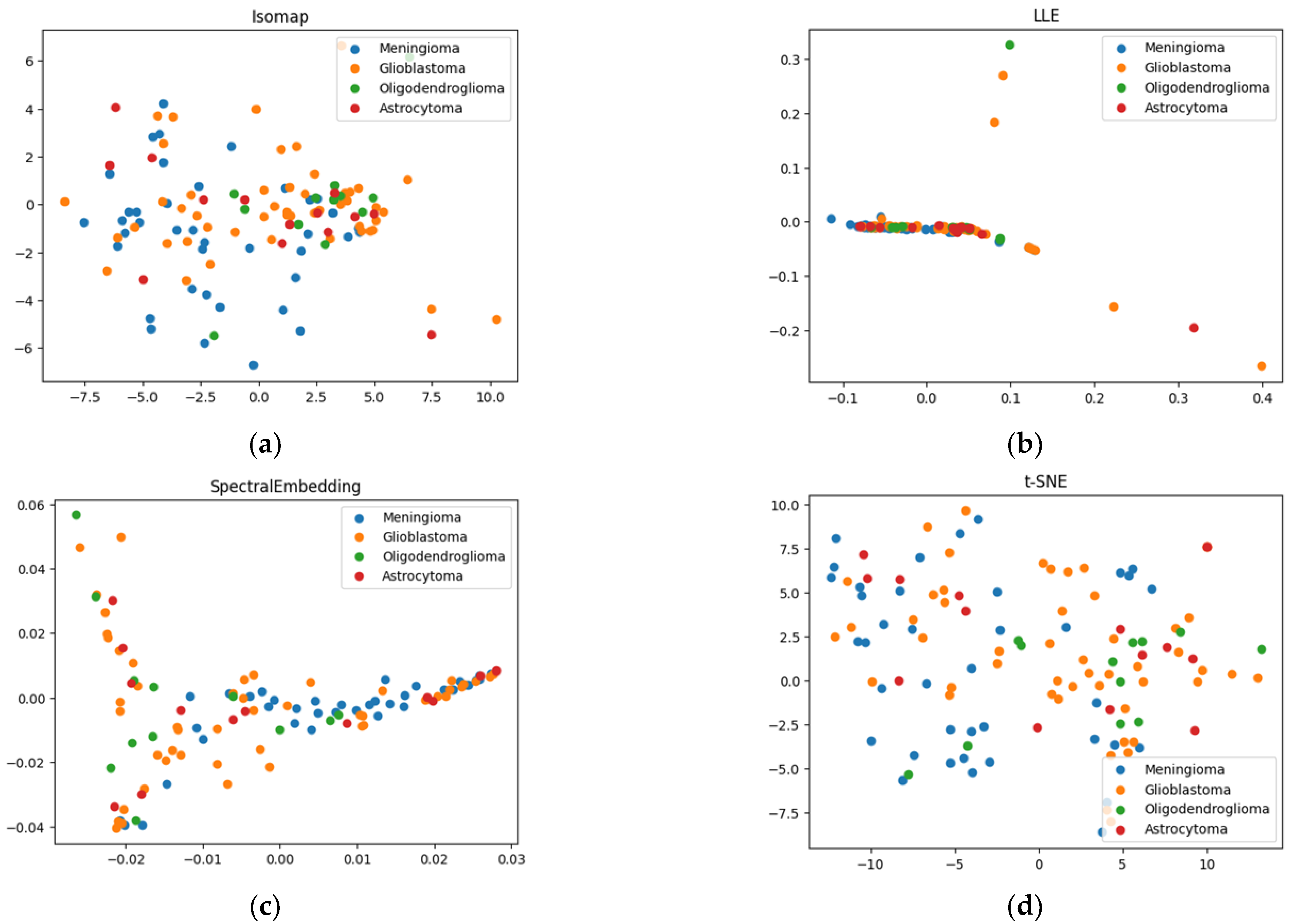
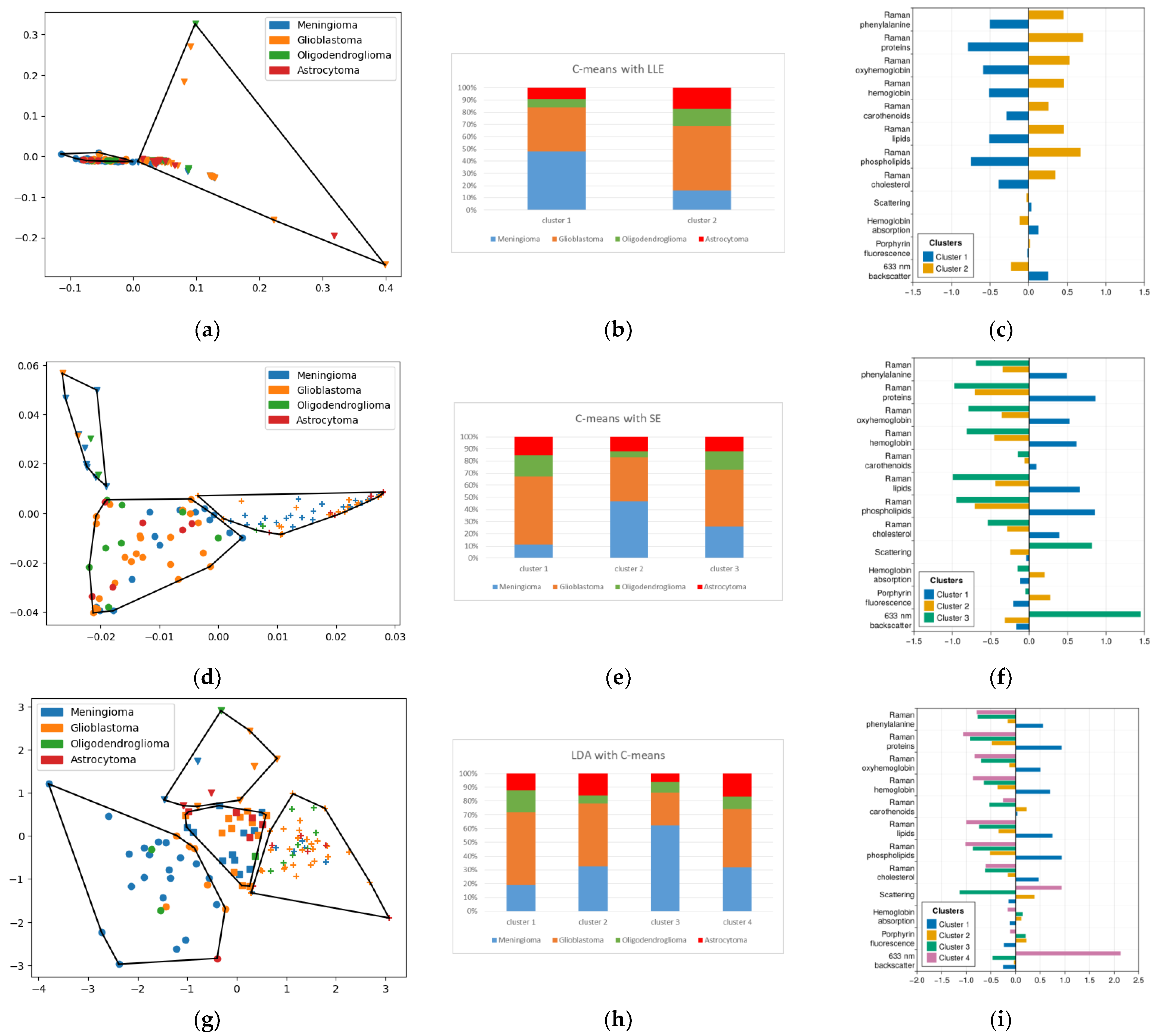
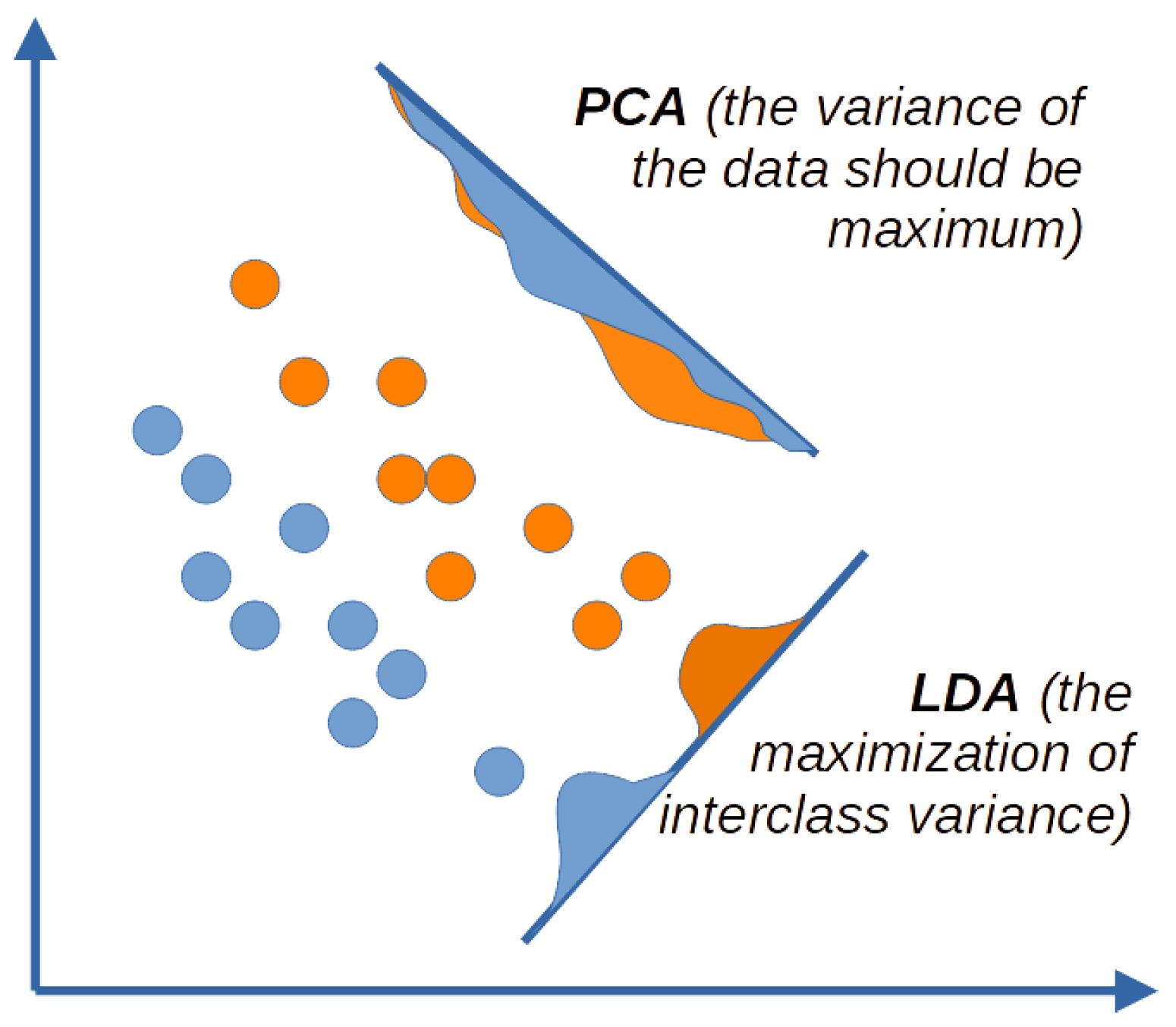
2.1. Results of Dimensionality Reduction
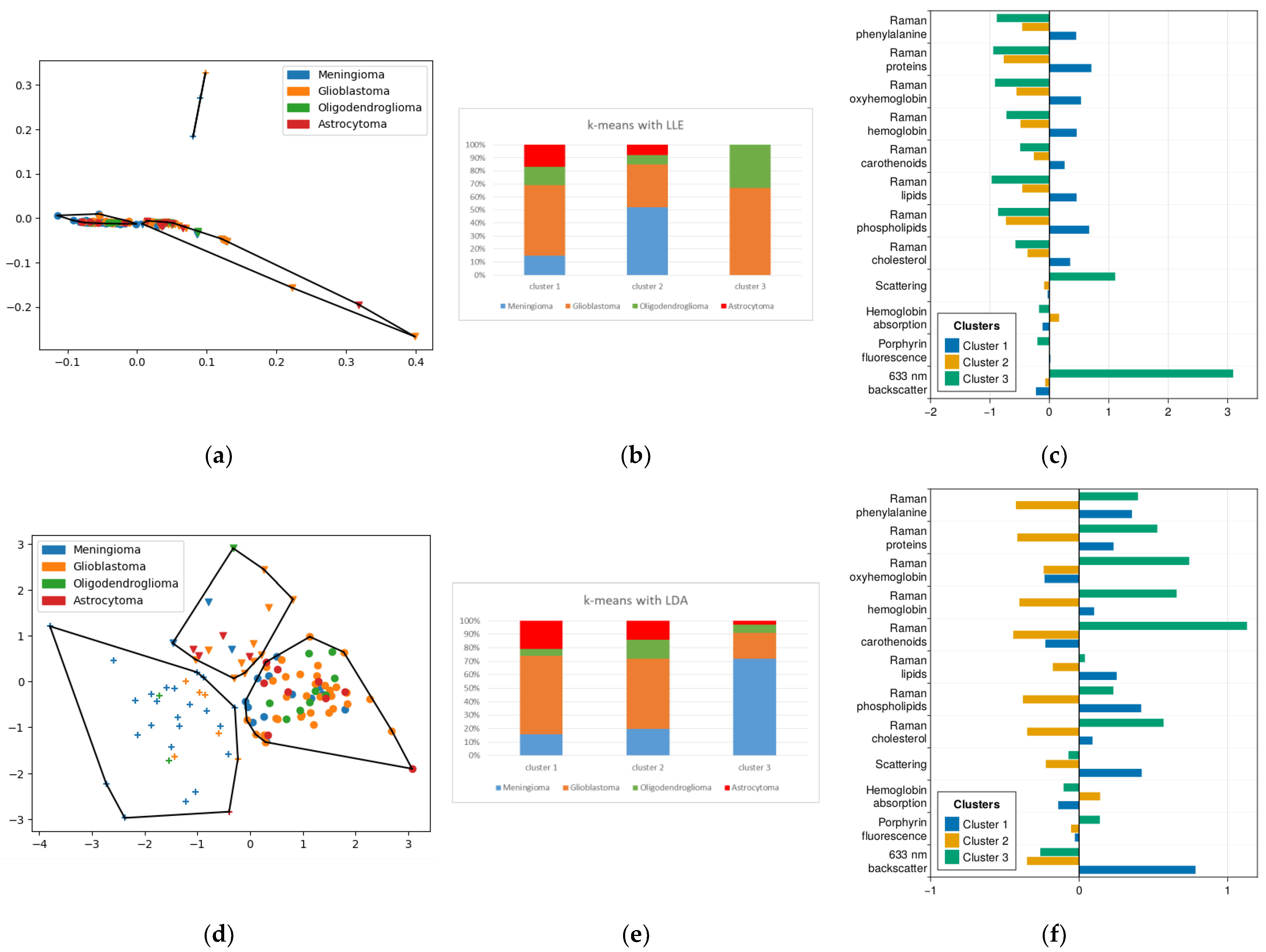
2.2. k-Means Method of Cluster Analysis
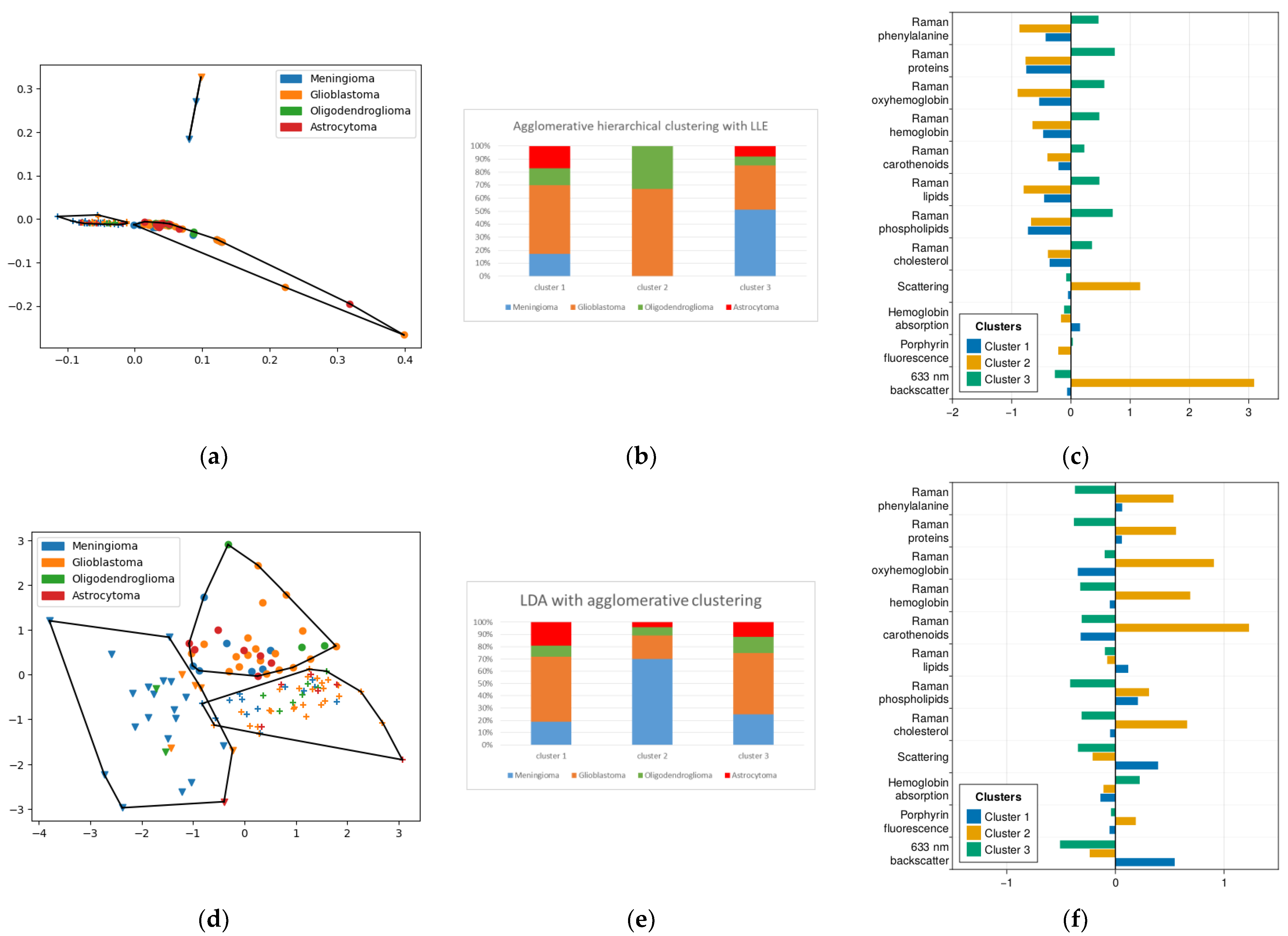
2.3. Method of Agglomerative Hierarchical Clustering
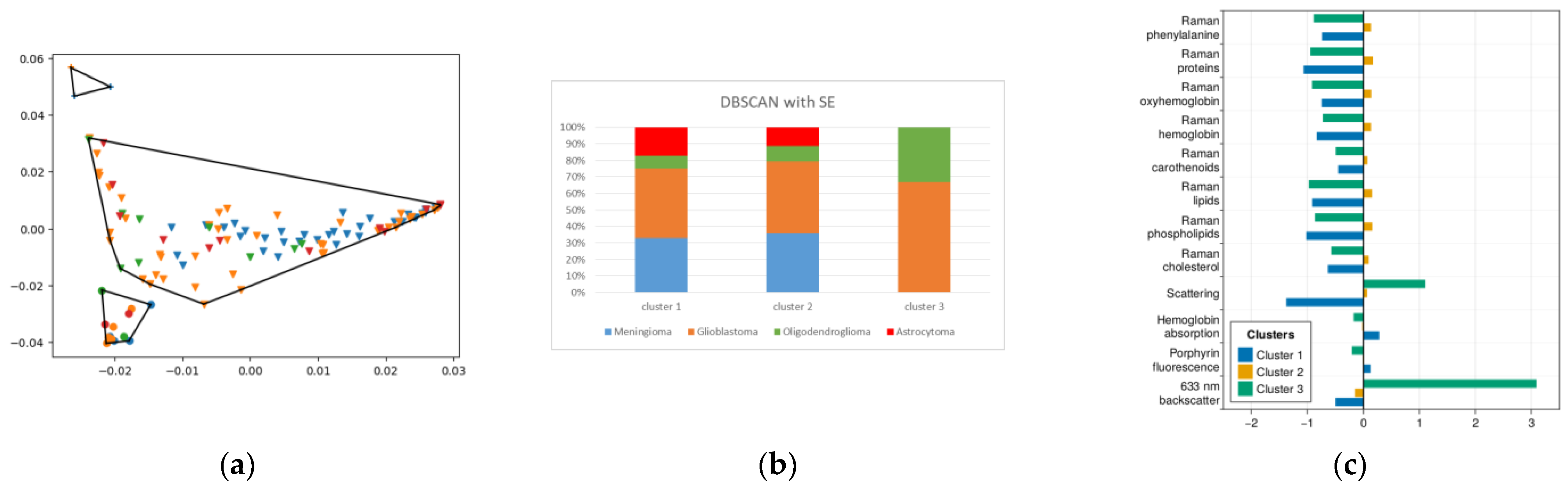
2.4. DBSCAN
2.5. Fuzzy Cluster Analysis
3. Discussion
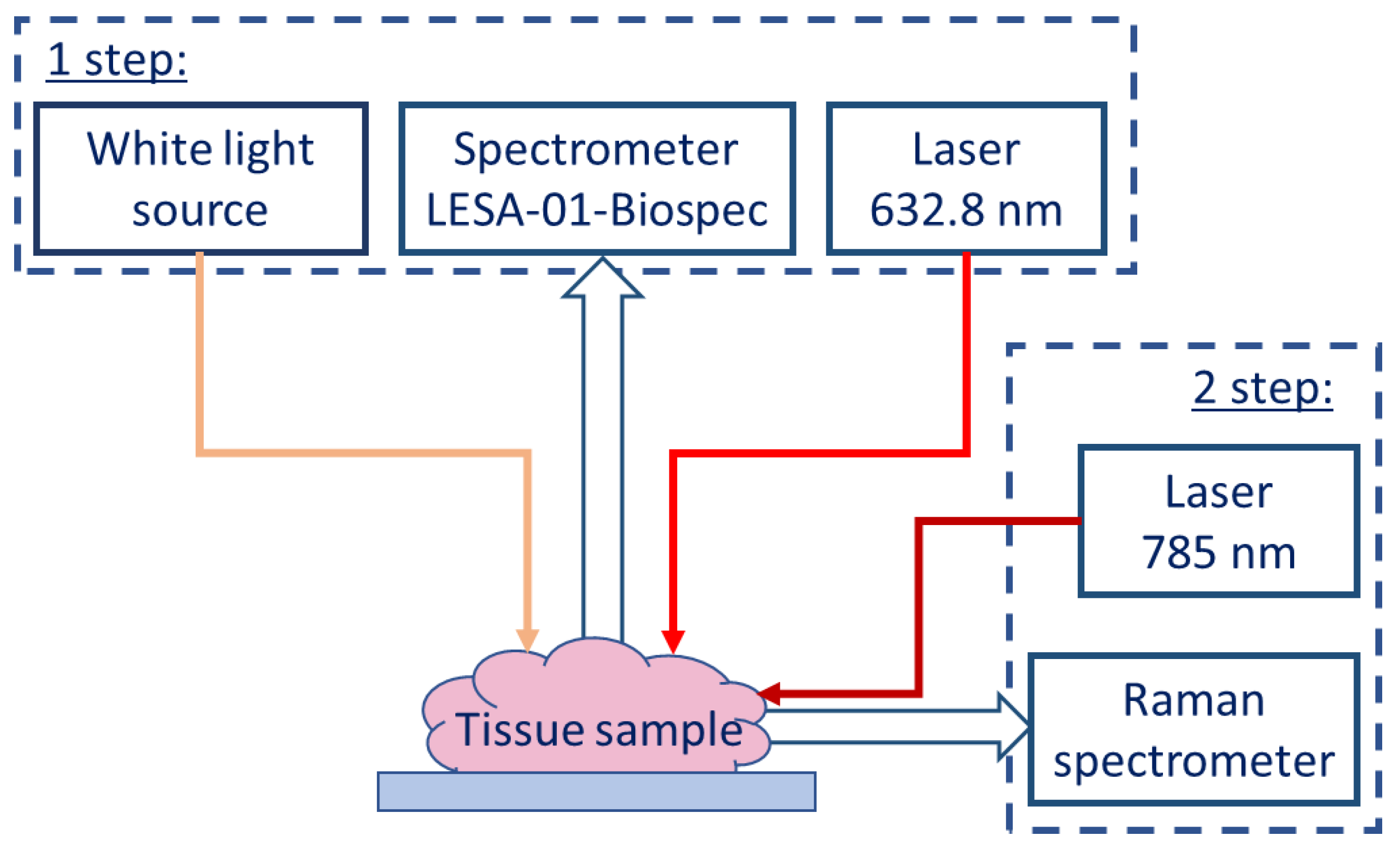
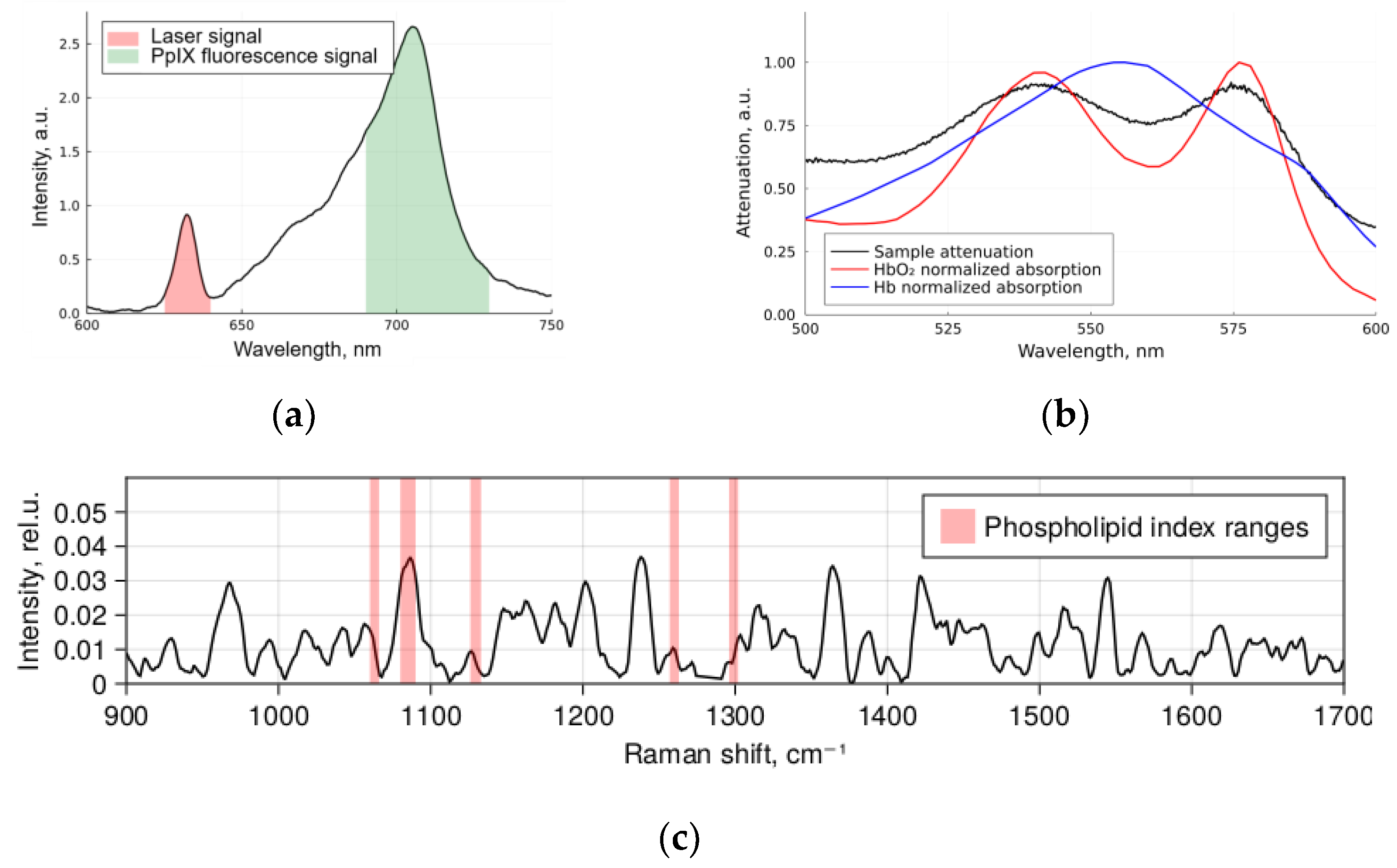
4. Materials and Methods
- Registration of diffuse reflectance spectra in white light and fluorescence spectra with 632.8 nm laser as an excitation source using the LESA-01-BIOSPEC spectrometer;
- Registration of the spontaneous Raman spectra of a sample excited at 785 nm using the Raman-HR-TEC-785 spectrometer.
- hard clustering: each object belongs to only one of the clusters;
- fuzzy clustering: each object belongs to each cluster to some extent; i.e., the algorithms fix the probabilities of a given object belonging to each cluster, and these probabilities must sum to “1”.
- centroid-based clustering;
- hierarchical clustering;
- density-based clustering;
- distribution-based clustering.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Potapov, A.A.; Goryaynov, S.A.; Okhlopkov, V.A.; Pitskhelauri, D.I.; Kobyakov, G.L.; Zhukov, V.Y.; Gol’bin, D.A.; Svistov, D.V.; Martynov, B.V.; Krivoshapkin, A.L.; et al. Clinical guidelines for the use of intraoperative fluorescence diagnosis in brain tumor surgery. Zhurnal Vopr. Nejrokhirurgii Im. N. N. Burdenko 2015, 79, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Stummer, W.; Novotny, A.; Stepp, H.; Goetz, C.; Bise, K.; Reulen, H.J. Fluorescence-guided resection of glioblastoma multiforme by using 5-aminolevulinic acid-induced porphyrins: A prospective study in 52 consecutive patients. J. Neurosurg. 2000, 93, 1003–1013. [Google Scholar] [CrossRef] [PubMed]
- Stummer, W.; Tonn, J.C.; Goetz, C.; Ullrich, W.; Stepp, H.; Bink, A.; Pietsch, T.; Pichlmeier, U. 5-Aminolevulinic acid-derived tumor fluorescence: The diagnostic accuracy of visible fluorescence qualities as corroborated by spectrometry and histology and postoperative imaging. Neurosurgery 2014, 74, 310–320. [Google Scholar] [CrossRef] [PubMed]
- Stummer, W.; Suero Molina, E. Fluorescence Imaging/Agents in Tumor Resection. Neurosurg. Clin. N. Am. 2017, 28, 569–583. [Google Scholar] [CrossRef] [PubMed]
- Feigl, G.C.; Ritz, R.; Moraes, M.; Klein, J.; Ramina, K.; Gharabaghi, A.; Krischek, B.; Danz, S.; Bornemann, A.; Liebsch, M.; et al. Resection of malignant brain tumors in eloquent cortical areas: A new multimodal approach combining 5-aminolevulinic acid and intraoperative monitoring. J. Neurosurg. 2010, 113, 352–357. [Google Scholar] [CrossRef]
- Duffau, H. Long-term outcomes after supratotal resection of diffuse low-grade gliomas: A consecutive series with 11-year follow-up. Acta Neurochir. 2016, 158, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Goryaynov, S.A.; Buklina, S.B.; Khapov, I.V.; Batalov, A.I.; Potapov, A.A.; Pronin, I.N.; Belyaev, A.U.; Aristov, A.A.; Zhukov, V.U.; Pavlova, G.V.; et al. 5-ALA-guided tumor resection during awake speech mapping in gliomas located in eloquent speech areas: Single-center experience. Front. Oncol. 2022, 12, 940951. [Google Scholar] [CrossRef] [PubMed]
- Marbacher, S.; Klinger, E.; Schwyzer, L.; Fischer, I.; Nevzati, E.; Diepers, M.; Roelcke, U.; Fathi, A.R.; Coluccia, D.; Fandino, J. Use of fluorescence to guide resection or biopsy of primary brain tumors and brain metastases. Neurosurg. Focus 2014, 36, E10. [Google Scholar] [CrossRef]
- Goryaynov, S.A.; Okhlopkov, V.A.; Golbin, D.A.; Chernyshov, K.A.; Svistov, D.V.; Martynov, B.V.; Kim, A.V.; Byvaltsev, V.A.; Pavlova, G.V.; Batalov, A.; et al. Fluorescence Diagnosis in Neurooncology: Retrospective Analysis of 653 Cases. Front. Oncol. 2019, 9, 830. [Google Scholar] [CrossRef]
- Shofty, B.; Richetta, C.; Haim, O.; Kashanian, A.; Gurevich, A.; Grossman, R. 5-ALA-assisted stereotactic brain tumor biopsy improve diagnostic yield. Eur. J. Surg. Oncol. 2019, 45, 2375–2378. [Google Scholar] [CrossRef]
- Strickland, B.A.; Zada, G. 5-ALA Enhanced Fluorescence-Guided Microscopic to Endoscopic Resection of Deep Frontal Subcortical Glioblastoma Multiforme. World Neurosurg. 2021, 148, 65. [Google Scholar] [CrossRef] [PubMed]
- Rynda, A.Y.; Olyushin, V.E.; Rostovtsev, D.M.; Zabrodskaya, Y.M.; Papayan, G.V. Fluorescent diagnostics with chlorin e6 in surgery of low-grade glioma. Biomed. Photonics 2021, 10, 35–43. [Google Scholar] [CrossRef]
- Manoharan, R.; Parkinson, J. Sodium Fluorescein in Brain Tumor Surgery: Assessing Relative Fluorescence Intensity at Tumor Margins. Asian J. Neurosurg. 2020, 15, 88–93. [Google Scholar] [CrossRef] [PubMed]
- Teng, C.W.; Huang, V.; Arguelles, G.R.; Zhou, C.; Cho, S.S.; Harmsen, S.; Lee, J.Y.K. Applications of indocyanine green in brain tumor surgery: Review of clinical evidence and emerging technologies. Neurosurg. Focus 2021, 50, E4. [Google Scholar] [CrossRef] [PubMed]
- Schwake, M.; Stummer, W.; Suero Molina, E.J.; Wölfer, J. Simultaneous fluorescein sodium and 5-ALA in fluorescence-guided glioma surgery. Acta Neurochir. 2015, 157, 877–879. [Google Scholar] [CrossRef] [PubMed]
- Widhalm, G.; Kiesel, B.; Woehrer, A.; Traub-Weidinger, T.; Preusser, M.; Marosi, C.; Prayer, D.; Hainfellner, J.A.; Knosp, E.; Wolfsberger, S. 5-Aminolevulinic acid induced fluorescence is a powerful intraoperative marker for precise histopathological grading of gliomas with non-significant contrast-enhancement. PLoS ONE 2013, 8, e76988. [Google Scholar] [CrossRef]
- Aiman, W.; Gasalberti, D.P.; Rayi, A. Low-Grade Gliomas. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2023. [Google Scholar]
- Romanishkin, I.D.; Ospanov, A.; Savelyeva, T.A.; Shugay, S.V.; Goryainov, S.A.; Pavlova, G.V.; Pronin, I.N.; Loshchenov, V.B. Multimodal Method of Tissue Differentiation in Neurooncology Using Raman Spectroscopy, Fluorescence and Diffuse Reflectance Spectroscopy. Vopr. Neirokhirurgii 2022, 86, 5–12. [Google Scholar] [CrossRef]
- Fürtjes, G.; Reinecke, D.; Von Spreckelsen, N.; Meißner, A.-K.; Rueß, D.; Timmer, M.; Freudiger, C.; Ion-Margineanu, A.; Khalid, F.; Watrinet, K.; et al. Intraoperative Microscopic Autofluorescence Detection and Characterization in Brain Tumors Using Stimulated Raman Histology and Two-Photon Fluorescence. Front. Oncol. 2023, 13, 1146031. [Google Scholar] [CrossRef]
- Santos, L.F.; Wolthuis, R.; Koljenović, S.; Almeida, R.M.; Puppels, G.J. Fiber-Optic Probes for in Vivo Raman Spectroscopy in the High-Wavenumber Region. Anal. Chem. 2005, 77, 6747–6752. [Google Scholar] [CrossRef]
- Koljenović, S.; Bakker Schut, T.C.; Wolthuis, R.; De Jong, B.; Santos, L.; Caspers, P.J.; Kros, J.M.; Puppels, G.J. Tissue Characterization Using High Wave Number Raman Spectroscopy. J. Biomed. Opt. 2005, 10, 031116. [Google Scholar] [CrossRef]
- Jermyn, M.; Mok, K.; Mercier, J.; Desroches, J.; Pichette, J.; Saint-Arnaud, K.; Bernstein, L.; Guiot, M.-C.; Petrecca, K.; Leblond, F. Intraoperative Brain Cancer Detection with Raman Spectroscopy in Humans. Sci. Transl. Med. 2015, 7, 274ra19. [Google Scholar] [CrossRef] [PubMed]
- Desroches, J.; Jermyn, M.; Mok, K.; Lemieux-Leduc, C.; Mercier, J.; St-Arnaud, K.; Urmey, K.; Guiot, M.-C.; Marple, E.; Petrecca, K.; et al. Characterization of a Raman Spectroscopy Probe System for Intraoperative Brain Tissue Classification. Biomed. Opt. Express 2015, 6, 2380–2397. [Google Scholar] [CrossRef]
- Lu, H.; Grygoryev, K.; Bermingham, N.; Jansen, M.; O’Sullivan, M.; Nunan, G.; Buckley, K.; Manley, K.; Burke, R.; Andersson-Engels, S. Combined Autofluorescence and Diffuse Reflectance for Brain Tumour Surgical Guidance: Initial Ex Vivo Study Results. Biomed. Opt. Express 2021, 12, 2432–2446. [Google Scholar] [CrossRef] [PubMed]
- Baria, E.; Giordano, F.; Guerrini, R.; Caporalini, C.; Buccoliero, A.M.; Cicchi, R.; Pavone, F.S. Dysplasia and Tumor Discrimination in Brain Tissues by Combined Fluorescence, Raman, and Diffuse Reflectance Spectroscopies. Biomed. Opt. Express 2023, 14, 1256–1275. [Google Scholar] [CrossRef] [PubMed]
- Crase, S.; Hall, B.; Thennadil, S.N. Cluster Analysis for IR and NIR Spectroscopy: Current Practices to Future Perspectives. Comput. Mater. Contin. 2021, 69, 1945–1965. [Google Scholar] [CrossRef]
- Wahl, J.; Klint, E.; Hallbeck, M.; Hillman, J.; Wårdell, K.; Ramser, K. Impact of Preprocessing Methods on the Raman Spectra of Brain Tissue. Biomed. Opt. Express 2022, 13, 6763–6777. [Google Scholar] [CrossRef]
- Romanishkin, I.; Savelieva, T.; Kosyrkova, A.; Okhlopkov, V.; Shugai, S.; Orlov, A.; Kravchuk, A.; Goryaynov, S.; Golbin, D.; Pavlova, G.; et al. Differentiation of Glioblastoma Tissues Using Spontaneous Raman Scattering with Dimensionality Reduction and Data Classification. Front. Oncol. 2022, 12, 944210. [Google Scholar] [CrossRef]
- Gierlinger, N.; Schwanninger, M.; Wimmer, R. Characteristics and Classification of Fourier-Transform near Infrared Spectra of the Heartwood of Different Larch Species (Larix Sp.). J. Near Infrared Spectrosc. 2004, 12, 113–119. [Google Scholar] [CrossRef]
- Gautam, R.; Vanga, S.; Ariese, F.; Umapathy, S. Review of multidimensional data processing approaches for Raman and infrared spectroscopy. EPJ Tech. Instrum. 2015, 2, 8. [Google Scholar] [CrossRef]

| Algorithm | Silhouette Index | Calinski- Harbasz Index | Davies- Bouldin Index | Sensitivity/Specificity of the Meningioma Differentiation |
|---|---|---|---|---|
| LLE with k-means | 0.64 | 256.68 | 0.46 | 52%/92.5% |
| LDA with k-means | 0.37 | 125.57 | 0.89 | 72%/82% |
| LLE with agglomerative clustering | 0.75 | 148.17 | 0.39 | 51%/91.5% |
| LDA with agglomerative clustering | 0.32 | 101.58 | 0.99 | 70%/78% |
| Spectral embedding with DBSCAN | 0.40 | 76.52 | 0.56 | 36.1%/83.5% |
| Algorithm | Partition Coefficient | Partition Entropy Coefficient | Sensitivity/Specificity of the Meningioma Differentiation |
|---|---|---|---|
| LDA with C-means | 0.11 | 0.26 | 63%/72% |
| LLE with C-means | 0.16 | 0.12 | 48%/84% |
| Spectral embedding with C-means | 0.14 | 0.18 | 47%/81.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ospanov, A.; Romanishkin, I.; Savelieva, T.; Kosyrkova, A.; Shugai, S.; Goryaynov, S.; Pavlova, G.; Pronin, I.; Loschenov, V. Optical Differentiation of Brain Tumors Based on Raman Spectroscopy and Cluster Analysis Methods. Int. J. Mol. Sci. 2023, 24, 14432. https://doi.org/10.3390/ijms241914432
Ospanov A, Romanishkin I, Savelieva T, Kosyrkova A, Shugai S, Goryaynov S, Pavlova G, Pronin I, Loschenov V. Optical Differentiation of Brain Tumors Based on Raman Spectroscopy and Cluster Analysis Methods. International Journal of Molecular Sciences. 2023; 24(19):14432. https://doi.org/10.3390/ijms241914432
Chicago/Turabian StyleOspanov, Anuar, Igor Romanishkin, Tatiana Savelieva, Alexandra Kosyrkova, Svetlana Shugai, Sergey Goryaynov, Galina Pavlova, Igor Pronin, and Victor Loschenov. 2023. "Optical Differentiation of Brain Tumors Based on Raman Spectroscopy and Cluster Analysis Methods" International Journal of Molecular Sciences 24, no. 19: 14432. https://doi.org/10.3390/ijms241914432
APA StyleOspanov, A., Romanishkin, I., Savelieva, T., Kosyrkova, A., Shugai, S., Goryaynov, S., Pavlova, G., Pronin, I., & Loschenov, V. (2023). Optical Differentiation of Brain Tumors Based on Raman Spectroscopy and Cluster Analysis Methods. International Journal of Molecular Sciences, 24(19), 14432. https://doi.org/10.3390/ijms241914432







