TRAX-CHEMxt: Towards the Homogeneous Chemical Stage of Radiation Damage
Abstract
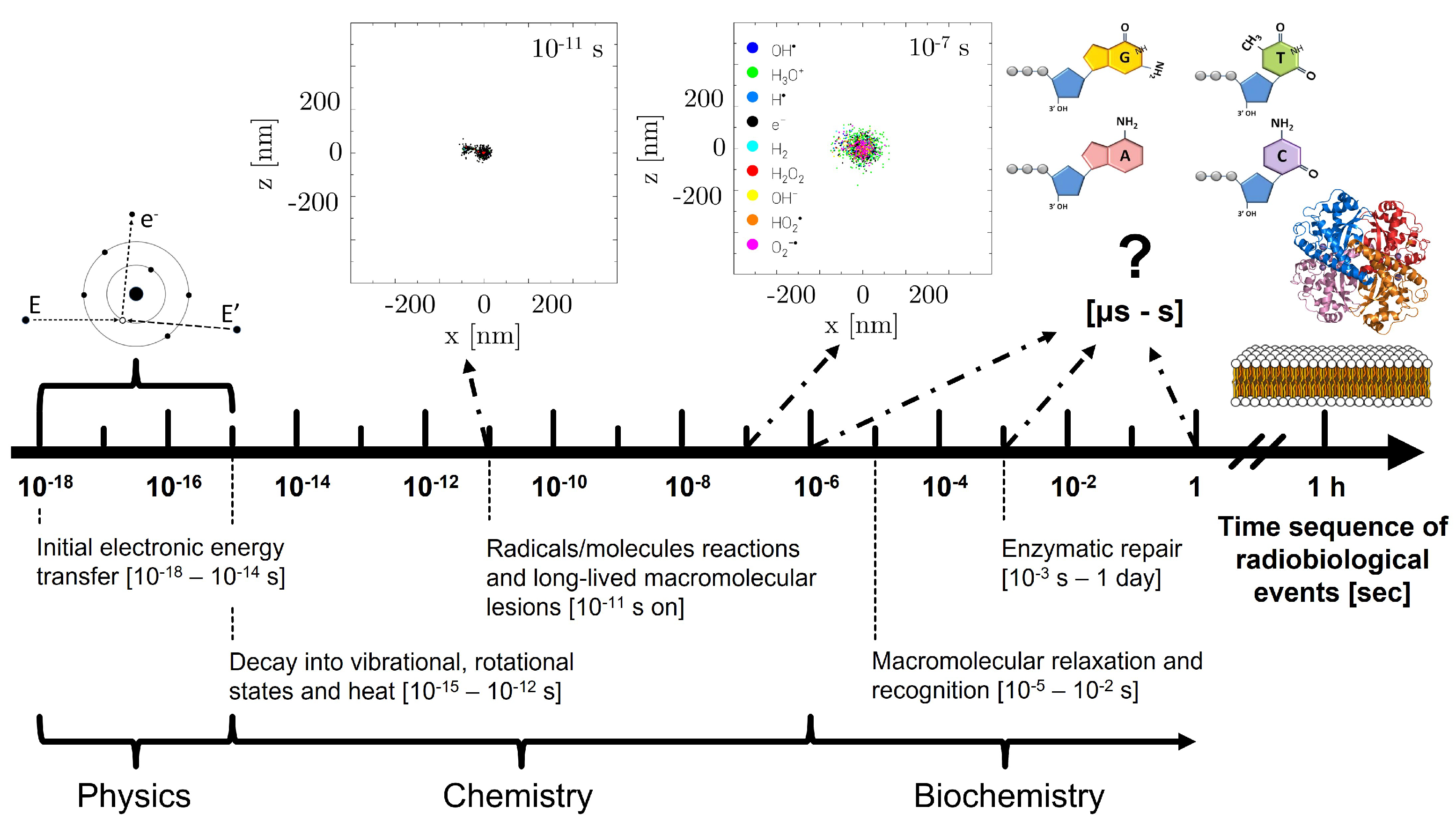
1. Introduction
2. Results
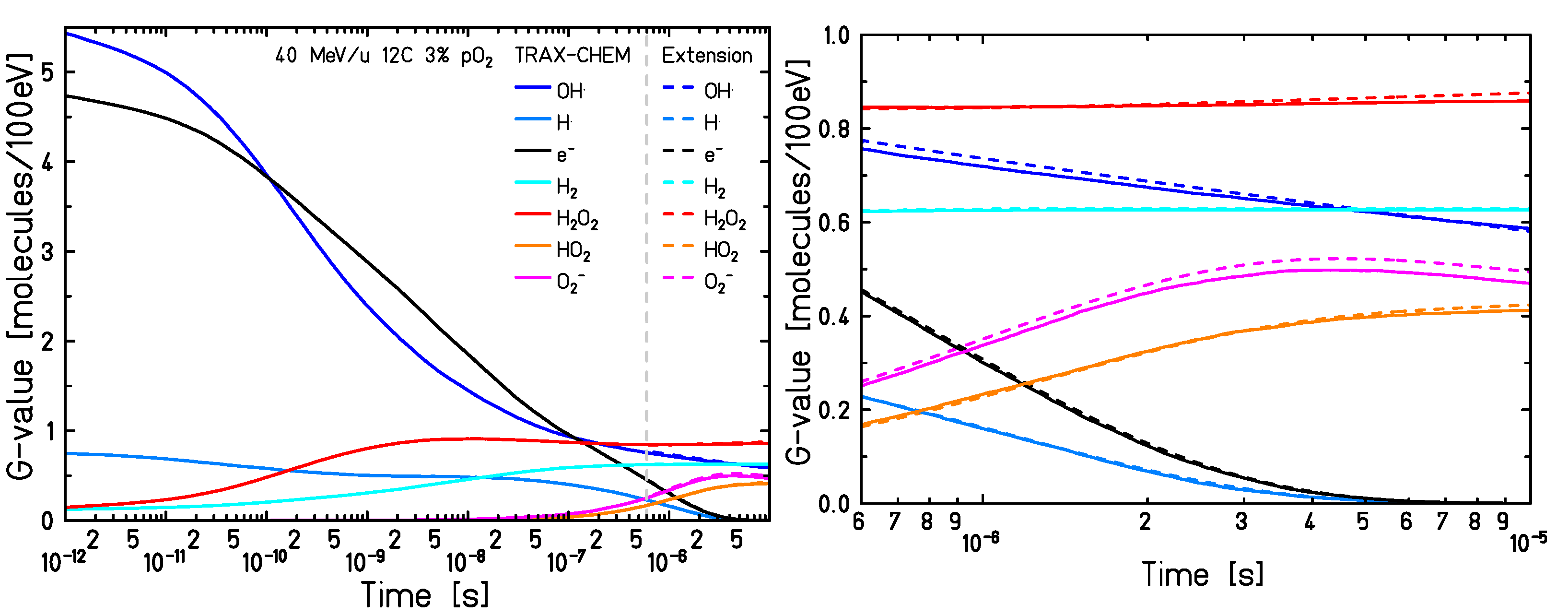
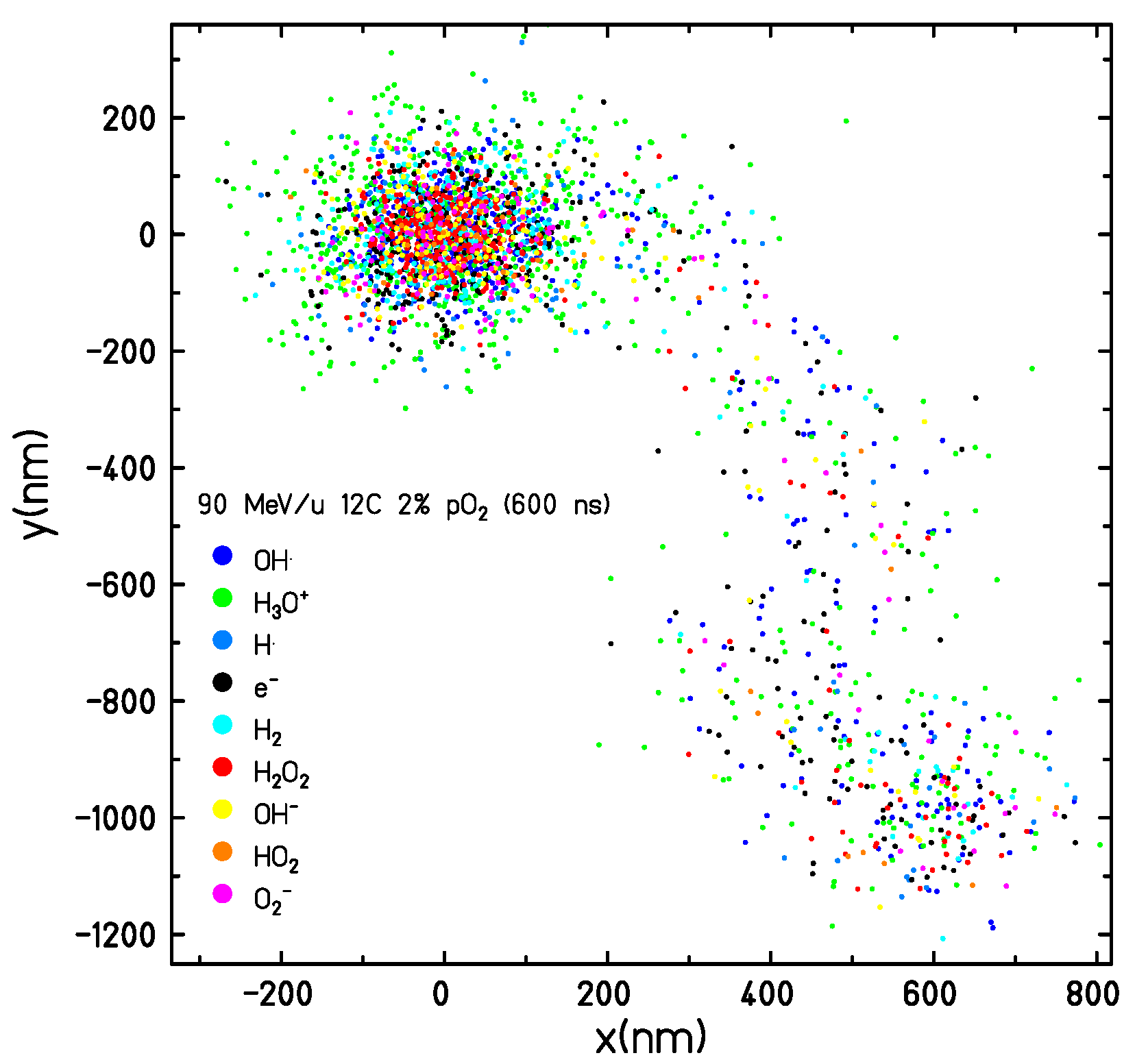
2.1. Transition Time and Chemical Track Evolution at the ms Scale
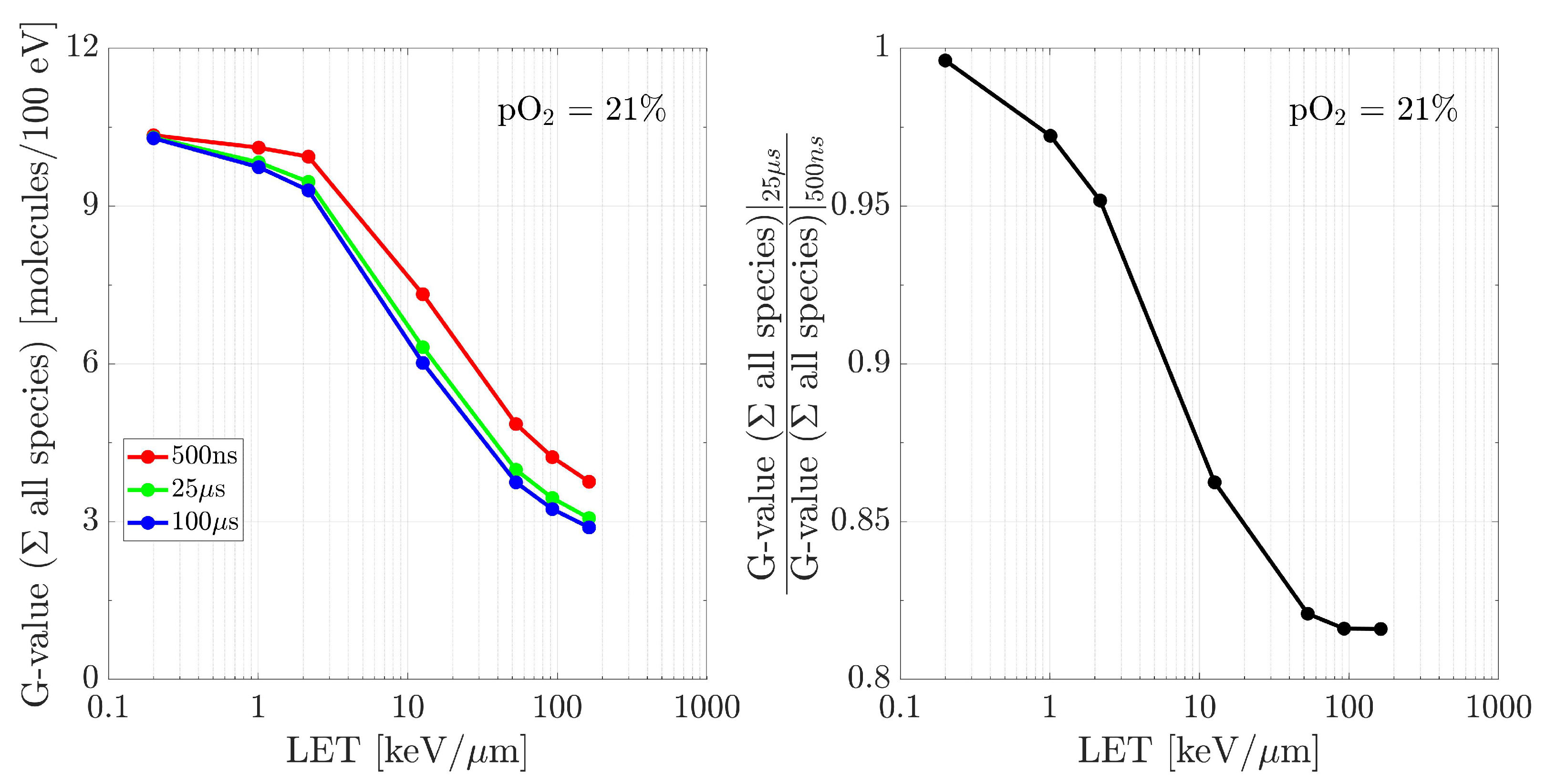
2.2. LET Impact
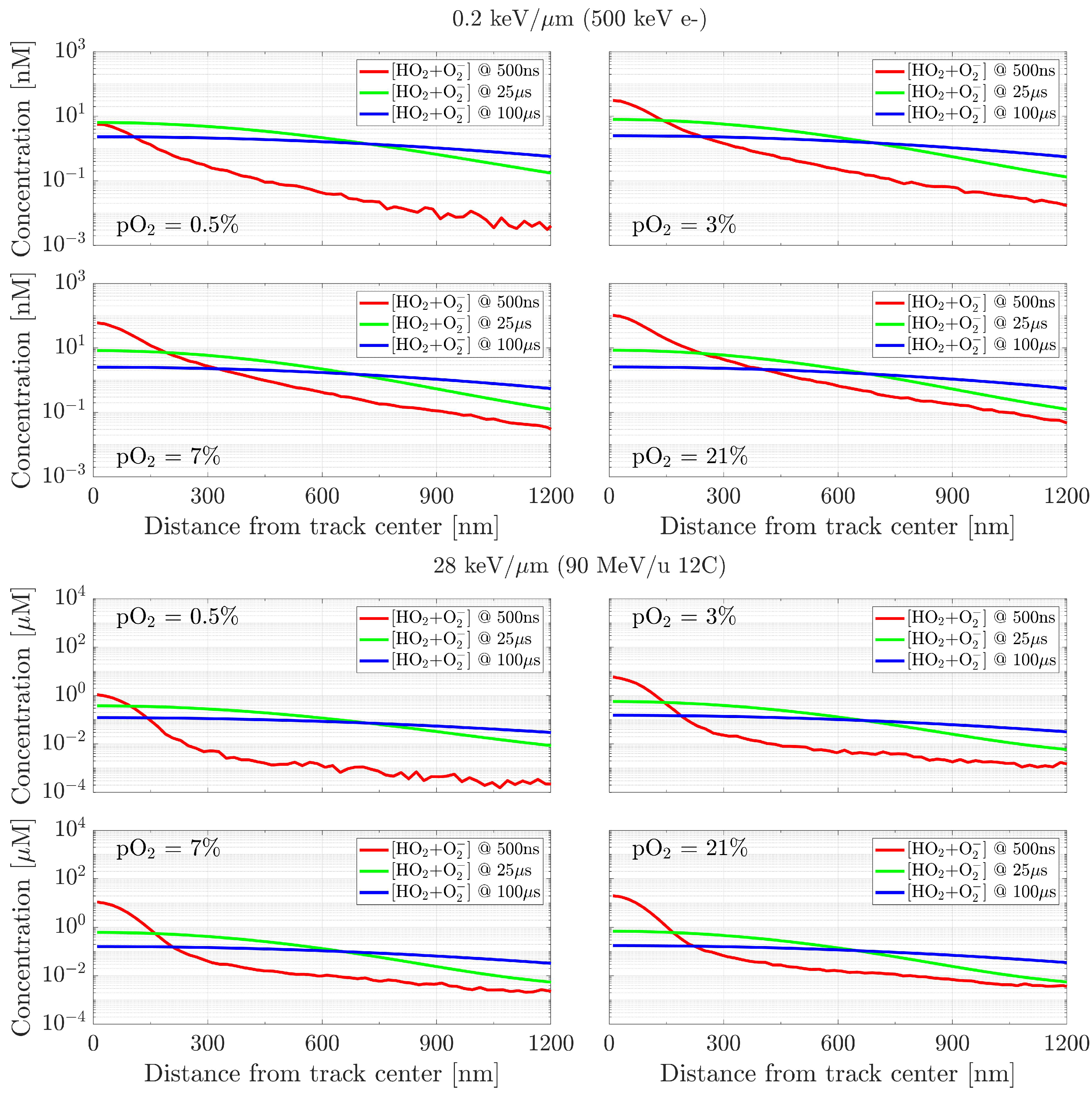
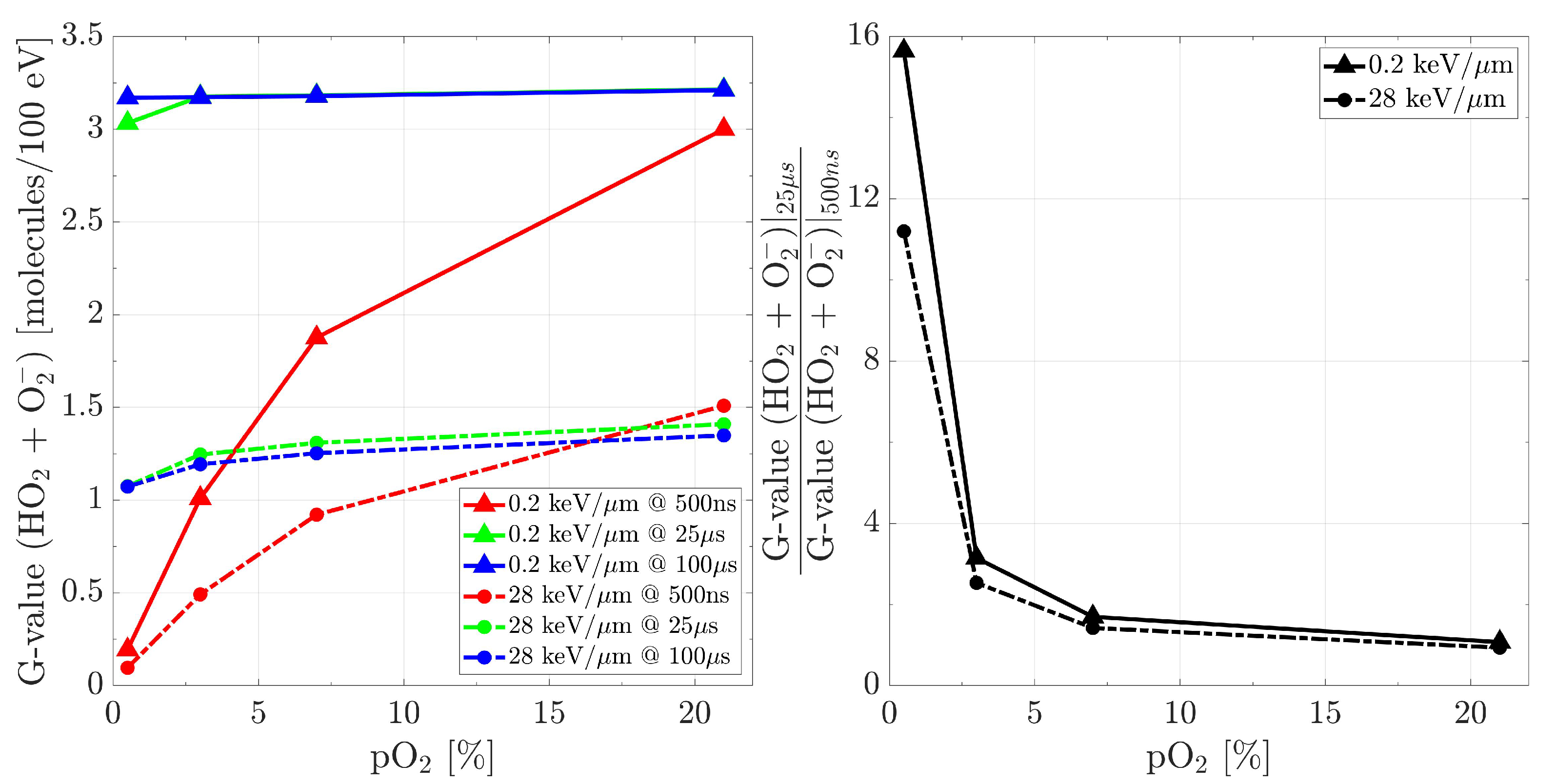
2.3. Oxygenation Impact
2.4. Comparisons with Previous Approaches
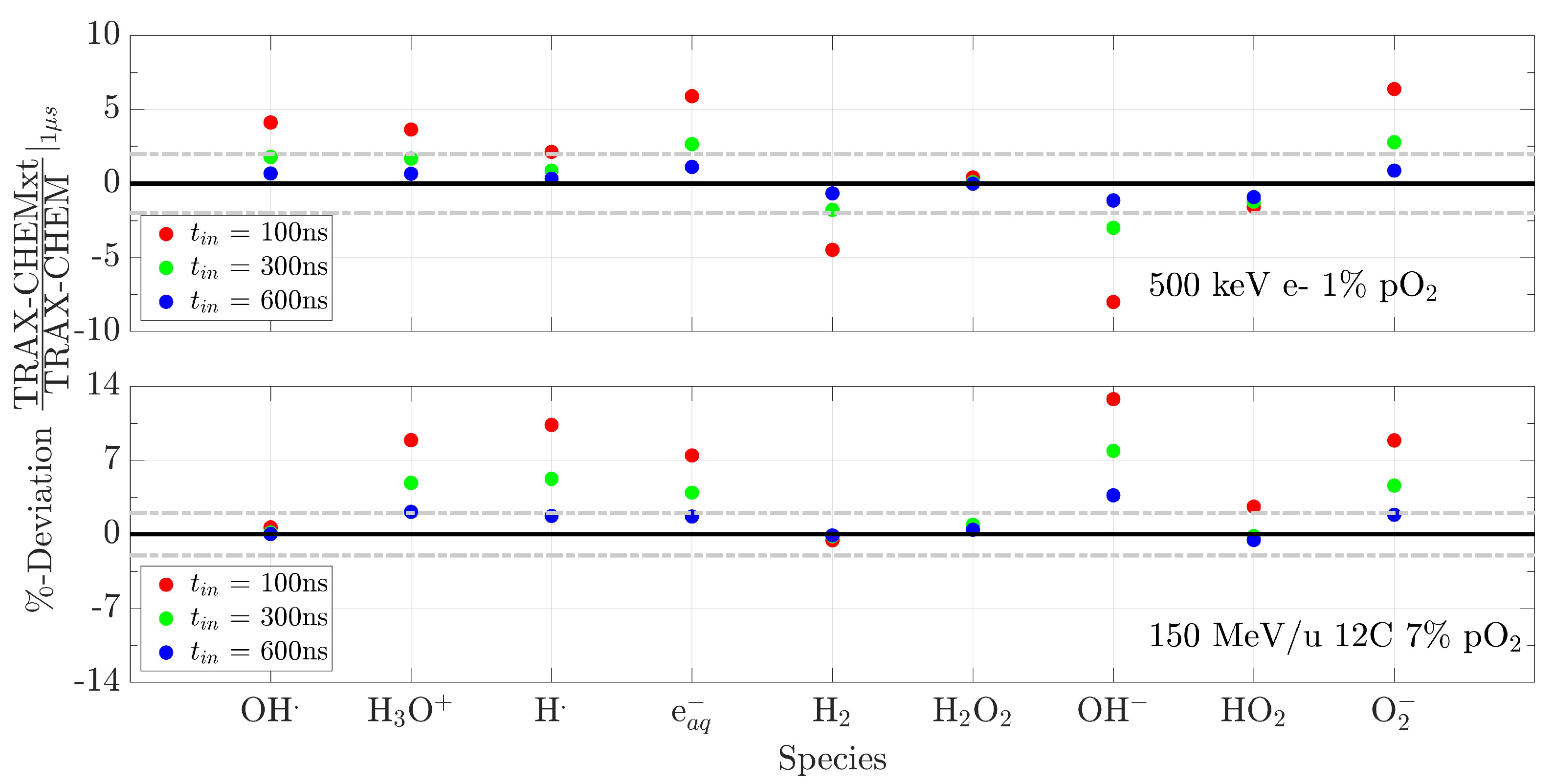
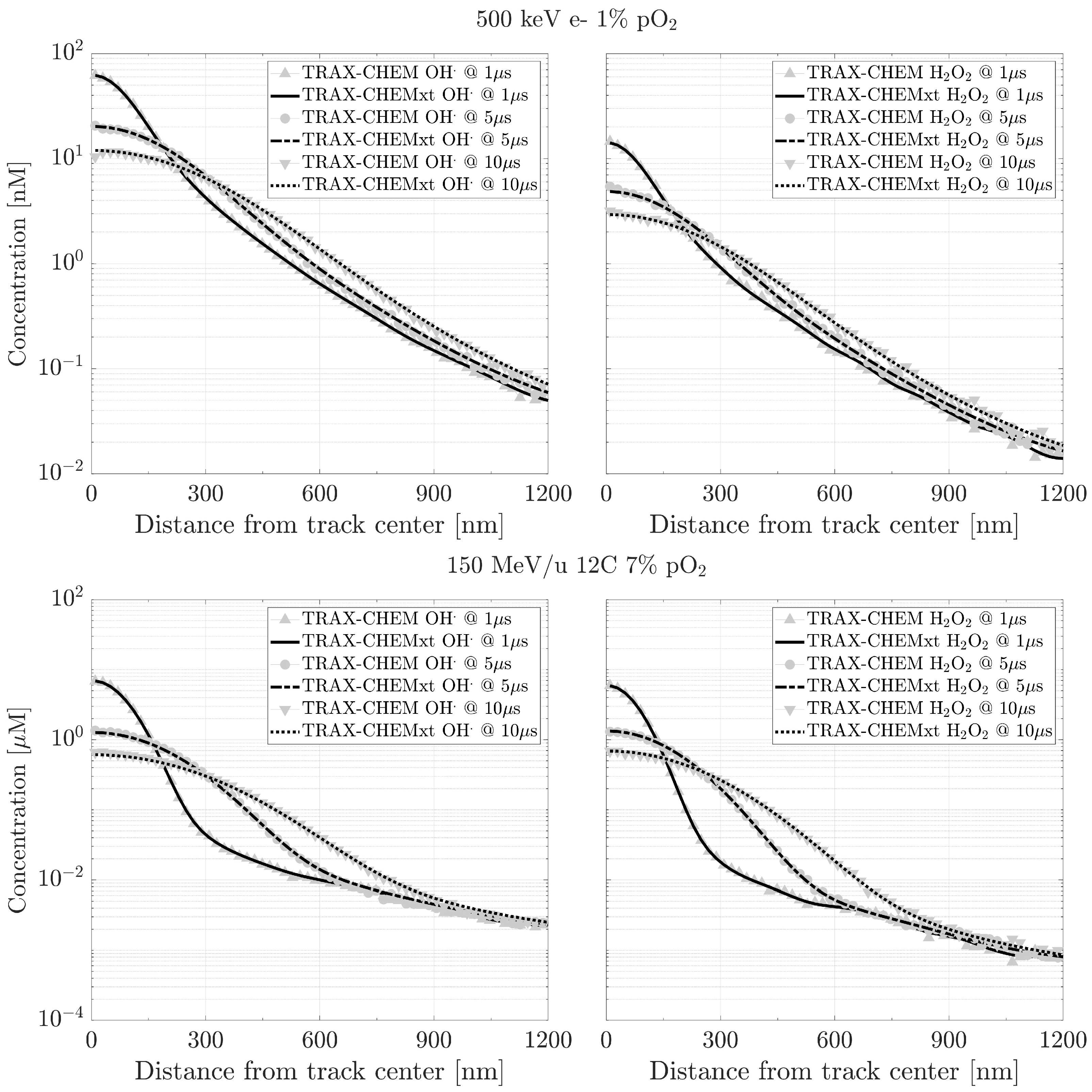
2.4.1. Comparison with TRAX-CHEM (Monte Carlo Domain)
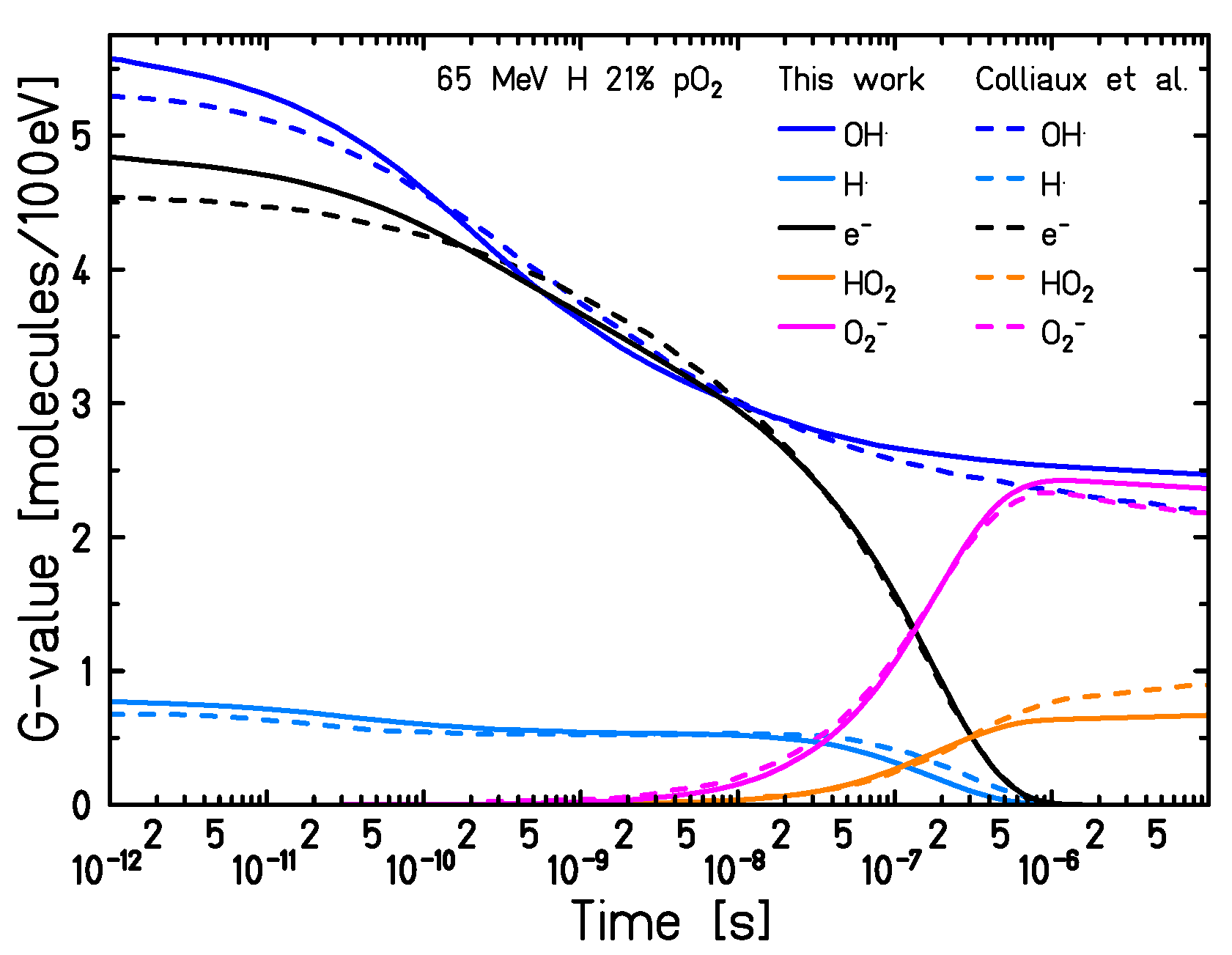
2.4.2. Comparison with Experimental Data and a Different Monte Carlo Algorithm
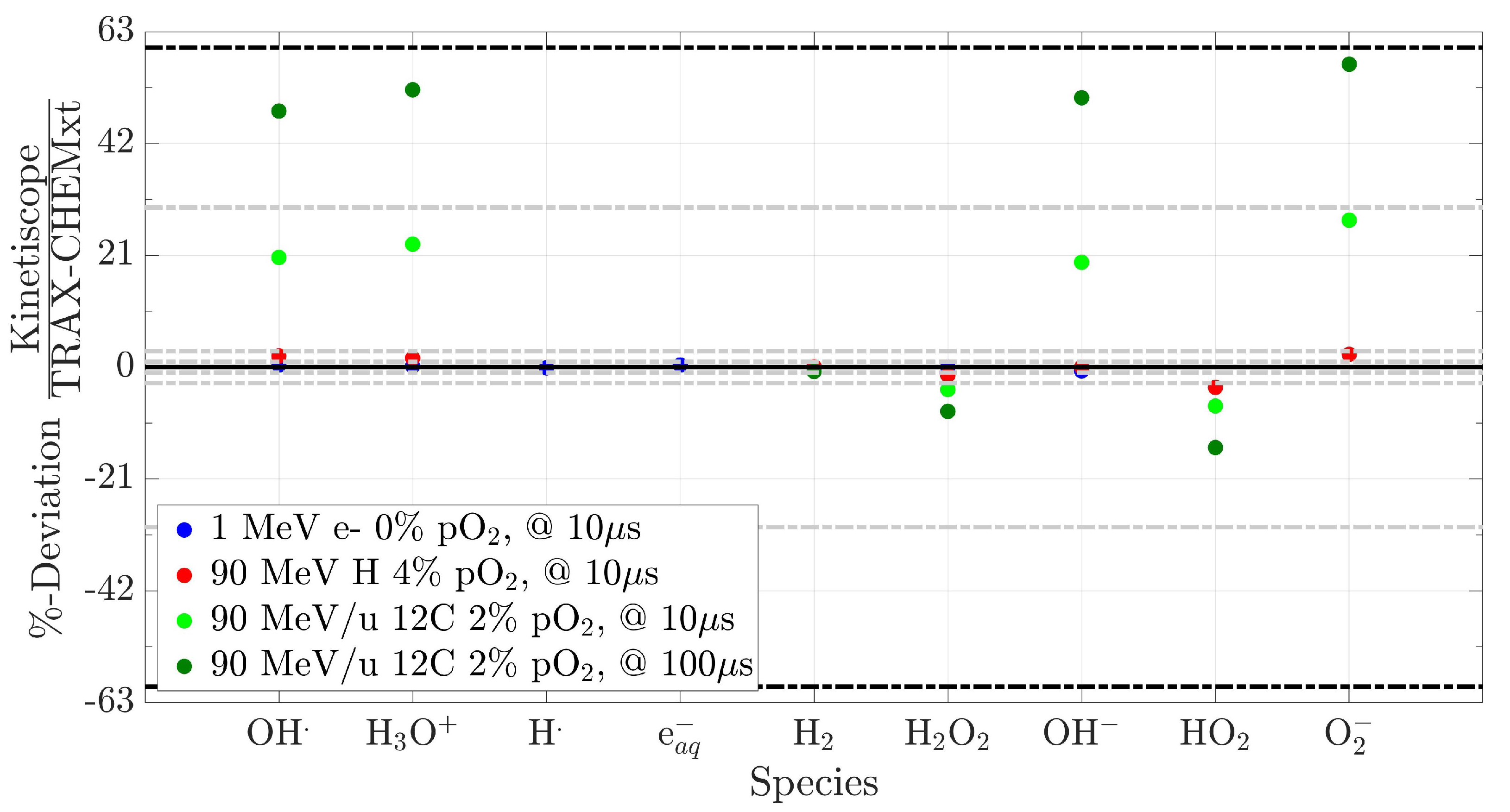
2.4.3. Comparison with Kinetiscope (Pure Homogeneous Domain)
3. Discussion
4. Materials and Methods
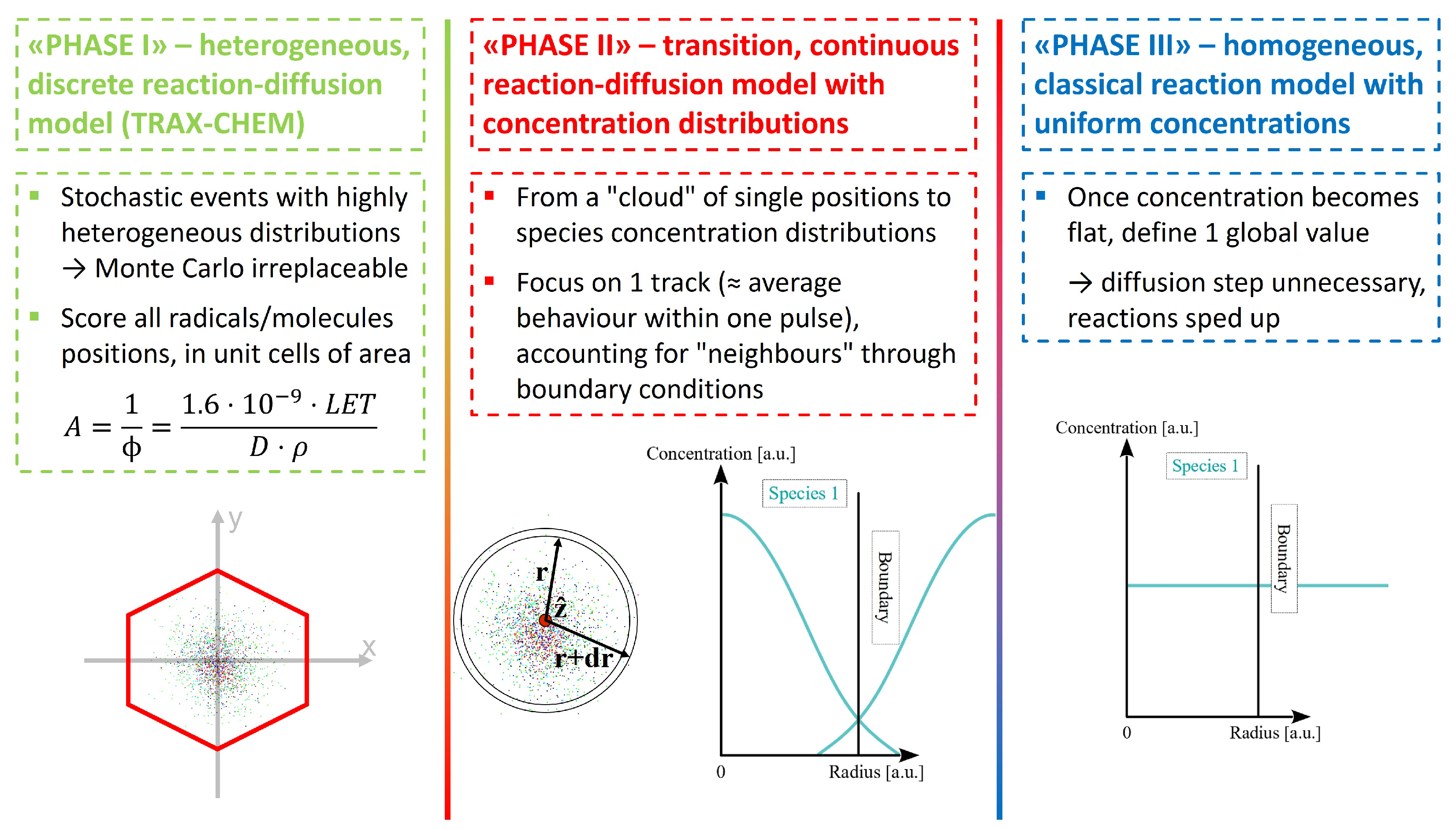
4.1. Code Implementation
4.2. Simulation Settings
4.3. Time Step and Transitional Time Point between TRAX-CHEM and TRAX-CHEMxt
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| e- | Electron beam |
| H | Proton beam |
| 12C | Carbon ion beam |
| LET | Linear energy transfer |
| IRT | Independent reaction time |
| B.C. | Boundary conditions |
| SOD | Superoxide dismutase |
| CAT | Catalase |
| GSH | Glutathione |
References
- Scifoni, E. Radiation biophysical aspects of charged particles: From the nanoscale to therapy. Mod. Phys. Lett. A 2015, 30, 1540019. [Google Scholar] [CrossRef]
- Mairani, A.; Mein, S.; Blakely, E.; Debus, J.; Durante, M.; Ferrari, A.; Fuchs, H.; Georg, D.; Grosshans, D.R.; Guan, F.; et al. Roadmap: Helium ion therapy. Phys. Med. Biol. 2022, 67, 15. [Google Scholar] [CrossRef] [PubMed]
- Alanazi, A.; Meesungnoen, J.; Jay-Gerin, J.P. A computer modeling study of water radiolysis at high dose rates. Relevance to FLASH radiotherapy. Radiat. Res. 2020, 195, 149–162. [Google Scholar] [CrossRef] [PubMed]
- Michaels, H.B.; Hunt, J.W. A model for radiation damage in cells by direct effect and by indirect effect: A radiation chemistry approach. Radiat. Res. 1978, 74, 23–34. [Google Scholar] [CrossRef]
- Meesat, R.; Sanguanmith, S.; Meesungnoen, J.; Lepage, M.; Khalil, A.; Jay-Gerin, J.P. Utilization of the ferrous sulfate (Fricke) dosimeter for evaluating the radioprotective potential of cystamine: Experiment and Monte Carlo simulation. Radiat. Res. 2012, 177, 813–826. [Google Scholar] [CrossRef]
- Kreipl, M.S.; Friedland, W.; Paretzke, H.G. Interaction of ion tracks in spatial and temporal proximity. Radiat. Environ. Biophys. 2009, 48, 349–359. [Google Scholar] [CrossRef]
- Ito, A.; Nakano, H.; Kusano, Y.; Hirayama, R.; Furusawa, Y.; Murayama, C.; Mori, T.; Katsumura, Y.; Shinohara, K. Contribution of indirect action to radiation-induced mammalian cell inactivation: Dependence on photon energy and heavy-ion LET. Radiat. Res. 2006, 165, 703–712. [Google Scholar] [CrossRef]
- Schlathölter, T.; Eustache, P.; Porcel, E.; Salado, D.; Stefancikova, L.; Tillement, O.; Lux, F.; Mowat, P.; Biegun, A.; van Goethem, M.; et al. Improving proton therapy by metal-containing nanoparticles: Nanoscale insights. Int. J. Nanomed. 2016, 11, 1549–1556. [Google Scholar] [CrossRef]
- Hirayama, R.; Matsumoto, Y.; Kase, Y.; Noguchi, M.; Ando, K.; Ito, A.; Okayasu, R.; Furusawa, Y. Radioprotection by DMSO in nitrogen-saturated mammalian cells exposed to helium ion beams. Radiat. Phys. Chem. 2009, 78, 1175–1178. [Google Scholar] [CrossRef]
- Chapman, J.D.; Doern, S.D.; Reuvers, A.P.; Gillespie, C.J.; Chatterjee, A.; Blakely, E.A.; Smith, K.C.; Tobias, C.A. Radioprotection by DMSO of mammalian cells exposed to X-rays and to heavy charged-particle beams. Radiat. Environ. Biophys. 1979, 16, 29–41. [Google Scholar] [CrossRef]
- O’Neill, P.; Wardman, P. Radiation chemistry comes before radiation biology. Int. J. Radiat. Biol. 2009, 85, 9–25. [Google Scholar] [CrossRef] [PubMed]
- Grün, R.; Friedrich, T.; Traneus, E.; Scholz, M. Is the dose-averaged LET a reliable predictor for the relative biological effectiveness? Med. Phys. 2019, 46, 1064–1074. [Google Scholar] [CrossRef] [PubMed]
- Friedl, A.A.; Prise, K.M.; Butterworth, K.T.; Montay-Gruel, P.; Favaudon, V. Radiobiology of the FLASH effect. Med. Phys. 2022, 49, 1993–2013. [Google Scholar] [CrossRef] [PubMed]
- Kacem, H.; Almeida, A.; Cherbuin, N.; Vozenin, M.C. Understanding the FLASH effect to unravel the potential of ultra-high dose rate irradiation. Int. J. Radiat. Biol. 2022, 98, 506–516. [Google Scholar] [CrossRef] [PubMed]
- Vozenin, M.C.; Hendry, J.H.; Limoli, C.L. Biological benefits of ultra-high dose rate FLASH radiotherapy: Sleeping beauty awoken. Clin. Oncol. 2019, 31, 407–415. [Google Scholar] [CrossRef]
- Montay-Gruel, P.; Corde, S.; Laissue, J.A.; Bazalova-Carter, M. FLASH radiotherapy with photon beams. Med. Phys. 2022, 49, 2055–2067. [Google Scholar] [CrossRef]
- Tinganelli, W.; Sokol, O.; Quartieri, M.; Puspitasari, A.; Dokic, I.; Abdollahi, A.; Durante, M.; Haberer, T.; Debus, J.; Boscolo, D.; et al. Ultra-high dose rate (FLASH) carbon ion irradiation: Dosimetry and first cell experiments. Int. J. Radiat. Oncol. Biol. Phys. 2022, 112, 1012–1022. [Google Scholar] [CrossRef]
- Tinganelli, W.; Weber, U.; Puspitasari, A.; Simoniello, P.; Abdollahi, A.; Oppermann, J.; Schuy, C.; Horst, F.; Helm, A.; Fournier, C.; et al. FLASH with carbon ions: Tumor control, normal tissue sparing, and distal metastasis in a mouse osteosarcoma model. Radiother. Oncol. 2022, 175, 185–190. [Google Scholar] [CrossRef]
- Weber, U.A.; Scifoni, E.; Durante, M. FLASH radiotherapy with carbon ion beams. Med. Phys. 2022, 49, 1974–1992. [Google Scholar] [CrossRef]
- Colliaux, A.; Gervais, B.; Rodriguez-Lafrasse, C.; Beuve, M. Simulation of ion-induced water radiolysis in different conditions of oxygenation. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2015, 365, 596–605. [Google Scholar] [CrossRef]
- Boscolo, D.; Krämer, M.; Fuss, M.C.; Durante, M.; Scifoni, E. Impact of target oxygenation on the chemical track evolution of ion and electron radiation. Int. J. Mol. Sci. 2020, 21, 424. [Google Scholar] [CrossRef] [PubMed]
- Karamitros, M.; Luan, S.; Bernal, M.; Allison, J.; Baldacchino, G.; Davidkova, M.; Francis, Z.; Friedland, W.; Ivantchenko, V.; Ivantchenko, A.; et al. Diffusion-controlled reactions modeling in Geant4-DNA. J. Comput. Phys. 2014, 274, 841–882. [Google Scholar] [CrossRef]
- Schuemann, J.; McNamara, A.L.; Ramos-Méndez, J.; Perl, J.; Held, K.D.; Paganetti, H.; Incerti, S.; Faddegon, B. TOPAS-nBio: An extension to the TOPAS simulation toolkit for cellular and sub-cellular radiobiology. Radiat. Res. 2019, 191, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, R.; Saito, K. Monte Carlo simulation of water radiolysis in oxygenated condition for monoenergetic electrons from 100 eV to 1 MeV. Radiat. Phys. Chem. 2001, 62, 217–228. [Google Scholar] [CrossRef]
- Plante, I. A Monte-Carlo step-by-step simulation code of the non-homogeneous chemistry of the radiolysis of water and aqueous solutions. Part I: Theoretical framework and implementation. Radiat. Environ. Biophys. 2011, 50, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Plante, I. A Monte-Carlo step-by-step simulation code of the non-homogeneous chemistry of the radiolysis of water and aqueous solutions. Part II: Calculation of radiolytic yields under different conditions of LET, pH, and temperature. Radiat. Environ. Biophys. 2011, 50, 405–415. [Google Scholar] [CrossRef]
- Zhu, H.; Li, J.; Deng, X.; Qiu, R.; Wu, Z.; Zhang, H. Modeling of cellular response after FLASH irradiation: A quantitative analysis based on the radiolytic oxygen depletion hypothesis. Phys. Med. Biol. 2021, 66, 185009. [Google Scholar] [CrossRef]
- Hu, A.; Qiu, R.; Wu, Z.; Zhang, H.; Li, J. CPU-GPU coupling independent reaction times method in NASIC and application in water radiolysis by FLASH irradiation. Biomed. Phys. Eng. Express 2022, 8, 025015. [Google Scholar] [CrossRef]
- Tian, Z.; Jiang, S.B.; Jia, X. Accelerated Monte Carlo simulation on the chemical stage in water radiolysis using GPU. Phys. Med. Biol. 2017, 62, 3081–3096. [Google Scholar] [CrossRef]
- Lai, Y.; Jia, X.; Chi, Y. Modeling the effect of oxygen on the chemical stage of water radiolysis using GPU-based microscopic Monte Carlo simulations, with an application in FLASH radiotherapy. Phys. Med. Biol. 2021, 66, 025004. [Google Scholar] [CrossRef]
- Plante, I. A review of simulation codes and approaches for radiation chemistry. Phys. Med. Biol. 2021, 66, 03TR02. [Google Scholar] [CrossRef]
- Labarbe, R.; Hotoiu, L.; Barbier, J.; Favaudon, V. A physicochemical model of reaction kinetics supports peroxyl radical recombination as the main determinant of the FLASH effect. Radiother. Oncol. 2020, 153, 303–310. [Google Scholar] [CrossRef] [PubMed]
- Colliaux, A.; Gervais, B.; Rodriguez-Lafrasse, C.; Beuve, M. O2 and glutathione effects on water radiolysis: A simulation study. J. Phys. Conf. Ser. 2011, 261, 012007. [Google Scholar] [CrossRef]
- Boscolo, D.; Krämer, M.; Durante, M.; Fuss, M.C.; Scifoni, E. TRAX-CHEM: A pre-chemical and chemical stage extension of the particle track structure code TRAX in water targets. Chem. Phys. Lett. 2018, 698, 11–18. [Google Scholar] [CrossRef]
- Krämer, M.; Kraft, G. Calculations of heavy-ion track structure. Radiat. Environ. Biophys. 1994, 33, 91–109. [Google Scholar] [CrossRef] [PubMed]
- Wälzlein, C.; Krämer, M.; Scifoni, E.; Durante, M. Advancing the modeling in particle therapy: From track structure to treatment planning. Appl. Radiat. Isot. 2014, 83, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Boscolo, D.; Scifoni, E.; Durante, M.; Krämer, M.; Fuss, M.C. May oxygen depletion explain the FLASH effect? A chemical track structure analysis. Radiother. Oncol. 2021, 162, 68–75. [Google Scholar] [CrossRef]
- Boscolo, D.; Scifoni, E.; Durante, M.; Krämer, M.; Fuss, M.C. Response to “Comment on: May oxygen depletion explain the FLASH effect? A chemical track structure analysis”. Radiother. Oncol. 2021, 163, 237–239. [Google Scholar] [CrossRef]
- Delattre, J.; Beaudeux, J.L.; Bonnefont-Rousselot, D. Radicaux Libres et Stress Oxydant: Aspects Biologiques et Pathologiques; Tec & Doc Éditions Médicales Internationales: Paris, France; London, UK; New York, NY, USA, 2005. [Google Scholar]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Autsavapromporn, N.; Meesungnoen, J.; Plante, I.; Jay-Gerin, J.P. Monte Carlo simulation study of the effects of acidity and LET on the primary free-radical and molecular yields of water radiolysis—Application to the Fricke dosimeter. Can. J. Chem. 2007, 85, 214–229. [Google Scholar] [CrossRef]
- Blain, G.; Vandenborre, J.; Villoing, D.; Fiegel, V.; Fois, G.R.; Haddad, F.; Koumeir, C.; Maigne, L.; Métivier, V.; Poirier, F.; et al. Proton irradiations at ultra-high dose rate vs. conventional dose rate: Strong impact on hydrogen peroxide yield. Radiat. Res. 2022, 198, 318–324. [Google Scholar] [CrossRef] [PubMed]
- Kacem, H.; Psoroulas, S.; Boivin, G.; Folkerts, M.; Grilj, V.; Lomax, T.; Martinotti, A.; Meer, D.; Ollivier, J.; Petit, B.; et al. Comparing radiolytic production of H2O2 and development of Zebrafish embryos after ultra high dose rate exposure with electron and transmission proton beams. Radiother. Oncol. 2022, 175, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Tran, H.N.; Chappuis, F.; Incerti, S.; Bochud, F.; Desorgher, L. Geant4-DNA modeling of water radiolysis beyond the microsecond: An on-lattice stochastic approach. Int. J. Mol. Sci. 2021, 22, 6023. [Google Scholar] [CrossRef] [PubMed]
- Ramos-Méndez, J.; Domínguez-Kondo, N.; Schuemann, J.; McNamara, A.; Moreno-Barbosa, E.; Faddegon, B. LET-dependent intertrack yields in proton irradiation at ultra-high dose rates relevant for FLASH therapy. Radiat. Res. 2020, 194, 351–362. [Google Scholar] [CrossRef]
- Froidevaux, P.; Grilj, V.; Bailat, C.; Geyer, W.R.; Bochud, F.; Vozenin, M.C. FLASH irradiation does not induce lipid peroxidation in lipids micelles and liposomes. Radiat. Phys. Chem. 2023, 205, 110733. [Google Scholar] [CrossRef]
- Clifford, P.; Green, N.J.B.; Oldfield, M.J.; Pilling, M.J.; Pimblott, S.M. Stochastic models of multi-species kinetics in radiation-induced spurs. J. Chem. Soc. Faraday Trans. 1 1986, 82, 2673–2689. [Google Scholar] [CrossRef]
- Quarteroni, A. Numerical Models for Differential Problems; Springer: Milan, Italy, 2014. [Google Scholar] [CrossRef]
- Brezis, H. Functional Analysis, Sobolev Spaces and Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Usmani, R.A. Inversion of Jacobi’s tridiagonal matrix. Comput. Math. Appl. 1994, 27, 59–66. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, R.; Esipova, T.V.; Allu, S.R.; Ashraf, R.; Rahman, M.; Gunn, J.R.; Bruza, P.; Gladstone, D.J.; Williams, B.B.; et al. Quantification of oxygen depletion during FLASH irradiation in vitro and in vivo. Int. J. Radiat. Oncol. Biol. Phys. 2021, 111, 240–248. [Google Scholar] [CrossRef]
- Jansen, J.; Knoll, J.; Beyreuther, E.; Pawelke, J.; Skuza, R.; Hanley, R.; Brons, S.; Pagliari, F.; Seco, J. Does FLASH deplete oxygen? Experimental evaluation for photons, protons, and carbon ions. Med. Phys. 2021, 48, 3982–3990. [Google Scholar] [CrossRef]



| Particle Type | pO (atm) | Species | Yield |
|---|---|---|---|
| 500 keV e− | 0% | 3.19 | |
| 21% | 3.21 | ||
| 90 MeV H | 0% | 3.12 | |
| 21% | 3.15 | ||
| 90 MeV/u 12C | 0% | 1.40 | |
| 21% | 1.56 |
| Initial Conditions | (10 µs)—TRAX-CHEM 1 | (10 µs)—TRAX-CHEMxt | (1 ms)—TRAX-CHEMxt | Computational Gain (10 µs) |
|---|---|---|---|---|
| 500 keV e−, 1% pO | ∼12 h | 75 s | 27 min | 1369 |
| 150 MeV/u 12C, 7% pO | >2 days | 80 s | 30 min | 2189 |
| Species | Experiment [39] | Colliaux et al. [20] | This Work |
|---|---|---|---|
| 2.7 | 2.8 | 2.7 | |
| + | 3.3 | 3.4 | 3.2 |
| 0.67 | 0.61 | 0.61 |
| Time Interval | (ns) |
|---|---|
| –1 µs | 0.5 |
| 1 µs–10 µs | 1 |
| 10 µs–100 µs | 2.5 |
| 100 µs–1 ms | 5 |
| 1 ms– | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camazzola, G.; Boscolo, D.; Scifoni, E.; Dorn, A.; Durante, M.; Krämer, M.; Abram, V.; Fuss, M.C. TRAX-CHEMxt: Towards the Homogeneous Chemical Stage of Radiation Damage. Int. J. Mol. Sci. 2023, 24, 9398. https://doi.org/10.3390/ijms24119398
Camazzola G, Boscolo D, Scifoni E, Dorn A, Durante M, Krämer M, Abram V, Fuss MC. TRAX-CHEMxt: Towards the Homogeneous Chemical Stage of Radiation Damage. International Journal of Molecular Sciences. 2023; 24(11):9398. https://doi.org/10.3390/ijms24119398
Chicago/Turabian StyleCamazzola, Gianmarco, Daria Boscolo, Emanuele Scifoni, Alexander Dorn, Marco Durante, Michael Krämer, Valentino Abram, and Martina C. Fuss. 2023. "TRAX-CHEMxt: Towards the Homogeneous Chemical Stage of Radiation Damage" International Journal of Molecular Sciences 24, no. 11: 9398. https://doi.org/10.3390/ijms24119398
APA StyleCamazzola, G., Boscolo, D., Scifoni, E., Dorn, A., Durante, M., Krämer, M., Abram, V., & Fuss, M. C. (2023). TRAX-CHEMxt: Towards the Homogeneous Chemical Stage of Radiation Damage. International Journal of Molecular Sciences, 24(11), 9398. https://doi.org/10.3390/ijms24119398










