Structural Insights into Phosphorylation-Mediated Polymerase Function Loss for DNA Polymerase β Bound to Gapped DNA
Abstract
1. Introduction
2. Results and Discussion
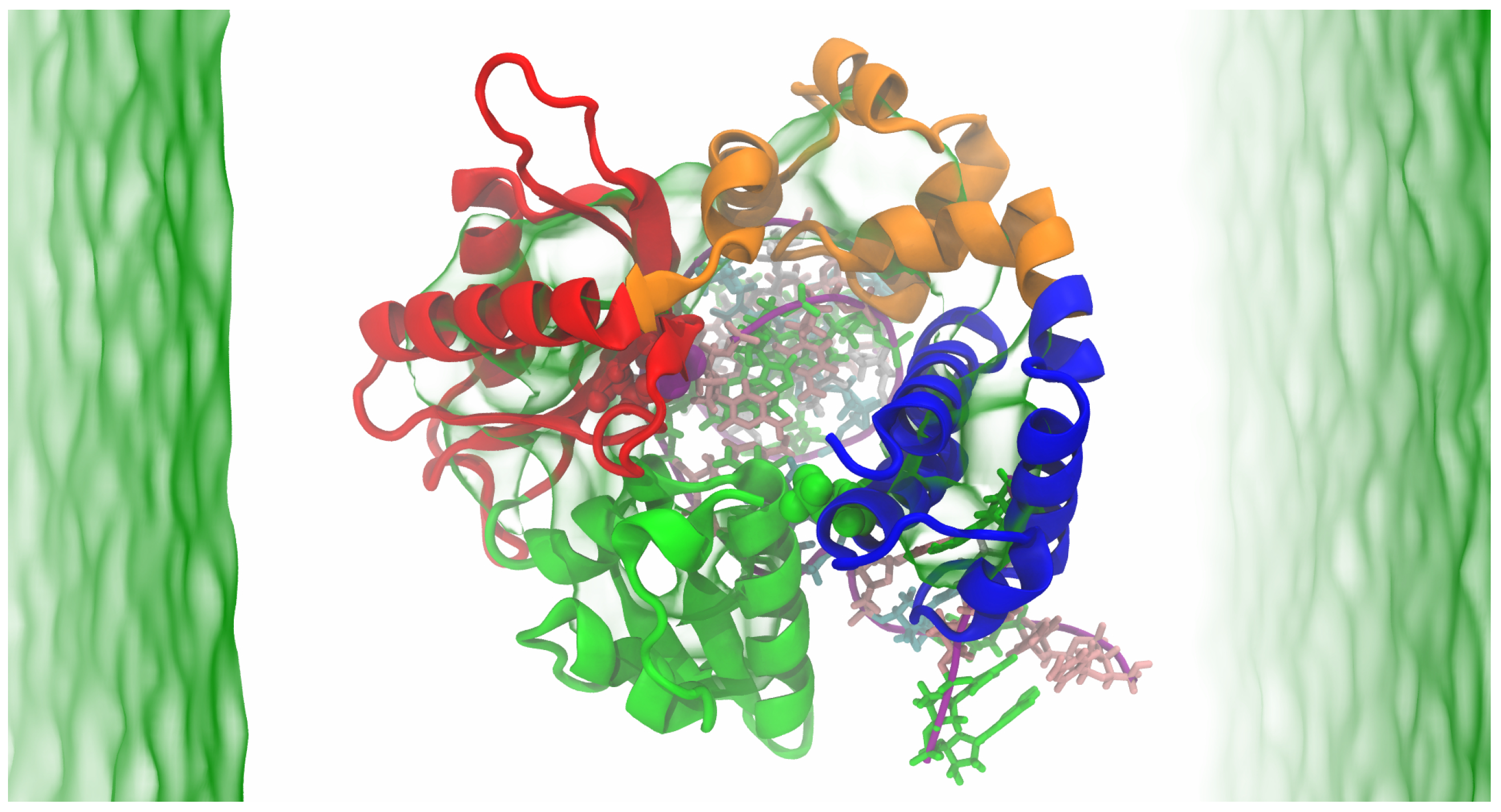
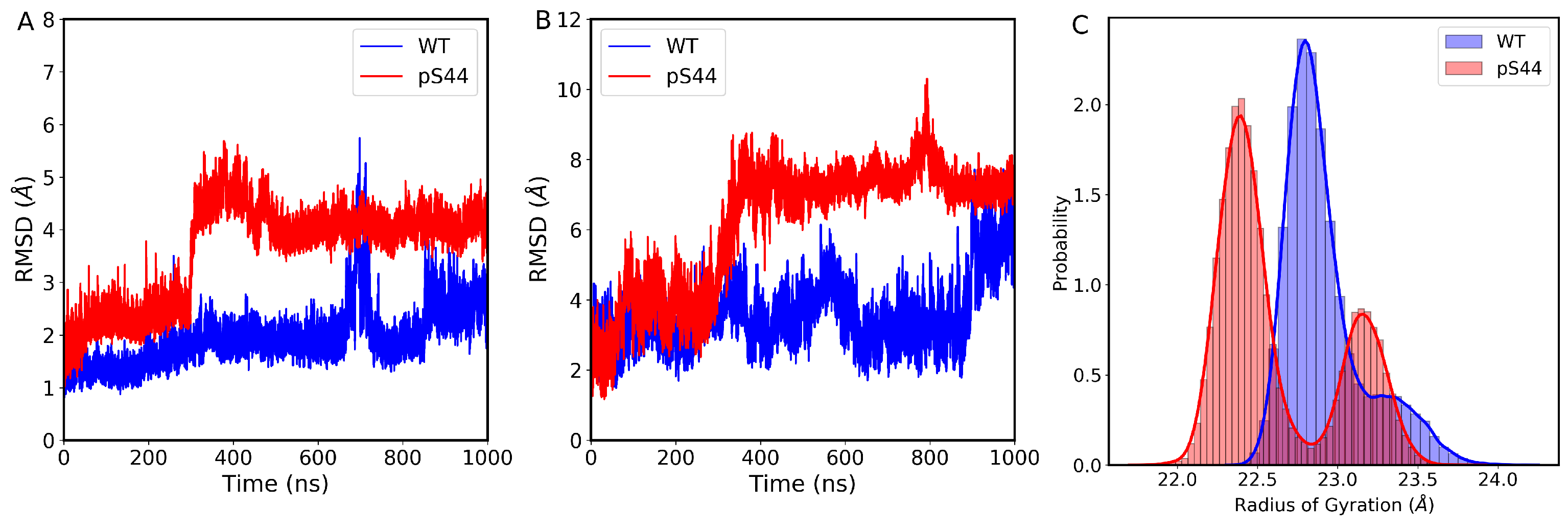
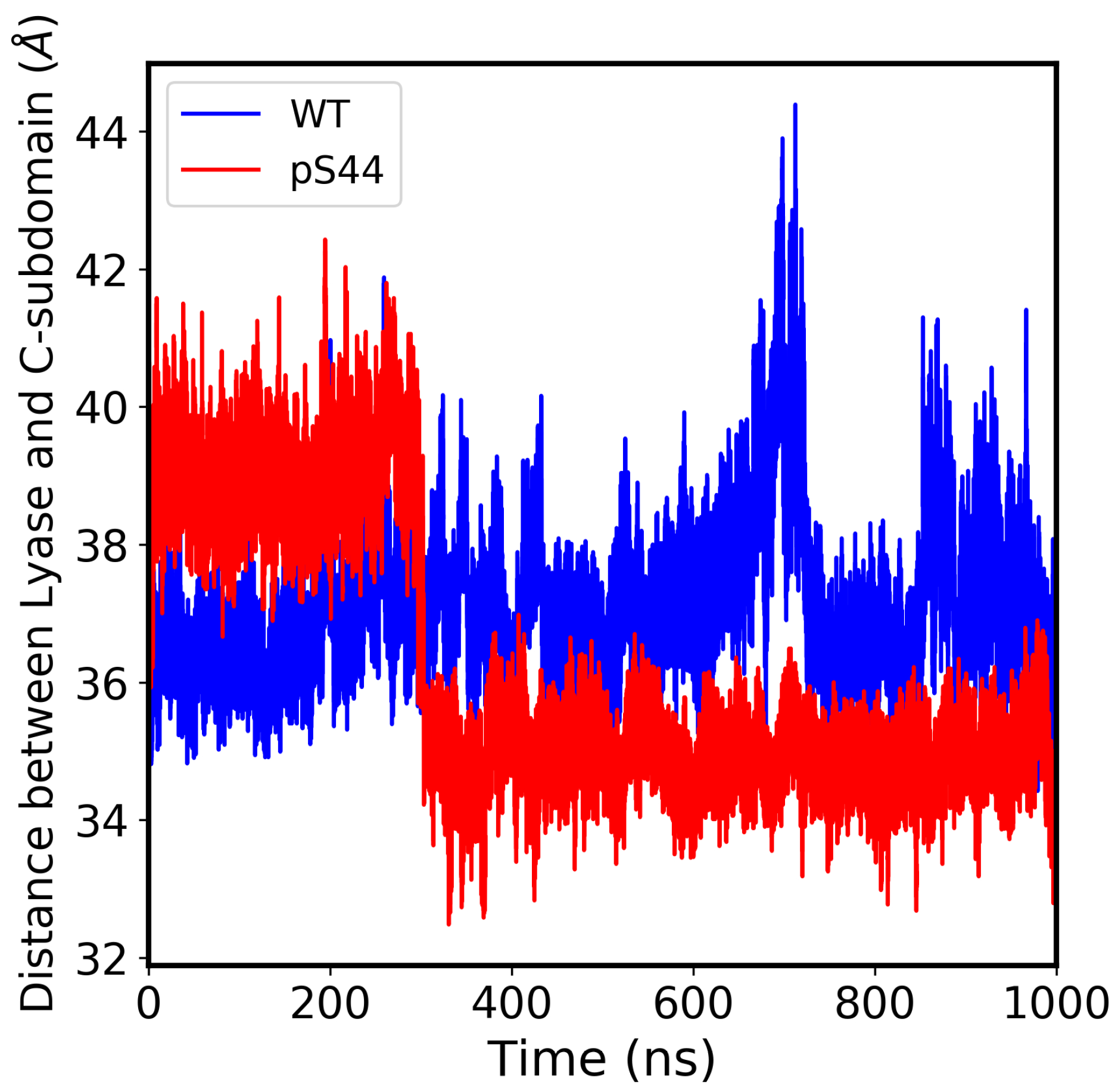
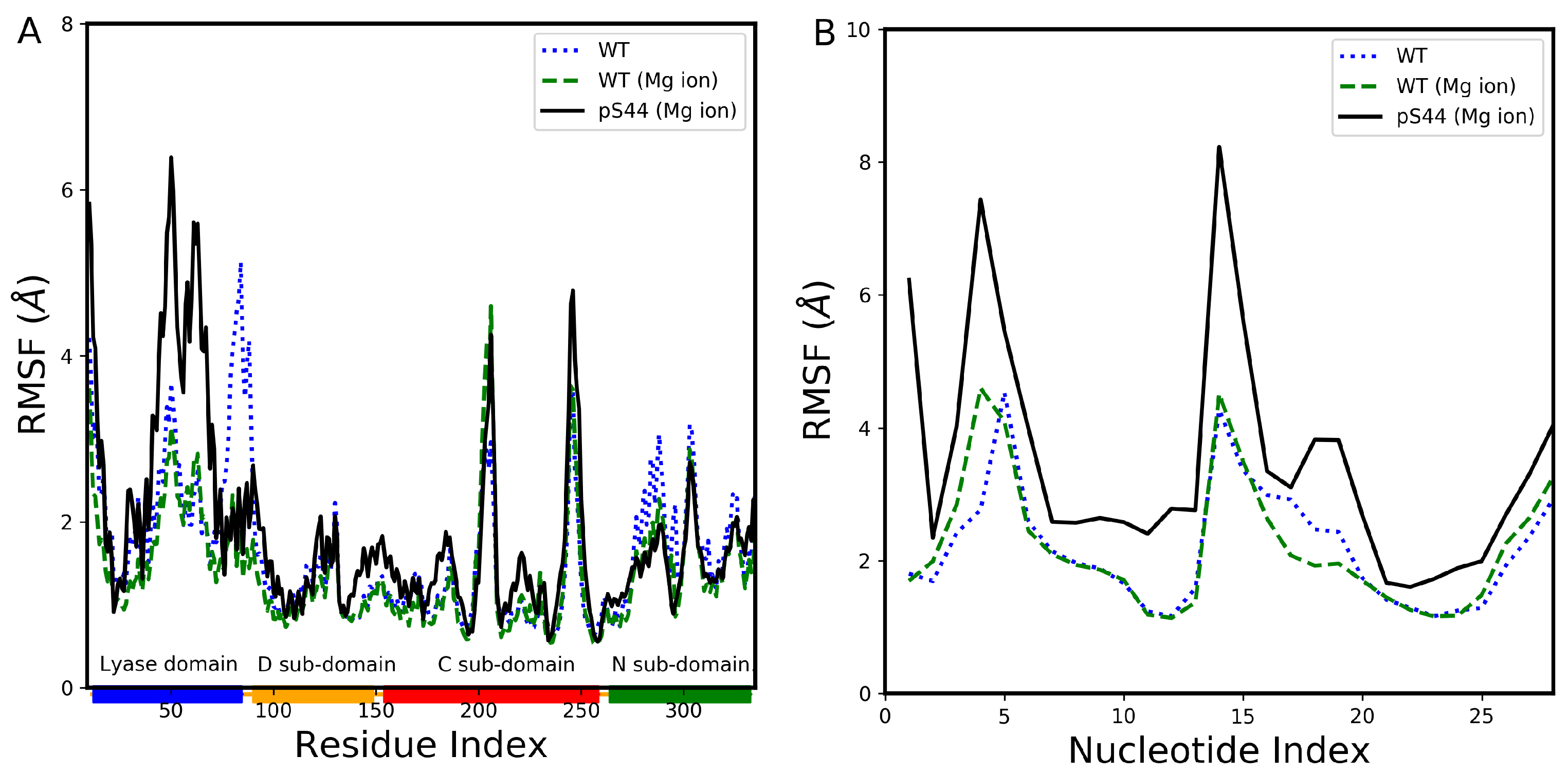
2.1. Structural Stability and Flexibility Analysis
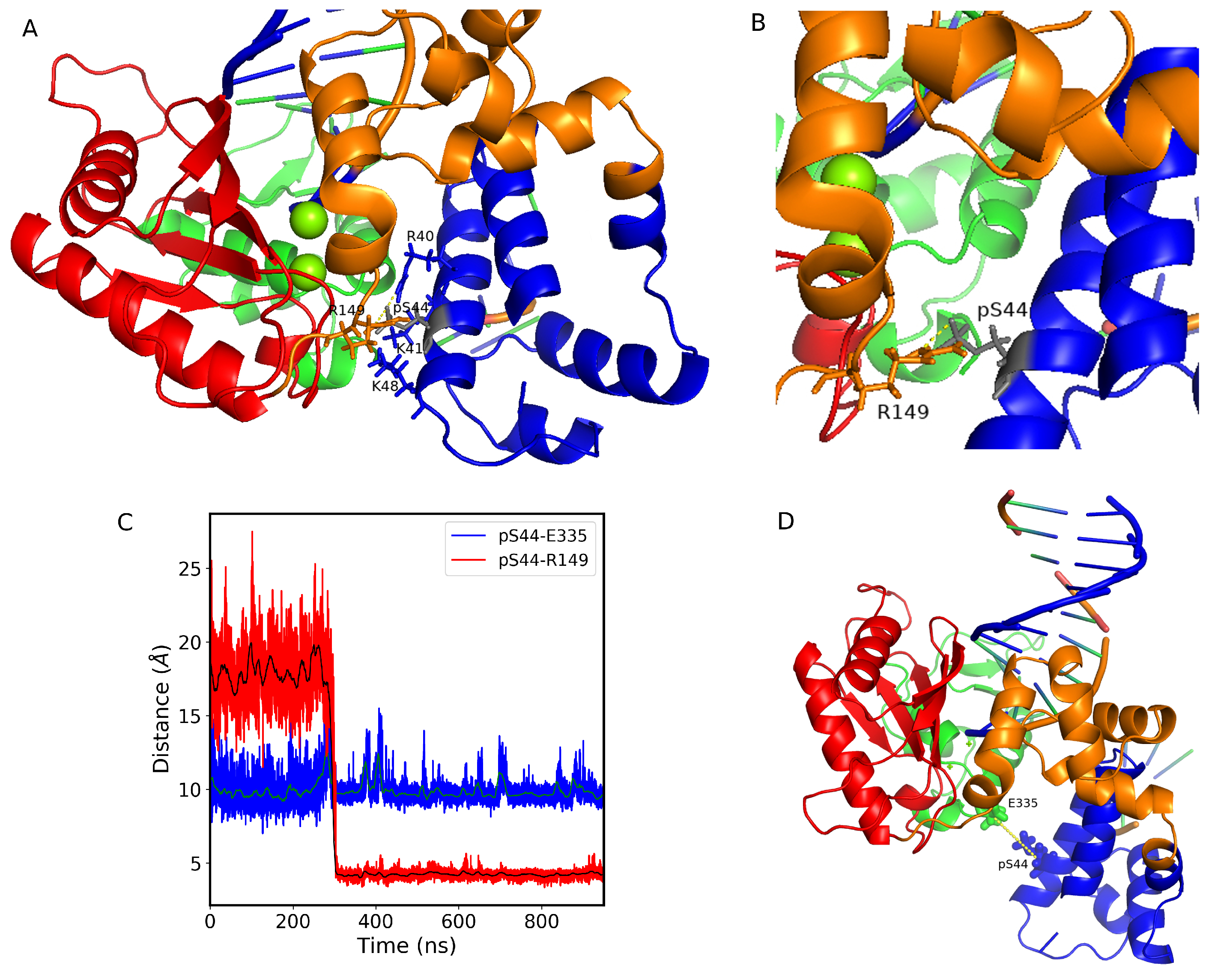
2.2. Newly Formed Salt Bridges Due to the Phosphorylation
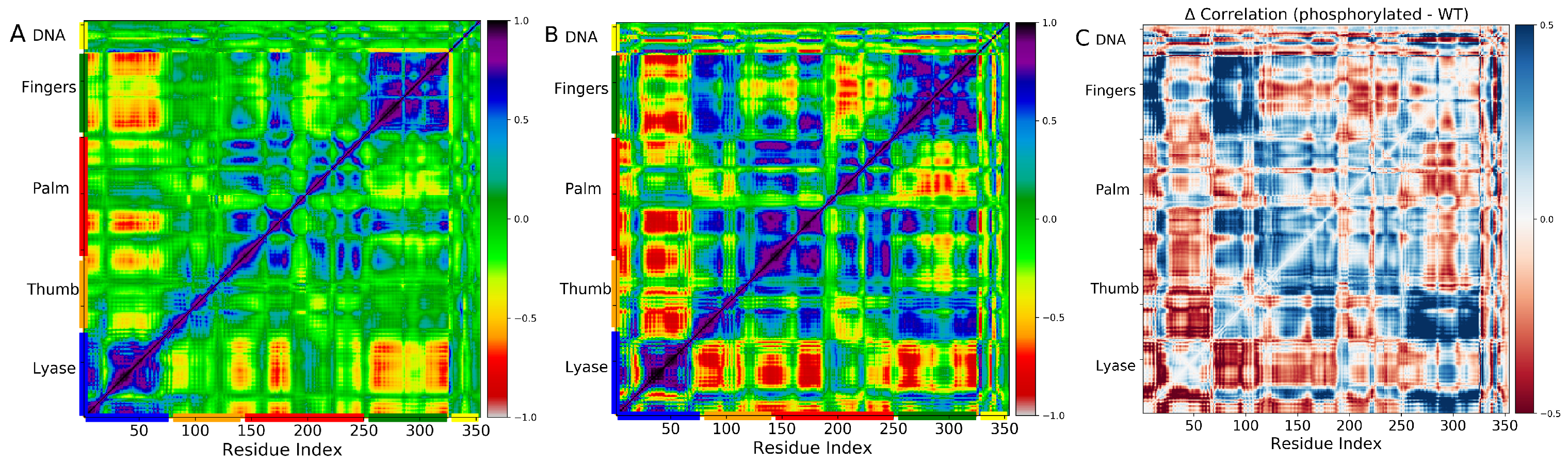
2.3. Phosphorylated S44 Enhances the Correlated Motions in Subdomains of DNA Polymerase Complex
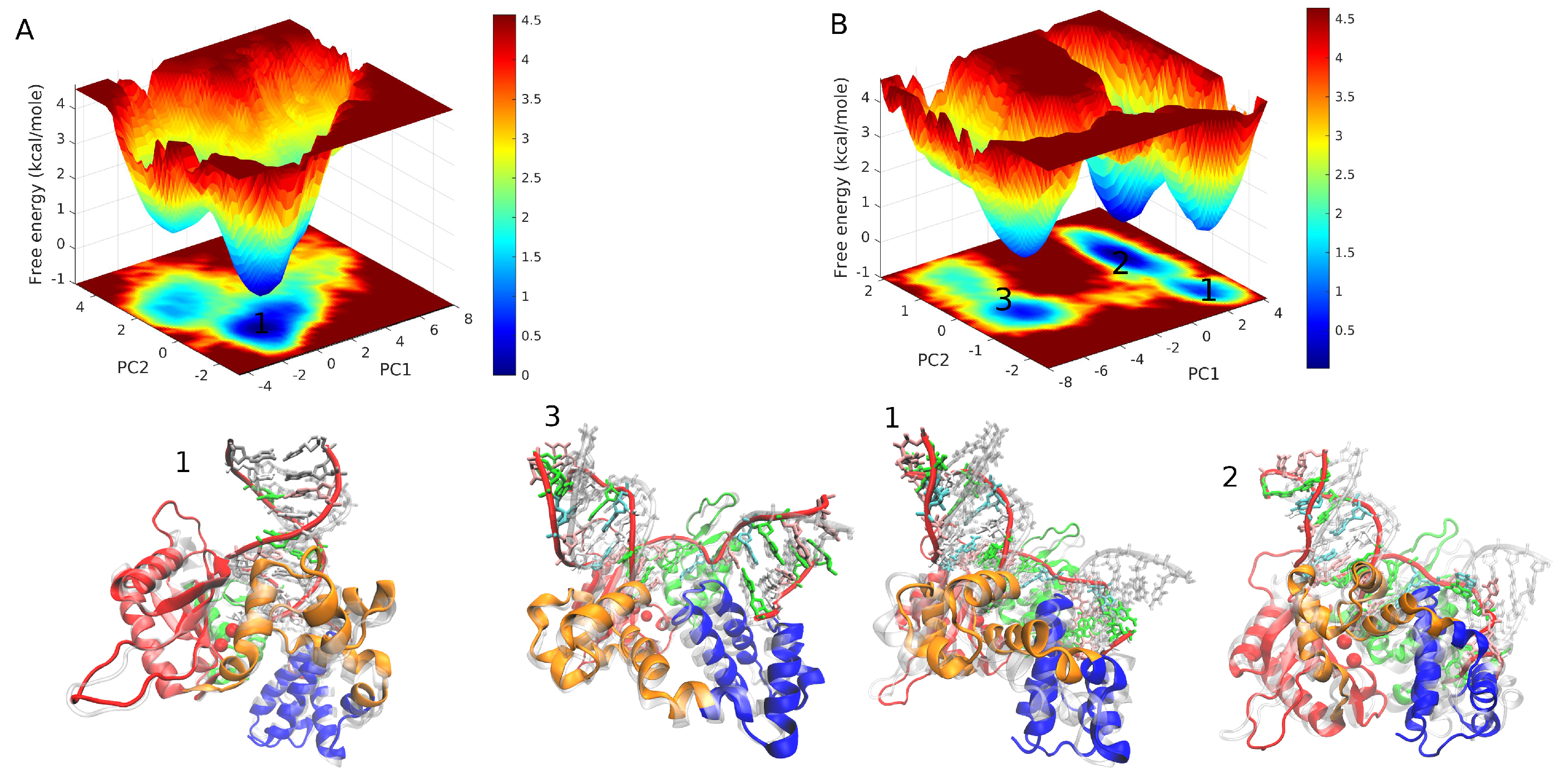
2.4. Principal Component Analysis
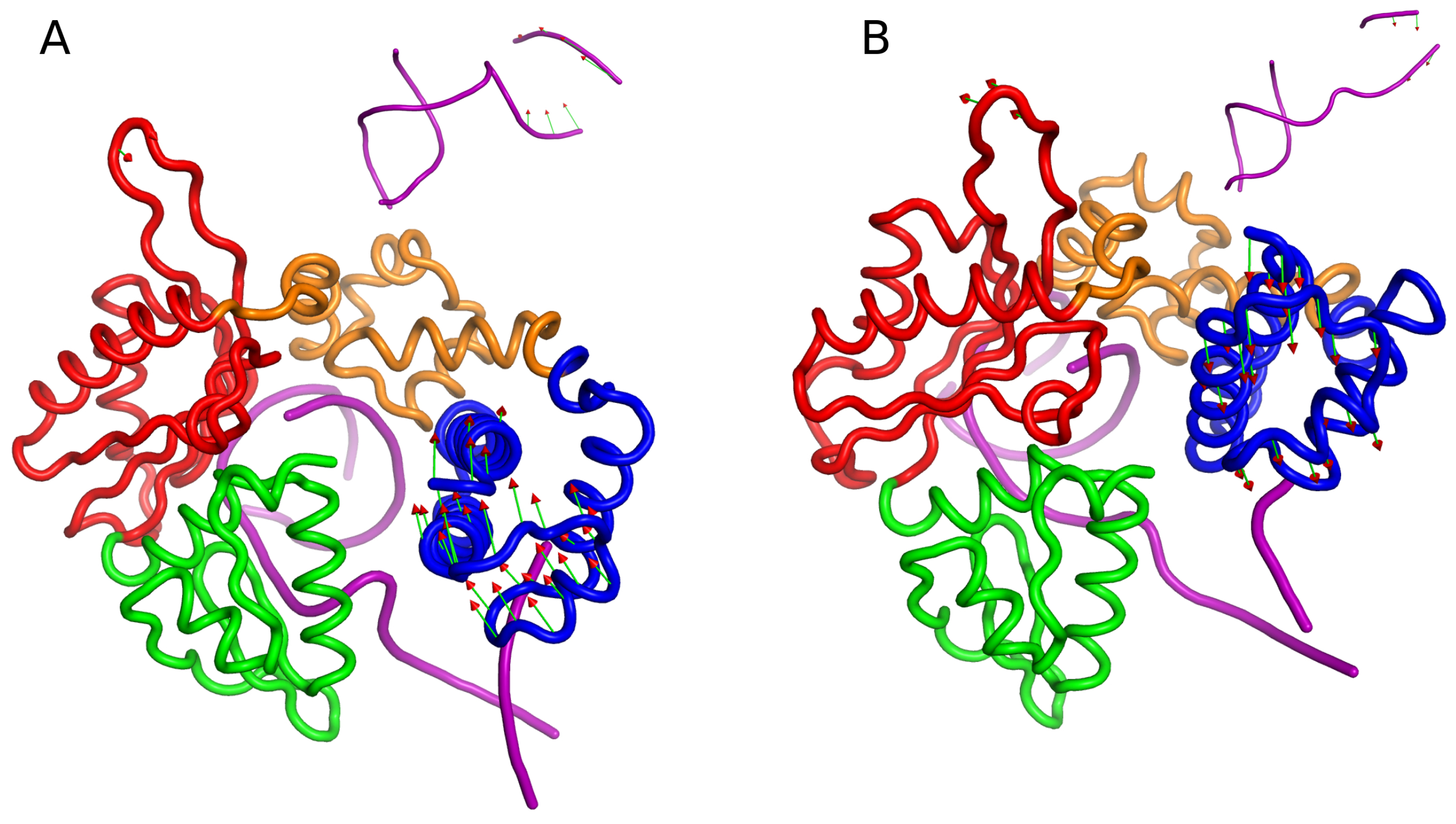
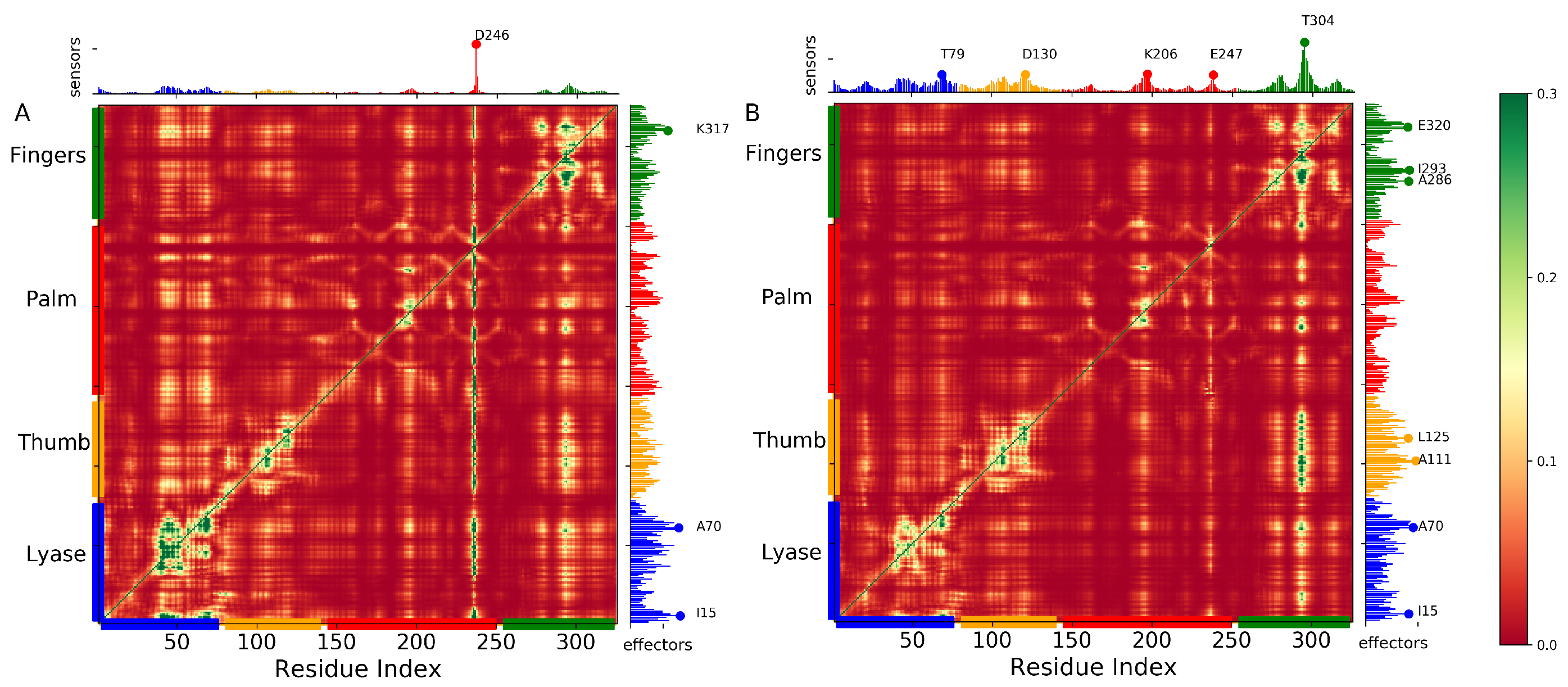
2.5. Phosphorylation of S44 Changes the Influence/Sensitivity Profile of DNA Polymerase Complex
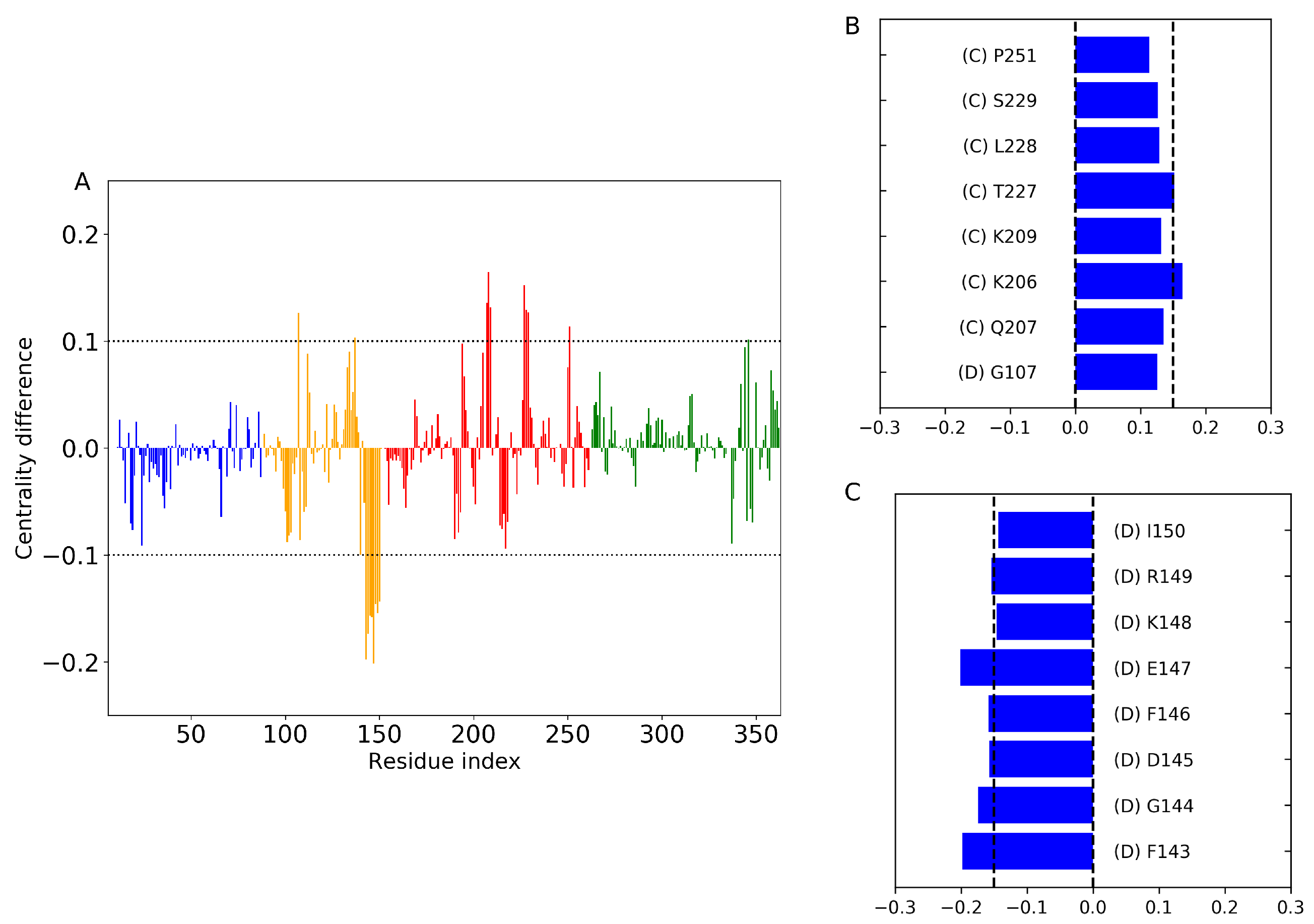
2.6. Structural Network Analysis
3. Materials and Methods
3.1. Simulation Protocol
3.2. Structural Analysis and Visualization
3.3. Dynamic Cross-Correlation
3.4. Principal Component Analysis
3.5. Perturbation Response Scanning
3.6. Structural Network Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lindahl, T. Instability and decay of the primary structure of DNA. Nature 1993, 362, 709–715. [Google Scholar] [CrossRef] [PubMed]
- Starcevic, D.; Dalal, S.; Sweasy, J.B. Is There a Link between Dna Polymerase β and Cancer? Chem. Commun. 2004, 3, 998–1001. [Google Scholar] [CrossRef]
- Leob, L.A.; Monnat, R.J. DNA Polymerases and Human Disease. Nat. Rev. Genet. 2008, 9, 594–604. [Google Scholar] [CrossRef] [PubMed]
- Lange, S.S.; Takata, K.-I.; Wood, R.D. DNA Polymerases and Cancer. Nat. Rev. Cancer 2011, 11, 96–110. [Google Scholar] [CrossRef]
- Kunkel, T.A. DNA Replication Fidelity. J. Biol. Chem. 2004, 279, 16895–16898. [Google Scholar] [CrossRef] [PubMed]
- Mullholland, A.J.; Roitberg, A.E.; Tunon, I. Enzyme Dynamics and Catalysis in the Mechanism of DNA Polymerase. Theor. Chem. Accounts 2012, 131, 1286. [Google Scholar] [CrossRef]
- Idriss, H.T.; Al-Assar, O.; Wilson, S.H. DNA Polymerase β. Int. J. Biochem. Cell Biol. 2002, 34, 321–324. [Google Scholar] [CrossRef]
- Beard, W.A.; Wilson, S.H. Structure and mechanism of DNA Polymerase β. Chem. Rev. 2006, 106, 361–382. [Google Scholar] [CrossRef]
- Kohlstaedt, L.A.; Wang, J.; Friedman, J.M.; Rice, P.A.; Steitz, T.A. Crystal structure at 3.5 Åresolution of HIV-1 reverse transcriptase complexed with an inhibitor. Science 1992, 256, 1783–1790. [Google Scholar] [CrossRef]
- Joyce, C.M.; Steitz, T.A. Function and structure relationships in DNA Polymerases. Annu. Rev. Biochem. 1994, 63, 777–822. [Google Scholar] [CrossRef]
- Florian, J.; Goodman, M.F.; Warshel, A. Computer simulation studies of the fidelity of DNA Polymerases. Biopolymers 2003, 68, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Rucker, R.; Oelschlaeger, P.; Warshel, A. A binding free energy decomposition approach for accurate calculations of the fidelity of DNA Polymerases. Proteins 2009, 78, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Meli, M.; Sustarsic, M.; Craggs, T.D.; Kapanidis, A.N.; Colombo, G. DNA Polymerase conformational dynamics and the role of fidelity-conferring residues: Insight from computer simulations. Front. Mol. Biosci. 2016, 3, 20. [Google Scholar] [CrossRef] [PubMed]
- Walker, A.R.; Cisneros, G.A. Computational simulations of DNA Polymerases: Detailed insights on structure/function/mechanism from native proteins to cancer variants. Chem. Res. Toxicol. 2017, 30, 1922–1935. [Google Scholar] [CrossRef]
- Wang, Y.; Schlick, T. Distinct energetics and closing pathways for DNA polymerase β with 8-oxoG template and different incoming nucleotides. BMC Struct. Biol. 2007, 7, 7. [Google Scholar] [CrossRef]
- Arora, K.; Schlick, T. In Silico Evidence for DNA Polymerase-β’s Substrate-Induced Conformational Change. Biophys. J. 2004, 87, 3088–3099. [Google Scholar] [CrossRef]
- Yang, L.; Arora, K.; Beard, W.A.; Wilson, S.H.; Schlick, T. Critical Role of Magnesium Ions in DNA Polymerase β’s Closing and Active Site Assembly. J. Am. Chem. Soc. 2004, 126, 8441–8453. [Google Scholar] [CrossRef]
- Beard, W.A.; Wilson, S.H. Structure and mechanism of DNA Polymerase β. Biochemistry 2014, 53, 2768–2780. [Google Scholar] [CrossRef]
- Jonniya, N.A.; Fulbabu, M.S.; Kar, P. Investigating Phosphorylation-Induced Conformational Changes in Wnk1 Kinase by Molecular Dynamics Simulations. ACS Omega 2019, 4, 17404–17416. [Google Scholar] [CrossRef]
- Smith, I.N.; Dawson, J.E.; Kriger, J.; Thacker, S.; Bahar, I.; Eng, C. Structural and Dynamic effects of PTEN C-terminal Tail Phosphorylation. J. Chem. Inf. Model 2022, 62, 4175–4190. [Google Scholar] [CrossRef]
- Tokui, T.; Inagaki, M.; Nishizawa, K.; Yatani, R.; Kusagawa, M.; Ajiro, K.; Nishimoto, Y.; Date, T.; Matsukage, A. Inactivation of DNA Polymerase β by In Vitro Phosphorylation with Protein Kinase C. J. Biol. Chem. 1991, 266, 10820–10824. [Google Scholar] [CrossRef] [PubMed]
- Beard, W.A. DNA Polymerase β: Closing the gap between structure and function. DNA Repair 2020, 93, 102910. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Idriss, H.; Taha, K.; Lee, S.; Homouz, D. Phosphorylation induced conformational transitions in DNA Polymerase β. Front. Mol. Biosci. 2022, 9, 900771. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.; Werneburg, B.G.; Tsai, M.D. DNA Polymerase β: Structure—Fidelity relationship from pre-steady-state kinetic analyses of all possible correct and incorrect base pairs for wild type and R283A mutant. Biochemistry 1997, 36, 1100–1107. [Google Scholar] [CrossRef] [PubMed]
- Vande Berg, B.J.; Beard, W.A.; Wilson, S.H. DNA structure and aspartate 276 influence nucleotide binding to human DNA Polymerase β. J. Biol. Chem. 2001, 276, 3408–3416. [Google Scholar] [CrossRef]
- Yang, L.; Beard, W.A.; Wilson, S.H.; Broyde, S.; Schlick, T. Highly organized but pliant active site of DNA Polymerase β: Compensatory mechanisms in mutant enzymes revealed by dynamics simulations and energy analyses. Biophys. J. 2004, 86, 3392–3408. [Google Scholar] [CrossRef]
- Sawaya, M.R.; Pelletier, H.; Kumar, A.; Wilson, S.H.; Kraut, J. Crystal structure of rat DNA polymerase beta: Evidence for a common polymerase mechanism. Science 1994, 264, 1930–1935. [Google Scholar] [CrossRef]
- Sawaya, M.R.; Prasad, R.; Wilson, S.H.; Kraut, J.; Pelletier, H. Crystal structures of human DNA polymerase beta complexed with gapped and nicked DNA: Evidence for an induced fit mechanism. Biochemistry 1997, 36, 11205–11215. [Google Scholar] [CrossRef]
- Beard, W.A.; Shock, D.D.; Batra, V.K.; Pedersen, L.C.; Wilson, S.H. DNA polymerase beta substrate specificity: Sie chain modulation of the “A-rule”. J. Biol. Chem. 2009, 284, 31680–31689. [Google Scholar] [CrossRef]
- Batra, V.K.; Beard, W.A.; Shock, D.D.; Krahn, J.M.; Pedersen, L.C.; Wilson, S.H. Magnesium-induced Assembly of a Complete DNA Polymerase Catalytic Complex. Structure 2006, 14, 757–766. [Google Scholar] [CrossRef]
- Freudenthal, B.D.; Beard, W.A.; Wilson, S.H. Structure of dNTP intermediate states during DNA Polymerase active site assembly. Structure 2012, 20, 1829–1837. [Google Scholar] [CrossRef]
- Rivalta, I.; Sultan, M.M.; Lee, N.-S.; Manley, G.A.; Loria, J.P.; Batista, V.S. Allosteric pathways in imidazole glycerol phosphate synthase. Proc. Natl. Acad. Sci. USA 2012, 109, E1428–E1436. [Google Scholar] [CrossRef]
- Lange, O.F.; Grubmuller, H. Generalized correlations for biomolecular dynamics. Proteins 2006, 62, 1053–1061. [Google Scholar] [CrossRef]
- Amitai, G.; Shemesh, A.; Sitbon, E.; Shklar, M.; Netanely, D.; Venger, I.; Pietrokovski, S. Network Analysis of Protein Structures Identifies Functional Residues. J. Mol. Biol. 2004, 344, 1135–1146. [Google Scholar] [CrossRef]
- Whitley, M.; Lee, A. Frameworks for understanding long-range intra-protein communication. Curr. Protein Pept. Sci. 2009, 10, 116–127. [Google Scholar] [CrossRef] [PubMed]
- De Ruvo, M.; Giuliani, A.; Paci, P.; Santoni, D.; Di Paola, L. Shedding light on protein-ligand binding by graph theory: The topological nature of allostery. Biophys. Chem. 2012, 165-166, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Saltalamacchia, A.; Casalino, L.; Borisek, J.; Batista, V.S.; Rivalta, I.; Magistrato, A. Decrypting the information exchange pathways across the Spliceosome machinery. J. Am. Chem. Soc. 2020, 142, 8403–8411. [Google Scholar] [CrossRef]
- Lee, Y.; Choi, S.; Hyeon, C. Mapping the intramolecular signal transduction of G-protein coupled receptors. Proteins 2014, 82, 727–743. [Google Scholar] [CrossRef]
- Verkhivker, G.M. Molecular simulations and network modeling reveal an allosteric signaling in the SARS-CoV-2 spike proteins. J. Proteome Res. 2020, 19, 4587–4608. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. Gromacs 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; MacKerell, A.D., Jr. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Perrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, T. Particle Mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2d Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Schrodinger, L.; DeLano, W. Pymol. 2015. Available online: http://www.pymol.org/pymol (accessed on 1 May 2021).
- Ichiye, T.; Karplus, M. Collective Motions in Proteins: A Covariance Analysis of Atomic Fluctuations in Molecular Dynamics and Normal Mode Simulations. Proteins 1991, 11, 205–217. [Google Scholar] [CrossRef]
- The Mathworks, Inc. MATLAB version: 9.13.0 (R2022b). 2022. Available online: https://www.mathworks.com (accessed on 15 March 2022).
- Atilgan, C.; Atilgan, A.R. Perturbation-response scanning reveals ligand entry-exit mechanisms of Ferric binding protein. PLoS Comput. Biol. 2009, 5, e1000544. [Google Scholar] [CrossRef] [PubMed]
- Bakan, A.; Meireles, L.M.; Bahar, I. Prody: Protein Dynamics Inferred from Theory and Experiments. Bioinformatics 2011, 27, 1575–1577. [Google Scholar] [CrossRef] [PubMed]
- Atilgan, A.R.; Durell, S.R.; Jernigan, R.L.; Demirel, M.C.; Keskin, O.; Bahar, I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef] [PubMed]
- General, I.J.; Liu, Y.; Blackburn, M.E.; Mao, W.; Giearsch, L.M.; Bahar, I. Atpase subdomain IA is a mediator of inter-domain allostery in HSP70 molecular chaperones. PLoS Comput. Biol. 2014, 10, e1003624. [Google Scholar] [CrossRef]
- Negre, C.F.A.; Morzan, U.N.; Hendrickson, H.P.; Batista, V.S. Eigenvector centrality for characterization of protein allosteric pathways. Proc. Natl. Acad. Sci. USA 2018, 252, E12201–E12208. [Google Scholar] [CrossRef] [PubMed]
- Howard, M.J.; Rodriguez, Y.; Wilson, S.H. DNA polymerase β uses its lyase domain in a processive search for DNA damage. Nucleic Acids Res. 2017, 45, 3822–3832. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, A.; Idriss, H.; Homouz, D. Structural Insights into Phosphorylation-Mediated Polymerase Function Loss for DNA Polymerase β Bound to Gapped DNA. Int. J. Mol. Sci. 2023, 24, 8988. https://doi.org/10.3390/ijms24108988
Srivastava A, Idriss H, Homouz D. Structural Insights into Phosphorylation-Mediated Polymerase Function Loss for DNA Polymerase β Bound to Gapped DNA. International Journal of Molecular Sciences. 2023; 24(10):8988. https://doi.org/10.3390/ijms24108988
Chicago/Turabian StyleSrivastava, Amit, Haitham Idriss, and Dirar Homouz. 2023. "Structural Insights into Phosphorylation-Mediated Polymerase Function Loss for DNA Polymerase β Bound to Gapped DNA" International Journal of Molecular Sciences 24, no. 10: 8988. https://doi.org/10.3390/ijms24108988
APA StyleSrivastava, A., Idriss, H., & Homouz, D. (2023). Structural Insights into Phosphorylation-Mediated Polymerase Function Loss for DNA Polymerase β Bound to Gapped DNA. International Journal of Molecular Sciences, 24(10), 8988. https://doi.org/10.3390/ijms24108988




