Using Multiscale Simulations as a Tool to Interpret Equatorial X-ray Fiber Diffraction Patterns from Skeletal Muscle
Abstract
1. Introduction
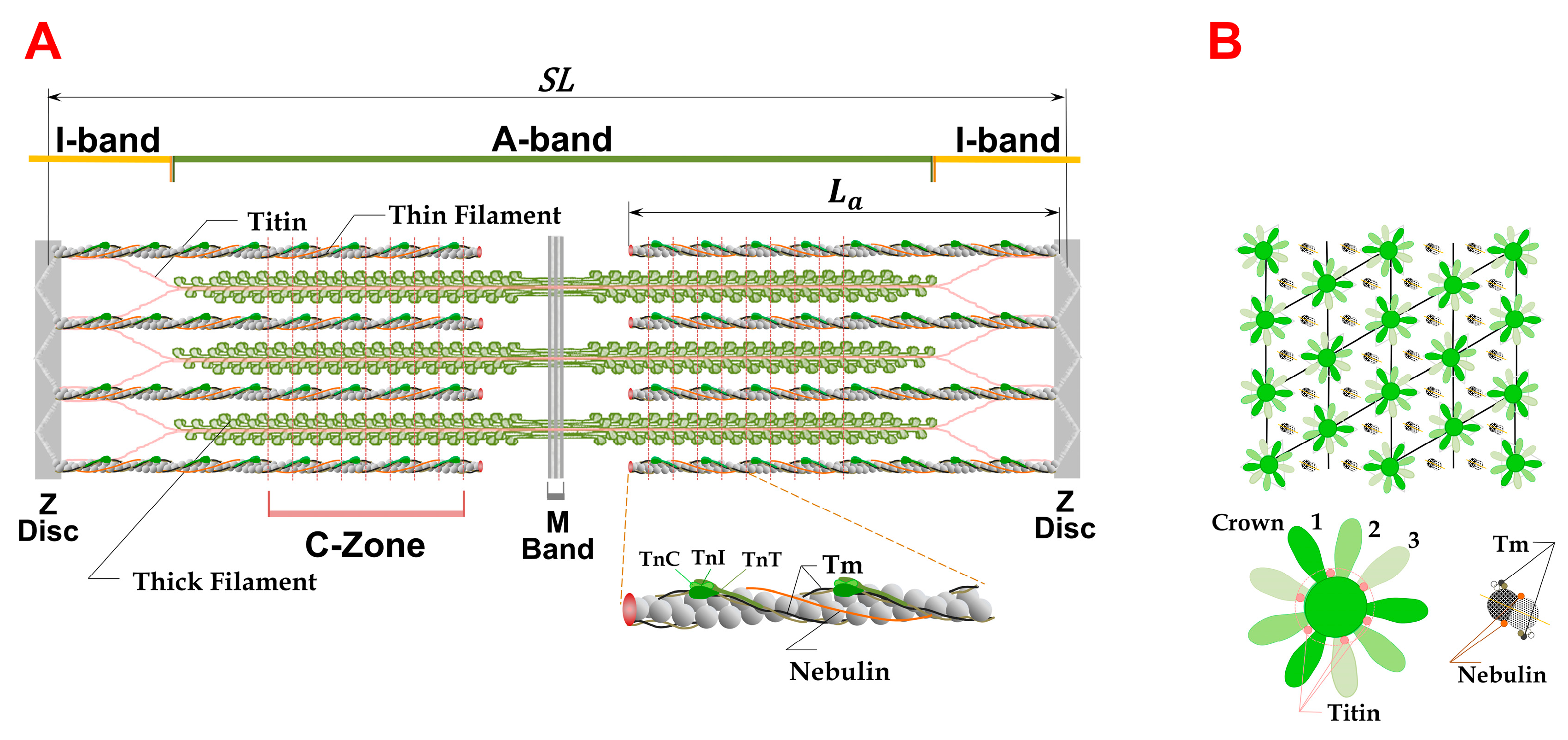
1.1. Sarcomere Structure
1.2. The Equatorial X-ray Diffraction Pattern from Striated Muscle
1.3. Using Multiscale Simulations to Predict X-ray Fiber Diffraction Patterns from Muscle
2. Results
2.1. Estimation of Number of Bound Myosin Heads during Isometric Contraction Using MUSICO
2.2. Comparison of Experimental and Simulated Equatorial X-ray Reflection Intensities
2.3. Refinement of Thick Filament Backbone Parameters for the Thick Filament Electron Density Model
2.4. Simulation of Equatorial Diffraction Pattern from Contracting Muscle
3. Discussion
3.1. Overview
3.2. Significance of Study
3.3. Future Directions
4. Materials and Methods
4.1. Simulation of Myosin Head Distributions from Mechanical Data
4.2. Electron Densities
4.2.1. Thick Filament Backbone Densities
4.2.2. Myosin S2 Region Densities
4.2.3. Titin Densities and Densities of Unbound Myosin Heads Centered on the Thick Filament
4.2.4. Thin Filament Densities
4.2.5. Densities for Pre- and Post-Powerstroke Myosin Heads
4.3. Calculation of Predicted Equatorial Diffraction Pattern from the Electron Densities
4.4. Experimental Equatorial X-ray Diffraction Intensity Measurements
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Squire, J. The Structural Basis of Muscular Contraction; Plenum Press: New York, NY, USA, 1981; 698p. [Google Scholar]
- Ma, W.; Irving, T.C. Small Angle X-ray Diffraction as a Tool for Structural Characterization of Muscle Disease. Int. J. Mol. Sci. 2022, 23, 3052. [Google Scholar] [CrossRef] [PubMed]
- Squire, J.M.; Knupp, C. Analysis methods and quality criteria for investigating muscle physiology using x-ray diffraction. J. Gen. Physiol. 2021, 153, e202012778. [Google Scholar] [CrossRef] [PubMed]
- Granzier, H.L.; Irving, T.C. Passive tension in cardiac muscle: Contribution of collagen, titin, microtubules, and intermediate filaments. Biophys. J. 1995, 68, 1027–1044. [Google Scholar] [CrossRef] [PubMed]
- Liversage, A.D.; Holmes, D.; Knight, P.J.; Tskhovrebova, L.; Trinick, J. Titin and the sarcomere symmetry paradox. J. Mol. Biol. 2001, 305, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Tskhovrebova, L.; Trinick, J. Roles of titin in the structure and elasticity of the sarcomere. J. Biomed. Biotechnol. 2010, 2010, 612482. [Google Scholar] [CrossRef]
- Mijailovich, S.M.; Stojanovic, B.; Nedic, D.; Svicevic, M.; Geeves, M.A.; Irving, T.C.; Granzier, H. Nebulin and Titin Modulate Crossbridge Cycling and Length Dependent Calcium Sensitivity. J. Gen. Physiol. 2019, 151, 680–704. [Google Scholar] [CrossRef]
- Trinick, J. Titin and nebulin: Protein rulers in muscle? Trends Biochem. Sci. 1994, 19, 405–409. [Google Scholar] [CrossRef]
- Horowits, R. Nebulin regulation of actin filament lengths: New angles. Trends Cell Biol. 2006, 16, 121–124. [Google Scholar] [CrossRef]
- Wang, Z.; Grange, M.; Pospich, S.; Wagner, T.; Kho, A.L.; Gautel, M.; Raunser, S. Structures from intact myofibrils reveal mechanism of thin filament regulation through nebulin. Science 2022, 375, eabn1934. [Google Scholar] [CrossRef]
- Haselgrove, J.C.; Huxley, H.E. X-ray evidence for radial cross-bridge movement and for the sliding filament model in actively contracting skeletal muscle. J. Mol. Biol. 1973, 77, 549–568. [Google Scholar] [CrossRef]
- Matsubara, I. X-ray diffraction studies of the heart. Annu. Rev. Biophys. Bioeng. 1980, 9, 81–105. [Google Scholar] [CrossRef] [PubMed]
- Brunello, E.; Fusi, L.; Ghisleni, A.; Park-Holohan, S.J.; Ovejero, J.G.; Narayanan, T.; Irving, M. Myosin filament-based regulation of the dynamics of contraction in heart muscle. Proc. Natl. Acad. Sci. USA 2020, 117, 8177–8186. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Gong, H.; Irving, T. Myosin Head Configurations in Resting and Contracting Murine Skeletal Muscle. Int. J. Mol. Sci. 2018, 19, 2643. [Google Scholar] [CrossRef] [PubMed]
- Brunello, E.; Bianco, P.; Piazzesi, G.; Linari, M.; Reconditi, M.; Panine, P.; Narayanan, T.; Helsby, W.I.; Irving, M.; Lombardi, V. Structural changes in the myosin filament and cross-bridges during active force development in single intact frog muscle fibres: Stiffness and X-ray diffraction measurements. J. Physiol. 2006, 577, 971–984. [Google Scholar] [CrossRef]
- Anderson, R.L.; Trivedi, D.V.; Sarkar, S.S.; Henze, M.; Ma, W.; Gong, H.; Rogers, C.S.; Gorham, J.M.; Wong, F.L.; Morck, M.M.; et al. Deciphering the super relaxed state of human beta-cardiac myosin and the mode of action of mavacamten from myosin molecules to muscle fibers. Proc. Natl. Acad. Sci. USA 2018, 115, E8143–E8152. [Google Scholar] [CrossRef]
- Ma, W.; Gong, H.; Jani, V.; Landim-Vieira, M.P.; Pinto, J.R.; Aslam, M.I.; Cammarato, A.; Irving, T. Myofibril orientation as a metric for characterizing heart disease. Biophys. J. 2022, 121, 565–574. [Google Scholar] [CrossRef]
- Colson, B.A.; Bekyarova, T.; Locher, M.R.; Fitzsimons, D.P.; Irving, T.C.; Moss, R.L. Protein kinase A-mediated phosphorylation of cMyBP-C increases proximity of myosin heads to actin in resting myocardium. Circ. Res. 2008, 103, 244–251. [Google Scholar] [CrossRef]
- Palmer, B.M.; Sadayappan, S.; Wang, Y.; Weith, A.E.; Previs, M.J.; Bekyarova, T.; Irving, T.C.; Robbins, J.; Maughan, D.W. Roles for cardiac MyBP-C in maintaining myofilament lattice rigidity and prolonging myosin cross-bridge lifetime. Biophys. J. 2011, 101, 1661–1669. [Google Scholar] [CrossRef]
- Yuan, C.C.; Muthu, P.; Kazmierczak, K.; Liang, J.; Huang, W.; Irving, T.C.; Kanashiro-Takeuchi, R.M.; Hare, J.M.; Szczesna-Cordary, D. Constitutive phosphorylation of cardiac myosin regulatory light chain prevents development of hypertrophic cardiomyopathy in mice. Proc. Natl. Acad. Sci. USA 2015, 112, E4138–E4146. [Google Scholar] [CrossRef]
- Ma, W.; McMillen, T.S.; Childers, M.C.; Gong, H.; Regnier, M.; Irving, T. Structural OFF/ON transitions of myosin in relaxed porcine myocardium predict calcium-activated force. Proc. Natl. Acad. Sci. USA 2023, 120, e2207615120. [Google Scholar] [CrossRef]
- Mijailovich, S.M.; Prodanovic, M.; Poggesi, C.; Geeves, M.A.; Regnier, M. Multiscale Modeling of Twitch Contractions in Cardiac Trabeculae. J. Gen. Physiol. 2021, 153, e202012604. [Google Scholar] [CrossRef] [PubMed]
- Irving, T.C.; Millman, B.M. Changes in thick filament structure during compression of the filament lattice in relaxed frog sartorius muscle. J. Muscle Res. Cell Motil. 1989, 10, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Malinchik, S.; Yu, L.C. Analysis of equatorial x-ray diffraction patterns from muscle fibers: Factors that affect the intensities. Biophys. J. 1995, 68, 2023–2031. [Google Scholar] [CrossRef] [PubMed]
- Ait-Mou, Y.; Hsu, K.; Farman, G.P.; Kumar, M.; Greaser, M.L.; Irving, T.C.; de Tombe, P.P. Titin strain contributes to the Frank-Starling law of the heart by structural rearrangements of both thin- and thick-filament proteins. Proc. Natl. Acad. Sci. USA 2016, 113, 2306–2311. [Google Scholar] [CrossRef] [PubMed]
- Eakins, F.; Pinali, C.; Gleeson, A.; Knupp, C.; Squire, J.M. X-ray Diffraction Evidence for Low Force Actin-Attached and Rigor-Like Cross-Bridges in the Contractile Cycle. Biology 2016, 5, 41. [Google Scholar] [CrossRef]
- Eakins, F.; Harford, J.J.; Knupp, C.; Roessle, M.; Squire, J.M. Different Myosin Head Conformations in Bony Fish Muscles Put into Rigor at Different Sarcomere Lengths. Int. J. Mol. Sci. 2018, 19, 2091. [Google Scholar] [CrossRef]
- Reconditi, M.; Brunello, E.; Fusi, L.; Linari, M.; Martinez, M.F.; Lombardi, V.; Irving, M.; Piazzesi, G. Sarcomere-length dependence of myosin filament structure in skeletal muscle fibres of the frog. J. Physiol. 2014, 592, 1119–1137. [Google Scholar] [CrossRef]
- Mijailovich, S.M.; Kayser-Herold, O.; Stojanovic, B.; Nedic, D.; Irving, T.C.; Geeves, M.A. Three-dimensional stochastic model of actin-myosin binding in the sarcomere lattice. J. Gen. Physiol. 2016, 148, 459–488. [Google Scholar] [CrossRef]
- Prodanovic, M.; Irving, T.C.; Mijailovich, S.M. X-ray diffraction from nonuniformly stretched helical molecules. J. Appl. Crystallogr. 2016, 49, 784–797. [Google Scholar] [CrossRef]
- Irving, M. Regulation of Contraction by the Thick Filaments in Skeletal Muscle. Biophys. J. 2017, 113, 2579–2594. [Google Scholar] [CrossRef]
- Greaser, M.L.; Pleitner, J.M. Titin isoform size is not correlated with thin filament length in rat skeletal muscle. Front. Physiol. 2014, 5, 35. [Google Scholar] [CrossRef]
- Prodanovic, M.; Geeves, M.A.; Poggesi, C.; Regnier, M.; Mijailovich, S.M. Effect of Myosin Isoforms on Cardiac Muscle Twitch of Mice, Rats and Humans. Int. J. Mol. Sci. 2022, 23, 1135. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.C. Analysis of equatorial x-ray diffraction patterns from skeletal muscle. Biophys. J. 1989, 55, 433–440. [Google Scholar] [CrossRef] [PubMed]
- Squire, J.M.; Knupp, C. X-ray diffraction studies of muscle and the crossbridge cycle. Adv. Protein. Chem. 2005, 71, 195–255. [Google Scholar] [CrossRef] [PubMed]
- Bershitsky, S.Y.; Koubassova, N.A.; Bennett, P.M.; Ferenczi, M.A.; Shestakov, D.A.; Tsaturyan, A.K. Myosin heads contribute to the maintenance of filament order in relaxed rabbit muscle. Biophys. J. 2010, 99, 1827–1834. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Namba, K.; Fujii, T. Cardiac muscle thin filament structures reveal calcium regulatory mechanism. Nat. Commun. 2020, 11, 153. [Google Scholar] [CrossRef] [PubMed]
- Risi, C.M.; Belknap, B.; White, H.D.; Dryden, K.; Pinto, J.R.; Chase, P.B.; Galkin, V.E. High-resolution cryo-EM structure of the junction region of the native cardiac thin filament in relaxed state. PNAS Nexus 2023, 2, pgac298. [Google Scholar] [CrossRef]
- Risi, C.M.; Pepper, I.; Belknap, B.; Landim-Vieira, M.; White, H.D.; Dryden, K.; Pinto, J.R.; Chase, P.B.; Galkin, V.E. The structure of the native cardiac thin filament at systolic Ca(2+) levels. Proc. Natl. Acad. Sci. USA 2021, 118, e2024288118. [Google Scholar] [CrossRef]
- Risi, C.M.; Villanueva, E.; Belknap, B.; Sadler, R.L.; Harris, S.P.; White, H.D.; Galkin, V.E. Cryo-Electron Microscopy Reveals Cardiac Myosin Binding Protein-C M-Domain Interactions with the Thin Filament. J. Mol. Biol. 2022, 434, 167879. [Google Scholar] [CrossRef]
- Wang, Z.; Grange, M.; Wagner, T.; Kho, A.L.; Gautel, M.; Raunser, S. The molecular basis for sarcomere organization in vertebrate skeletal muscle. Cell 2021, 184, 2135–2150. [Google Scholar] [CrossRef]
- Li, J.; Rahmani, H.; Yeganeh, F.A.; Rastegarpouyani, H.; Taylor, D.W.; Wood, N.B.; Previs, M.J.; Iwamoto, H.; Taylor, K.A. Structure of the Flight Muscle Thick Filament from the Bumble Bee, Bombus ignitus, at 6 Å Resolution. Int. J. Mol. Sci. 2022, 24, 377. [Google Scholar] [CrossRef] [PubMed]
- Daneshparvar, N.; Taylor, D.W.; O’Leary, T.S.; Rahmani, H.; Abbasiyeganeh, F.; Previs, M.J.; Taylor, K.A. CryoEM structure of Drosophila flight muscle thick filaments at 7 Å resolution. Life Sci. Alliance 2020, 3, e202000823. [Google Scholar] [CrossRef] [PubMed]
- Mijailovich, S.M.; Prodanovic, M.; Poggesi, C.; Powers, J.D.; Davis, J.; Geeves, M.A.; Regnier, M. The effect of variable troponin C mutation thin filament incorporation on cardiac muscle twitch contractions. J. Mol. Cell. Cardiol. 2021, 155, 112–124. [Google Scholar] [CrossRef] [PubMed]
- Mijailovich, S.M.; Kayser-Herald, O.; Moss, R.L.; Geeves, M.A. Thin Filament Regulation of Relaxation in 3D Multi-Sarcomere Geometry. Biophys. J. 2009, 96, 201a. [Google Scholar] [CrossRef]
- Geeves, M.; Griffiths, H.; Mijailovich, S.; Smith, D. Cooperative [Ca(2)+]-dependent regulation of the rate of myosin binding to actin: Solution data and the tropomyosin chain model. Biophys. J. 2011, 100, 2679–2687. [Google Scholar] [CrossRef]
- Mijailovich, S.M.; Kayser-Herold, O.; Li, X.; Griffiths, H.; Geeves, M.A. Cooperative regulation of myosin-S1 binding to actin filaments by a continuous flexible Tm-Tn chain. Eur. Biophys. J. 2012, 41, 1015–1032. [Google Scholar] [CrossRef]
- Holmes, K.C.; Schröder, R.R.; Sweeney, H.L.; Houdusse, A. The structure of the rigor complex and its implications for the power stroke. Philos. Trans. R. Soc. B Biol. Sci. 2004, 359, 1819–1828. [Google Scholar] [CrossRef]
- Rahmani, H.; Ma, W.; Hu, Z.; Daneshparvar, N.; Taylor, D.W.; McCammon, J.A.; Irving, T.C.; Edwards, R.J.; Taylor, K.A. The myosin II coiled-coil domain atomic structure in its native environment. Proc. Natl. Acad. Sci. USA 2021, 118, e2024151118. [Google Scholar] [CrossRef]
- Squire, J.M. General model of myosin filament structure. 3. Molecular packing arrangements in myosin filaments. J. Mol. Biol. 1973, 77, 291–323. [Google Scholar] [CrossRef]
- Squire, J.; Cantino, M.; Chew, M.; Denny, R.; Harford, J.; Hudson, L.; Luther, P. Myosin rod-packing schemes in vertebrate muscle thick filaments. J. Struct. Biol. 1998, 122, 128–138. [Google Scholar] [CrossRef]
- Skubiszak, L.; Kowalczyk, L. Myosin molecule packing within the vertebrate skeletal muscle thick filaments. A complete bipolar model. Acta Biochim. Pol. 2002, 49, 829–840. [Google Scholar] [CrossRef] [PubMed]
- Kensler, R.W.; Stewart, M. Frog skeletal muscle thick filaments are three-stranded. J. Cell Biol. 1983, 96, 1797–1802. [Google Scholar] [CrossRef] [PubMed]
- Blankenfeldt, W.; Thoma, N.H.; Wray, J.S.; Gautel, M.; Schlichting, I. Crystal structures of human cardiac beta-myosin II S2-Delta provide insight into the functional role of the S2 subfragment. Proc. Natl. Acad. Sci. USA 2006, 103, 17713–17717. [Google Scholar] [CrossRef] [PubMed]
- Adamovic, I.; Mijailovich, S.M.; Karplus, M. The elastic properties of the structurally characterized myosin II S2 subdomain: A molecular dynamics and normal mode analysis. Biophys. J. 2008, 94, 3779–3789. [Google Scholar] [CrossRef]
- Al-Khayat, H.A. Three-dimensional structure of the human myosin thick filament: Clinical implications. Glob. Cardiol. Sci. Pract. 2013, 2013, 280–302. [Google Scholar] [CrossRef]
- Koubassova, N.A.; Bershitsky, S.Y.; Ferenczi, M.A.; Tsaturyan, A.K. Direct modeling of X-ray diffraction pattern from contracting skeletal muscle. Biophys. J. 2008, 95, 2880–2894. [Google Scholar] [CrossRef]
- Vainshtein, B.K. Diffraction of X-rays by Chain Molecules; Elsevier: Amsterdam, The Netherlands, 1966. [Google Scholar]
- Gong, H.M.; Ma, W.; Regnier, M.; Irving, T.C. Thick filament activation is different in fast- and slow-twitch skeletal muscle. J. Physiol. 2022, 600, 5247–5266. [Google Scholar] [CrossRef]
- Jiratrakanvong, J.; Shao, J.; Menendez, M.; Li, X.; Li, J.; Nabon, J.; Agam, W.M.G.; Irving, T. MuscleX: Software suite for diffraction X-ray imaging (v1.21.0). Available online: https://zenodo.org/record/7468634#.ZFnmqXZBxPa (accessed on 1 March 2023). [CrossRef]
- Yu, L.C.; Steven, A.C.; Naylor, G.R.; Gamble, R.C.; Podolsky, R.J. Distribution of mass in relaxed frog skeletal muscle and its redistribution upon activation. Biophys. J. 1985, 47, 311–321. [Google Scholar] [CrossRef]
- Duke, T.A. Molecular model of muscle contraction. Proc. Natl. Acad. Sci. USA 1999, 96, 2770–2775. [Google Scholar] [CrossRef]
- Smith, D.A.; Geeves, M.A. Cooperative regulation of myosin-actin interactions by a continuous flexible chain II: Actin-tropomyosin-troponin and regulation by calcium. Biophys. J. 2003, 84, 3168–3180. [Google Scholar] [CrossRef]
- Kreutziger, K.L.; Piroddi, N.; McMichael, J.T.; Tesi, C.; Poggesi, C.; Regnier, M. Calcium binding kinetics of troponin C strongly modulate cooperative activation and tension kinetics in cardiac muscle. J. Mol. Cell Cardiol. 2011, 50, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; McCully, M.E.; Luo, Z.; McMichael, J.; Tu, A.Y.; Daggett, V.; Regnier, M. Structural and functional consequences of cardiac troponin C L57Q and I61Q Ca(2+)-desensitizing variants. Arch. Biochem. Biophys. 2013, 535, 68–75. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Robertson, I.M.; Li, M.X.; McCully, M.E.; Crane, M.L.; Luo, Z.; Tu, A.Y.; Daggett, V.; Sykes, B.D.; Regnier, M. Structural and functional consequences of the cardiac troponin C L48Q Ca(2+)-sensitizing mutation. Biochemistry 2012, 51, 4473–4487. [Google Scholar] [CrossRef] [PubMed]
- Poole, K.J.; Lorenz, M.; Evans, G.; Rosenbaum, G.; Pirani, A.; Craig, R.; Tobacman, L.S.; Lehman, W.; Holmes, K.C. A comparison of muscle thin filament models obtained from electron microscopy reconstructions and low-angle X-ray fibre diagrams from non-overlap muscle. J. Struct. Biol. 2006, 155, 273–284. [Google Scholar] [CrossRef]
- Pirani, A.; Xu, C.; Hatch, V.; Craig, R.; Tobacman, L.S.; Lehman, W. Single particle analysis of relaxed and activated muscle thin filaments. J. Mol. Biol. 2005, 346, 761–772. [Google Scholar] [CrossRef]
- Robinson, T.F.; Winegrad, S. Variation of thin filament length in heart muscles. Nature 1977, 267, 74–75. [Google Scholar] [CrossRef]
- Robinson, T.F.; Winegrad, S. The measurement and dynamic implications of thin filament lengths in heart muscle. J. Physiol. 1979, 286, 607–619. [Google Scholar] [CrossRef]
- Irving, T.C.; Maughan, D.W. In vivo x-ray diffraction of indirect flight muscle from Drosophila melanogaster. Biophys. J. 2000, 78, 2511–2515. [Google Scholar] [CrossRef]
- Huxley, H.E.; Stewart, A.; Sosa, H.; Irving, T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 1994, 67, 2411–2421. [Google Scholar] [CrossRef]
- Kojima, H.; Ishijima, A.; Yanagida, T. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA 1994, 91, 12962–12966. [Google Scholar] [CrossRef]
- Deacon, J.C.; Bloemink, M.J.; Rezavandi, H.; Geeves, M.A.; Leinwand, L.A. Identification of functional differences between recombinant human alpha and beta cardiac myosin motors. Cell Mol. Life Sci. 2012, 69, 2261–2277, Erratum in Cell Mol. Life Sci. 2012, 69, 4239–4255. [Google Scholar] [CrossRef] [PubMed]
- Mijailovich, S.M.; Nedic, D.; Svicevic, M.; Stojanovic, B.; Walklate, J.; Ujfalusi, Z.; Geeves, M.A. Modeling the Actin.myosin ATPase Cross-Bridge Cycle for Skeletal and Cardiac Muscle Myosin Isoforms. Biophys. J. 2017, 112, 984–996. [Google Scholar] [CrossRef] [PubMed]
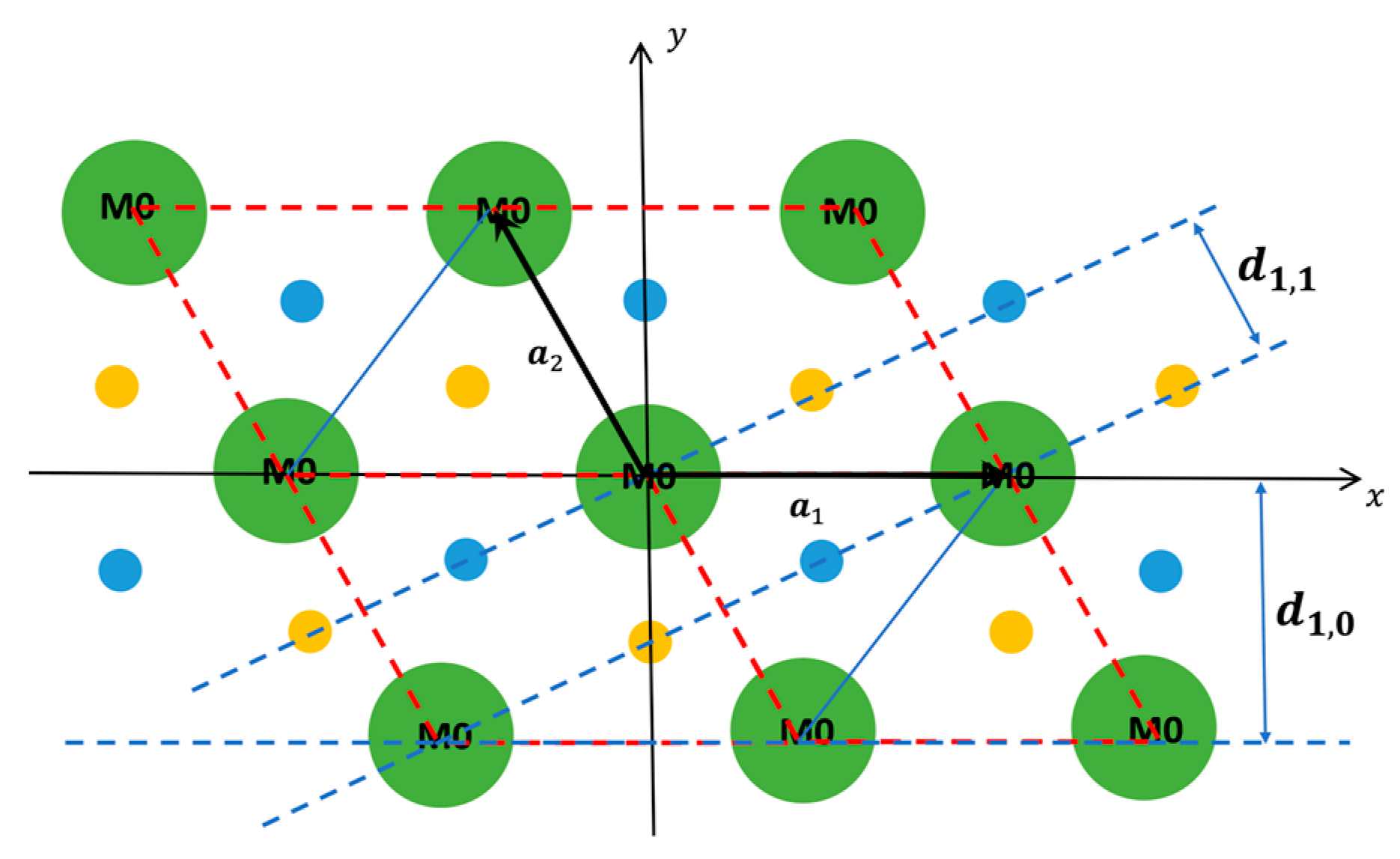



| Description | Parameter | Value |
|---|---|---|
| Sarcomere length | SL (μm) | 2.862 |
| Interfilament spacing | d10 (nm) | 34.21 |
| Distance between actin and myosin | dAM (nm) | 22.81 |
| Description | Parameter | Value |
|---|---|---|
| Myosin–actin binding rate | (s−1) | 100 |
| ADP release rate | (s−1) | 300 |
| Parked-state amplitude | (s−1) | 220 |
| Parked-state baseline rate | (s−1) | 40 |
| Experiment (kPa) | MUSICO (kPa) | |
|---|---|---|
| Mean isometric tension (avg. over 6 trials) | 66.3 ± 13.7 | 66.15 |
| Relaxed | Contracted | |
|---|---|---|
| Fraction of bound crossbridges % | 1.95 | 22.93 |
| Fraction of unbound crossbridges % | 17.67 | 42.67 |
| Fraction of crossbridges in PS % | 80.38 | 34.40 |
| Reflection Phase | (1.0) + | (1.1) + | (2.0) − | (2.1) − | (3.0) + | (2.2) + | (3.1) − | (4.0) − | R-Factor | |
|---|---|---|---|---|---|---|---|---|---|---|
| Experimental Resting | Mean | 100.00 | 36.34 | 15.72 | 6.24 | 6.73 | 0.31 | 2.36 | 1.24 | |
| Error | 3.49 | 1.43 | 1.07 | 1.13 | 0.23 | 0.46 | 0.27 | |||
| Simulation = 2.58 nm = 2.15 nm | Mean | 100.00 | 34.05 | 18.73 | 9.13 | 1.77 | 0.35 | 1.17 | 0.22 | 0.0043 |
| Error | 0.46 | 0.05 | 0.08 | 0.02 | 0.01 | 0.01 | 0.00 | |||
| Experimental Contracting | Mean | 100.00 | 68.75 | 20.49 | 12.96 | 2.51 | 3.78 | 0.60 | 1.36 | |
| Error | 3.72 | 5.27 | 1.00 | 2.25 | 0.38 | 9.75 | 3.72 | |||
| Simulation = 2.58 nm = 1.72 nm | Mean | 100.00 | 70.12 | 20.34 | 15.69 | 2.96 | 0.81 | 2.49 | 0.41 | 0.00082 |
| Error | 3.31 | 0.38 | 0.50 | 0.18 | 0.08 | 0.06 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prodanovic, M.; Wang, Y.; Mijailovich, S.M.; Irving, T. Using Multiscale Simulations as a Tool to Interpret Equatorial X-ray Fiber Diffraction Patterns from Skeletal Muscle. Int. J. Mol. Sci. 2023, 24, 8474. https://doi.org/10.3390/ijms24108474
Prodanovic M, Wang Y, Mijailovich SM, Irving T. Using Multiscale Simulations as a Tool to Interpret Equatorial X-ray Fiber Diffraction Patterns from Skeletal Muscle. International Journal of Molecular Sciences. 2023; 24(10):8474. https://doi.org/10.3390/ijms24108474
Chicago/Turabian StyleProdanovic, Momcilo, Yiwei Wang, Srboljub M. Mijailovich, and Thomas Irving. 2023. "Using Multiscale Simulations as a Tool to Interpret Equatorial X-ray Fiber Diffraction Patterns from Skeletal Muscle" International Journal of Molecular Sciences 24, no. 10: 8474. https://doi.org/10.3390/ijms24108474
APA StyleProdanovic, M., Wang, Y., Mijailovich, S. M., & Irving, T. (2023). Using Multiscale Simulations as a Tool to Interpret Equatorial X-ray Fiber Diffraction Patterns from Skeletal Muscle. International Journal of Molecular Sciences, 24(10), 8474. https://doi.org/10.3390/ijms24108474







