Insights into Infusion-Based Targeted Drug Delivery in the Brain: Perspectives, Challenges and Opportunities
Abstract
:1. Introduction
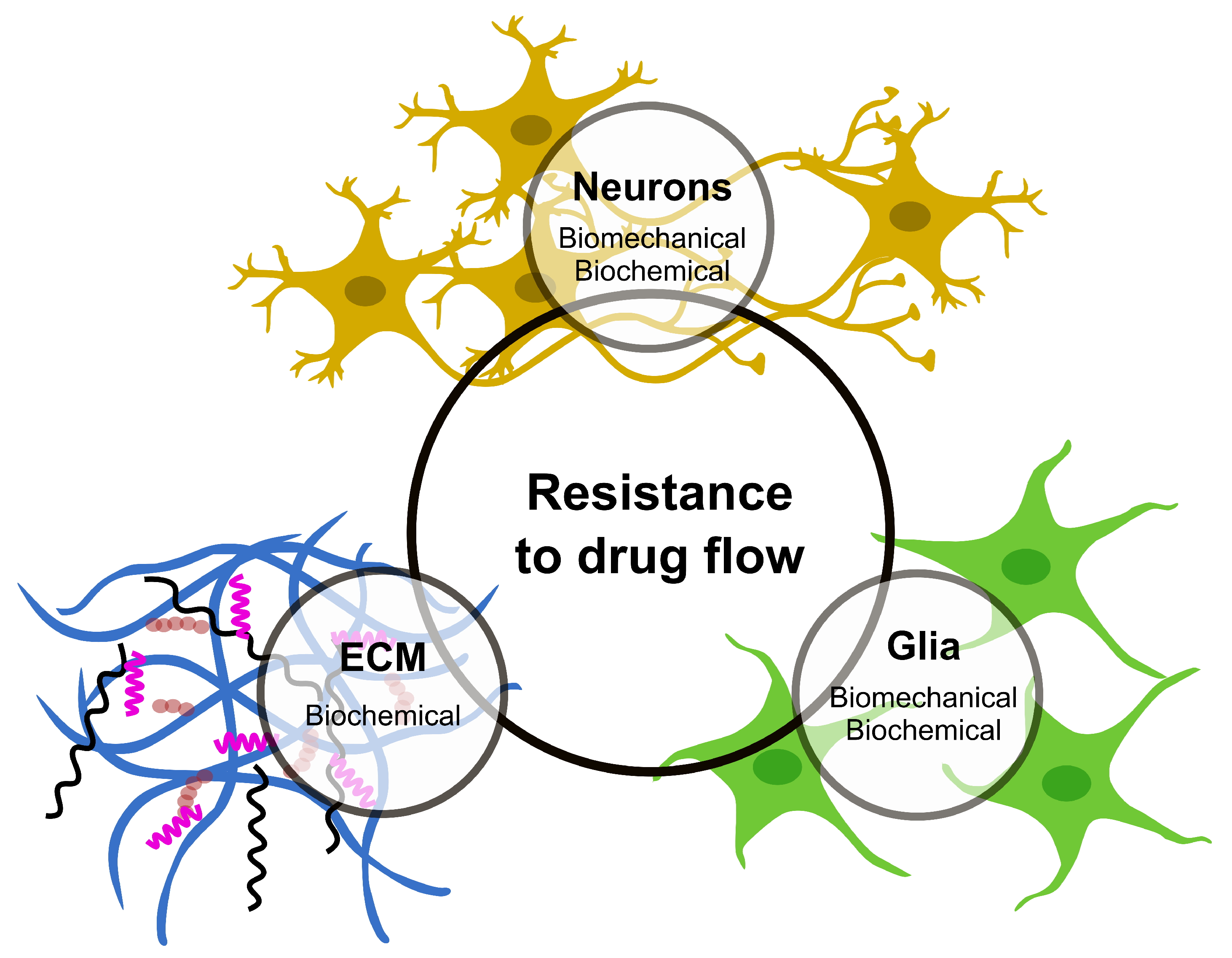
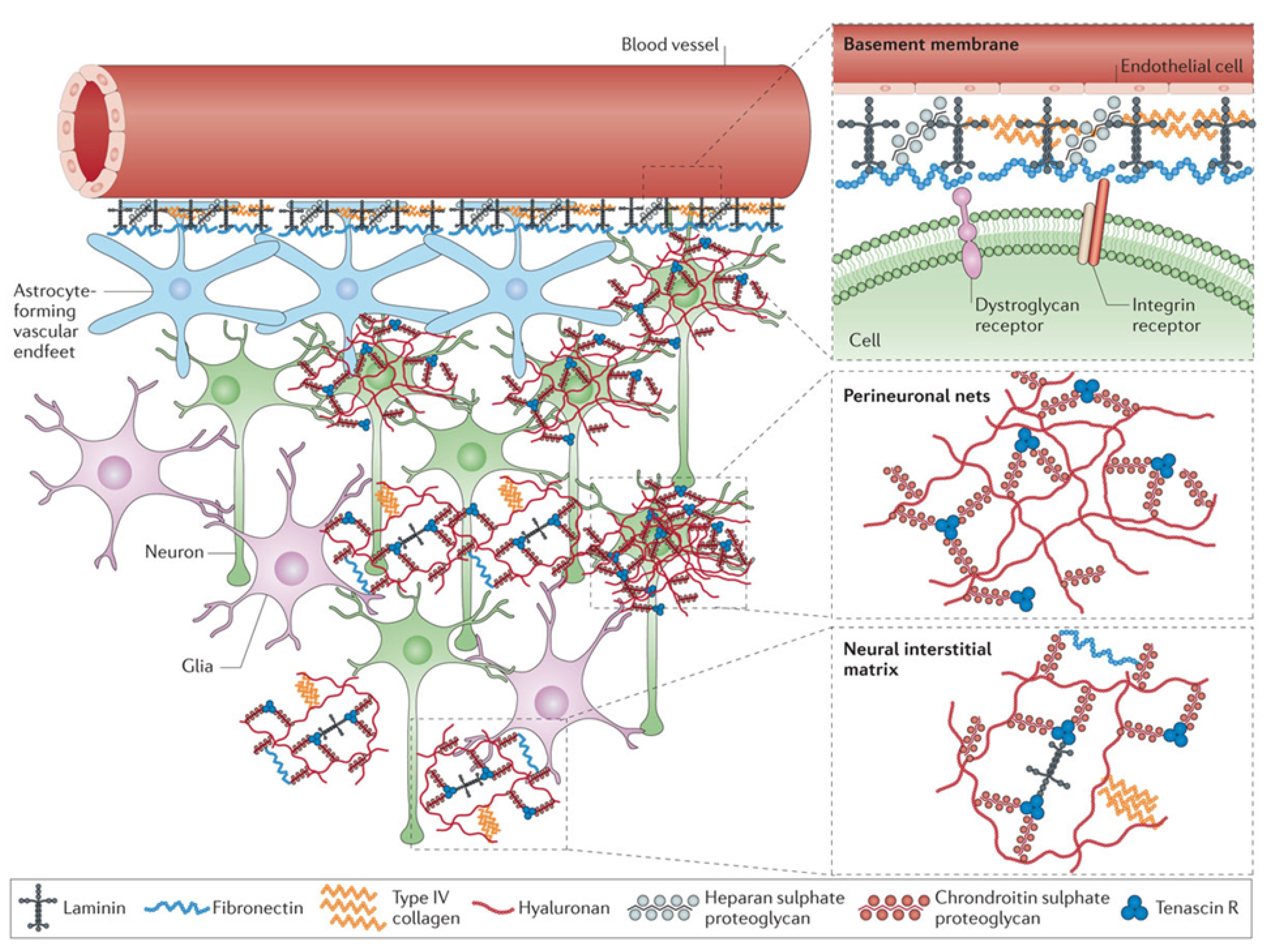
2. Brain Tissue: A Complex System for Diffusion-Based Drug Delivery
3. Infusion-Based Drug Delivery in CNS Tissue
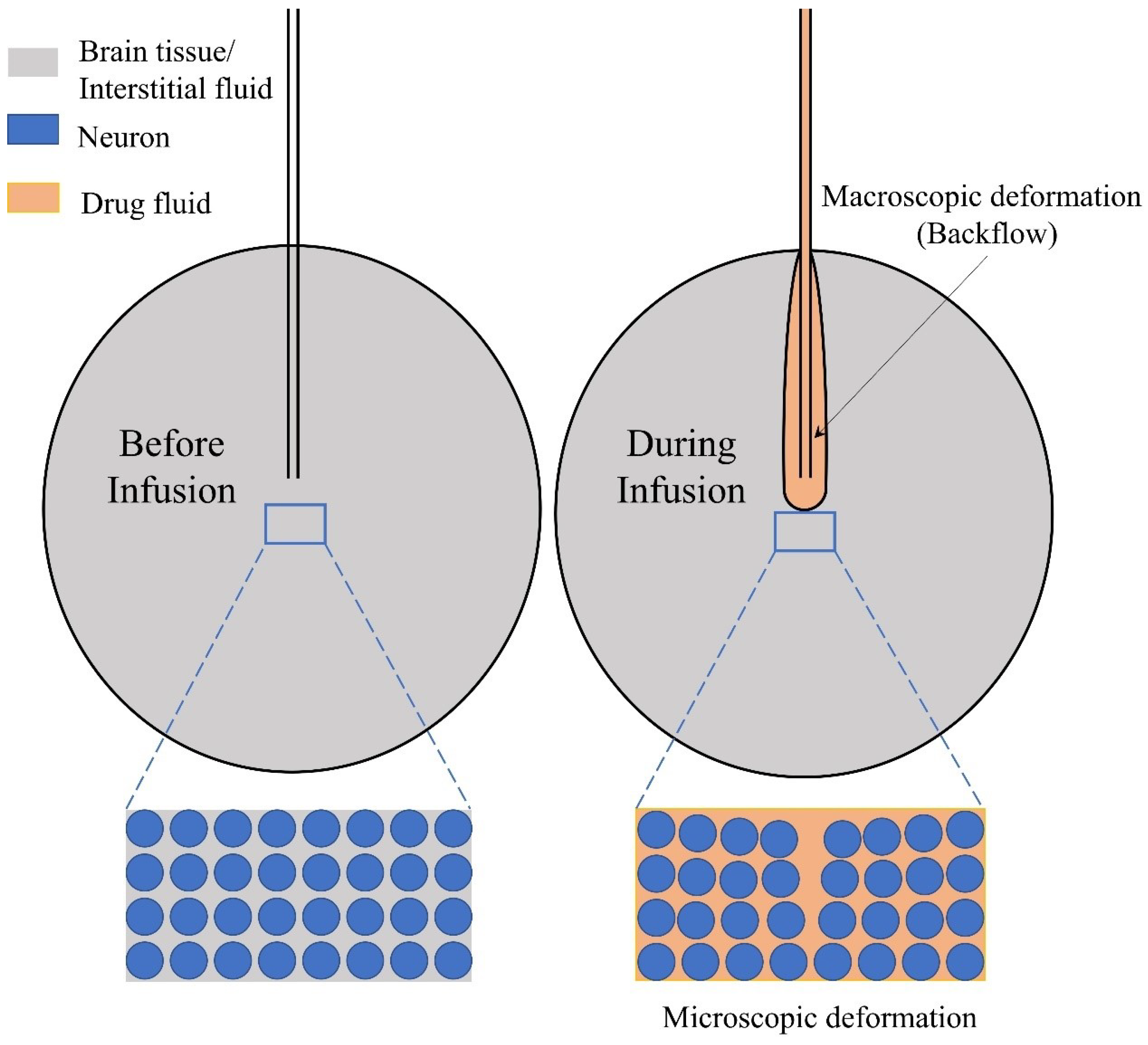
3.1. Biomechanical Aspects of Infusion-Based Drug Flow
3.2. Chemical Aspects of Infusion-Based Drug Flow: Molecular-Level Mechanisms
4. Simulations and Existing Models for Infusion-Based Drug Delivery
4.1. Mathematical Models
4.1.1. Single-Phase Model
4.1.2. Biphasic Model: Fluid Flow and Solid Response
4.1.3. Multiphasics Model
4.2. Mathematical Models for Particle Distribution in CNS
4.3. Modelling Molecular Interactions
4.4. Geometric Models
4.4.1. Idealised Models
4.4.2. Realistic Models Using MRI and DTI as Input
4.5. Limitations and Perspectives
4.5.1. On Mathematical Models
4.5.2. On Model Compatibility
5. Robotics Solutions
5.1. Planning
5.2. Needle Tracking
5.3. Brain Deformation Sensing
5.4. Software
6. Clinical Implications
7. Conclusions and Future Perspectives
- Consider tumour growth and expansion according to computational evolution data and, from these data, achieve procedure-optimised therapy plans which account for patient-specific anatomy.
- Obtain a better understanding of molecular-level processes that govern drug uptake, interaction with the tissue and ultimately drug reach and efficacy.
- Pair diffusion imaging data with histology, microstructural measurements and high-fidelity diffusion models based on computational fluid dynamics and finite element analysis to improve our understanding of the brain biphasic nature.
- Develop better bottom-up models and associated experimental techniques that enable to describe drug diffusion and convection across the scales and quantify its uptake considering the complexity of the tissue and its variability.
- Target the main diffusion tracts along and within the tumour and deploy CED systems that can deliver various molecules in various areas of the tumour.
- Rely on a single, integrated platform for neuro-oncological treatment and a spectrum of other uses, ranging from degenerative disease management and structural definition to stem cell therapy and localised tissue ablation.
- Integrate pre-operative imaging with online imaging via save modalities, such as ultrasound, to correct for brain shift and to ensure a more accurate targeting, overcoming most of the limitations of current systems for catheter insertion based on preoperative imaging alone and reducing the cost of those few systems (e.g., MR Interventions’ ClearPoint) which rely on an interventional MRI or CT suite.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFT | Adaptive Fractal Trees |
| BBB | Blood–Brain Barrier |
| CED | Convection-Enhanced Delivery |
| CFD | Computational Fluid Dynamics |
| CNS | Central Nervous System |
| CSF | Cerebrospinal Fluid |
| CT | Computed Tomography |
| DPD | Dissipative Particle Dynamics |
| DoF | Degrees of Freedom |
| DTI | Diffusion Tensor Imaging |
| E | Young’s Modulus |
| ECS | Extracellular Space |
| ESF | Extracellular Fluid |
| ECM | Extracellular Matrix |
| FBG | Fiber Bragg Grating |
| GBM | Glioblastoma Multiforme |
| GPU | Graphic Processing Unit |
| if | Interstitial Fluid |
| Hydraulic Permeability | |
| MC | Monte Carlo |
| MD | Molecular Dynamics |
| MIKT | Medical Imaging Interaction Toolkit |
| MRI | Magnetic Resonance Imaging |
| MSD | Mean Square Displacement |
| NODDI | Neurite Orientation Dispersion and Density Imaging |
| NPs | Nanoparticles |
| PBNs | Programmable Bevel-Tip Steerable Needles |
| PVE | Poro-Viscoelastic |
| RRT | Rapidly exploring Random Trees |
| ROI | Region of Interest |
| SOFA | Simulation Open Framework Architecture |
| TCs | Tissue Components |
| US | Ultrasound |
| UX | User Experience |
| UI | User Interface |
References
- Alphandéry, E. Glioblastoma treatments: An account of recent industrial developments. Front. Pharmacol. 2018, 9, 879. [Google Scholar] [CrossRef] [Green Version]
- Bush, N.A.O.; Chang, S.M.; Berger, M.S. Current and future strategies for treatment of glioma. Neurosurg. Rev. 2017, 40, 1–14. [Google Scholar] [CrossRef]
- Olesen, J.; Gustavsson, A.; Svensson, M.; Wittchen, H.U.; Jönsson, B. The economic cost of brain disorders in Europe. Eur. J. Neurol. 2012, 19, 155–162. [Google Scholar] [CrossRef]
- Harder, B.G.; Blomquist, M.R.; Wang, J.; Kim, A.J.; Woodworth, G.F.; Winkles, J.A.; Loftus, J.C.; Tran, N.L. Developments in Blood-Brain Barrier Penetrance and Drug Repurposing for Improved Treatment of Glioblastoma. Front. Oncol. 2018, 8, 462. [Google Scholar] [CrossRef] [Green Version]
- Weidle, U.H.; Niewohner, J.; Tiefenthaler, G. The blood-brain barrier challenge for the treatment of brain cancer, secondary brain metastases, and neurological diseases. Cancer Genom. Proteom. 2015, 12, 167–178. [Google Scholar]
- Yuan, F. Transvascular drug delivery in solid tumors. Semin. Radiat. Oncol. 1998, 8, 164–175. [Google Scholar] [CrossRef]
- Mehta, A.M.; Sonabend, A.M.; Bruce, J.N. Convection-Enhanced Delivery. Neurotherapeutics 2017, 14, 358–371. [Google Scholar] [CrossRef] [Green Version]
- Lonser, R.R.; Sarntinoranont, M.; Morrison, P.F.; Oldfield, E.H. Convection-enhanced delivery to the central nervous system. J. Neurosurg. 2015, 122, 697–706. [Google Scholar] [CrossRef] [Green Version]
- Audette, M.A.; Bordas, S.P.; Blatt, J.E. Robotically Steered Needles: A Survey of Neurosurgical Applications and Technical Innovations. Robot. Surg. Res. Rev. 2020, 7, 1–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Terzano, M.; Dini, D.; Rodriguez y Baena, F.; Spagnoli, A.; Oldfield, M. An adaptive finite element model for steerable needles. Biomech. Model. Mechanobiol. 2020, 19, 1809–1825. [Google Scholar] [CrossRef] [Green Version]
- Vogelbaum, M.A. Convection enhanced delivery for treating brain tumors and selected neurological disorders: Symposium review. J. Neuro-Oncol. 2007, 83, 97–109. [Google Scholar] [CrossRef] [Green Version]
- Azevedo, F.A.; Carvalho, L.R.; Grinberg, L.T.; Farfel, J.M.; Ferretti, R.E.; Leite, R.E.; Filho, W.J.; Lent, R.; Herculano-Houzel, S. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. The J. Comp. Neurol. 2009, 513, 532–541. [Google Scholar] [CrossRef]
- Daneman, R. The blood-brain barrier in health and disease. Ann. Neurol. 2012, 72, 648–672. [Google Scholar] [CrossRef]
- Daneman, R.; Prat, A. The Blood–Brain Barrier. Cold Spring Harb. Perspect. Biol. 2015, 7, a020412. [Google Scholar] [CrossRef] [Green Version]
- Hammarlund-Udenaes, M.; Paalzow, L.K.; de Lange, E.C. Drug equilibration across the blood-brain barrier–pharmacokinetic considerations based on the microdialysis method. Pharm. Res. 1997, 14, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, C. Diffusion and related transport mechanisms in brain tissue. Rep. Prog. Phys. 2001, 64, 815–884. [Google Scholar] [CrossRef]
- Nicholson, C.; Phillips, J.M. Ion diffusion modified by tortuosity and volume fraction in the extracellular microenvironment of the rat cerebellum. J. Physiol. 1981, 321, 225–257. [Google Scholar] [CrossRef] [PubMed]
- Jamal, A.; Mongelli, M.T.; Vidotto, M.; Madekurozwa, M.; Bernardini, A.; Overby, D.R.; De Momi, E.; Rodriguez y Baena, F.; Sherwood, J.M.; Dini, D. Infusion Mechanisms in Brain White Matter and Their Dependence on Microstructure: An Experimental Study of Hydraulic Permeability. IEEE Trans. Biomed. Eng. 2021, 68, 1229–1237. [Google Scholar] [CrossRef] [PubMed]
- Vidotto, M.; Bernardini, A.; Trovatelli, M.; Momi, E.D.; Dini, D. On the Microstructural Origin of Brain White Matter Hydraulic Permeability. Proc. Natl. Acad. Sci. USA 2021, 118, e2105328118. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.K.; Stylianopoulos, T. Delivering nanomedicine to solid tumors. Nat. Rev. Clin. Oncol. 2010, 7, 653–664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Y.; Chen, X.; Cao, J.; Gao, H. Overcoming the biological barriers in the tumor microenvironment for improving drug delivery and efficacy. J. Mater. Chem. B 2020, 8, 6765–6781. [Google Scholar] [CrossRef] [PubMed]
- Bertrand, N.; Wu, J.; Xu, X.; Kamaly, N.; Farokhzad, O.C. Cancer nanotechnology: The impact of passive and active targeting in the era of modern cancer biology. Adv. Drug Deliv. Rev. 2014, 66, 2–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lieleg, O.; Baumgärtel, R.M.; Bausch, A.R. Selective Filtering of Particles by the Extracellular Matrix: An Electrostatic Bandpass. Biophys. J. 2009, 97, 1569–1577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarntinoranont, M.; Banerjee, R.K.; Lonser, R.R.; Morrison, P.F. A Computational Model of Direct Interstitial Infusion of Macromolecules into the Spinal Cord. Ann. Biomed. Eng. 2003, 31, 448–461. [Google Scholar] [CrossRef] [PubMed]
- Prange, M.T.; Margulies, S.S. Regional, directional, and age-dependent properties of the brain undergoing large deformation. J. Biomech. Eng. 2002, 124, 244–252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, K. Constitutive model of brain tissue suitable for finite element analysis of surgical procedures. J. Biomech. 1999, 32, 531–537. [Google Scholar] [CrossRef]
- Miller, K.; Chinzei, K. Constitutive modelling of brain tissue: Experiment and theory. J. Biomech. 1997, 30, 1115–1121. [Google Scholar] [CrossRef]
- Mendis, K.K.; Stalnaker, R.L.; Advani, S.H. A constitutive relationship for large deformation finite element modeling of brain tissue. J. Biomech. Eng. 1995, 117, 279–285. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, B.R.; Medige, J. Shear properties of human brain tissue. J. Biomech. Eng. 1997, 119, 423–432. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.; Chinzei, K. Mechanical properties of brain tissue in tension. J. Biomech. 2002, 35, 483–490. [Google Scholar] [CrossRef] [Green Version]
- Franceschini, G.; Bigoni, D.; Regitnig, P.; Holzapfel, G.A. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. J. Mech. Phys. Solids 2006, 54, 2592–2620. [Google Scholar] [CrossRef]
- Goriely, A.; Geers, M.G.; Holzapfel, G.A.; Jayamohan, J.; Jérusalem, A.; Sivaloganathan, S.; Squier, W.; van Dommelen, J.A.; Waters, S.; Kuhl, E. Mechanics of the brain: Perspectives, challenges, and opportunities. Biomech. Model. Mechanobiol. 2015, 14, 931–965. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Budday, S.; Ovaert, T.C.; Holzapfel, G.A.; Steinmann, P.; Kuhl, E. Fifty Shades of Brain: A Review on the Mechanical Testing and Modeling of Brain Tissue. Arch. Comput. Methods Eng. 2019, 27, 1187–1230. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Sarntinoranont, M. Biphasic finite element model of solute transport for direct infusion into nervous tissue. Ann. Biomed. Eng. 2007, 35, 2145–2158. [Google Scholar] [CrossRef] [PubMed]
- Ehlers, W.; Wagner, A. Multi-component modelling of human brain tissue: A contribution to the constitutive and computational description of deformation, flow and diffusion processes with application to the invasive drug-delivery problem. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 861–879. [Google Scholar] [CrossRef] [PubMed]
- Vidotto, M.; Botnariuc, D.; De Momi, E.; Dini, D. A computational fluid dynamics approach to determine white matter permeability. Biomech. Model. Mechanobiol. 2019, 18, 1111–1122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tavner, A.C.; Roy, T.D.; Hor, K.W.; Majimbi, M.; Joldes, G.R.; Wittek, A.; Bunt, S.; Miller, K. On the appropriateness of modelling brain parenchyma as a biphasic continuum. J. Mech. Behav. Biomed. Mater. 2016, 61, 511–518. [Google Scholar] [CrossRef] [PubMed]
- Støverud, K.H.; Darcis, M.; Helmig, R.; Hassanizadeh, S.M. Modeling Concentration Distribution and Deformation During Convection-Enhanced Drug Delivery into Brain Tissue. Transp. Porous Media 2012, 92, 119–143. [Google Scholar] [CrossRef] [Green Version]
- Raghavan, R.; Brady, M. Predictive models for pressure-driven fluid infusions into brain parenchyma. Phys. Med. Biol. 2011, 56, 6179–6204. [Google Scholar] [CrossRef] [PubMed]
- Linninger, A.A.; Somayaji, M.R.; Erickson, T.; Guo, X.; Penn, R.D. Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue. J. Biomech. 2008, 41, 2176–2187. [Google Scholar] [CrossRef] [PubMed]
- Forte, A.E.; Gentleman, S.M.; Dini, D. On the characterization of the heterogeneous mechanical response of human brain tissue. Biomech. Model. Mechanobiol. 2017, 16, 907–920. [Google Scholar] [CrossRef] [Green Version]
- Budday, S.; Sommer, G.; Haybaeck, J.; Steinmann, P.; Holzapfel, G.A.; Kuhl, E. Rheological characterization of human brain tissue. Acta Biomater. 2017, 60, 315–329. [Google Scholar] [CrossRef] [PubMed]
- Budday, S.; Nay, R.; de Rooij, R.; Steinmann, P.; Wyrobek, T.; Ovaert, T.C.; Kuhl, E. Mechanical properties of gray and white matter brain tissue by indentation. J. Mech. Behav. Biomed. Mater. 2015, 46, 318–330. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Clarke, E.C.; Bilston, L.E. Rheological properties of the tissues of the central nervous system: A review. Med. Eng. Phys. 2008, 30, 1318–1337. [Google Scholar] [CrossRef]
- Feng, Y.; Okamoto, R.J.; Namani, R.; Genin, G.M.; Bayly, P.V. Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J. Mech. Behav. Biomed. Mater. 2013, 23, 117–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, Y.; Lee, C.H.; Sun, L.; Ji, S.; Zhao, X. Characterizing white matter tissue in large strain via asymmetric indentation and inverse finite element modeling. J. Mech. Behav. Biomed. Mater. 2017, 65, 490–501. [Google Scholar] [CrossRef] [Green Version]
- Greiner, A.; Reiter, N.; Paulsen, F.; Holzapfel, G.A.; Steinmann, P.; Comellas, E.; Budday, S. Poro-Viscoelastic Effects During Biomechanical Testing of Human Brain Tissue. Front. Mech. Eng. 2021, 7, 708350. [Google Scholar] [CrossRef]
- Vunjak-Novakovic, G.; Martin, I.; Obradovic, B.; Treppo, S.; Grodzinsky, A.J.; Langer, R.; Freed, L. Bioreactor Cultivation Conditions Modulate the Composition and Mechanical Properties of Tissue-Engineered Cartilage. J. Orthop. Res. 1999, 17, 130–138. [Google Scholar] [CrossRef]
- Gu, W.Y.; Yao, H. Effects of hydration and fixed charge density on fluid transport in charged hydrated soft tissues. Ann. Biomed. Eng. 2003, 31, 1162–1170. [Google Scholar] [CrossRef] [PubMed]
- Heneghan, P.; Riches, P.E. Determination of the strain-dependent hydraulic permeability of the compressed bovine nucleus pulposus. J. Biomech. 2008, 41, 903–906. [Google Scholar] [CrossRef] [PubMed]
- Reynaud, B.; Quinn, T.M. Anisotropic hydraulic permeability in compressed articular cartilage. J. Biomech. 2006, 39, 131–137. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Luck, J.; Dewhirst, M.W.; Yuan, F. Interstitial hydraulic conductivity in a fibrosarcoma. Am. J. Physiol.-Heart Circ. Physiol. 2000, 279, 2726–2734. [Google Scholar] [CrossRef] [PubMed]
- Boucher, Y.; Brekken, C.; Netti, P.A.; Baxter, L.T.; Jain, R.K. Intratumoral infusion of fluid: Estimation of hydraulic conductivity and implications for the delivery of therapeutic agents. Br. J. Cancer 1998, 78, 1442–1448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milosevic, M.; Lunt, S.J.; Leung, E.; Skliarenko, J.; Shaw, P.; Fyles, A.; Hill, R.P. Interstitial permeability and elasticity in human cervix cancer. Microvasc. Res. 2008, 75, 381–390. [Google Scholar] [CrossRef] [PubMed]
- Walhovd, K.B.; Johansen-Berg, H.; Káradóttir, R.T. Unraveling the secrets of white matter-Bridging the gap between cellular, animal and human imaging studies. Neuroscience 2014, 276, 2–13. [Google Scholar] [CrossRef] [Green Version]
- Pieri, V.; Trovatelli, M.; Cadioli, M.; Zani, D.D.; Brizzola, S.; Ravasio, G.; Acocella, F.; Giancamillo, M.D.; Castellano, A. In vivo Diffusion Tensor Magnetic Resonance Tractography of the Sheep Brain: An Atlas of the Ovine White Matter Fiber Bundles. Front. Vet. Sci. 2019, 6, 345. [Google Scholar] [CrossRef]
- Zhan, W.; Rodriguez y Baena, F.; Dini, D. Effect of tissue permeability and drug diffusion anisotropy on convection-enhanced delivery. Drug Deliv. 2019, 26, 773–781. [Google Scholar] [CrossRef] [Green Version]
- Bernardini, A.; Trovatelli, M.; Kłosowski, M.M.; Pederzani, M.; Zani, D.D.; Brizzola, S.; Porter, A.; Rodriguez y Baena, F.; Dini, D. Imaging and reconstruction of the cytoarchitecture of axonal fibres: Enabling biomedical engineering studies involving brain microstructure. Res. Sq. 2021, 1–22. [Google Scholar] [CrossRef]
- Kroppenstedt, S.N.; Thomale, U.W.; Griebenow, M.; Sakowitz, O.W.; Schaser, K.D.; Mayr, P.S.; Unterberg, A.W.; Stover, J.F. Effects of early and late intravenous norepinephrine infusion on cerebral perfusion, microcirculation, brain-tissue oxygenation, and edema formation in brain-injured rats. Crit. Care Med. 2003, 31, 2211–2221. [Google Scholar] [CrossRef]
- Vardakis, J.C.; Chou, D.; Tully, B.J.; Hung, C.C.; Lee, T.H.; Tsui, P.H.; Ventikos, Y. Investigating cerebral oedema using poroelasticity. Med. Eng. Phys. 2016, 38, 48–57. [Google Scholar] [CrossRef]
- Jamal, A.; Bernardini, A.; Dini, D. Microscale characterisation of the time-dependent mechanical behaviour of brain white matter. J. Mech. Behav. Biomed. Mater. 2022, 125, 104917. [Google Scholar] [CrossRef] [PubMed]
- Hosseini-Farid, M.; Ramzanpour, M.; McLean, J.; Ziejewski, M.; Karami, G. A poro-hyper-viscoelastic rate-dependent constitutive modeling for the analysis of brain tissues. J. Mech. Behav. Biomed. Mater. 2020, 102, 103475. [Google Scholar] [CrossRef] [PubMed]
- Mow, V.C.; Kuei, S.C.; Lai, W.M.; Armstrong, C.G. Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. J. Biomech. Eng. 1980, 102, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Lai, W.M.; Mow, V.C.; Roth, V. Effects of Nonlinear Strain-Dependent Permeability and Rate of Compression on the Stress Behavior of Articular Cartilage. J. Biomech. Eng. 1981, 103, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Holmes, M.H. Finite Deformation of Soft Tissue: Analysis of a Mixture Model in Uni-Axial Compression. J. Biomech. Eng. 1986, 108, 372–381. [Google Scholar] [CrossRef]
- Mak, A.F. The apparent viscoelastic behavior of articular cartilage–the contributions from the intrinsic matrix viscoelasticity and interstitial fluid flows. J. Biomech. Eng. 1986, 108, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Mak, A.F. Unconfined compression of hydrated viscoelastic tissues: A biphasic poroviscoelastic analysis. Biorheology 1986, 23, 371–383. [Google Scholar] [CrossRef]
- Wang, R.; Sarntinoranont, M. Biphasic analysis of rat brain slices under creep indentation shows nonlinear tension-compression behavior. J. Mech. Behav. Biomed. Mater. 2019, 89, 1–8. [Google Scholar] [CrossRef]
- Suh, J.K.; DiSilvestro, M.R. Biphasic Poroviscoelastic Behavior of Hydrated Biological Soft Tissue. J. Appl. Mech. 1999, 66, 528–535. [Google Scholar] [CrossRef]
- Cheng, S.; Bilston, L.E. Unconfined compression of white matter. J. Biomech. 2007, 40, 117–124. [Google Scholar] [CrossRef]
- Mehrabian, A.; Abousleiman, Y.N.; Mapstone, T.B.; El-Amm, C.A. Dual-porosity poroviscoelasticity and quantitative hydromechanical characterization of the brain tissue with experimental hydrocephalus data. J. Theor. Biol. 2015, 384, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Mehrabian, A.; Abousleiman, Y. General solutions to poroviscoelastic model of hydrocephalic human brain tissue. J. Theor. Biol. 2011, 291, 105–118. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, H.; Nauman, E.; Shi, R. Contribution of cytoskeletal elements to the axonal mechanical properties. J. Biol. Eng. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wells, R.G. The role of matrix stiffness in regulating cell behavior. Hepatology 2008, 47, 1394–1400. [Google Scholar] [CrossRef] [PubMed]
- Yuan, T.; Zhan, W.; Jamal, A.; Dini, D. On the Microstructurally-Driven Heterogenous Response of Brain White Matter to Drug Infusion Pressure. Biomech. Model. Mechanobiol. 2022; under review. [Google Scholar]
- Novak, U.; Kaye, A.H. Extracellular matrix and the brain: Components and function. J. Clin. Neurosci. 2000, 7, 280–290. [Google Scholar] [CrossRef] [PubMed]
- Bandtlow, C.E.; Zimmermann, D.R. Proteoglycans in the Developing Brain: New Conceptual Insights for Old Proteins. Physiol. Rev. 2000, 80, 1267–1290. [Google Scholar] [CrossRef]
- Nicholson, C.; Syková, E. Extracellular space structure revealed by diffusion analysis. Trends Neurosci. 1998, 21, 207–215. [Google Scholar] [CrossRef]
- Zamecnik, J. The extracellular space and matrix of gliomas. Acta Neuropathol. 2005, 110, 435–442. [Google Scholar] [CrossRef] [PubMed]
- Lau, L.W.; Cua, R.; Keough, M.B.; Haylock-Jacobs, S.; Yong, V.W. Pathophysiology of the brain extracellular matrix: A new target for remyelination. Nat. Rev. Neurosci. 2013, 14, 722–729. [Google Scholar] [CrossRef]
- Engin, A.B.; Nikitovic, D.; Neagu, M.; Henrich-Noack, P.; Docea, A.O.; Shtilman, M.I.; Golokhvast, K.; Tsatsakis, A.M. Mechanistic understanding of nanoparticles’ interactions with extracellular matrix: The cell and immune system. Part. Fibre Toxicol. 2017, 14, 22. [Google Scholar] [CrossRef] [PubMed]
- Stylianopoulos, T.; Poh, M.Z.; Insin, N.; Bawendi, M.G.; Fukumura, D.; Munn, L.L.; Jain, R.K. Diffusion of Particles in the Extracellular Matrix: The Effect of Repulsive Electrostatic Interactions. Biophys. J. 2010, 99, 1342–1349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Asadi, A.; Monroe, M.R.; Douglas, E.P. pH effects on collagen fibrillogenesis in vitro: Electrostatic interactions and phosphate binding. Mater. Sci. Eng. C 2009, 29, 1643–1649. [Google Scholar] [CrossRef]
- Mertz, E.L.; Leikin, S. Interactions of Inorganic Phosphate and Sulfate Anions with Collagen. Biochemistry 2004, 43, 14901–14912. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, G.; Deen, W.M. Effects of Charge on Osmotic Reflection Coefficients of Macromolecules in Fibrous Membranes. Biophys. J. 2009, 97, 1595–1605. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thorne, R.G.; Lakkaraju, A.; Rodriguez-Boulan, E.; Nicholson, C. In vivo diffusion of lactoferrin in brain extracellular space is regulated by interactions with heparan sulfate. Proc. Natl. Acad. Sci. USA 2008, 105, 8416–8421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arends, F.; Baumgärtel, R.; Lieleg, O. Ion-Specific Effects Modulate the Diffusive Mobility of Colloids in an Extracellular Matrix Gel. Langmuir 2013, 29, 15965–15973. [Google Scholar] [CrossRef] [PubMed]
- Braunger, J.A.; Björnmalm, M.; Isles, N.A.; Cui, J.; Henderson, T.M.A.; O’Connor, A.J.; Caruso, F. Interactions between circulating nanoengineered polymer particles and extracellular matrix components in vitro. Biomater. Sci. 2017, 5, 267–273. [Google Scholar] [CrossRef] [Green Version]
- Winter, R.; Jeworrek, C. Effect of pressure on membranes. Soft Matter 2009, 5, 3157. [Google Scholar] [CrossRef]
- Augustine, R.; Hasan, A.; Primavera, R.; Wilson, R.J.; Thakor, A.S.; Kevadiya, B.D. Cellular uptake and retention of nanoparticles: Insights on particle properties and interaction with cellular components. Mater. Today Commun. 2020, 25, 101692. [Google Scholar] [CrossRef]
- Mohammad-Beigi, H.; Hayashi, Y.; Zeuthen, C.M.; Eskandari, H.; Scavenius, C.; Juul-Madsen, K.; Vorup-Jensen, T.; Enghild, J.J.; Sutherland, D.S. Mapping and identification of soft corona proteins at nanoparticles and their impact on cellular association. Nat. Commun. 2020, 11, 4535. [Google Scholar] [CrossRef] [PubMed]
- Price, E.; Gesquiere, A.J. Author Correction: An in vitro assay and artificial intelligence approach to determine rate constants of nanomaterial-cell interactions. Sci. Rep. 2019, 9, 19906. [Google Scholar] [CrossRef] [PubMed]
- Jang, Y.H.; Jin, X.; Shankar, P.; Lee, J.H.; Jo, K.; Lim, K.I. Molecular-level interactions between engineered materials and cells. Int. J. Mol. Sci. 2019, 20, 4142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, P.H.; Kumar, S.; Schaffer, D.V. Novel biomaterials to study neural stem cell mechanobiology and improve cell-replacement therapies. Curr. Opin. Biomed. Eng. 2017, 4, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Muhamed, I.; Chowdhury, F.; Maruthamuthu, V. Biophysical tools to study cellular mechanotransduction. Bioengineering 2017, 4, 12. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, E. The role of surface charge in cellular uptake and cytotoxicity of medical nanoparticles. Int. J. Nanomed. 2012, 7, 5577. [Google Scholar] [CrossRef] [Green Version]
- Salatin, S.; Maleki Dizaj, S.; Yari Khosroushahi, A. Effect of the surface modification, size, and shape on cellular uptake of nanoparticles. Cell Biol. Int. 2015, 39, 881–890. [Google Scholar] [CrossRef]
- Villanueva-Flores, F.; Castro-Lugo, A.; Ramírez, O.T.; Palomares, L.A. Understanding cellular interactions with nanomaterials: Towards a rational design of medical nanodevices. Nanotechnology 2020, 31, 132002. [Google Scholar] [CrossRef]
- Yuan, T.; Gao, L.; Zhan, W.; Dini, D. Effect of Particle Size and Surface Charge on Nanoparticles Diffusion in the Brain White Matter. Pharm. Res. 2022; accepted. [Google Scholar] [CrossRef]
- Kalyanasundaram, S.; Calhoun, V.D.; Leong, K.W. A finite element model for predicting the distribution of drugs delivered intracranially to the brain. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1997, 273, R1810–R1821. [Google Scholar] [CrossRef]
- Linninger, A.A.; Somayaji, M.R.; Mekarski, M.; Zhang, L. Prediction of convection-enhanced drug delivery to the human brain. J. Theor. Biol. 2008, 250, 125–138. [Google Scholar] [CrossRef]
- Somayaji, M.R.; Xenos, M.; Zhang, L.; Mekarski, M.; Linninger, A.A. Systematic design of drug delivery therapies. Comput. Chem. Eng. 2008, 32, 89–98. [Google Scholar] [CrossRef]
- Kim, J.H.; Astary, G.W.; Chen, X.; Mareci, T.H.; Sarntinoranont, M. Voxelized Model of Interstitial Transport in the Rat Spinal Cord Following Direct Infusion Into White Matter. J. Biomech. Eng. 2009, 131, 071007. [Google Scholar] [CrossRef]
- Kim, J.H.; Mareci, T.H.; Sarntinoranont, M. A voxelized model of direct infusion into the corpus callosum and hippocampus of the rat brain: Model development and parameter analysis. Med. Biol. Eng. Comput. 2010, 48, 203–214. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.H.; Astary, G.W.; Kantorovich, S.; Mareci, T.H.; Carney, P.R.; Sarntinoranont, M. Voxelized Computational Model for Convection-Enhanced Delivery in the Rat Ventral Hippocampus: Comparison with In Vivo MR Experimental Studies. Ann. Biomed. Eng. 2012, 40, 2043–2058. [Google Scholar] [CrossRef] [Green Version]
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Vidotto, M.; Pederzani, M.; Castellano, A.; Pieri, V.; Falini, A.; Dini, D.; De Momi, E. Integrating Diffusion Tensor Imaging and Neurite Orientation Dispersion and Density Imaging to Improve the Predictive Capabilities of CED Models. Ann. Biomed. Eng. 2021, 49, 689–702. [Google Scholar] [CrossRef]
- Bernal, R.; Pullarkat, P.A.; Melo, F. Mechanical Properties of Axons. Phys. Rev. Lett. 2007, 99, 018301. [Google Scholar] [CrossRef] [Green Version]
- Javid, S.; Rezaei, A.; Karami, G. A micromechanical procedure for viscoelastic characterization of the axons and ECM of the brainstem. J. Mech. Behav. Biomed. Mater. 2014, 30, 290–299. [Google Scholar] [CrossRef]
- Chen, Z.-J.; Broaddus, W.; Viswanathan, R.; Raghavan, R.; Gillies, G. Intraparenchymal drug delivery via positive-pressure infusion: Experimental and modeling studies of poroelasticity in brain phantom gels. IEEE Trans. Biomed. Eng. 2002, 49, 85–96. [Google Scholar] [CrossRef]
- García, J.J.; Smith, J.H. A Biphasic Hyperelastic Model for the Analysis of Fluid and Mass Transport in Brain Tissue. Ann. Biomed. Eng. 2009, 37, 375–386. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.H.; García, J.J. A nonlinear biphasic model of flow-controlled infusion in brain: Fluid transport and tissue deformation analyses. J. Biomech. 2009, 42, 2017–2025. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.H.; Jaime García, J. A nonlinear biphasic model of flow-controlled infusions in brain: Mass transport analyses. J. Biomech. 2011, 44, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Ivanchenko, O.; Sindhwani, N.; Linninger, A. Experimental Techniques for Studying Poroelasticity in Brain Phantom Gels Under High Flow Microinfusion. J. Biomech. Eng. 2010, 132, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lueshen, E.; Tangen, K.; Mehta, A.I.; Linninger, A. Backflow-free catheters for efficient and safe convection-enhanced delivery of therapeutics. Med. Eng. Phys. 2017, 45, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Orozco, G.A.; Smith, J.H.; García, J.J. Three-dimensional nonlinear finite element model to estimate backflow during flow-controlled infusions into the brain. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2020, 234, 1018–1028. [Google Scholar] [CrossRef]
- García, J.J.; Molano, A.B.; Smith, J.H. Description and Validation of a Finite Element Model of Backflow During Infusion Into a Brain Tissue Phantom. J. Comput. Nonlinear Dyn. 2013, 8, 011017. [Google Scholar] [CrossRef]
- Stine, C.A.; Munson, J.M. Convection-Enhanced Delivery: Connection to and Impact of Interstitial Fluid Flow. Front. Oncol. 2019, 9, 966. [Google Scholar] [CrossRef] [Green Version]
- Linninger, A.; Tsakiris, C.; Zhu, D.; Xenos, M.; Roycewicz, P.; Danziger, Z.; Penn, R. Pulsatile Cerebrospinal Fluid Dynamics in the Human Brain. IEEE Trans. Biomed. Eng. 2005, 52, 557–565. [Google Scholar] [CrossRef]
- Linninger, A.A.; Xenos, M.; Zhu, D.C.; Somayaji, M.R.; Kondapalli, S.; Penn, R.D. Cerebrospinal Fluid Flow in the Normal and Hydrocephalic Human Brain. IEEE Trans. Biomed. Eng. 2007, 54, 291–302. [Google Scholar] [CrossRef]
- Smith, J.H.; Starkweather, K.A.; García, J.J. Implications of Transvascular Fluid Exchange in Nonlinear, Biphasic Analyses of Flow-Controlled Infusion in Brain. Bull. Math. Biol. 2012, 74, 881–907. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A.; Ehlers, W. Continuum-Mechanical Analysis of Human Brain Tissue. PAMM 2010, 10, 99–100. [Google Scholar] [CrossRef]
- Wagner, A.; Ehlers, W. Computational modelling of drug infusion into the anisotropic white-matter tracts of the human brain. PAMM 2011, 11, 133–134. [Google Scholar] [CrossRef]
- Magdoom, K.N.; Pishko, G.L.; Rice, L.; Pampo, C.; Siemann, D.W.; Sarntinoranont, M. MRI-Based Computational Model of Heterogeneous Tracer Transport following Local Infusion into a Mouse Hind Limb Tumor. PLoS ONE 2014, 9, e89594. [Google Scholar] [CrossRef] [Green Version]
- Zhan, W.; Arifin, D.Y.; Lee, T.K.; Wang, C.H. Mathematical Modelling of Convection Enhanced Delivery of Carmustine and Paclitaxel for Brain Tumour Therapy. Pharm. Res. 2017, 34, 860–873. [Google Scholar] [CrossRef]
- Zhan, W.; Wang, C.H. Convection enhanced delivery of liposome encapsulated doxorubicin for brain tumour therapy. J. Control Release 2018, 285, 212–229. [Google Scholar] [CrossRef] [PubMed]
- Zhan, W.; Wang, C.H. Convection enhanced delivery of chemotherapeutic drugs into brain tumour. J. Control Release 2018, 271, 74–87. [Google Scholar] [CrossRef]
- Zhan, W. Convection enhanced delivery of anti-angiogenic and cytotoxic agents in combination therapy against brain tumour. Eur. J. Pharm. Sci. 2020, 141, 105094. [Google Scholar] [CrossRef]
- Kamali-Zare, P.; Nicholson, C. Brain extracellular space: Geometry, matrix and physiological importance. Basic Clin. Neurosci. 2013, 4, 4–8. [Google Scholar]
- Nicholson, C.; Hrabětová, S. Brain Extracellular Space: The Final Frontier of Neuroscience. Biophys. J. 2017, 113, 2133–2142. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, C.; Kamali-Zare, P.; Tao, L. Brain extracellular space as a diffusion barrier. Comput. Vis. Sci. 2011, 14, 309–325. [Google Scholar] [CrossRef] [Green Version]
- Thorne, R.G.; Nicholson, C. In vivo diffusion analysis with quantum dots and dextrans predicts the width of brain extracellular space. Proc. Natl. Acad. Sci. USA 2006, 103, 5567–5572. [Google Scholar] [CrossRef] [Green Version]
- Syková, E.; Nicholson, C. Diffusion in Brain Extracellular Space. Physiol. Rev. 2008, 88, 1277–1340. [Google Scholar] [CrossRef] [Green Version]
- Tao, L.; Nicholson, C. Maximum geometrical hindrance to diffusion in brain extracellular space surrounding uniformly spaced convex cells. J. Theor. Biol. 2004, 229, 59–68. [Google Scholar] [CrossRef]
- Nicholson, C.; Kamali-Zare, P. Reduction of Dimensionality in Monte Carlo Simulation of Diffusion in Extracellular Space Surrounding Cubic Cells. Neurochem. Res. 2020, 45, 42–52. [Google Scholar] [CrossRef]
- Fieremans, E.; De Deene, Y.; Delputte, S.; Özdemir, M.S.; D’Asseler, Y.; Vlassenbroeck, J.; Deblaere, K.; Achten, E.; Lemahieu, I. Simulation and experimental verification of the diffusion in an anisotropic fiber phantom. J. Magn. Reson. 2008, 190, 189–199. [Google Scholar] [CrossRef]
- Nilsson, M.; Lätt, J.; Ståhlberg, F.; van Westen, D.; Hagslätt, H. The importance of axonal undulation in diffusion MR measurements: A Monte Carlo simulation study. NMR Biomed. 2012, 25, 795–805. [Google Scholar] [CrossRef]
- Su, D.; Ma, R.; Salloum, M.; Zhu, L. Multi-scale study of nanoparticle transport and deposition in tissues during an injection process. Med. Biol. Eng. Comput. 2010, 48, 853–863. [Google Scholar] [CrossRef]
- Su, D.; Ma, R.; Zhu, L. Numerical study of nanofluid infusion in deformable tissues for hyperthermia cancer treatments. Med. Biol. Eng. Comput. 2011, 49, 1233–1240. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular Dynamics Simulation for All. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef] [Green Version]
- Dror, R.O.; Jensen, M.Ø.; Borhani, D.W.; Shaw, D.E. Exploring atomic resolution physiology on a femtosecond to millisecond timescale using molecular dynamics simulations. J. Gen. Physiol. 2010, 135, 555–562. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett. (EPL) 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Dai, X.; Ding, H.; Yin, Q.; Wan, G.; Shi, X.; Qiao, Y. Dissipative particle dynamics study on self-assembled platycodin structures: The potential biocarriers for drug delivery. J. Mol. Graph. Model. 2015, 57, 20–26. [Google Scholar] [CrossRef]
- Sweetman, B.; Xenos, M.; Zitella, L.; Linninger, A.A. Three-dimensional computational prediction of cerebrospinal fluid flow in the human brain. Comput. Biol. Med. 2011, 41, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Messaritaki, E.; Rudrapatna, S.U.; Parker, G.D.; Gray, W.P.; Jones, D.K. Improving the Predictions of Computational Models of Convection-Enhanced Drug Delivery by Accounting for Diffusion Non-gaussianity. Front. Neurol. 2018, 9, 1092. [Google Scholar] [CrossRef]
- Brady, M.; Raghavan, R.; Sampson, J. Determinants of Intraparenchymal Infusion Distributions: Modeling and Analyses of Human Glioblastoma Trials. Pharmaceutics 2020, 12, 895. [Google Scholar] [CrossRef]
- Bander, E.D.; Tizi, K.; Wembacher-Schroeder, E.; Thomson, R.; Donzelli, M.; Vasconcellos, E.; Souweidane, M.M. Deformational changes after convection-enhanced delivery in the pediatric brainstem. Neurosurg. Focus 2020, 48, E3. [Google Scholar] [CrossRef] [Green Version]
- Cheng, A.D. Material coefficients of anisotropic poroelasticity. Int. J. Rock Mech. Min. Sci. 1997, 34, 199–205. [Google Scholar] [CrossRef]
- Multiphysics, C. The COMSOL Multiphysics Reference Manual. 2015. Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 9 March 2022).
- Hrabetova, S.; Cognet, L.; Rusakov, D.A.; Nägerl, U.V. Unveiling the extracellular space of the brain: From super-resolved microstructure to in vivo function. J. Neurosci. 2018, 38, 9355–9363. [Google Scholar] [CrossRef] [Green Version]
- Faria, C.; Erlhagen, W.; De Momi, E.; Ferrigno, G.; Bicho, E. Review of Robotic Technology for Stereotactic Neurosurgery. IEEE Rev. Biomed. Eng. 2015, 8, 125–137. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.A.; Jivraj, J.; Wong, R.; Yang, V. 30 Years of Neurosurgical Robots: Review and Trends for Manipulators and Associated Navigational Systems. Ann. Biomed. Eng. 2016, 44, 836–846. [Google Scholar] [CrossRef]
- Fomenko, A.; Serletis, D. Robotic Stereotaxy in Cranial Neurosurgery: A Qualitative Systematic Review. Neurosurgery 2017, 83, 642–650. [Google Scholar] [CrossRef]
- Wang, M.Y.; Goto, T.; Tessitore, E.; Veeravagu, A. Introduction. Robotics in neurosurgery. Neurosurg. Focus FOC 2017, 42, E1. [Google Scholar] [CrossRef]
- Kwoh, Y.S.; Hou, J.; Jonckheere, E.A.; Hayati, S. A robot with improved absolute positioning accuracy for CT guided stereotactic brain surgery. IEEE Trans. Biomed. Eng. 1988, 35, 153–160. [Google Scholar] [CrossRef]
- Drake, J.M.; Joy, M.; Goldenberg, A.; Kreindler, D. Computer- and robot-assisted resection of thalamic astrocytomas in children. Neurosurgery 1991, 29, 27–33. [Google Scholar] [CrossRef]
- Li, Q.H.; Zamorano, L.; Pandya, A.; Perez, R.; Gong, J.; Diaz, F. The application accuracy of the NeuroMate robot—A quantitative comparison with frameless and frame-based surgical localization systems. Comput. Aided Surg. 2002, 7, 90–98. [Google Scholar] [CrossRef]
- Lewis, O.; Woolley, M.; Johnson, D.; Rosser, A.; Barua, N.U.; Bienemann, A.S.; Gill, S.S.; Evans, S. Chronic, intermittent convection-enhanced delivery devices. J. Neurosci. Methods 2016, 259, 47–56. [Google Scholar] [CrossRef] [Green Version]
- van de Berg, N.J.; van Gerwen, D.J.; Dankelman, J.; van den Dobbelsteen, J.J. Design Choices in Needle Steering—A Review. IEEE/ASME Trans. Mechatron. 2015, 20, 2172–2183. [Google Scholar] [CrossRef]
- EDEN2020. Enhanced Delivery Ecosystem for Neurosurgery in 2020. Available online: https://www.eden2020.eu. (accessed on 29 October 2021).
- Blumenfeld, P.; Hata, N.; DiMaio, S.; Zou, K.; Haker, S.; Fichtinger, G.; Tempany, C.M. Transperineal prostate biopsy under magnetic resonance image guidance: A needle placement accuracy study. J. Magn. Reson. Imaging Off. J. Int. Soc. Magn. Reson. Med. 2007, 26, 688–694. [Google Scholar] [CrossRef]
- Schouten, M.G.; Bomers, J.G.; Yakar, D.; Huisman, H.; Rothgang, E.; Bosboom, D.; Scheenen, T.W.; Misra, S.; Fütterer, J.J. Evaluation of a robotic technique for transrectal MRI-guided prostate biopsies. Eur. Radiol. 2012, 22, 476–483. [Google Scholar] [CrossRef] [Green Version]
- Patil, S.; Burgner, J.; Webster, R.J.; Alterovitz, R. Needle Steering in 3-D Via Rapid Replanning. IEEE Trans. Robot. 2014, 30, 853–864. [Google Scholar] [CrossRef] [PubMed]
- Essert, C.; Haegelen, C.; Lalys, F.; Abadie, A.; Jannin, P. Automatic computation of electrode trajectories for deep brain stimulation: A hybrid symbolic and numerical approach. Int. J. Comput. Assist. Radiol. Surg. 2012, 7, 517–532. [Google Scholar] [CrossRef]
- Segato, A.; Sestini, L.; Castellano, A.; De Momi, E. GA3C Reinforcement Learning for Surgical Steerable Catheter Path Planning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2429–2435. [Google Scholar] [CrossRef]
- Favaro, A.; Segato, A.; Muretti, F.; Momi, E.D. An Evolutionary-Optimized Surgical Path Planner for a Programmable Bevel-Tip Needle. IEEE Trans. Robot. 2021, 37, 1039–1050. [Google Scholar] [CrossRef]
- Likhachev, M.; Ferguson, D.; Gordon, G.; Stentz, A.; Thrun, S. Anytime Dynamic A*: An Anytime, Replanning Algorithm. In Proceedings of the Fifteenth International Conference on International Conference on Automated Planning and Scheduling (ICAPS’05), Monterey, CA, USA, 5–10 July 2005; pp. 262–271. [Google Scholar]
- Leibrandt, K.; Bergeles, C.; Yang, G.Z. Concentric Tube Robots: Rapid, Stable Path-Planning and Guidance for Surgical Use. IEEE Robot. Autom. Mag. 2017, 24, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Patil, S.; Alterovitz, R. Interactive motion planning for steerable needles in 3D environments with obstacles. In Proceedings of the 2010 3rd IEEE RAS EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 893–899. [Google Scholar] [CrossRef] [Green Version]
- Fauser, J.; Sakas, G.; Mukhopadhyay, A. Planning nonlinear access paths for temporal bone surgery. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 637–646. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, K.; Sukkarieh, S. 3D smooth path planning for a UAV in cluttered natural environments. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 794–800. [Google Scholar] [CrossRef]
- Favaro, A.; Cerri, L.; Galvan, S.; Baena, F.R.Y.; De Momi, E. Automatic Optimized 3D Path Planner for Steerable Catheters with Heuristic Search and Uncertainty Tolerance. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 9–16. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Garriga-Casanovas, A.; Secoli, R.; Rodriguez y Baena, F. Fast and Adaptive Fractal Tree-Based Path Planning for Programmable Bevel Tip Steerable Needles. IEEE Robot. Autom. Lett. 2016, 1, 601–608. [Google Scholar] [CrossRef] [Green Version]
- Pinzi, M.; Galvan, S.; Rodriguez y Baena, F. The Adaptive Hermite Fractal Tree (AHFT): A novel surgical 3D path planning approach with curvature and heading constraints. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 659–670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, M.; Salzman, O.; Alterovitz, R. Toward Certifiable Motion Planning for Medical Steerable Needles. Proceedings of Robotics: Science and Systems. arXiv 2021, arXiv:2107.04939. [Google Scholar]
- Barraquand, J.; Latombe, J.C. Nonholonomic multibody mobile robots: Controllability and motion planning in the presence of obstacles. In Proceedings of the Proceedings. 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 3, pp. 2328–2335. [Google Scholar] [CrossRef]
- Lindemann, S.; LaValle, S. Multiresolution approach for motion planning under differential constraints. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 139–144. [Google Scholar] [CrossRef] [Green Version]
- Pinzi, M.; Watts, T.; Secoli, R.; Galvan, S.; Baena, F.R.y. Path Replanning for Orientation-Constrained Needle Steering. IEEE Trans. Biomed. Eng. 2021, 68, 1459–1466. [Google Scholar] [CrossRef]
- Quinlan, S.; Khatib, O. Elastic bands: Connecting path planning and control. In Proceedings of the [1993] Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; Volume 2, pp. 802–807. [Google Scholar] [CrossRef]
- Lee, C.T.; Tsai, C.C. 3D Collision-Free Trajectory Generation Using Elastic Band Technique for an Autonomous Helicopter. In Next Wave in Robotics; Li, T.H.S., Tu, K.Y., Tsai, C.C., Hsu, C.C., Tseng, C.C., Vadakkepat, P., Baltes, J., Anderson, J., Wong, C.C., Jesse, N., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 34–41. [Google Scholar]
- Zhu, Z.; Schmerling, E.; Pavone, M. A convex optimization approach to smooth trajectories for motion planning with car-like robots. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 835–842. [Google Scholar] [CrossRef] [Green Version]
- Brainlab AG. Cranial Navigation Application. Available online: https://www.brainlab.com/surgery-products/overview-neurosurgery-products/cranial-navigation/ (accessed on 29 October 2021).
- Medtronic plc.Stealth Navigation for Neurosurgery. Available online: https://www.medtronic.com/us-en/healthcare-professionals/products/neurological/surgical-navigation-systems.html (accessed on 29 October 2021).
- Renishaw plc.Neuroinspire. Available online: https://www.renishaw.com/en/neuroinspire-neurosurgical-planning-software–8244 (accessed on 29 October 2021).
- Chittiboina, P.; Heiss, J.D.; Lonser, R.R. Accuracy of direct magnetic resonance imaging-guided placement of drug infusion cannulae. J. Neurosurg. 2015, 122, 1173–1179. [Google Scholar] [CrossRef]
- Chen, Y.; Godage, I.S.; Sengupta, S.; Liu, C.L.; Weaver, K.D.; Barth, E.J. MR-conditional steerable needle robot for intracerebral hemorrhage removal. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Patel, N.A.; van Katwijk, T.; Li, G.; Moreira, P.; Shang, W.; Misra, S.; Fischer, G.S. Closed-loop asymmetric-tip needle steering under continuous intraoperative MRI guidance. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015; pp. 4869–4874. [Google Scholar] [CrossRef]
- Matheson, E.; Rodriguez y Baena, F. Biologically Inspired Surgical Needle Steering: Technology and Application of the Programmable Bevel-Tip Needle. Biomimetics 2020, 5, 68. [Google Scholar] [CrossRef]
- Boviatsis, E.J.; Kouyialis, A.T.; Stranjalis, G.; Korfias, S.; Sakas, D.E. CT-guided stereotactic aspiration of brain abscesses. Neurosurg. Rev. 2003, 26, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharji, P.; Moore, W. Application of real-time 3D navigation system in CT-guided percutaneous interventional procedures: A feasibility study. Radiol. Res. Pract. 2017, 2017, 3151694. [Google Scholar] [CrossRef] [PubMed]
- Lo Presti, D.; Massaroni, C.; Jorge Leitão, C.S.; De Fátima Domingues, M.; Sypabekova, M.; Barrera, D.; Floris, I.; Massari, L.; Oddo, C.M.; Sales, S.; et al. Fiber Bragg Gratings for Medical Applications and Future Challenges: A Review. IEEE Access 2020, 8, 156863–156888. [Google Scholar] [CrossRef]
- Chevrie, J.; Shahriari, N.; Babel, M.; Krupa, A.; Misra, S. Flexible Needle Steering in Moving Biological Tissue With Motion Compensation Using Ultrasound and Force Feedback. IEEE Robot. Autom. Lett. 2018, 3, 2338–2345. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.; Denasi, A.; Barrera, D.; Madrigal, J.; Sales, S.; Misra, S. Multi-Core Optical Fibers With Bragg Gratings as Shape Sensor for Flexible Medical Instruments. IEEE Sens. J. 2019, 19, 5878–5884. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.; Donder, A.; Galvan, S.; Baena, F.R.y.; Misra, S. Pose Measurement of Flexible Medical Instruments Using Fiber Bragg Gratings in Multi-Core Fiber. IEEE Sens. J. 2020, 20, 10955–10962. [Google Scholar] [CrossRef]
- Brainlab AG. Intraoperative Ultrasound. Available online: https://www.brainlab.com/surgery-products/overview-neurosurgery-products/intraoperative-ultrasound/ (accessed on 9 March 2022).
- Scholten, H.; Pourtaherian, A.; Mihajlovic, N.; Korsten, H.; A. Bouwman, R. Improving needle tip identification during ultrasound-guided procedures in anaesthetic practice. Anaesthesia 2017, 72, 889–904. [Google Scholar] [CrossRef] [PubMed]
- Denasi, A.; Khan, F.; Boskma, K.J.; Kaya, M.; Hennersperger, C.; Göbl, R.; Tirindelli, M.; Navab, N.; Misra, S. An Observer-Based Fusion Method Using Multicore Optical Shape Sensors and Ultrasound Images for Magnetically-Actuated Catheters. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 50–57. [Google Scholar] [CrossRef] [Green Version]
- Gerard, I.J.; Kersten-Oertel, M.; Petrecca, K.; Sirhan, D.; Hall, J.A.; Collins, D.L. Brain shift in neuronavigation of brain tumors: A review. Med. Image Anal. 2017, 35, 403–420. [Google Scholar] [CrossRef] [PubMed]
- Fuerst, B.; Wein, W.; Müller, M.; Navab, N. Automatic ultrasound–MRI registration for neurosurgery using the 2D and 3D LC2 Metric. Med. Image Anal. 2014, 18, 1312–1319. [Google Scholar] [CrossRef] [PubMed]
- Drobny, D.; Ranzini, M.; Ourselin, S.; Vercauteren, T.; Modat, M. Landmark-Based Evaluation of a Block-Matching Registration Framework on the RESECT Pre- and Intra-operative Brain Image Data Set. In Large-Scale Annotation of Biomedical Data and Expert Label Synthesis and Hardware Aware Learning for Medical Imaging and Computer Assisted Intervention; Zhou, L., Heller, N., Shi, Y., Xiao, Y., Sznitman, R., Cheplygina, V., Mateus, D., Trucco, E., Hu, X.S., Chen, D., et al., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 136–144. [Google Scholar] [CrossRef]
- Heinrich, M.P.; Jenkinson, M.; Papież, B.W.; Brady, M.; Schnabel, J.A. Towards realtime multimodal fusion for image-guided interventions using self-similarities. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2013; pp. 187–194. [Google Scholar] [CrossRef] [Green Version]
- Göbl, R.; Navab, N.; Hennersperger, C. SUPRA: Open-source software-defined ultrasound processing for real-time applications. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 759–767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forte, A.E.; Galvan, S.; Dini, D. Models and tissue mimics for brain shift simulations. Biomech. Model. Mechanobiol. 2018, 17, 249–261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leibinger, A.; Forte, A.E.; Tan, Z.; Oldfield, M.J.; Beyrau, F.; Dini, D.; Rodriguez y Baena, F. Soft Tissue Phantoms for Realistic Needle Insertion: A Comparative Study. Ann. Biomed. Eng. 2016, 44, 2442–2452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, Z.; Dini, D.; Rodriguez y Baena, F.; Forte, A.E. Composite hydrogel: A high fidelity soft tissue mimic for surgery. Mater. Des. 2018, 160, 886–894. [Google Scholar] [CrossRef]
- Budday, S.; Sommer, G.; Birkl, C.; Langkammer, C.; Haybaeck, J.; Kohnert, J.; Bauer, M.; Paulsen, F.; Steinmann, P.; Kuhl, E.; et al. Mechanical characterization of human brain tissue. Acta Biomater. 2017, 48, 319–340. [Google Scholar] [CrossRef] [PubMed]
- Comellas, E.; Budday, S.; Pelteret, J.P.; Holzapfel, G.A.; Steinmann, P. Modeling the porous and viscous responses of human brain tissue behavior. Comput. Methods Appl. Mech. Eng. 2020, 369, 113128. [Google Scholar] [CrossRef]
- Rasin, I.; Pekar, Z.; Sadowsky, O.; Forte, A.; Galvan, S.; Dini, D.; Shoham, M.; Joskowicz, L. Real-time modeling of intra-operative brain shift based on video tracking. In Proceedings of the Hamlyn Symposium on Medical Robotics, London, UK, 12–15 July 2014. [Google Scholar]
- Dumpuri, P.; Thompson, R.C.; Dawant, B.M.; Cao, A.; Miga, M.I. An atlas-based method to compensate for brain shift: Preliminary results. Med. Image Anal. 2007, 11, 128–145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- BWH. 3D Slicer. Available online: https://www.slicer.org/ (accessed on 29 October 2021).
- DFKZ. The Medical Imaging Interaction Toolkit (MITK). Available online: https://www.mitk.org (accessed on 29 October 2021).
- Tokuda, J.; Fischer, G.S.; Papademetris, X.; Yaniv, Z.; Ibanez, L.; Cheng, P.; Liu, H.; Blevins, J.; Arata, J.; Golby, A.J.; et al. OpenIGTLink: An open network protocol for image-guided therapy environment. Int. J. Med. Robot. Comput. Assist. Surg. 2009, 5, 423–434. [Google Scholar] [CrossRef] [PubMed]
- SOFA. Simulation Open Framework Architecture. Available online: https://www.sofa-framework.org (accessed on 29 October 2021).
- Kitware. Interactive Medical Simulation Toolkit. Available online: https://www.imstk.org (accessed on 29 October 2021).
- Mueller, S.; Polley, M.Y.; Lee, B.; Kunwar, S.; Pedain, C.; Wembacher-Schröder, E.; Mittermeyer, S.; Westphal, M.; Sampson, J.H.; Vogelbaum, M.A.; et al. Effect of imaging and catheter characteristics on clinical outcome for patients in the PRECISE study. J. Neuro-Oncol. 2011, 101, 267–277. [Google Scholar] [CrossRef] [Green Version]
- Matheson, E.; Secoli, R.; Galvan, S.; Rodriguez y Baena, F. Human-robot visual interface for 3D steering of a flexible, bioinspired needle for neurosurgery. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 5426–5431. [Google Scholar] [CrossRef] [Green Version]
- Mulder, M.; Mulder, J.; Stassen, H. Cybernetics of tunnel-in-the-sky displays. II. Curved trajectories. In Proceedings of the IEEE SMC’99 Conference Proceedings. 1999 IEEE International Conference on Systems, Man, and Cybernetics (Cat. No. 99CH37028), Tokyo, Japan, 12–15 October 1999; Volume 5, pp. 1088–1093. [Google Scholar] [CrossRef]
- Yuan, C.; Recktenwald, F.; Mallot, H.A. Visual steering of UAV in unknown environments. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 3906–3911. [Google Scholar] [CrossRef]
- Castellano, A.; Falini, A. Progress in neuro-imaging of brain tumors. Curr. Opin. Oncol. 2016, 28, 484–493. [Google Scholar] [CrossRef] [PubMed]
- Riva, M.; Lopci, E.; Gay, L.G.; Nibali, M.C.; Rossi, M.; Sciortino, T.; Castellano, A.; Bello, L. Advancing Imaging to Enhance Surgery: From Image to Information Guidance. Neurosurg. Clin. N. Am. 2021, 32, 31–46. [Google Scholar] [CrossRef] [PubMed]
- Jahangiri, A.; Chin, A.T.; Flanigan, P.M.; Chen, R.; Bankiewicz, K.; Aghi, M.K. Convection-enhanced delivery in glioblastoma: A review of preclinical and clinical studies. J. Neurosurg. 2017, 126, 191–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lonser, R.R. Imaging of Convective Drug Delivery in the Nervous System. Neurosurg. Clin. N. Am. 2017, 28, 615–622. [Google Scholar] [CrossRef] [PubMed]
- Castellano, A.; Cirillo, S.; Bello, L.; Riva, M.; Falini, A. Functional MRI for Surgery of Gliomas. Curr. Treat. Opt. Neurol. 2017, 19, 34. [Google Scholar] [CrossRef] [PubMed]
- Pieri, V.; Sanvito, F.; Riva, M.; Petrini, A.; Rancoita, P.M.V.; Cirillo, S.; Iadanza, A.; Bello, L.; Castellano, A.; Falini, A. Along-tract statistics of neurite orientation dispersion and density imaging diffusion metrics to enhance MR tractography quantitative analysis in healthy controls and in patients with brain tumors. Hum. Brain Mapp. 2021, 42, 1268–1286. [Google Scholar] [CrossRef] [PubMed]
- Castellano, A.; Bello, L.; Michelozzi, C.; Gallucci, M.; Fava, E.; Iadanza, A.; Riva, M.; Casaceli, G.; Falini, A. Role of diffusion tensor magnetic resonance tractography in predicting the extent of resection in glioma surgery. Neuro Oncol. 2012, 14, 192–202. [Google Scholar] [CrossRef] [PubMed]
- Altabella, L.; Broggi, S.; Mangili, P.; Conte, G.M.; Pieri, V.; Iadanza, A.; Del Vecchio, A.; Anzalone, N.; di Muzio, N.; Calandrino, R.; et al. Integration of Diffusion Magnetic Resonance Tractography into tomotherapy radiation treatment planning for high-grade gliomas. Phys. Med. 2018, 55, 127–134. [Google Scholar] [CrossRef] [PubMed]
- Segato, A.; Pieri, V.; Favaro, A.; Riva, M.; Falini, A.; De Momi, E.; Castellano, A. Automated Steerable Path Planning for Deep Brain Stimulation Safeguarding Fiber Tracts and Deep Gray Matter Nuclei. Front. Robot. AI 2019, 6, 70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Amico, R.S.; Neira, J.A.; Yun, J.; Alexiades, N.G.; Banu, M.; Englander, Z.K.; Kennedy, B.C.; Ung, T.H.; Rothrock, R.J.; Romanov, A.; et al. Validation of an effective implantable pump-infusion system for chronic convection-enhanced delivery of intracerebral topotecan in a large animal model. J. Neurosurg. 2019, 133, 614–623. [Google Scholar] [CrossRef] [PubMed]
- Gimenez, F.; Krauze, M.T.; Valles, F.; Hadaczek, P.; Bringas, J.; Sharma, N.; Forsayeth, J.; Bankiewicz, K.S. Image-guided convection-enhanced delivery of GDNF protein into monkey putamen. NeuroImage 2011, 54 (Suppl. 1), S189–S195. [Google Scholar] [CrossRef] [PubMed]
- van der Bom, I.M.; Moser, R.P.; Gao, G.; Sena-Esteves, M.; Aronin, N.; Gounis, M.J. Frameless multimodal image guidance of localized convection-enhanced delivery of therapeutics in the brain. J. Neurointerv. Surg. 2013, 5, 69–72. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sewing, A.C.P.; Lagerweij, T.; van Vuurden, D.G.; Meel, M.H.; Veringa, S.J.E.; Carcaboso, A.M.; Gaillard, P.J.; Peter Vandertop, W.; Wesseling, P.; Noske, D.; et al. Preclinical evaluation of convection-enhanced delivery of liposomal doxorubicin to treat pediatric diffuse intrinsic pontine glioma and thalamic high-grade glioma. J. Neurosurg. Pediatr. 2017, 19, 518–530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tromp, D.P.; Adluru, N.; Alexander, A.L.; Emborg, M.E. Simulating convection-enhanced delivery in the putamen using probabilistic tractography. Proc. IEEE Int. Symp. Biomed. Imaging 2011, 2011, 787–790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosenbluth, K.H.; Martin, A.J.; Bringas, J.; Bankiewicz, K.S. Evaluation of pressure-driven brain infusions in nonhuman primates by intra-operative 7 Tesla MRI. J. Magn. Reson. Imaging 2012, 36, 1339–1346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raghavan, R.; Brady, M.L.; Rodríguez-Ponce, M.I.; Hartlep, A.; Pedain, C.; Sampson, J.H. Convection-enhanced delivery of therapeutics for brain disease, and its optimization. Neurosurg. Focus 2006, 20, E12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arifin, D.Y.; Lee, K.Y.; Wang, C.H.; Smith, K.A. Role of convective flow in carmustine delivery to a brain tumor. Pharm. Res. 2009, 26, 2289–2302. [Google Scholar] [CrossRef] [PubMed]
- Banks, J. The Neurotechnological Revolution: Unlocking the brain’s secrets to develop innovative technologies as well as treatments for neurological diseases. IEEE Pulse 2015, 6, 10–15. [Google Scholar] [CrossRef]
- Murray, C.J.; Lopez, A.D. Global mortality, disability, and the contribution of risk factors: Global Burden of Disease Study. Lancet 1997, 349, 1436–1442. [Google Scholar] [CrossRef]
- DiLuca, M.; Olesen, J. The Cost of Brain Diseases: A Burden or a Challenge? Neuron 2014, 82, 1205–1208. [Google Scholar] [CrossRef] [Green Version]
- Sobocki, P.; Lekander, I.; Berwick, S.; Olesen, J.; Jönsson, B. Resource allocation to brain research in Europe (RABRE). Eur. J. Neurosci. 2006, 24, 2691–2693. [Google Scholar] [CrossRef] [PubMed]
- Kesari, S. Understanding Glioblastoma Tumor Biology: The Potential to Improve Current Diagnosis and Treatments. Semin. Oncol. 2011, 38, S2–S10. [Google Scholar] [CrossRef] [PubMed]
- Portnow, J.; Badie, B.; Chen, M.; Liu, A.; Blanchard, S.; Synold, T.W. The Neuropharmacokinetics of Temozolomide in Patients with Resectable Brain Tumors: Potential Implications for the Current Approach to Chemoradiation. Clin. Cancer Res. 2009, 15, 7092–7098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ostermann, S.; Csajka, C.; Buclin, T.; Leyvraz, S.; Lejeune, F.; Decosterd, L.A.; Stupp, R. Plasma and Cerebrospinal Fluid Population Pharmacokinetics of Temozolomide in Malignant Glioma Patients. Clin. Cancer Res. 2004, 10, 3728–3736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamal, A.; Yuan, T.; Galvan, S.; Castellano, A.; Riva, M.; Secoli, R.; Falini, A.; Bello, L.; Rodriguez y Baena, F.; Dini, D. Insights into Infusion-Based Targeted Drug Delivery in the Brain: Perspectives, Challenges and Opportunities. Int. J. Mol. Sci. 2022, 23, 3139. https://doi.org/10.3390/ijms23063139
Jamal A, Yuan T, Galvan S, Castellano A, Riva M, Secoli R, Falini A, Bello L, Rodriguez y Baena F, Dini D. Insights into Infusion-Based Targeted Drug Delivery in the Brain: Perspectives, Challenges and Opportunities. International Journal of Molecular Sciences. 2022; 23(6):3139. https://doi.org/10.3390/ijms23063139
Chicago/Turabian StyleJamal, Asad, Tian Yuan, Stefano Galvan, Antonella Castellano, Marco Riva, Riccardo Secoli, Andrea Falini, Lorenzo Bello, Ferdinando Rodriguez y Baena, and Daniele Dini. 2022. "Insights into Infusion-Based Targeted Drug Delivery in the Brain: Perspectives, Challenges and Opportunities" International Journal of Molecular Sciences 23, no. 6: 3139. https://doi.org/10.3390/ijms23063139
APA StyleJamal, A., Yuan, T., Galvan, S., Castellano, A., Riva, M., Secoli, R., Falini, A., Bello, L., Rodriguez y Baena, F., & Dini, D. (2022). Insights into Infusion-Based Targeted Drug Delivery in the Brain: Perspectives, Challenges and Opportunities. International Journal of Molecular Sciences, 23(6), 3139. https://doi.org/10.3390/ijms23063139






