Testing of Exchange-Correlation Functionals of DFT for a Reliable Description of the Electron Density Distribution in Organic Molecules
Abstract
:1. Introduction
2. Results and Discussion
2.1. Testing of DFT Functionals for the Electron Density Distribution in Bond Critical Points
2.2. Testing of DFT Functionals for the Electron Density Distribution in a Ring Critical Point
2.3. Testing of DFT Functionals for the Bond Delocalization Index
3. Crystal Structure and Methodology
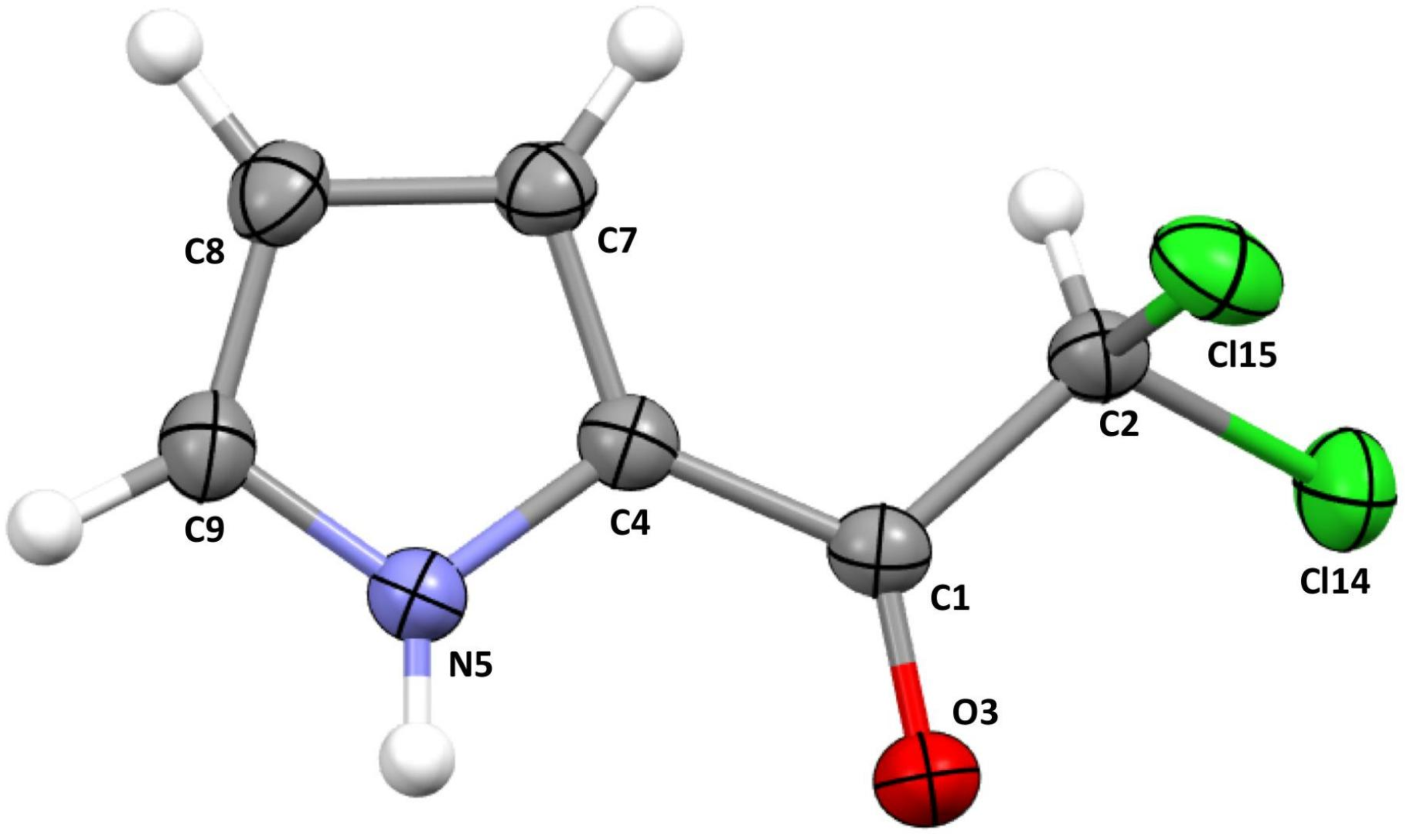
3.1. Crystal Structure of 2,2-Dichloro-1-(1H-pyrrol-2-yl)ethan-1-one
3.2. Methodology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| EDD | electron density distribution |
| QTAIM | Quantum Theory of Atoms in Molecules |
| BCP | bond critical point |
| RCP | ring critical point |
| LDA | Local Density Approximation |
| GGA | Generalized Gradient Approximation method |
| M-GGA | meta-GGA functional |
| H-GGA | hybrid GGA functional |
| HM-GGA | hybrid M-GGA functional |
| DH-GGA | double-hybrid GGA functional |
References
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Peverati, R.; Truhlar, D.G. Quest for a universal density functional: The accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos. Trans. R. Soc. A 2014, 372, 20120476. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef] [Green Version]
- Boyd, R.J.; Wang, J.; Eriksson, L.A. The Electron Density as Calculated From Density Functional Theory. In Recent Advances in Computational Chemistry: Recent Advances in Density Functional Methods; Chong, D.P., Ed.; World Scientific: Singapore, 1995. [Google Scholar]
- Csonka, G.I.; Nguyen, N.A.; Kolossvary, I. Simple Tests for Density Functional Methods. J. Comput. Chem. 1997, 18, 1534–1545. [Google Scholar] [CrossRef]
- Brothers, E.N.; Merz, K.M., Jr. Performance of Density Functionals with Small Split Valence Basis Sets. J. Phys. Chem A 2004, 108, 2904–2911. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Hybrid Meta Density Functional Theory Methods for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions: The MPW1B95 and MPWB1K Models and Comparative Assessments for Hydrogen Bonding and van der Waals Interactions. J. Phys. Chem. A 2004, 108, 6908–6918. [Google Scholar] [CrossRef]
- Zhao, Y.; Pu, J.; Benjamin, J.L.; Truhlar, D.G. Tests of second-generation and third-generation density functionals for thermochemical kinetics. Phys. Chem. Chem. Phys. 2004, 6, 673–676. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Benchmark Databases for Nonbonded Interactions and Their Use To Test Density Functional Theory. J. Chem. Theory Comput. 2005, 1, 415–432. [Google Scholar] [CrossRef]
- Zhao, Y.; González-García, N.; Truhlar, D.G. Benchmark Database of Barrier Heights for Heavy Atom Transfer, Nucleophilic Substitution, Association, and Unimolecular Reactions and Its Use to Test Theoretical Methods. J. Phys. Chem. A 2005, 109, 2012–2018. [Google Scholar] [CrossRef]
- Schultz, N.E.; Zhao, Y.; Truhlar, D.G. Databases for Transition Element Bonding: Metal–Metal Bond Energies and Bond Lengths and Their Use To Test Hybrid, Hybrid Meta, and Meta Density Functionals and Generalized Gradient Approximations. J. Phys. Chem. A 2005, 109, 4388–4403. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. A 2005, 109, 5656–5667. [Google Scholar] [CrossRef]
- Schultz, N.E.; Zhao, Y.; Truhlar, D.G. Density Functionals for Inorganometallic and Organometallic Chemistry. J. Phys. Chem. A 2005, 109, 11127–11143. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Assessment of Gaussian-3 and density-functional theories on the G3/05 test set of experimental energies. J. Chem. Phys. 2005, 123, 124107. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Comparative DFT Study of van der Waals Complexes: Rare-Gas Dimers, Alkaline-Earth Dimers, Zinc Dimer, and Zinc-Rare-Gas Dimers. J. Phys. Chem. A 2006, 110, 5121–5129. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. Assessment of Density Functionals for π Systems: Energy Differences between Cumulenes and Poly-ynes; Proton Affinities, Bond Length Alternation, and Torsional Potentials of Conjugated Polyenes; and Proton Affinities of Conjugated Shiff Bases. J. Phys. Chem. A 2006, 110, 10478–10486. [Google Scholar] [CrossRef]
- Riley, K.E.; Op’t Holt, B.T.; Merz, K.M., Jr. Critical Assessment of the Performance of Density Functional Methods for Several Atomic and Molecular Properties. J. Chem. Theory Comput. 2007, 3, 407–433. [Google Scholar] [CrossRef]
- Sousa, S.F.; Fernandes, P.A.; Ramos, M.J. General Performance of Density Functionals. J. Phys. Chem. A 2007, 111, 10439–10452. [Google Scholar] [CrossRef] [PubMed]
- Bochevarov, A.D.; Friesner, R.A. The densities produced by the density functional theory: Comparison to full configuration interaction. J. Chem. Phys. 2008, 128, 034102. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg. H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Rayne, S.; Forest, K. Performance of the major semiempirical, ab initio, and density functional theory methods in evaluating isomerization enthalpies for linear to branched heptanes. Nat. Prec. 2010. [Google Scholar] [CrossRef]
- Tognetti, V.; Joubert, L. On the Influence of Density Functional Approximations on Some Local Bader’s Atoms-in-Molecules Properties. J. Phys. Chem. A 2011, 115, 5505–5515. [Google Scholar] [CrossRef]
- Thanthiriwatte, K.S.; Hohenstein, E.G.; Burns, L.A.; Sherrill, C.D. Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions. J. Chem. Theory Comput. 2011, 7, 88–96. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density Functional Theory for Reaction Energies: Test of Meta and Hybrid Meta Functionals, Range-Separated Functionals, and Other High-Performance Functionals. J. Chem. Theory Comput. 2011, 7, 669–676. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef]
- Mardirossian, N.; Parkhill, J.A.; Head-Gordon, M. Benchmark results for empirical post-GGA functionals: Difficult exchange problems and independent tests. Phys. Chem. Chem. Phys. 2011, 13, 19325–19337. [Google Scholar] [CrossRef] [PubMed]
- Leang, S.S.; Zahariev, F.; Gordon, M.S. Benchmarking the performance of time-dependent density functional methods. J. Chem. Phys. 2012, 136, 104101. [Google Scholar] [CrossRef] [Green Version]
- Boese, A.D. Density Functional Theory and Hydrogen Bonds: Are We There Yet? ChemPhysChem 2015, 16, 978–985. [Google Scholar] [CrossRef]
- Brémond, É.; Savarese, M.; Pérez-Jiménez, Á.J.; Sancho-García, J.C.; Adamo, C. Systematic Improvement of Density Functionals through Parameter-Free Hybridization Schemes. J. Phys. Chem. Lett. 2015, 6, 3540–3545. [Google Scholar] [CrossRef] [PubMed]
- Matczak, P. Assessment of various density functionals for intermolecular N → Sn interactions: The test case of poly(trimethyltin cyanide). Comput. Theor. Chem. 2015, 1051, 110–122. [Google Scholar] [CrossRef]
- Rybarczyk-Pirek, A.J.; Małecka, M.; Palusiak, M. Use of Quantum Theory of Atoms in Molecules in the Search for Appropriate Hydrogen Atom Locations in X-ray Diffraction Based Studies. Cryst. Growth Des. 2016, 16, 6841–6848. [Google Scholar] [CrossRef]
- Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef]
- Brorsen, K.R.; Yang, Y.; Pak, M.V.; Hammes-Schiffer, S. Is the Accuracy of Density Functional Theory for Atomization Energies and Densities in Bonding Regions Correlated? J. Phys. Chem. Lett. 2017, 8, 2076–2081. [Google Scholar] [CrossRef]
- Gould, T. What Makes a Density Functional Approximation Good? Insights from the Left Fukui Function. J. Chem. Theory Comput. 2017, 13, 2373–2377. [Google Scholar] [CrossRef]
- Mezei, P.D.; Csonka, G.I.; Kállay, M. Electron Density Errors and Density-Driven Exchange-Correlation Energy Errors in Approximate Density Functional Calculations. J. Chem. Theory Comput. 2017, 13, 4753–4764. [Google Scholar] [CrossRef] [Green Version]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef] [Green Version]
- Brémond, É; Savarese, M.; Pérez-Jiménez, Á.J.; Sancho-García, J.C.; Adamo, C. Speed-Up of the Excited-State Benchmarking: Double-Hybrid Density Functionals as Test Cases. J. Chem. Theory Comput. 2017, 13, 5539–5551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, P.; Truhlar, D.G. Can Kohn–Sham density functional theory predict accurate charge distributions for both single-reference and multi-reference molecules? Phys. Chem. Chem. Phys. 2017, 19, 12898–12912. [Google Scholar] [CrossRef]
- Su, N.Q.; Zhu, Z.; Xu, X. Doubly hybrid density functionals that correctly describe both density and energy for atoms. Proc. Natl. Acad. Sci. USA 2018, 115, 2287–2292. [Google Scholar] [CrossRef] [PubMed]
- Hait, D.; Head-Gordon, M. How Accurate Is Density Functional Theory at Predicting Dipole Moments? An Assessment Using a New Database of 200 Benchmark Values. J. Chem. Theory Comput. 2018, 14, 1969–1981. [Google Scholar] [CrossRef] [Green Version]
- Adamson, J.; Nazarski, R.B.; Jarvet, J.; Pehk, T.; Aav, R. Shortfall of B3LYP in Reproducing NMR JCH Couplings in Some Isomeric Epoxy Structures with Strong Stereoelectronic Effects: A Benchmark Study on DFT Functionals. ChemPhysChem 2018, 19, 631–642. [Google Scholar] [CrossRef]
- Cui, C.X.; Xu, D.; Ding, B.-W.; Qu, L.-B.; Zhang, Y.-P.; Lan, Y. Benchmark Study of Popular Density Functionals for Calculating Binding Energies of Three-Center Two-Electron Bonds. J. Comput. Chem. 2019, 40, 657–670. [Google Scholar] [CrossRef] [PubMed]
- Seeger, Z.L.; Izgorodina, E.I. A Systematic Study of DFT Performance for Geometry Optimizations of Ionic Liquid Clusters. J. Chem. Theory Comput. 2020, 16, 6735–6753. [Google Scholar] [CrossRef]
- Jabłoński, M.; Krygowski, T.M. Dependence of the substituent energy on the level of theory. J. Comput. Chem. 2021, 42, 2079–2088. [Google Scholar] [CrossRef]
- Mendes, R.A.; Haiduke, R.L.A. Performance of new exchange–correlation functionals in providing vertical excitation energies of metal complexes. Theor. Chem. Acc. 2021, 140, 146. [Google Scholar] [CrossRef]
- Brémond, É.; Tognetti, V.; Chermette, H.; Sancho-García, J.C.; Joubert, L.; Adamo, C. Electronic Energy and Local Property Errors at QTAIM Critical Points while Climbing Perdew’s Ladder of Density-Functional Approximations. J. Chem. Theory Comput. 2022, 18, 293–308. [Google Scholar] [CrossRef]
- Jabłoński, M. Determining Repulsion in Cyclophane Cages. Molecules 2022, 27, 3969. [Google Scholar] [CrossRef]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1–20. [Google Scholar]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Jabłoński, M.; Palusiak, M. Basis Set and Method Dependence in Atoms in Molecules Calculations. J. Phys. Chem. A 2010, 114, 2240–2244. [Google Scholar] [CrossRef] [PubMed]
- Jabłoński, M.; Palusiak, M. Basis Set and Method Dependence in Quantum Theory of Atoms in Molecules Calculations for Covalent Bonds. J. Phys. Chem. A 2010, 114, 12498–12505. [Google Scholar] [CrossRef]
- Nicolau, I.; Demopoulus, V.J. A Study of the Friedel-Crafts Acylation of 1-Benzenesulfonyl-1H-pyrrole in the Preparation of 3-Aroylpyrroles. J. Heterocycl. Chem. 1998, 35, 1345–1348. [Google Scholar] [CrossRef]
- Chȩcińska, L.; Mebs, S.; Hübschle, C.B.H.; Förster, D.; Morgenroth, W.; Luger, P. Reproducibility and transferability of topological data: Experimental charge density study of two modifications of L-alanyl-L-tyrosyl-L-alanine. Org. Biomol. Chem. 2006, 4, 3242–3251. [Google Scholar] [CrossRef]
- Palusiak, M.; Krygowski, T.M. Application of AIM Parameters at Ring Critical Points for Estimation of π-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings. Chem. Eur. J. 2007, 13, 7996–8006. [Google Scholar] [CrossRef] [PubMed]
- Fradera, X.; Austen, M.A.; Bader, R.F.W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304–314. [Google Scholar] [CrossRef]
- Fradera, X.; Poater, J.; Simon, S.; Duran, M.; Solà, M. Electron-pairing analysis from localization and delocalization indices in the framework of the atoms-in-molecules theory. Theor. Chem. Acc. 2002, 108, 214–224. [Google Scholar] [CrossRef]
- Matta, C.F.; Boyd, R.J. (Eds.) The Quantum Theory of Atoms in Molecules—From Solid to DNA and Drug Design; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Bader, R.F.W.; Stephens, M.E. Spatial Localization of the Electronic Pair and Number Distributions in Molecules. J. Am. Chem. Soc. 1975, 97, 7391–7399. [Google Scholar] [CrossRef]
- García-Revilla, M.; Francisco, E.; Popelier, P.L.A.; Pendás, A.M. Domain-Averaged Exchange-Correlation Energies as a Physical Underpinning for Chemical Graphs. ChemPhysChem 2013, 14, 1211–1218. [Google Scholar] [CrossRef]
- These Data Can Be Obtained Free of Charge via Website (or from 565 CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; Fax: +44 1223 336033; E-mail: deposit@ccdc.cam.ac.uk). Available online: http://www.ccdc.cam.ac.uk/conts/retrieving.html (accessed on 22 November 2022).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Keith, T.A. AIMAll; Version 15.05.18; TK Gristmill Software: Overland Park, KS, USA, 2015; Available online: aim.tkgristmill.com (accessed on 17 September 2022).
- Slater, J.C. The Self-Consistent Field for Molecular and Solids. Quantum Theory of Molecules and Solids; McGraw-Hill: New York, NY, USA, 1974; Volume 4. [Google Scholar]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-fnnctional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Handy, N.C.; Cohen, A.J. Left–right correlation energy. Mol. Phys. 2001, 99, 403–412. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Boese, A.D.; Handy, N.C. A new parametrization of exchange–correlation generalized gradient approximation functionals. J. Chem. Phys. 2001, 114, 5497–5503. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [Green Version]
- Voorhis, T.V.; Scuseria, G.E. A novel form for the exchange-correlation energy functional. J. Chem. Phys. 1998, 109, 400–410. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Goddard, W.A., III. The X3LYP extended density functional for accurate descriptions of nonbond interactions, spin states, and thermochemical properties. Proc. Natl. Acad. Sci. USA 2004, 101, 2673–2677. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef] [Green Version]
- Peverati, R.; Truhlar, D.G. Communication: A global hybrid generalized gradient approximation to the exchange-correlation functional that satisfies the second-order density-gradient constraint and has broad applicability in chemistry. J. Chem. Phys. 2011, 135, 191102. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Peverati, R.; Truhlar, D.G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Charge-Transfer States, and Better Performance on Average than B3LYP for Ground States. J. Phys. Chem. A 2006, 110, 13126–13130. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Truhlar, D.G. Screened-exchange density functionals with broad accuracy for chemistry and solid-state physics. Phys. Chem. Chem. Phys. 2012, 14, 16187–16191. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [Green Version]
- Schwabe, T.; Grimme, S. Towards chemical accuracy for the thermodynamics of large molecules: New hybrid density functionals including non-local correlation effects. Phys. Chem. Chem. Phys. 2006, 8, 4398–4401. [Google Scholar] [CrossRef]
- Brémond, E.; Adamo, C. Seeking for parameter-free double-hybrid functionals: The PBE0-DH model. J. Chem. Phys. 2011, 135, 024106. [Google Scholar] [CrossRef] [PubMed]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry. Introduction to Advanced Electronic Structure Theory; Dover Publications, Inc.: Mineola, NY, USA, 1982. [Google Scholar]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. IV. Calculation of static electrical response properties. J. Chem. Phys. 1994, 100, 2975–2988. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef] [Green Version]
- Čížek, J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256–4266. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A Fifth-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
- Head-Gordon, M.; Pople, J.A.; Frisch, M.J. MP2 Energy Evaluation by Direct Methods. Chem. Phys. Lett. 1988, 153, 503–506. [Google Scholar] [CrossRef]
- Pople, J.A.; Binkley, J.S.; Seeger, R. Theoretical Models Incorporating Electron Correlation. Int. J. Quant. Chem. 1976, 10, 1–19. [Google Scholar] [CrossRef]
- Pople, J.A.; Seeger, R.; Krishnan, R. Variational Configuration Interaction Methods and Comparison with Perturbation Theory. Int. J. Quant. Chem. 1977, 12, 149–163. [Google Scholar] [CrossRef]
- Krishnan, R.; Pople, J.A. Approximate Fourth-Order Perturbation Theory of the Electron Correlation Energy. Int. J. Quant. Chem. 1978, 14, 91–100. [Google Scholar] [CrossRef]
- STOE IPDS-Software, Version 2.89; STOE & CIE GmbH: Darmstadt, Germany, 1998.
- Altomare, A.; Burla, M.C.; Camalli, M.; Cascarano, G.L.; Giacovazzo, C.; Guagliardi, A.; Moliterni, A.G.G.; Polidori, G.; Spagna, R. SIR97: A new tool for crystal structure determination and refinement. J. Appl. Cryst. 1999, 32, 115–119. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spek, A.L. Structure Validation in chemical crystallography. Acta Cryst. D 2009, 65, 148–155. [Google Scholar] [CrossRef] [Green Version]
- Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Cryst. 2020, 53, 226–235. [Google Scholar] [CrossRef]







| Property | Bond | RCP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C4–N5 | C9–N5 | C8–C9 | C7–C8 | C4–C7 | C1–C4 | C1–O3 | C1–C2 | C2–Cl14 | C2–Cl15 | ||
| 0.2953 | 0.3172 | 0.3186 | 0.3059 | 0.3090 | 0.3021 | 0.3992 | 0.2453 | 0.1947 | 0.1909 | 0.0520 | |
| −0.7219 | −0.6682 | −1.0319 | −0.9526 | −0.9594 | −0.9792 | −0.3405 | −0.6098 | −0.2816 | −0.2684 | −0.0471 | |
| H | −0.4399 | −0.4970 | −0.3816 | −0.3486 | −0.3561 | −0.3328 | −0.7094 | −0.2103 | −0.1414 | −0.1383 | 0.1767 |
| 0.8968 | 0.9530 | 1.1614 | 1.1016 | 1.1222 | 0.9080 | 1.1287 | 0.7359 | 0.8636 | 0.8459 | n/a | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domagała, M.; Jabłoński, M.; Dubis, A.T.; Zabel, M.; Pfitzner, A.; Palusiak, M. Testing of Exchange-Correlation Functionals of DFT for a Reliable Description of the Electron Density Distribution in Organic Molecules. Int. J. Mol. Sci. 2022, 23, 14719. https://doi.org/10.3390/ijms232314719
Domagała M, Jabłoński M, Dubis AT, Zabel M, Pfitzner A, Palusiak M. Testing of Exchange-Correlation Functionals of DFT for a Reliable Description of the Electron Density Distribution in Organic Molecules. International Journal of Molecular Sciences. 2022; 23(23):14719. https://doi.org/10.3390/ijms232314719
Chicago/Turabian StyleDomagała, Małgorzata, Mirosław Jabłoński, Alina T. Dubis, Manfred Zabel, Arno Pfitzner, and Marcin Palusiak. 2022. "Testing of Exchange-Correlation Functionals of DFT for a Reliable Description of the Electron Density Distribution in Organic Molecules" International Journal of Molecular Sciences 23, no. 23: 14719. https://doi.org/10.3390/ijms232314719
APA StyleDomagała, M., Jabłoński, M., Dubis, A. T., Zabel, M., Pfitzner, A., & Palusiak, M. (2022). Testing of Exchange-Correlation Functionals of DFT for a Reliable Description of the Electron Density Distribution in Organic Molecules. International Journal of Molecular Sciences, 23(23), 14719. https://doi.org/10.3390/ijms232314719