DRPreter: Interpretable Anticancer Drug Response Prediction Using Knowledge-Guided Graph Neural Networks and Transformer
Abstract
1. Introduction
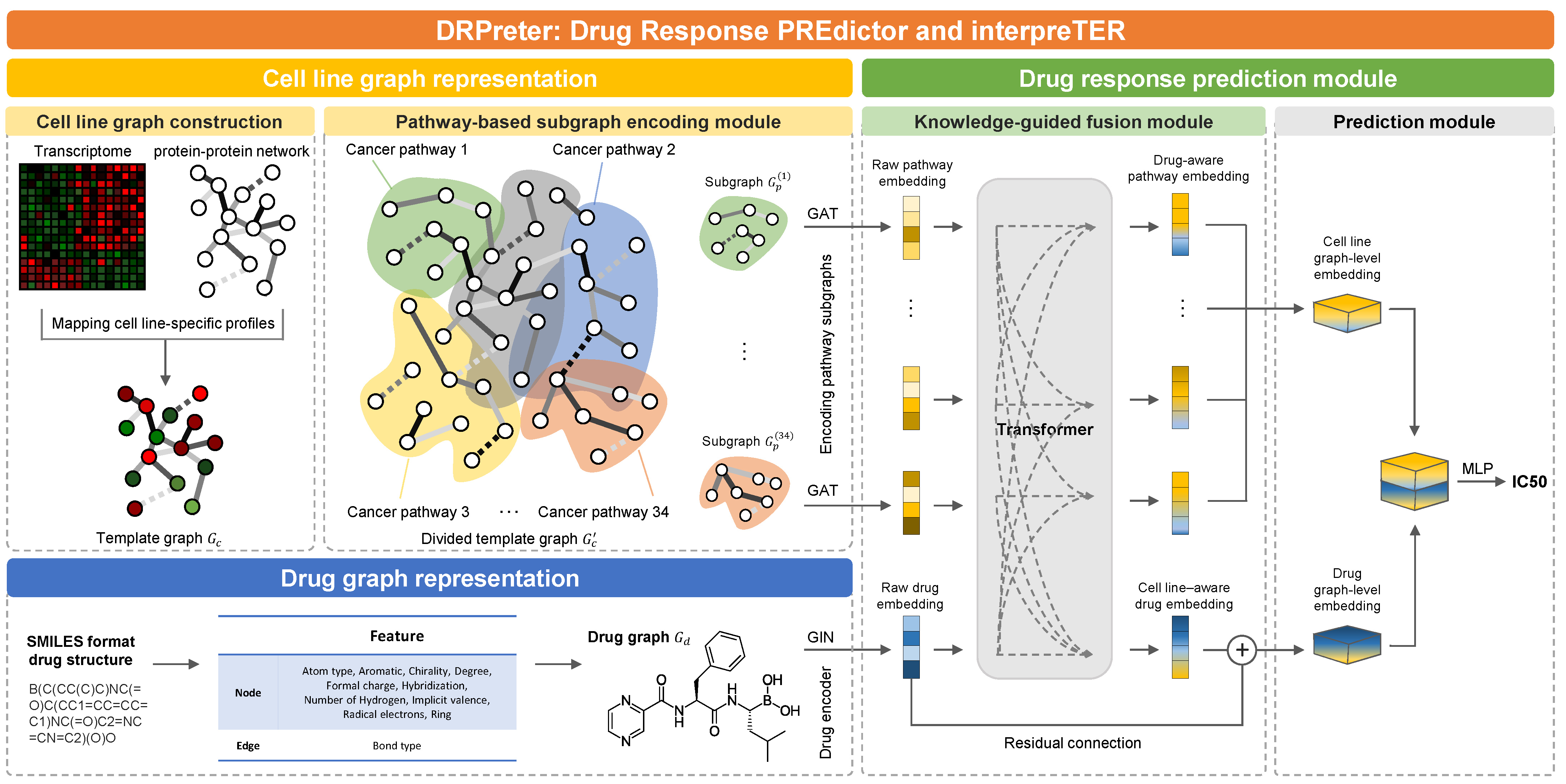
- Knowledge-guided cell representation with graphs. DRPreter constructs a cell line network as a set of subgraphs that correspond to cancer-related pathways for the detailed representation of the biological mechanism.
- Interpretability of drug mechanisms of action. Using the transformer’s encoder, the interactions between drugs and pathways are derived from the model, and putative key pathways for the drug mechanism can be highlighted.
- Enhanced performance. DRPreter outperforms state-of-the-art drug-response prediction models, as demonstrated by comparative experiments on the GDSC drug-sensitivity dataset.
2. Results and Discussion
2.1. Performance Comparison
2.1.1. Dataset
2.1.2. Experimental Setups
2.1.3. Rediscovered Responses of Known Pairs
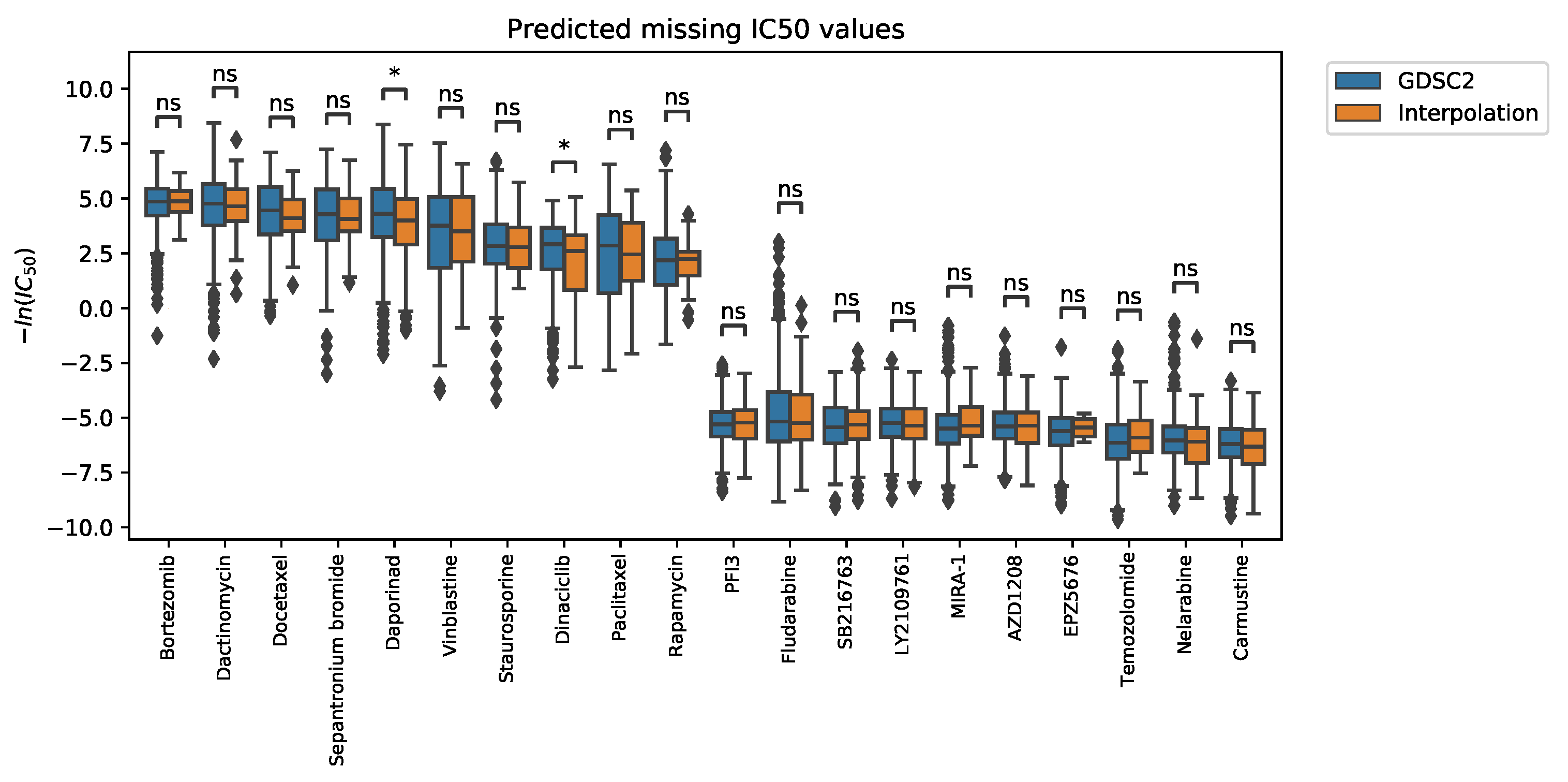
2.2. Case Study
2.2.1. Interpolation of Unknown Values
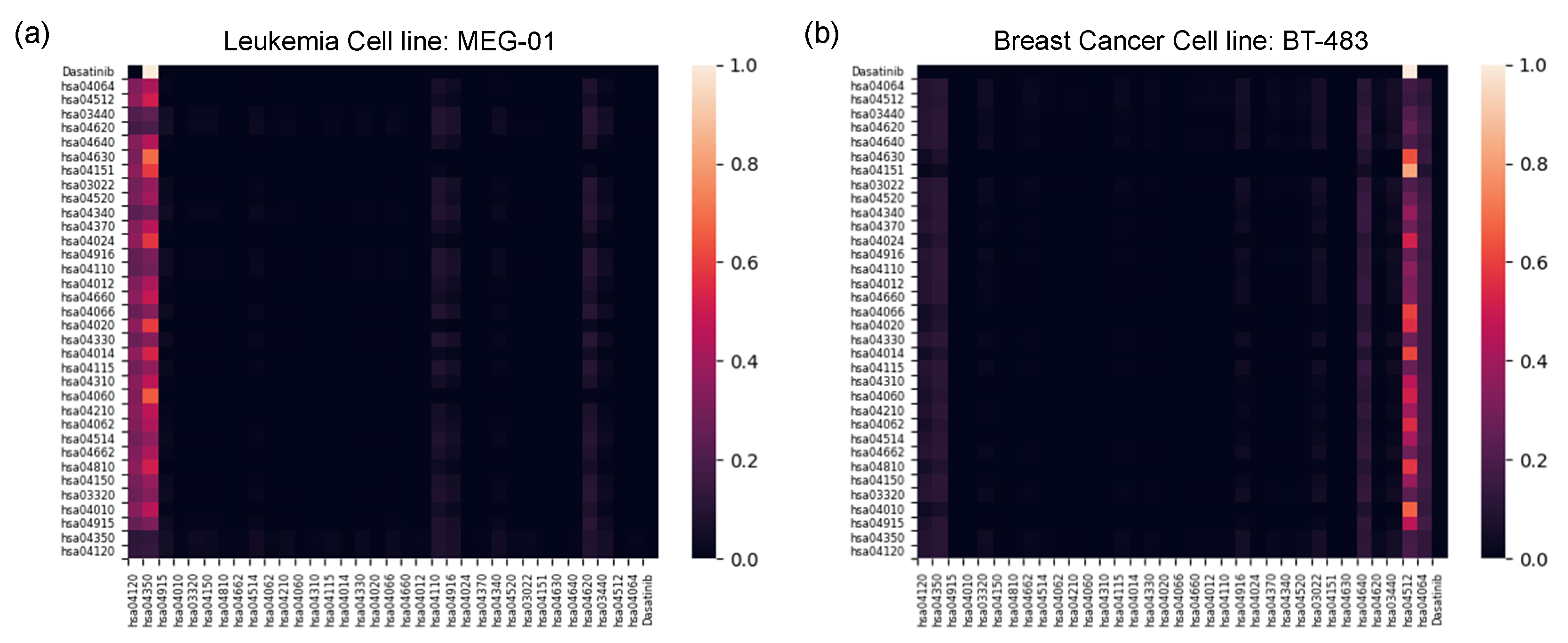
2.2.2. Gradient-Weighted Gene Nodes Interpretation
2.2.3. Pathway-Level Interpretation Using the Transformer
3. Materials and Methods
3.1. Graph Neural Networks
3.2. Cell-Line Graph Representation
3.2.1. Cell-Line Graph Construction
3.2.2. Cell-Line Graph Encoder on Pathway Subgraphs
3.3. Drug Graph Representation
3.3.1. Drug Graph Construction
3.3.2. Drug Graph Encoder
3.4. Drug Response Prediction Module
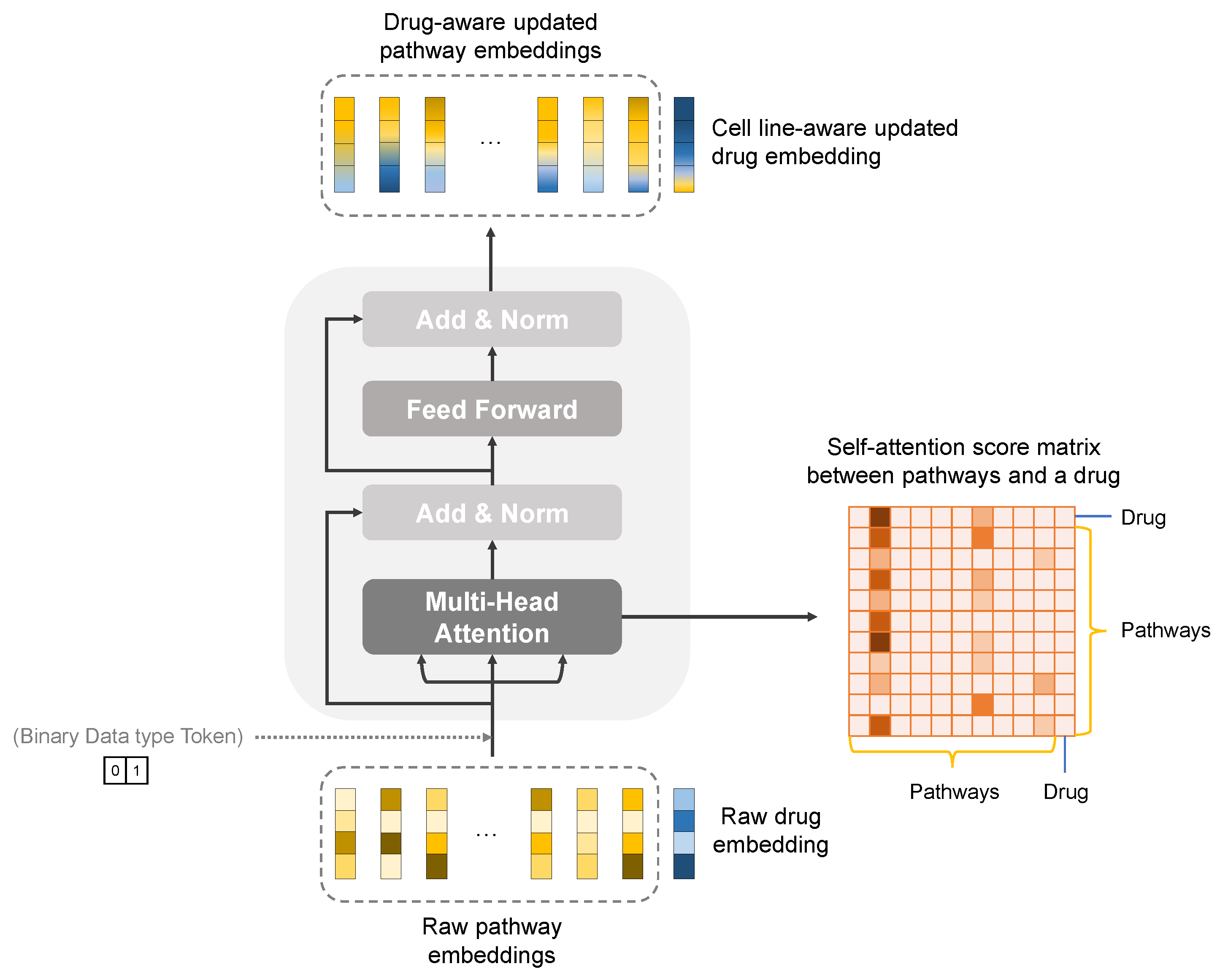
3.4.1. Knowledge-Guided Cell-Line–Drug Fusion Module Using Transformer
3.4.2. Improving Predictive Performance Using a Similarity Graph
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| mut | Mutation of gene |
| exp | Gene expression |
| cnv | Copy number variation |
| CCLE | Cancer Cell Line Encyclopedia |
| CNN | Convolutional Neural Network |
| COSMIC | Catalogue of Somatic Mutations in Cancer |
| GAT | Graph Attention Network |
| GCN | Graph Convolutional Network |
| GDSC | Genomics of Drug Sensitivity in Cancer |
| GIN | Graph Isomorphism Network |
| GNN | Graph Neural Network |
| GradCAM | Gradient-weighted Class Activation Mapping |
| IC50 | half maximal inhibitory concentration |
| MLP | Multi-Layer Perceptron |
| RSEM | RNA-Seq by Expectation Maximization |
| TGF | Transforming Growth Factor |
| TPM | Transcripts Per Kilobase Million |
Appendix A
| Pathway Name | KEGG Identifier | Number of Genes | Number of Edges |
|---|---|---|---|
| Ubiquitin mediated proteolysis | hsa04120 | 142 | 534 |
| TGF- signaling pathway | hsa04350 | 94 | 228 |
| Estrogen signaling pathway | hsa04915 | 137 | 222 |
| MAPK signaling pathway | hsa04010 | 294 | 692 |
| PPAR signaling pathway | hsa03320 | 74 | 28 |
| mTOR signaling pathway | hsa04150 | 155 | 688 |
| Regulation of actin cytoskeleton | hsa04810 | 218 | 552 |
| B cell receptor signaling pathway | hsa04662 | 79 | 208 |
| Cell adhesion molecules | hsa04514 | 146 | 150 |
| Chemokine signaling pathway | hsa04062 | 190 | 514 |
| Apoptosis | hsa04210 | 136 | 424 |
| Cytokine-cytokine receptor interaction | hsa04060 | 293 | 588 |
| Wnt signaling pathway | hsa04310 | 167 | 384 |
| p53 signaling pathway | hsa04115 | 73 | 180 |
| Ras signaling pathway | hsa04014 | 232 | 600 |
| Notch signaling pathway | hsa04330 | 59 | 76 |
| Calcium signaling pathway | hsa04020 | 239 | 218 |
| HIF-1 signaling pathway | hsa04066 | 109 | 204 |
| T cell receptor signaling pathway | hsa04660 | 104 | 336 |
| ErbB signaling pathway | hsa04012 | 85 | 326 |
| Cell cycle | hsa04110 | 126 | 1076 |
| Melanogenesis | hsa04916 | 101 | 110 |
| cAMP signaling pathway | hsa04024 | 221 | 222 |
| VEGF signaling pathway | hsa04370 | 59 | 102 |
| Hedgehog signaling pathway | hsa04340 | 56 | 80 |
| Adherens junction | hsa04520 | 71 | 172 |
| Basal transcription factors | hsa03022 | 44 | 470 |
| PI3K-Akt signaling pathway | hsa04151 | 351 | 1030 |
| JAK-STAT signaling pathway | hsa04630 | 162 | 508 |
| Hematopoietic cell lineage | hsa04640 | 96 | 102 |
| Toll-like receptor signaling pathway | hsa04620 | 102 | 328 |
| Homologous recombination | hsa03440 | 41 | 140 |
| ECM-receptor interaction | hsa04512 | 88 | 120 |
| NF-B signaling pathway | hsa04064 | 102 | 392 |
| Feature | Size | Description | |
|---|---|---|---|
| Node | Atom type | 43 | [B, C, N, O, F, …] (one-hot) |
| Aromatic | 1 | Whether the atom is in aromatic system (binary) | |
| Chirality | 2 | [R, S] (one-hot or null) | |
| Degree | 11 | [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] (one-hot) | |
| Formal charge | 1 | electric charge (integer) | |
| Hybridization | 5 | [, , , , ] (one-hot or null) | |
| Number of Hydrogens | 5 | [0, 1, 2, 3, 4] (one-hot) | |
| Implicit valence | 7 | [0, 1, 2, 3, 4, 5, 6] (one-hot) | |
| Radical electrons | 1 | Number of radical electrons (integer) | |
| Ring | 1 | Whether the atom is in ring (binary) | |
| Edge | Bond type | 4 | [single, double, triple, aromatic] (one-hot) |
References
- Kellogg, R.A.; Dunn, J.; Snyder, M.P. Personal omics for precision health. Circ. Res. 2018, 122, 1169–1171. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, Z. Practicing precision medicine with intelligently integrative clinical and multi-omics data analysis. Hum. Genom. 2020, 14, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Kalamara, A.; Tobalina, L.; Saez-Rodriguez, J. How to find the right drug for each patient? Advances and challenges in pharmacogenomics. Curr. Opin. Syst. Biol. 2018, 10, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.B. The impact of pharmacogenomics in personalized medicine. Curr. Appl. Pharm. Biotechnol. 2019, 171, 369–394. [Google Scholar]
- Cho, S.Y. Patient-derived xenografts as compatible models for precision oncology. Lab. Anim. Res. 2020, 36, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.P.; Pratap, K.; Sinha, J.; Desiraju, K.; Bahal, D.; Kukreti, R. Critical evaluation of challenges and future use of animals in experimentation for biomedical research. Int. J. Immunopathol. Pharmacol. 2016, 29, 551–561. [Google Scholar] [CrossRef]
- Rees, M.G.; Seashore-Ludlow, B.; Cheah, J.H.; Adams, D.J.; Price, E.V.; Gill, S.; Javaid, S.; Coletti, M.E.; Jones, V.L.; Bodycombe, N.E.; et al. Correlating chemical sensitivity and basal gene expression reveals mechanism of action. Nat. Chem. Biol. 2016, 12, 109–116. [Google Scholar] [CrossRef]
- Seyhan, A.A. Lost in translation: The valley of death across preclinical and clinical divide–identification of problems and overcoming obstacles. Transl. Med. Commun. 2019, 4, 1–19. [Google Scholar] [CrossRef]
- Kuenzi, B.M.; Park, J.; Fong, S.H.; Sanchez, K.S.; Lee, J.; Kreisberg, J.F.; Ma, J.; Ideker, T. Predicting drug response and synergy using a deep learning model of human cancer cells. Cancer Cell 2020, 38, 672–684. [Google Scholar] [CrossRef]
- Savage, N. Tapping into the drug discovery potential of AI. Biopharma Deal 2021. [Google Scholar] [CrossRef]
- Shoemaker, R.H. The NCI60 human tumour cell line anticancer drug screen. Nat. Rev. Cancer 2006, 6, 813–823. [Google Scholar] [CrossRef]
- Barretina, J.; Caponigro, G.; Stransky, N.; Venkatesan, K.; Margolin, A.A.; Kim, S.; Wilson, C.J.; Lehár, J.; Kryukov, G.V.; Sonkin, D.; et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature 2012, 483, 603–607. [Google Scholar] [CrossRef]
- Yang, W.; Soares, J.; Greninger, P.; Edelman, E.J.; Lightfoot, H.; Forbes, S.; Bindal, N.; Beare, D.; Smith, J.A.; Thompson, I.R.; et al. Genomics of Drug Sensitivity in Cancer (GDSC): A resource for therapeutic biomarker discovery in cancer cells. Nucleic Acids Res. 2012, 41, D955–D961. [Google Scholar] [CrossRef]
- Basu, A.; Bodycombe, N.E.; Cheah, J.H.; Price, E.V.; Liu, K.; Schaefer, G.I.; Ebright, R.Y.; Stewart, M.L.; Ito, D.; Wang, S.; et al. An interactive resource to identify cancer genetic and lineage dependencies targeted by small molecules. Cell 2013, 154, 1151–1161. [Google Scholar] [CrossRef]
- Seashore-Ludlow, B.; Rees, M.G.; Cheah, J.H.; Cokol, M.; Price, E.V.; Coletti, M.E.; Jones, V.; Bodycombe, N.E.; Soule, C.K.; Gould, J.; et al. Harnessing Connectivity in a Large-Scale Small-Molecule Sensitivity DatasetHarnessing Connectivity in a Sensitivity Dataset. Cancer Discov. 2015, 5, 1210–1223. [Google Scholar] [CrossRef]
- Iorio, F.; Knijnenburg, T.A.; Vis, D.J.; Bignell, G.R.; Menden, M.P.; Schubert, M.; Aben, N.; Gonçalves, E.; Barthorpe, S.; Lightfoot, H.; et al. A landscape of pharmacogenomic interactions in cancer. Cell 2016, 166, 740–754. [Google Scholar] [CrossRef]
- Güvenç Paltun, B.; Mamitsuka, H.; Kaski, S. Improving drug response prediction by integrating multiple data sources: Matrix factorization, kernel and network-based approaches. Brief. Bioinform. 2021, 22, 346–359. [Google Scholar] [CrossRef]
- Adam, G.; Rampášek, L.; Safikhani, Z.; Smirnov, P.; Haibe-Kains, B.; Goldenberg, A. Machine learning approaches to drug response prediction: Challenges and recent progress. NPJ Precis. Oncol. 2020, 4, 1–10. [Google Scholar] [CrossRef]
- Firoozbakht, F.; Yousefi, B.; Schwikowski, B. An overview of machine learning methods for monotherapy drug response prediction. Brief. Bioinform. 2022, 23, bbab408. [Google Scholar] [CrossRef]
- Riddick, G.; Song, H.; Ahn, S.; Walling, J.; Borges-Rivera, D.; Zhang, W.; Fine, H.A. Predicting in vitro drug sensitivity using Random Forests. Bioinformatics 2011, 27, 220–224. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, N.; Li, C.; Wang, H.; Fang, Y.; Wang, J.; Zheng, X. Anticancer drug sensitivity prediction in cell lines from baseline gene expression through recursive feature selection. BMC Cancer 2015, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, X.; Zhang, L.; Gao, Q. Improved anticancer drug response prediction in cell lines using matrix factorization with similarity regularization. BMC Cancer 2017, 17, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Guan, N.N.; Zhao, Y.; Wang, C.C.; Li, J.Q.; Chen, X.; Piao, X. Anticancer drug response prediction in cell lines using weighted graph regularized matrix factorization. Mol. Ther. Nucleic Acids 2019, 17, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Baptista, D.; Ferreira, P.G.; Rocha, M. Deep learning for drug response prediction in cancer. Brief. Bioinform. 2021, 22, 360–379. [Google Scholar] [CrossRef] [PubMed]
- Sakellaropoulos, T.; Vougas, K.; Narang, S.; Koinis, F.; Kotsinas, A.; Polyzos, A.; Moss, T.J.; Piha-Paul, S.; Zhou, H.; Kardala, E.; et al. A deep learning framework for predicting response to therapy in cancer. Cell Rep. 2019, 29, 3367–3373. [Google Scholar] [CrossRef]
- Chiu, Y.C.; Chen, H.I.H.; Zhang, T.; Zhang, S.; Gorthi, A.; Wang, L.J.; Huang, Y.; Chen, Y. Predicting drug response of tumors from integrated genomic profiles by deep neural networks. BMC Med. Genom. 2019, 12, 143–155. [Google Scholar]
- Sharifi-Noghabi, H.; Zolotareva, O.; Collins, C.C.; Ester, M. MOLI: Multi-omics late integration with deep neural networks for drug response prediction. Bioinformatics 2019, 35, i501–i509. [Google Scholar] [CrossRef]
- Liu, P.; Li, H.; Li, S.; Leung, K.S. Improving prediction of phenotypic drug response on cancer cell lines using deep convolutional network. BMC Bioinform. 2019, 20, 1–14. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, Z.; Jiang, R.; Zhou, M. DeepCDR: A hybrid graph convolutional network for predicting cancer drug response. Bioinformatics 2020, 36, i911–i918. [Google Scholar] [CrossRef]
- Nguyen, T.; Nguyen, G.T.; Nguyen, T.; Le, D.H. Graph convolutional networks for drug response prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 19, 146–154. [Google Scholar] [CrossRef]
- Kim, S.; Bae, S.; Piao, Y.; Jo, K. Graph convolutional network for drug response prediction using gene expression data. Mathematics 2021, 9, 772. [Google Scholar] [CrossRef]
- Zhu, Y.; Ouyang, Z.; Chen, W.; Feng, R.; Chen, D.Z.; Cao, J.; Wu, J. TGSA: Protein–protein association-based twin graph neural networks for drug response prediction with similarity augmentation. Bioinformatics 2022, 38, 461–468. [Google Scholar] [CrossRef]
- Feng, R.; Xie, Y.; Lai, M.; Chen, D.Z.; Cao, J.; Wu, J. AGMI: Attention-Guided Multi-omics Integration for Drug Response Prediction with Graph Neural Networks. In Proceedings of the 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Houston, TX, USA, 9–12 December 2021; pp. 1295–1298. [Google Scholar]
- Peng, W.; Liu, H.; Dai, W.; Yu, N.; Wang, J. Predicting cancer drug response using parallel heterogeneous graph convolutional networks with neighborhood interactions. Bioinformatics 2022, 38, 4546–4553. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, P.; Chen, X.; Tian, L.; Ge, H.; Qian, D. SWnet: A deep learning model for drug response prediction from cancer genomic signatures and compound chemical structures. BMC Bioinform. 2021, 22, 1–16. [Google Scholar] [CrossRef]
- Deng, L.; Cai, Y.; Zhang, W.; Yang, W.; Gao, B.; Liu, H. Pathway-guided deep neural network toward interpretable and predictive modeling of drug sensitivity. J. Chem. Inf. Model. 2020, 60, 4497–4505. [Google Scholar] [CrossRef]
- DepMap Broad. DepMap 21Q4 Public. Figshare. Dataset. 2021. Available online: https://portals.broadinstitute.org/ccle (accessed on 3 December 2021).
- Szklarczyk, D.; Gable, A.L.; Lyon, D.; Junge, A.; Wyder, S.; Huerta-Cepas, J.; Simonovic, M.; Doncheva, N.T.; Morris, J.H.; Bork, P.; et al. STRING v11: Protein–Protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res. 2019, 47, D607–D613. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, J.; Suzek, T.O.; Zhang, J.; Wang, J.; Bryant, S.H. PubChem: A public information system for analyzing bioactivities of small molecules. Nucleic Acids Res. 2009, 37, W623–W633. [Google Scholar] [CrossRef]
- Sondka, Z.; Bamford, S.; Cole, C.G.; Ward, S.A.; Dunham, I.; Forbes, S.A. The COSMIC Cancer Gene Census: Describing genetic dysfunction across all human cancers. Nat. Rev. Cancer 2018, 18, 696–705. [Google Scholar] [CrossRef]
- Field-Smith, A.; Morgan, G.J.; Davies, F.E. Bortezomib (Velcade™) in the treatment of multiple myeloma. Ther. Clin. Risk Manag. 2006, 2, 271. [Google Scholar] [CrossRef]
- Kouroukis, T.; Baldassarre, F.; Haynes, A.; Imrie, K.; Reece, D.; Cheung, M. Bortezomib in multiple myeloma: Systematic review and clinical considerations. Curr. Oncol. 2014, 21, 573–603. [Google Scholar] [CrossRef] [PubMed]
- Récher, C.; Beyne-Rauzy, O.; Demur, C.; Chicanne, G.; Dos Santos, C.; Mas, V.M.D.; Benzaquen, D.; Laurent, G.; Huguet, F.; Payrastre, B. Antileukemic activity of rapamycin in acute myeloid leukemia. Blood 2005, 105, 2527–2534. [Google Scholar] [CrossRef] [PubMed]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Wishart, D.S.; Knox, C.; Guo, A.C.; Cheng, D.; Shrivastava, S.; Tzur, D.; Gautam, B.; Hassanali, M. DrugBank: A knowledgebase for drugs, drug actions and drug targets. Nucleic Acids Res. 2008, 36, D901–D906. [Google Scholar] [CrossRef] [PubMed]
- Safran, M.; Dalah, I.; Alexander, J.; Rosen, N.; Iny Stein, T.; Shmoish, M.; Nativ, N.; Bahir, I.; Doniger, T.; Krug, H.; et al. GeneCards Version 3: The human gene integrator. Database 2010, 2010, baq020. [Google Scholar] [CrossRef] [PubMed]
- Rouillard, A.D.; Gundersen, G.W.; Fernandez, N.F.; Wang, Z.; Monteiro, C.D.; McDermott, M.G.; Ma’ayan, A. The harmonizome: A collection of processed datasets gathered to serve and mine knowledge about genes and proteins. Database 2016, 2016, baw100. [Google Scholar] [CrossRef]
- Ioannou, N.; Dalgleish, A.; Seddon, A.; Mackintosh, D.; Guertler, U.; Solca, F.; Modjtahedi, H. Anti-tumour activity of afatinib, an irreversible ErbB family blocker, in human pancreatic tumour cells. Br. J. Cancer 2011, 105, 1554–1562. [Google Scholar] [CrossRef]
- Fernandes, M.T.; Dejardin, E.; dos Santos, N.R. Context-dependent roles for lymphotoxin-𝛽 receptor signaling in cancer development. Biochim. Biophys. Acta BBA Rev. Cancer 2016, 1865, 204–219. [Google Scholar] [CrossRef]
- Canale, M.; Andrikou, K.; Priano, I.; Cravero, P.; Pasini, L.; Urbini, M.; Delmonte, A.; Crinò, L.; Bronte, G.; Ulivi, P. The Role of TP53 Mutations in EGFR-Mutated Non-Small-Cell Lung Cancer: Clinical Significance and Implications for Therapy. Cancers 2022, 14, 1143. [Google Scholar] [CrossRef]
- Tishler, R.B.; Lamppu, D.M.; Park, S.; Price, B.D. Microtubule-active drugs taxol, vinblastine, and nocodazole increase the levels of transcriptionally active p53. Cancer Res. 1995, 55, 6021–6025. [Google Scholar]
- Tanaka, M.; Shibahara, J.; Fukushima, N.; Shinozaki, A.; Umeda, M.; Ishikawa, S.; Kokudo, N.; Fukayama, M. Claudin-18 is an early-stage marker of pancreatic carcinogenesis. J. Histochem. Cytochem. 2011, 59, 942–952. [Google Scholar] [CrossRef]
- Stewart, D.J. Wnt signaling pathway in non–small cell lung cancer. J. Natl. Cancer Inst. 2014, 106, djt356. [Google Scholar] [CrossRef]
- Hah, Y.S.; Cho, H.Y.; Lim, T.Y.; Park, D.H.; Kim, H.M.; Yoon, J.; Kim, J.G.; Kim, C.Y.; Yoon, T.J. Induction of melanogenesis by rapamycin in human MNT-1 melanoma cells. Ann. Dermatol. 2012, 24, 151–157. [Google Scholar] [CrossRef]
- Mehnert, J.M.; Tan, A.R.; Moss, R.; Poplin, E.; Stein, M.N.; Sovak, M.; Levinson, K.; Lin, H.; Kane, M.; Gounder, M.; et al. Rationally Designed Treatment for Solid Tumors with MAPK Pathway Activation: A Phase I Study of Paclitaxel and Bortezomib Using an Adaptive Dose-Finding ApproachPaclitaxel and Bortezomib for Tumors with MAPK Activation. Mol. Cancer Ther. 2011, 10, 1509–1519. [Google Scholar] [CrossRef]
- Izzi, L.; Attisano, L. Regulation of the TGF-𝛽 signalling pathway by ubiquitin-mediated degradation. Oncogene 2004, 23, 2071–2078. [Google Scholar] [CrossRef]
- Huang, F.; Chen, Y.G. Regulation of TGF-𝛽 receptor activity. Cell Biosci. 2012, 2, 1–10. [Google Scholar] [CrossRef]
- Iyengar, P.V. Regulation of Ubiquitin Enzymes in the TGF-𝛽 Pathway. Int. J. Mol. Sci. 2017, 18, 877. [Google Scholar] [CrossRef]
- Seoane, J.; Gomis, R.R. TGF-𝛽 family signaling in tumor suppression and cancer progression. Cold Spring Harb. Perspect. Biol. 2017, 9, a022277. [Google Scholar] [CrossRef]
- Keskin, D.; Sadri, S.; Eskazan, A.E. Dasatinib for the treatment of chronic myeloid leukemia: Patient selection and special considerations. Drug Des. Dev. Ther. 2016, 10, 3355. [Google Scholar] [CrossRef]
- Sun, H.; Kapuria, V.; Peterson, L.F.; Fang, D.; Bornmann, W.G.; Bartholomeusz, G.; Talpaz, M.; Donato, N.J. Bcr-Abl ubiquitination and Usp9x inhibition block kinase signaling and promote CML cell apoptosis. Blood J. Am. Soc. Hematol.y 2011, 117, 3151–3162. [Google Scholar] [CrossRef]
- Bartscht, T.; Rosien, B.; Rades, D.; Kaufmann, R.; Biersack, H.; Lehnert, H.; Gieseler, F.; Ungefroren, H. Dasatinib blocks transcriptional and promigratory responses to transforming growth factor-beta in pancreatic adenocarcinoma cells through inhibition of Smad signalling: Implications for in vivo mode of action. Mol. Cancer 2015, 14, 1–12. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, L.; Shi, L.; Yun, F.; Liu, X.; Chen, Y.; Chen, C.; Ren, Y.; Jia, Y. Transcriptome profiling revealed multiple genes and ECM-receptor interaction pathways that may be associated with breast cancer. Cell. Mol. Biol. Lett. 2019, 24, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning (PMLR), Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Li, M.M.; Huang, K.; Zitnik, M. Graph Representation Learning in Biomedicine. arXiv 2021, arXiv:2104.04883. [Google Scholar]
- Dai, E.; Zhao, T.; Zhu, H.; Xu, J.; Guo, Z.; Liu, H.; Tang, J.; Wang, S. A Comprehensive Survey on Trustworthy Graph Neural Networks: Privacy, Robustness, Fairness, and Explainability. arXiv 2022, arXiv:2204.08570. [Google Scholar]
- Lee, S.; Lim, S.; Lee, T.; Sung, I.; Kim, S. Cancer subtype classification and modeling by pathway attention and propagation. Bioinformatics 2020, 36, 3818–3824. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Zhang, M.; Cui, Z.; Neumann, M.; Chen, Y. An end-to-end deep learning architecture for graph classification. In Proceedings of the AAAI conference on Artificial Intelligence, New Orleans, LA, USA, 2 February 2018; Volume 32. [Google Scholar]
- Gao, H.; Ji, S. Graph u-nets. In Proceedings of the International Conference On Machine Learning (PMLR), Long Beach, CA, USA, 9–15 June 2019; pp. 2083–2092. [Google Scholar]
- Lee, J.; Lee, I.; Kang, J. Self-attention graph pooling. In Proceedings of the International Conference on Machine Learning (PMLR), Long Beach, CA, USA, 9–15 June 2019; pp. 3734–3743. [Google Scholar]
- Landrum, G. RDKit: A Software Suite for Cheminformatics, Computational Chemistry, and Predictive Modeling. 2013. Available online: http://rdkit.sourceforge.net (accessed on 16 September 2021).
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Weisfeiler, B.; Leman, A. The reduction of a graph to canonical form and the algebra which appears therein. NTI Ser. 1968, 2, 12–16. [Google Scholar]
- Zheng, K.; Zhao, H.; Zhao, Q.; Wang, B.; Gao, X.; Wang, J. NASMDR: A framework for miRNA-drug resistance prediction using efficient neural architecture search and graph isomorphism networks. Brief. Bioinform. 2022, 20, bbac338. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1025–1035. [Google Scholar]
| Structural Settings of DRPreter | Data | MSE (↓) | MAE (↓) | PCC (↑) | SCC (↑) |
|---|---|---|---|---|---|
| Template graph | COSMIC 1 | 0.8926 ± 0.0363 | 0.6909 ± 0.0146 | 0.9423 ± 0.0027 | 0.9196 ± 0.0034 |
| Template graph | Pathway 2 | 0.8536 ± 0.0420 | 0.6759 ± 0.0161 | 0.9449 ± 0.0032 | 0.9224 ± 0.0035 |
| Pathway | Pathway 2 | 0.8645 ± 0.0277 | 0.6791 ± 0.0113 | 0.9446 ± 0.0014 | 0.9233 ± 0.0008 |
| Pathway + Transformer | Pathway 2 | 0.8302 ± 0.0156 | 0.6676 ± 0.0051 | 0.9465 ± 0.0015 | 0.9242 ± 0.0015 |
| Pathway + Transformer + Similarity | Pathway 2 | 0.8251 ± 0.0122 | 0.6682 ± 0.0047 | 0.9467 ± 0.0013 | 0.9248 ± 0.0014 |
| Model | Cell Encoder | Data | MSE (↓) | MAE (↓) | PCC (↑) | SCC (↑) |
|---|---|---|---|---|---|---|
| SVM 1 | - | Pathway | 8.5780 ± 2.0615 | 2.2976 ± 0.3005 | 0.5282 ± 0.0355 | 0.4471 ± 0.0476 |
| RF 2 | - | Pathway | 1.6711 ± 0.0422 | 0.9608 ± 0.0100 | 0.8887 ± 0.0021 | 0.8497 ± 0.0034 |
| GraphDRP | 1D CNN | COSMIC | 1.0110 ± 0.0157 | 0.7618 ± 0.0083 | 0.9386 ± 0.0018 | 0.9151 ± 0.0021 |
| TGDRP | GNN | COSMIC | 0.9004 ± 0.0341 | 0.6933 ± 0.0148 | 0.9417 ± 0.0026 | 0.9188 ± 0.0040 |
| TGSA | GNN | COSMIC | 0.8955 ± 0.0536 | 0.6913 ± 0.0238 | 0.9425 ± 0.0043 | 0.9201 ± 0.0051 |
| DRPreter | Knowledge-guided GNN | Pathway | 0.8251±0.0122 | 0.6682±0.0047 | 0.9467±0.0013 | 0.9248±0.0014 |
| Comparison Models | Data | MSE (↓) | MAE (↓) | PCC (↑) | SCC (↑) |
|---|---|---|---|---|---|
| TGDRP | COSMIC 1 | 1.9398 ± 0.0231 | 1.0435 ± 0.0058 | 0.8665 ± 0.0026 | 0.8164 ± 0.0074 |
| DRPreter Template graph | COSMIC 1 | 1.9665 ± 0.0323 | 1.0435 ± 0.0089 | 0.8685 ± 0.0018 | 0.8232 ± 0.0022 |
| DRPreter Template graph | Pathway 2 | 1.9276 ± 0.0495 | 1.0351 ± 0.0130 | 0.8711 ± 0.0034 | 0.8270 ± 0.0042 |
| DRPreter w/o Trans 3 and Similarity | Pathway 2 | 1.8536 ± 0.0548 | 1.0085 ± 0.0123 | 0.8820±0.0049 | 0.8445±0.0094 |
| DRPreter w/o similarity | Pathway 2 | 1.8317±0.0276 | 1.0076±0.0067 | 0.8778 ± 0.0018 | 0.8356 ± 0.0022 |
| Drug | Cell Line | Disease | Top 5 Significant Genes | ln(IC50) | |
|---|---|---|---|---|---|
| True | Predicted | ||||
| Afatinib | GMS-10 | Glioblastoma | ACTR3B, PRR5, PRKCZ, ERBB2, LTBR | 0.5372 | 0.5324 |
| Vinblastine | NCI-H1792 | NSCLC | CYP7A1, GTF2H2, DVL2, RAB5B, TP53 | −5.9258 | −5.27633 |
| Docetaxel | PANC0327 | Pancreatic cancer | CLDN18, SOX17, FGF19, WNT7A, CDH5 | −3.7668 | −3.8204 |
| Rapamycin | IGR1 | Melanoma | TYRP1, DCT, TYR, FRZB, CDK2 | −1.6747 | −1.7651 |
| Bortezomib | EBC-1 | Lung squamous cell carcinoma Derived from metastatic site: Skin | SHC4, TNR, IL17RA, MAPK12, SMURF1 | −5.7714 | −6.0714 |
| Notation | Description |
|---|---|
| G | A graph. |
| V | Set of nodes of a graph. |
| v | A node included in V. |
| Indexes of the nodes. | |
| l | Index of the layer of a graph. |
| i-th node in V. | |
| Node feature of node | |
| N(i) | Set of neighbor nodes of a node |
| E | Set of edges of a graph. |
| A | Adjacency matrix between nodes. |
| Trainable parameter matrix of l-th layer. | |
| Node feature matrix of l-th layer. | |
| Nonlinear activation function softmax. | |
| Learnable parameter. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, J.; Piao, Y.; Bang, D.; Kim, S.; Jo, K. DRPreter: Interpretable Anticancer Drug Response Prediction Using Knowledge-Guided Graph Neural Networks and Transformer. Int. J. Mol. Sci. 2022, 23, 13919. https://doi.org/10.3390/ijms232213919
Shin J, Piao Y, Bang D, Kim S, Jo K. DRPreter: Interpretable Anticancer Drug Response Prediction Using Knowledge-Guided Graph Neural Networks and Transformer. International Journal of Molecular Sciences. 2022; 23(22):13919. https://doi.org/10.3390/ijms232213919
Chicago/Turabian StyleShin, Jihye, Yinhua Piao, Dongmin Bang, Sun Kim, and Kyuri Jo. 2022. "DRPreter: Interpretable Anticancer Drug Response Prediction Using Knowledge-Guided Graph Neural Networks and Transformer" International Journal of Molecular Sciences 23, no. 22: 13919. https://doi.org/10.3390/ijms232213919
APA StyleShin, J., Piao, Y., Bang, D., Kim, S., & Jo, K. (2022). DRPreter: Interpretable Anticancer Drug Response Prediction Using Knowledge-Guided Graph Neural Networks and Transformer. International Journal of Molecular Sciences, 23(22), 13919. https://doi.org/10.3390/ijms232213919







