Probing Surface and Interfacial Tension of Ionic Liquids in Vacuum with the Pendant Drop and Sessile Drop Method
Abstract
1. Introduction
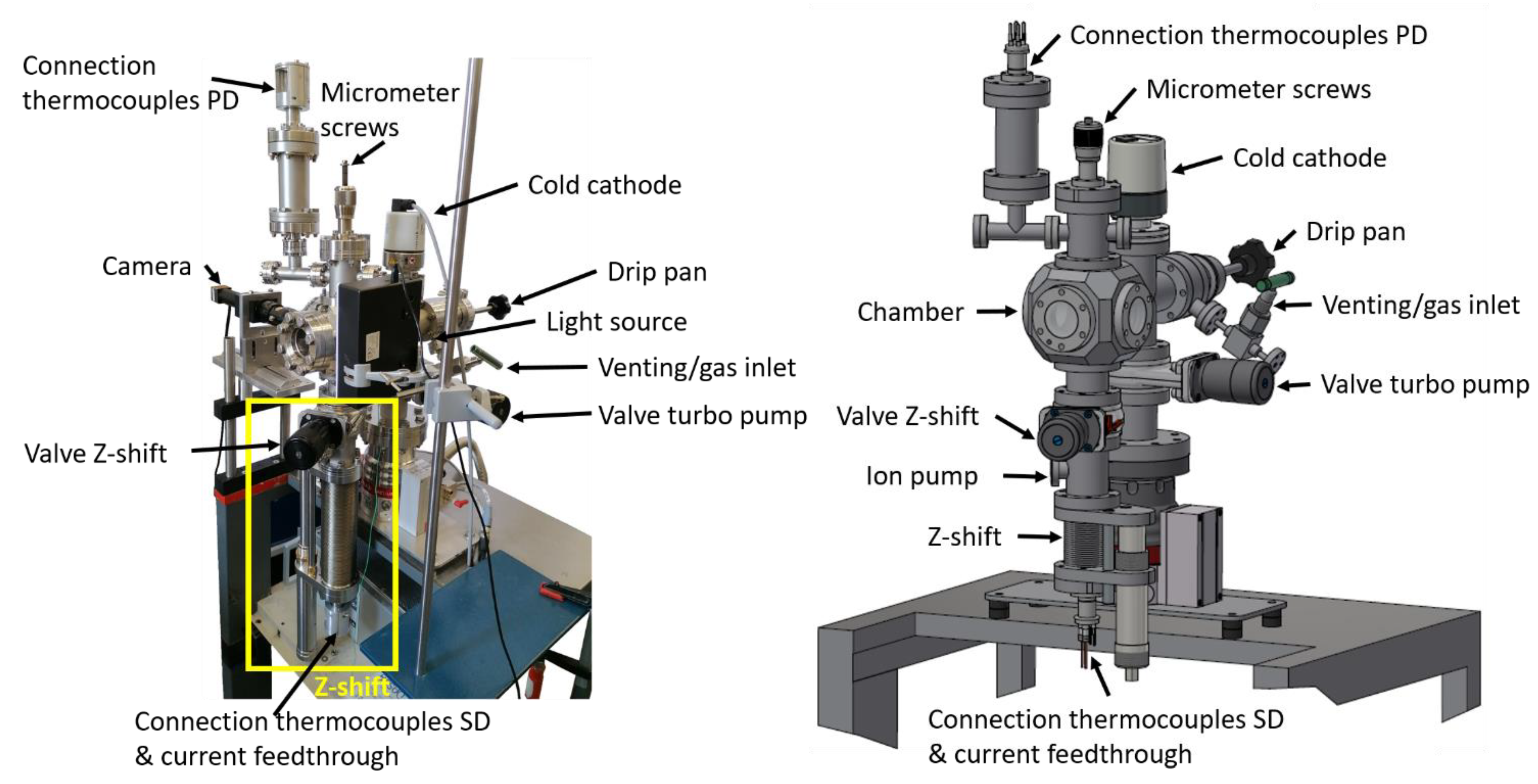
2. Setup
2.1. General Setup
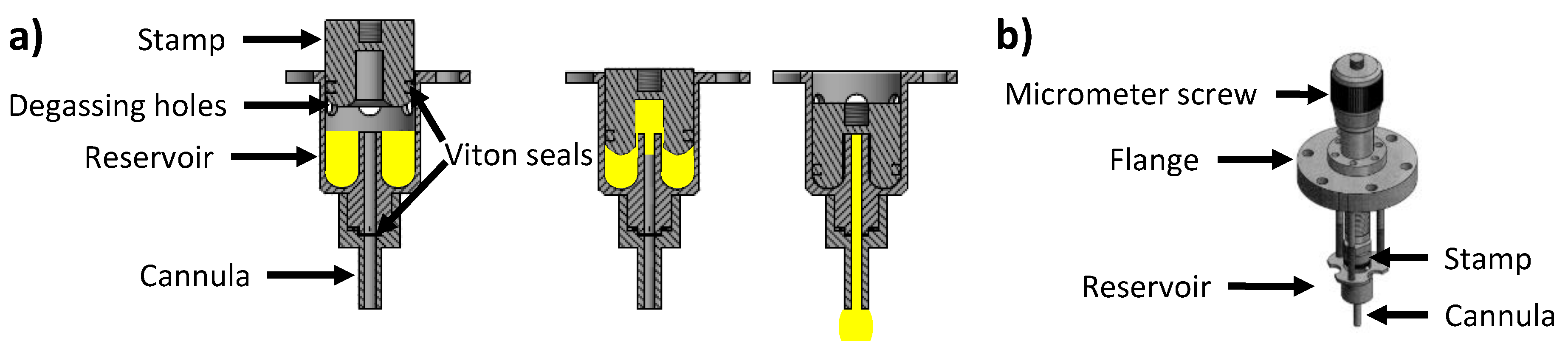
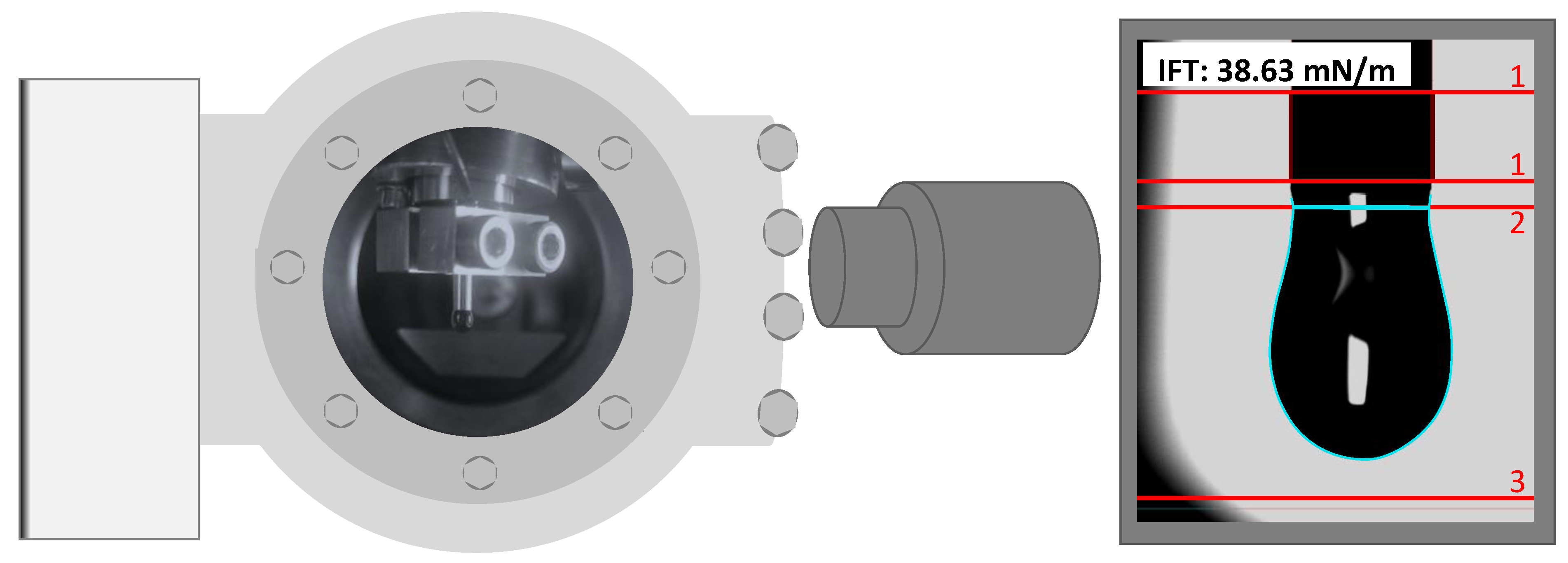
2.2. Pendant Drop
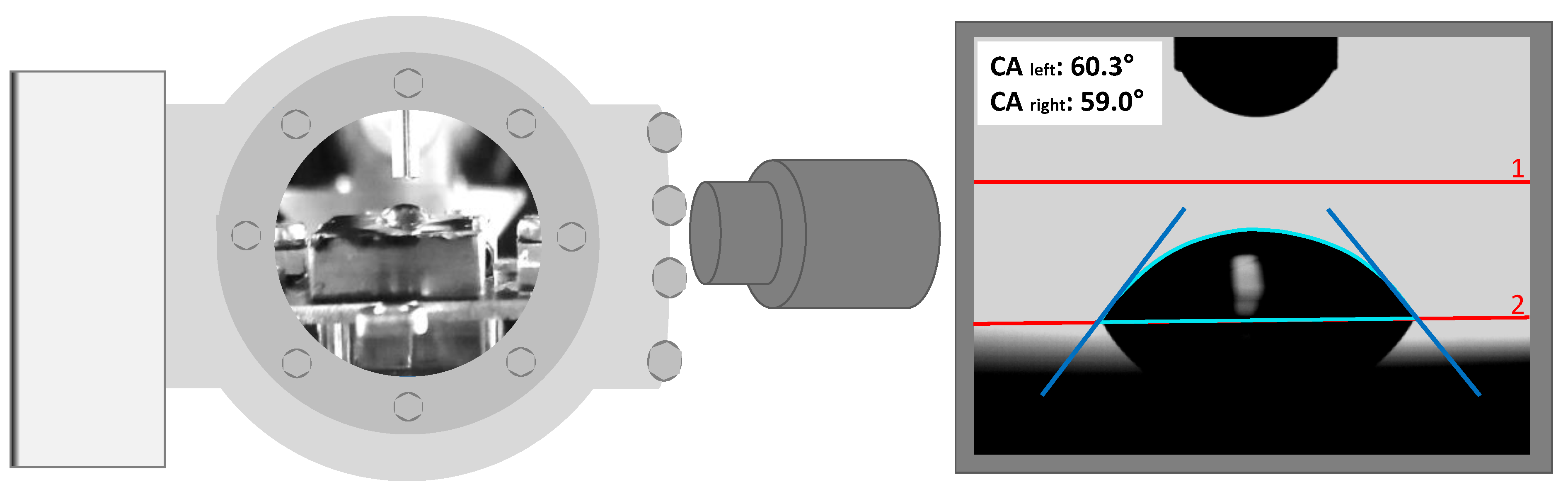
2.3. Sessile Drop
3. Reference Pendant Drop Measurements in Air
3.1. Water
3.2. Benzene
4. Pendant Drop Measurements on Ionic Liquids in High Vacuum
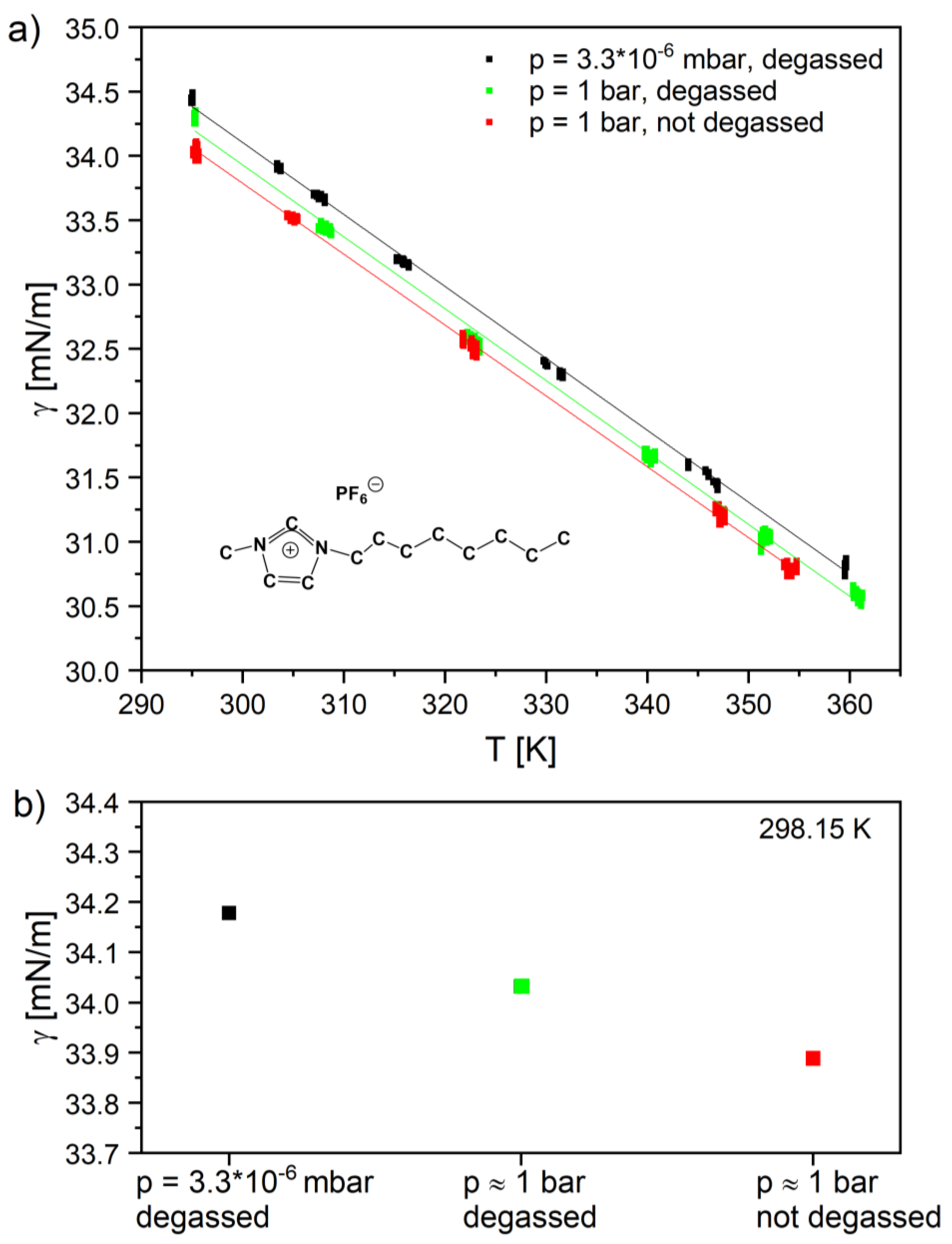
4.1. 1-Methly-3-Octylimidazolium Hexafluorophosphate [C8C1Im][PF6] in Vacuum and Air
4.2. Bis-Polyethylene Glycol-Functionalized Imidazolium Iodides [(mPEGn)2Im]I in Vacuum
5. Summary and Conclusions
6. Materials
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sedev, R. Surface tension, interfacial tension and contact angles of ionic liquids. Curr. Opin. Colloid Interface Sci. 2011, 16, 310–316. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Mahmoudi, B. Development of robust model to estimate gas–oil interfacial tension using least square support vector machine: Experimental and modeling study. J. Supercrit. Fluids 2016, 107, 122–128. [Google Scholar] [CrossRef]
- Langmuir, I. Forces Near the Surfaces of Molecules. Chem. Rev. 1930, 6, 451–479. [Google Scholar] [CrossRef]
- Pádua, A.A.; Costa Gomes, M.F.; Canongia Lopes, J.N. Molecular solutes in ionic liquids: A structural perspective. Acc. Chem. Res. 2007, 40, 1087–1096. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Y.; Yan, T.; Voth, G.A. A multiscale coarse-graining study of the liquid/vacuum interface of room-temperature ionic liquids with alkyl substituents of different lengths. J. Phys. Chem. C 2008, 112, 1132–1139. [Google Scholar] [CrossRef]
- Plechkova, N.V.; Seddon, K.R. Applications of ionic liquids in the chemical industry. Chem. Soc. Rev. 2008, 37, 123–150. [Google Scholar] [CrossRef]
- Kaur, G.; Kumar, H.; Singla, M. Diverse applications of ionic liquids: A comprehensive review. J. Mol. Liq. 2022, 351, 118556. [Google Scholar] [CrossRef]
- Shimizu, K.; Heller, B.S.J.; Maier, F.; Steinrück, H.-P.; Lopes, J.N.C. Probing the surface tension of ionic liquids using the langmuir principle. Langmuir 2018, 34, 4408–4416. [Google Scholar] [CrossRef]
- Massoudi, R.; King, A.D. Effect of pressure on the surface tension of water. Adsorption of low molecular weight gases on water at 25. deg. J. Phys. Chem. 1974, 78, 2262–2266. [Google Scholar] [CrossRef]
- Sachs, W.; Meyn, V. Pressure and temperature dependence of the surface tension in the system natural gas/water principles of investigation and the first precise experimental data for pure methane/water at 25 °C up to 46.8 MPa. Colloids Surf. A Physicochem. Eng. Asp. 1995, 94, 291–301. [Google Scholar] [CrossRef]
- Steinrück, H.-P.; Libuda, J.; Wasserscheid, P.; Cremer, T.; Kolbeck, C.; Laurin, M.; Maier, F.; Sobota, M.; Schulz, P.S.; Stark, M. Surface science and model catalysis with ionic liquid-modified materials. Adv. Mater. 2011, 23, 2571–2587. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, H.; Ohno, A.; Nakajima, K.; Suzuki, M.; Tsuji, H.; Kimura, K. Surface characterization of imidazolium ionic liquids by high-resolution Rutherford backscattering spectroscopy and X-ray photoelectron spectroscopy. Surf. Sci. 2010, 604, 464–469. [Google Scholar] [CrossRef]
- Smith, E.F.; Rutten, F.J.M.; Villar-Garcia, I.J.; Briggs, D.; Licence, P. Ionic liquids in vacuo: Analysis of liquid surfaces using ultra-high-vacuum techniques. Langmuir 2006, 22, 9386–9392. [Google Scholar] [CrossRef] [PubMed]
- Santos, C.S.; Baldelli, S. Gas–liquid interface of room-temperature ionic liquids. Chem. Soc. Rev. 2010, 39, 2136–2145. [Google Scholar] [CrossRef] [PubMed]
- Goodman, D.W. Model studies in catalysis using surface science probes. Chem. Rev. 1995, 95, 523–536. [Google Scholar] [CrossRef]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.C.; Tabor, R.F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef]
- Franses, E.I.; Basaran, O.A.; Chang, C.-H. Techniques to measure dynamic surface tension. Curr. Opin. Colloid Interface Sci. 1996, 1, 296–303. [Google Scholar] [CrossRef]
- Tariq, M.; Freire, M.G.; Saramago, B.; Coutinho, J.A.; Lopes, J.N.C.; Rebelo, L.P.N. Surface tension of ionic liquids and ionic liquid solutions. Chem. Soc. Rev. 2012, 41, 829–868. [Google Scholar] [CrossRef]
- Hoorfar, M.; Kurz, M.A.; Neumann, A.W. Evaluation of the surface tension measurement of axisymmetric drop shape analysis (ADSA) using a shape parameter. Colloids Surf. A Physicochem. Eng. Asp. 2005, 260, 277–285. [Google Scholar] [CrossRef]
- Ferrera, C.; Montanero, J.M.; Cabezas, M.G. An analysis of the sensitivity of pendant drops and liquid bridges to measure the interfacial tension. Meas. Sci. Technol. 2007, 18, 3713–3723. [Google Scholar] [CrossRef]
- Saad, S.M.; Policova, Z.; Acosta, E.J.; Neumann, W.A. Range of validity of drop shape techniques for surface tension measurement. Langmuir 2010, 26, 14004–14013. [Google Scholar] [CrossRef] [PubMed]
- Worthington, A.M. II. On pendent drops. Proc. R. Soc. Lond. 1881, 32, 362–377. [Google Scholar]
- Worthington, A.M. IV. Note on a point in the theory of pendent drops. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1885, 19, 46–48. [Google Scholar] [CrossRef][Green Version]
- Ferguson, A. Photographic measurements of pendant drops. Philos. Mag. 1911, 23, 417–430. [Google Scholar] [CrossRef]
- Bashforth, F.; Adams, J.C. An Attempt to Test the Theories of Capillary Action by Comparing the Theoretical and Measured Forms of Drops of Fluid; University Press: Cambridge, UK, 1883. [Google Scholar]
- Merrington, A.C.; Richardson, E.G. The break-up of liquid jets. Proc. Phys. Soc. 1947, 59, 1–13. [Google Scholar] [CrossRef]
- Andreas, J.M.; Hauser, E.A.; Tucker, W.B. Boundary tension by pendant drops. J. Phys. Chem. 1938, 42, 1001–1019. [Google Scholar] [CrossRef]
- Fordham, S.; Freeth, F.A. On the calculation of surface tension from measurements of pendant drops. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 194, 1–16. [Google Scholar]
- Cheng, P.; Li, D.; Boruvka, L.; Rotenberg, Y.; Neumann, W.A. Automation of axisymmetric drop shape analysis for measurements of interfacial tensions and contact angles. Colloids Surf. 1990, 43, 151–167. [Google Scholar] [CrossRef]
- Del Río, O.I.; Neumann, A.W. Axisymmetric drop shape analysis: Computational methods for the measurement of interfacial properties from the shape and dimensions of pendant and sessile drops. J. Colloid Interface Sci. 1997, 196, 136–147. [Google Scholar]
- Rotenberg, Y.; Boruvka, L.; Neumann, A.W. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces. J. Colloid Interface Sci. 1983, 93, 169–183. [Google Scholar] [CrossRef]
- Hoorfar, M.; Neumann, A.W. Recent progress in axisymmetric drop shape analysis (ADSA). Adv. Colloid Interface Sci. 2006, 121, 25–49. [Google Scholar] [CrossRef] [PubMed]
- Huh, C.; Reed, R.L. A method for estimating interfacial tensions and contact angles from sessile and pendant drop shapes. J. Colloid Interface Sci. 1983, 91, 472–484. [Google Scholar] [CrossRef]
- Schuster, J.M.; Schvezov, C.E.; Rosenberger, M.R. Influence of experimental variables on the measure of contact angle in metals using the sessile drop method. Procedia Mater. Sci. 2015, 8, 742–751. [Google Scholar] [CrossRef]
- Young, T. III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar]
- Spelt, J.K.; Absolom, D.R.; Neumann, A.W. Solid surface tension: The interpretation of contact angles by the equation of state approach and the theory of surface tension components. Langmuir 1986, 2, 620–625. [Google Scholar] [CrossRef]
- Niedermaier, I.; Kolbeck, C.; Steinrück, H.-P.; Maier, F. Dual analyzer system for surface analysis dedicated for angle-resolved photoelectron spectroscopy at liquid surfaces and interfaces. Rev. Sci. Instrum. 2016, 87, 045105. [Google Scholar] [CrossRef]
- Saad, S.M.I.; Policova, Z.; Neumann, A.W. Design and accuracy of pendant drop methods for surface tension measurement. Colloids Surf. A Physicochem. Eng. Asp. 2011, 384, 442–452. [Google Scholar] [CrossRef]
- Kaelble, D.H.; Cirlin, E.H. Dispersion and polar contributions to surface tension of poly (methylene oxide) and Na-treated polytetrafluoroethylene. J. Polym. Sci. Part A-2 Polym. Phys. 1971, 9, 363–368. [Google Scholar] [CrossRef]
- Blythe, A.R.; Briggs, D.; Kendall, C.R.; Rance, D.G.; Zichy, V.J.I. Surface modification of polyethylene by electrical discharge treatment and the mechanism of autoadhesion. Polymer 1978, 19, 1273–1278. [Google Scholar] [CrossRef]
- Fowkes, F.M.; McCarthy, D.C.; Mostafa, M.A. Contact angles and the equilibrium spreading pressures of liquids on hydrophobic solids. J. Colloid Interface Sci. 1980, 78, 200–206. [Google Scholar] [CrossRef]
- Rudawska, A.; Jacniacka, E. Analysis for determining surface free energy uncertainty by the Owen–Wendt method. Int. J. Adhes. Adhes. 2009, 29, 451–457. [Google Scholar] [CrossRef]
- Vuckovac, M.; Latikka, M.; Liu, K.; Huhtamäki, T.; Ras, R.H.A. Uncertainties in contact angle goniometry. Soft Matter 2019, 15, 7089–7096. [Google Scholar] [CrossRef] [PubMed]
- Rietzler, F.; Nagengast, J.; Steinrück, H.P.; Maier, F. Interface of ionic liquids and carbon: Ultrathin [C1C1Im][Tf2N] films on graphite and graphene. J. Phys. Chem. C 2015, 119, 28068–28076. [Google Scholar] [CrossRef]
- Vargaftik, N.B.; Volkov, B.N.; Voljak, L.D. International tables of the surface tension of water. J. Phys. Chem. Ref. Data 1983, 12, 817–820. [Google Scholar] [CrossRef]
- Kell, G.S. Density, thermal expansivity, and compressibility of liquid water from 0. deg. to 150. deg. Correlations and tables for atmospheric pressure and saturation reviewed and expressed on 1968 temperature scale. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar] [CrossRef]
- Parkhurst, H.J., Jr.; Jonas, J. Dense liquids. II. The effect of density and temperature on viscosity of tetramethylsilane and benzene. J. Chem. Phys. 1975, 63, 2705–2709. [Google Scholar] [CrossRef]
- Sugden, S. VI—The variation of surface tension with temperature and some related functions. J. Chem. Soc. Trans. 1924, 125, 32–41. [Google Scholar] [CrossRef]
- Sánchez, L.G.; Espel, J.R.; Onink, F.; Meindersma, G.W.; Haan, A.B.D. Density, viscosity, and surface tension of synthesis grade imidazolium, pyridinium, and pyrrolidinium based room temperature ionic liquids. J. Chem. Eng. Data 2009, 54, 2803–2812. [Google Scholar] [CrossRef]
- Naser, M.A.; Permadi, A.K.; Bae, W.; Ryoo, W.; Siregar, S. A laboratory investigation of the effects of saturated steam properties on the interfacial tension of heavy-oil/steam system using pendant drop method. Energy Environ. Res. 2015, 5, 94. [Google Scholar] [CrossRef]
- Kahl, H.; Wadewitz, T.; Winkelmann, J. Surface tension of pure liquids and binary liquid mixtures. J. Chem. Eng. Data 2003, 48, 580–586. [Google Scholar] [CrossRef]
- Gardas, R.L.; Freire, M.G.; Carvalho, P.J.; Marrucho, I.M.; Fonseca, I.M.A.; Ferreira, A.G.M.; Coutinho, J.A.P. High-pressure densities and derived thermodynamic properties of imidazolium-based ionic liquids. J. Chem. Eng. Data 2007, 52, 80–88. [Google Scholar] [CrossRef]
- Klomfar, J.; Součková, M.; Pátek, J. Surface tension measurements for four 1-alkyl-3-methylimidazolium-based ionic liquids with hexafluorophosphate anion. J. Chem. Eng. Data 2009, 54, 1389–1394. [Google Scholar] [CrossRef]
- Freire, M.G.; Carvalho, P.J.; Fernandes, A.M.; Marrucho, I.M.; Queimada, A.J.; Coutinho, J.A.P. Surface tensions of imidazolium based ionic liquids: Anion, cation, temperature and water effect. J. Colloid Interface Sci. 2007, 314, 621–630. [Google Scholar] [CrossRef] [PubMed]
- Freire, M.G.; Neves, C.M.S.S.; Marrucho, I.M.; Coutinho, J.A.P.; Fernandes, A.M. Hydrolysis of tetrafluoroborate and hexafluorophosphate counter ions in imidazolium-based ionic liquids. J. Phys. Chem. A 2010, 114, 3744–3749. [Google Scholar] [CrossRef] [PubMed]
- Seidl, V.; Bosch, M.; Paap, U.; Livraghi, M.; Zhai, Z.; Wick, C.; Koller, T.M.; Wasserscheid, P.; Maier, F.; Smith, A.-S.; et al. Bis-polyethylene glycol-functionalized imidazolium ionic liquids: A multi-method approach towards bulk and surface properties. J. Ion. Liq. 2022, 2, 100041. [Google Scholar] [CrossRef]
- Lin, S.-Y.; Hwang, H.-F. Measurement of low interfacial tension by pendant drop digitization. Langmuir 1994, 10, 4703–4709. [Google Scholar] [CrossRef]
- Morita, A.; Carastan, D.; Demarquette, N. Influence of drop volume on surface tension evaluated using the pendant drop method. Colloid Polym. Sci. 2002, 280, 857–864. [Google Scholar] [CrossRef]
- Alvarez, N.J.; Walker, L.M.; Anna, S.L. A non-gradient based algorithm for the determination of surface tension from a pendant drop: Application to low Bond number drop shapes. J. Colloid Interface Sci. 2009, 333, 557–562. [Google Scholar] [CrossRef]
- Yang, J.; Yu, K.; Zuo, Y.Y. Accuracy of Axisymmetric Drop Shape Analysis in Determining Surface and Interfacial Tensions. Langmuir 2017, 33, 8914–8923. [Google Scholar] [CrossRef]
- Hoorfar, M.; Neumann, A.W. Axsymmetric drop shape analysis (ADSA) for the determination of surface tension and contact angle of water. J. Adhes. 2004, 80, 727–743. [Google Scholar] [CrossRef]



| Reference Liquid | T (K) | ρ (g/cm3) | γ (mN/m) | γ (mN/m) Literature | Standard Deviaton Δγ (mN/m) | Maximum Deviaton (mN/m) | Deviation from Literature Value (%) |
|---|---|---|---|---|---|---|---|
| MP-water | 295.45 | 0.9990 [46] | 72.40 ± 0.06 | 72.34 [45] | 0.06 | <0.1 | |
| Benzene | 295.15 | 0.8767 [47] | 28.85 ± 0.03 | 28.62 [48] | 0.23 | 0.03 | 0.8 |
| Condition | p (mbar) | γ (mN/m) (T = 298.15 K) | γ (mN/m) from Ref [53] (T = 298.13 K) | γ0 (mN/m) | γ1 (mN/m·K−1) | R2 |
|---|---|---|---|---|---|---|
| Degassed | 3.3·10−6 | 34.18 | 50.88 | –0.0559 | 0.999 | |
| Degassed | 1.0·103 | 34.03 | 33.95 | 50.69 | –0.0559 | 0.997 |
| Non-degassed | 1.0·103 | 33.89 | 50.32 | –0.0551 | 0.999 |
| IL | γ (mN/m) at 5·10−6 mbar (T = 298.15 K) | γ (mN/m) from Ref. [56] at 1 bar Ar (T = 298.15 K) | γ0 (mN/m) | γ1 (mN/m·K−1) | R2 |
|---|---|---|---|---|---|
| [(mPEG2)2Im]I | 46.72 | 46.26 | 72.17 | –0.0854 | 0.997 |
| [(mPEG4)2Im]I | 43.95 | 43.94 | 71.05 | –0.0909 | 0.999 |
| [(mPEG6)2Im]I | 43.17 | 42.96 | 72.87 | –0.0996 | 0.997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paap, U.; Kreß, B.; Steinrück, H.-P.; Maier, F. Probing Surface and Interfacial Tension of Ionic Liquids in Vacuum with the Pendant Drop and Sessile Drop Method. Int. J. Mol. Sci. 2022, 23, 13158. https://doi.org/10.3390/ijms232113158
Paap U, Kreß B, Steinrück H-P, Maier F. Probing Surface and Interfacial Tension of Ionic Liquids in Vacuum with the Pendant Drop and Sessile Drop Method. International Journal of Molecular Sciences. 2022; 23(21):13158. https://doi.org/10.3390/ijms232113158
Chicago/Turabian StylePaap, Ulrike, Bernd Kreß, Hans-Peter Steinrück, and Florian Maier. 2022. "Probing Surface and Interfacial Tension of Ionic Liquids in Vacuum with the Pendant Drop and Sessile Drop Method" International Journal of Molecular Sciences 23, no. 21: 13158. https://doi.org/10.3390/ijms232113158
APA StylePaap, U., Kreß, B., Steinrück, H.-P., & Maier, F. (2022). Probing Surface and Interfacial Tension of Ionic Liquids in Vacuum with the Pendant Drop and Sessile Drop Method. International Journal of Molecular Sciences, 23(21), 13158. https://doi.org/10.3390/ijms232113158






