Comprehensive Empirical Model of Substitution—Influence on Hydrogen Bonding in Aromatic Schiff Bases
Abstract
1. Introduction
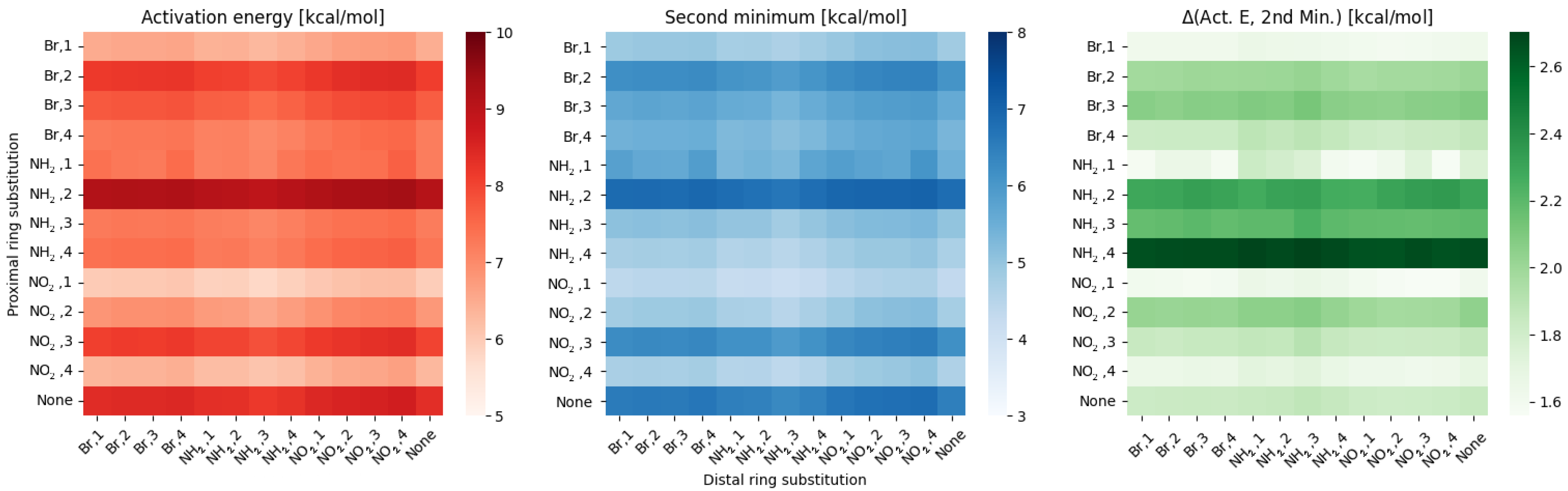
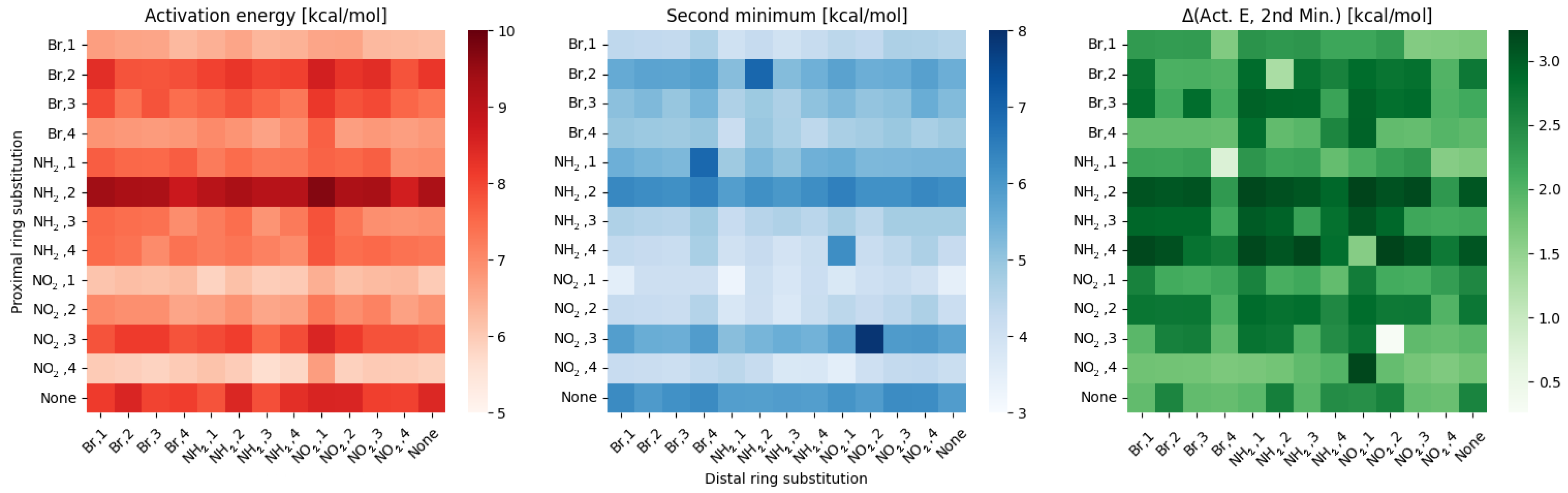
2. Results
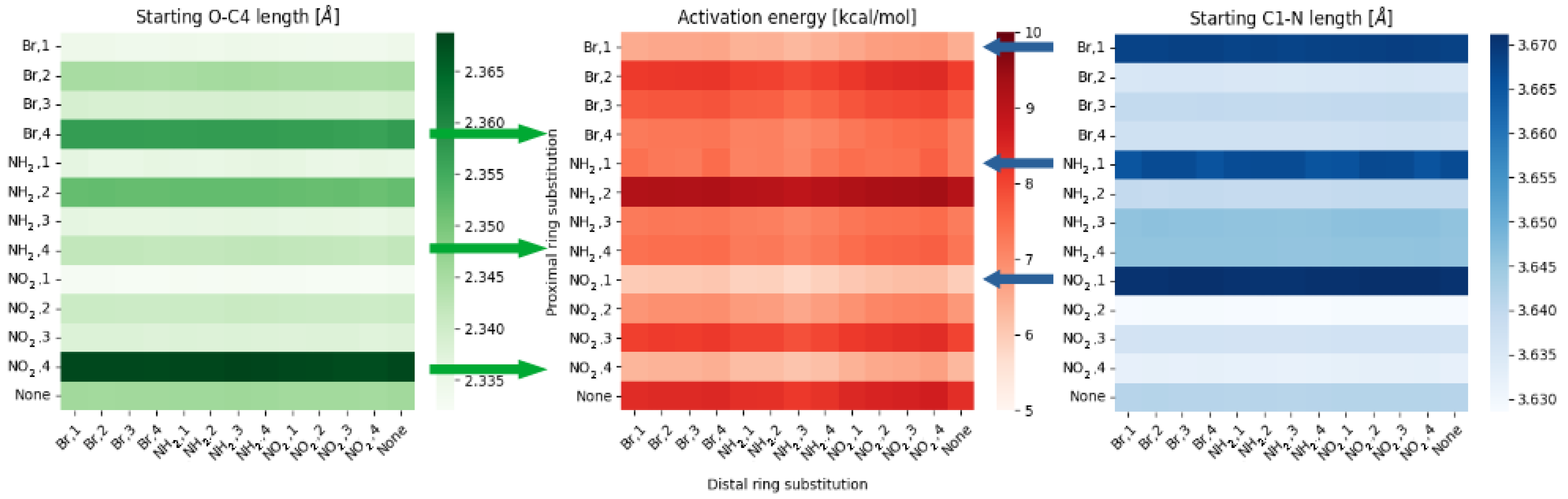
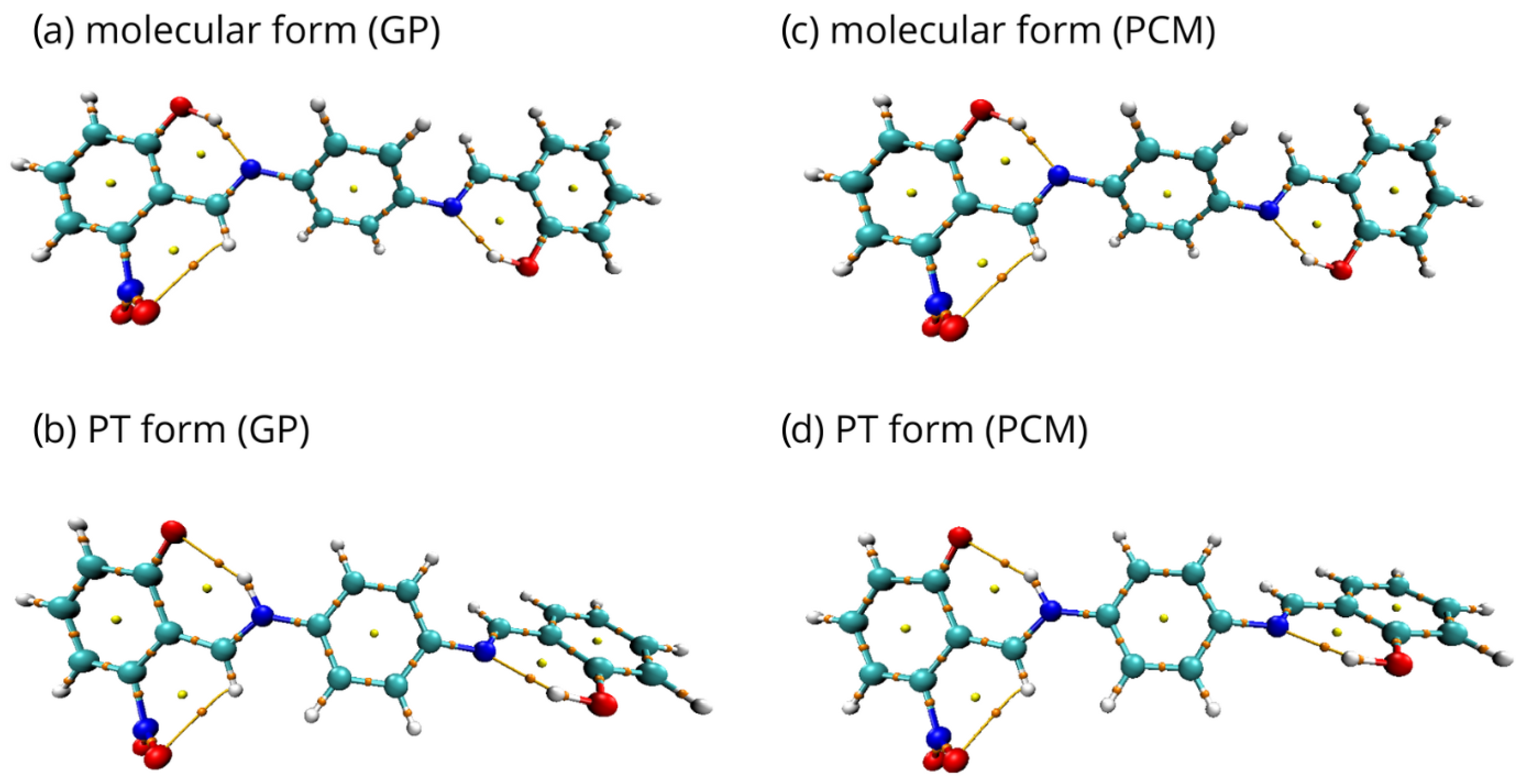
2.1. Density Functional Theory (DFT)
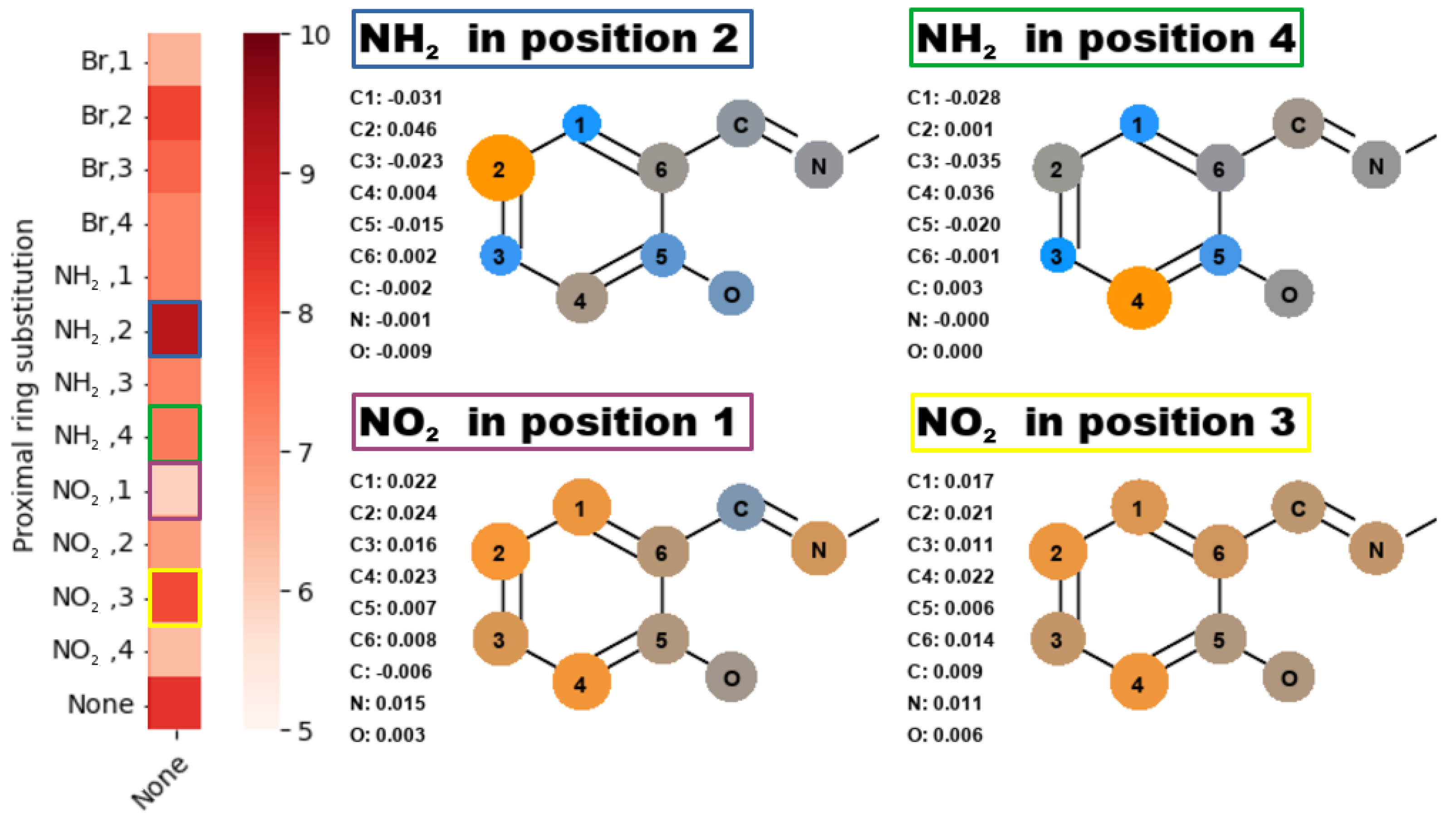
2.2. Quantum Theory of Atoms in Molecules
2.3. Non-Covalent Interactions Index
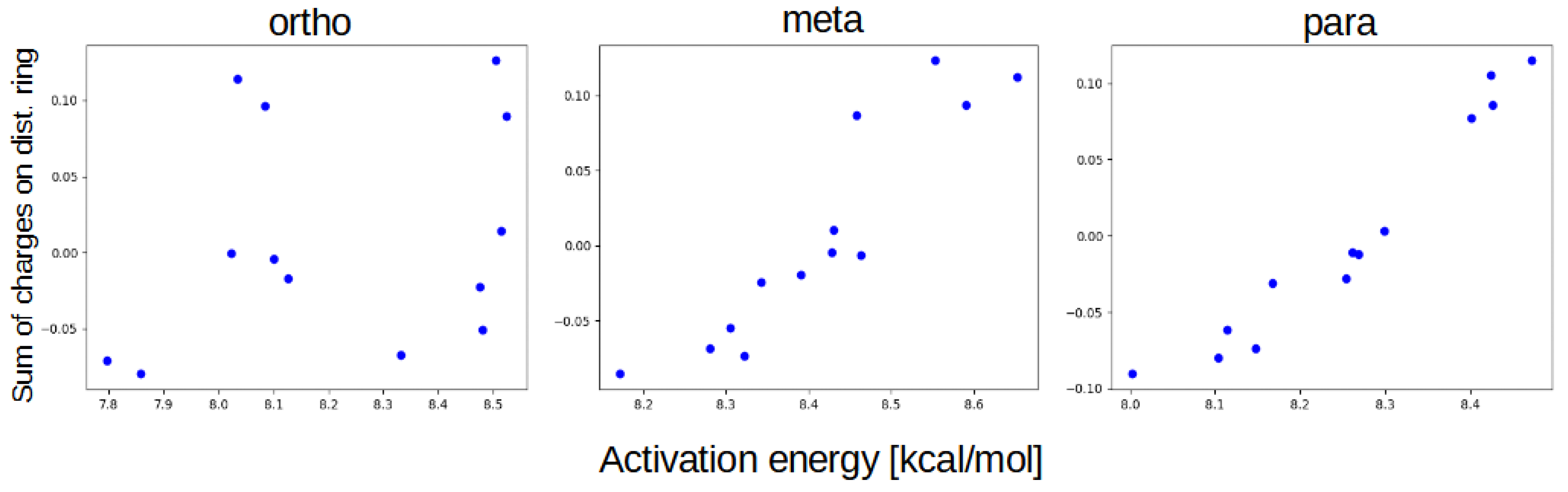
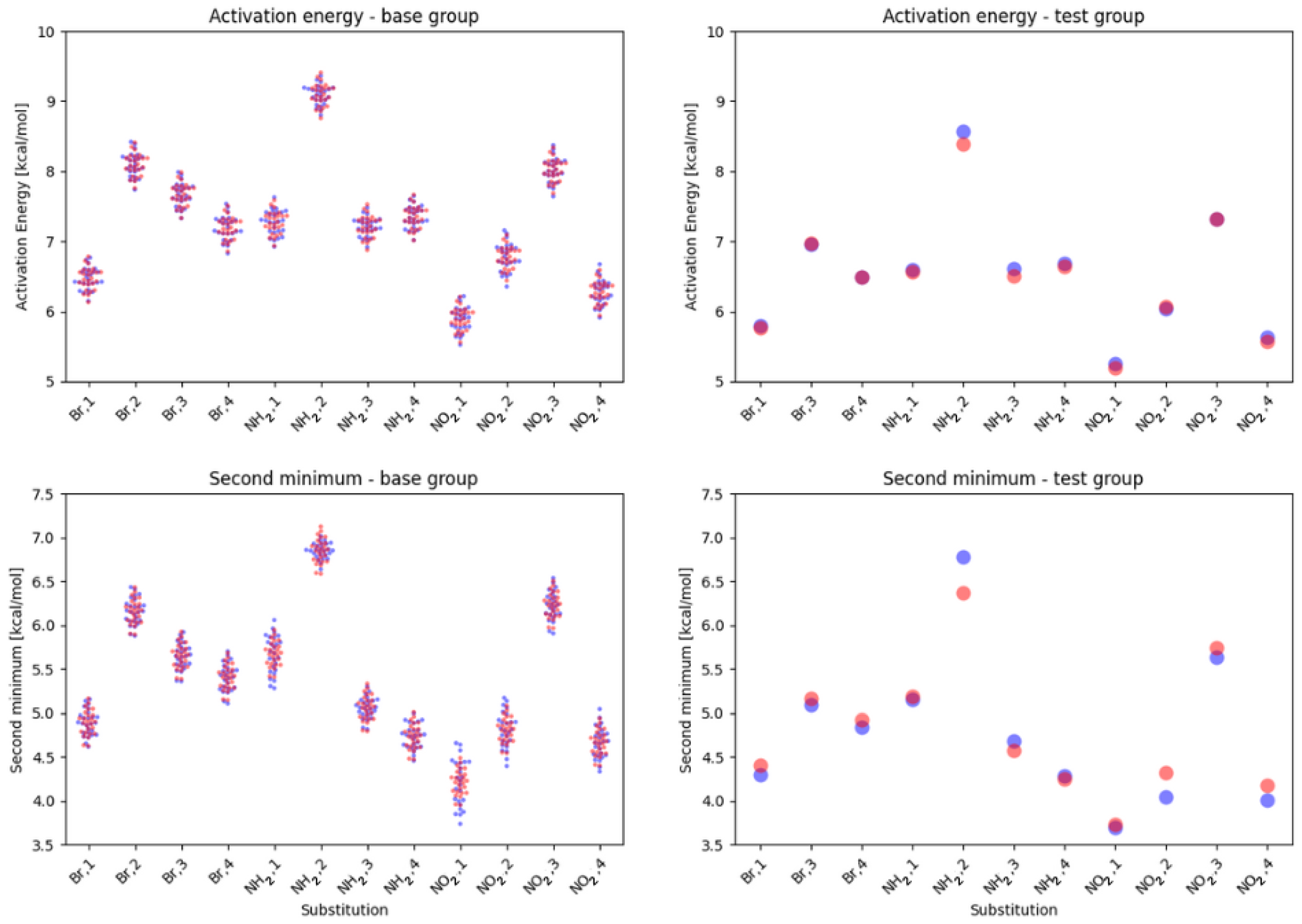
3. Discussion
- classical substituent effect, affecting the hydrogen bridge via resonance and induction effects;
- ‘steric’ effect—some of the substituents can have additional, non-trivial effect while in positions 1 or 4.
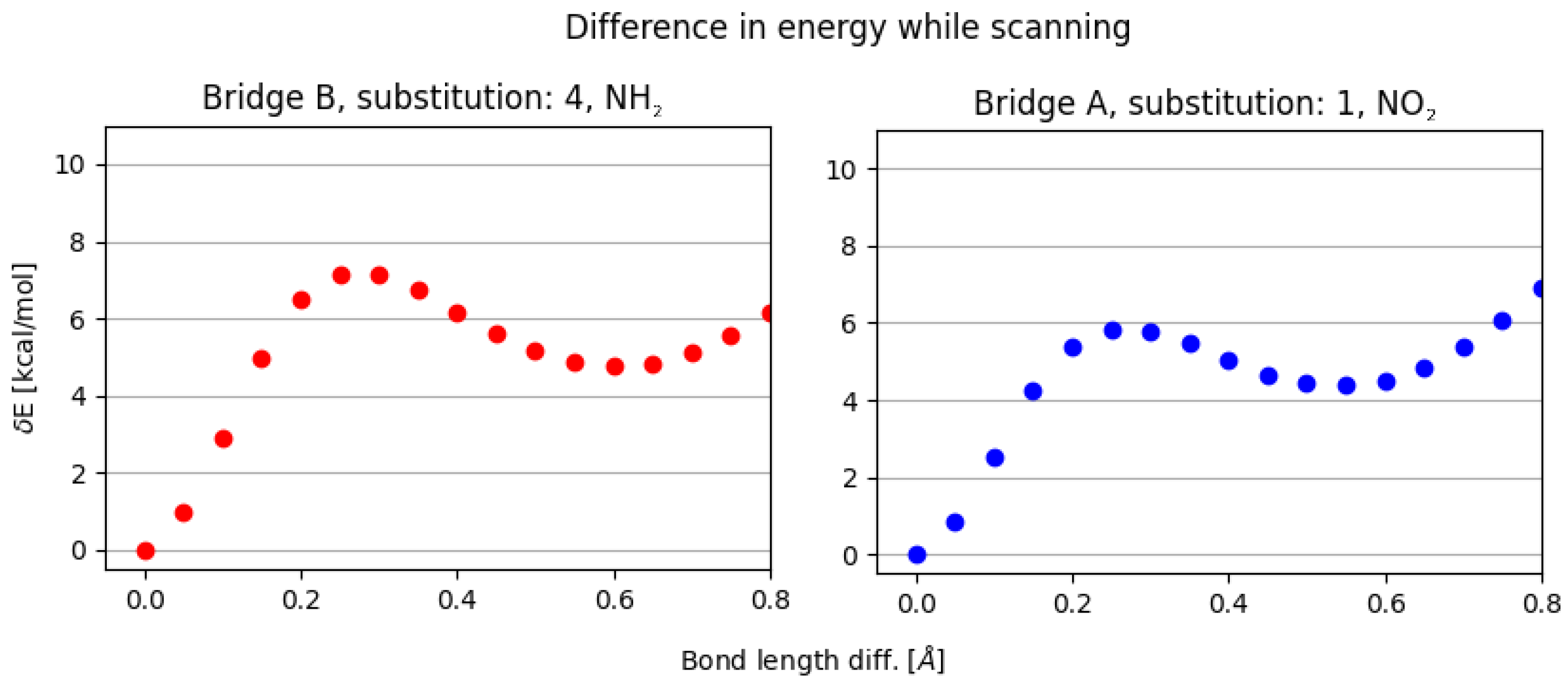
- NO, 1; NO, 4—the sterical increments should result in more pronounced lowering of the parameters, but experimental values of the activation energy and the second minimum are higher than expected. We believe, this is the effect of the repulsion between O and N in the hydrogen bridge, acting like a spring—the more it is compressed, the more force is needed to further shorten it.
- NO, 1; NH, 4—the model value is larger than the experimental one, because of the NH–OH interaction, which can act as dampener for the counteractive effect described above.
- NO, 2; NH, 3 and NH, 2; NO, 3—this is the most elaborate effect, as it does not affect the molecules geometry explicitly, but rather modulates both of the substituents by the formation of the additional bridge between them. This will highly impact the effect each one has on the ring via resonance and induction.
4. Materials and Methods
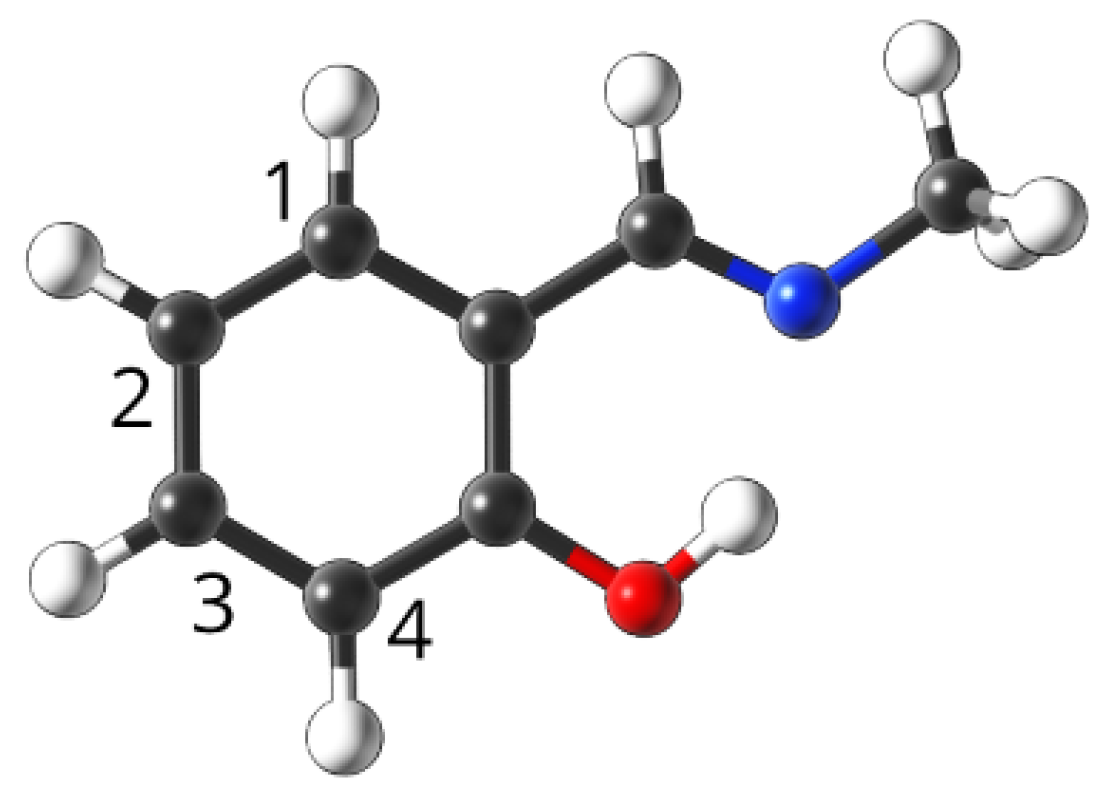
4.1. Studied Compounds
4.2. Density Functional Theory
4.3. Topological Analysis Methods—Quantum Theory of Atoms in Molecules (QTAIM) and Non-Covalent Interactions (NCI) Index
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| PCM | Polarizable Continuum Model |
| QTAIM | Quantum Theory of Atoms In Molecules |
| NCI | Non-Covalent Interactions index |
| HB | Hydrogen Bond |
| GP | Gas Phase |
| PT | Proton Transfer |
| BCP | Bond Critical Point |
| RCP | Ring Critical Point |
| RDG | Reduced Density Gradient |
| CCDC | Cambridge Crystallographic Data Centre |
| PES | Potential Energy Surface |
References
- Mahadevi, A.S.; Sastry, G.N. Cation-π Interaction: Its Role and Relevance in Chemistry, Biology, and Material Science. Chem. Rev. 2012, 113, 2100–2138. [Google Scholar] [CrossRef] [PubMed]
- Hartley, C.S. Folding of ortho-Phenylenes. Acc. Chem. Res. 2016, 49, 646–654. [Google Scholar] [CrossRef] [PubMed]
- Deb, T.; Tu, J.; Franzini, R.M. Mechanisms and Substituent Effects of Metal-Free Bioorthogonal Reactions. Chem. Rev. 2021, 121, 6850–6914. [Google Scholar] [CrossRef] [PubMed]
- Hammett, L.P. Some Relations between Reaction Rates and Equilibrium Constants. Chem. Rev. 1935, 17, 125–136. [Google Scholar] [CrossRef]
- Hammett, L.P. The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives. J. Am. Chem. Soc. 1937, 59, 96–103. [Google Scholar] [CrossRef]
- Sadlej-Sosnowska, N. Substituent active region—A gate for communication of substituent charge with the rest of a molecule: Monosubstituted benzenes. Chem. Phys. Lett. 2007, 447, 192–196. [Google Scholar] [CrossRef]
- George, P.; Trachtman, M.; Bock, C.W.; Brett, A.M. Homodesmotic reactions for the assessment of stabilization energies in benzenoid and other conjugated cyclic hydrocarbons. J. Chem. Soc. Perkin Trans. 2 1976, 11, 1222–1227. [Google Scholar] [CrossRef]
- Pross, A.; Radom, L.; Taft, R.W. Theoretical approach to substituent effects. Phenols and phenoxide ions. J. Org. Chem. 1980, 45, 818–826. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Stępień, B.T. Sigma- and Pi-Electron Delocalization: Focus on Substituent Effects. Chem. Rev. 2005, 105, 3482–3512. [Google Scholar] [CrossRef]
- Wells, P.R. Linear Free Energy Relationships. Chem. Rev. 1963, 63, 171–219. [Google Scholar] [CrossRef]
- Johnson, C.D. Linear free energy relations and the reactivity-selectivity principle. Chem. Rev. 1975, 75, 755–765. [Google Scholar] [CrossRef]
- Pocheć, M.; Kułacz, K.; Panek, J.J.; Jezierska, A. How Substitution Combines with Non-Covalent Interactions to Modulate 1,4-Naphthoquinone and Its Derivatives Molecular Features—Multifactor Studies. Int. J. Mol. Sci. 2021, 22, 10357. [Google Scholar] [CrossRef] [PubMed]
- Latimer, W.M.; Rodebush, W.H. Polarity and ionization from the standpoint of the Lewis theory of valence. J. Am. Chem. Soc. 1920, 42, 1419–1433. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond; Cornell University Press: Ithaca, NY, USA, 1939. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: London, UK, 1992. [Google Scholar]
- Szalewicz, K. Hydrogen Bond, Encyclopedia of Physical Science and Technology, 3rd ed.; Academic Press: Cambridge, MA, USA, 2001; pp. 505–538. [Google Scholar]
- Clements, R.; Dean, R.L.; Singh, T.R.; Wood, J.L. Proton double minimum potentials in symmetric hydrogen bonds. J. Chem. Soc. D Chem. Commun. 1971, 18, 1125–1126. [Google Scholar] [CrossRef]
- Jaffé, H.H. Inter- and Intramolecular Hydrogen Bonds1. J. Am. Chem. Soc. 1957, 79, 2373–2375. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Bickelhaupt, F.M.; Snijders, J.G.; Baerends, E.J. The Nature of the Hydrogen Bond in DNA Base Pairs: The Role of Charge Transfer and Resonance Assistance. Chem. Eur. J. 1999, 5, 3581–3594. [Google Scholar] [CrossRef]
- Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef]
- Jeffrey, G.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Scheiner, S. Hydrogen Bonding: A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Jeffrey, G. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Herschlag, D.; Pinney, M.M. Hydrogen Bonds: Simple after All? Biochemistry 2018, 57, 3338–3352. [Google Scholar] [CrossRef]
- Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Interrelation between H-Bond and Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3513–3560. [Google Scholar] [CrossRef]
- Filarowski, A.; Koll, A.; Sobczyk, L. Intramolecular Hydrogen Bonding in o-hydroxy Aryl Schiff Bases. Curr. Org. Chem. 2009, 13, 172–193. [Google Scholar] [CrossRef]
- Pimentel, G.M.A. The Hydrogen Bond; Freeman: Dallas, TX, USA, 1960. [Google Scholar]
- Huyskens, P.; Luck, W.; Zeegers-Huyskens, T. Intermolecular Forces: An Introduction to Modern Methods and Results; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Hobza, P.; Havlas, Z. Blue-Shifting Hydrogen Bonds. Chem. Rev. 2000, 100, 4253–4264. [Google Scholar] [CrossRef]
- Belkova, N.V.; Shubina, E.S.; Epstein, L.M. Diverse World of Unconventional Hydrogen Bonds. Acc. Chem. Res. 2005, 38, 624–631. [Google Scholar] [CrossRef] [PubMed]
- Kułacz, K.; Pocheć, M.; Jezierska, A.; Panek, J.J. Naphthazarin Derivatives in the Light of Intra- and Intermolecular Forces. Molecules 2021, 26, 5642. [Google Scholar] [CrossRef]
- Filarowski, A.; Koll, A. Specificity of the intramolecular hydrogen bond. The differences in spectroscopic characteristics of the intermolecular and intramolecular H-bonds. Vib. Spectrosc. 1998, 17, 123–131. [Google Scholar] [CrossRef]
- Jezierska, A.; Panek, J.J.; Koll, A. Spectroscopic Properties of a Strongly Anharmonic Mannich Base N-oxide. ChemPhysChem 2008, 9, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Moss, G.P.; Smith, P.A.S.; Tavernier, D. Glossary of class names of organic compounds and reactivity intermediates based on structure (IUPAC Recommendations 1995). Pure Appl. Chem. 1995, 67, 1307–1375. [Google Scholar] [CrossRef]
- Bhat, K.; Chang, K.; Aggarwal, M.; Wang, W.; Penn, B.; Frazier, D. Synthesis and characterization of various Schiff bases for non-linear optical applications. Mater. Chem. Phys. 1996, 44, 261–266. [Google Scholar] [CrossRef]
- dos Santos, J.E.; Dockal, E.R.; Cavalheiro, É.T. Synthesis and characterization of Schiff bases from chitosan and salicylaldehyde derivatives. Carbohydr. Polym. 2005, 60, 277–282. [Google Scholar] [CrossRef]
- Borisova, N.E.; Reshetova, M.D.; Ustynyuk, Y.A. Metal-Free Methods in the Synthesis of Macrocyclic Schiff Bases. Chem. Rev. 2006, 107, 46–79. [Google Scholar] [CrossRef]
- Bryant, D.A.; Hunter, C.N.; Warren, M.J. Biosynthesis of the modified tetrapyrroles—The pigments of life. J. Biol. Chem. 2020, 295, 6888–6925. [Google Scholar] [CrossRef] [PubMed]
- Schiff, H. Mittheilungen aus dem Universitätslaboratorium in Pisa: Eine neue Reihe organischer Basen. Liebigs Ann. 1864, 131, 118–119. [Google Scholar] [CrossRef]
- Schiff, H. Eine neue Reihe organischer Diamine. Ann. Chem. Pharm. 1866, 140, 92–137. [Google Scholar] [CrossRef]
- O’Donnell, M.J. The Enantioselective Synthesis of α-Amino Acids by Phase-Transfer Catalysis with Achiral Schiff Base Esters. Acc. Chem. Res. 2004, 37, 506–517. [Google Scholar] [CrossRef] [PubMed]
- Filarowski, A.; Lopatkova, M.; Lipkowski, P.; der Auweraer, M.V.; Leen, V.; Dehaen, W. Solvatochromism of BODIPY-Schiff Dye. J. Phys. Chem. B 2014, 119, 2576–2584. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Li, J. Molecular Assembly of Schiff Base Interactions: Construction and Application. Chem. Rev. 2015, 115, 1597–1621. [Google Scholar] [CrossRef]
- Wang, J.; Meng, Q.; Yang, Y.; Zhong, S.; Zhang, R.; Fang, Y.; Gao, Y.; Cui, X. Schiff Base Aggregation-Induced Emission Luminogens for Sensing Applications: A Review. ACS Sens. 2022, 7, 2521–2536. [Google Scholar] [CrossRef]
- Chen, J.; Peng, Q.; Peng, X.; Zhang, H.; Zeng, H. Probing and Manipulating Noncovalent Interactions in Functional Polymeric Systems. Chem. Rev. 2022, 122, 14594–14678. [Google Scholar] [CrossRef]
- Kumari, S.; Chauhan, G.S. New Cellulose–Lysine Schiff-Base-Based Sensor–Adsorbent for Mercury Ions. ACS Appl. Mater. Interfaces 2014, 6, 5908–5917. [Google Scholar] [CrossRef]
- Raczuk, E.; Dmochowska, B.; Samaszko-Fiertek, J.; Madaj, J. Different Schiff Bases–Structure, Importance and Classification. Molecules 2022, 27, 787. [Google Scholar] [CrossRef]
- Catalano, A.; Sinicropi, M.S.; Iacopetta, D.; Ceramella, J.; Mariconda, A.; Rosano, C.; Scali, E.; Saturnino, C.; Longo, P. A Review on the Advancements in the Field of Metal Complexes with Schiff Bases as Antiproliferative Agents. Appl. Sci. 2021, 11, 6027. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Chygorin, E.N.; Kokozay, V.N.; Bon, V.V.; Boča, R.; Kozlov, Y.N.; Shul’pina, L.S.; Jezierska, J.; Ozarowski, A.; Pombeiro, A.J.L.; et al. Heterometallic Schiff Base Complex: Structure, Electron Paramagnetic Resonance, and Alkane Oxidation Catalytic Activity. Inorg. Chem. 2012, 51, 9110–9122. [Google Scholar] [CrossRef] [PubMed]
- Lagerspets, E.; Lagerblom, K.; Heliövaara, E.; Hiltunen, O.M.; Moslova, K.; Nieger, M.; Repo, T. Schiff base Cu(I) catalyst for aerobic oxidation of primary alcohols. Mol. Catal. 2019, 468, 75–79. [Google Scholar] [CrossRef]
- Shirase, S.; Shinohara, K.; Tsurugi, H.; Mashima, K. Oxidation of Alcohols to Carbonyl Compounds Catalyzed by Oxo-Bridged Dinuclear Cerium Complexes with Pentadentate Schiff-Base Ligands under a Dioxygen Atmosphere. ACS Catal. 2018, 8, 6939–6947. [Google Scholar] [CrossRef]
- Barluenga, J.; Aznar, F.; Valdés, C. N-Trialkylsilylimines as Coupling Partners for Pd-Catalyzed C–N Bond-Forming Reactions: One-Step Synthesis of Imines and Azadienes from Aryl and Alkenyl Bromides. Angew. Chem. Int. Ed. 2004, 43, 343–345. [Google Scholar] [CrossRef]
- Barluenga, J.; Jiménez-Aquino, A.; Fernández, M.A.; Aznar, F.; Valdés, C. Multicomponent and one-pot synthesis of trisubstituted pyridines through a Pd-catalyzed cross-coupling/cross-coupling/cycloaddition sequence. Tetrahedron 2008, 64, 778–786. [Google Scholar] [CrossRef]
- Nichols, A.W.; Chatterjee, S.; Sabat, M.; Machan, C.W. Electrocatalytic Reduction of CO2 to Formate by an Iron Schiff Base Complex. Inorg. Chem. 2018, 57, 2111–2121. [Google Scholar] [CrossRef]
- Güngör, Ö.; Gürkan, P. Synthesis and characterization of higher amino acid Schiff bases, as monosodium salts and neutral forms. Investigation of the intramolecular hydrogen bonding in all Schiff bases, antibacterial and antifungal activities of neutral forms. J. Mol. Struct. 2014, 1074, 62–70. [Google Scholar] [CrossRef]
- Kumar, K.S.; Ganguly, S.; Veerasamy, R.; Clercq, E.D. Synthesis, antiviral activity and cytotoxicity evaluation of Schiff bases of some 2-phenyl quinazoline-4(3)H-ones. Eur. J. Med. Chem. 2010, 45, 5474–5479. [Google Scholar] [CrossRef]
- Sriram, D.; Yogeeswari, P.; Myneedu, N.S.; Saraswat, V. Abacavir prodrugs: Microwave-assisted synthesis and their evaluation of anti-HIV activities. Bioorg. Med. Chem. Lett. 2006, 16, 2127–2129. [Google Scholar] [CrossRef]
- Bensaber, S.M.; Allafe, H.A.; Ermeli, N.B.; Mohamed, S.B.; Zetrini, A.A.; Alsabri, S.G.; Erhuma, M.; Hermann, A.; Jaeda, M.I.; Gbaj, A.M. Chemical synthesis, molecular modelling, and evaluation of anticancer activity of some pyrazol-3-one Schiff base derivatives. Med. Chem. Res. 2014, 23, 5120–5134. [Google Scholar] [CrossRef]
- Desai, S.B.; Desai, P.; Desai, K. Synthesis of some Schiff bases, thiazolidinones and azetidinones derived from 2, 6-diaminobenzo[1, 2-d:4, 5-d’] bisthiazole and their anticancer activities. Heterocycl. Comm. 2001, 7, 83–90. [Google Scholar] [CrossRef]
- Saravanan, G.; Pannerselvam, P.; Prakash, C. Synthesis and anti-microbial screening of novel schiff bases of 3-amino-2-methyl quinazolin 4-(3H)-one. J. Adv. Pharm. Technol. Res. 2010, 1, 320–325. [Google Scholar] [CrossRef] [PubMed]
- Imran, S.; Taha, M.; Ismail, N.; Khan, K.; Naz, F.; Hussain, M.; Tauseef, S. Synthesis of Novel Bisindolylmethane Schiff bases and Their Antibacterial Activity. Molecules 2014, 19, 11722–11740. [Google Scholar] [CrossRef]
- You, Z.L.; Zhu, H.L. Syntheses, Crystal Structures, and Antibacterial Activities of Four Schiff Base Complexes of Copper and Zinc. Z. Anorg. Allg. Chem. 2004, 630, 2754–2760. [Google Scholar] [CrossRef]
- Jarrahpour, A.; Sheikh, J.; Mounsi, I.E.; Juneja, H.; Hadda, T.B. Computational evaluation and experimental in vitro antibacterial, antifungal and antiviral activity of bis-Schiff bases of isatin and its derivatives. Med. Chem. Res. 2012, 22, 1203–1211. [Google Scholar] [CrossRef]
- Abd-Elzaher, M.M.; Labib, A.A.; Mousa, H.A.; Moustafa, S.A.; Ali, M.M.; El-Rashedy, A.A. Synthesis, anticancer activity and molecular docking study of Schiff base complexes containing thiazole moiety. Beni-Suef Univ. J. Basic Appl. Sci. 2016, 5, 85–96. [Google Scholar] [CrossRef]
- Uddin, M.N.; Ahmed, S.S.; Alam, S.M.R. REVIEW: Biomedical applications of Schiff base metal complexes. J. Coord. Chem. 2020, 73, 3109–3149. [Google Scholar] [CrossRef]
- Cheng, J.; Wei, K.; Ma, X.; Zhou, X.; Xiang, H. Synthesis and Photophysical Properties of Colorful Salen-Type Schiff Bases. J. Phys. Chem. C 2013, 117, 16552–16563. [Google Scholar] [CrossRef]
- Niu, C.; Zhao, L.; Fang, T.; Deng, X.; Ma, H.; Zhang, J.; Na, N.; Han, J.; Ouyang, J. Color- and Morphology-Controlled Self-Assembly of New Electron-Donor-Substituted Aggregation-Induced Emission Compounds. Langmuir 2014, 30, 2351–2359. [Google Scholar] [CrossRef]
- Safin, D.A.; Robeyns, K.; Garcia, Y. Solid-state thermo- and photochromism in N, N′-bis(5-X-salicylidene)diamines (X = H, Br). RSC Adv. 2012, 2, 11379. [Google Scholar] [CrossRef]
- Tsumaki, T. Nebenvalenzringverbindungen. IV. Über einige innerkomplexe Kobaltsalze der Oxyaldimine. Bull. Chem. Soc. Jpn. 1938, 13, 252–260. [Google Scholar] [CrossRef]
- Coggon, P.; McPhail, A.T.; Mabbs, F.E.; Richards, A.; Thornley, A.S. Preparation, magnetic, and electronic spectral properties of some chromium(III)–NN′-ethylenebis(salicylideneiminato) complexes: Crystal and molecular structure of NN′-ethylenebis(salicylideneiminato)diaquochromium(III) chloride. J. Chem. Soc. A Inorganic Phys. Theor. 1970, 3296–3303. [Google Scholar] [CrossRef]
- Chen, H.; Han, D.; Li, T.; Yan, H.; Tang, W.; Chen, J.; Zheng, P.; Chen, C. Synthesis and Crystal Structure of Organocobalt(III) Complexes with Secondary Alkyls or Bulky Schiff Base Equatorial Ligands. Inorg. Chem. 1996, 35, 1502–1508. [Google Scholar] [CrossRef]
- Atwood, D.A.; Remington, M.P.; Rutherford, D. Use of the Salan Ligands To Form Bimetallic Aluminum Complexes. Organometallics 1996, 15, 4763–4769. [Google Scholar] [CrossRef]
- Pfeiffer, P.; Breith, E.; Lübbe, E.; Tsumaki, T. Tricyclische orthokondensierte Nebenvalenzringe. Liebigs Ann. 1933, 503, 84–130. [Google Scholar] [CrossRef]
- Zhang, W.; Loebach, J.L.; Wilson, S.R.; Jacobsen, E.N. Enantioselective epoxidation of unfunctionalized olefins catalyzed by salen manganese complexes. J. Am. Chem. Soc. 1990, 112, 2801–2803. [Google Scholar] [CrossRef]
- Irie, R.; Noda, K.; Ito, Y.; Matsumoto, N.; Katsuki, T. Catalytic asymmetric epoxidation of unfunctionalized olefins using chiral (salen)manganese(III) complexes. Tetrahedron Asymmetry 1991, 2, 481–494. [Google Scholar] [CrossRef]
- Jacobsen, E.N.; Zhang, W.; Muci, A.R.; Ecker, J.R.; Deng, L. Highly enantioselective epoxidation catalysts derived from 1, 2-diaminocyclohexane. J. Am. Chem. Soc. 1991, 113, 7063–7064. [Google Scholar] [CrossRef]
- Jacobsen, E.N.; Deng, L.; Furukawa, Y.; Martínez, L.E. Enantioselective catalytic epoxidation of cinnamate esters. Tetrahedron 1994, 50, 4323–4334. [Google Scholar] [CrossRef]
- Mazlan, N.F.; Tan, L.L.; Karim, N.H.A.; Heng, L.Y.; Reza, M.I.H. Optical biosensing using newly synthesized metal salphen complexes: A potential DNA diagnostic tool. Sens. Actuators B Chem. 2017, 242, 176–188. [Google Scholar] [CrossRef]
- Hsieh, W.H.; Wan, C.F.; Liao, D.J.; Wu, A.T. A turn-on Schiff base fluorescence sensor for zinc ion. Tetrahedron Lett. 2012, 53, 5848–5851. [Google Scholar] [CrossRef]
- Benjamin, M.; Manoj, D.; Thenmozhi, K.; Bhagat, P.R.; Saravanakumar, D.; Senthilkumar, S. A bioinspired ionic liquid tagged cobalt-salophen complex for nonenzymatic detection of glucose. Biosens. Bioelectron. 2017, 91, 380–387. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, K.; Saito, B.; Katsuki, T. Asymmetric catalysis of metal complexes with non-planar ONNO ligands: Salen, salalen and salan. Chem. Commun. 2007, 35, 3619–3627. [Google Scholar] [CrossRef]
- Cozzi, P.G. Metal–Salen Schiff base complexes in catalysis: Practical aspects. Chem. Soc. Rev. 2004, 33, 410–421. [Google Scholar] [CrossRef]
- Canali, L.; Sherrington, D.C. Utilisation of homogeneous and supported chiral metal(salen) complexes in asymmetric catalysis. Chem. Soc. Rev. 1999, 28, 85–93. [Google Scholar] [CrossRef]
- Mir, N.A.; Dubey, R.; Tothadi, S.; Desiraju, G.R. Combinatorial crystal synthesis of ternary solids based on 2-methylresorcinol. CrystEngComm 2015, 17, 7866–7869. [Google Scholar] [CrossRef]
- Sato, I.; Umemura, M.; Mitsudo, K.; Fukumura, H.; Kim, J.H.; Hoshino, Y.; Nakashima, H.; Kioi, M.; Nakakaji, R.; Sato, M.; et al. Simultaneous hyperthermia-chemotherapy with controlled drug delivery using single-drug nanoparticles. Sci. Rep. 2016, 6, 24629. [Google Scholar] [CrossRef]
- Graf, N.; Lippard, S.J. Redox activation of metal-based prodrugs as a strategy for drug delivery. Adv. Drug Deliv. Rev. 2012, 64, 993–1004. [Google Scholar] [CrossRef]
- Raczyński, K.; Pihut, A.; Panek, J.J.; Jezierska, A. Competition of Intra- and Intermolecular Forces in Anthraquinone and Its Selected Derivatives. Molecules 2021, 26, 3448. [Google Scholar] [CrossRef]
- Kizior, B.; Panek, J.J.; Szyja, B.M.; Jezierska, A. Structure-Property Relationship in Selected Naphtho- and Anthra-Quinone Derivatives on the Basis of Density Functional Theory and Car–Parrinello Molecular Dynamics. Symmetry 2021, 13, 564. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Sato, H.; Sakaki, S. Comparison of Electronic Structure Theories for Solvated Molecules: RISM-SCF versus PCM. J. Phys. Chem. A 2004, 108, 1629–1634. [Google Scholar] [CrossRef]
- Aihara, J. Topological Charge Stabilization Rule and Quasi-Aromaticity. Bull. Chem. Soc. Jpn. 1987, 60, 2268–2270. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- CCDC Structural Database. Available online: https://www.ccdc.cam.ac.uk/ (accessed on 10 June 2022).
- Pahor, N.B.; Calligaris, M.; Delise, P.; Dodic, G.; Nardin, G.; Randaccio, L. Structural effects of the co-ordination of quadridentate Schiff bases to transition-metal atoms. Structure of NN′-(o-phenylene)bis(salicylideneamine) and of its cobalt(II) complex. J. Chem. Soc. Dalton Trans. 1976, 2478–2483. [Google Scholar] [CrossRef]
- OneAngstrom. SAMSON 2022 R1 Platform for Molecular Design. Available online: https://www.samson-connect.net/ (accessed on 11 September 2022).
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision C.01, 2016; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Pocheć, M. GaussianMaster Python Package; Zenodo: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]
- Pocheć, M. Schiff Bases Library Preparation Script. Available online: https://github.com/panpochec/LibCompiler4Scans (accessed on 15 August 2022).
- Pocheć, M. Schiff Bases Library Analysis Script. Available online: https://github.com/panpochec/LibraryAnalysis (accessed on 15 August 2022).
- Pocheć, M. Model Builder and Tester Script. Available online: https://github.com/panpochec/SchiffModel/ (accessed on 15 August 2022).
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- pandas-dev/pandas: Pandas; Zenodo: Geneva, Switzerland, 2020. [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Williams, T.; Kelley, C. Gnuplot 5.4.4: An Interactive Plotting Program. 2022. Available online: https://sourceforge.net/projects/gnuplot/files/gnuplot/5.4.4/ (accessed on 18 August 2022).
- Adobe Inc. Adobe Photoshop, Version 23.5; Adobe Inc.: San Jose, CA, USA, 2022.


| Gas Phase | PCM | |||
|---|---|---|---|---|
| BCP | BCP [e*] | ∇2BCP [e*] | BCP [e*] | ∇2BCP [e*] |
| Molecular form | ||||
| O-H | 0.336 | −2.525 | 0.333 | −2.492 |
| H...N | 0.056 | 0.112 | 0.058 | 0.112 |
| Proton-transferred form | ||||
| O...H | 0.025 | 0.082 | 0.025 | 0.081 |
| H-N | 0.357 | −2.206 | 0.358 | −2.210 |
| Net Atomic Charge [e] | Gas Phase | PCM |
|---|---|---|
| Molecular form | ||
| O | −1.202 | −1.187 |
| H | 0.664 | 0.650 |
| N | −0.111 | −1.123 |
| C | 0.613 | 0.651 |
| C6 | −0.019 | −0.011 |
| C5 | 0.651 | 0.634 |
| SUM | −0.404 | −0.386 |
| Proton-transferred form | ||
| O | −1.146 | −1.143 |
| H | 0.503 | 0.505 |
| N | −1.184 | −1.184 |
| C | 0.529 | 0.529 |
| C6 | −0.038 | −0.041 |
| C5 | 0.899 | 0.898 |
| SUM | -0.437 | −0.436 |
| Substitution Pattern | I [kcal/mol] | I [kcal/mol] |
|---|---|---|
| Br,1 or Br,3 | −0.670 | −0.905 |
| Br,2 or Br,4 | −0.244 | −0.396 |
| NO, 1 or NO, 3 | −0.322 | −1.496 |
| NO, 2 or NO, 4 | −1.56 | 0.297 |
| NH, 1 or NH, 3 | −1.12 | −0.324 |
| NH, 2 or NH, 4 | 0.754 | −1.747 |
| Substitution Pattern | I [kcal/mol] | I [kcal/mol] |
| Br,1 | −1.199 | −0.759 |
| Br,4 | −0.902 | −0.750 |
| NO, 1 | −2.127 | 0.613 |
| NO, 4 | −0.501 | −2.116 |
| NH, 1 | −0.060 | −2.016 |
| NH, 4 | −1.743 | −0.141 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krupka, K.M.; Pocheć, M.; Panek, J.J.; Jezierska, A. Comprehensive Empirical Model of Substitution—Influence on Hydrogen Bonding in Aromatic Schiff Bases. Int. J. Mol. Sci. 2022, 23, 12439. https://doi.org/10.3390/ijms232012439
Krupka KM, Pocheć M, Panek JJ, Jezierska A. Comprehensive Empirical Model of Substitution—Influence on Hydrogen Bonding in Aromatic Schiff Bases. International Journal of Molecular Sciences. 2022; 23(20):12439. https://doi.org/10.3390/ijms232012439
Chicago/Turabian StyleKrupka, Katarzyna M., Michał Pocheć, Jarosław J. Panek, and Aneta Jezierska. 2022. "Comprehensive Empirical Model of Substitution—Influence on Hydrogen Bonding in Aromatic Schiff Bases" International Journal of Molecular Sciences 23, no. 20: 12439. https://doi.org/10.3390/ijms232012439
APA StyleKrupka, K. M., Pocheć, M., Panek, J. J., & Jezierska, A. (2022). Comprehensive Empirical Model of Substitution—Influence on Hydrogen Bonding in Aromatic Schiff Bases. International Journal of Molecular Sciences, 23(20), 12439. https://doi.org/10.3390/ijms232012439