Multiphoton Bleaching of Red Fluorescent Proteins and the Ways to Reduce It
Abstract
:1. Introduction
2. Results
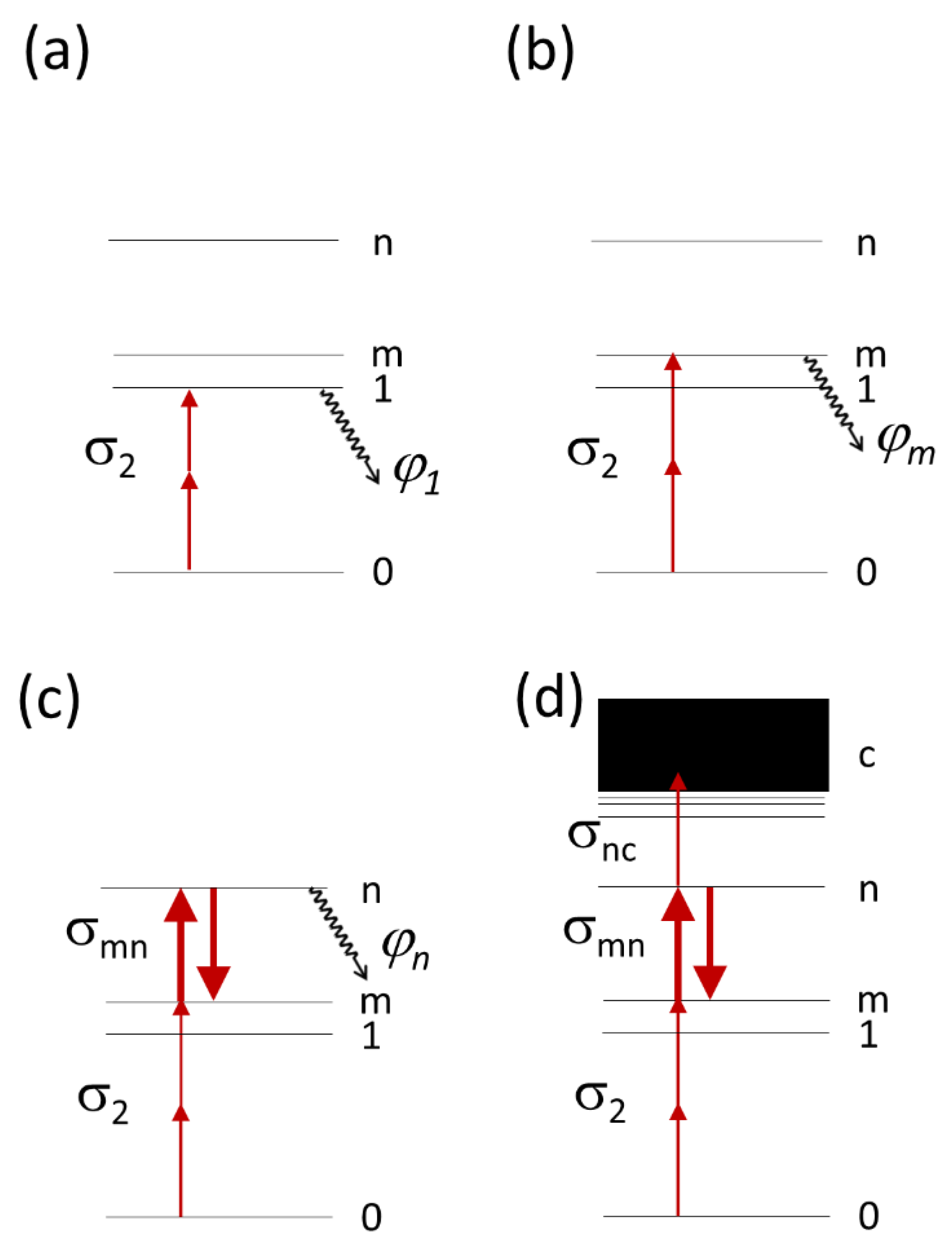
2.1. Physical Model of Multiphoton Bleaching in a Thin Colony of Cells Containing Fluorescing Molecules
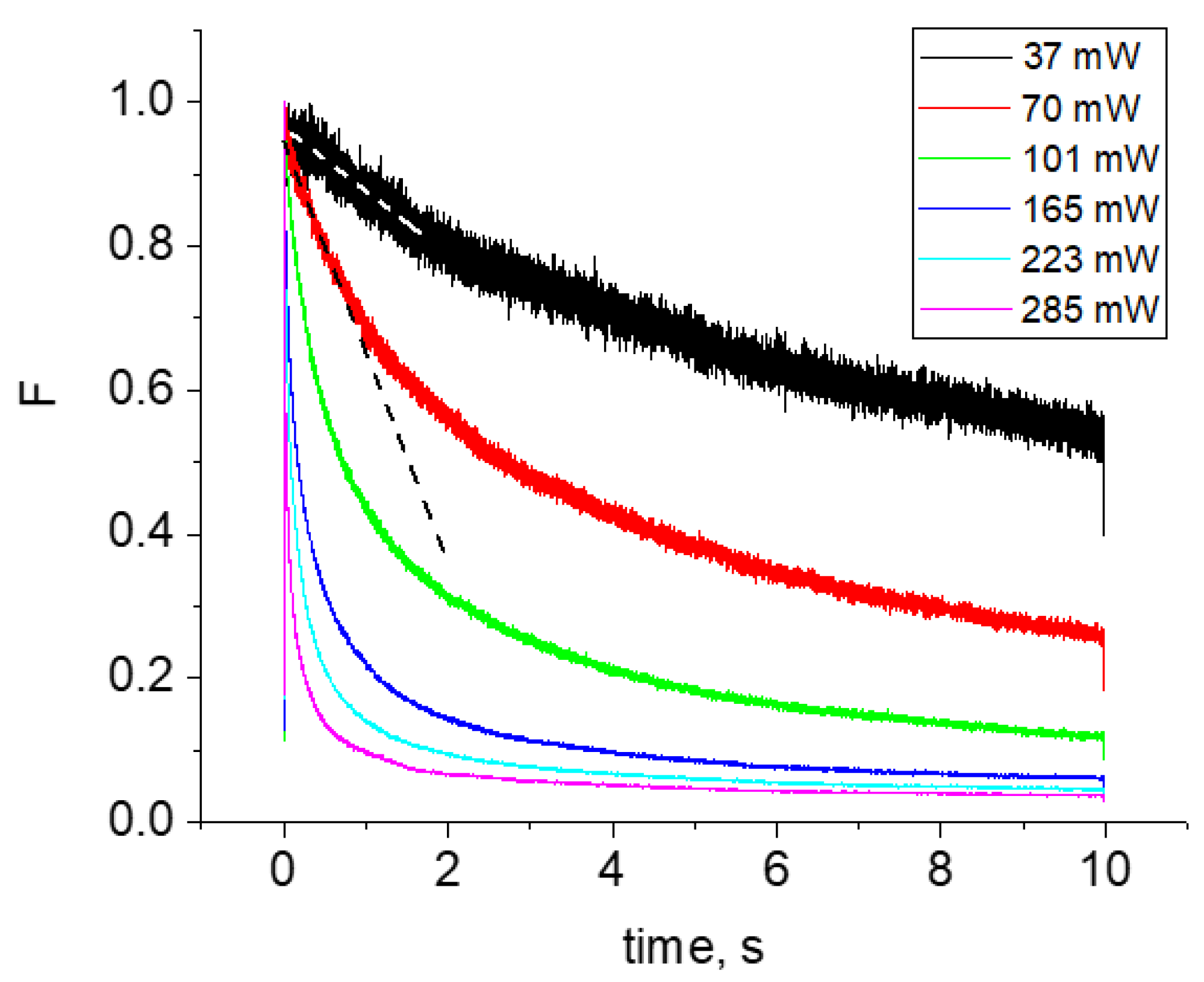
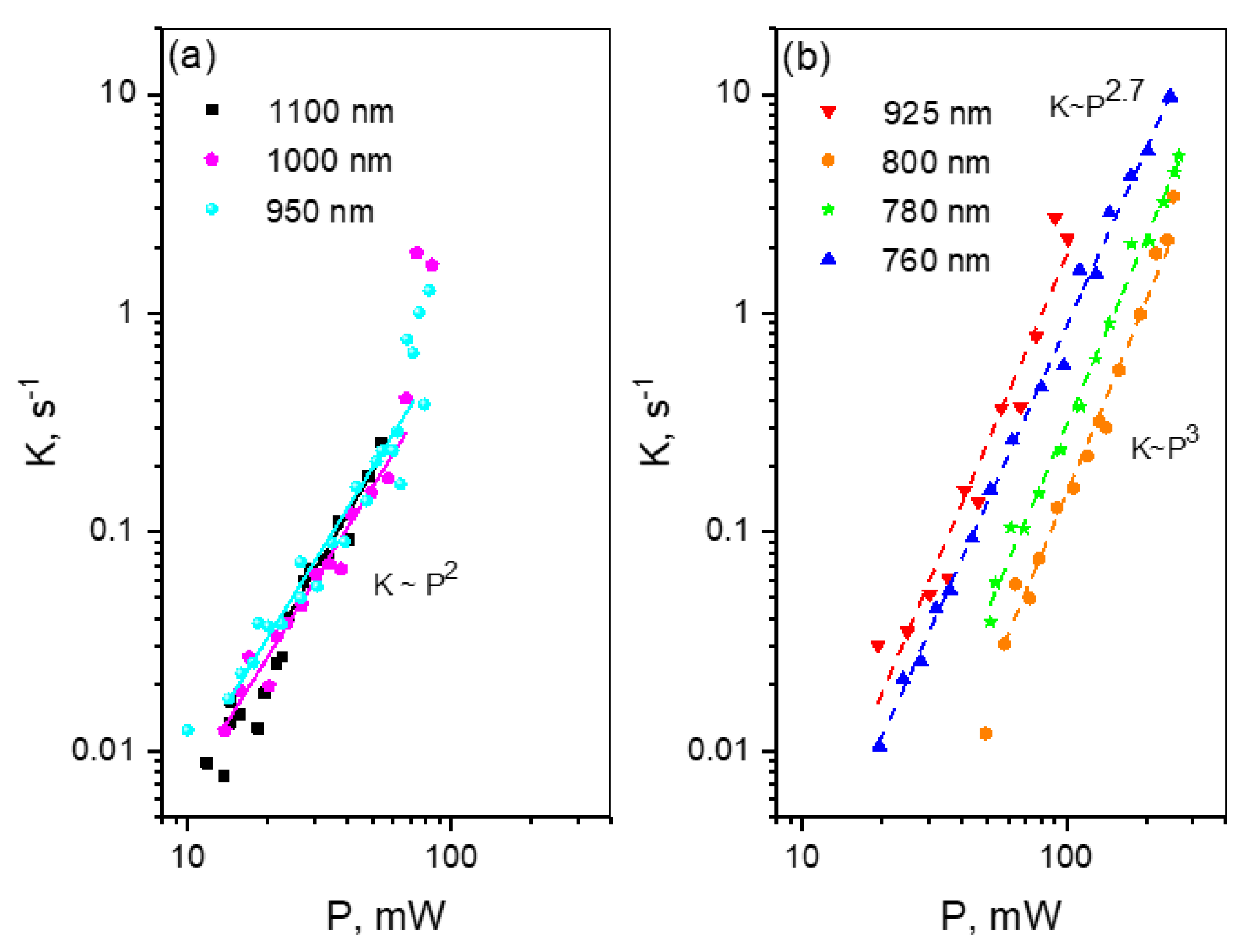
2.2. Multiphoton Bleaching of mCherry in E. coli Colonies
- (1)
- For each wavelength, there is a range of power values where the bleaching rate depends quadratically on power. Although this behavior is natural and reflects the fundamental bleaching limit corresponding to photochemical reaction starting just after absorption of two photons, to the best of our knowledge there are no publications where quadratic law was shown for any FP. After reaching a certain threshold, the dependence switches to super-quadratic, with α = 3.3–3.6. Note that previously the bleaching of mCherry was measured at 790 nm at similar excitation conditions (same objective lens, similar colony thickness and pulse duration) with the laser power of 40–150 mW [28], and the K~P3.4 dependence was observed. As one can see from Figure 4, these power levels were higher than the threshold (at 780–800 nm) and therefore the quadratic part was missed there.
- (2)
- The power threshold P* for the super-quadratic transition is observed for wavelengths 760–800 nm, and it shifts to lower power values as the wavelengths becomes shorter.
- (3)
- We did not observe a transition from quadratic to super quadratic dependence for wavelengths of 1100 (black squares) and 1000 nm (data not shown), at least for highest available power levels. Given the vertical electron detachment energy of mCherry is 5.52 eV [28], one can predict that the absorption of four photons with energy less than 1.57 eV (>900 nm) would not suffice to photodetach an electron. As a result, we would not anticipate the transition from P2 to P3.5 dependence for wavelengths longer than 900 nm. This imposes a critical wavelength for two-photon excitation of mCherry, λ = 900 nm, suggesting that using the lowest, S0 → S1 transition at 1000–1100 nm should result in slower (quadratic) multiphoton bleaching even at high powers.
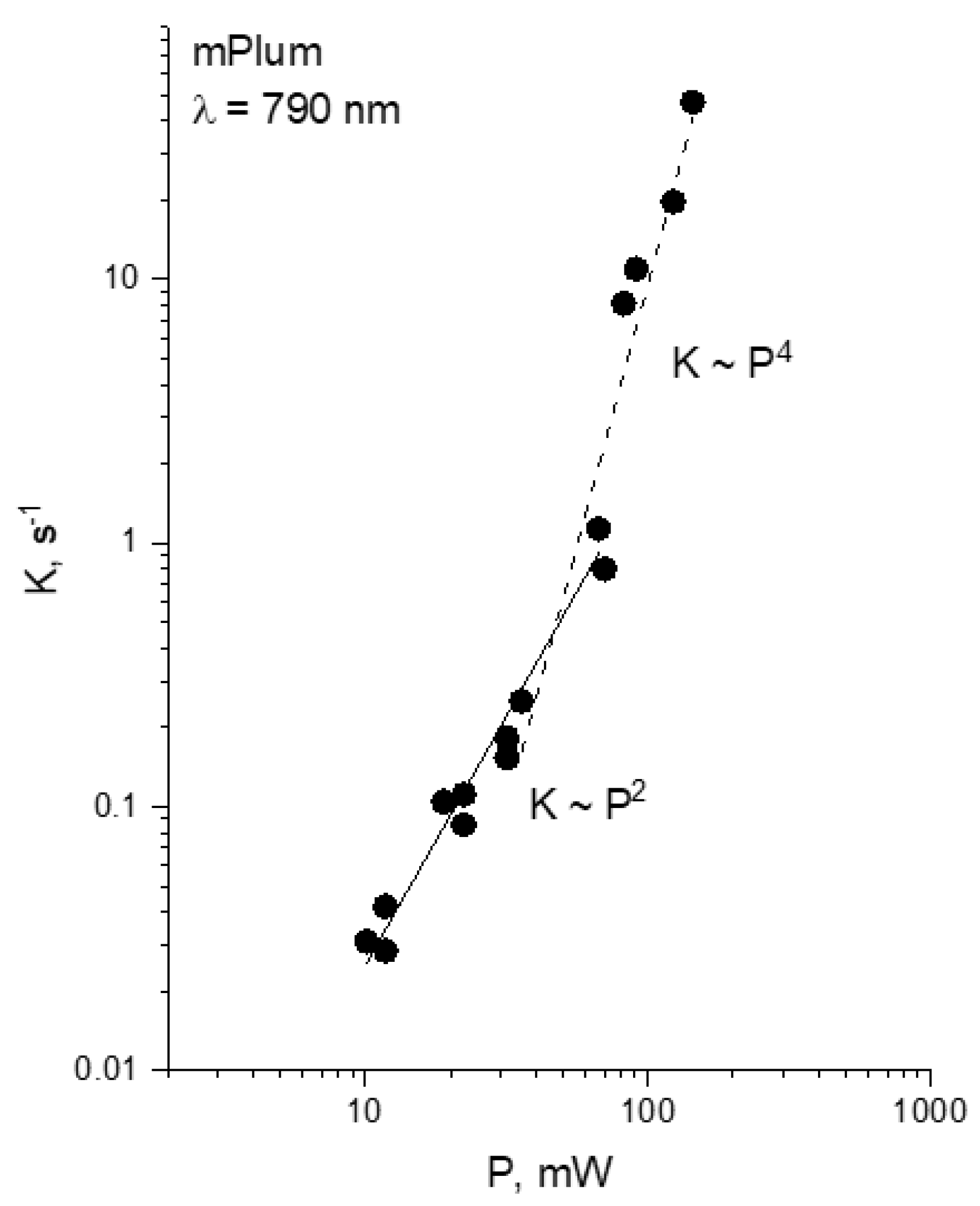
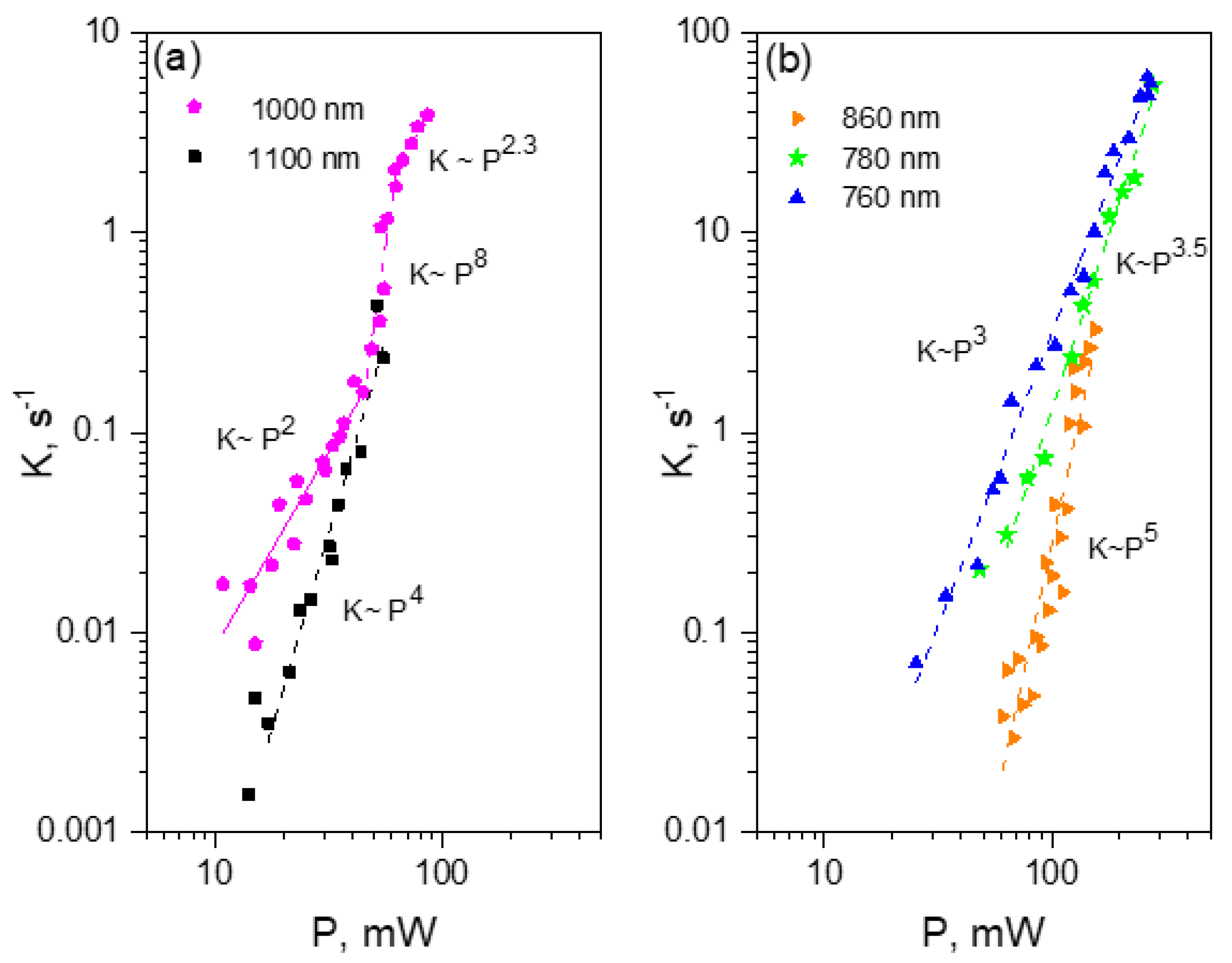
2.3. Multiphoton Bleaching of mPlum in E. coli Colonies
2.4. Multiphoton Bleaching of jREX-GECO1 in E. coli Colonies
2.5. Multiphoton Bleaching of tdTomato in E. coli Colonies
3. Discussion
4. Materials and Methods
4.1. Expressing RFPs in E. coli Colonies
4.2. Preparing Plates with E. coli Colonies
4.3. Optical Instrument
4.4. Photobleaching Experiments
4.5. Characterizing Laser Beam Parameters in Focal Area
4.6. Colony Thickness, Rayleigh Length, and Focal Spot Size inside a Colony
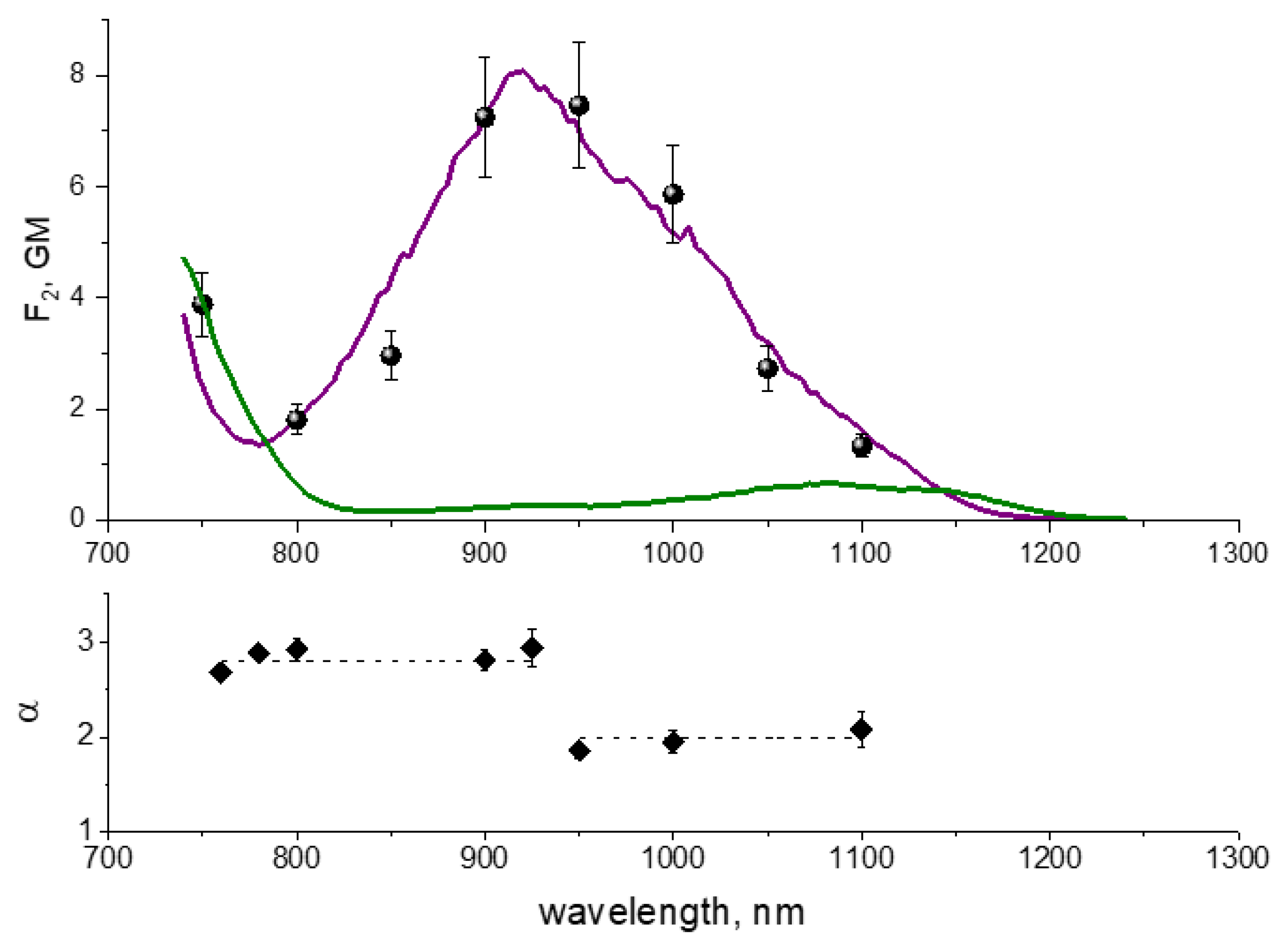
4.7. Two-Photon Excitation Spectra of RFPs inside E. coli Colonies
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Shaner, N.C.; Campbell, R.E.; Steinbach, P.A.; Giepmans, B.N.G.; Palmer, A.E.; Tsien, R.Y. Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein. Nat. Biotechnol. 2004, 22, 1567–1572. [Google Scholar] [CrossRef]
- Lin, M.Z.; McKeown, M.R.; Ng, H.-L.; Aguilera, T.A.; Shaner, N.C.; Campbell, R.E.; Adams, S.R.; Gross, L.A.; Ma, W.; Alber, T.; et al. Autofluorescent proteins with excitation in the optical window for intravital imaging in mammals. Chem. Biol. 2009, 16, 1169–1179. [Google Scholar] [CrossRef] [Green Version]
- Chudakov, D.M.; Matz, M.V.; Lukyanov, S.; Lukyanov, K.A. Fluorescent proteins and their applications in imaging living cells and tissues. Physiol. Rev. 2010, 90, 1103–1163. [Google Scholar] [CrossRef]
- Dana, H.; Mohar, B.; Sun, Y.; Narayan, S.; Gordus, A.; Hasseman, J.P.; Tsegaye, G.; Holt, G.T.; Hu, A.; Walpita, D.; et al. Sensitive red protein calcium indicators for imaging neural activity. eLife 2016, 5, e12727. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Nasu, Y.; Shkolnikov, I.; Kim, A.; Campbell, R.E. Engineering genetically encoded fluorescent indicators for imaging of neuronal activity: Progress and prospects. Neurosci. Res. 2020, 152, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Denk, W.; Strickler, J.H.; Webb, W.W. Two-photon laser scanning fluorescence microscopy. Science 1990, 248, 73–76. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Zipfel, W.; Shear, J.B.; Williams, R.M.; Webb, W.W. Multiphoton fluorescence excitation: New spectral windows for biological nonlinear microscopy. Proc. Natl. Acad. Sci. USA 1996, 93, 10763–10768. [Google Scholar] [CrossRef] [Green Version]
- Kazemipour, A.; Novak, O.; Flickinger, D.; Marvin, J.S.; Abdelfattah, A.S.; King, J.; Borden, P.M.; Kim, J.J.; Al-Abdullatif, S.H.; Deal, P.E.; et al. Kilohertz frame-rate two-photon tomography. Nat. Methods 2019, 16, 778–786. [Google Scholar] [CrossRef]
- Lu, R.; Liang, Y.; Meng, G.; Zhou, P.; Svoboda, K.; Paninski, L.; Ji, N. Rapid mesoscale volumetric imaging of neural activity with synaptic resolution. Nat. Methods 2020, 17, 291–294. [Google Scholar] [CrossRef]
- Drobizhev, M.; Makarov, N.S.; Tillo, S.E.; Hughes, T.E.; Rebane, A. Two-photon absorption properties of fluorescent proteins. Nat. Methods 2011, 8, 393–399. [Google Scholar] [CrossRef] [PubMed]
- Drobizhev, M.; Tillo, S.; Makarov, N.S.; Hughes, T.E.; Rebane, A. Absolute two-photon absorption spectra and two-photon brightness of orange and red fluorescent proteins. J. Phys. Chem. B 2009, 113, 855–859. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, A.M.; Mancini, M.C.; Nie, S. Bioimaging: Second window for in vivo imaging. Nat. Nanotechnol. 2009, 4, 710–711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nifosì, R.; Luo, Y. Predictions of novel two-photon absorption bands in fluorescent proteins. J. Phys. Chem. B 2007, 111, 14043–14050. [Google Scholar] [CrossRef] [PubMed]
- Drobizhev, M.; Makarov, N.S.; Hughes, T.; Rebane, A. Resonance enhancement of two-photon absorption in fluorescent proteins. J. Phys. Chem. B 2007, 111, 14051–14054. [Google Scholar] [CrossRef]
- Tillo, S.E.; Hughes, T.E.; Makarov, N.S.; Rebane, A.; Drobizhev, M. A new approach to dual-color two-photon microscopy with fluorescent proteins. BMC Biotechnol. 2010, 10, 6. [Google Scholar] [CrossRef] [Green Version]
- Patterson, G.H.; Piston, D.W. Photobleaching in two-photon excitation microscopy. Biophys. J. 2000, 78, 2159–2162. [Google Scholar] [CrossRef] [Green Version]
- Goodman, L.; Philis, J. Multiphoton Absorption Spectroscopy: Techniques, Instrumentation, and Applications. In Applied Laser Spectroscopy; Andrews, D.L., Ed.; VCH Publishers: New York, NY, USA, 1992; Chapter 8; pp. 319–364. [Google Scholar]
- Lougnot, D.-J.; Goldschmidt, C.R. Photoionization of fluorescein via excited triplet and singlet states. J. Photochem. 1980, 12, 215–224. [Google Scholar] [CrossRef]
- Redchenko, V.V.; Safronov, A.I.; Kirpichenok, M.A.; Grandberg, I.I.; Traven, V. Electronic Structure of π-Systems. XV. Photoelectron spectra of 7-aminocoumarin derivatives. J. Gen. Chem. USSR 1992, 62, 2313–2318. [Google Scholar]
- Marchant, J.S.; Stutzmann, G.E.; Leissring, M.A.; LaFerla, F.M.; Parker, I. Multiphoton-evoked color change of DsRed as an optical highlighter for cellular and subcellular labeling. Nat. Biotechnol. 2001, 19, 645–649. [Google Scholar] [CrossRef]
- Robinson, L.C.; Marchant, J.S. Improved “optical highlighter” probes derived from discosoma red fluorescent protein. Biophys. J. 2005, 88, 1444–1457. [Google Scholar] [CrossRef] [Green Version]
- Andresen, V.; Alexander, S.; Heupel, W.-M.; Hirschberg, M.; Hoffman, R.M.; Friedl, P. Infrared multiphoton microscopy: Subcellular-resolved deep tissue imaging. Curr. Opin. Biotechnol. 2009, 20, 54–62. [Google Scholar] [CrossRef]
- Herz, J.; Siffrin, V.; Hauser, A.E.; Brandt, A.U.; Leuenberger, T.; Radbruch, H.; Zipp, F.; Niesner, R.A. Expanding two-photon intravital microscopy to the infrared by means of optical parametric oscillator. Biophys. J. 2010, 98, 715–723. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.-S.; Zeng, S.-Q.; Luo, Q.-M.; Zhang, Z.-H.; Zhou, W. High-order photobleaching of green fluorescent protein inside live cells in two-photon excitation microscopy. Biochem. Biophys. Res. Commun. 2002, 291, 1272–1275. [Google Scholar] [CrossRef] [PubMed]
- Drummond, D.R.; Carter, N.; Cross, R.A. Multiphoton versus confocal high resolution z-sectioning of enhanced green fluorescent microtubules: Increased multiphoton photobleaching within the focal plane can be compensated using a Pockels cell and dual widefield detectors. J. Microsc. 2002, 206, 161–169. [Google Scholar] [CrossRef]
- Kalies, S.; Kuetemeyer, K.; Heisterkamp, A. Mechanisms of high-order photobleaching and its relationship to intracellular ablation. Biomed. Opt. Express 2011, 2, 805–816. [Google Scholar] [CrossRef] [PubMed]
- Graham, D.J.L.; Tseng, S.-F.; Hsieh, J.-T.; Chen, D.J.; Alexandrakis, G. Dependence of Two-Photon eGFP Bleaching on Femtosecond Pulse Spectral Amplitude and Phase. J. Fluoresc. 2015, 25, 1775–1785. [Google Scholar] [CrossRef] [PubMed]
- Drobizhev, M.; Stoltzfus, C.; Topol, I.; Collins, J.; Wicks, G.; Mikhaylov, A.; Barnett, L.; Hughes, T.E.; Rebane, A. Multiphoton photochemistry of red fluorescent proteins in solution and live cells. J. Phys. Chem. B 2014, 118, 9167–9179. [Google Scholar] [CrossRef] [PubMed]
- Ji, N.; Magee, J.C.; Betzig, E. High-speed, low-photodamage nonlinear imaging using passive pulse splitters. Nat. Methods 2008, 5, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Donnert, G.; Eggeling, C.; Hell, S.W. Major signal increase in fluorescence microscopy through dark-state relaxation. Nat. Methods 2007, 4, 81–86. [Google Scholar] [CrossRef]
- Kawano, H.; Nabekawa, Y.; Suda, A.; Oishi, Y.; Mizuno, H.; Miyawaki, A.; Midorikawa, K. Attenuation of photobleaching in two-photon excitation fluorescence from green fluorescent protein with shaped excitation pulses. Biochem. Biophys. Res. Commun. 2003, 311, 592–596. [Google Scholar] [CrossRef]
- Field, J.J.; Carriles, R.; Sheetz, K.E.; Chandler, E.V.; Hoover, E.E.; Tillo, S.E.; Hughes, T.E.; Sylvester, A.W.; Kleinfeld, D.; Squier, J.A. Optimizing the fluorescent yield in two-photon laser scanning microscopy with dispersion compensation. Opt. Express 2010, 18, 13661–13672. [Google Scholar] [CrossRef] [Green Version]
- Xi, P.; Andegeko, Y.; Weisel, L.R.; Lozovoy, V.V.; Dantus, M. Greater signal, increased depth, and less photobleaching in two-photon microscopy with 10fs pulses. Opt. Commun. 2008, 281, 1841–1849. [Google Scholar] [CrossRef]
- Wang, L.; Jackson, W.C.; Steinbach, P.A.; Tsien, R.Y. Evolution of new nonantibody proteins via iterative somatic hypermutation. Proc. Natl. Acad. Sci. USA 2004, 101, 16745–16749. [Google Scholar] [CrossRef] [Green Version]
- Molina, R.S.; Qian, Y.; Wu, J.; Shen, Y.; Campbell, R.E.; Drobizhev, M.; Hughes, T.E. Understanding the Fluorescence Change in Red Genetically Encoded Calcium Ion Indicators. Biophys. J. 2019, 116, 1873–1886. [Google Scholar] [CrossRef] [Green Version]
- Drobizhev, M.; Hughes, T.E.; Stepanenko, Y.; Wnuk, P.; O’Donnell, K.; Scott, J.N.; Callis, P.R.; Mikhaylov, A.; Dokken, L.; Rebane, A. Primary role of the chromophore bond length alternation in reversible photoconversion of red fluorescence proteins. Sci. Rep. 2012, 2, 688. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Habuchi, S.; Cotlet, M.; Gensch, T.; Bednarz, T.; Haber-Pohlmeier, S.; Rozenski, J.; Dirix, G.; Michiels, J.; Vanderleyden, J.; Heberle, J.; et al. Evidence for the isomerization and decarboxylation in the photoconversion of the red fluorescent protein DsRed. J. Am. Chem. Soc. 2005, 127, 8977–8984. [Google Scholar] [CrossRef] [Green Version]
- Shu, X.; Shaner, N.C.; Yarbrough, C.A.; Tsien, R.Y.; Remington, S.J. Novel chromophores and buried charges control color in mFruits. Biochemistry 2006, 45, 9639–9647. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, D.; Acharya, A.; Tiwari, S.C.; Krylov, A.I. Toward understanding the redox properties of model chromophores from the green fluorescent protein family: An interplay between conjugation, resonance stabilization, and solvent effects. J. Phys. Chem. B 2012, 116, 12398–12405. [Google Scholar] [CrossRef] [PubMed]
- Fuenzalida Werner, J.P.; Huang, Y.; Mishra, K.; Janowski, R.; Vetschera, P.; Heichler, C.; Chmyrov, A.; Neufert, C.; Niessing, D.; Ntziachristos, V.; et al. Challenging a Preconception: Optoacoustic Spectrum Differs from the Optical Absorption Spectrum of Proteins and Dyes for Molecular Imaging. Anal. Chem. 2020, 92, 10717–10724. [Google Scholar] [CrossRef]
- Molina, R.S.; King, J.; Franklin, J.; Clack, N.; McRaven, C.; Goncharov, V.; Flickinger, D.; Svoboda, K.; Drobizhev, M.; Hughes, T.E. High throughput instrument to screen fluorescent proteins under two-photon excitation. Biomed. Opt. Express 2020, 11, 7192–7203. [Google Scholar] [CrossRef]
- Guild, J.B.; Xu, C.; Webb, W.W. Measurement of group delay dispersion of high numerical aperture objective lenses using two-photon excited fluorescence. Appl. Opt. 1997, 36, 397–401. [Google Scholar] [CrossRef]
- Dickson, L.D. Characteristics of a propagating gaussian beam. Appl. Opt. 1970, 9, 1854–1861. [Google Scholar] [CrossRef]
- Drobizhev, M.; Molina, R.S.; Hughes, T.E. Characterizing the Two-photon Absorption Properties of Fluorescent Molecules in the 680–1300 nm Spectral Range. Bio-Protocol 2020, 10, e3498. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7409827/ (accessed on 23 December 2021). [CrossRef]
- Xu, C.; Webb, W.W. Multiphoton Excitation of Molecular Fluorophores and Nonlinera Laser Microscopy. In Topics in Fluorescence Spectroscopy, Vol. 5, Nonlinear and Two-Photon Induced Fluorescence; Lakowicz, J.R., Ed.; Plenum Press: New York, NY, USA; London, UK, 1997; Chapter 11; pp. 471–540. [Google Scholar]



| λ, nm | n | σ2, GM (a) | φ1,m (b) | σmnσnc, cm4 (c) | σmn, cm2 (d) | σnc, cm2 (d) |
|---|---|---|---|---|---|---|
| 1100 | 2 | 24 | (1.6 ± 0.3) × 10−5 | -- | -- | -- |
| 1000 | 2 | 6.2 | (1.0 ± 0.2) × 10−4 | -- | -- | -- |
| 800 | 2 to 4 | 22 | (1.0 ± 0.2) × 10−4 | (5.0 ± 0.8) × 10−36 | (3.7 ± 1.4) × 10−17 | (1.3 ± 0.5) × 10−19 * |
| 780 | 2 to 4 | 42 | (8.5 ± 1.7) × 10−5 | (1.7 ± 0.3) × 10−35 | (5.0 ± 1.6) × 10−17 | (3.4 ± 0.9) × 10−19 |
| 760 | 2 to 4 | 71 | (1.0 ± 0.2) × 10−4 | (3.3 ± 0.5) × 10−35 | (8.8 ± 1.9) × 10−17 | (7.3 ± 1.2) × 10−19 |
| λ, nm | (φm/σmnσnc)1/2, cm−2 | w02, cm2 | P* Predicted, mW (I0*, photons/cm2/s) | P* Observed, mW (I0*, photons/cm2/s) |
|---|---|---|---|---|
| 760 | 1.7 × 1015 | 1.32 × 10−7 | 26 (3.6 × 1028) | 19 (2.6 × 1028) |
| 780 | 2.2 × 1015 | 1.37 × 10−7 | 34 (3.9 × 1028) | 28 (3.2 × 1028) |
| 800 | 4.5 × 1015 | 1.43 × 10−7 | 68 (5.4 × 1028) | 61 (4.8 × 1028) |
| λ, nm | n | σ2, GM (a) | φ1 (b) | σmnφn, cm2 (c) | σmn, cm2 (d) | φn |
|---|---|---|---|---|---|---|
| 1100 | 2 | 7.9 | (2.1 ± 0.3) × 10−4 | -- | -- | -- |
| 1000 | 2 | 25 | (5.7 ± 0.9) × 10−5 | -- | -- | -- |
| 950 | 2 | 34 | (5.0 ± 0.8) × 10−5 | -- | -- | -- |
| 925 | 3 | 38 | -- | (1.2 ± 0.2) × 10−20 (m = 1) | -- | -- |
| 900 | 3 | 35 | (2.0 ± 0.3) × 10−20 (m = 1) | -- | -- | |
| 800 | 3 | 8.8 | -- | (7.7 ± 1.1) × 10−21 (m = 1) | -- | -- |
| 780 | 3 | 6.5 | -- | (1.5 ± 0.2) × 10−20 (m = 1) | -- | -- |
| 760 | 3 | 8.7 | -- | (3.0 ± 0.5) × 10−20 (m > 1) | (1.4 ± 0.4) × 10−17 | (2.2 ± 0.7) × 10−3 |
| λ, nm | n | σ2, GM (a) | φ1,m (b) | σmnσnc, cm4 (c) | σmn, cm2 (d) | σnc, cm2 (d) |
|---|---|---|---|---|---|---|
| 1100 | 4 | 80 | -- | (2.3 ± 0.4) × 10−36 | -- | -- |
| 1000 | 2 to 8 | 56 | (3.7 ± 0.6) × 10−5 | -- | -- | -- |
| 970 | 2 to 10 | 42 | (1.6 ± 0.2) × 10−5 | -- | ||
| 860 | 5 | 22 | -- | -- | -- | -- |
| 820 | 4 | 3.2 | -- | (4.3 ± 0.2) × 10−36 | -- | -- |
| 780 | 4 | 8.7 | -- | (1.6 ± 0.8) × 10−35 | (4.3 ± 1.5) × 10−17 | (3.8 ± 1.3) × 10−20 |
| 760 | 4 (α = 3) | 31 | -- | -- | -- | (4.8 ± 0.7) × 10−19 |
| Protein | λ, nm | σ2, GM (a) | σmnσnc, cm4 | φF (b) | FOM (4) [×10−8] |
|---|---|---|---|---|---|
| mCherry | 800 | 22 | 5.0 × 10−36 | 0.24 | 5 |
| 780 | 42 | 1.7 × 10−35 | 0.24 | 3.8 | |
| 760 | 71 | 3.3 × 10−35 | 0.24 | 3.5 | |
| mPlum | 790 | 43 | 1.6 × 10−35 | 0.13 | 2.1 |
| tdTomato | 1100 | 80 | 2.3 × 10−36 | 0.72 | 43 |
| 820 | 3.2 | 4.3 × 10−36 | 0.72 | 6.2 | |
| 780 | 8.7 | 1.6 × 10−35 | 0.72 | 5.3 |
| Protein | λ, nm | φ1,m(a) | φF(b) | FOM (2) [×103] |
|---|---|---|---|---|
| mCherry | 1100 | 1.6 × 10−5 | 0.24 | 15 |
| 1000 | 1.0 × 10−4 | 0.24 | 2.4 | |
| 800 | 1.0 × 10−4 | 0.24 | 2.4 | |
| 780 | 8.5 × 10−5 | 0.24 | 2.8 | |
| 760 | 1.0 × 10−4 | 0.24 | 2.4 | |
| mPlum | 790 | 1.3 × 10−4 | 0.13 | 1 |
| jREX-GECO1 | 1100 | 2.1 × 10−4 | 0.21 | 1 |
| tdTomato | 1000 | 5.7 × 10−5 | 0.21 | 3.7 |
| 950 | 5.0 × 10−5 | 0.21 | 4.2 | |
| 1000 | 3.7 × 10−5 | 0.72 | 20 | |
| 970 | 1.6 × 10−5 | 0.72 | 45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drobizhev, M.; Molina, R.S.; Franklin, J. Multiphoton Bleaching of Red Fluorescent Proteins and the Ways to Reduce It. Int. J. Mol. Sci. 2022, 23, 770. https://doi.org/10.3390/ijms23020770
Drobizhev M, Molina RS, Franklin J. Multiphoton Bleaching of Red Fluorescent Proteins and the Ways to Reduce It. International Journal of Molecular Sciences. 2022; 23(2):770. https://doi.org/10.3390/ijms23020770
Chicago/Turabian StyleDrobizhev, Mikhail, Rosana S. Molina, and Jacob Franklin. 2022. "Multiphoton Bleaching of Red Fluorescent Proteins and the Ways to Reduce It" International Journal of Molecular Sciences 23, no. 2: 770. https://doi.org/10.3390/ijms23020770
APA StyleDrobizhev, M., Molina, R. S., & Franklin, J. (2022). Multiphoton Bleaching of Red Fluorescent Proteins and the Ways to Reduce It. International Journal of Molecular Sciences, 23(2), 770. https://doi.org/10.3390/ijms23020770





