Tracking Topological and Electronic Effects on the Folding and Stability of Guanine-Deficient RNA G-Quadruplexes, Engineered with a New Computational Tool for De Novo Quadruplex Folding
Abstract
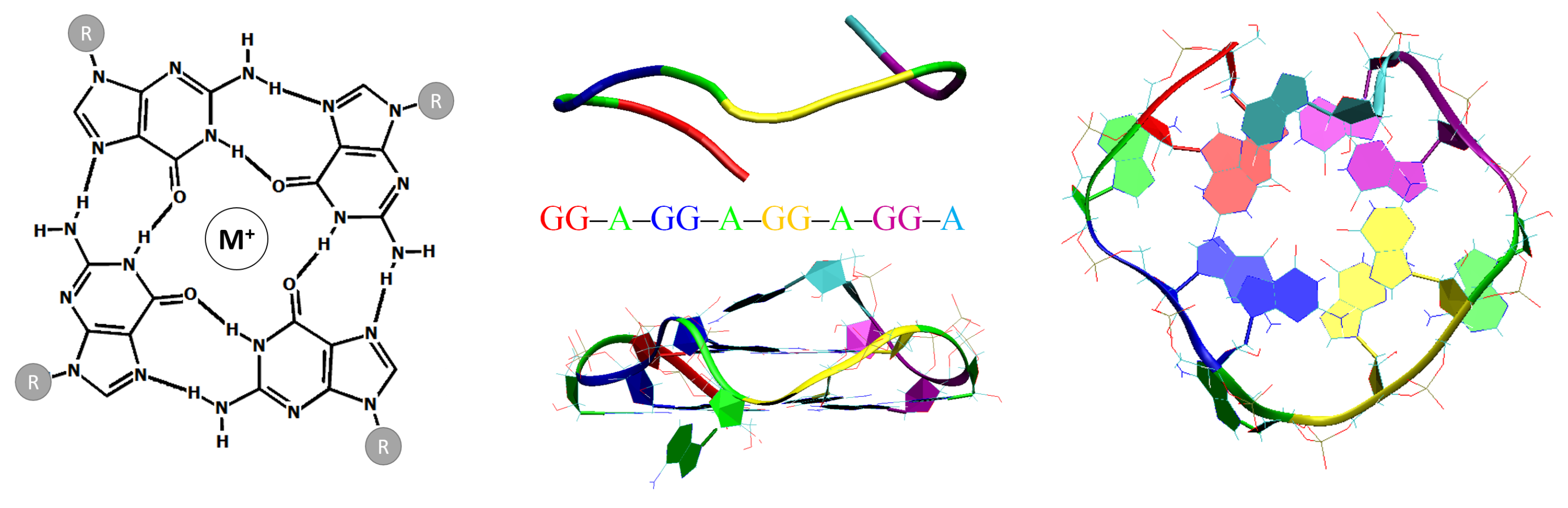
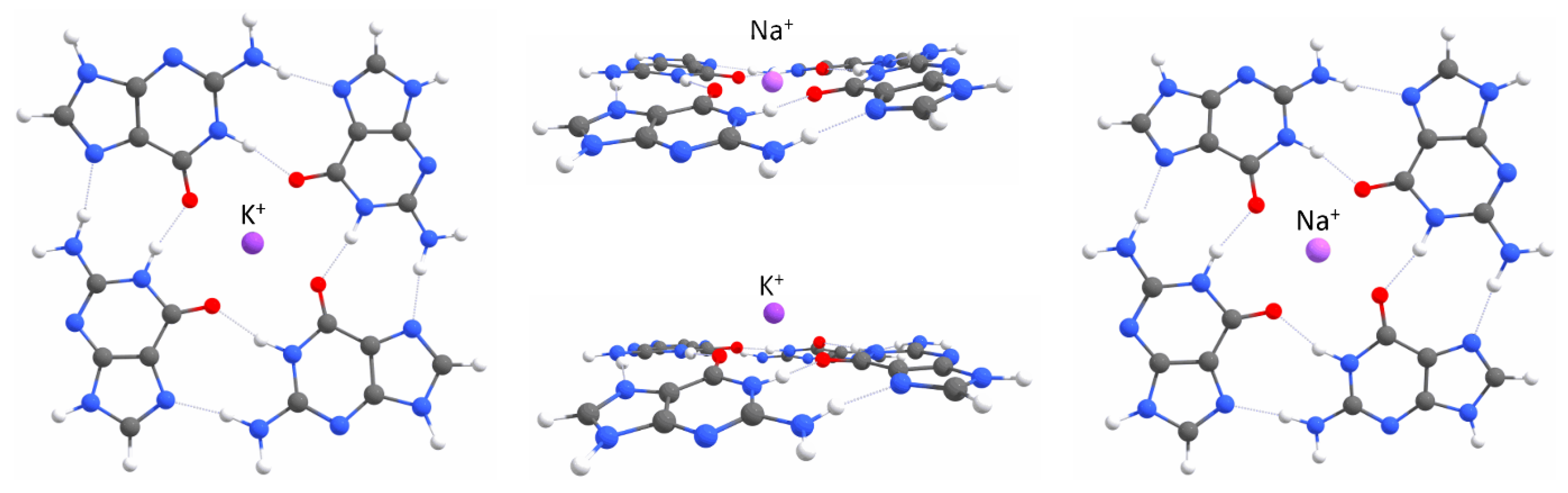
1. Introduction
2. Materials and Methods
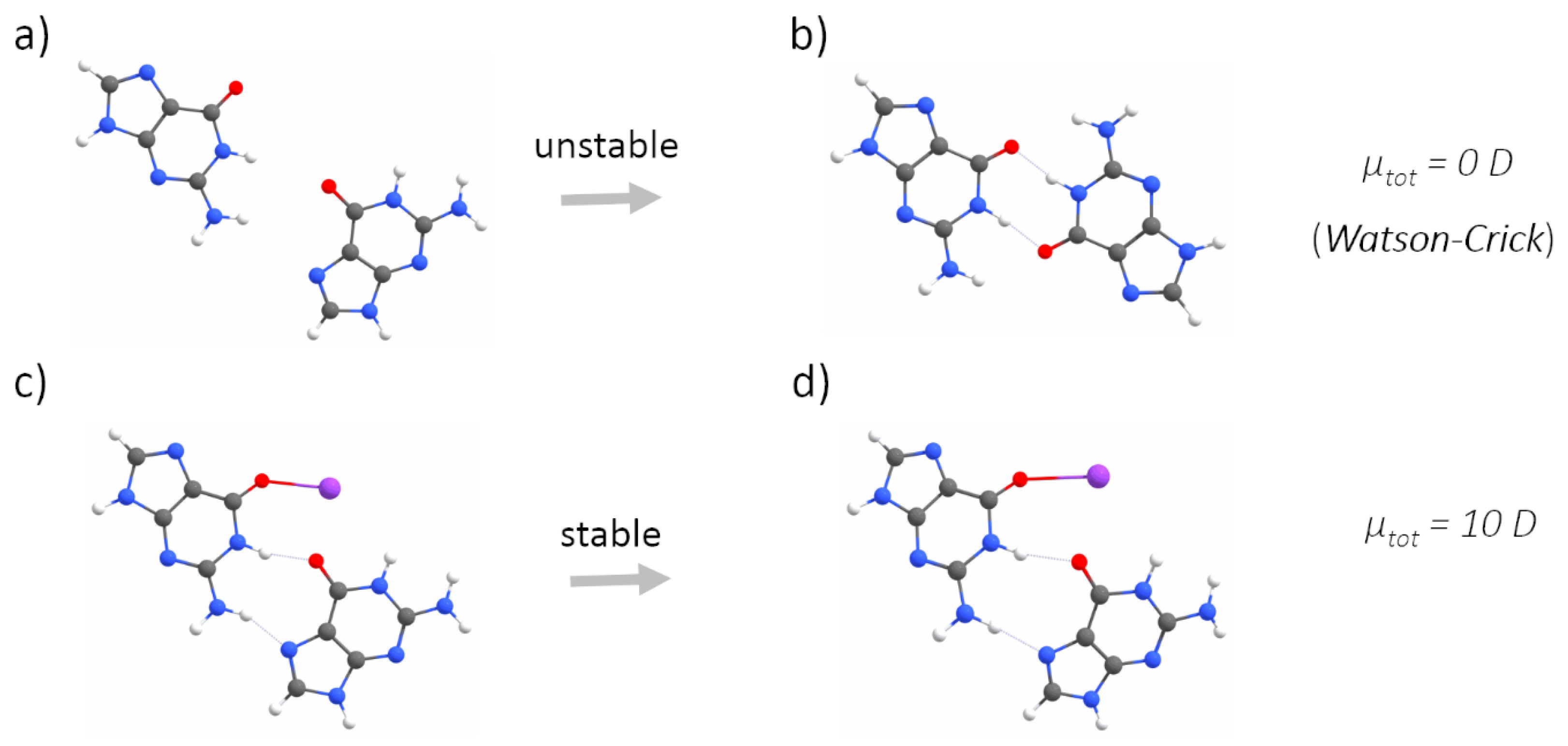
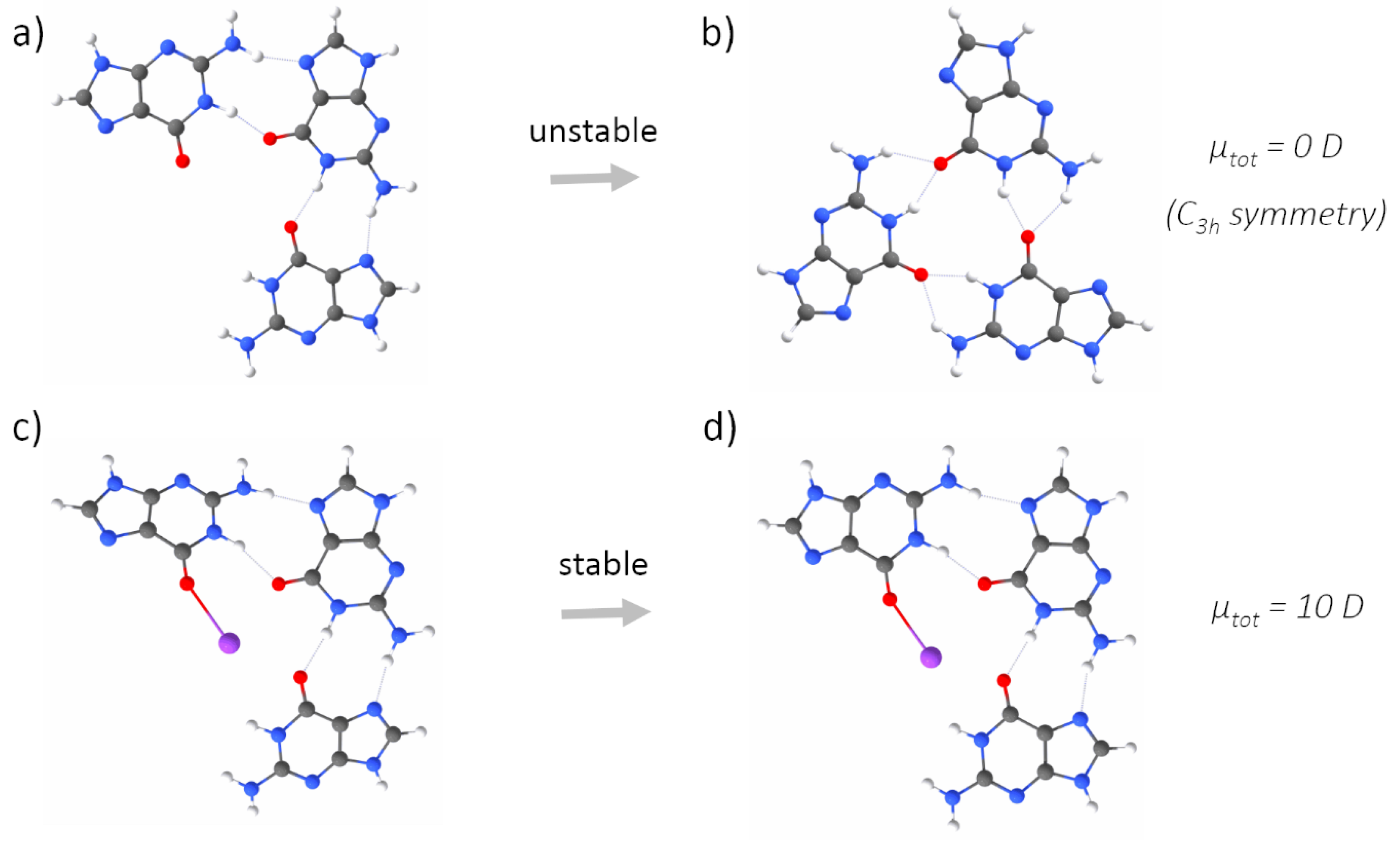
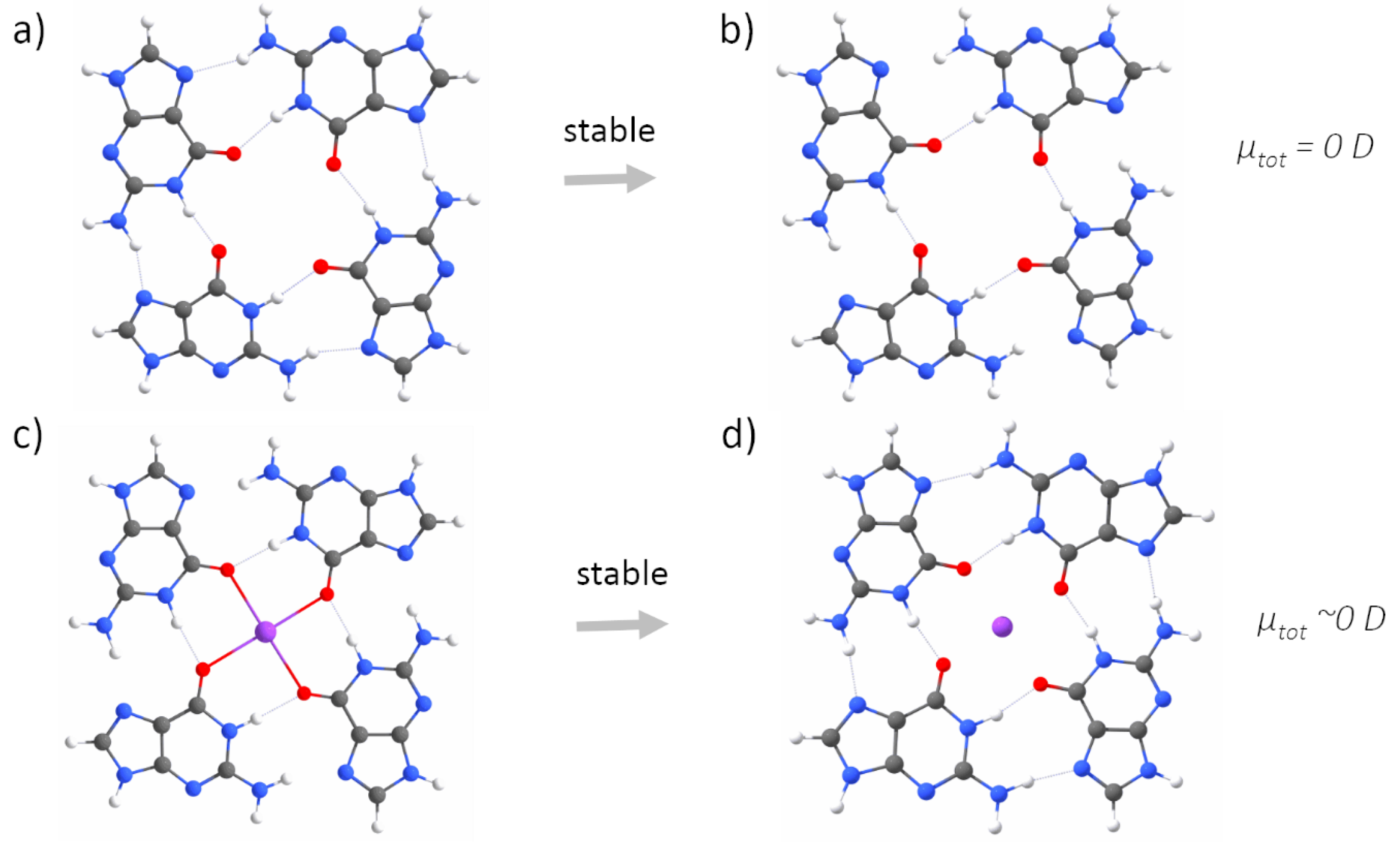
2.1. Quantum Mechanical Calculations
2.2. Molecular Dynamics Simulations
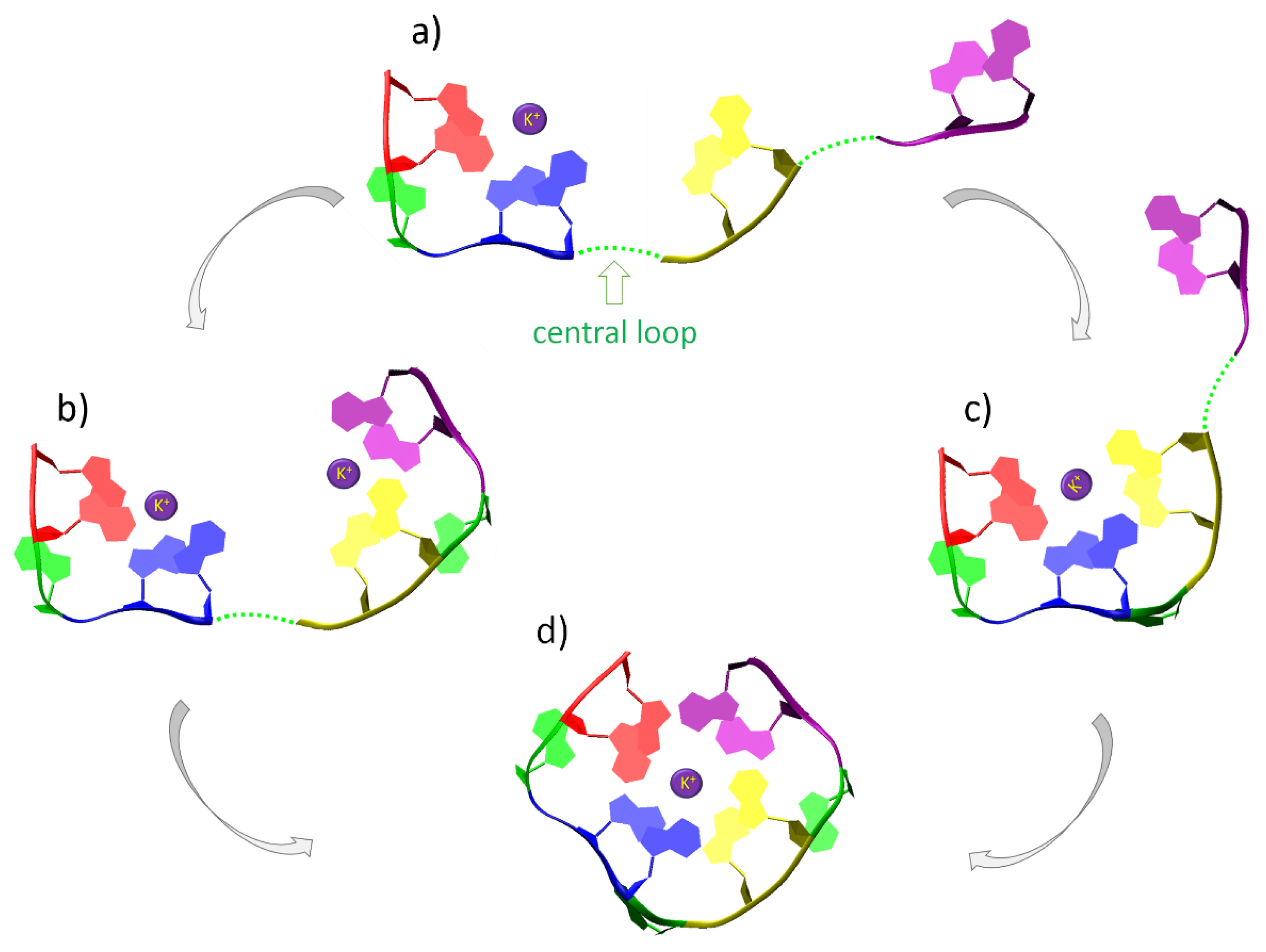
2.3. De Novo Modelling of G-Quadruplex Topologies
- Adding a new nucleotide to the model. The orientation of the new nucleotide with respect to the already built ones (if any) resembles that in canonical helical nucleic acids—with adjacent nucleotides interacting via pi-stacking.
- Application of the geometric restraints to the model based on user’s input and a predefined set of templates, consisting of pairs of nucleotides involved in hydrogen bonds via Hoogsteen edges, and pairs of pi-stacking nucleotides.
- Concerted pulling of residues, based on the imposed restraints. The conjugated gradient (CG) algorithm is used for this purpose, as implemented in NAB for “rigid body transformations”. The structure with the lowest potential energy is chosen as the input configuration for the next step.
- The backbone with restrained nucleobases is optimized using the Generalized Born implicit solvent model [53].
- The optional removal of the cap prior to the addition of a new nucleotide.
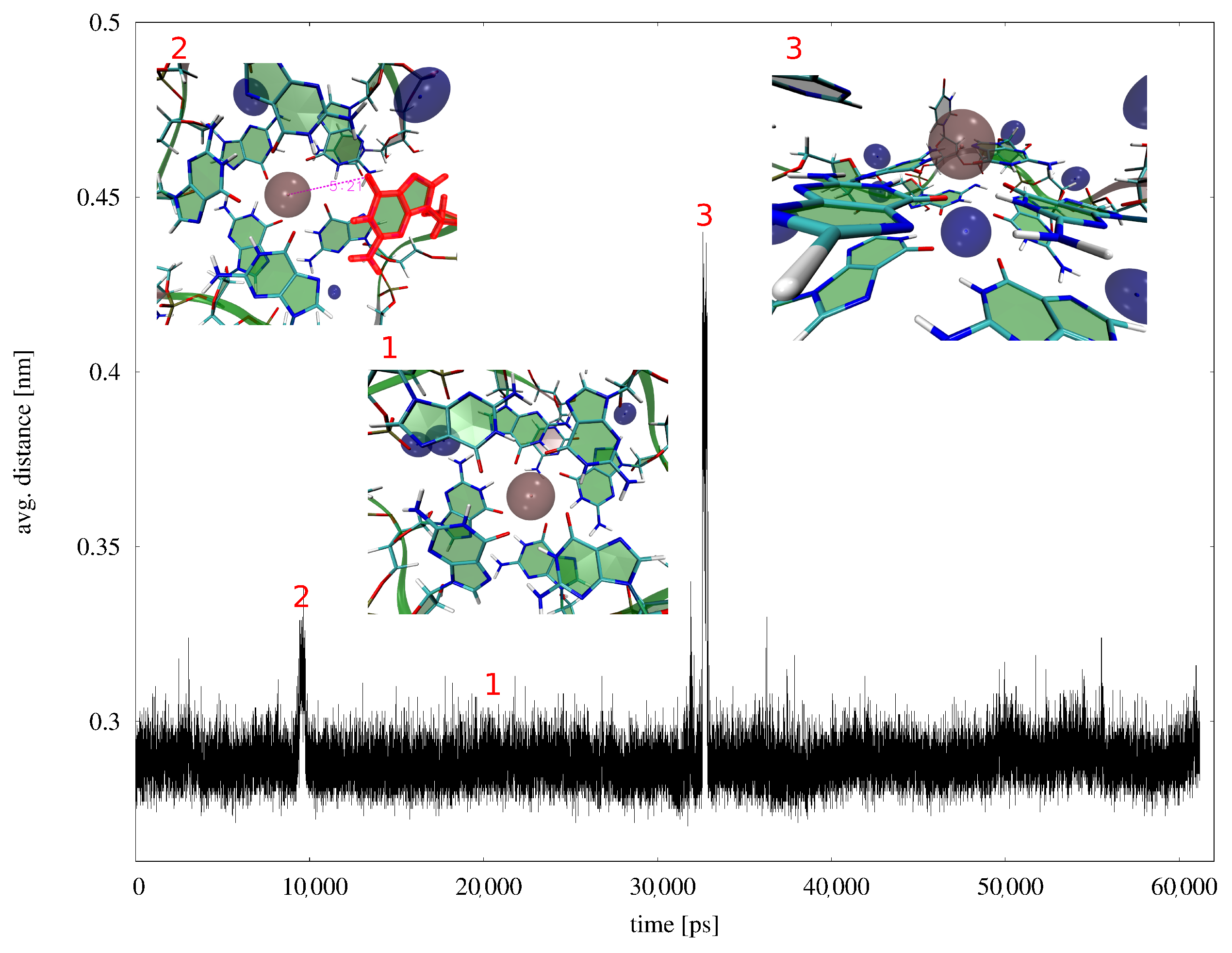
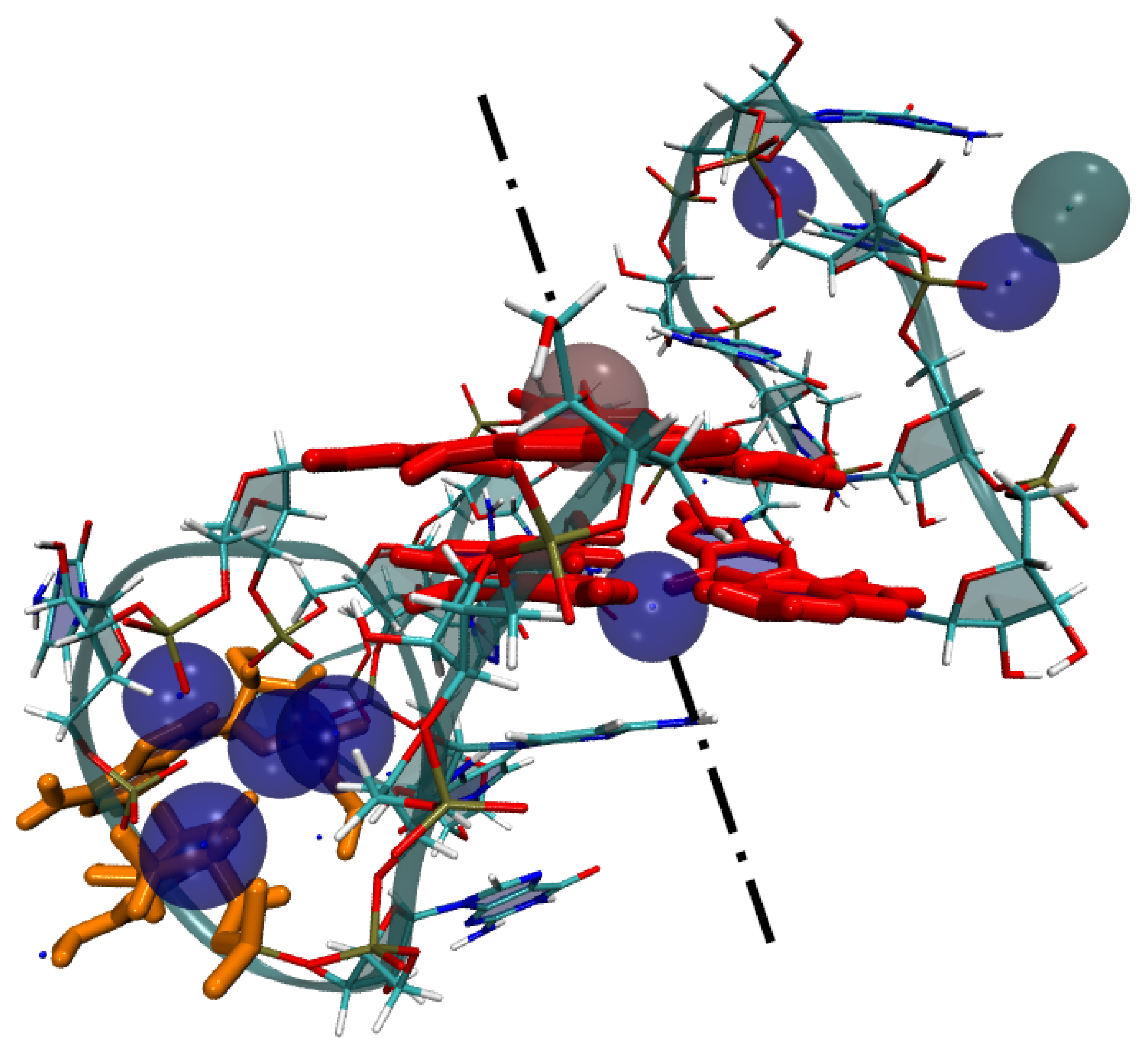
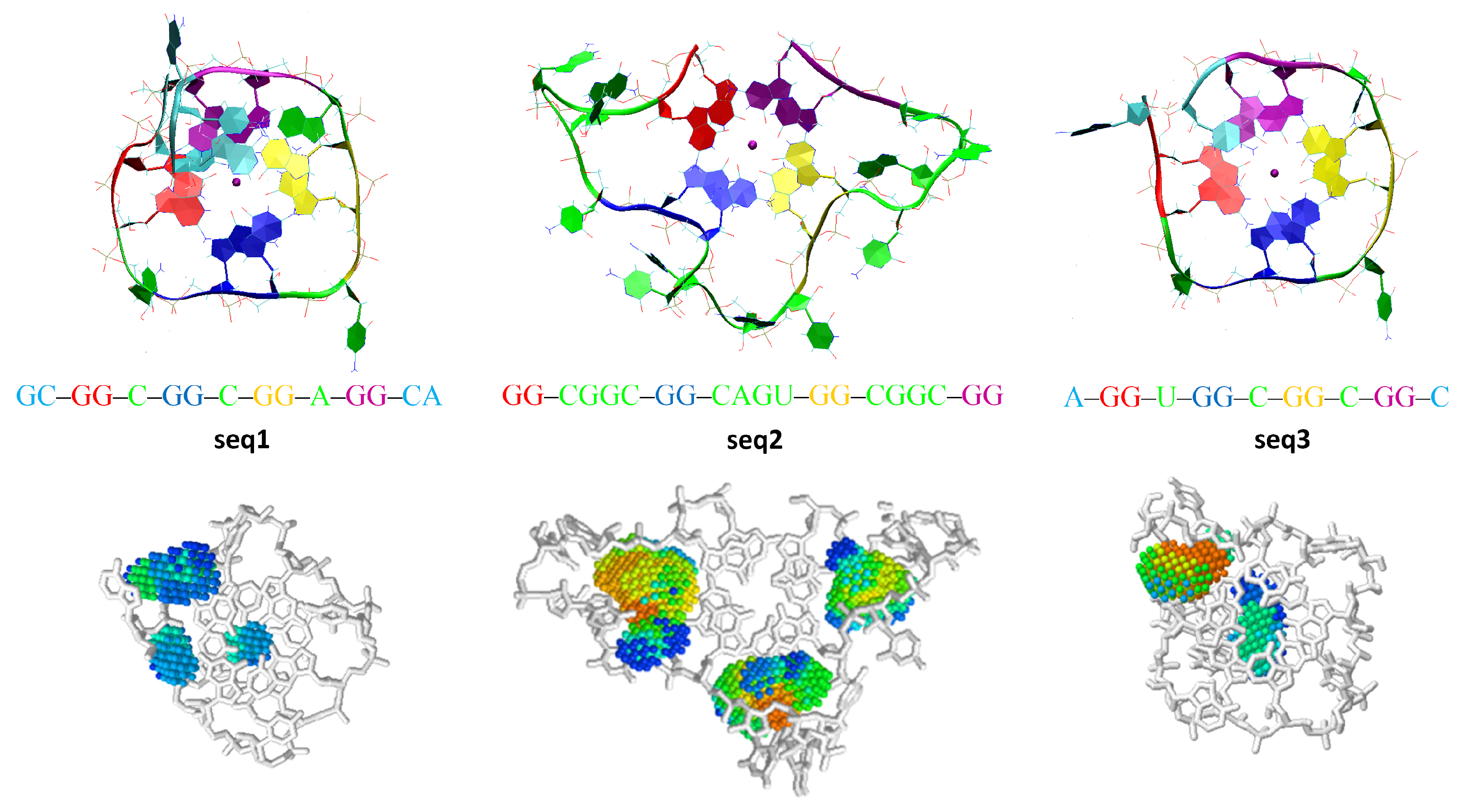
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 5-UTR | 5-untranslated region |
| DFT | density functional theory |
| GQ | guanine quadruplex |
| MD | molecular dynamics |
| NAB | Nucleic Acid Builder |
| PDB | Protein Data Bank |
| QM | quantum mechanics |
| NMR | nuclear magnetic resonance |
Appendix A. QM Results
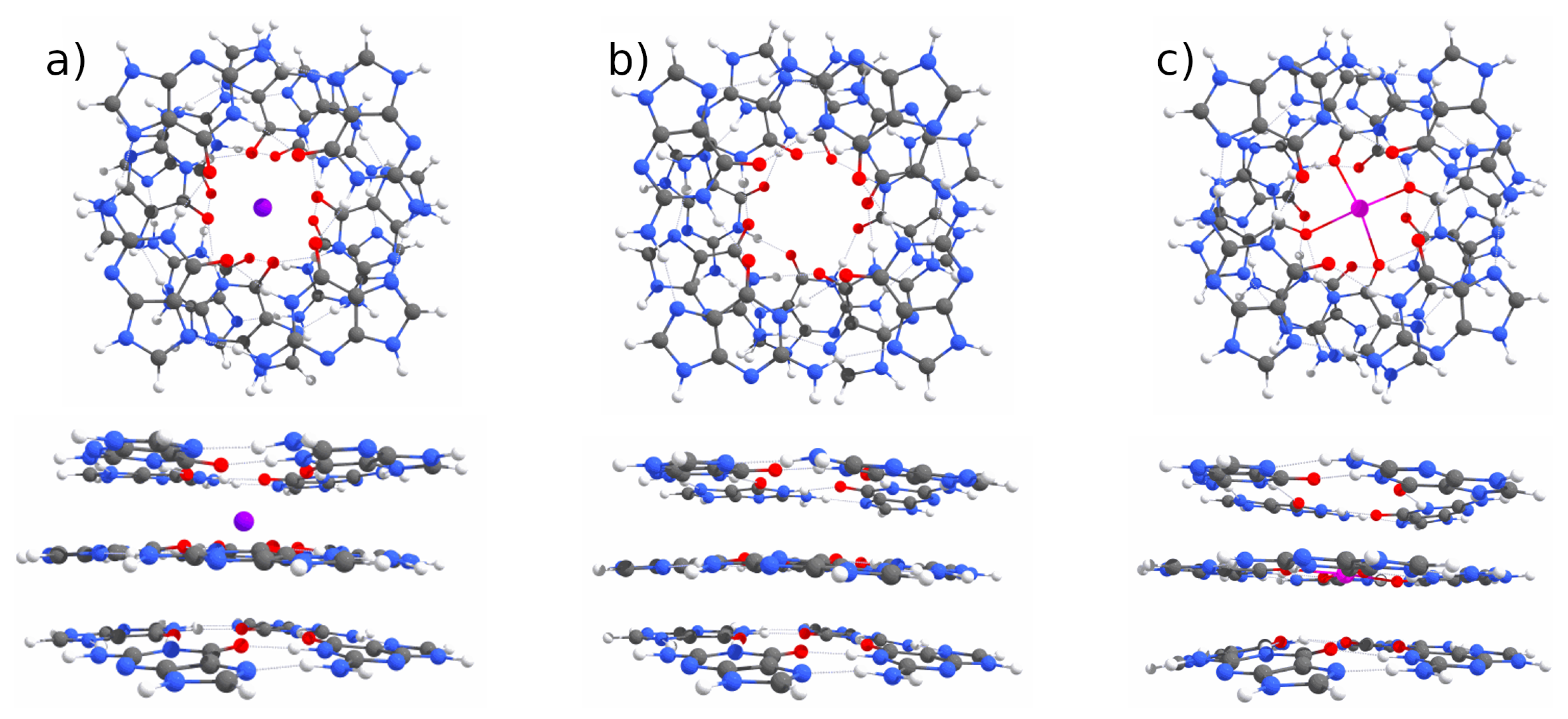
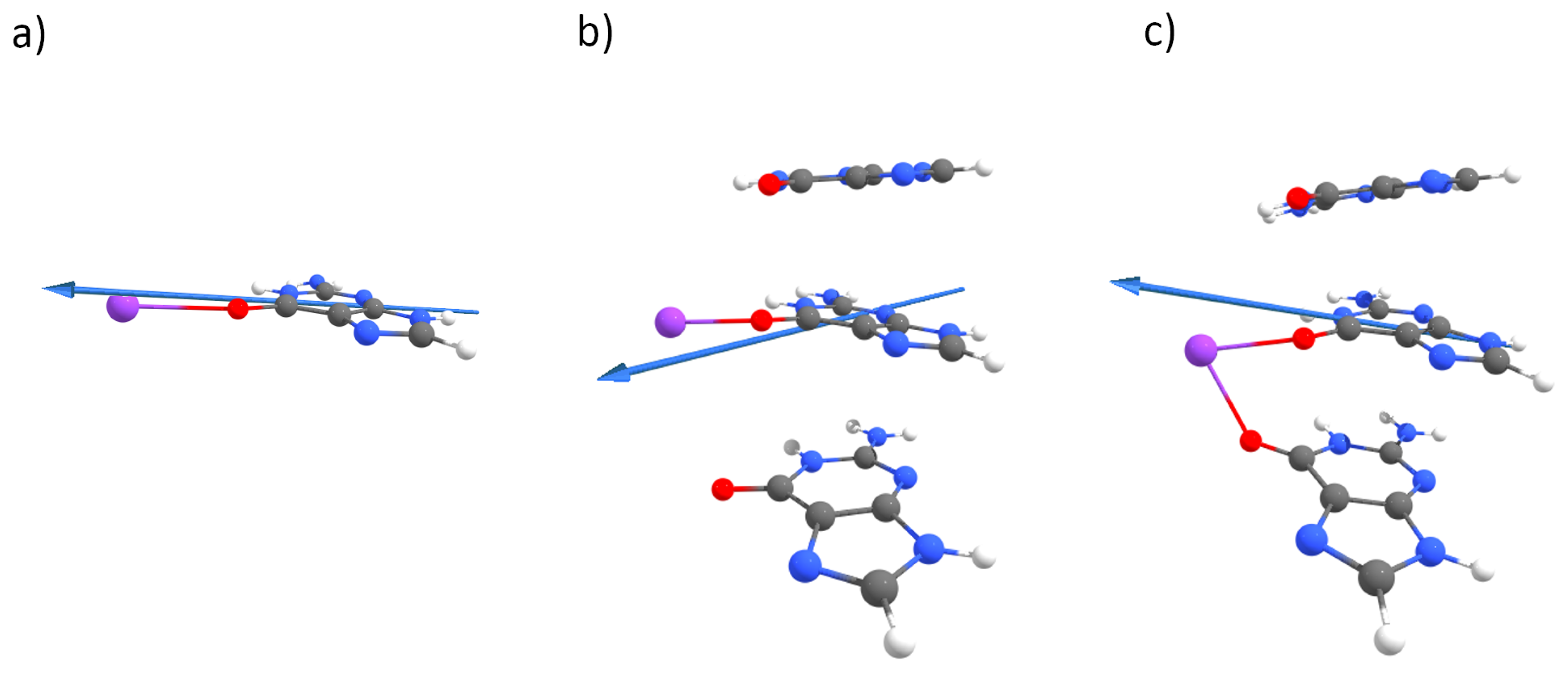
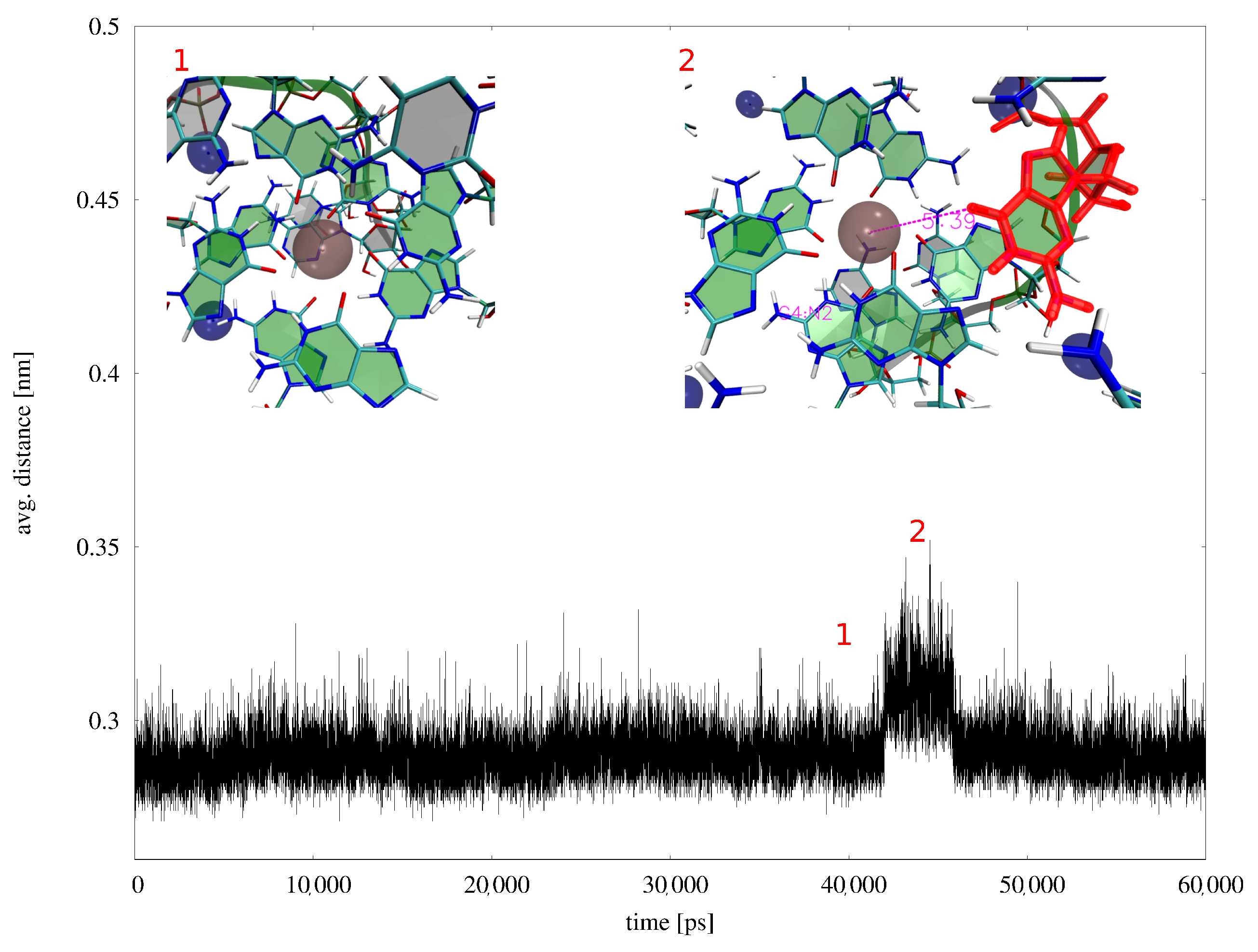
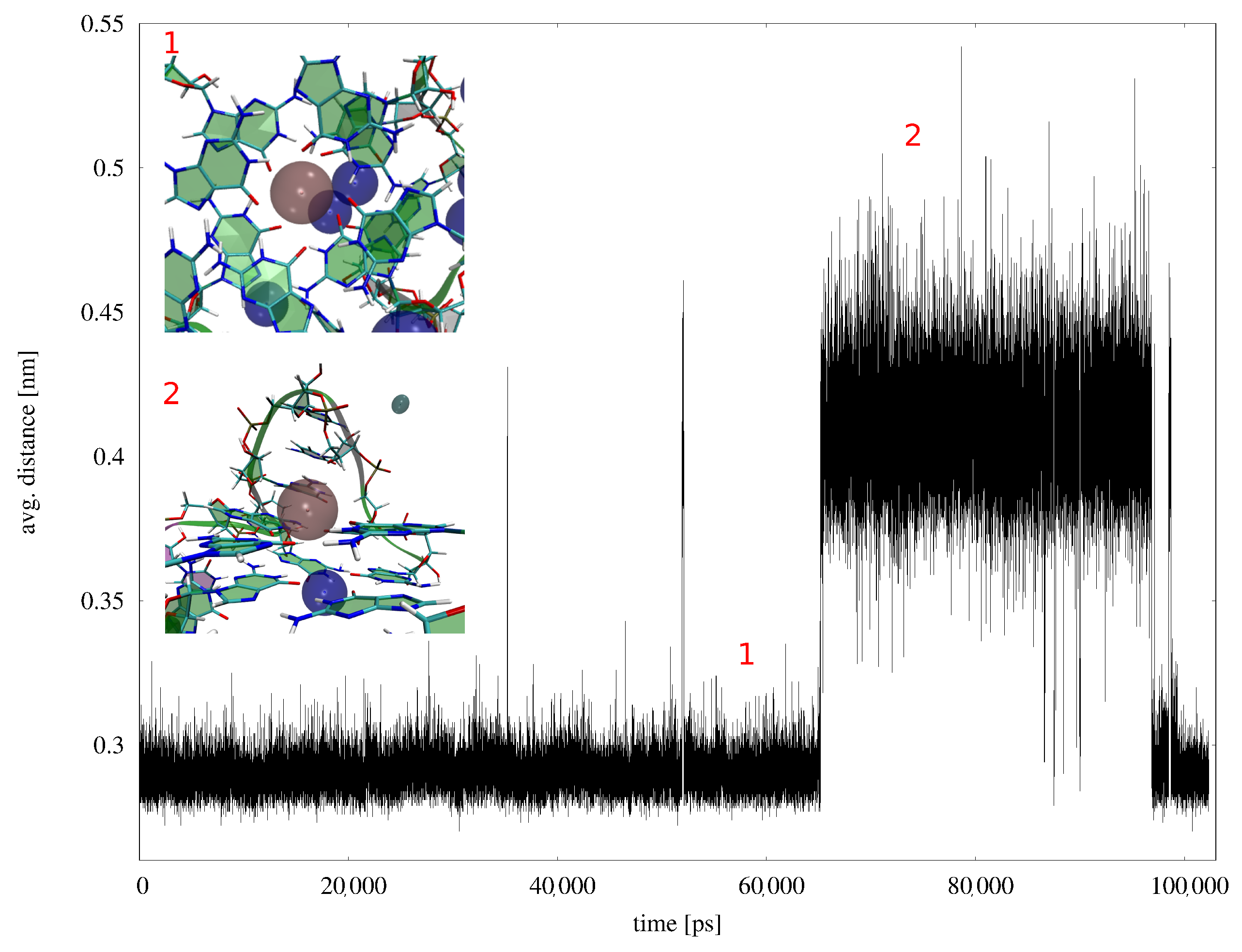
Appendix B. MD Results
| Model | Type | Sequence | MD Time | Result | Ion Escape | Dissociation |
|---|---|---|---|---|---|---|
| 1 | RNA | AGGAGGAGGAGG-GGAGGAGGAGGA | 100 | stable | - | - |
| 2 | RNA | GGAGGAGGAGGA | 100 | stable | - | - |
| 3 | RNA | GGAGGGGGAGGA | 100 | stable | - | - |
| 4 | RNA | GGAGGUGGAGGA | 100 | stable | - | - |
| 5 | RNA | GGGGGGGGGGGA | 100 | stable | - | - |
| 6 | RNA | GGUGGUGGUGGA | 100 | stable | - | - |
| 7 | RNA | GGAAGGAAGGAAGGA | 100 | destroyed | 10 | 9.8 |
| 8 | RNA | GGGGGGGGGGGGGGA | 100 | destroyed | 63 | 49 |
| 9 | RNA | GGAGGAGAGGAGGA | 100 | destroyed | 26.1 | 26 |
| 10 | RNA | GGAGGGAGGGAGGA | 100 | destroyed | 19.1 | 19 |
| 11 | RNA | GGACGGACGGACGGA | 100 | destroyed | 11 | 13 |
| 12 | RNA | GGUUGGUUGGUUGGA | 100 | destroyed | 17 | 14 |
| 13 | RNA | GGCACGGCACGGCACGGA | 191.6 | destroyed | 141.8 | 141.3 |
| 14 | RNA | GGACAGGACAGGACAGGA | 95.8 | destroyed | 23 | 14 |
| 15 | RNA | GGAGCGGAGCGGAGCGGA | 191.6 | destroyed | 181.8 | 120.8 |
| 16 | RNA | GGAGGAGGAGG | 100 | stable | - | - |
| 17 | RNA | ACGGGGGGGGGGGGGGCA | 100 | destroyed | - | 97 |
| 18 | RNA | ACGGUUGGUUGGUUGGCA | 194 | destroyed | 117.1 | 117 |
| 19 | RNA | GCGGUUGGUUGGUUGGCG | 194 | stable | - | - |
| 20 | RNA | AUGGUUGGUUGGUUGGUA | 194 | stable | - | - |
| 21 | RNA | ACGGCCGGCCGGCCGGCA | 194 | destroyed | 22 | 10 |
| 22 | RNA | CAGGUUGGUUGGUUGGAC | 194 | stable | - | - |
| 23 | RNA | AGGUUGGUUGGUUGGA | 194 | destroyed | - | 170 |
| 24 | RNA | GGGGGGGGGGG | 100 | destroyed | 7 | 6.5 |
| 25 | RNA | GGCGGCGGCGG | 100 | stable | - | - |
| 26 | RNA | GGUGGUGGUGG | 100 | stable | - | - |
| 27 | RNA | AGGAGCGGAGCGGAGCGGA | 100 | destroyed | 17 | 14 |
| 28 | RNA | AGGCACGGCACGGCACGGA | 100 | destroyed | 13 | 5 |
| 29 | RNA | GCGGCACGGCACGGCACGGCG | 96 | destroyed | 11 | 6 |
| 30 | RNA | AGGGGGGGGGGG-GGGGGGGGGGGA | 100 | stable | - | - |
| 31 | RNA | AGGUGGUGGUGG-GGUGGUGGUGGA | 100 | stable | - | - |
| 32 | RNA | AGGCGGCGGCGG-GGCGGCGGCGGA | 100 | stable | - | - |
| 33 | DNA | GGAGGAGGAGG | 100 | stable | - | - |
| 34 | DNA | GGGGGGGGGGG | 100 | destroyed | 2.1 | 2 |
| 35 | DNA | GGCGGCGGCGG | 100 | destroyed | 2.9 | 2 |
| 36 | DNA | GGTGGTGGTGG | 100 | destroyed | 34 | 33 |
| 37 | RNA | GGUUGGUUGGUUGG | 100 | destroyed | 46 | 45 |
| 38 | RNA | GUGGUUGGUUGGUUGGUG | 100 | destroyed | - | 100 |
| 39 (seq1) | RNA | GCGGCGGCGGAGGCA | 100 | stable | - | - |
| 40 (seq2) | RNA | GGCGGCGGCAGUGGCGGCGG | 100 | destroyed | 7 | 5 |
| 41 (seq3) | RNA | AGGUGGCGGCGGC | 100 | stable | - | - |
| 42 | DNA | GCGGCGGCGGAGGCA | 100 | stable | - | - |
| 43 | DNA | GGCGGCGGCAGTGGCGGCGG | 100 | destroyed | 9 | 8 |
| 44 | DNA | AGGTGGCGGCGGC | 100 | stable | - | - |
Appendix B.1. MD Simulations with Amber ff99-ILDN-Bsc0 Force Field
Appendix B.2. MD Simulations with AMOEBA Polarizable Force Field
Appendix C. The Process of De Novo Quadruplex Folding with the NAB-GQ- Builder Tool

References
- Lim, K.W.; Amrane, S.; Bouaziz, S.; Xu, W.; Mu, Y.; Patel, D.J.; Phan, A.T. Structure of the human telomere in K+ solution: A stable basket-type G-quadruplex with only two G-tetrad layers. J. Am. Chem. Soc. 2009, 131, 4301–4309. [Google Scholar] [CrossRef] [PubMed]
- Varshney, D.; Spiegel, J.; Zyner, K.; Tannahill, D.; Balasubramanian, S. The regulation and functions of DNA and RNA G-quadruplexes. Nat. Rev. Mol. Cell Biol. 2020, 21, 459–474. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.S.M.; Ghanem, L.R.; Barash, Y. Integrative analysis reveals RNA G-quadruplexes in UTRs are selectively constrained and enriched for functional associations. Nat. Commun. 2020, 11, 527. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Hurley, L.H.; Neidle, S. Targeting G-quadruplexes in gene promoters: A novel anticancer strategy? Nat. Rev. Drug Discov. 2011, 10, 261–275. [Google Scholar] [CrossRef] [PubMed]
- Fay, M.M.; Lyons, S.M.; Ivanov, P. RNA G-Quadruplexes in biology: Principles and molecular mechanisms. J. Mol. Biol. 2017, 429, 2127–2147. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, I.; Shafer, R.H. Effect of loop sequence and size on DNA aptamer stability. Biochemistry 2000, 39, 1462–1468. [Google Scholar] [CrossRef]
- Hazel, P.; Huppert, J.; Balasubramanian, S.; Neidle, S. Loop-length-dependent folding of G-quadruplexes. J. Am. Chem. Soc. 2004, 126, 16405–16415. [Google Scholar] [CrossRef]
- Pandey, S.; Agarwala, P.; Maiti, S. Effect of loops and G-quartets on the stability of RNA G-quadruplexes. J. Phys. Chem. B 2013, 117, 6896–6905. [Google Scholar] [CrossRef]
- Zhang, D.H.; Fujimoto, T.; Saxena, S.; Yu, H.Q.; Miyoshi, D.; Sugimoto, N. Monomorphic RNA G-quadruplex and polymorphic DNA G-quadruplex structures responding to cellular environmental factors. Biochemistry 2010, 49, 4554–4563. [Google Scholar] [CrossRef]
- Dai, J.; Chen, D.; Jones, R.A.; Hurley, L.H.; Yang, D. NMR solution structure of the major G-quadruplex structure formed in the human BCL2 promoter region. Nucleic Acids Res. 2006, 34, 5133–5144. [Google Scholar] [CrossRef]
- Karsisiotis, A.I.; O’Kane, C.; Webba da Silva, M. DNA quadruplex folding formalism—A tutorial on quadruplex topologies. Methods 2013, 64, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Kejnovská, I.; Stadlbauer, P.; Trantŕek, L.; Renc̆iuk, D.; Gajarský, M.; Krafc̆ík, D.; Palacký, J.; Bednár̆ová, K.; S̆poner, J.; Mergny, J.-L.; et al. G-quadruplex formation by DNA sequences deficient in guanines: Two tetrad parallel quadruplexes do not fold intramolecularly. Chem. Eur. J. 2021, 27, 12115–12125. [Google Scholar] [CrossRef] [PubMed]
- Largy, E.; Mergny, J.L.; Gabelica, V. Role of alkali metal ions in G-quadruplex nucleic acid structure and stability. In The Alkali Metal Ions: Their Role for Life; Springer: Cham, Switzerland, 2016; pp. 203–258. [Google Scholar]
- Bhattacharyya, D.; Mirihana Arachchilage, G.; Basu, S. Metal cations in G-quadruplex folding and stability. Front. Chem. 2016, 4, 38. [Google Scholar] [CrossRef]
- Bugaut, A.; Murat, P.; Balasubramanian, S. An RNA hairpin to G-quadruplex conformational transition. J. Am. Chem. Soc. 2012, 134, 19953–19956. [Google Scholar] [CrossRef]
- Risitano, A.; Fox, K.R. Stability of intramolecular DNA quadruplexes: Comparison with DNA duplexes. Biochemistry 2003, 42, 6507–6513. [Google Scholar] [CrossRef]
- Mergny, J.L.; De Cian, A.; Ghelab, A.; Sacca, B.; Lacroix, L. Kinetics of tetramolecular quadruplexes. Nucleic Acids Res. 2005, 33, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Joachimi, A.; Benz, A.; Hartig, J.S. A comparison of DNA and RNA quadruplex structures and stabilities. Bioorg. Med. Chem. 2009, 17, 6811–6815. [Google Scholar] [CrossRef] [PubMed]
- Zaccaria, F.; Fonseca Guerra, C. RNA versus DNA G-quadruplex: The origin of increased stability. Chem. Eur. J. 2018, 24, 16315–16322. [Google Scholar] [CrossRef]
- Neidle, S. Structured waters mediate small molecule binding to G-quadruplex nucleic acids. Pharmaceuticals 2021, 15, 7. [Google Scholar] [CrossRef]
- Esposito, V.; Virgilio, A.; Randazzo, A.; Galeone, A.; Mayol, L. A new class of DNA quadruplexes formed by oligodeoxyribonucleotides containing a 3′-3′ or 5′-5′ inversion of polarity site. Chem. Commun. 2005, 31, 3953–3955. [Google Scholar] [CrossRef]
- Puig Lombardi, E.; Londoño Vallejo, A. A guide to computational methods for G-quadruplex prediction. Nucleic Acids Res. 2020, 48, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Kuhrova, P.; Best, R.B.; Bottaro, S.; Bussi, G.; Sponer, J.; Otyepka, M.; Banas, P. Computer folding of RNA tetraloops: Identification of key force field deficiencies. J. Chem. Theory Comput. 2016, 12, 4534–4548. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Gao, Y.; Qiu, F.; Zhu, T. Benchmark force fields for the molecular dynamic simulation of G-quadruplexes. Molecules 2021, 26, 5379. [Google Scholar] [CrossRef]
- Haider, S. Computational methods to study G-quadruplex–ligand complexes. J. Indian Inst. Sci. 2018, 98, 325–339. [Google Scholar] [CrossRef]
- S̆poner, J.; Bussi, G.; Stadlbauer, P.; Kuhrová, P.; Banás̆, P.; Islam, B.; Haider, S.; Neidle, S.; Otyepka, M. Folding of guanine quadruplex molecules–funnel-like mechanism or kinetic partitioning? An overview from MD simulation studies. Biochim. Biophys. Acta. Gen. Subj. 2017, 1861, 1246–1263. [Google Scholar] [CrossRef] [PubMed]
- Ortiz de Luzuriaga, I.; Lopez, X.; Gil, A. Learning to model G-quadruplexes: Current methods and perspectives. Annu. Rev. Biophys. 2021, 50, 209–243. [Google Scholar] [CrossRef] [PubMed]
- Hong, F.; Schreck, J.S.; S̆ulc, P. Understanding DNA interactions in crowded environments with a coarse-grained model. Nucleic Acids Res. 2020, 48, 10726–10738. [Google Scholar] [CrossRef]
- Mulholland, K.; Sullivan, H.J.; Garner, J.; Cai, J.; Chen, B.; Wu, C. Three-dimensional structure of RNA monomeric G-quadruplex containing ALS and FTD related G4C2 repeat and its binding with TMPyP4 probed by homology modeling based on experimental constraints and molecular dynamics simulations. ACS Chem. Neurosci. 2020, 11, 57–75. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Frisch, M.J.; Fox, D.J. Gaussian 09, revision C.01; Gaussian Inc.: Wallingfort, CT, USA, 2009; Available online: http://www.gaussian.com (accessed on 29 July 2022).
- S̆poner, J.; Mládek, A.; S̆pac̆ková, N.; Cang, X.; Cheatham, T.E., III; Grimme, S. Relative stability of different DNA guanine quadruplex stem topologies derived using large-scale quantum-chemical computations. J. Am. Chem. Soc. 2013, 135, 9785–9796. [Google Scholar] [CrossRef] [PubMed]
- Ortiz de Luzuriaga, I.; Elleuchi, S.; Jarraya, K.; Artacho, E.; López, X.; Gil, A. Semi-empirical and linear-scaling DFT methods to characterize duplex DNA and G-quadruplexes in the presence of interacting small molecules. Phys. Chem. Chem. Phys. 2022, 24, 11510–11519. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar] [CrossRef]
- Pérez, A.; Marchán, I.; Svozil, D.; Sponer, J.; Cheatham III, T.E.; Laughton, C.E.; Orozco, M. Refinement of the AMBER force field for nucleic acids: Improving the description of α/γ conformers. Biophys. J. 2007, 92, 3817–3829. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Guy, A.T.; Piggot, T.J.; Khalid, S. Single-stranded DNA within nanopores: Conformational dynamics and implications for sequencing; a molecular dynamics simulation study. Biophys. J. 2012, 103, 1028–1036. [Google Scholar] [CrossRef]
- Ando, T.; Skolnick, J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc. Natl. Acad. Sci. USA 2010, 107, 18457–18462. [Google Scholar] [CrossRef]
- Salsbury, A.M.; Lemkul, J.A. Molecular dynamics simulations of the c-kit1 promoter G-quadruplex: Importance of electronic polarization on stability and cooperative ion binding. J. Phys. Chem. B 2019, 123, 148–159. [Google Scholar] [CrossRef]
- Singh, A.; Singh, N. Effect of salt concentration on the stability of heterogeneous DNA. Physica A 2015, 419, 328–334. [Google Scholar] [CrossRef]
- Rackers, J.A.; Wang, Z.; Lu, C.; Laury, M.L.; Lagardère, L.; Schnieders, M.J.; Piquemal, J.P.; Ren, P.; Ponder, J.W. Tinker 8: Software tools for molecular design. J. Chem. Theory Comput. 2018, 14, 5273–5289. [Google Scholar] [CrossRef] [PubMed]
- Rackers, J.A.; Wang, Q.; Liu, C.; Piquemal, J.P.; Ren, P.; Ponder, J.W. An optimized charge penetration model for use with the AMOEBA force field. Phys. Chem. Chem. Phys. 2017, 19, 276–291. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. Tinker9: Next Generation of Tinker with GPU Support; Washington University: St. Louis, MO, USA, 2021; Available online: https://github.com/TinkerTools/tinker9 (accessed on 20 April 2022).
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Kawabata, T. Detection of multiscale pockets on protein surfaces using mathematical morphology. Proteins Struct. Funct. Bioinf. 2010, 78, 1195–1211. [Google Scholar] [CrossRef]
- Macke, T.; Case, D.A. Modeling unusual nucleic acid structures. In Molecular Modeling of Nucleic Acids; American Chemical Society: Washington, DC, USA, 1998; pp. 379–393. [Google Scholar]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Wang, J.; Cieplak, P.; Kollman, P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000, 21, 1049–1074. [Google Scholar] [CrossRef]
- Zgarbová, M.; Otyepka, M.; Sponer, J.; Mládek, A.; Banás̆, P.; Cheatham, T.E., 3rd; Jurec̆ka, P. Refinement of the Cornell et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J. Chem. Theory Comput. 2011, 7, 2886–2902. [Google Scholar] [CrossRef]
- Brown, R.A.; Case, D.A. Second derivatives in generalized Born theory. J. Comput. Chem. 2006, 27, 1662–1675. [Google Scholar] [CrossRef]
- Miglietta, G.; Cogoi, S.; Marinello, J.; Capranico, G.; Tikhomirov, A.S.; Shchekotikhin, A.; Xodo, L.E. RNA G-Quadruplexes in Kirsten Ras (KRAS) oncogene as targets for small molecules inhibiting translation. J. Med. Chem. 2017, 60, 9448–9461. [Google Scholar] [CrossRef]
- Mashima, T.; Matsugami, A.; Nishikawa, F.; Nishikawa, S.; Katahira, M. Unique quadruplex structure and interaction of an RNA aptamer against bovine prion protein. Nucleic Acids Res. 2009, 37, 6249–6258. [Google Scholar] [CrossRef] [PubMed]
- Ambrus, A.; Chen, D.; Dai, J.; Jones, R.A.; Yang, D. Solution structure of the biologically relevant G-quadruplex element in the human c-MYC promoter. Implications for G-quadruplex stabilization. Biochemistry 2005, 44, 2048–2058. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Cheng, Y.; Hao, J.; Jia, G.; Zhou, J.; Mergny, J.L.; Li, C. Loop permutation affects the topology and stability of G-quadruplexes. Nucleic Acids Res. 2018, 46, 9264–9275. [Google Scholar] [CrossRef] [PubMed]
- Hao, F.; Ma, Y.; Guan, Y. Effects of central loop length and metal ions on the thermal stability of G-quadruplexes. Molecules 2019, 24, 1863. [Google Scholar] [CrossRef] [PubMed]
- Stadlbauer, P.; Trantírek, L.; Cheatham III, T.E.; Koc̆a, J.; Sponer, J. Triplex intermediates in folding of human telomeric quadruplexes probed by microsecond-scale molecular dynamics simulations. Biochimie 2014, 105, 22–35. [Google Scholar] [CrossRef]
- Stefl, R.; Cheatham, T.E., 3rd; Spacková, N.A.; Fadrná, E.; Berger, I.; Koca, J.; Sponer, J. Formation pathways of a guanine-quadruplex DNA revealed by molecular dynamics and thermodynamic analysis of the substates. Biophys. J. 2003, 85, 1787–1804. [Google Scholar] [CrossRef]
- Mashimo, T.; Yagi, H.; Sannohe, Y.; Rajendran, A.; Sugiyama, H. Folding pathways of human telomeric type-1 and type-2 G-quadruplex structures. J. Am. Chem. Soc. 2010, 132, 14910–14918. [Google Scholar] [CrossRef]
- Heddi, B.; Martín-Pintado, N.; Serimbetov, Z.; Kari, T.M.A.; Phan, A.T. G-quadruplexes with (4n - 1) guanines in the G-tetrad core: Formation of a G-triad–water complex and implication for small-molecule binding. Nucleic Acids Res. 2016, 44, 910–916. [Google Scholar] [CrossRef]
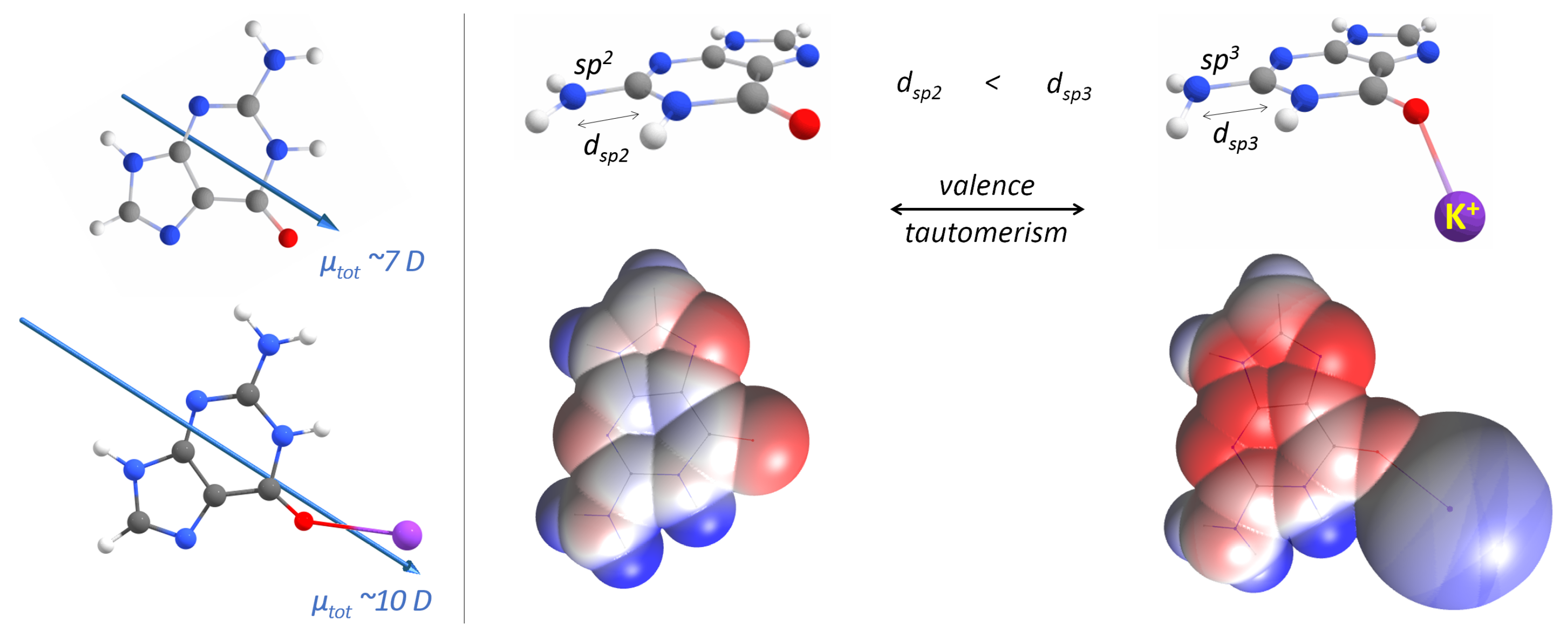
- Singh, V.; Fedeles, B.I.; Essigmann, J.M. Role of tautomerism in RNA biochemistry. RNA 2015, 21, 1–13. [Google Scholar] [CrossRef]
- Halder, A.; Bhattacharya, S.; Datta, A.; Bhattacharyyac, D.; Mitra, A. The role of N7 protonation of guanine in determining the structure, stability and function of RNA base pairs. Phys. Chem. Chem. Phys. 2015, 17, 26249–26263. [Google Scholar] [CrossRef]
- Matulis, V.E.; Lyakhov, A.S.; Gaponik, P.N.; Voitekhovich, S.V.; Ivashkevich, O.A. 1,5-Diamino-1H-1,2,3,4-tetrazolium picrate: X-ray molecular and crystal structures and ab initio MO calculations. J. Mol. Struct. 2003, 649, 309–314. [Google Scholar] [CrossRef]
- Niedzialek, D.; Urbanczyk-Lopkowska, Z. New crystalline form of 7-amino-4-methylcoumarin (coumarin 120)—A polymorph with 1:1 valence tautomers. Cryst. Eng. Comm. 2007, 9, 735–739. [Google Scholar] [CrossRef]
- Orłowski, R.; Clark, J.; Derr, J.B.; Espinoza, E.M.; Mayther, M.F.; Staszewska-Krajewska, O.; Winkler, J.R.; Jȩdrzejewska, H.; Szumna, A.; Gray, H.B.; et al. Role of intramolecular hydrogen bonds in promoting electron flow through amino acid andoligopeptide conjugates. Proc. Natl. Acad. Sci. USA 2021, 118, e2026462118. [Google Scholar] [CrossRef] [PubMed]
- Vovusha, H.; Amorim, R.G.; Scheicher, R.H.; Sanyal, B. Controlling the orientation of nucleobases by dipole moment interaction with graphene/h-BN interfaces. RSC Adv. 2018, 8, 6527–6531. [Google Scholar] [CrossRef] [PubMed]
- Yamauchi, Y.; Yoshizawa, M.; Akita, M.; Fujita, M. Molecular recognition and self-assembly special feature: Discrete stack of an odd number of polarized aromatic compounds revealing the importance of net vs. local dipoles. Proc. Natl. Acad. Sci. USA 2009, 106, 10435–10437. [Google Scholar] [CrossRef]
- Kulkarni, C.; Bejagam, K.K.; Senanayak, S.P.; Narayan, K.S.; Balasubramanian, S.; George, S.J. Dipole-moment-driven cooperative supramolecular polymerization. J. Am. Chem. Soc. 2015, 137, 3924–3932. [Google Scholar] [CrossRef]
- Shu, D.; Moll, W.D.; Deng, Z.; Mao, C.; Guo, P. Bottom-up assembly of RNA arrays and superstructures as potential parts in nanotechnology. Nano Lett. 2004, 4, 1717–1723. [Google Scholar] [CrossRef]
- Khisamutdinov, E.F.; Li, H.; Jasinski, D.L.; Chen, J.; Fu, J.; Guo, P. Enhancing immunomodulation on innate immunity by shape transition among RNA triangle, square and pentagon nanovehicles. Nucleic Acids Res. 2014, 42, 9996–10004. [Google Scholar] [CrossRef]
- Li, H.; Lee, T.; Dziubla, T.; Pi, F.; Guo, S.; Xu, J.; Li, C.; Haque, F.; Liang, X.J.; Guo, P. RNA as a stable polymer to build controllable and defined nanostructures for material and biomedical applications. Nano Today 2015, 10, 631–655. [Google Scholar] [CrossRef]
- Jasinski, D.; Haque, F.; Binzel, D.W.; Guo, P. Advancement of the emerging field of RNA nanotechnology. ACS Nano 2017, 11, 1142–1164. [Google Scholar] [CrossRef]
- Ferino, A.; Nicoletto, G.; D’Este, F.; Zorzet, S.; Lago, S.; Richter, S.N.; Tikhomirov, A.; Shchekotikhin, A.; Xodo, L.E. Photodynamic therapy for ras-driven cancers: Targeting G-quadruplex RNA structures with bifunctional alkyl-modified porphyrins. J. Med. Chem. 2020, 63, 1245–1260. [Google Scholar] [CrossRef] [PubMed]
- Kosiol, N.; Juranek, S.; Brossart, P.; Heine, A.; Paeschke, K. G-quadruplexes: A promising target for cancer therapy. Mol. Cancer 2021, 20, 40. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Sánchez-Ferrer, A.; Bagnani, M.; Adamcik, J.; Azzari, P.; Hao, J.; Song, A.; Liu, H.; Mezzenga, R. Metal ions confinement defines the architecture of G-quartet, G-quadruplex fibrils and their assembly into nematic tactoids. Proc. Natl. Acad. Sci. USA 2020, 117, 9832–9839. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Göç, Y.B.; Poziemski, J.; Smolińska, W.; Suwała, D.; Wieczorek, G.; Niedzialek, D. Tracking Topological and Electronic Effects on the Folding and Stability of Guanine-Deficient RNA G-Quadruplexes, Engineered with a New Computational Tool for De Novo Quadruplex Folding. Int. J. Mol. Sci. 2022, 23, 10990. https://doi.org/10.3390/ijms231910990
Göç YB, Poziemski J, Smolińska W, Suwała D, Wieczorek G, Niedzialek D. Tracking Topological and Electronic Effects on the Folding and Stability of Guanine-Deficient RNA G-Quadruplexes, Engineered with a New Computational Tool for De Novo Quadruplex Folding. International Journal of Molecular Sciences. 2022; 23(19):10990. https://doi.org/10.3390/ijms231910990
Chicago/Turabian StyleGöç, Yavuz Burak, Jakub Poziemski, Weronika Smolińska, Dominik Suwała, Grzegorz Wieczorek, and Dorota Niedzialek. 2022. "Tracking Topological and Electronic Effects on the Folding and Stability of Guanine-Deficient RNA G-Quadruplexes, Engineered with a New Computational Tool for De Novo Quadruplex Folding" International Journal of Molecular Sciences 23, no. 19: 10990. https://doi.org/10.3390/ijms231910990
APA StyleGöç, Y. B., Poziemski, J., Smolińska, W., Suwała, D., Wieczorek, G., & Niedzialek, D. (2022). Tracking Topological and Electronic Effects on the Folding and Stability of Guanine-Deficient RNA G-Quadruplexes, Engineered with a New Computational Tool for De Novo Quadruplex Folding. International Journal of Molecular Sciences, 23(19), 10990. https://doi.org/10.3390/ijms231910990






