Protein–Protein Interaction Prediction for Targeted Protein Degradation
Abstract
:1. Introduction
2. Methods
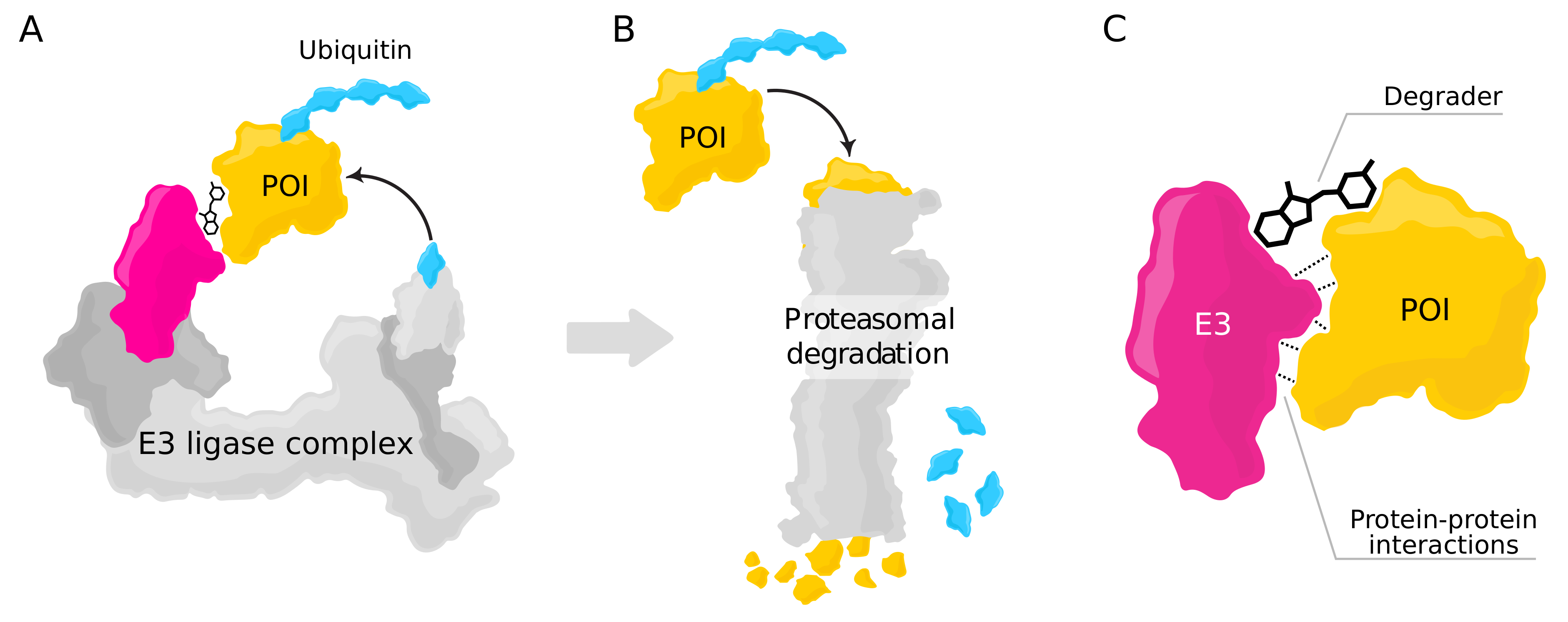
- Binding site prediction: One PDB file is used as model input, and the binary output describes whether a particular location on the protein surface constitutes a possible site for protein interactions (see Figure 2A).
- Interaction prediction: Two PDB files are processed, and the binary output describes whether the two proteins interact at a particular site (see Figure 2B).
2.1. Model Overview
2.2. (Pre-)Processing of 3D Structures into Graph Representations
2.3. Chemo-Geometric Feature Generation
2.3.1. Chemical Features
2.3.2. Geometric Features
2.4. Main DGRL Pipeline
2.5. Model Training
2.6. Implementation
3. Results
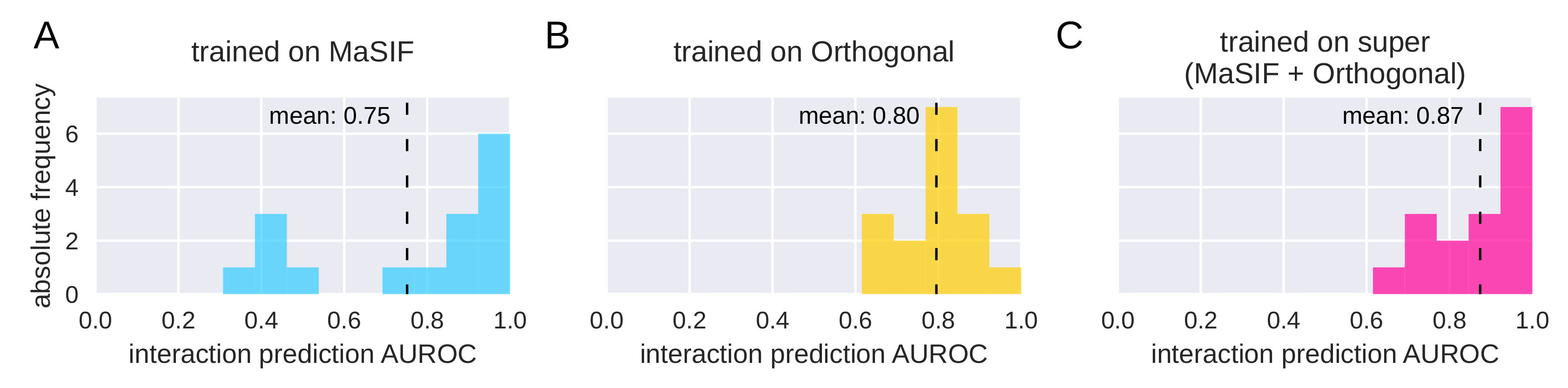
3.1. The Orthogonal Dataset
3.2. PPI Prediction on Protein Pairs
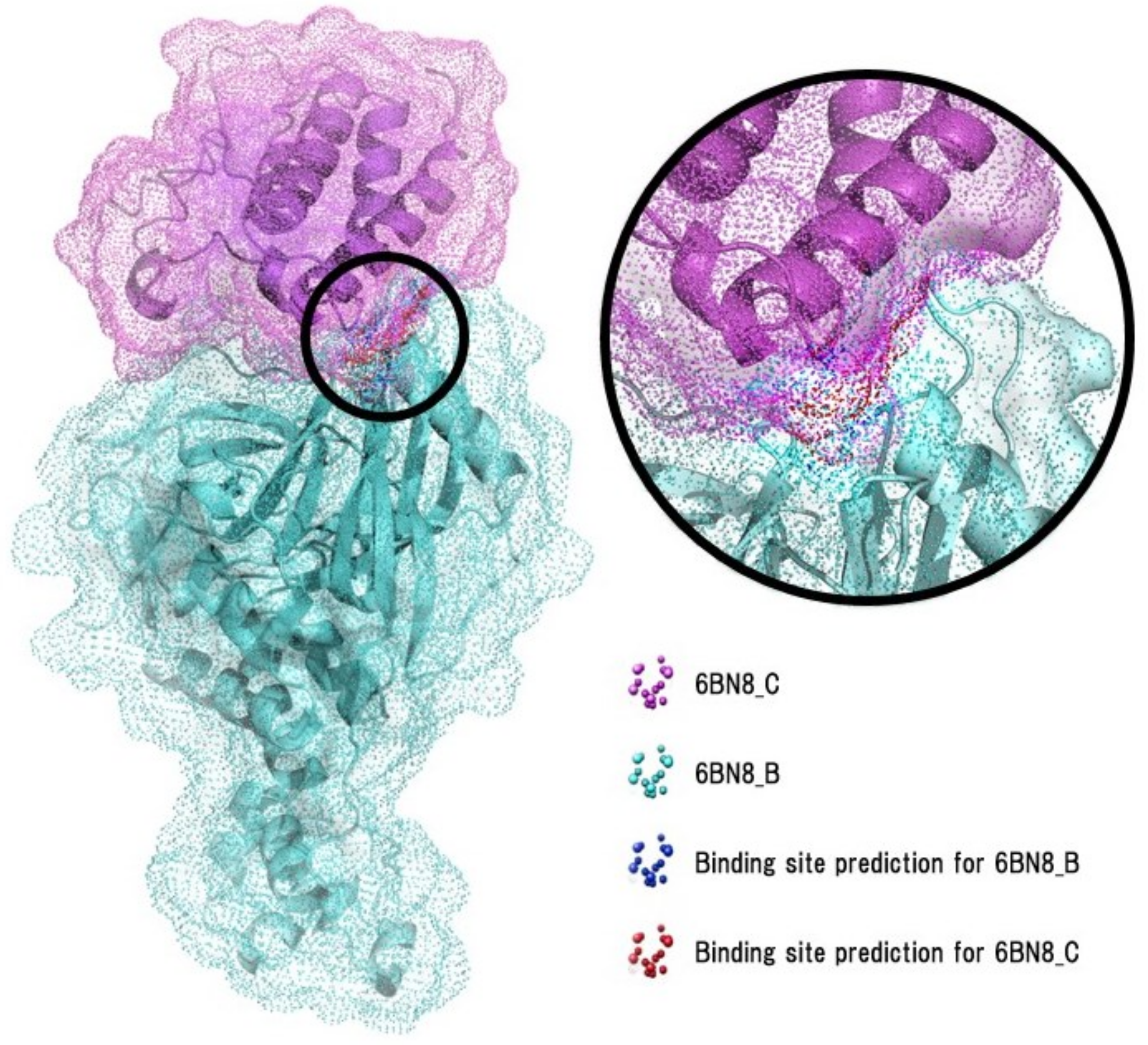
3.3. Evaluation on Ternary Complex Data
4. Discussion
4.1. Related Work
4.2. The Importance of Diverse Datasets for PPI Prediction
4.3. Using PPI Prediction for Targeted Protein Degradation
4.4. PPI Prediction and Complementary Experimental Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PPI | protein–protein interaction |
| CNS | central nervous system |
| POI | protein of interest |
| PIC | proximity-inducing compound |
| TPD | targeted protein degradation |
| CRBN | Cereblon |
| VHL | Von Hippel–Lindau tumor suppressor |
| DGRL | deep graph representation learning |
| PDB | Protein Data Bank |
| k-NN | k nearest neighbors |
| MLP | multilayer perceptron |
| AUROC | area under the receiver operating characteristic curve |
Appendix A. Confusion Matrices on MaSIF and Orthogonal Datasets
| Predicted | |||
|---|---|---|---|
| interaction | no interaction | ||
| Actual | interaction | 3273 (32.7%) | 1380 (13.8%) |
| no interaction | 882 (8.8%) | 4465 (44.6%) | |
| Predicted | |||
|---|---|---|---|
| interaction | no interaction | ||
| Actual | interaction | 3418 (34.2%) | 1314 (13.1%) |
| no interaction | 712 (7.1%) | 4556 (45.5%) | |
| Predicted | |||
|---|---|---|---|
| binding site | no binding site | ||
| Actual | binding site | 3210 (32.1%) | 1714 (17.1%) |
| no binding site | 926 (9.2%) | 4150 (41.5%) | |
| Predicted | |||
|---|---|---|---|
| interaction | no interaction | ||
| Actual | interaction | 3503 (35.1%) | 914 (9.1%) |
| no interaction | 1107 (11.0%) | 4476 (44.7%) | |
Appendix B. Prediction Results for the Known Ternary Complexes
| PDB ID | Chains | PPIs AUROC |
|---|---|---|
| 5T35 | A, D | 0.40 |
| 6BN7 | B, C | 0.93 |
| 6BN8 | B, C | 0.95 |
| 6BN9 | B, C | 0.95 |
| 6BNB | B, C | 0.86 |
| 6BOY | B, C | 0.95 |
| 6HAX | A, B | 0.46 |
| 6HAY | E, F | 0.45 |
| 6HR2 | E, F | 0.51 |
| 6SIS | E, H | 0.38 |
| 6W7O | B, D | 0.72 |
| 6W8I | A, D | 0.89 |
| 6W8I | B, E | 0.80 |
| 6W8I | C, F | 0.81 |
| 6ZHC | A, D | 0.95 |
| 7KHH | C, D | 0.93 |
| PDB ID | Chains | PPI AUROC |
|---|---|---|
| 5T35 | A, D | 0.76 |
| 6BN7 | B, C | 0.78 |
| 6BN8 | B, C | 0.86 |
| 6BN9 | B, C | 0.78 |
| 6BNB | B, C | 0.83 |
| 6BOY | B, C | 0.81 |
| 6HAX | A, B | 0.67 |
| 6HAY | E, F | 0.66 |
| 6HR2 | E, F | 0.67 |
| 6SIS | E, H | 0.71 |
| 6W7O | B, D | 0.84 |
| 6W8I | A, D | 0.92 |
| 6W8I | B, E | 0.96 |
| 6W8I | C, F | 0.77 |
| 6ZHC | A, D | 0.91 |
| 7KHH | C, D | 0.78 |
| PDB ID | Chains | PPI AUROC |
|---|---|---|
| 5T35 | A, D | 0.76 |
| 6BN7 | B, C | 0.98 |
| 6BN8 | B, C | 0.99 |
| 6BN9 | B, C | 0.97 |
| 6BNB | B, C | 0.94 |
| 6BOY | B, C | 0.98 |
| 6HAX | A, B | 0.84 |
| 6HAY | E, F | 0.74 |
| 6HR2 | E, F | 0.69 |
| 6SIS | E, H | 0.72 |
| 6W7O | B, D | 0.81 |
| 6W8I | A, D | 0.86 |
| 6W8I | B, E | 0.87 |
| 6W8I | C, F | 0.91 |
| 6ZHC | A, D | 0.97 |
| 7KHH | C, D | 0.97 |
| Predicted | |||
|---|---|---|---|
| interaction | no interaction | ||
| Actual | interaction | 4423 (44.2%) | 112 (1.1%) |
| no interaction | 92(1.0%) | 5373(53.7%) | |
| Predicted | |||
|---|---|---|---|
| interaction | no interaction | ||
| Actual | interaction | 2943 (29.4%) | 2382 (27.8%) |
| no interaction | 1108 (11.1%) | 3567 (35.6%) | |
References
- Koshland, D.E., Jr. The Key–Lock Theory and the Induced Fit Theory. Angew. Chem. Int. Ed. 1995, 33, 2375–2378. [Google Scholar] [CrossRef]
- Hopkins, A.L.; Groom, C.R. The druggable genome. Nat. Rev. Drug Discov. 2002, 1, 727–730. [Google Scholar] [CrossRef]
- Overington, J.P.; Al-Lazikani, B.; Hopkins, A.L. How many drug targets are there? Nat. Rev. Drug Discov. 2006, 5, 993–996. [Google Scholar] [CrossRef]
- Santos, R.; Ursu, O.; Gaulton, A.; Bento, A.P.; Donadi, R.S.; Bologa, C.G.; Karlsson, A.; Al-Lazikani, B.; Hersey, A.; Oprea, T.I.; et al. A comprehensive map of molecular drug targets. Nat. Rev. Drug Discov. 2016, 16, 19–34. [Google Scholar] [CrossRef] [PubMed]
- Lo, T.W.; Pickle, C.S.; Lin, S.; Ralston, E.J.; Gurling, M.; Schartner, C.M.; Bian, Q.; Doudna, J.A.; Meyer, B.J. Precise and Heritable Genome Editing in Evolutionarily Diverse Nematodes Using TALENs and CRISPR/Cas9 to Engineer Insertions and Deletions. Genetics 2013, 195, 331–348. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Jiang, X.; Huang, L. 5.42-RNA Interference Technology. In Comprehensive Biotechnology, 3rd ed.; Moo-Young, M., Ed.; Pergamon: Oxford, UK, 2019; pp. 560–575. [Google Scholar] [CrossRef]
- Wei, M.; Zhao, R.; Cao, Y.; Wei, Y.; Li, M.; Dong, Z.; Liu, Y.; Ruan, H.; Li, Y.; Cao, S.; et al. First orally bioavailable prodrug of proteolysis targeting chimera (PROTAC) degrades cyclin-dependent kinases 2/4/6 in vivo. Eur. J. Med. Chem. 2021, 209, 112903. [Google Scholar] [CrossRef]
- Gerry, C.J.; Schreiber, S.L. Unifying principles of bifunctional, proximity-inducing small molecules. Nat. Chem. Biol. 2020, 16, 369–378. [Google Scholar] [CrossRef]
- Siriwardena, S.U.; Godage, D.N.P.M.; Shoba, V.M.; Lai, S.; Shi, M.; Wu, P.; Chaudhary, S.K.; Schreiber, S.L.; Choudhary, A. Phosphorylation-Inducing Chimeric Small Molecules. J. Am. Chem. Soc. 2020, 142, 14052–14057. [Google Scholar] [CrossRef]
- Yamazoe, S.; Tom, J.; Fu, Y.; Wu, W.; Zeng, L.; Sun, C.; Liu, Q.; Lin, J.; Lin, K.; Fairbrother, W.J.; et al. Heterobifunctional Molecules Induce Dephosphorylation of Kinases–A Proof of Concept Study. J. Med. Chem. 2019, 63, 2807–2813. [Google Scholar] [CrossRef]
- Wang, W.W.; Chen, L.Y.; Wozniak, J.M.; Jadhav, A.M.; Anderson, H.; Malone, T.E.; Parker, C.G. Targeted Protein Acetylation in Cells Using Heterobifunctional Molecules. J. Am. Chem. Soc. 2021, 143, 16700–16708. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, K.M.; Kim, K.B.; Kumagai, A.; Mercurio, F.; Crews, C.M.; Deshaies, R.J. Protacs: Chimeric molecules that target proteins to the Skp1–Cullin–F box complex for ubiquitination and degradation. Proc. Natl. Acad. Sci. USA 2001, 98, 8554–8559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ciechanover, A.; Schwartz, A.L. The ubiquitin-proteasome pathway: The complexity and myriad functions of proteins death. Proc. Natl. Acad. Sci. USA 1998, 95, 2727–2730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, A.C.; Crews, C.M. Induced protein degradation: An emerging drug discovery paradigm. Nat. Rev. Drug Discov. 2016, 16, 101–114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nalawansha, D.A.; Crews, C.M. PROTACs: An Emerging Therapeutic Modality in Precision Medicine. Cell Chem. Biol. 2020, 27, 998–1114. [Google Scholar] [CrossRef] [PubMed]
- Pettersson, M.; Crews, C.M. PROteolysis TArgeting Chimeras (PROTACs)—Past, present and future. Drug Discov. Today 2019, 31, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Békés, M.; Langley, D.R.; Crews, C.M. PROTAC targeted protein degraders: The past is prologue. Nat. Rev. Drug Discov. 2022, 21, 181–200. [Google Scholar] [CrossRef]
- Hughes, S.J.; Ciulli, A. Molecular recognition of ternary complexes: A new dimension in the structure-guided design of chemical degraders. Essays Biochem. 2017, 61, 505–516. [Google Scholar] [CrossRef] [Green Version]
- Ishida, T.; Ciulli, A. E3 Ligase Ligands for PROTACs: How They Were Found and How to Discover New Ones. SLAS Discov. 2021, 26, 484–502. [Google Scholar] [CrossRef]
- Seychell, B.C.; Beck, T. Molecular basis for protein–protein interactions. Beilstein Org. Chem. 2021, 17, 1–10. [Google Scholar] [CrossRef]
- Takeuchi, K.; Baskaran, K.; Arthanari, H. Structure determination using solution NMR: Is it worth the effort? J. Magn. Reson. 2019, 306, 195–201. [Google Scholar] [CrossRef]
- Renaud, J.P.; Chari, A.; Ciferri, C.; Liu, W.; Rémigy, H.W.; Stark, H.; Wiesmann, C. Cryo-EM in drug discovery: Achievements, limitations and prospects. Nat. Rev. Drug Discov. 2018, 17, 471–492. [Google Scholar] [CrossRef]
- Sunny, S.; Jayaraj, P.B. Protein–Protein Docking: Past, Present, and Future. Protein J. 2021, 41, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.; O’Neill, M.; Pritzel, A.; Antropova, N.; Senior, A.; Green, T.; Žídek, A.; Bates, R.; Blackwell, S.; Yim, J.; et al. Protein complex prediction with AlphaFold-Multimer. bioRxiv 2021. [Google Scholar] [CrossRef]
- Dequeker, C.; Behbahani, Y.M.; David, L.; Laine, E.; Carbone, A. From complete cross-docking to partners identification and binding sites predictions. PLoS Comput. Biol. 2022, 18, e1009825. [Google Scholar] [CrossRef]
- Sverrisson, F.; Feydy, J.; Correia, B.E.; Bronstein, M.M. Fast end-to-end learning on protein surfaces. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021. [Google Scholar] [CrossRef]
- Szilagyi, A.; Zhang, Y. Template-based structure modeling of protein–protein interactions. Curr. Opin. Struct. Biol. 2014, 24, 10–23. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Dauzhenka, T.; Kundrotas, P.J.; Sternberg, M.J.E.; Vakser, I.A. Application of docking methodologies to modeled proteins. Proteins Struct. Funct. Bioinform. 2020, 88, 1180–1188. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Gainza, P.; Sverrisson, F.; Monti, F.; Rodolà, E.; Boscaini, D.; Bronstein, M.M.; Correia, B.E. Deciphering interaction fingerprints from protein molecular surfaces using geometric deep learning. Nat. Methods 2019, 17, 184–192. [Google Scholar] [CrossRef]
- Hamilton, W.L. Graph Representation Learning. Synth. Lect. Artif. Intell. Mach. Learn. 2020, 14, 1–159. [Google Scholar] [CrossRef]
- Lim, S.; Lu, Y.; Cho, C.Y.; Sung, I.; Kim, J.; Kim, Y.; Park, S.; Kim, S. A review on compound-protein interaction prediction methods: Data, format, representation and model. Comput. Struct. Biotechnol. J. 2021, 19, 1541–1556. [Google Scholar] [CrossRef]
- Torrey, L.; Shavlik, J. Transfer Learning. In Handbook of Research on Machine Learning Applications and Trends; IGI Global: Hershey, PA, USA, 2010; pp. 242–264. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y. Generating Triangulated Macromolecular Surfaces by Euclidean Distance Transform. PLoS ONE 2009, 4, e8140. [Google Scholar] [CrossRef]
- Xu, D.; Li, H.; Zhang, Y. Protein Depth Calculation and the Use for Improving Accuracy of Protein Fold Recognition. J. Comput. Biol. 2013, 20, 805–816. [Google Scholar] [CrossRef] [Green Version]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar] [CrossRef]
- Chiang, W.L.; Liu, X.; Si, S.; Li, Y.; Bengio, S.; Hsieh, C.J. Cluster-GCN. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2019, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef] [Green Version]
- Stärk, H.; Beaini, D.; Corso, G.; Tossou, P.; Dallago, C.; Günnemann, S.; Liò, P. 3D Infomax improves GNNs for Molecular Property Prediction. arXiv 2021, arXiv:2110.04126. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Lawrence, M.C.; Colman, P.M. Shape Complementarity at Protein/Protein Interfaces. J. Mol. Biol. 1993, 234, 946–950. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Proctor, E.A.; Lugovskoy, A.A.; Dokholyana, N.V. Fast screening of protein surfaces using geometric invariant fingerprints. Proc. Natl. Acad. Sci. USA 2009, 109, 16622–16626. [Google Scholar] [CrossRef] [Green Version]
- Weisstein, E.W. Gaussian Curvature (Wolfram MathWorld). Available online: https://mathworld.wolfram.com/GaussianCurvature.html (accessed on 14 October 2021).
- Weisstein, E.W. Mean Curvature (Wolfram MathWorld). Available online: https://mathworld.wolfram.com/MeanCurvature.html (accessed on 14 October 2021).
- Koenderink, J.J.; van Doorn, A.J. Surface shape and curvature scales. Image Vis. Comput. 1992, 10, 557–564. [Google Scholar] [CrossRef]
- Weisstein, E.W. Principal Curvatures (Wolfram MathWorld). Available online: https://mathworld.wolfram.com/PrincipalCurvatures.html (accessed on 9 May 2022).
- Weisstein, E.W. Shape Operator (Wolfram MathWorld). Available online: https://mathworld.wolfram.com/ShapeOperator.html (accessed on 14 October 2021).
- Cao, Y.; Li, D.; Sun, H.; Assadi, A.H.; Zhang, S. Efficient Weingarten map and curvature estimation on manifolds. Mach. Learn. 2021, 110, 1319–1344. [Google Scholar] [CrossRef]
- Charlier, B.; Feydy, J.; Glaunès, J.A.; Collin, F.D.; Durif, G. Kernel Operations on the GPU, with Autodiff, without Memory Overflows. J. Mach. Learn. Res. 2021, 22, 1–6. Available online: http://jmlr.org/papers/v22/20-275.html (accessed on 9 May 2022).
- Reddi, S.J.; Kale, S.; Kumar, S. On the Convergence of Adam and Beyond. arXiv 2019, arXiv:1904.09237. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef] [Green Version]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. Available online: http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf (accessed on 9 May 2022).
- Blum, M.; Chang, H.Y.; Chuguransky, S.; Grego, T.; Kandasaamy, S.; Mitchell, A.; Nuka, G.; Paysan-Lafosse, T.; Qureshi, M.; Raj, S.; et al. The InterPro protein families and domains database: 20 years on. Nucleic Acids Res. 2020, 49, D344–D354. [Google Scholar] [CrossRef]
- Lučić, B.; Batista, J.; Bojović, A.; Sović K., A.; Bešlo, D.; Nadramija, D.; Vikić-Topić, D. Estimation of Random Accuracy and its Use in Validation of Predictive Quality of Classification Models within Predictive Challenges. Croat. Chem. Acta 2019, 92, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Batista, J.; Vikić-Topić, D.; Lučić, B. The Difference Between the Accuracy of Real and the Corresponding Random Model is a Useful Parameter for Validation of Two-State Classification Model Quality. Croat. Chem. Acta 2016, 86, 527–534. [Google Scholar] [CrossRef]
- Weng, G.; Li, D.; Kang, Y.; Hou, T. Integrative Modeling of PROTAC-Mediated Ternary Complexes. J. Med. Chem. 2021, 64, 16271–16281. [Google Scholar] [CrossRef] [PubMed]
- Zaidman, D.; Prilusky, J.; London, N. PRosettaC: Rosetta Based Modeling of PROTAC Mediated Ternary Complexes. J. Chem. Inf. Model. 2020, 60, 4894–4903. [Google Scholar] [CrossRef]
- Huang, H.; Zeng, C.; Gong, X. Inter-protein contact map generated only from intra-monomer by image inpainting. In Proceedings of the 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Houston, TX, USA, 9–12 December 2021; pp. 131–136. [Google Scholar] [CrossRef]
- Dai, B.; Bailey-Kellogg, C. Protein interaction interface region prediction by geometric deep learning. Bioinformatics 2021, 37, 2580–2588. [Google Scholar] [CrossRef]
- Yang, F.; Fan, K.; Song, D.; Lin, H. Graph-based prediction of Protein-protein interactions with attributed signed graph embedding. BMC Bioinform. 2020, 21, 323. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Wu, L.; Yu, X.; Chu, Z.; Jin, S.; Liu, J. Prediction of Protein–Protein Interaction Sites Based on Stratified Attentional Mechanisms. Front. Genet. 2021, 12. [Google Scholar] [CrossRef]
- Yuan, Q.; Chen, J.; Zhao, H.; Zhou, Y.; Yang, Y. Structure-aware protein–protein interaction site prediction using deep graph convolutional network. Bioinformatics 2021, 38, 125–132. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Renaud, N.; Geng, C.; Georgievska, S.; Ambrosetti, F.; Ridder, L.; Marzella, D.F.; Réau, M.F.; Bonvin, A.M.J.J.; Xue, L.C. DeepRank: A deep learning framework for data mining 3D protein-protein interfaces. Nat. Commun. 2021, 12, 7068. [Google Scholar] [CrossRef]
- Zollman, D.; Ciulli, A. Structural and Biophysical Principles of Degrader Ternary Complexes. In Protein Degradation with New Chemical Modalities; Royal Society of Chemistry: London, UK, 2020; pp. 14–54. [Google Scholar]
- Unke, O.T.; Meuwly, M. PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges. J. Chem. Theory Comput. 2019, 15, 3678–3693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gasteiger, J.; Groß, J.; Günnemann, S. Directional Message Passing for Molecular Graphs. arXiv 2020, arXiv:2003.03123. [Google Scholar] [CrossRef]
- Alabi, S. Novel Mechanisms of Molecular Glue-Induced Protein Degradation. Biochemistry 2021, 60, 2371–2373. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer, B.; Predki, P.; Snyder, M. Microarrays to characterize protein interactions on a whole-proteome scale. Proteomics 2003, 3, 2190–2199. [Google Scholar] [CrossRef]
- Lin, J.S.; Lai, E.M. Protein–Protein Interactions: Co-Immunoprecipitation. In Methods in Molecular Biology; Springer: New York, NY, USA, 2017; pp. 211–219. [Google Scholar] [CrossRef]
- Michnick, S.W.; Ear, P.H.; Landry, C.; Malleshaiah, M.K.; Messier, V. Protein-Fragment Complementation Assays for Large-Scale Analysis, Functional Dissection and Dynamic Studies of Protein–Protein Interactions in Living Cells. In Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2011; pp. 395–425. [Google Scholar] [CrossRef]
- Rainey, K.H.; Patterson, G.H. Photoswitching FRET to monitor protein–protein interactions. Proc. Natl. Acad. Sci. USA 2018, 116, 864–873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfleger, K.D.G.; Seeber, R.M.; Eidne, K.A. Bioluminescence resonance energy transfer (BRET) for the real-time detection of protein-protein interactions. Nat. Protoc. 2006, 1, 337–345. [Google Scholar] [CrossRef]
- Slaughter, B.D.; Schwartz, J.W.; Li, R. Mapping dynamic protein interactions in MAP kinase signaling using live-cell fluorescence fluctuation spectroscopy and imaging. Proc. Natl. Acad. Sci. USA 2007, 104, 20320–20325. [Google Scholar] [CrossRef] [Green Version]
- Marcuello, C.; de Miguel, R.; Lostao, A. Molecular Recognition of Proteins through Quantitative Force Maps at Single Molecule Level. Biomolecules 2022, 12, 594. [Google Scholar] [CrossRef]
- Tapia-Rojo, R.; Alonso-Caballero, A.; Fernandez, J.M. Direct observation of a coil-to-helix contraction triggered by vinculin binding to talin. Sci. Adv. 2020, 6, aaz4707. [Google Scholar] [CrossRef] [PubMed]
- Villanueva, R.; Ferreira, P.; Marcuello, C.; Usón, A.; Miramar, M.D.; Peleato, M.L.; Lostao, A.; Susin, S.A.; Medina, M. Key Residues Regulating the Reductase Activity of the Human Mitochondrial Apoptosis Inducing Factor. Biochemistry 2015, 54, 5175–5184. [Google Scholar] [CrossRef] [PubMed]
- Sevrioukova, I.F. Apoptosis-Inducing Factor: Structure, Function, and Redox Regulation. Antioxid. Redox Signal. 2011, 14, 2545–2579. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Dataset | Task | Subset | PDB IDs | Resolution (Å) | Mol. w. per Model (kDa) | Tot. Polymer Residues per Model | Polymer Entity seq. Length | Mol. Entity w. (kDa) |
|---|---|---|---|---|---|---|---|---|
| MaSIF | binding site | train. | 2809 | 2.27 | 99.08 | 873.58 | 220.32 | 24.7 |
| test | 368 | 2.35 | 142.42 | 1270.48 | 343.61 | 38.21 | ||
| interactions | train. | 4833 | 2.35 | 117.92 | 1043.45 | 264.32 | 29.67 | |
| test | 970 | 2.28 | 99.31 | 876.54 | 235.81 | 29.9 | ||
| Orthogonal | binding site | train. | 2373 | 1.75 | 66.07 | 547.07 | 246.82 | 27.94 |
| test | 1111 | 1.81 | 105.54 | 880.11 | 297.68 | 33.81 | ||
| interactions | train. | 3201 | 1.77 | 80.86 | 657.90 | 214.36 | 26.82 | |
| test | 1431 | 1.74 | 65.06 | 566.08 | 249.67 | 28.21 |
| Dataset | Task | MaSIF [30] | dMaSIF [26] | Ours |
|---|---|---|---|---|
| MaSIF | binding site | 0.85 | 0.87 | 0.82 |
| interactions | 0.81 | 0.82 | 0.88 | |
| Orthogonal | binding site | - | 0.77 | 0.79 |
| interactions | - | 0.77 | 0.88 |
| PDB ID | Chains | E3 ligase | Target |
|---|---|---|---|
| 5T35 | A, D | VHL | BRD4 BD2 |
| 6BN7 | B, C | CRBN | BRD4 BD1 |
| 6BN8 | B, C | CRBN | BRD4 BD1 |
| 6BN9 | B, C | CRBN | BRD4 BD1 |
| 6BNB | B, C | CRBN | BRD4 BD1 |
| 6BOY | B, C | CRBN | BRD4 BD1 |
| 6HAX | A, B | VHL | SMARCA2 |
| 6HAY | E, F | VHL | SMARCA2 |
| 6HR2 | E, F | VHL | SMARCA4 |
| 6SIS | E, H | VHL | BRD4 BD2 |
| 6W7O | B, D | cIAP1-BIR3 | BTK |
| 6W8I | A, D ∣ B, E ∣ C, F | cIAP1-BIR3 | BTK |
| 6ZHC | AD | VHL | Bcl-xL |
| 7KHH | CD | VHL | BRD4 BD1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orasch, O.; Weber, N.; Müller, M.; Amanzadi, A.; Gasbarri, C.; Trummer, C. Protein–Protein Interaction Prediction for Targeted Protein Degradation. Int. J. Mol. Sci. 2022, 23, 7033. https://doi.org/10.3390/ijms23137033
Orasch O, Weber N, Müller M, Amanzadi A, Gasbarri C, Trummer C. Protein–Protein Interaction Prediction for Targeted Protein Degradation. International Journal of Molecular Sciences. 2022; 23(13):7033. https://doi.org/10.3390/ijms23137033
Chicago/Turabian StyleOrasch, Oliver, Noah Weber, Michael Müller, Amir Amanzadi, Chiara Gasbarri, and Christopher Trummer. 2022. "Protein–Protein Interaction Prediction for Targeted Protein Degradation" International Journal of Molecular Sciences 23, no. 13: 7033. https://doi.org/10.3390/ijms23137033
APA StyleOrasch, O., Weber, N., Müller, M., Amanzadi, A., Gasbarri, C., & Trummer, C. (2022). Protein–Protein Interaction Prediction for Targeted Protein Degradation. International Journal of Molecular Sciences, 23(13), 7033. https://doi.org/10.3390/ijms23137033






