Direct Metal-Free Transformation of Alkynes to Nitriles: Computational Evidence for the Precise Reaction Mechanism
Abstract
1. Introduction
2. Results and Discussion
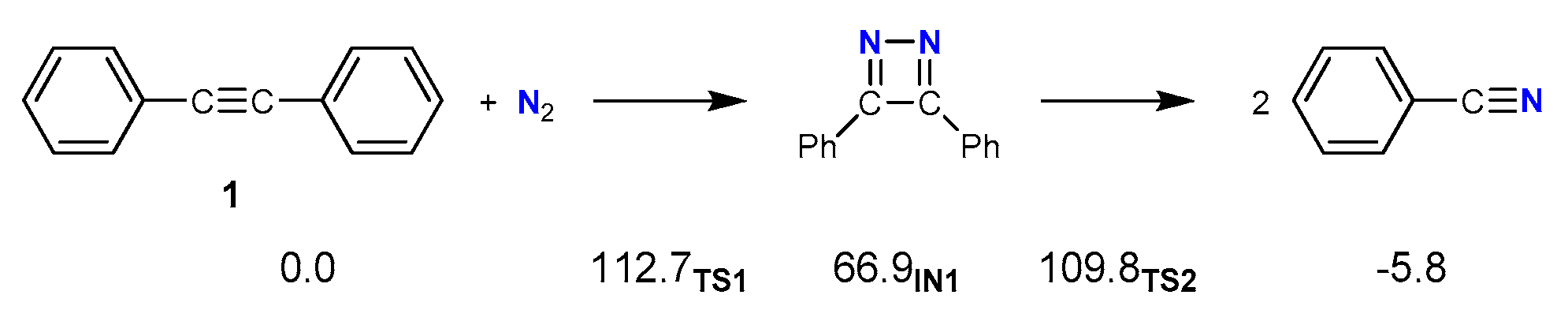
2.1. The Uncatalyzed Reaction with N2 as a Nitrogen Source in Acetonitrile
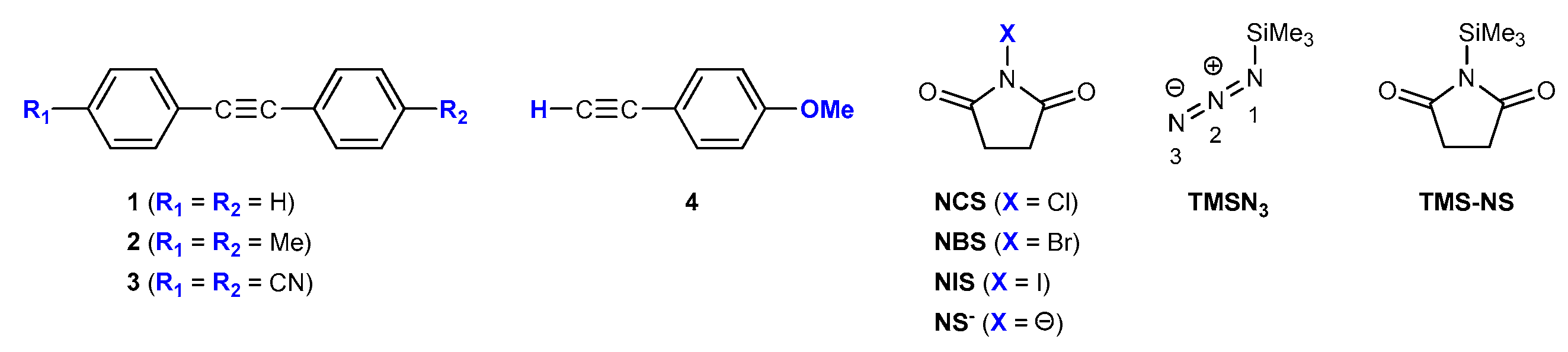
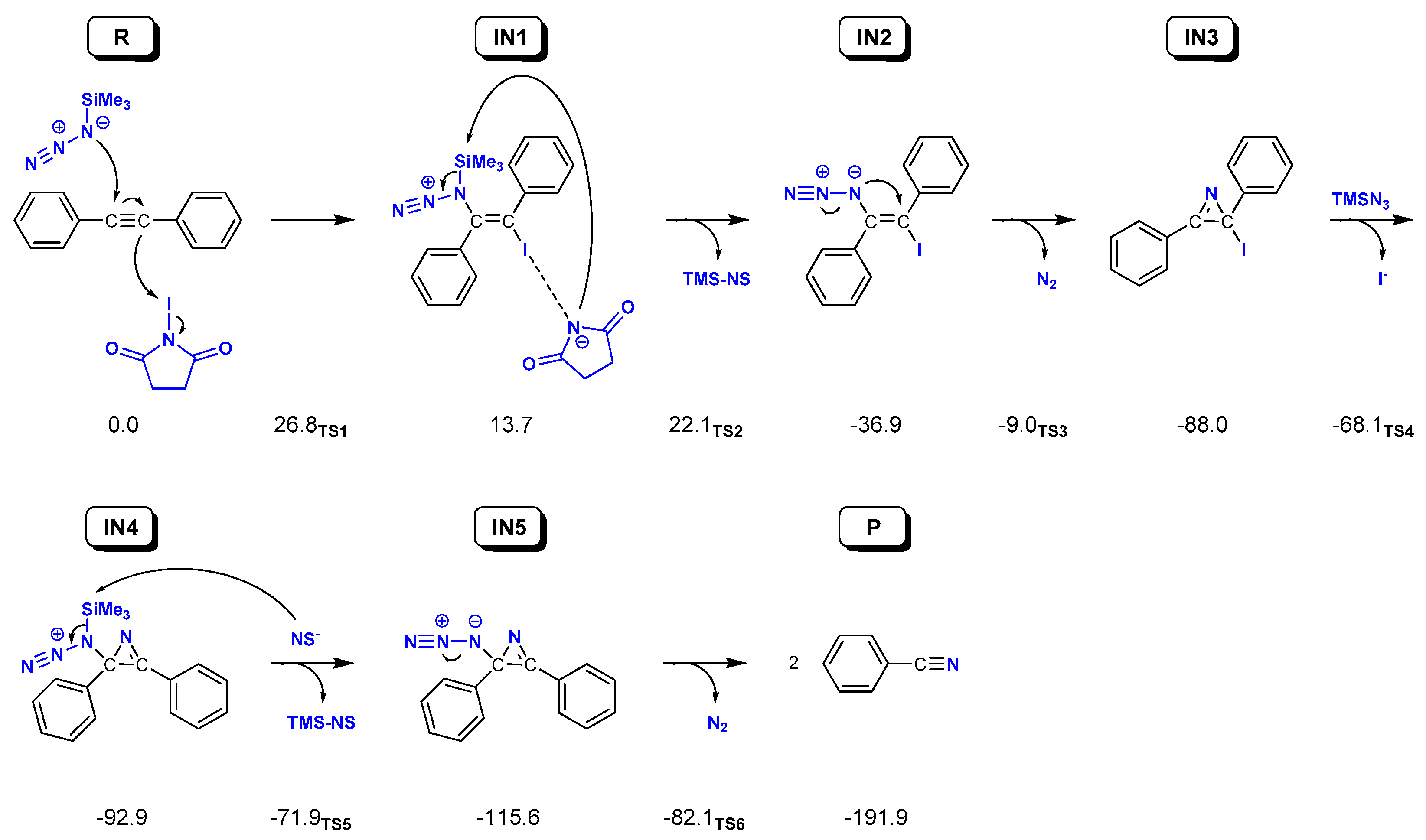
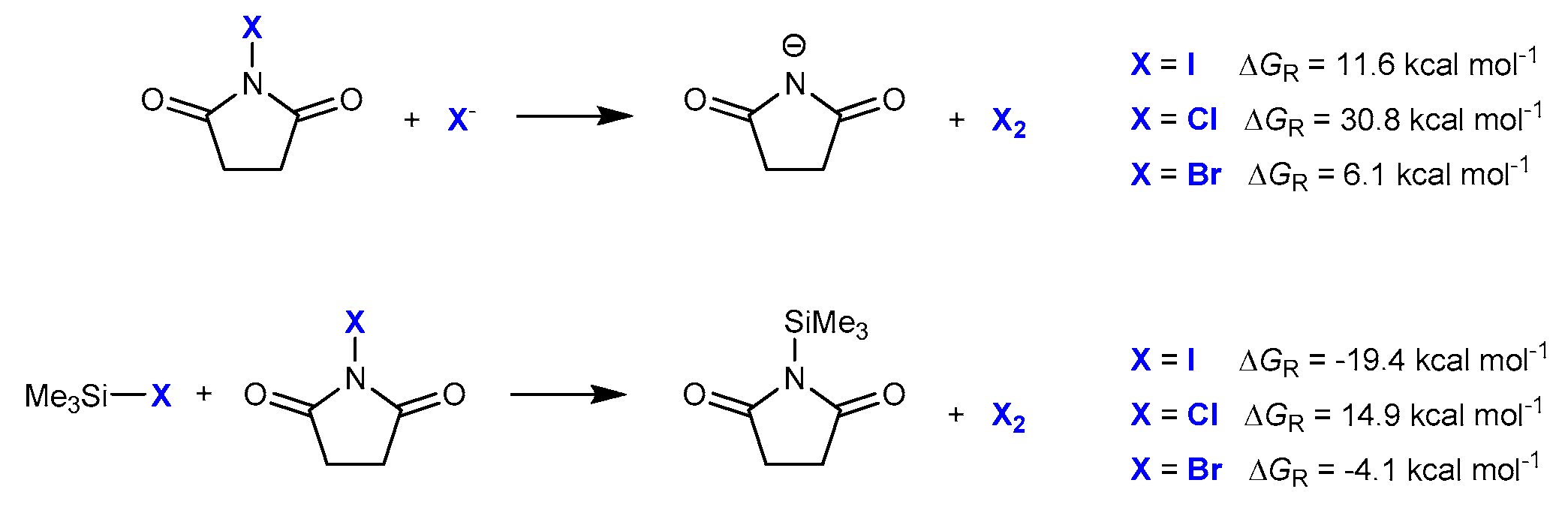
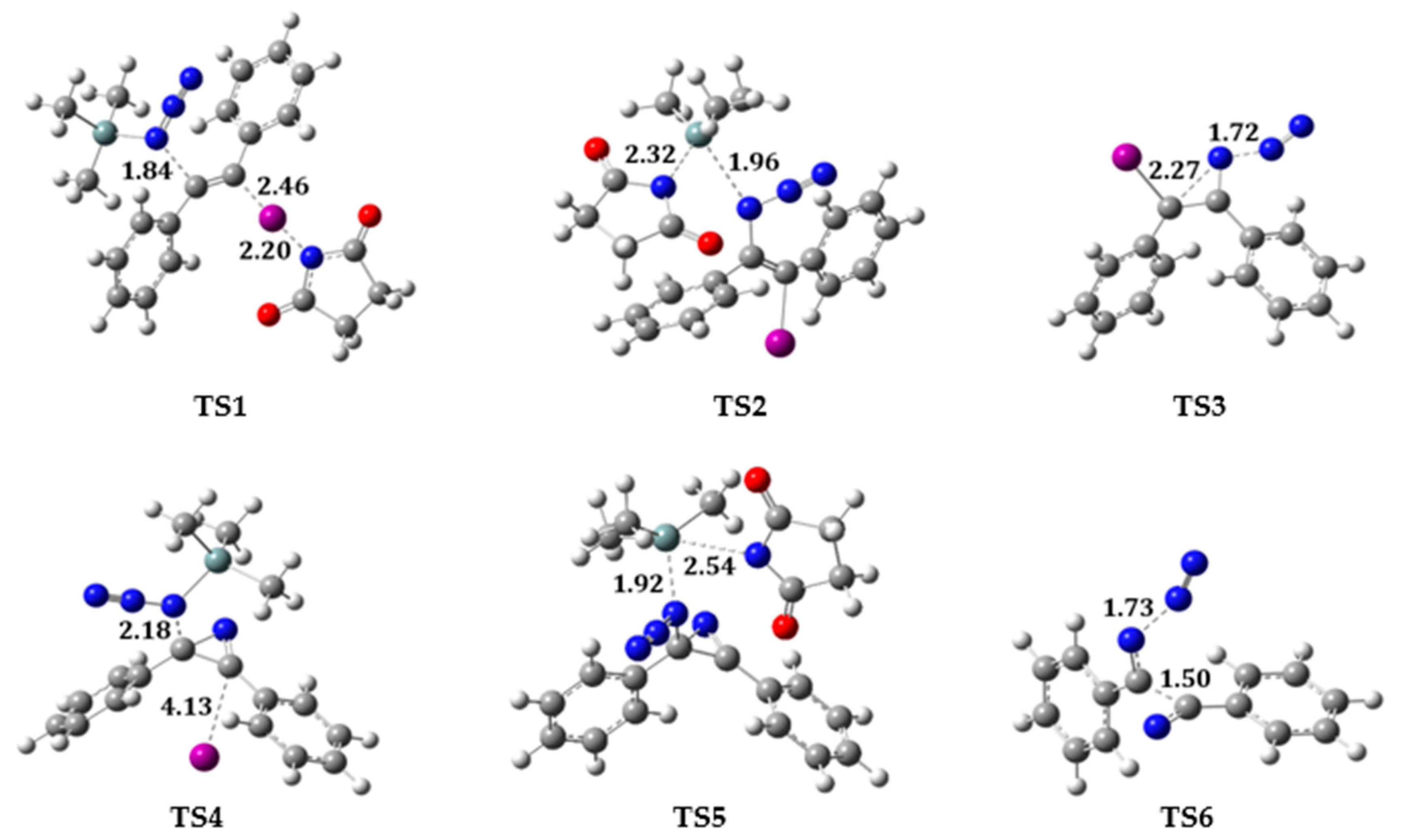
2.2. Reaction on Diphenylacetylene with NIS and TMSN3 in Acetonitrile
2.3. Reaction on Diphenylacetylene Derivatives with NIS and TMSN3 in Acetonitrile
2.4. Reaction on Terminal Alkynes with NIS and TMSN3 in Acetonitrile
2.5. Changing Oxidant to NCS and NBS in Acetonitrile
2.6. Changing Nitrogen Source to NaN3 in Acetonitrile
2.7. Changing Solvent Polarity
3. Calculation Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiong, H.; Ramkumar, N.; Chiou, M.F.; Jian, W.; Li, Y.; Su, J.H.; Zhang, X.; Bao, H. Iron-catalyzed carboazidation of alkenes and alkynes. Nat. Commun. 2019, 10, 122. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Gurbanov, A.V.; Guseinov, F.I.; da Silva, M.F.C.G. Noncovalent interactions in metal complex catalysis. Coord. Chem. Rev. 2019, 387, 32–46. [Google Scholar] [CrossRef]
- Wen, H.; Liu, G.; Huang, Z. Recent advances in tridentate iron and cobalt complexes for alkene and alkyne hydrofunctionalizations. Coord. Chem. Rev. 2019, 386, 138. [Google Scholar] [CrossRef]
- Liu, B.; Ning, Y.; Virelli, M.; Zanoni, G.; Anderson, E.A.; Bi, X. Direct Transformation of Terminal Alkynes into Amidines by a Silver-Catalyzed Four-Component Reaction. J. Am. Chem. Soc. 2019, 141, 1593–1598. [Google Scholar] [CrossRef]
- Haley, M.M. Modern Alkyne Chemistry: Catalytic and Atom-Economic Transformations; Trost, B.M., Li, C.-J., Eds.; Wiley: New York, NY, USA, 2014. [Google Scholar]
- Mizushima, E.; Sato, K.; Hayashi, T.; Tanaka, M. Highly efficient AuI-catalyzed hydration of alkynes. Angew. Chem. Int. Ed. Engl. 2002, 41, 4563. [Google Scholar] [CrossRef]
- Marion, N.; Ramón, R.S.; Nolan, S.P. [(NHC)AuI]-Catalyzed Acid-Free Alkyne Hydration at Part-per-Million Catalyst Loadings. J. Am. Chem. Soc. 2009, 131, 448. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Jiao, N. Dioxygen Activation under Ambient Conditions: Cu-Catalyzed Oxidative Amidation-Diketonization of Terminal Alkynes Leading to α-Ketoamides. J. Am. Chem. Soc. 2010, 132, 28–29. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.E.; Deng, G. Synthesis of α-Diketones from Alkylaryl- and Diarylalkynes Using Mercuric Salts. Org. Lett. 2014, 16, 2142–2145. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Zhao, A.; Xu, B.; Jia, J.; Liu, X.; Guo, C. PIFA-Mediated Esterification Reaction of Alkynes with Alcohols via Oxidative Cleavage of Carbon Triple Bonds. J. Org. Chem. 2014, 79, 2709–2715. [Google Scholar] [CrossRef]
- Kolle, S.; Batra, S. Transformations of alkynes to carboxylic acids and their derivatives via C≡C bond cleavage. Org. Biomol. Chem. 2016, 14, 11048–11060. [Google Scholar] [CrossRef]
- Dighe, S.U.; Batra, S. Visible Light-Induced Iodine-Catalyzed Transformation of Terminal Alkynes to Primary Amides via C≡C Bond Cleavage under Aqueous Conditions. Adv. Synth. Catal. 2016, 358, 500. [Google Scholar] [CrossRef]
- Song, S.; Li, X.; Sun, X.; Yuan, Y.; Jiao, N. Efficient bromination of olefins, alkynes, and ketones with dimethyl sulfoxide and hydrobromic acid. Green Chem. 2015, 17, 3285–3289. [Google Scholar] [CrossRef]
- Ferris, T.; Carroll, L.; Mease, R.C.; Spivey, A.C.; Aboagye, E.O. Iodination of terminal alkynes using KI/CuSO4—A facile method with potential for radio-iodination. Tetrahedron Lett. 2019, 60, 936–939. [Google Scholar] [CrossRef]
- Liu, Y.; Song, F.; Guo, S. Cleavage of a Carbon-Carbon Triple Bond via Gold-Catalyzed Cascade Cyclization/Oxidative Cleavage Reactions of (Z)-Enynols with Molecular Oxygen. J. Am. Chem. Soc. 2006, 128, 11332–11333. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, J.Y.; Zhang, T.S.; Li, G.; Hao, W.J.; Tu, S.J.; Jiang, B. Arylacetylenes as two-carbon synthons: Synthesis of eight-membered rings via C≡C bond cleavage. Chem. Commun. 2018, 54, 164. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.Y.; Gao, Y.C.; Zheng, W.; Tang, R.Y. Oxidative Radical Cyclization of N-methyl-N-arylpropiolamide to Isatins via Cleavage of the Carbon-carbon Triple Bond. Adv. Synth. Catal. 2018, 360, 3391–3400. [Google Scholar] [CrossRef]
- Park, Y.T.; Park, J.W.; Jun, C.H. Metal-organic cooperative catalysis in C-H and C-C bond activation and its concurrent recovery. Acc. Chem. Res. 2008, 41, 222. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Jiao, N. Direct approaches to nitriles via highly efficient nitrogenation strategy through C-H or C-C bond cleavage. Acc. Chem. Res. 2014, 47, 1137. [Google Scholar] [CrossRef]
- Dutta, U.; Lupton, D.W.; Maiti, D. Aryl Nitriles from Alkynes Using tert-Butyl Nitrite: Metal-Free Approach to C≡C Bond Cleavage. Org. Lett. 2016, 18, 860–863. [Google Scholar] [CrossRef]
- Shen, T.; Wang, T.; Qin, C.; Jiao, N. Silver-catalyzed nitrogenation of alkynes: A direct approach to nitriles through C≡C bond cleavage. Angew. Chem. Int. Ed. Engl. 2013, 52, 6677–6680. [Google Scholar] [CrossRef]
- Okamoto, N.; Ishikura, M.; Yanada, R. Cleavage of Carbon-Carbon Triple Bond: Direct Transformation of Alkynes to Nitriles. Org. Lett. 2013, 15, 2571–2573. [Google Scholar] [CrossRef] [PubMed]
- Keerthika, K.; Nath, S.; Geetharani, K. Transition-metal-free trifluoromethylative difunctionalization of olefins and alkynes: Approaches and challenges ahead. Catal. Sci. Technol. 2020, 10, 7142–7159. [Google Scholar] [CrossRef]
- Su, D.S.; Zhang, J.; Frank, B.; Thomas, A.; Wang, X.; Paraknowitsch, J.; Schlögl, R. Metal-free heterogeneous catalysis for sustainable chemistry. ChemSusChem 2010, 3, 169–180. [Google Scholar] [CrossRef]
- Lin, Y.; Song, Q. Cleavage of the Carbon-Carbon Triple Bonds of Arylacetylenes for the Synthesis of Arylnitriles without a Metal Catalyst. Eur. J. Org. Chem. 2016, 2016, 3056–3059. [Google Scholar] [CrossRef]
- Asakawa, H.; Lee, K.H.; Lin, Z.; Yamashita, M. Facile scission of isonitrile carbon-nitrogen triple bond using a diborane(4) reagent. Nat. Commun. 2014, 5, 4245. [Google Scholar] [CrossRef]
- Chan, A.P.Y.; Sergeev, A.G. Metal-mediated cleavage of unsaturated C-C bonds. Coord. Chem. Rev. 2020, 413, 213213. [Google Scholar] [CrossRef]
- Qin, C.; Su, Y.; Shen, T.; Shi, X.; Jiao, N. Splitting a Substrate into Three Parts: Gold-Catalyzed Nitrogenation of Alkynes by C-C and C≡C Bond Cleavage. Angew. Chem. 2016, 55, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Jiang, H. Palladium-Catalyzed Cleavage Reaction of Carbon-Carbon Triple Bond with Molecular Oxygen Promoted by Lewis Acid. J. Am. Chem. Soc. 2008, 130, 5030–5031. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, P.; Liu, G. Palladium-Catalyzed C-C Triple Bond Cleavage: Efficient Synthesis of 4H-Benzo[d][1,3]oxazin-4-ones. ACS Catal. 2013, 3, 178–181. [Google Scholar] [CrossRef]
- Shimada, T.; Yamamoto, Y. Carbon-Carbon Bond Cleavage of Diynes through the Hydroamination with Transition Metal Catalysts. J. Am. Chem. Soc. 2003, 125, 6646–6647. [Google Scholar] [CrossRef]
- Datta, S.; Chang, C.L.; Yeh, K.L.; Liu, R.S. A New Ruthenium-Catalyzed Cleavage of a Carbon-Carbon Triple Bond: Efficient Transformation of Ethynyl Alcohol into Alkene and Carbon Monoxide. J. Am. Chem. Soc. 2003, 125, 9294–9295. [Google Scholar] [CrossRef] [PubMed]
- Jun, C.H.; Lee, H.; Lim, S.G. The C-C bond activation and skeletal rearrangement of cycloalkanone imine by Rh (I) catalysts. J. Am. Chem. Soc. 2001, 123, 751–752. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Li, X.; Jiao, N. Copper-catalyzed direct transformation of simple alkynes to alkenyl nitriles via aerobic oxidative N-incorporation. Chem. Sci. 2015, 6, 6355–6360. [Google Scholar] [CrossRef]
- The Cyano Group; Rappoport, Z., Ed.; Wiley: London, UK, 1970. [Google Scholar]
- Fadda, A.A.; Mukhtar, M.M.; Refat, H.M. Utility of new activated nitriles in the synthesis of some new heterocyclic compounds. Am. J. Org. Chem. 2012, 2, 32–40. [Google Scholar] [CrossRef]
- Ghosh, T.; Si, A.; Misra, A.K. Facile Transformation of Nitriles into Thioamides: Application to C-Glycosyl Nitrile Derivatives. ChemistrySelect 2017, 2, 1366–1369. [Google Scholar] [CrossRef]
- Fleming, F.F.; Lihua, Y.; Ravikumar, P.C.; Funk, L.; Shook, B.C. Nitrile-containing pharmaceuticals: Efficacious roles of the nitrile pharmacophore. J. Med. Chem. 2010, 53, 7902–7917. [Google Scholar] [CrossRef]
- Colombier, M.A.; Molina, J.M. Doravirine: A review. Curr. Opin. HIV AIDS 2018, 13, 308–314. [Google Scholar] [CrossRef]
- Nassereddine, S.; Lap, C.J.; Tabbara, I.A. Evaluating ivosidenib for the treatment of relapsed/refractory AML: Design, development, and place in therapy. Onco. Targets Ther. 2018, 12, 303–308. [Google Scholar] [CrossRef]
- Yang, J.; Gong, W. Lorlatinib for the treatment of anaplastic lymphoma kinase-positive non-small cell lung cancer. Expert Rev. Clin. Pharmacol. 2019, 12, 173–178. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.S.; Manson, J.L. Designer magnets containing cyanides and nitriles. Acc. Chem. Res. 2001, 34, 563–570. [Google Scholar] [CrossRef] [PubMed]
- Goujon, L.J.; Khaldi, A.; Maziz, A.; Plesse, C.; Nguyen, G.T.M.; Aubert, P.H.; Vidal, F.; Chevrot, C.; Teyssié, D. Flexible Solid Polymer Electrolytes Based on Nitrile Butadiene Rubber/Poly (ethylene oxide) Interpenetrating Polymer Networks Containing Either LiTFSI or EMITFSI. Macromolecules 2011, 44, 9683–9691. [Google Scholar] [CrossRef]
- Fleming, F.F.; Wang, Q. Unsaturated nitriles: Conjugate additions of carbon nucleophiles to a recalcitrant class of acceptors. Chem. Rev. 2003, 103, 2035–2078. [Google Scholar] [CrossRef]
- Sandmeyer, T. Ueber die Ersetzung der Amidgruppe durch Chlor in den aromatischen Substanzen. Chem. Ber. 1884, 17, 1633–1635. [Google Scholar] [CrossRef]
- Rosenmund, K.W.; Struck, E. Das am Ringkohlenstoff gebundene Halogen und sein Ersatz durch andere Substituenten. I. Mitteilung: Ersatz des Halogens durch die Carboxylgruppe. Chem. Ber. 1919, 52, 1749–1756. [Google Scholar] [CrossRef]
- Ellis, G.P.; Romney-Alexander, T. Cyanation of aromatic halides. Chem. Rev. 1987, 87, 779–794. [Google Scholar] [CrossRef]
- Erker, T.; Nemec, S. Palladium-Catalyzed Cyanation Reactions of Thiophene Halides. Synthesis 2004, 1, 23–25. [Google Scholar]
- Anbarasan, P.; Schareina, T.; Beller, M. Recent developments and perspectives in palladium-catalyzed cyanation of aryl halides: Synthesis of benzonitriles. Chem. Soc. Rev. 2011, 40, 5049–5067. [Google Scholar] [CrossRef] [PubMed]
- Cohen, D.T.; Buchwald, S.L. Mild Palladium-Catalyzed Cyanation of (Hetero)aryl Halides and Triflates in Aqueous Media. Org. Lett. 2015, 17, 202–205. [Google Scholar] [CrossRef] [PubMed]
- Bisseret, P.; Duret, G.; Blanchard, N. Chopping unfunctionalized carbon-carbon bonds: A new paradigm for the synthesis of organonitriles. Org. Chem. Front. 2014, 1, 825–833. [Google Scholar] [CrossRef]
- John, P.C.S.; Guan, Y.; Kim, Y.; Kim, S.; Paton, R.S. Prediction of organic homolytic bond dissociation enthalpies at near chemical accuracy with sub-second computational cost. Nat. Commun. 2020, 11, 2328. [Google Scholar] [CrossRef]
- Jasiński, R.; Dresler, E. On the Question of Zwitterionic Intermediates in the [3 + 2] Cycloaddition Reactions: A Critical Review. Organics 2020, 1, 5. [Google Scholar] [CrossRef]
- García-Lacuna, J.; Domínguez, G.; Pérez-Castells, J. Flow Chemistry for Cycloaddition Reactions. ChemSusChem 2020, 13, 1. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.-L.; Chiou, W.-H. Diastereocontrolled Formal Syntheses of (±)-Lepadiformines A, B, and C and the Divergent Synthesis of 2-epi-Lepadiformine C through Unexpected Double Consecutive Epimerizations. J. Org. Chem. 2020, 85, 9051–9063. [Google Scholar] [CrossRef]
- Krištofíková, D.; Modrocká, V.; Mečiarová, M.; Šebesta, R. Green Asymmetric Organocatalysis. ChemSusChem 2020, 13, 2828. [Google Scholar] [CrossRef] [PubMed]
- Gawronski, J.; Wascinska, N.; Gajewy, J. Recent Progress in Lewis Base Activation and Control of Stereoselectivity in the Additions of Trimethylsilyl Nucleophiles. Chem. Rev. 2008, 108, 5227–5252. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef] [PubMed]
- Ptiček, L.; Hok, L.; Grbčić, P.; Topić, F.; Cetina, M.; Rissanen, K.; Pavelić, S.K.; Vianello, R.; Racané, L. Amidino substituted 2-aminophenols: Biologically important building blocks for the amidino-functionalization of 2-substituted benzoxazoles. Org. Biomol. Chem. 2021. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Božičević, L.; Lapić, J.; Đaković, S.; Šakić, D.; Tandarić, T.; Vianello, R.; Vrček, V. Transacylation in Ferrocenoyl-Purines. NMR and Computational Study of the Isomerization Mechanism. J. Org. Chem. 2019, 84, 12471. [Google Scholar] [CrossRef]
- Cindrić, M.; Sović, I.; Mioč, M.; Hok, L.; Boček, I.; Roškarić, P.; Butković, K.; Martin-Kleiner, I.; Starčević, K.; Vianello, R.; et al. Experimental and Computational Study of the Antioxidative Potential of Novel Nitro and Amino Substituted Benzimidazole/Benzothiazole-2-Carboxamides with Antiproliferative Activity. Antioxidants 2019, 8, 477. [Google Scholar] [CrossRef]
- Juraj, N.P.; Miletić, G.I.; Perić, B.; Popović, Z.; Smrečki, N.; Vianello, R.; Kirin, S.I. Stereochemistry of Hexacoordinated Zn(II), Cu(II), Ni(II), and Co(II) Complexes with Iminodiacetamide Ligands. Inorg. Chem. 2019, 58, 16445–16457. [Google Scholar] [CrossRef]
- Juraj, N.P.; Krklec, M.; Novosel, T.; Perić, B.; Vianello, R.; Raić-Malić, S.; Kirin, S.I. Copper(II) and Zinc(II) Complexes of Mono- and Bis-1,2,3-triazole substituted Heterocyclic Ligands. Dalton Transact. 2020, 49, 9002. [Google Scholar] [CrossRef] [PubMed]
- Melekhova, A.A.; Smirnov, A.S.; Novikov, A.S.; Panikorovskii, T.L.; Bokach, N.A.; Yu, V. Kukushkin, Copper(I)-Catalyzed 1,3-Dipolar Cycloaddition of Ketonitrones to Dialkylcyanamides: A Step toward Sustainable Generation of 2,3-Dihydro-1,2,4-oxadiazoles. ACS Omega 2017, 2, 1380–1391. [Google Scholar] [CrossRef] [PubMed]
- Bolotin, D.S.; Demakova, M.Y.; Novikov, A.S.; Avdontceva, M.S.; Kuznetsov, M.L.; Bokach, N.A.; Yu, V. Kukushkin, Bifunctional Reactivity of Amidoximes Observed upon Nucleophilic Addition to Metal-Activated Nitriles. Inorg. Chem. 2015, 54, 4039. [Google Scholar] [CrossRef] [PubMed]
- Tandarić, T.; Vianello, R. Computational Insight into the Mechanism of the Irreversible Inhibition of Monoamine Oxidase Enzymes by the Antiparkinsonian Propargylamine Inhibitors Rasagiline and Selegiline. ACS Chem. Neurosci. 2019, 10, 3532–3542. [Google Scholar] [CrossRef] [PubMed]
- Maršavelski, A.; Vianello, R. What a difference a methyl group makes—The selectivity of monoamine oxidase B towards histamine and N-methylhistamine. Chem. Eur. J. 2017, 23, 2915–2925. [Google Scholar] [CrossRef]
- Foster, J.P.; Weinhold, F. Natural hybrid orbitals. J. Am. Chem. Soc. 1980, 102, 7211–7218. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]


| Solvent | Acetonitrile | Toluene | Water | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Oxidant | NIS | NIS | NIS | NIS | NCS | NBS | NIS | NIS | NIS |
| Nitrogen Source | TMSN3 | TMSN3 | TMSN3 | TMSN3 | TMSN3 | TMSN3 | NaN3 | TMSN3 | TMSN3 |
| Alkyne | 1 | 2 | 3 | 4 | 2 | 2 | 2 | 1 | 1 |
| Stationary Point | |||||||||
| R | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| TS1 | 26.8 | 26.8 | 26.8 | 22.7 | 35.8 | 30.0 | 24.7 | 29.6 | 24.5 |
| IN1 | 13.7 | 12.9 | 14.6 | 3.4 | –5.5 | 1.7 | 16.1 | 9.7 | |
| TS2 | 22.1 | 20.7 | 22.2 | 8.4 | 1.0 | 8.3 | 20.7 | 18.6 | |
| IN2 | −36.9 | –37.6 | –37.2 | –43.4 | –57.3 | –50.9 | –50.5 | –38.5 | –38.5 |
| TS3 | −9.0 | –9.3 | –9.4 | –14.3 | –28.5 | –23.3 | –22.2 | –10.6 | –11.2 |
| IN3 | –88.0 | –88.9 | –87.2 | –94.9 | –110.8 | –104.7 | –101.9 | –89.2 | –93.9 |
| TS4 | –68.1 | –71.4 | –62.4 | –66.4 | –78.5 | –73.8 | –90.9 | –62.4 | –72.7 |
| IN4 | –92.9 | –93.8 | –92.9 | –88.1 | –103.4 | –91.4 | –77.4 | –98.9 | |
| TS5 | –71.9 | –73.7 | –72.5 | –69.4 | –64.0 | –76.8 | –74.9 | –80.2 | |
| IN5 | –115.6 | –116.3 | –116.8 | –112.9 | –106.6 | –119.4 | –142.6 | –118.6 | –124.0 |
| TS6 | –82.1 | –82.8 | –83.3 | –79.2 | –73.1 | –85.9 | –109.1 | –84.0 | –91.1 |
| P | –191.9 | –192.0 | –188.8 | –191.7 | –178.9 | –192.5 | –228.9 | –193.9 | –193.5 |
| Rate-limiting step | IN5→P | IN5→P | IN5→P | IN5→P | IN4→IN5 | IN5→P | IN5→P | IN5→P | IN5→P |
| Activation barrier ΔG‡ | 33.5 | 33.5 | 33.5 | 33.6 | 39.3 | 33.5 | 33.5 | 34.6 | 32.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hok, L.; Vianello, R. Direct Metal-Free Transformation of Alkynes to Nitriles: Computational Evidence for the Precise Reaction Mechanism. Int. J. Mol. Sci. 2021, 22, 3193. https://doi.org/10.3390/ijms22063193
Hok L, Vianello R. Direct Metal-Free Transformation of Alkynes to Nitriles: Computational Evidence for the Precise Reaction Mechanism. International Journal of Molecular Sciences. 2021; 22(6):3193. https://doi.org/10.3390/ijms22063193
Chicago/Turabian StyleHok, Lucija, and Robert Vianello. 2021. "Direct Metal-Free Transformation of Alkynes to Nitriles: Computational Evidence for the Precise Reaction Mechanism" International Journal of Molecular Sciences 22, no. 6: 3193. https://doi.org/10.3390/ijms22063193
APA StyleHok, L., & Vianello, R. (2021). Direct Metal-Free Transformation of Alkynes to Nitriles: Computational Evidence for the Precise Reaction Mechanism. International Journal of Molecular Sciences, 22(6), 3193. https://doi.org/10.3390/ijms22063193








