A Molecular Interpretation of the Dynamics of Diffusive Mass Transport of Water within a Glassy Polyetherimide
Abstract
1. Introduction
1.1. Background
1.1.1. Relevant Results on Equilibrium Thermodynamics of a PEI–Water System
1.1.2. Mutual vs. Intra-Diffusion Coefficients
2. Results and Discussion
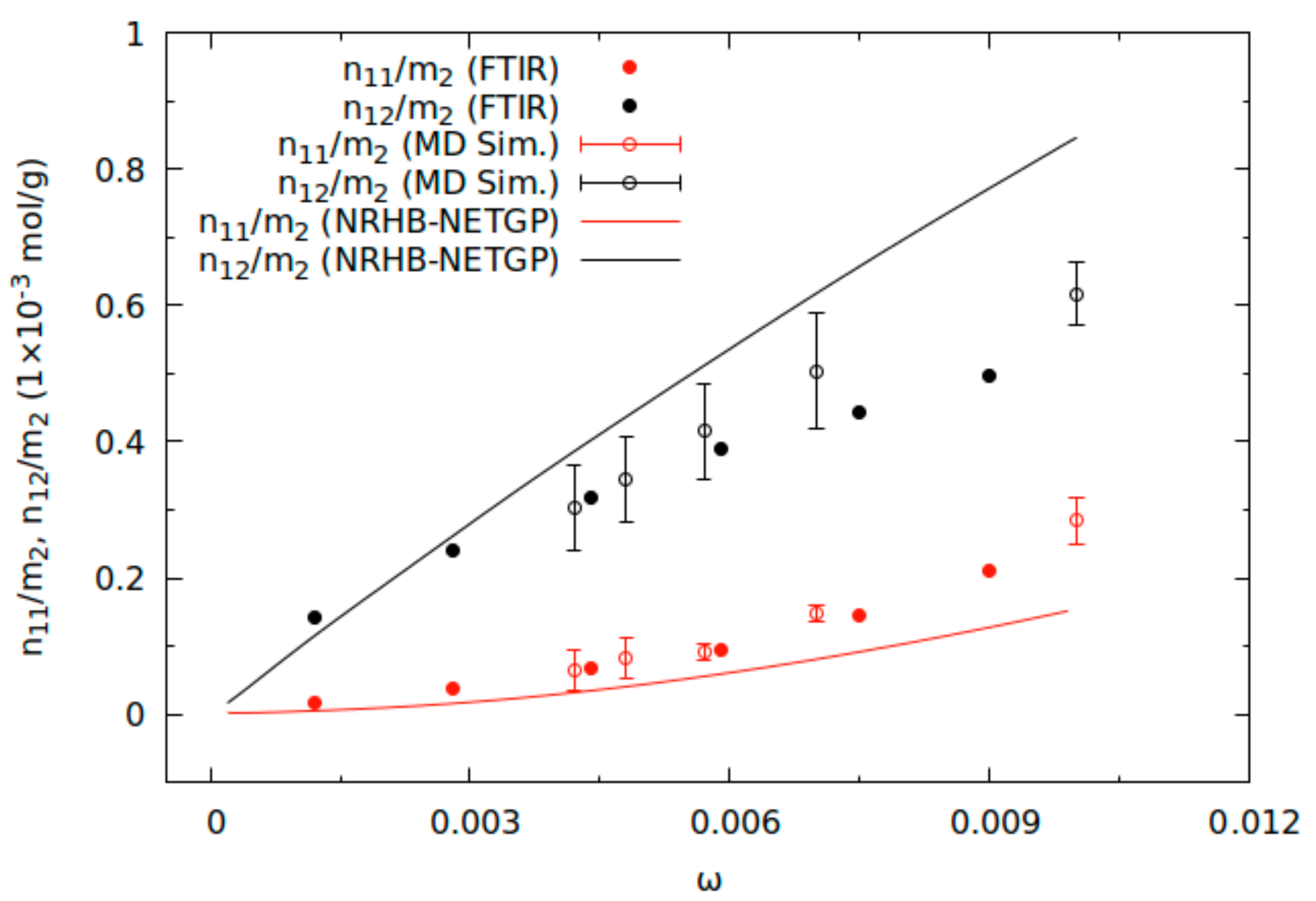
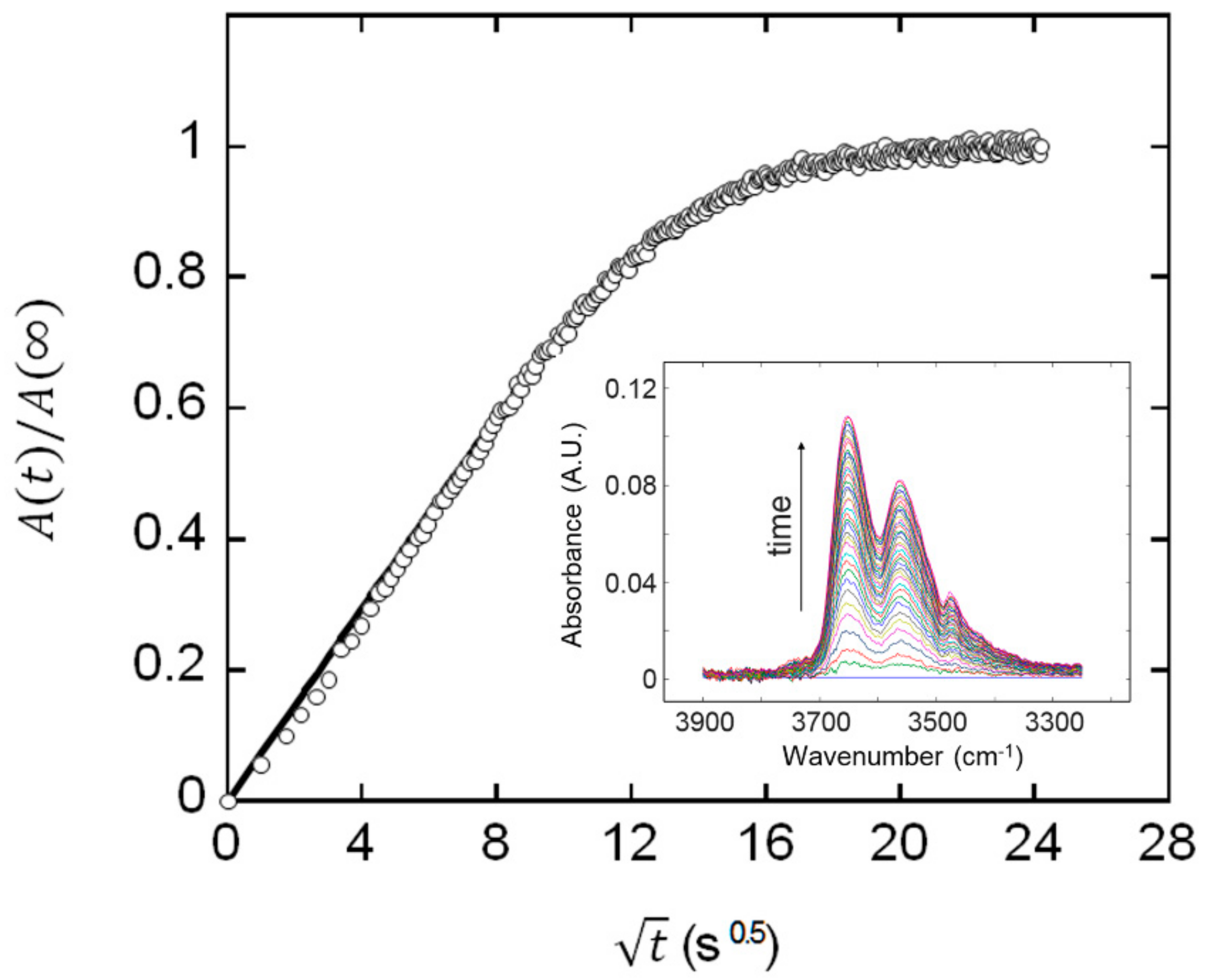
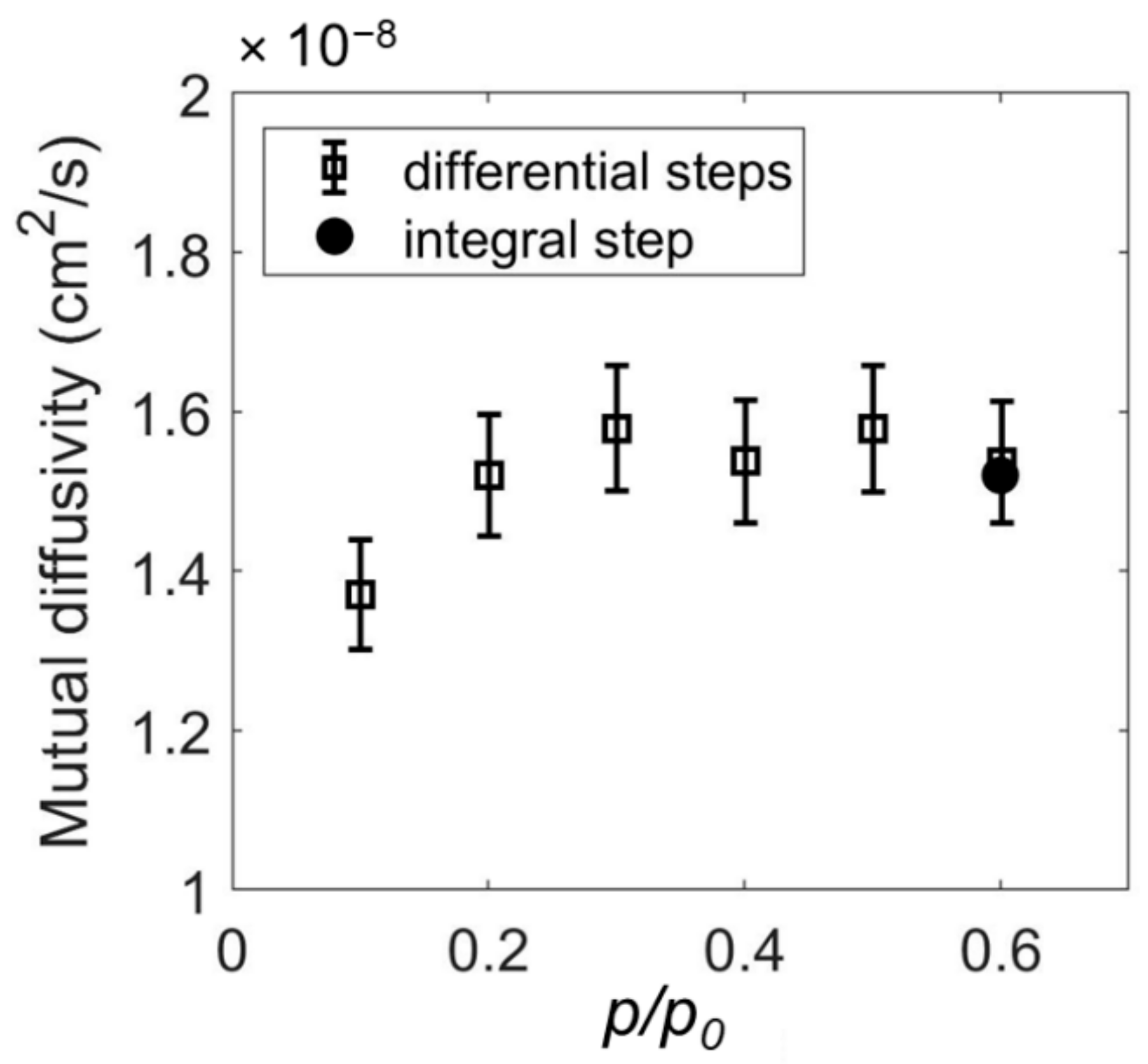
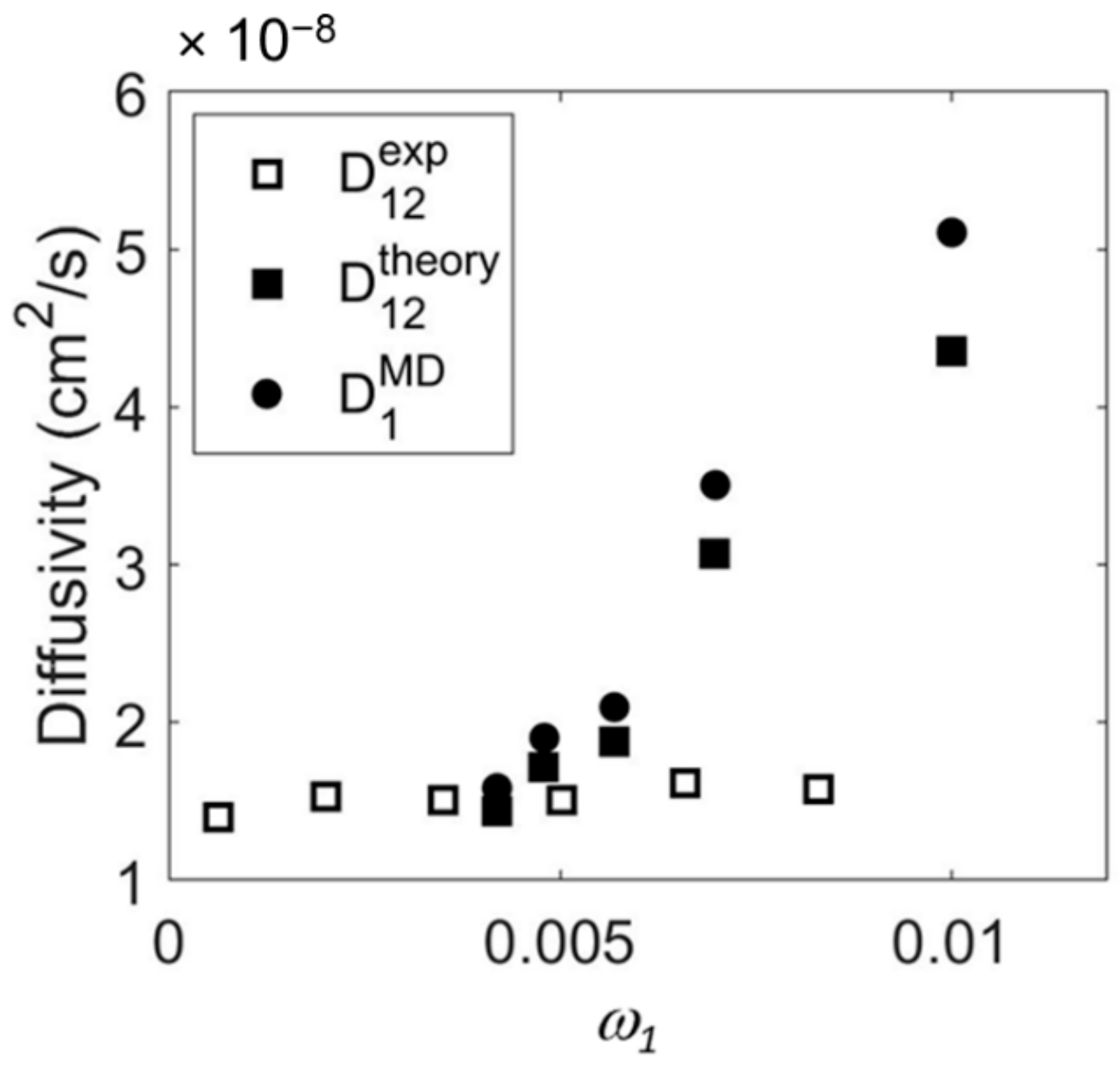
2.1. Determination of Mutual Diffusivity of the Water–PEI System from Vibrational Spectroscopy
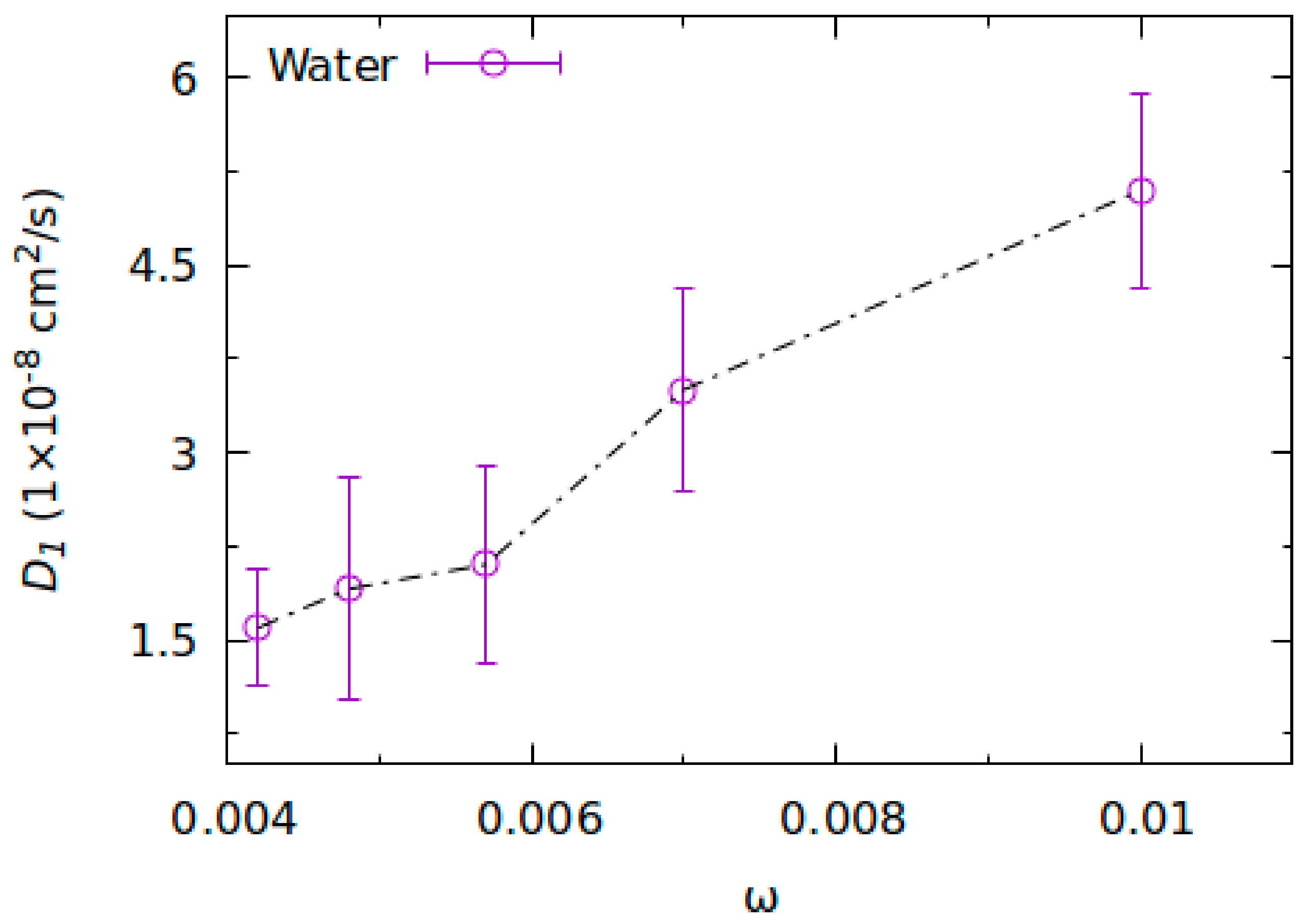
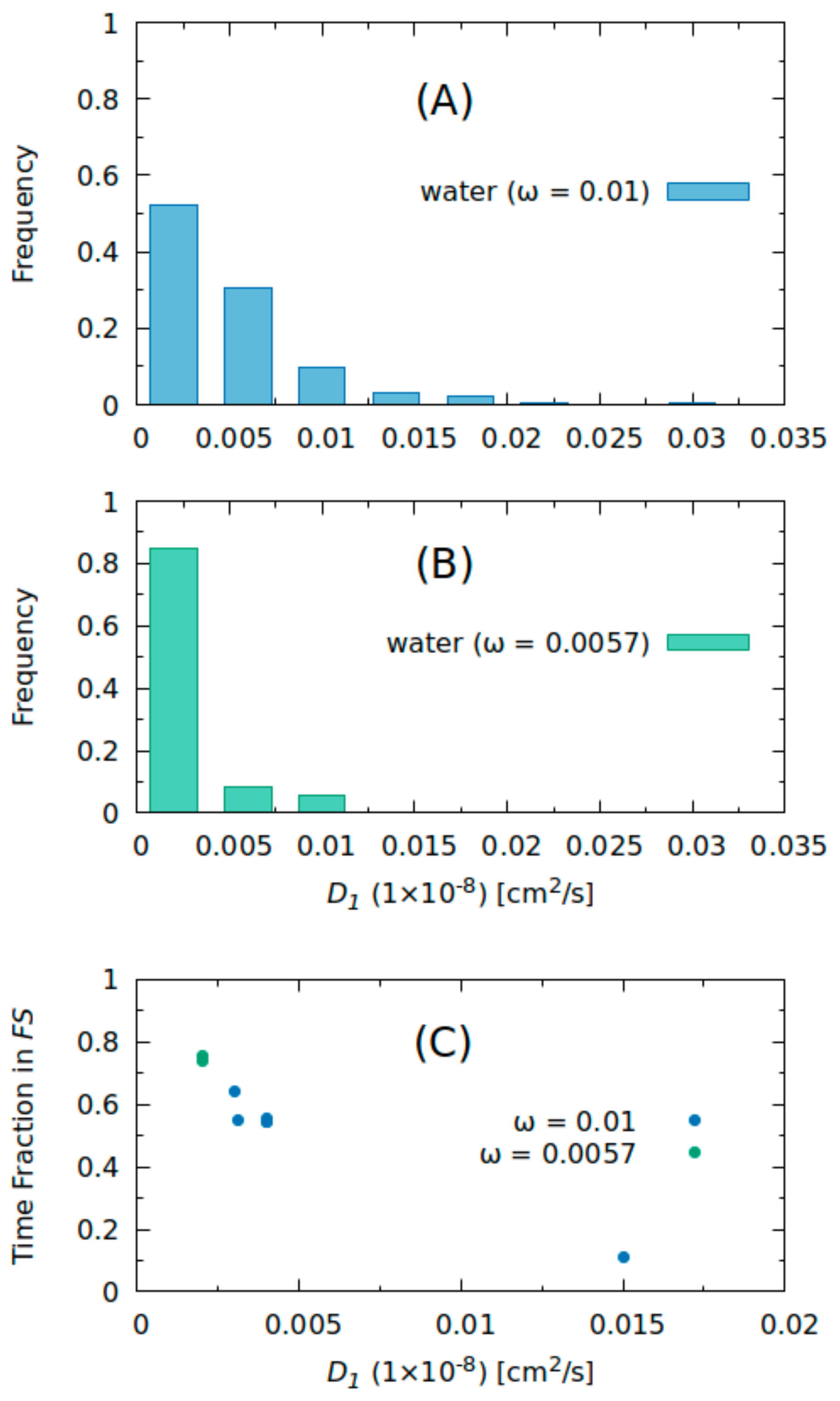
2.2. Molecular Dynamics Simulations
| System | Box (nm3) | Water Molecules | Total Particles | Simulation Time (ns) | |
|---|---|---|---|---|---|
| I | 6.31000 | - | 0 | 22,680 | 120 |
| II | 6.31308 | 0.0042 | 86 | 22,938 | 198 |
| III | 6.31358 | 0.0048 | 100 | 22,980 | 200 |
| IV | 6.31589 | 0.0057 | 120 | 23,040 | 200 |
| V | 6.31980 | 0.007 | 150 | 23,130 | 200 |
| VI | 6.32867 | 0.01 | 220 | 23,340 | 240 |
2.3. Comparison of Theoretical Predictions with Results of Vibrational Spectroscopy
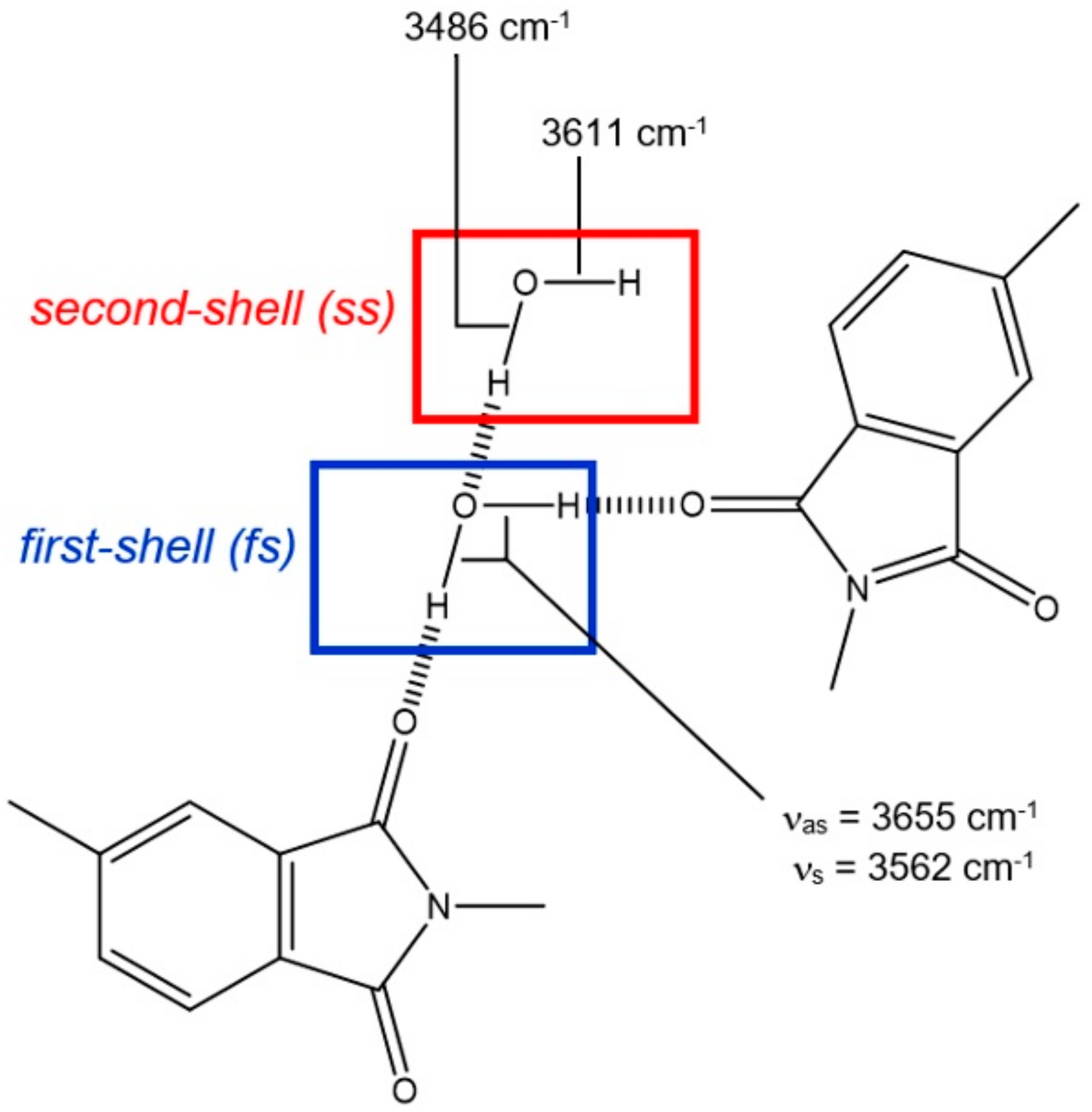
2.4. H-Bond Lifetimes
| System | τ1 | τ2 | A1 | A2 |
|---|---|---|---|---|
| II | 4.4 ps | 2362 ps | 0.62 | 0.38 |
| VI | 3.9 ps | 118 ps | 0.67 | 0.33 |
3. Experimental
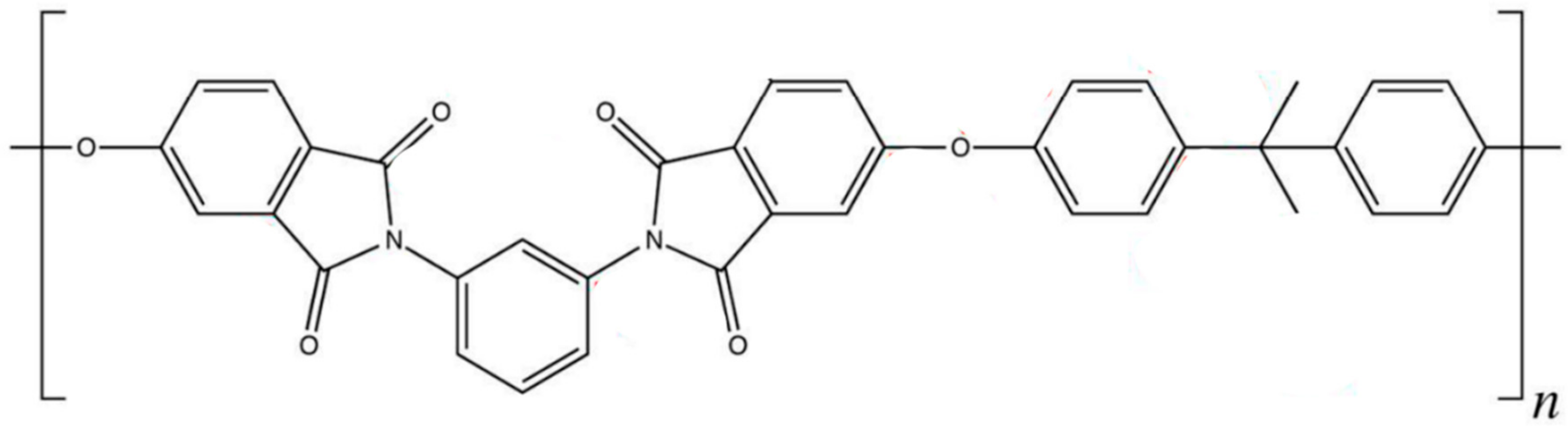
3.1. Materials
3.2. FTIR Spectroscopy
3.3. MD Simulations
3.3.1. Polymer Model
3.3.2. Simulation Details
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mensitieri, G.; Iannone, M. Modeling accelerated ageing in polymer compsites. In Ageing of Composites; Martin, R., Ed.; CRC Press: Boca Raton, FL, USA, 2008; pp. 224–282. [Google Scholar]
- Li, D.; Yao, J.; Wang, H. Thin films and membranes with hierarchical porosity. In Encyclopedia of Membrane Science and Technology; Hoek, E.M.V., Tarabara, V.V., Eds.; John Wiley & Sons, Inc.: Chichester, UK, 2013. [Google Scholar]
- Bernstein, R.; Kaufman, Y.; Freger, V. Porosity. In Encyclopedia of Membrane Science and Technology; Hoek, E.M.V., Tarabara, V.V., Eds.; John Wiley & Sons, Inc.: Chichester, UK, 2013. [Google Scholar]
- Brunetti, A.; Barbieri, G.; Drioli, E. Analytical applications of membranes. In Encyclopedia of Membrane Science and Technology; Hoek, E.M.V., Tarabara, V.V., Eds.; John Wiley & Sons, Inc.: Chichester, UK, 2013. [Google Scholar]
- Koros, W.J.; Fleming, G.K.; Jordan, S.M.; Kim, T.H.; Hoehn, H.H. Polymeric Membrane Materials for Solution-Diffusion Based Permeation Separations. Prog. Polym. Sci. 1988, 13, 339. [Google Scholar] [CrossRef]
- Christie, S.; Scorsone, E.; Persaud, K.; Kvasnik, F. Remote Detection of Gaseous Ammonia Using the near Infrared Transmission Properties of Polyaniline. Sens. Actuators B. Chem. 2003, 90, 163. [Google Scholar] [CrossRef]
- Scherillo, G.; Petretta, M.; Galizia, M.; La Manna, P.; Musto, P.; Mensitieri, G. Thermodynamics of Water Sorption in High Performance Glassy Thermoplastic Polymers. Front. Chem. 2014, 2, 25. [Google Scholar] [CrossRef] [PubMed]
- Scherillo, G.; Galizia, M.; Musto, P.; Mensitieri, G. Water Sorption Thermodynamics in Glassy and Rubbery Polymers: Modeling the Interactional Issues Emerging from Ftir Spectroscopy. Ind. Eng. Chem. Res. 2013, 52, 8674. [Google Scholar] [CrossRef]
- Scherillo, G.; Sanguigno, L.; Galizia, M.; Lavorgna, M.; Musto, P.; Mensitieri, G. Non-Equilibrium Compressible Lattice Theories Accounting for Hydrogen Bonding Interactions: Modelling Water Sorption Thermodynamics in Fluorinated Polyimides. Fluid Phase Equilib. 2012, 334, 166. [Google Scholar] [CrossRef]
- De Nicola, A.; Correa, A.; Milano, G.; La Manna, P.; Musto, P.; Mensitieri, G.; Scherillo, G. Local Structure and Dynamics of Water Absorbed in Poly(Ether Imide): A Hydrogen Bonding Anatomy. J. Phys. Chem. B 2017, 121, 3162–3176. [Google Scholar] [CrossRef]
- Mensitieri, G.; Scherillo, G.; Panayiotou, C.; Musto, P. Towards a Predictive Thermodynamic Description of Sorption Processes in Polymers: The Synergy between Theoretical Eos Models and Vibrational Spectroscopy. Mater. Sci. Eng. 2020, 140, 100525. [Google Scholar] [CrossRef]
- Panayiotou, C.; Pantoula, M.; Stefanis, E.; Tsivintzelis, I.; Economou, I.G. Nonrandom Hydrogen-Bonding Model of Fluids and Their Mixtures. 1. Pure Fluids. Ind. Eng. Chem. Res. 2004, 43, 6592. [Google Scholar] [CrossRef]
- Panayiotou, C.; Tsivintzelis, I.; Economou, I.G. Nonrandom Hydrogen-Bonding Model of Fluids and Their Mixtures. 2. Multicomponent Mixtures. Ind. Eng. Chem. Res. 2007, 46, 2628. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Claredon Press: Oxford, UK, 1975. [Google Scholar]
- Bearman, R.J. On the Molecular Basis of Some Current Theories of Diffusion1. J. Phys. Chem. 1961, 65, 1961–1968. [Google Scholar] [CrossRef]
- Caruthers, J.M.; Chao, K.C.; Venkatasubramanian, V.; Sy-Siong-Kiao, R.; Novenario, C.R.; Sundaram, A. Handbook of Diffusion and Thermal Properties of Polymers and Polymer Solutions; Design Institute for Physical Property Data, American Institute of Chemical Engineers: New York, NY, USA, 1998. [Google Scholar]
- Vrentas, J.S.; Duda, J.L. Diffusion in Polymer–Solvent Systems. Ii. A Predictive Theory for the Dependence of Diffusion Coefficients on Temperature, Concentration, and Molecular Weight. J. Polym. Sci. 1977, 15, 417. [Google Scholar] [CrossRef]
- Vrentas, J.S.; Vrentas, C.M. Predictive Methods for Self-Diffusion and Mutual Diffusion Coefficients in Polymer–Solvent Systems. Eur. Polym. J. 1998, 34, 797. [Google Scholar] [CrossRef]
- Musto, P.; La Manna, P.; Cimino, F.; Mensitieri, G.; Russo, P. Morphology, Molecular Interactions and H2O Diffusion in a Poly(Lactic-Acid)/Graphene Composite: A Vibrational Spectroscopy Study. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2019, 218, 40–50. [Google Scholar] [CrossRef]
- Musto, P.; Ragosta, G.; Mensitieri, G.; Lavorgna, M. On the Molecular Mechanism of H2o Diffusion into Polyimides: A Vibrational Spectroscopy Investigation. Macromolecules 2007, 40, 9614. [Google Scholar] [CrossRef]
- Milano, G.; Guerra, G.; Müller-Plathe, F. Anisotropic Diffusion of Small Penetrants in the Δ Crystalline Phase of Syndiotactic Polystyrene: A Molecular Dynamics Simulation Study. Chem. Mater. 2002, 14, 2977–2982. [Google Scholar] [CrossRef]
- Rapaport, D.C. Hydrogen Bonds in Water. Mol. Phys. 1983, 50, 1151–1162. [Google Scholar] [CrossRef]
- Chowdhuri, S.; Chandra, A. Dynamics of Halide Ion−Water Hydrogen Bonds in Aqueous Solutions: Dependence on Ion Size and Temperature. J. Phys. Chem. B 2006, 110, 9674–9680. [Google Scholar] [CrossRef] [PubMed]
- Luzar, A. Resolving the Hydrogen Bond Dynamics Conundrum. J. Chem. Phys. 2000, 113, 10663. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Hydrogen-Bond Kinetics in Liquid Water. Nature 1996, 379, 55–57. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Effect of Environment on Hydrogen Bond Dynamics in Liquid Water. Phys. Rev. Lett. 1996, 76, 928–931. [Google Scholar] [CrossRef] [PubMed]
- Mijović, J.; Zhang, H. Molecular Dynamics Simulation Study of Motions and Interactions of Water in a Polymer Network. J. Phys. Chem. B 2004, 108, 2557. [Google Scholar] [CrossRef]
- Cotugno, S.; Larobina, D.; Mensitieri, G.; Musto, P.; Ragosta, G. A Novel Spectroscopic Approach to Investigate Transport Processes in Polymers: The Case of Water–Epoxy System. Polymer 2001, 42, 6431. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Nguyen, T.B. Monte Carlo Simulations of the Hydration of Substituted Benzenes with Opls Potential Functions. J. Comput. Chem. 1993, 14, 195. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; TiradoRives, J. Development and Testing of the Opls All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225. [Google Scholar] [CrossRef]
- Price, M.L.P.; Ostrovsky, D.; Jorgensen, W.L. Gas-Phase and Liquid-State Properties of Esters, Nitriles, and Nitro Compounds with the Opls-Aa Force Field. J. Comput. Chem. 2001, 22, 1340. [Google Scholar] [CrossRef]
- Milano, G.; Muller-Plathe, F. Cyclohexane;Benzene Mixtures:Thermodynamics and Structure from Atomistic Simulations. J. Phys. Chem. B 2004, 108, 7415. [Google Scholar] [CrossRef]
- Tironi, I.G.; Sperb, R.; Smith, P.E.; van Gunsteren, W.F. A Generalized Reaction Field Method for Molecular Dynamics Simulations. J. Chem. Phys. 1995, 102, 5451. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J.; Pullman, B. Intermolecular Forces. In Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry, Jerusalem, Israel, 13–16 April 1981; p. 331. [Google Scholar]
- Milano, G.; Kawakatsu, T. Hybrid Particle-Field Molecular Dynamics Simulations for Dense Polymer Systems. J. Chem. Phys. 2009, 130, 214106. [Google Scholar] [CrossRef]
- Milano, G.; Kawakatsu, T. Pressure Calculation in Hybrid Particle-Field Simulations. J. Chem. Phys. 2010, 133, 214102. [Google Scholar] [CrossRef]
- Zhao, Y.; De Nicola, A.; Kawakatsu, T.; Milano, G. Hybrid Particle-Field Molecular Dynamics Simulations: Parallelization and Benchmarks. J. Comput. Chem. 2012, 33, 868. [Google Scholar] [CrossRef]
- De Nicola, A.; Kawakatsu, T.; Milano, G. Generation of Well-Relaxed All-Atom Models of Large Molecular Weight Polymer Melts: A Hybrid Particle-Continuum Approach Based on Particle-Field Molecular Dynamics Simulations. J. Chem. Theory Comput. 2014, 10, 5651. [Google Scholar] [CrossRef] [PubMed]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. Gromacs: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Postma, J.P.M.; Gunsteren, W.F.v.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correa, A.; De Nicola, A.; Scherillo, G.; Loianno, V.; Mallamace, D.; Mallamace, F.; Ito, H.; Musto, P.; Mensitieri, G. A Molecular Interpretation of the Dynamics of Diffusive Mass Transport of Water within a Glassy Polyetherimide. Int. J. Mol. Sci. 2021, 22, 2908. https://doi.org/10.3390/ijms22062908
Correa A, De Nicola A, Scherillo G, Loianno V, Mallamace D, Mallamace F, Ito H, Musto P, Mensitieri G. A Molecular Interpretation of the Dynamics of Diffusive Mass Transport of Water within a Glassy Polyetherimide. International Journal of Molecular Sciences. 2021; 22(6):2908. https://doi.org/10.3390/ijms22062908
Chicago/Turabian StyleCorrea, Andrea, Antonio De Nicola, Giuseppe Scherillo, Valerio Loianno, Domenico Mallamace, Francesco Mallamace, Hiroshi Ito, Pellegrino Musto, and Giuseppe Mensitieri. 2021. "A Molecular Interpretation of the Dynamics of Diffusive Mass Transport of Water within a Glassy Polyetherimide" International Journal of Molecular Sciences 22, no. 6: 2908. https://doi.org/10.3390/ijms22062908
APA StyleCorrea, A., De Nicola, A., Scherillo, G., Loianno, V., Mallamace, D., Mallamace, F., Ito, H., Musto, P., & Mensitieri, G. (2021). A Molecular Interpretation of the Dynamics of Diffusive Mass Transport of Water within a Glassy Polyetherimide. International Journal of Molecular Sciences, 22(6), 2908. https://doi.org/10.3390/ijms22062908










