Structural and Dynamical Behaviour of Colloids with Competing Interactions Confined in Slit Pores
Abstract
:1. Introduction
2. The Model and the Simulation Method
3. Results
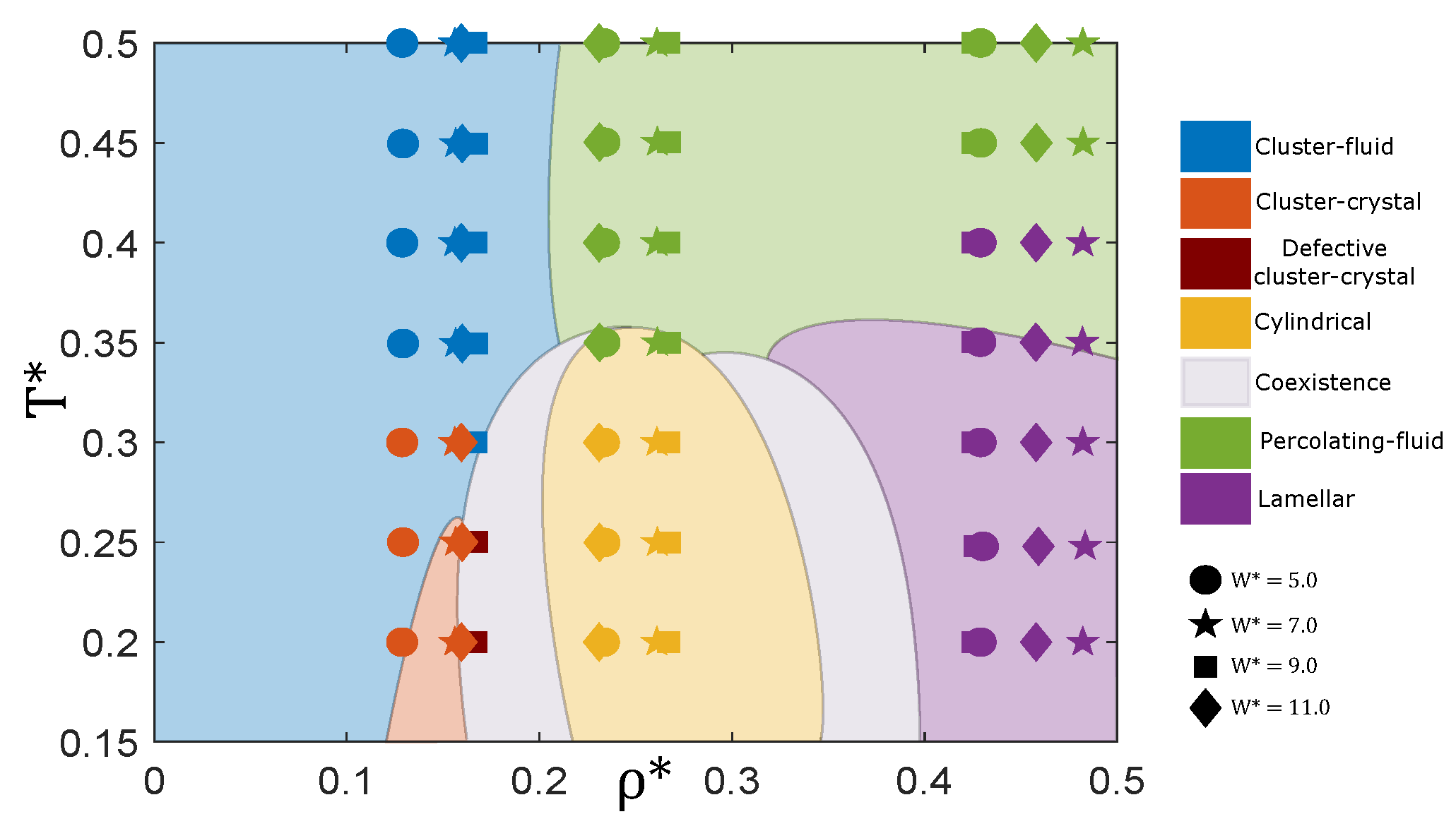
3.1. Equilibrium Properties
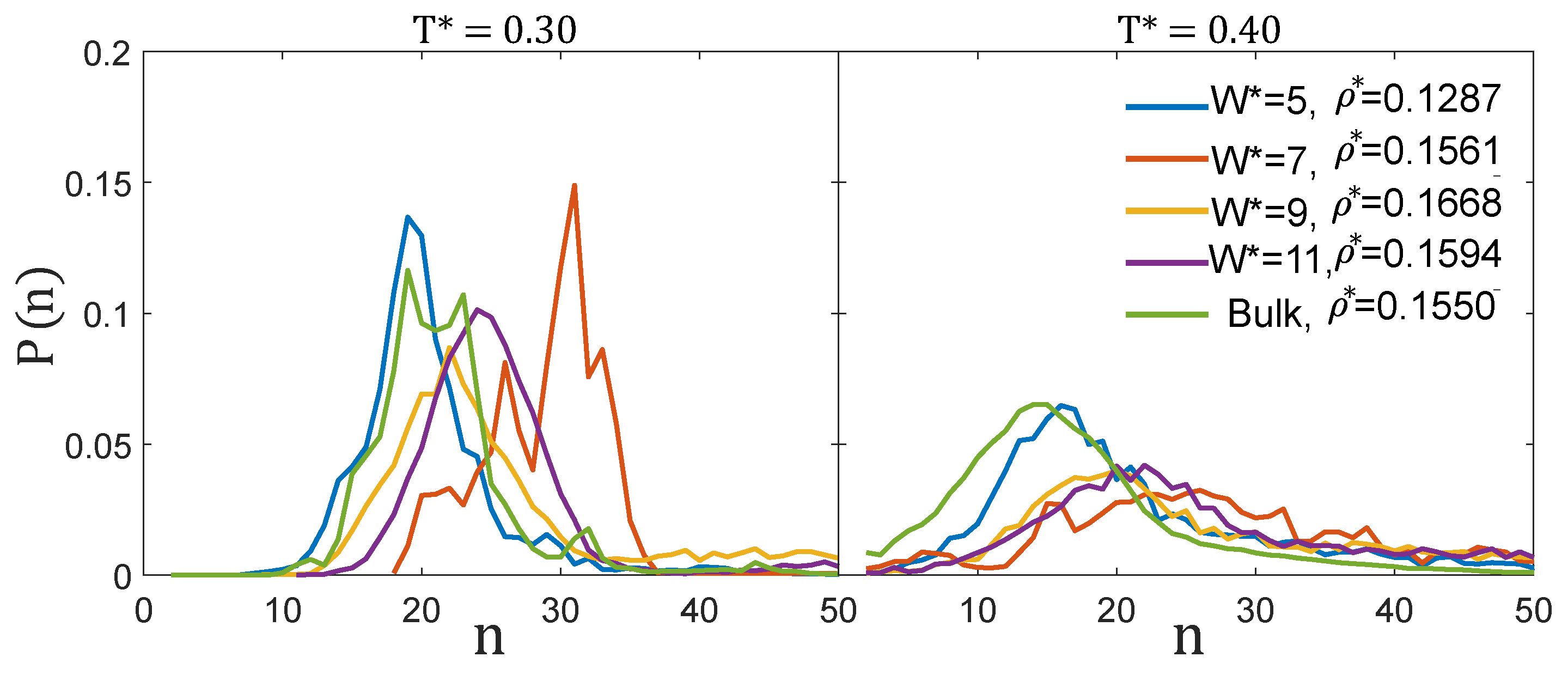
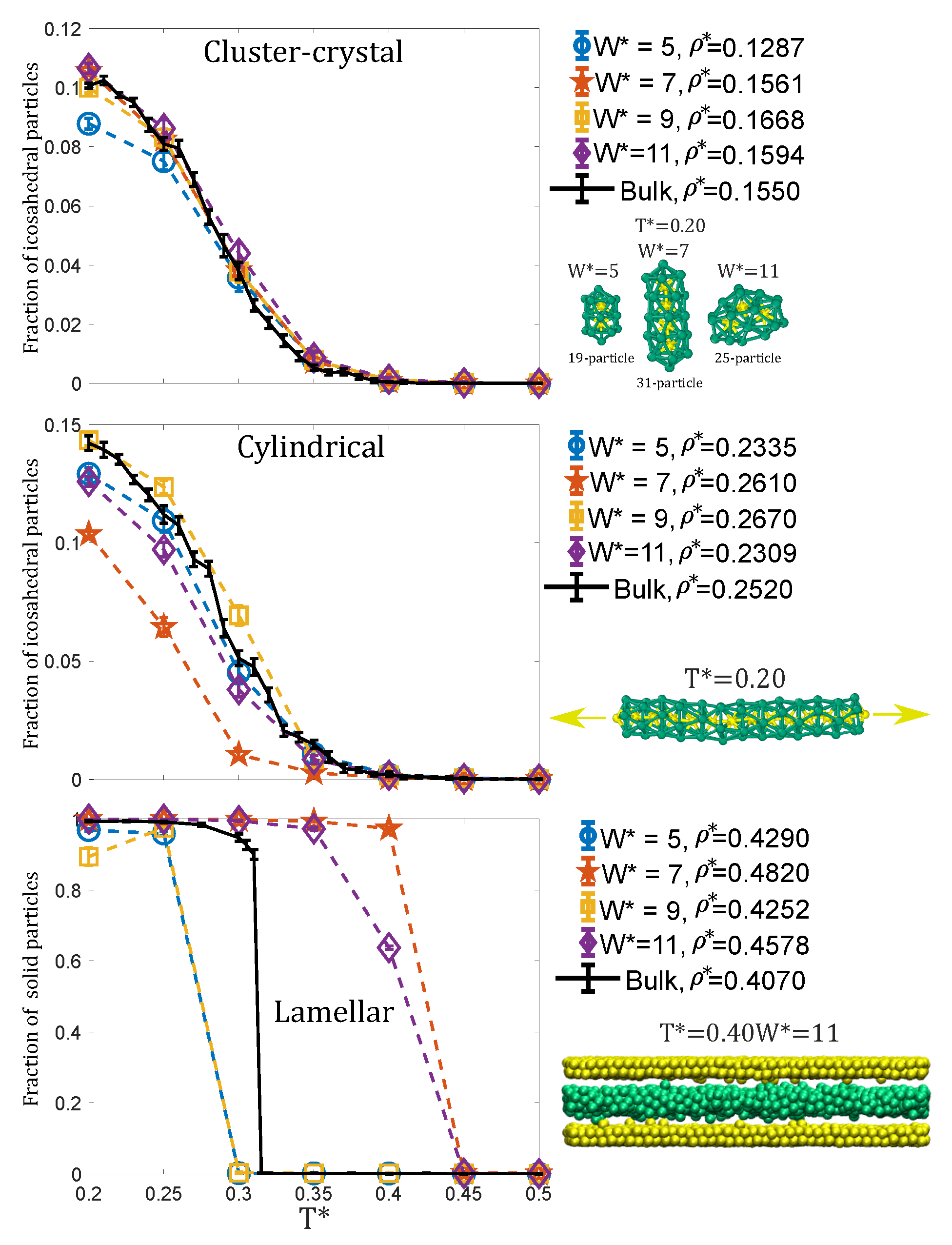
3.1.1. Low Density: The Cluster-Crystal
3.1.2. Intermediate Density: The Hexagonal Phase
3.1.3. High Density: The Lamellar Phase
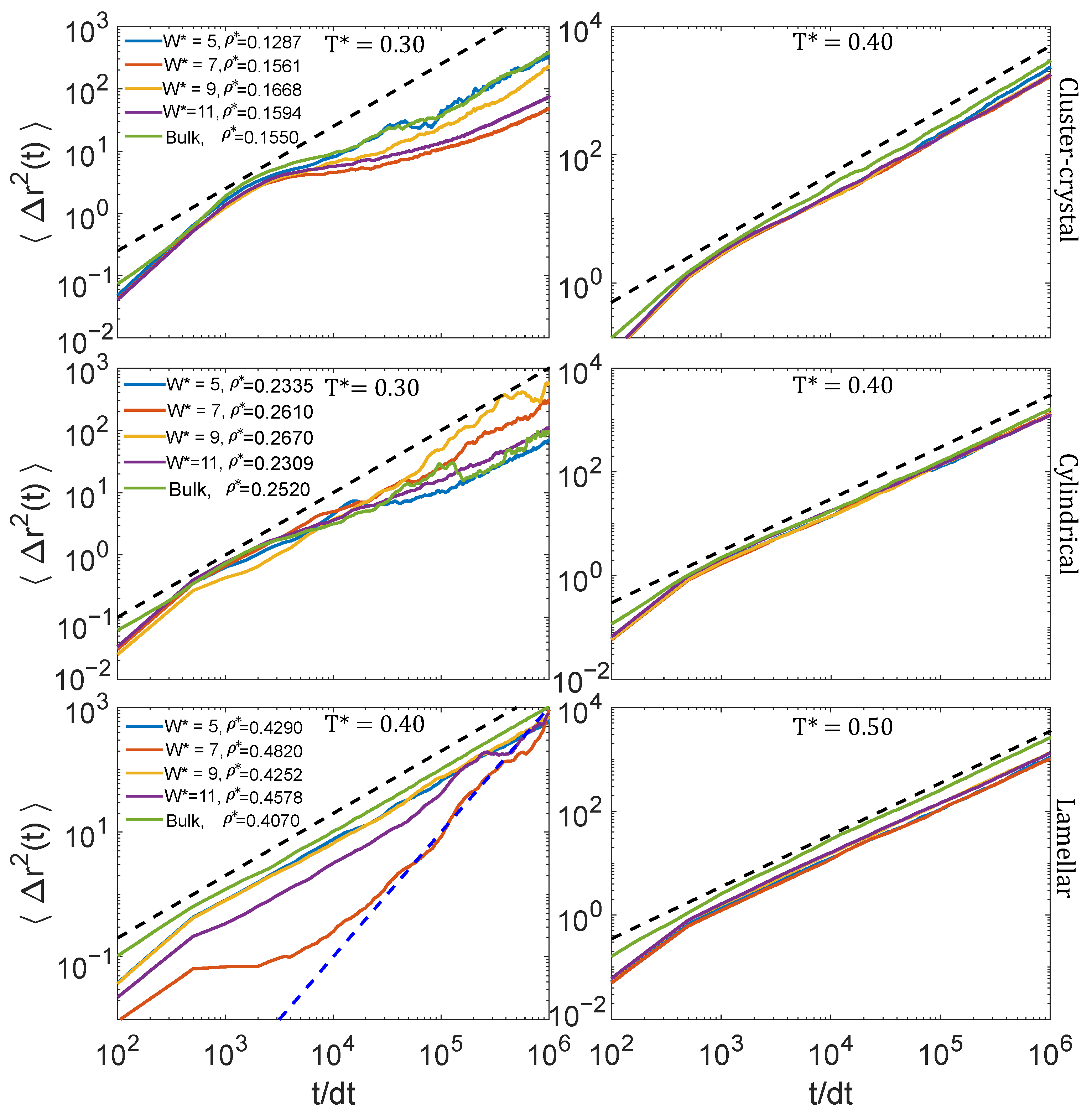
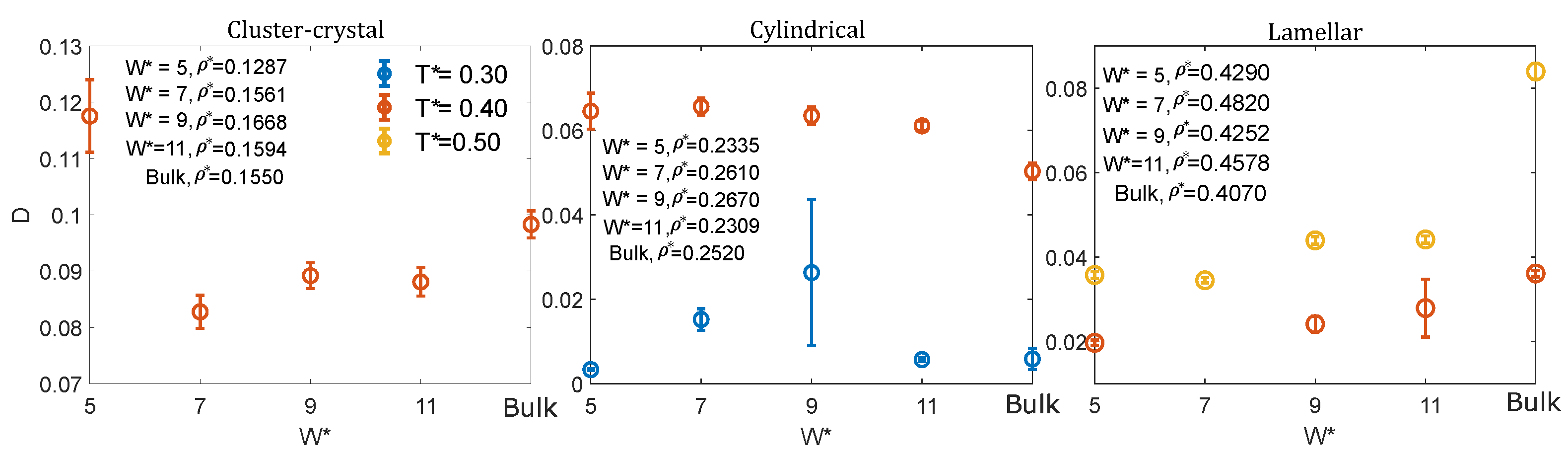
3.2. Dynamic Properties
3.2.1. Low Density: Cluster-Crystal
3.2.2. Intermediate Density: Cylindrical Phase
3.2.3. High Density: Lamellar Phase
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruiz-Franco, J.; Zaccarelli, E. On the role of competing interactions in charged colloids with short-range attraction. Annu. Rev. Condens. Matter Phys. 2021, 12, 51–70. [Google Scholar] [CrossRef]
- Ciach, A.; Pękalski, J.; Góźdź, W. Origin of similarity of phase diagrams in amphiphilic and colloidal systems with competing interactions. Soft Matter 2013, 9, 6301–6308. [Google Scholar] [CrossRef] [Green Version]
- Ciach, A. Universal sequence of ordered structures obtained from mesoscopic description of self-assembly. Phys. Rev. E 2008, 78, 061505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pini, D.; Parola, A. Pattern formation and self-assembly driven by competing interactions. Soft Matter 2017, 13, 9259–9272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhuang, Y.; Zhang, K.; Charbonneau, P. Equilibrium phase behavior of a continuous-space microphase former. Phys. Rev. Lett. 2016, 116, 098301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhuang, Y.; Charbonneau, P. Equilibrium phase behavior of the square-well linear microphase-forming model. J. Phys. Chem. B 2016, 120, 6178–6188. [Google Scholar] [CrossRef] [Green Version]
- Royall, C.P. Hunting mermaids in real space: Known knowns, known unknowns and unknown unknowns. Soft Matter 2018, 14, 4020–4028. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.H.; Kuipers, B.W.M.; de Tian, W.; Groenewold, J.; Kegel, W.K. Polydispersity and Gelation in Concentrated Colloids with Competing Interactions. Soft Matter 2015, 11, 297–302. [Google Scholar] [CrossRef] [Green Version]
- Toledano, J.C.F.; Sciortino, F.; Zaccarelli, E. Colloidal systems with competing interactions: From an arrested repulsive cluster phase to a gel. Soft Matter 2009, 5, 2390–2398. [Google Scholar] [CrossRef]
- Klix, C.L.; Royall, C.P.; Tanaka, H. Structural and dynamical features of multiple metastable glassy states in a colloidal system with competing interactions. Phys. Rev. Lett. 2010, 104, 165702. [Google Scholar] [CrossRef] [Green Version]
- Campbell, A.I.; Anderson, V.J.; van Duijneveldt, J.S.; Bartlett, P. Dynamical arrest in attractive colloids: The effect of long-range repulsion. Phys. Rev. Lett. 2005, 94, 208301. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Y.; Charbonneau, P. Recent advances in the theory and simulation of model colloidal microphase formers. J. Phys. Chem. B 2016, 120, 7775–7782. [Google Scholar] [CrossRef] [Green Version]
- Khandpur, A.K.; Foerster, S.; Bates, F.S.; Hamley, I.W.; Ryan, A.J.; Bras, W.; Almdal, K.; Mortensen, K. Polyisoprene-polystyrene diblock copolymer phase diagram near the order-disorder transition. Macromolecules 1995, 28, 8796–8806. [Google Scholar] [CrossRef]
- Hu, H.; Gopinadhan, M.; Osuji, C.O. Directed self-assembly of block copolymers: A tutorial review of strategies for enabling nanotechnology with soft matter. Soft Matter 2014, 10, 3867–3889. [Google Scholar] [CrossRef]
- Doerk, G.S.; Yager, K.G. Beyond native block copolymer morphologies. Mol. Syst. Des. Eng. 2017, 2, 518–538. [Google Scholar] [CrossRef]
- Guo, Y.; van Ravensteijn, B.G.P.; Kegel, W.K. Self-assembly of isotropic colloids into colloidal strings, Bernal spiral-like, and tubular clusters. Chem. Commun. 2020, 56, 6309–6312. [Google Scholar] [CrossRef] [PubMed]
- Serna, H.; Díaz Pozuelo, A.; Noya, E.G.; Góźdź, W.T. Formation and internal ordering of periodic microphases in colloidal models with competing interactions. Soft Matter 2021, 17, 4957. [Google Scholar] [CrossRef]
- Míguez, H.; Yang, S.M.; Ozin, G.A. Optical properties of colloidal photonic crystals confined in rectangular microchannels. Langmuir 2003, 19, 3479–3485. [Google Scholar] [CrossRef]
- Pękalski, J.; Rzadkowski, W.; Panagiotopoulos, A.Z. Shear-induced ordering in systems with competing interactions: A machine learning study. J. Chem. Phys. 2020, 152, 204905. [Google Scholar] [CrossRef] [PubMed]
- Imperio, A.; Reatto, L. Microphase morphology in two-dimensional fluids under lateral confinement. Phys. Rev. E 2007, 76, 040402(R). [Google Scholar] [CrossRef]
- Alba-Simionesco, A.; Coasne, B.; Dosseh, G.; Dudziak, G.; Gubbins, K.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Effects of confinement on freezing and melting. J. Phys. Condens. Matter 2006, 18, R15. [Google Scholar] [CrossRef]
- Nygård, K. Colloidal diffusion in confined geometries. Phys. Chem. Chem. Phys. 2017, 19, 23632. [Google Scholar] [CrossRef]
- Zangi, R. Water confined to a slab geometry: A review of recent computer simulation studies. J. Phys. Condens. Matter 2004, 16, S5371. [Google Scholar] [CrossRef]
- Martí, J.; Calero, C.; Franzese, G. Structure and dynamics of water at carbon-based interfaces. Entropy 2017, 19, 135. [Google Scholar] [CrossRef] [Green Version]
- Serna, H.; Noya, E.G.; Góźdź, W.T. Assembly of Helical Structures in Systems with Competing Interactions under Cylindrical Confinement. Langmuir 2018, 35, 702–708. [Google Scholar] [CrossRef]
- Serna, H.; Noya, E.G.; Góźdź, W.T. The influence of confinement on the structure of colloidal systems with competing interactions. Soft Matter 2020, 16, 718–727. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serna, H.; Noya, E.G.; Góźdź, W.T. Confinement of Colloids with Competing Interactions in Ordered Porous Materials. J. Phys. Chem. B 2020, 124, 10567–10577. [Google Scholar] [CrossRef] [PubMed]
- Pękalski, J.; Almarza, N.G.; Ciach, A. Effects of rigid or adaptive confinement on colloidal self-assembly. Fixed vs. fluctuating number of confined particles. J. Chem. Phys. 2015, 142, 204904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Almarza, N.G.; Pękalski, J.; Ciach, A. Effects of confinement on pattern formation in two dimensional systems with competing interactions. Soft Matter 2016, 12, 7551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwanzer, D.F.; Coslovich, D.; Kahl, G. Two-dimensional systems with competing interactions: Dynamic properties of single particles and of clusters. J. Phys. Condens. Matter 2016, 28, 414015. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18. [Google Scholar] [CrossRef]
- Bores, C.; Almarza, N.G.; Lomba, E.; Kahl, G. Inclusions of a two dimensional fluid with competing interactions in a disordered, porous matrix. J. Ournal. Phys. Condens. Matter 2015, 27, 194127. [Google Scholar] [CrossRef] [Green Version]
- Qiao, C.; Zhao, S.; Liu, H.; Dong, W. Connect the Thermodynamics of Bulk and Confined Fluids: Confinement-Adsorption Scaling. Langmuir 2019, 35, 3840–3847. [Google Scholar] [CrossRef] [PubMed]
- Lechner, W.; Dellago, C. Accurate determination of crystal structures based on averaged local bond order parameters. J. Chem. Phys. 2008, 129, 114707. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Li, B.; Jin, Q.; Ding, D.; Shi, A.C. Confined self-assembly of cylinder-forming diblock copolymers: Effects of confining geometries. Soft Matter 2011, 7, 10227–10240. [Google Scholar] [CrossRef]
- Mittal, J.; Truskett, T.M.; Errington, J.R.; Hummer, G. Layering and position-dependent diffusive dynamics of confined fluids. Phys. Rev. Lett. 2008, 100, 145901. [Google Scholar] [CrossRef] [Green Version]
- Litniewski, L.; Ciach, A. Effect of aggregation on adsorption phenomena. J. Chem. Phys. 2019, 150, 234702. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, W.; Zheng, X.; King, A.; Singh, A.; Rafailovich, M.; Sokolov, J.; Dai, K.; Kramer, E. Surface-induced ordering in asymmetric block copolymers. Macromolecules 1994, 27, 4000–4010. [Google Scholar] [CrossRef]



| Phase | ||||
| Cluster-Crystal | ||||
| Cylindrical | ||||
| Lamellar |
| Bulk | |||||
|---|---|---|---|---|---|
| Cluster-crystal | |||||
| Hexagonal | |||||
| Lamellar |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serna, H.; Góźdź, W.T.; Noya, E.G. Structural and Dynamical Behaviour of Colloids with Competing Interactions Confined in Slit Pores. Int. J. Mol. Sci. 2021, 22, 11050. https://doi.org/10.3390/ijms222011050
Serna H, Góźdź WT, Noya EG. Structural and Dynamical Behaviour of Colloids with Competing Interactions Confined in Slit Pores. International Journal of Molecular Sciences. 2021; 22(20):11050. https://doi.org/10.3390/ijms222011050
Chicago/Turabian StyleSerna, Horacio, Wojciech T. Góźdź, and Eva G. Noya. 2021. "Structural and Dynamical Behaviour of Colloids with Competing Interactions Confined in Slit Pores" International Journal of Molecular Sciences 22, no. 20: 11050. https://doi.org/10.3390/ijms222011050
APA StyleSerna, H., Góźdź, W. T., & Noya, E. G. (2021). Structural and Dynamical Behaviour of Colloids with Competing Interactions Confined in Slit Pores. International Journal of Molecular Sciences, 22(20), 11050. https://doi.org/10.3390/ijms222011050






