Structure and Thermal Stability of wtRop and RM6 Proteins through All-Atom Molecular Dynamics Simulations and Experiments
Abstract
1. Introduction
2. Results
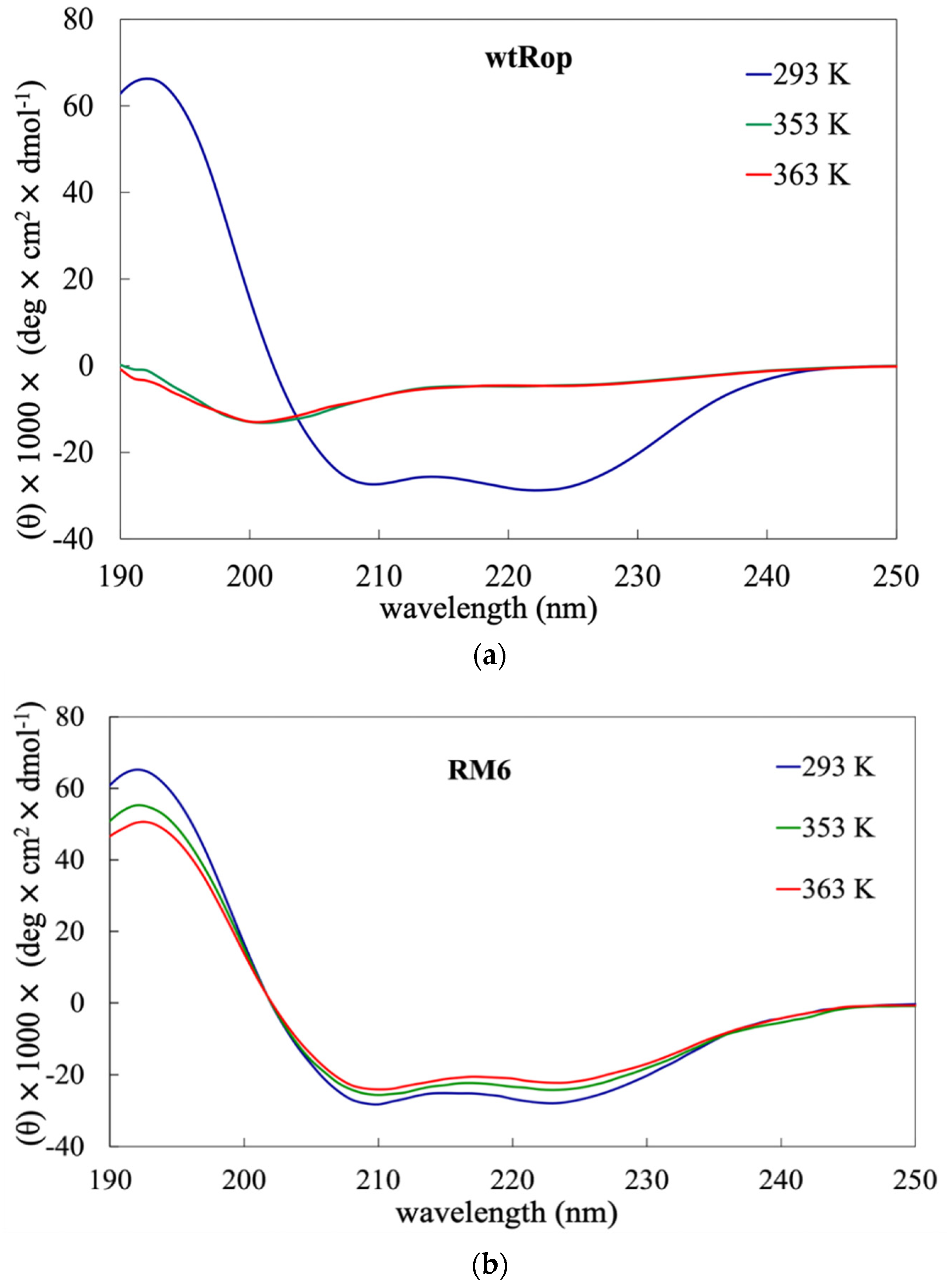
2.1. Experimental Probing the Thermal Stability of wtRop and RM6
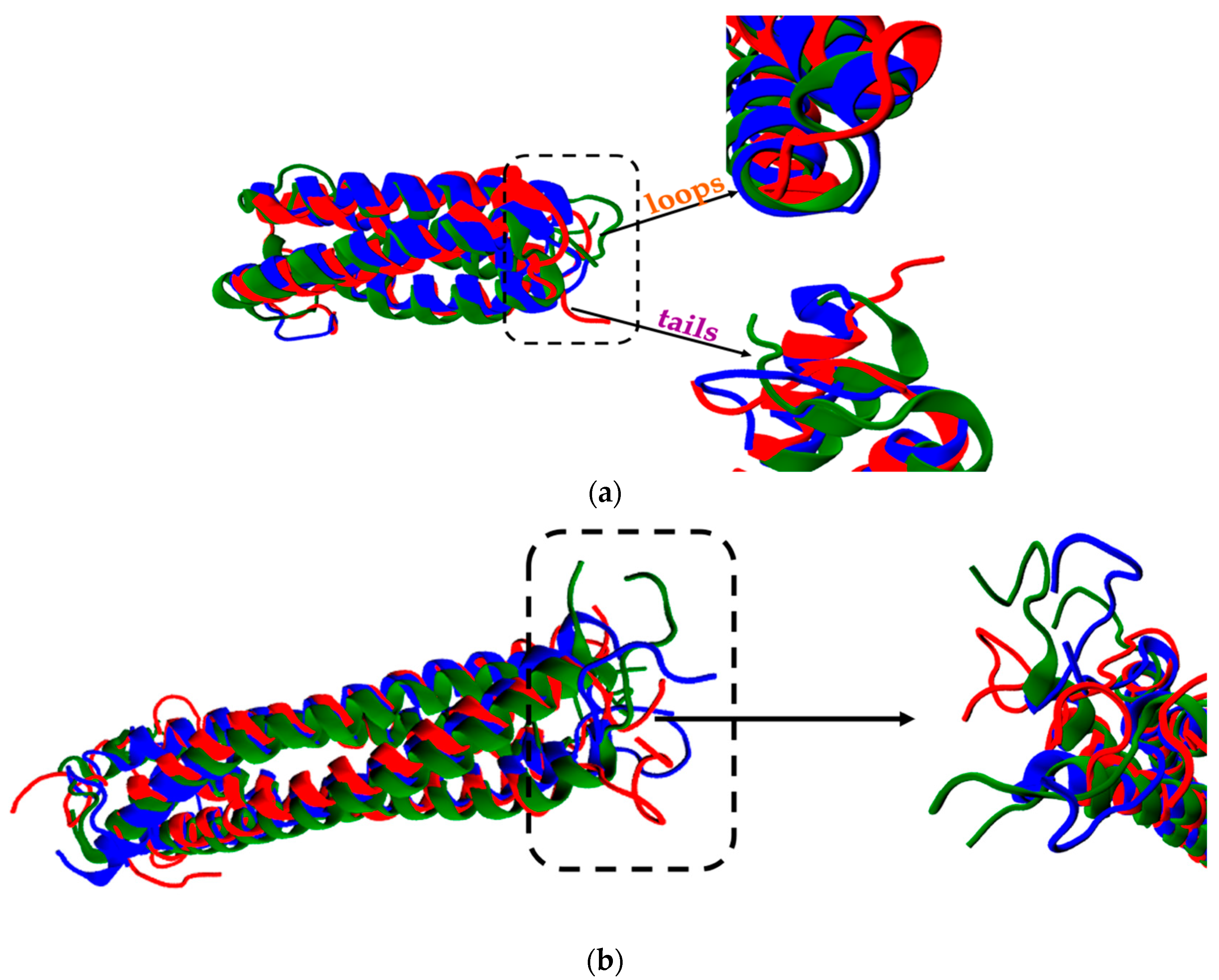
2.2. Structure Stability of wtRop and RM6 Proteins
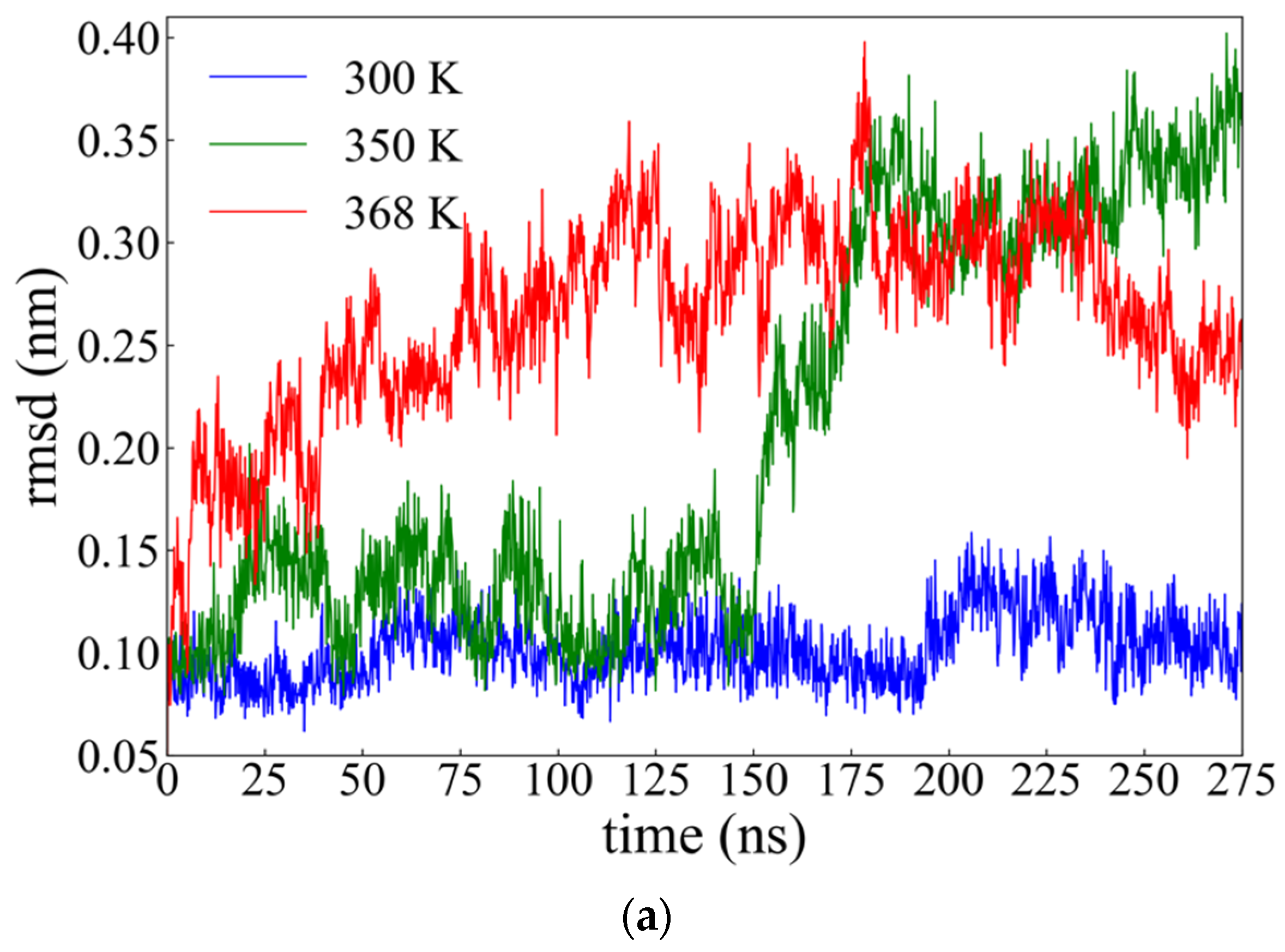
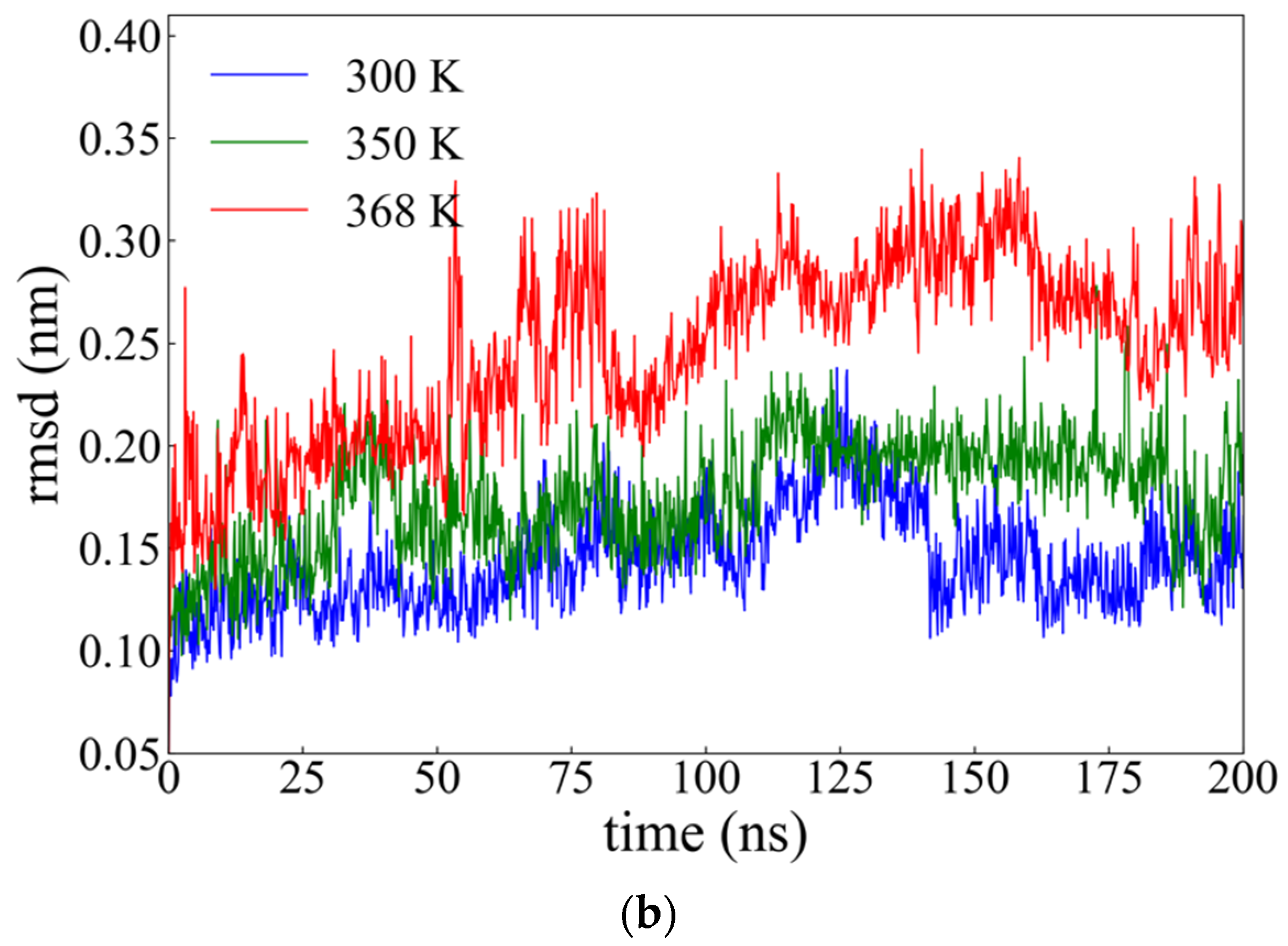
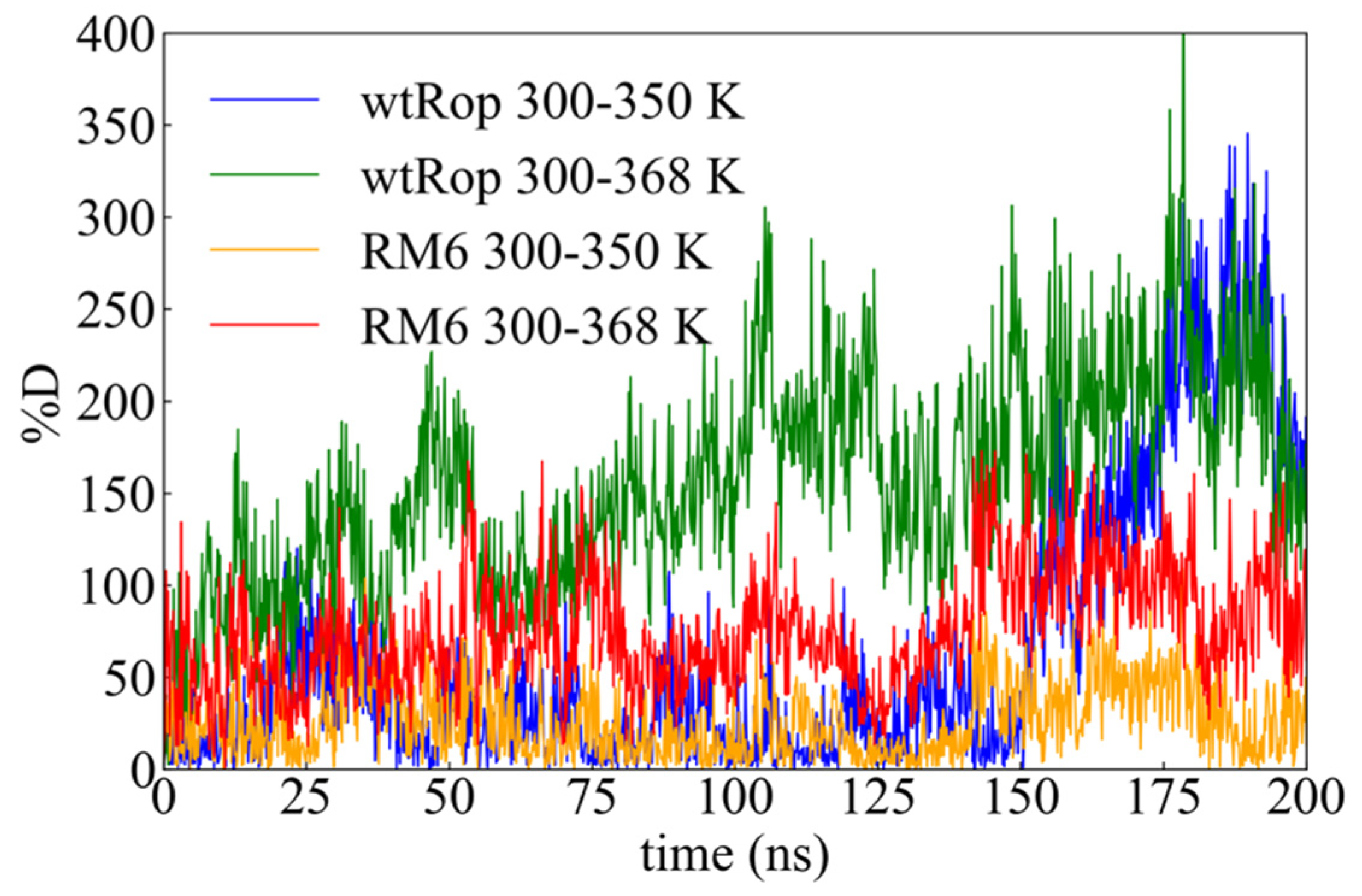
2.2.1. Root Mean Square Deviation (rmsd)
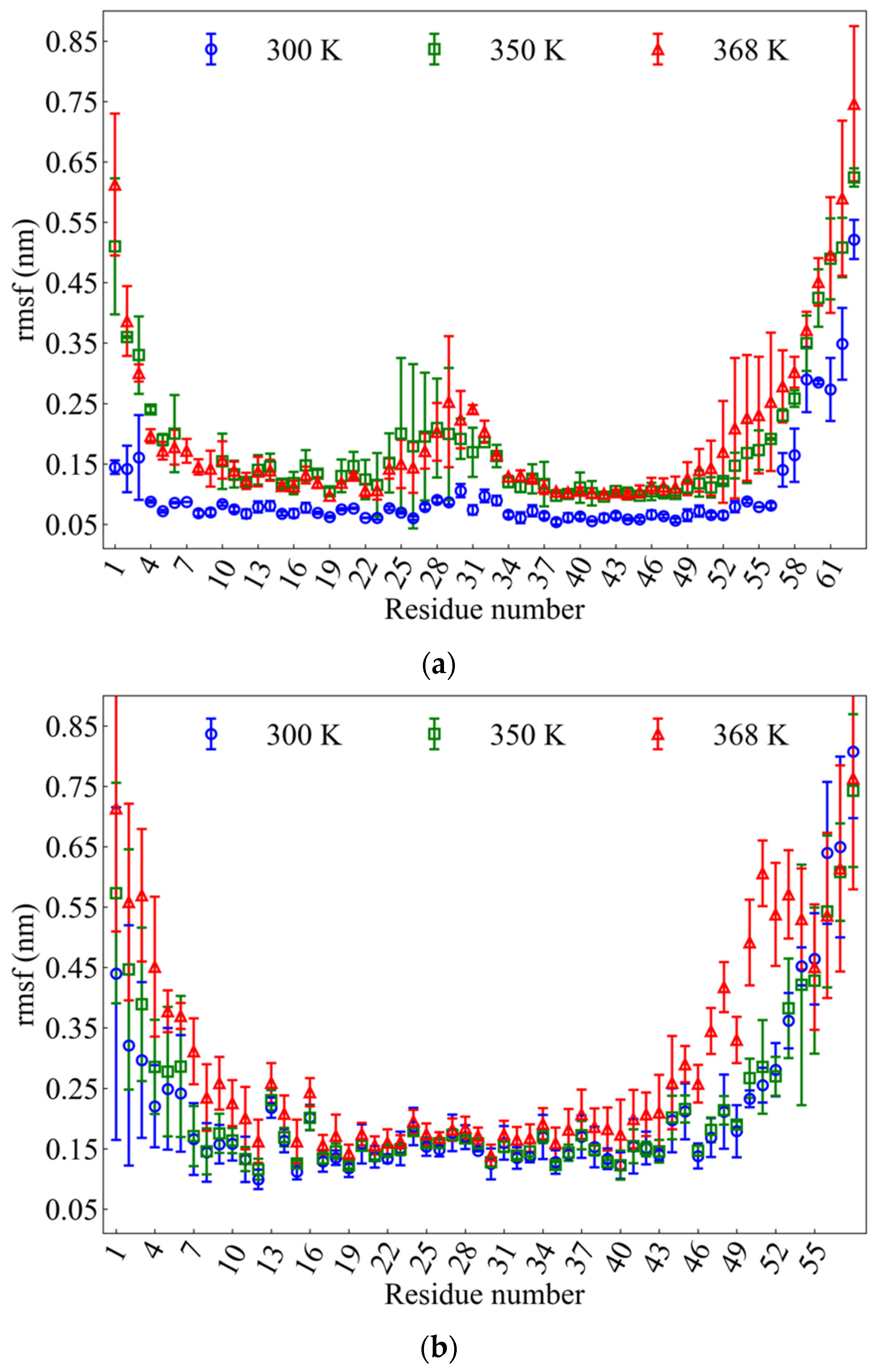
2.2.2. Root Mean Square Fluctuation (rmsf)
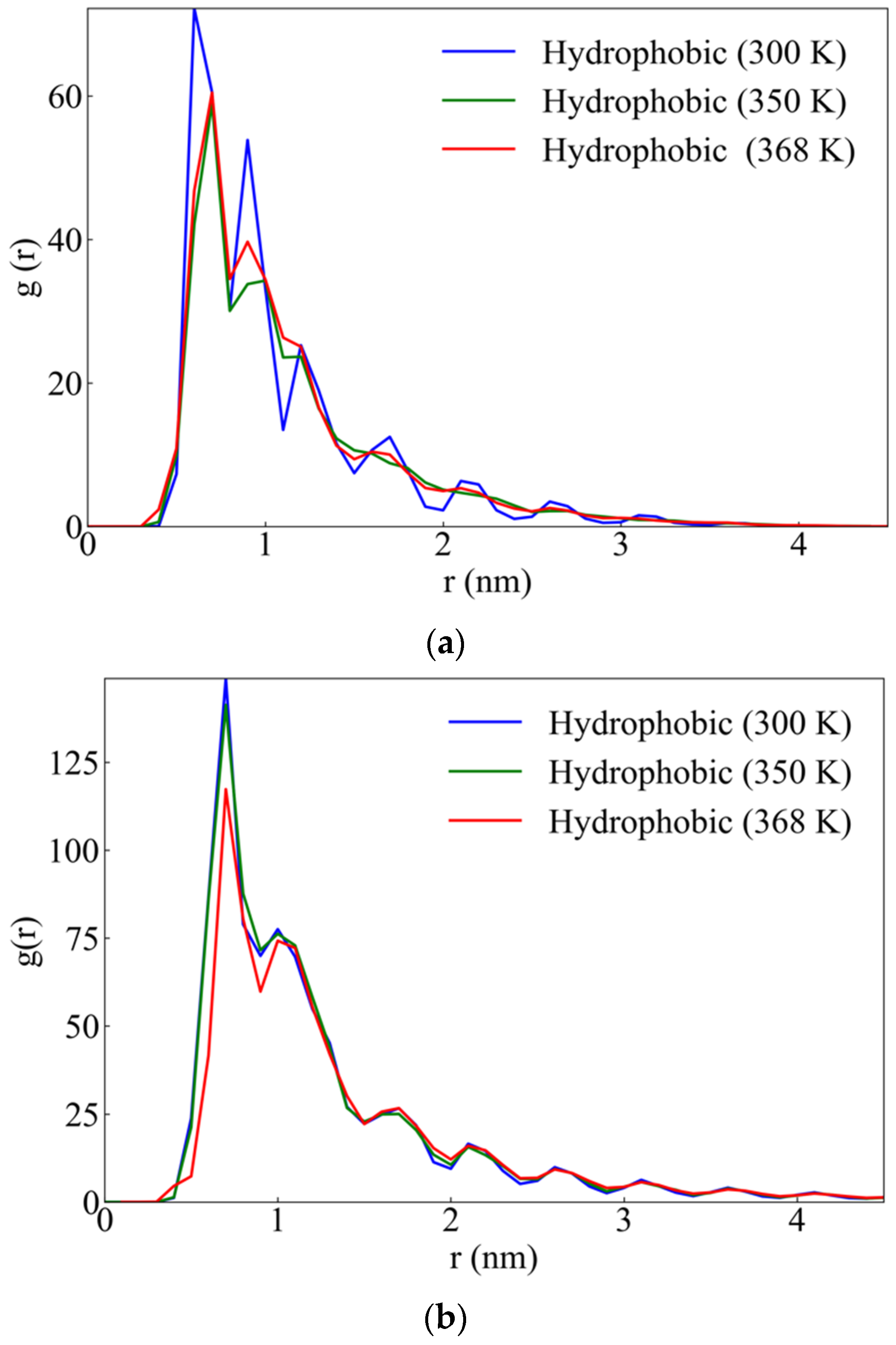
2.2.3. Hydrogen Bonds
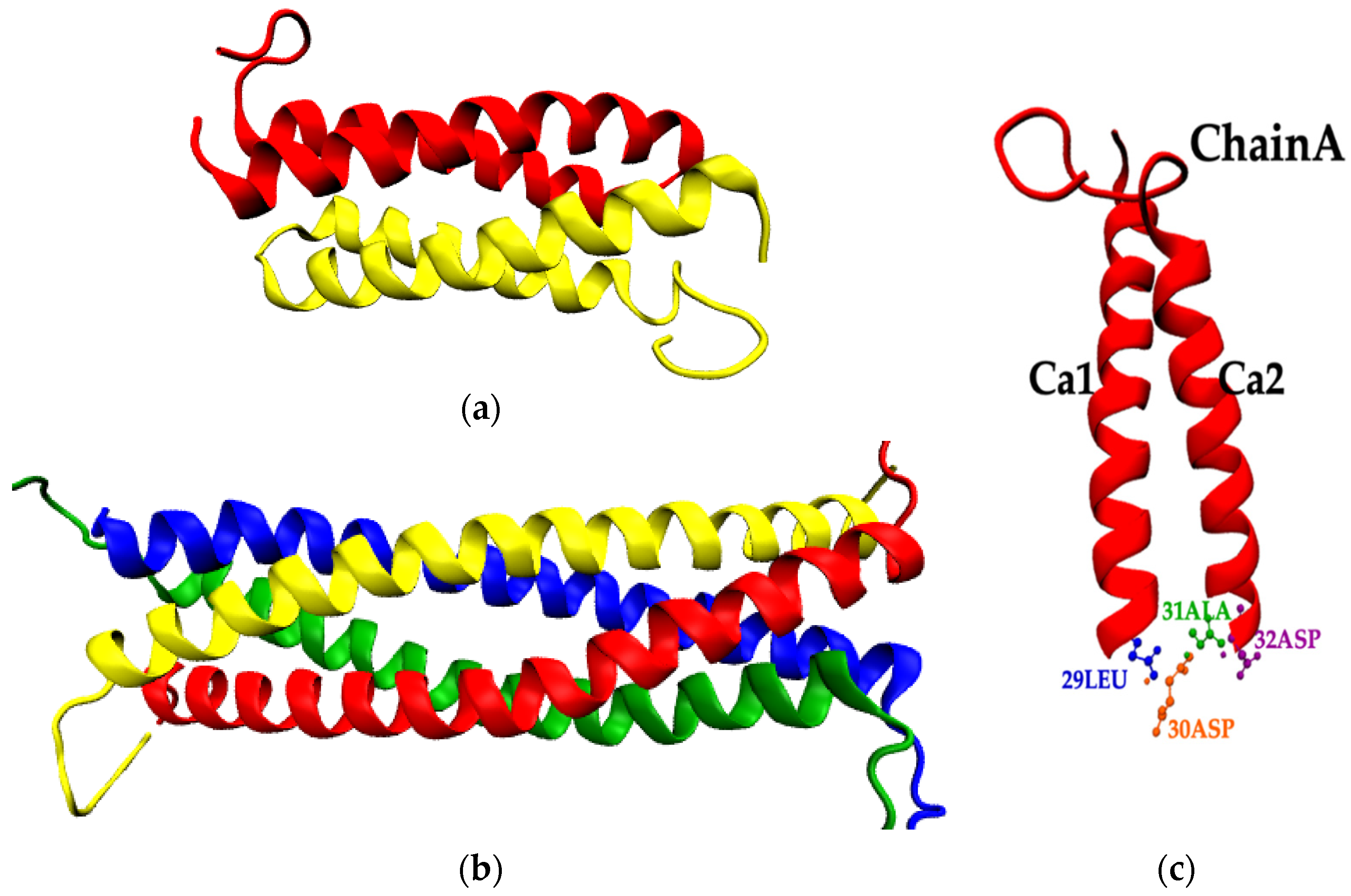
Alpha Helices
Hydrogen Bonds of Loop Region
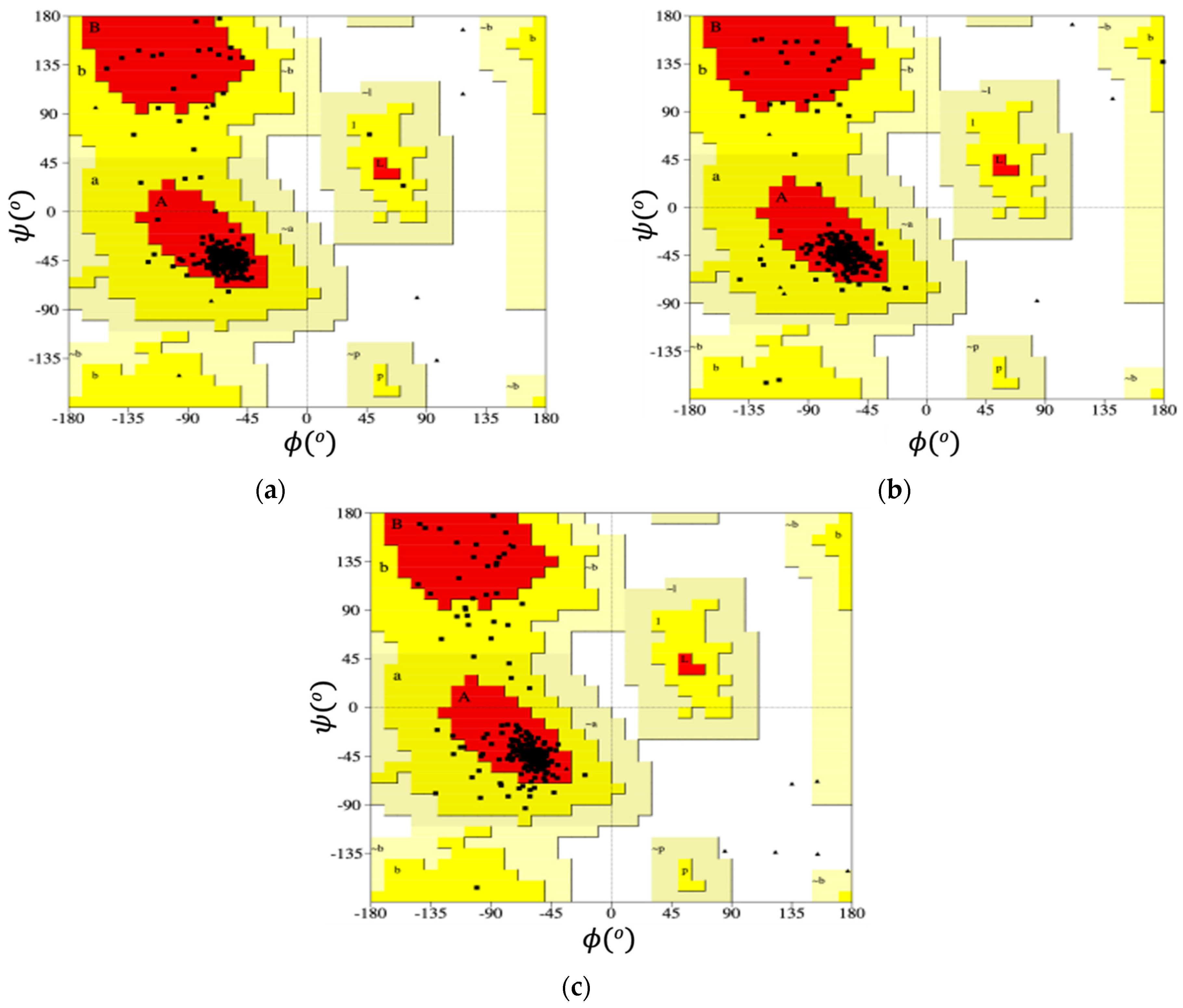
2.2.4. Ramachandran Plot
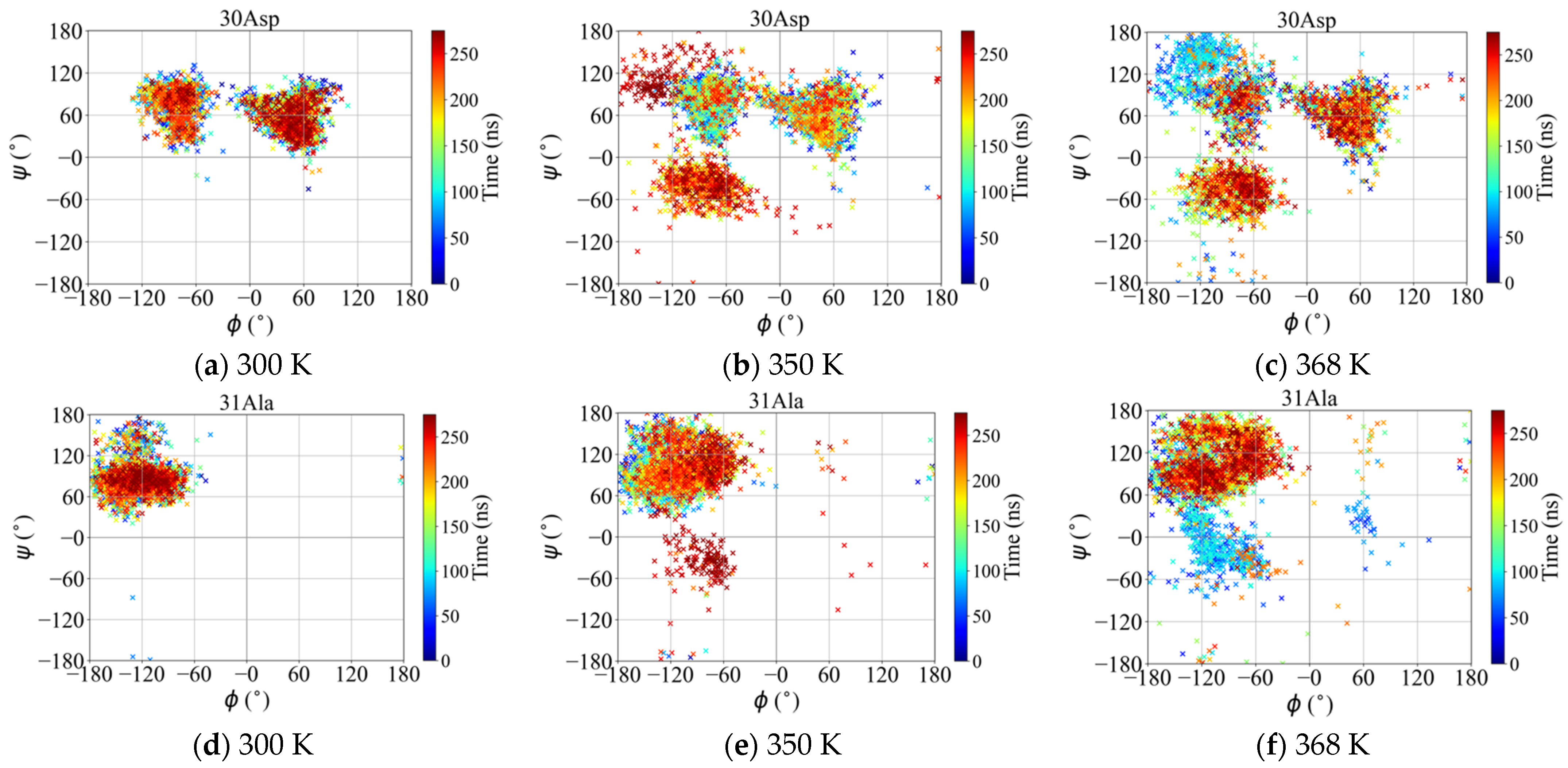
Map of Dihedral Angles of the Loop Residues
2.2.5. Local Conformation Analysis of Alpha-Helices: Helix Properties
3. Discussion
4. Systems and Methods
4.1. Experiments
4.2. Simulations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MD | Molecular dynamics |
| CD | Circular dichroism spectroscopy |
| rmsd | Root mean square deviation |
| rmsf | Root mean square fluctuation |
| PDB | Protein data bank |
| NMR | Nuclear magnetic resonance |
References
- Rajagopal, K.; Schneider, J.P. Self-Assembling Peptides and Proteins for Nanotechnological Applications. Curr. Opin. Struct. Biol. 2004, 14, 480–486. [Google Scholar] [CrossRef]
- Tsai, C.-J.; Zheng, J.; Zanuy, D.; Haspel, N.; Wolfson, H.; Alemán, C.; Nussinov, R. Principles of Nanostructure Design with Protein Building Blocks. Proteins 2007, 68, 1–12. [Google Scholar] [CrossRef]
- Pikkemaat, M.G.; Linssen, A.B.M.; Berendsen, H.J.C.; Janssen, D.B. Molecular Dynamics Simulations as a Tool for Improving Protein Stability. Protein Eng. Des. Sel. 2002, 15, 185–192. [Google Scholar] [CrossRef]
- Boyle, A.L.; Woolfson, D.N. De Novo Designed Peptides for Biological Applications. Chem. Soc. Rev. 2011, 40, 4295. [Google Scholar] [CrossRef] [PubMed]
- Maude, S.; Tai, L.R.; Davies, R.P.W.; Liu, B.; Harris, S.A.; Kocienski, P.J.; Aggeli, A. Peptide Synthesis and Self-Assembly. In Peptide-Based Materials; Deming, T., Ed.; Topics in Current Chemistry; Springer: Berlin/Heidelberg, Germany, 2011; Volume 310, pp. 27–69. [Google Scholar] [CrossRef]
- Khoury, G.A.; Smadbeck, J.; Kieslich, C.A.; Floudas, C.A. Protein Folding and de Novo Protein Design for Biotechnological Applications. Trends Biotechnol. 2014, 32, 99–109. [Google Scholar] [CrossRef]
- Argos, P.; Rossmann, M.G.; Grau, U.M.; Zuber, H.; Frank, G.; Tratschin, J.D. Thermal Stability and Protein Structure. Biochemistry 1979, 18, 5698–5703. [Google Scholar] [CrossRef] [PubMed]
- Nojima, H.; Hon-nami, K.; Oshima, T.; Noda, H. Reversible Thermal Unfolding of Thermostable Cytochrome C-552. J. Mol. Biol. 1978, 122, 33–42. [Google Scholar] [CrossRef]
- Nojima, H.; Ikai, A.; Oshima, T.; Noda, H. Reversible Thermal Unfolding of Thermostable Phosphoglycerate Kinase. Thermostability Associated with Mean Zero Enthalpy Change. J. Mol. Biol. 1977, 116, 429–442. [Google Scholar] [CrossRef]
- Predki, P.F.; Agrawal, V.; Brünger, A.T.; Regan, L. Amino-Acid Substitutions in a Surface Turn Modulate Protein Stability. Nat. Struct. Mol. Biol. 1996, 3, 54–58. [Google Scholar] [CrossRef]
- Pucci, F.; Bourgeas, R.; Rooman, M. High-Quality Thermodynamic Data on the Stability Changes of Proteins Upon Single-Site Mutations. J. Phys. Chem. Ref. Data 2016, 45, 023104. [Google Scholar] [CrossRef]
- Miotto, M.; Olimpieri, P.P.; Di Rienzo, L.; Ambrosetti, F.; Corsi, P.; Lepore, R.; Tartaglia, G.G.; Milanetti, E. Insights on Protein Thermal Stability: A Graph Representation of Molecular Interactions. Bioinformatics 2019, 35, 2569–2577. [Google Scholar] [CrossRef]
- Arnittali, M.; Rissanou, A.N.; Harmandaris, V. Structure of Biomolecules Through Molecular Dynamics Simulations. Procedia Comput. Sci. 2019, 156, 69–78. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Xu, W.; Li, M. Molecular Dynamics Simulation of Barnase: Contribution of Noncovalent Intramolecular Interaction to Thermostability. Math. Probl. Eng. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved Protein Structure Prediction Using Potentials from Deep Learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y. Pathways to a Protein Folding Intermediate Observed in a 1-Microsecond Simulation in Aqueous Solution. Science 1998, 282, 740–744. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Guo, X.; Cong, Y.; Feng, G.; Li, Y.; Zhang, J.Z.H. Accelerated Molecular Dynamics Simulation for Helical Proteins Folding in Explicit Water. Front. Chem. 2019, 7, 540. [Google Scholar] [CrossRef]
- Glykos, N.M.; Kokkinidis, M. Structural Polymorphism of a Marginally Stable 4-Alpha-Helical Bundle. Images of a Trapped Molten Globule? Proteins 2004, 56, 420–425. [Google Scholar] [CrossRef] [PubMed]
- Glykos, N.M.; Papanikolau, Y.; Vlassi, M.; Kotsifaki, D.; Cesareni, G.; Kokkinidis, M. Loopless Rop: Structure and Dynamics of an Engineered Homotetrameric Variant of the Repressor of Primer Protein. Biochemistry 2006, 45, 10905–10919. [Google Scholar] [CrossRef]
- Karplus, M.; McCammon, J.A. Molecular Dynamics Simulations of Biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Manjunath, K.; Sekar, K. Molecular Dynamics Perspective on the Protein Thermal Stability: A Case Study Using SAICAR Synthetase. J. Chem. Inf. Model. 2013, 53, 2448–2461. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L. Automatic Identification of Mobile and Rigid Substructures in Molecular Dynamics Simulations and Fractional Structural Fluctuation Analysis. PLoS ONE 2015, 10, e0119264. [Google Scholar] [CrossRef] [PubMed]
- Rissanou, A.N.; Georgilis, E.; Kasotakis, E.; Mitraki, A.; Harmandaris, V. Effect of Solvent on the Self-Assembly of Dialanine and Diphenylalanine Peptides. J. Phys. Chem. B 2013, 117, 3962–3975. [Google Scholar] [CrossRef] [PubMed]
- Tavernelli, I.; Cotesta, S.; Di Iorio, E.E. Protein Dynamics, Thermal Stability, and Free-Energy Landscapes: A Molecular Dynamics Investigation. Biophys. J. 2003, 85, 2641–2649. [Google Scholar] [CrossRef]
- Argos, P.; Rossmann, M.G.; Johnson, J.E. A Four-Helical Super-Secondary Structure. Biochem. Biophys. Res. Commun. 1977, 75, 83–86. [Google Scholar] [CrossRef]
- Cohen, C.; Parry, D.A.D. α-Helical Coiled Coils and Bundles: How to Design an α-Helical Protein. Proteins 1990, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Paliakasis, C.D.; Kokkinidis, M. Relationships between Sequence and Structure for the Four-α-Helix Bundle Tertiary Motif in Proteins. Protein Eng. Des. Sel. 1992, 5, 739–748. [Google Scholar] [CrossRef]
- Hill, R.B.; Raleigh, D.P.; Lombardi, A.; DeGrado, W.F. De Novo Design of Helical Bundles as Models for Understanding Protein Folding and Function. Acc. Chem. Res. 2000, 33, 745–754. [Google Scholar] [CrossRef]
- Betz, S.F.; Liebman, P.A.; DeGrado, W.F. De Novo Design of Native Proteins: Characterization of Proteins Intended to Fold into Antiparallel, Rop-like, Four-Helix Bundles. Biochemistry 1997, 36, 2450–2458. [Google Scholar] [CrossRef]
- Castagnoli, L.; Scarpa, M.; Kokkinidis, M.; Banner, D.W.; Tsernoglou, D.; Cesareni, G. Genetic and Structural Analysis of the ColE1 Rop (Rom) Protein. EMBO J. 1989, 8, 621–629. [Google Scholar] [CrossRef]
- Banner, D.W.; Kokkinidis, M.; Tsernoglou, D. Structure of the ColE1 Rop Protein at 1.7 Å Resolution. J. Mol. Biol. 1987, 19, 657–675. [Google Scholar] [CrossRef]
- Eberle, W.; Pastore, A.; Sander, C.; Rösch, P. The Structure of ColE1 Rop in Solution. J. Biomol. NMR 1991, 1, 71–82. [Google Scholar] [CrossRef] [PubMed]
- Munson, M.; Regan, L.; O’Brien, R.; Sturtevant, J.M. Redesigning the Hydrophobic Core of a Four-Helix-Bundle Protein. Protein Sci. 1994, 3, 2015–2022. [Google Scholar] [CrossRef] [PubMed]
- Vlassi, M.; Steif, C.; Weber, P.; Tsernoglou, D.; Wilson, K.S.; Hinz, H.-J.; Kokkinidis, M. Restored Heptad Pattern Continuity Does Not Alter the Folding of a Four-α-Helix Bundle. Nat. Struct. Mol. Biol. 1994, 1, 706–716. [Google Scholar] [CrossRef]
- Shukla, R.T.; Baliga, C.; Sasidhar, Y.U. The Role of Loop Closure Propensity in the Refolding of Rop Protein Probed by Molecular Dynamics Simulations. J. Mol. Graph. Model. 2013, 40, 10–21. [Google Scholar] [CrossRef] [PubMed]
- Lassalle, M.W.; Hinz, H.J.; Wenzel, H.; Vlassi, M.; Kokkinidis, M.; Cesareni, G. Dimer-to-Tetramer Transformation: Loop Excision Dramatically Alters Structure and Stability of the ROP Four Alpha-Helix Bundle Protein. J. Mol. Biol. 1998, 279, 987–1000. [Google Scholar] [CrossRef]
- Amprazi, M.; Kotsifaki, D.; Providaki, M.; Kapetaniou, E.G.; Fellas, G.; Kyriazidis, I.; Perez, J.; Kokkinidis, M. Structural Plasticity of 4-α-Helical Bundles Exemplified by the Puzzle-like Molecular Assembly of the Rop Protein. Proc. Natl. Acad. Sci. USA 2014, 111, 11049–11054. [Google Scholar] [CrossRef]
- Micsonai, A.; Wien, F.; Bulyáki, É.; Kun, J.; Moussong, É.; Lee, Y.-H.; Goto, Y.; Réfrégiers, M.; Kardos, J. BeStSel: A Web Server for Accurate Protein Secondary Structure Prediction and Fold Recognition from the Circular Dichroism Spectra. Nucleic Acids Res. 2018, 46, W315–W322. [Google Scholar] [CrossRef]
- Kabsch, W. A Solution for the Best Rotation to Relate Two Sets of Vectors. Acta Cryst. A 1976, 32, 922–923. [Google Scholar] [CrossRef]
- Kabsch, W. A Discussion of the Solution for the Best Rotation to Relate Two Sets of Vectors. Acta Cryst. A 1978, 34, 827–828. [Google Scholar] [CrossRef]
- Bolhuis, P.G. Sampling Kinetic Protein Folding Pathways Using All-Atom Models. In Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology Volume 1; Ferrario, M., Ciccotti, G., Binder, K., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2006; Volume 703, pp. 393–433. [Google Scholar] [CrossRef]
- Carugo, O. How Root-Mean-Square Distance (r.m.s.d.) Values Depend on the Resolution of Protein Structures That Are Compared. J. Appl. Cryst. 2003, 36, 125–128. [Google Scholar] [CrossRef]
- Amprazi, M. Production of Biomaterials Based on Specific Interactions of Protein Secondary Structures; Department of Biology, University of Crete: Crete, Greece, 2012. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Hubbard, R.E.; Kamran Haider, M. Hydrogen Bonds in Proteins: Role and Strength. In Encyclopedia of Life Sciences; John Wiley & Sons, Ltd.: Chichester, UK, 2010. [Google Scholar] [CrossRef]
- Kumar, R.; Schmidt, J.R.; Skinner, J.L. Hydrogen Bonding Definitions and Dynamics in Liquid Water. J. Chem. Phys. 2007, 126, 204107. [Google Scholar] [CrossRef] [PubMed]
- Kefala, A.; Amprazi, M.; Mylonas, E.; Kotsifaki, D.; Providaki, M.; Pozidis, C.; Fotiadou, M.; Kokkinidis, M. Probing Protein Folding with Sequence-Reversed α-Helical Bundles. Int. J. Mol. Sci. 2021, 22, 1955. [Google Scholar] [CrossRef]
- Kabsch, W.; Sander, C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Karplus, P.A. A Fresh Look at the Ramachandran Plot and the Occurrence of Standard Structures in Proteins. Biomol. Concepts 2010, 1, 271–283. [Google Scholar] [CrossRef] [PubMed]
- Janin, J.; Wodak, S.; Levitt, M.; Maigret, B. Conformation of Amino Acid Side-Chains in Proteins. J. Mol. Biol. 1978, 125, 357–386. [Google Scholar] [CrossRef]
- Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. Stereochemistry of Polypeptide Chain Configurations. J. Mol. Biol. 1963, 7, 95–99. [Google Scholar] [CrossRef]
- Laskowski, R.A.; Rullmannn, J.A.; MacArthur, M.W.; Kaptein, R.; Thornton, J.M. AQUA and PROCHECK-NMR: Programs for Checking the Quality of Protein Structures Solved by NMR. J. Biomol. NMR 1996, 8, 477–486. [Google Scholar] [CrossRef]
- Laskowski, R.A.; MacArthur, M.W.; Moss, D.S.; Thornton, J.M. PROCHECK: A Program to Check the Stereochemical Quality of Protein Structures. J. Appl. Cryst. 1993, 26, 283–291. [Google Scholar] [CrossRef]
- Nordlund, T.M.; Hoffmann, P.M. Quantitative Understanding of Biosystems: An Introduction to Biophysics, 2nd ed.; Foundations of Biochemistry and Biophysics; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Hauser, K.; He, Y.; Garcia-Diaz, M.; Simmerling, C.; Coutsias, E. Characterization of Biomolecular Helices and Their Complementarity Using Geometric Analysis. J. Chem. Inf. Model. 2017, 57, 864–874. [Google Scholar] [CrossRef]
- Krissinel, E.; Henrick, K. Inference of Macromolecular Assemblies from Crystalline State. J. Mol. Biol. 2007, 372, 774–797. [Google Scholar] [CrossRef]
- Schrodinger, L.L. The PyMOL; Molecular Graphics System: San Carlos, CA, USA, 2015. [Google Scholar]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A Message-Passing Parallel Molecular Dynamics Implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A Biomolecular Force Field Based on the Free Enthalpy of Hydration and Solvation: The GROMOS Force-Field Parameter Sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]

| System | Np | Ns | N | Nions | T (K) | L (nm) |
|---|---|---|---|---|---|---|
| NSR1 | 1 | 24,189 | 73,861 | 14 | 300 | 9.0 |
| NSR2 | 1 | 24,189 | 73,861 | 14 | 350 | 9.0 |
| NSR3 | 1 | 24,189 | 73,861 | 14 | 368 | 9.0 |
| MRM1 | 1 | 97,833 | 295,891 | 16 | 300 | 15.0 |
| MRM2 | 1 | 97,833 | 295,891 | 16 | 350 | 15.0 |
| MRM3 | 1 | 97,833 | 295,891 | 16 | 368 | 15.0 |
| Systems | <P-P> | <P-W> | <W-W>/W |
|---|---|---|---|
| NSR1 | 125.2 ± 1.9 | 303.3 ± 2.9 | 3.6 |
| NSR2 | 113.4 ± 1.7 | 293.8 ± 5.8 | 3.4 |
| NSR3 | 113.1 ± 2.1 | 283.2 ± 2.9 | 3.3 |
| MRM1 | 225.8 ± 3.5 | 517.4 ± 5.6 | 3.6 |
| MRM2 | 221.1 ± 0.8 | 481.5 ± 3.2 | 3.4 |
| MRM3 | 207.8 ± 2.4 | 482.1 ± 6.2 | 3.3 |
| Systems | HBα-helix (Ca1/Ca) | HBα-helix (Ca2/Cb) | HBα-helix (Cb1/Cc) | HBα-helix (Cb2/Cd) |
|---|---|---|---|---|
| NSR1 | 17.9 ± 0.13 | 15.9 ± 0.2 | 19.9 ± 0.1 | 19.7 ± 0.1 |
| NSR2 | 15.8 ± 0.4 | 13.0 ± 0.2 | 14.7 ± 2.0 | 19.0 ± 0.1 |
| NSR3 | 16.5 ± 0.9 | 15.2 ± 0.2 | 16.8 ± 0.3 | 14.2 ± 0.7 |
| MRM1 | 37.0 ± 0.6 | 28.6 ± 0.4 | 34.9 ± 0.6 | 40.1 ± 0.7 |
| MRM2 | 34.3 ± 1.6 | 36.7 ± 0.5 | 34.9 ± 0.4 | 37.7 ± 0.5 |
| MRM3 | 29.8 ± 1.5 | 30.8 ± 1.5 | 33.3 ± 0.4 | 29.5 ± 0.1 |
| <HBs> | NSR1 | NSR2 | NSR3 |
|---|---|---|---|
| 29Leu-Ca1 | 0.96 ± 0.01 | 0.9 ± 0.05 | 0.05 ± 0.04 |
| 29Leu-Ca2 | 0 | 0 | 0 |
| 29Leu-Cb1 | 0.97 ± 0.01 | 0.11 ± 0.02 | 0.9 ± 0.01 |
| 29Leu-Cb2 | 0 | 0 | 0 |
| 30Asp-Ca1 | 0.32 ± 0.11 | 0.5 ± 0.1 | 0.06 ± 0.04 |
| 30Asp-Ca2 | 0 | 0 | 0.3 ± 0.4 |
| 30Asp-Cb1 | 0.38 ± 0.2 | 0.05 ± 0.04 | 0.3 ± 0.35 |
| 30Asp-Cb2 | 0 | 0.01 ± 0.2 | 0 |
| 31Ala-Ca1 | 0.47 ± 0.17 | 0.55 ± 0.14 | 0 |
| 31Ala-Ca2 | 0.88 ± 0.07 | 0.72 ± 0.2 | 0.87 ± 0.13 |
| 31Ala-Cb1 | 0.47 ± 0.23 | 0 | 0.6 ± 0.03 |
| 31Ala-Cb2 | 0.92 ± 0.03 | 0.94 ± 0.03 | 0.77 ± 0.14 |
| 32Asp-Ca1 | 0 | 0 | 0 |
| 32Asp-Ca2 | 1.6 ± 0.04 | 1.51 ± 0.14 | 1.03 ± 0.14 |
| 32Asp-Cb1 | 0 | 0 | 0 |
| 32Asp-Cb2 | 1.54 ± 0.1 | 0.2 ± 0.1 | 1.4 ± 0.02 |
| Systems | d (nm) | L (nm) | r (nm) | θ (°) |
|---|---|---|---|---|
| NSR1 | 0.150 ± 0.005 | 3.46 ± 0.42 | 0.24 ± 0.01 | 99.09 ± 1.22 |
| NSR2 | 0.153 ± 0.004 | 3.57 ± 0.53 | 0.26 ± 0.02 | 90.46 ± 8.64 |
| NSR3 | 0.155 ± 0.005 | 3.63 ± 0.55 | 0.26 ± 0.02 | 90.01 ± 5.79 |
| MRM1 | 0.146 ± 0.001 | 6.62 ± 0.21 | 0.33 ± 0.01 | 76.67 ± 5.92 |
| MRM2 | 0.146 ± 0.001 | 6.64 ± 0.21 | 0.33 ± 0.01 | 78.16 ± 3.47 |
| MRM3 | 0.150 ± 0.004 | 6.79 ± 0.21 | 0.33 ± 0.04 | 82.80 ± 4.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnittali, M.; Rissanou, A.N.; Amprazi, M.; Kokkinidis, M.; Harmandaris, V. Structure and Thermal Stability of wtRop and RM6 Proteins through All-Atom Molecular Dynamics Simulations and Experiments. Int. J. Mol. Sci. 2021, 22, 5931. https://doi.org/10.3390/ijms22115931
Arnittali M, Rissanou AN, Amprazi M, Kokkinidis M, Harmandaris V. Structure and Thermal Stability of wtRop and RM6 Proteins through All-Atom Molecular Dynamics Simulations and Experiments. International Journal of Molecular Sciences. 2021; 22(11):5931. https://doi.org/10.3390/ijms22115931
Chicago/Turabian StyleArnittali, Maria, Anastassia N. Rissanou, Maria Amprazi, Michael Kokkinidis, and Vagelis Harmandaris. 2021. "Structure and Thermal Stability of wtRop and RM6 Proteins through All-Atom Molecular Dynamics Simulations and Experiments" International Journal of Molecular Sciences 22, no. 11: 5931. https://doi.org/10.3390/ijms22115931
APA StyleArnittali, M., Rissanou, A. N., Amprazi, M., Kokkinidis, M., & Harmandaris, V. (2021). Structure and Thermal Stability of wtRop and RM6 Proteins through All-Atom Molecular Dynamics Simulations and Experiments. International Journal of Molecular Sciences, 22(11), 5931. https://doi.org/10.3390/ijms22115931









