A Stochastic Petri Net-Based Model of the Involvement of Interleukin 18 in Atherosclerosis
Abstract
1. Introduction
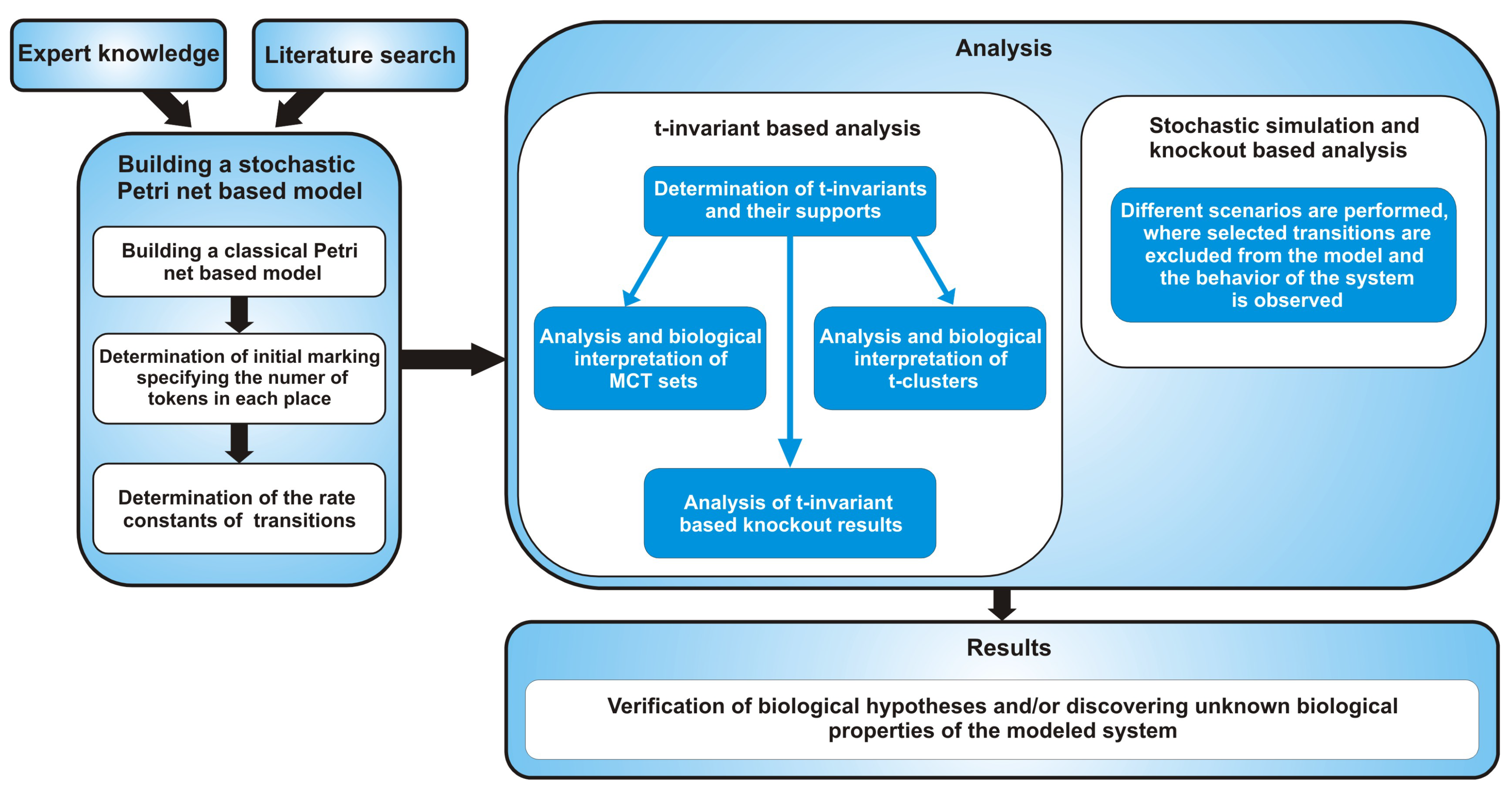
2. Methods
2.1. Petri Nets and Stochastic Petri Nets
2.1.1. t-Invariants
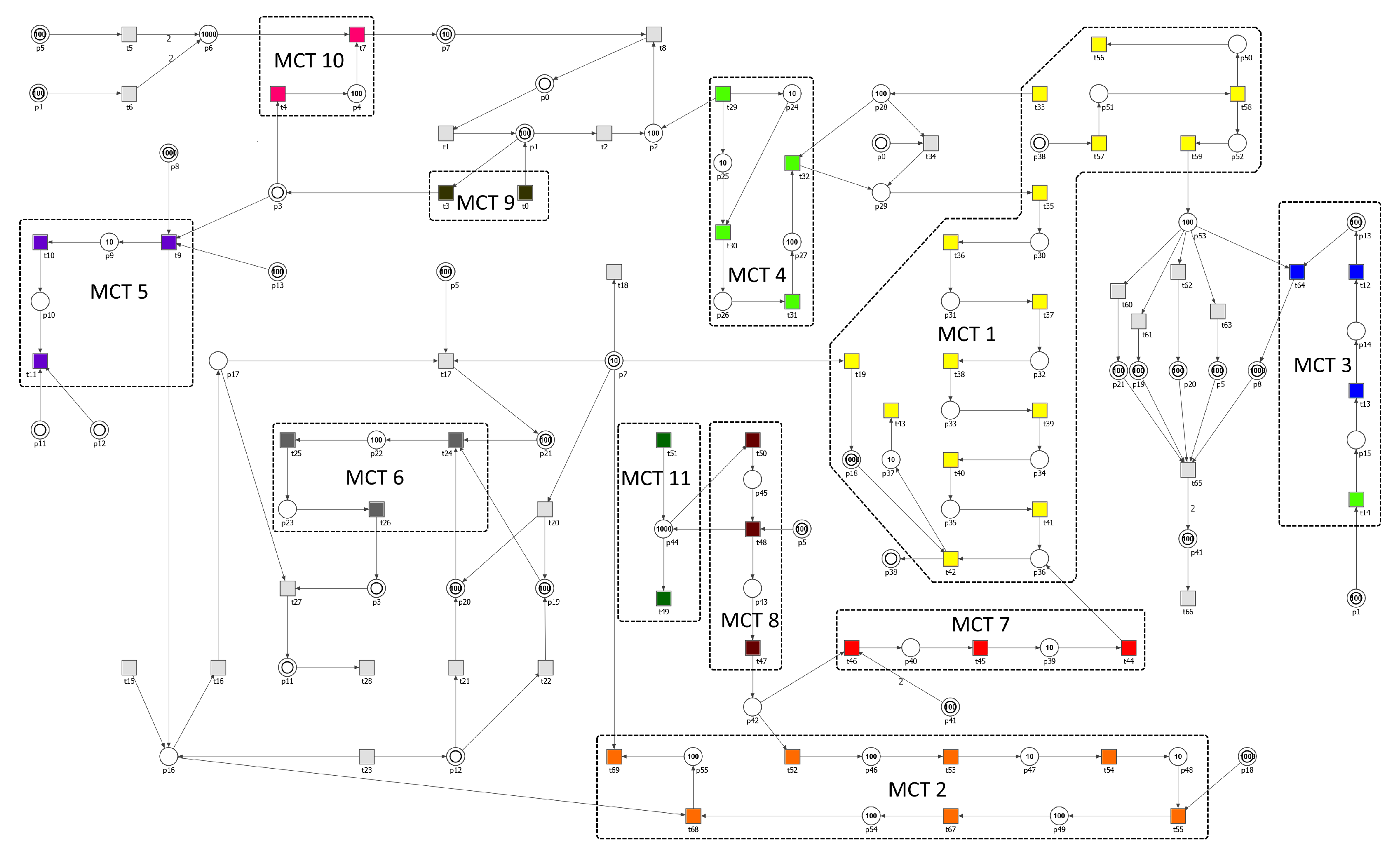
2.1.2. t-Clusters and MCT Sets
2.1.3. Knockout Analysis
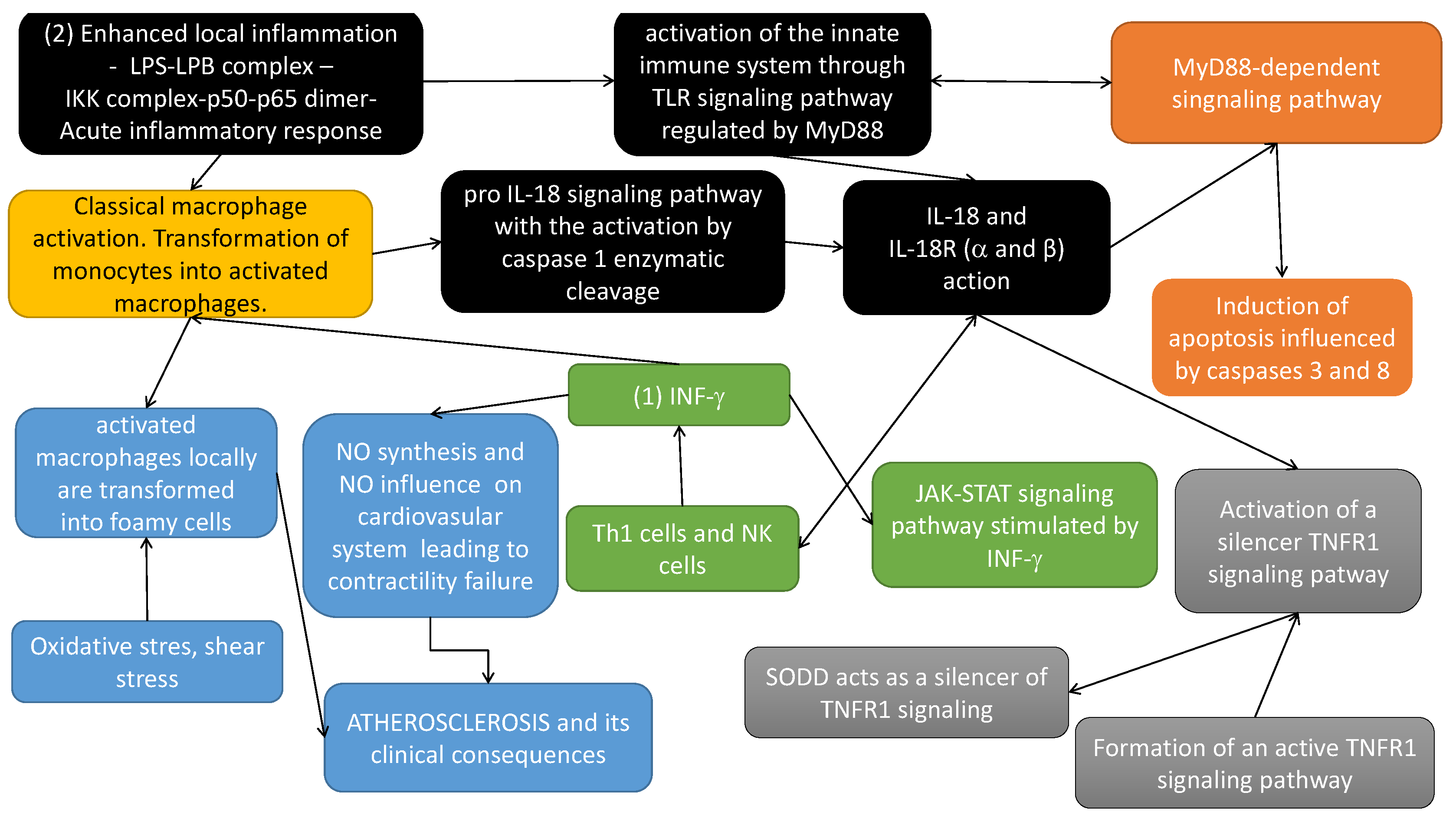
2.2. The Involvement of Interleukin 18 in Atherosclerosis Related Phenomena that Was Taken into Account for Building the Model
- (yellow box in Figure 2) Classical macrophage activation occurs in response to the action of: (1) IFN- (originally called macrophage-activating factor) and (2) lipopolysaccharide (LPS) (enhanced (severe) local inflammation-LPS-LPB complex-IKK complex phosphorylated and initiation cascade of phosphorylation leading finally to the translocation of p50–p65 to the nucleus and gene transcription of many inflammatory cytokines that activate inflammatory cascade).
- (black boxes in Figure 2) IL-18 is a proinflammatory cytokine, expressed mainly by activated macrophages. This cytokine facilitates IFN- production mainly by Th1 cells and NK (natural killers) cells. Induction of cellular immunity modulates acute phase reaction, in the model by affecting IL-18 receptors ( and ) action. It should be noted that IL-18 is synthesized as an inactive precursor (pro IL-18) requiring processing by caspase 1 into an active form of cytokine (pro IL-18 signalling pathway with the activation by caspase 1 enzymatic cleavage). Caspase 1 is activated within inflammasomes. Finally, activated IL-18 acts by binding to its receptors ( and ). Different types of macrophages (M1 and M2) are involved in its regulation [2].
- (blue boxes in Figure 2) Activated macrophages, influenced locally by enhanced oxidative stress, inflammatory process and shear stress, increase the atherosclerotic plaque formation, leading along with local changes of nitric oxide (NO), to the atherosclerosis-based clinical consequences.
- (green boxes in Figure 2) IFN- induces transcription of several proinflammatory genes, for example, inducible NO synthase (iNOS). IFN- signal transduction pathway starts with the recruitment of Janus kinases (JAK1 and JAK2), to the IFN- receptor inducing their phosphorylation in tyrosine. As a consequence, the transcription factor STAT1 is recruited to the IFN-R and phosphorylated by JAKs. Phosphorylated Stat1 dimerizes and translocates to the nucleus. Here it induces transcriptional activation of several genes by binding to the proper sites of their promoters. Among the genes induced, IFN regulatory factor (IRF) 1, is also transcription factor which mediates the transcriptional regulation induced by IFN- [34].
- (orange boxes in Figure 2) The cytoplasmic TIR domains of the IL-18R complex interact with myeloid differentiation factor 88 (MyD88). IL-18 together with MyD88 mediates apoptosis via extrinsic and intrinsic pathways. It up-regulates Fas, FasL, TNFR1 and induces TNF synthesis. The extrinsic pathways evolves the recruitment of FADD to Fas/FasL and TRADD to TNF/TNFR1, which activates caspase 8 and caspase 3 action [35].
3. Results and Discussion
3.1. Building a Stochastic Petri Net Based Model
3.2. The Analysis Based on T-Invariants
3.2.1. The Analysis and Biological Interpretation of MCT Sets
3.2.2. The Analysis and Biological Interpretation of T-Clusters
3.2.3. The Analysis of t-Invariants Based Knockout Results
- pathway (NO synthesis) (cardiac contractile dysfunction) (cardiovascular disease),
- pathway (lipids peroxydation) (transformation into foamy cells) (atherosclerotic plaque),
- (neighboring endothelial cells stimulation) required for tokens in (MCP1) which is not a serious problem because for production of tokens in is also responsible transition (MCP1 gene transcription).
- Disabling of (MCP1 gene transcription) results in a net covered (completely) by only 127 t-invariants, and , which means that none t-invariant with is disabled in the process (32 out of 32 remain) while only 17 t-invariants — with remain as a result.
- Disabling of (VCAM1 transcription): 151 t-invariants remain, net is fully covered, and .
- Disabling of (ICAM1 transcription): same as for .
- Disabling of (iNOS gene transcription): 71 t-invariants remain, net is not covered, and . As a result this scenario disables: MCT3, MCT7 and single transitions (colorredproinflammatory response), (no apoptosis) and the already mentioned path .
- Disabling of (TNF gene transcription): 22 t-invariants remain, net is not covered, and . As a result this scenario disables: MCT2, MCT7, MCT8 and single transitions (modulation by TNF), (neighboring endothelial cells stimulation), (proinflammatory response) and (no apoptosis).
- Disabling with or (or both of them): 51 t-invariants remain, the net is still fully covered, and . Disabled transitions and MCT sets are the same as described in scenario for disabling alone.
- Disabling (MCP1 gene transcription) and (iNOS gene transcription): 39 t-invariants remain, the net is not covered, and , so only 5 processed resulting in atherosclerotic plaque remain.
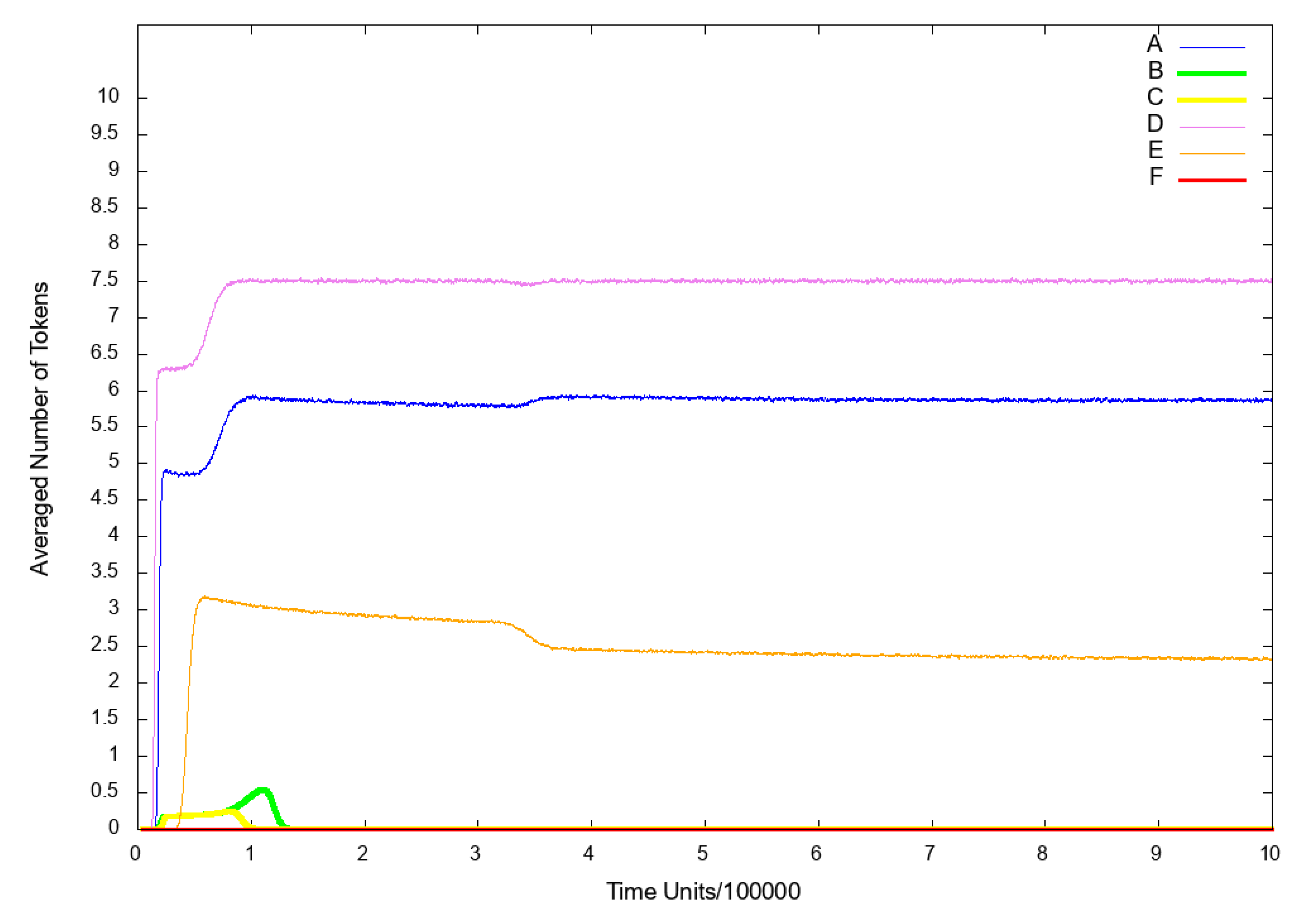
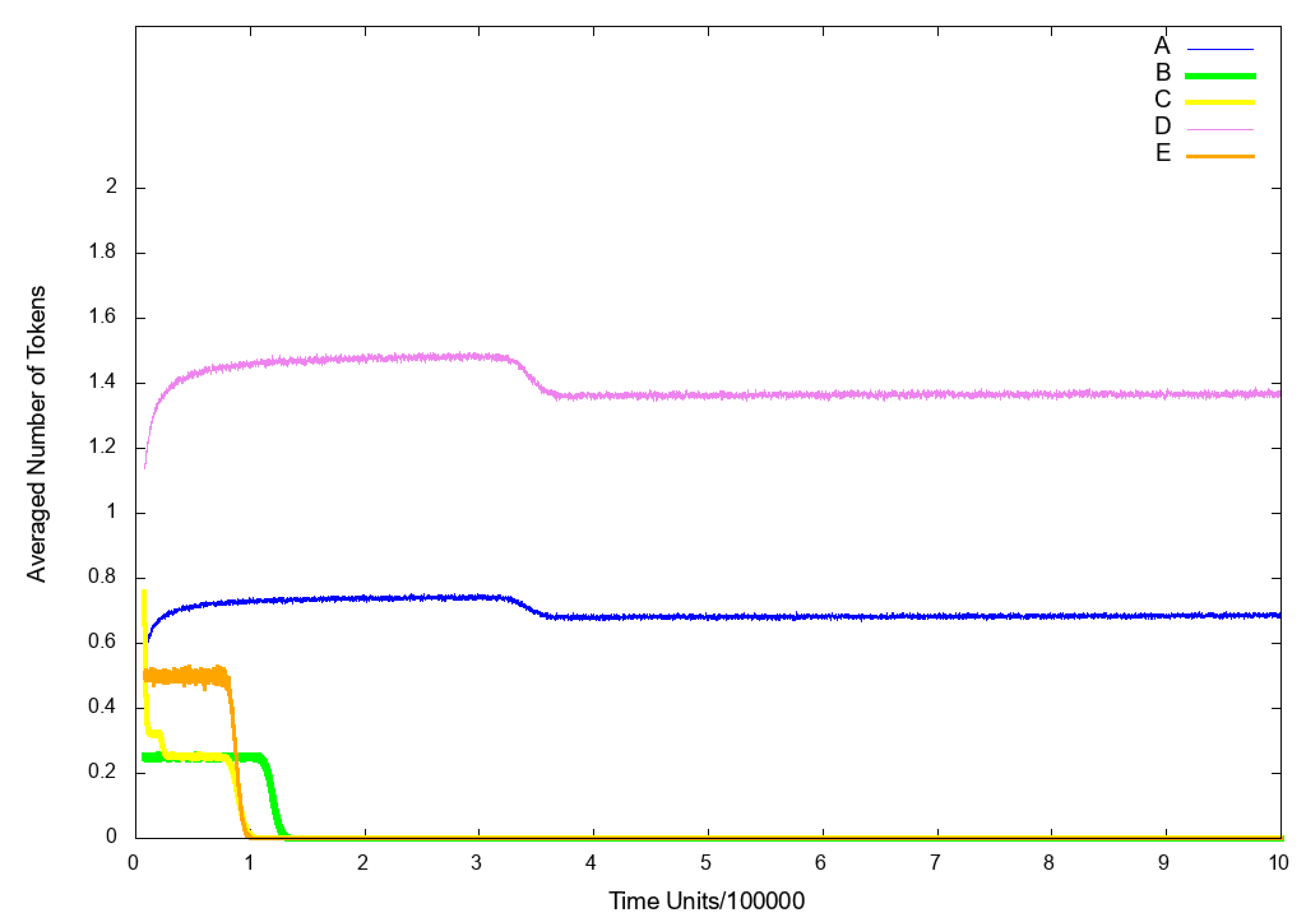
3.3. Stochastic Simulation and Knockout Based Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CD | cluster of differentiation |
| CKD | chronic kidney disease |
| DDs | Death Domains |
| DISC | death-inducing signaling complex |
| Fas | type I membrane protein that belongs to the tumor necrosis factor-nerve growth factor receptor family |
| FasL | Fas ligand (tumour necrosis factor superfamily) |
| FADD | Fas-associated protein with Death Domain |
| FLIPP | FADD-like-interleukin converting enzyme-like inhibitory protein |
| HD | haemodialysis |
| ICAM | intercellular adhesion molecule |
| ICE | caspase1-protease |
| IFR | interferon-related protein |
| IKK | IB kinase |
| IL-18 | interleukin 18 |
| IL-18Rs | Interleukin 18 receptors |
| INF- | interferon gamma |
| iNOS | inducible isoform nitric oxide synthase |
| IRAK | interleukin 1 receptor-associated kinase |
| IRAKP | interleukin 1 receptor-associated kinase phosphorylated |
| JAK/STAT | Janus kinase/signal transducers and activators of transcription |
| LBP | lipopolysaccharide binding protein |
| LPS | lipopolysaccharide |
| MAPK | mitogen-activated protein kinases |
| MCP1 | monocyte chemoattractant protein 1 |
| MCT sets | Maximal Common Transition sets |
| MPS | mononuclear phagocyte system |
| MSS | Mean Split Silhouette |
| MyD88 | myeloid differentiation primary response 88 |
| NADPH oxidase | nicotinamide adenine dinucleotide phosphate-oxidase |
| NK | natural killers |
| NO | nitric oxide |
| PN | Petri net |
| p38-MAPK | p38 mitogen-activated protein kinases |
| p50 | nuclear factor kappa-B p50 subunit |
| p65 | nuclear factor-kappa-B p65 subunit |
| RIP | receptor-interacting protein |
| SODD | silencer of death domains |
| SPN | stochastic Petri net |
| TAB | transforming growth factor activated kinase |
| TAK | transforming growth factor activated kinase-associated binding protein |
| TLR | Toll-like receptor |
| TNFR1 | tumor necrosis factor receptor 1 |
| TRADD | tumor necrosis factor receptor type 1—associated DEATH domain protein |
| TRAF | tumor necrosis factor receptor-associated factor |
| Uev1A-Ubc13 | ubiquitin-conjugating enzyme complex |
| VCAM | vascular cell adhesion molecule |
References
- Rżosińska, K.; Formanowicz, D.; Formanowicz, P. The study of the influence of micro-environmental signals on macrophage differentiation using a quantitative Petri net based model. Arch. Control. Sci. 2017, 27, 331–341. [Google Scholar] [CrossRef]
- Formanowicz, D.; Gutowska, K.; Formanowicz, P. Theoretical Studies on the Engagement of Interleukin 18 in the Immuno Inflammatory Processes Underlying Atherosclerosis. Int. J. Mol. Sci. 2018, 19, 3476. [Google Scholar] [CrossRef] [PubMed]
- Yasuda, K.; Nakanishi, K.; Tsutsui, H. Interleukin-18 in Health and Disease. Int. J. Mol. Sci. 2019, 20, 649. [Google Scholar] [CrossRef] [PubMed]
- Formanowicz, D.; Wanic-Kossowska, M.; Pawliczak, E.; Radom, M.; Formanowicz, P. Usefulness of serum interleukin-18 in predicting cardiovascular mortality in patients with chronic kidney disease-systems and clinical approach. Sci. Rep. 2015, 5, 18332. [Google Scholar] [CrossRef] [PubMed]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- David, R.; Alla, H. Discrete, Continuous and Hybrid Petri Nets; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Koch, I.; Reisig, W.; Schreiber, F. Modeling in Systems Biology; Springer: London, UK, 2011. [Google Scholar]
- Marsan, M. Stochastic Petri nets: An elementary introduction. Lect. Notes Comput. Sci. 1989, 424, 1–29. [Google Scholar]
- Bause, F.; Kritzinger, P. Stochastic Petri Nets—An Introduction to the Theory; Vieveg+Teubner Verlag: Wiesbaden, Germany, 2002. [Google Scholar]
- Heiner, M.; Herajy, M.; Liu, F.; Rohr, C.; Schwarick, M. Snoopy—A unifying Petri net tool. Lect. Notes Comput. Sci. 2012, 7347, 398–407. [Google Scholar]
- Heiner, M.; Gilbert, D.; Donaldson, R. Petri Nets for Systems and Synthetic Biology. Form. Methods Comput. Syst. Biol. 2008, 5016, 215–264. [Google Scholar] [CrossRef]
- Li, B.; Khlif-Bouassida, M.; Toguyéni, A. On-the-Fly Diagnosability Analysis of Bounded and Unbounded Labeled Petri Nets Using Verifier Nets. Int. J. Appl. Math. Comput. Sci. 2018, 28, 269–281. [Google Scholar] [CrossRef]
- Xu, X.G.; Shi, H.; Xu, D.H.; H-C, L. Picture Fuzzy Petri Nets for Knowledge Representation and Acquisition in Considering Conflicting Opinions. Appl. Sci. 2019, 9, 983. [Google Scholar] [CrossRef]
- Xu, X.G.; Xiong, Y.; Xu, D.H.; Liu, H.C. Bipolar fuzzy Petri nets for knowledge representation and acquisition considering non-cooperative behaviors. Int. J. Mach. Learn. Cybern. 2020, 11, 2297–2311. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P. (Eds.) Finding Groups in Data: An Introduction to Cluster Analysis; Wiley Series in Probability and Statistics; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar]
- Formanowicz, D.; Rybarczyk, A.; Radom, M.; Formanowicz, P. A role of inflammation and immunity in essential hypertension-modeled and analyzed using Petri nets. Int. J. Mol. Sci. 2020, 21, 3348. [Google Scholar] [CrossRef] [PubMed]
- Grafahrend-Belau, E.; Schreiber, F.; Heiner, M.; Sackmann, A.; Junker, B.H.; Grunwald, S.; Speer, A.; Winder, K.; Koch, I. Modularization of biochemical networks based on classification of Petri net t-invariants. BMC Bioinform. 2008, 9, 90. [Google Scholar] [CrossRef]
- Sackmann, A.; Heiner, M.; Koch, I. Application of Petri net based analysis techniques to signal transduction pathway. BMC Bioinform. 2006, 7, 482. [Google Scholar] [CrossRef]
- Sackmann, A.; Formanowicz, D.; Formanowicz, P.; Koch, I.; Błażewicz, J. An analysis of Petri net based model of the human body iron homeostasis process. Comput. Biol. Chem. 2007, 31, 1–10. [Google Scholar] [CrossRef]
- Kielbassa, J.; Bortfeldt, R.; Schuster, S.; Koch, I. Modeling of the U1 snRNP assembly pathway in alternative splicing in human cells using Petri nets. Comput. Biol. Chem. 2009, 33, 46–61. [Google Scholar] [CrossRef]
- Grunwald, S.; Speer, A.; Ackermann, J.; Koch, I. Petri net modelling of gene regulation of the Duchenne muscular dystrophy. Biosystems 2008, 92, 189–205. [Google Scholar] [CrossRef]
- Ivashkiv, L. IFN γ: Signalling, epigenetics and roles in immunity, metabolism, disease and cancer immunotherapy. Nat. Rev. Immunol. 2018, 18, 545–558. [Google Scholar] [CrossRef]
- Takeda, K.; Akira, S. TLR signaling pathways. Semin. Immunol. 2004, 16, 3–9. [Google Scholar] [CrossRef]
- Bousoik, E.; Aliabadi, H. “Do We Know Jack” About JAK? A Closer Look at JAK/STAT Signaling Pathway. Front. Oncol. 2018, 8, 287. [Google Scholar] [CrossRef] [PubMed]
- Fatkhullina, A.; Peshkova, I.; Koltsova, E. The Role of Cytokines in the Development of Atherosclerosis. Biochemistry 2016, 81, 1358–1370. [Google Scholar] [CrossRef]
- Sedger, L.; McDermott, M. TNF and TNF-receptors: From mediators of cell death and inflammation to therapeutic giants—past, present and future. Cytokine Growth Factor Rev. 2014, 25, 453–472. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zhang, L.; Joo, D.; Sun, S. NF-κB signaling in inflammation. Signal Transduct. Target. Ther. 2017, 71, e17023. [Google Scholar] [CrossRef]
- Kreckel, J.; Anany, M.; Siegmund, D.; Wajant, H. TRAF2 Controls Death Receptor-Induced Caspase-8 Processing and Facilitates Proinflammatory Signaling. Front. Immunol. 2019, 10, 2024. [Google Scholar] [CrossRef] [PubMed]
- Naseem, K. The role of nitric oxide in cardiovascular diseases. Mol. Aspects Med. 2005, 26, 33–65. [Google Scholar] [CrossRef] [PubMed]
- Carracedo, J.; Ramirez, R.; Madueno, J.; Soriano, S.; Rodriguez-Benot, A.; Rodriguez, M.; Martin-Malo, A.; Aljama, P. Cell apoptosis and hemodialysis-induced inflammation. Kidney Int. Suppl. 2002, 80, 89–93. [Google Scholar] [CrossRef]
- Knapp, S.; de Vos, A.; Florquin, S.; Golenbock, D.; van der Poll, T. Lipopolysaccharide Binding Protein Is an Essential Component of the Innate Immune Response to Escherichia coli Peritonitis in Mice. Infect. Immun. 2003, 71, 6747–6753. [Google Scholar] [CrossRef]
- Tedgui, A.; Mallat, Z. Cytokines in Atherosclerosis: Pathogenic and Regulatory Pathways. Physiol. Rev. 2006, 86, 515–581. [Google Scholar] [CrossRef]
- Vila-del Sol, V.; Punzón, C.; Fresno, M. IFN-γ-Induced TNF-α Expression Is Regulated by Interferon Regulatory Factors 1 and 8 in Mouse Macrophages. J. Immunol. 2008, 181, 4461–4470. [Google Scholar] [CrossRef]
- Gurung, P.; Kanneganti, T. Novel roles for caspase-8 in IL-1β and inflammasome regulation. Am. J. Pathol. 2015, 185, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Scheidel, J.; Lindauer, K.; Ackermann, J.; Koch, I. Quasi-Steady-State Analysis based on Structural Modules and Timed Petri Net Predict System’s Dynamics: The Life Cycle of the Insulin Receptor. Metabolites 2015, 5, 766–793. [Google Scholar] [CrossRef] [PubMed]
- Palsson, S.; Hickling, T.; Bradshaw-Pierce, E.; Zager, M.; Jooss, K.; Brien, P.; Spilker, M.; Palsson, B.; Vicini, P. The development of a fully-integrated immune response model (FIRM) simulator of the immune response through integration of multiple subset models. BMC Syst. Biol. 2013, 7, 95. [Google Scholar] [CrossRef] [PubMed]
- Formanowicz, D.; Rybarczyk, A.; Formanowicz, P. Factors influencing essential hypertension and cardiovascular disease modeled and analyzed using stochastic Petri nets. Fundam. Inform. 2018, 160, 143–165. [Google Scholar] [CrossRef]
- MacEwan, D. TNF ligands and receptors—A matter of life and death. Br. J. Pharmacol. 2002, 135, 855–875. [Google Scholar] [CrossRef]
- Atluri, P.; Karakousis, G.; Porrett, P.; Kaiser, L. The Surgical Review: An Integrated Basic and Clinical Science Study Guide, 2nd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2006. [Google Scholar]
- Takahashi, K.; Takeya, M.; Sakashita, N. Multifunctional roles of macrophages in the development and progression of atherosclerosis in humans and experimental animals. Med. Electron Microsc. 2002, 35, 179–203. [Google Scholar] [CrossRef] [PubMed]
- Heiner, M.; Lehrack, S.; Gilbert, D.; Marwan, W. Extended Stochastic Petri Nets for Model-Based Design of Wetlab Experiments. In Transactions on Computational Systems Biology XI; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5750, pp. 138–163. [Google Scholar] [CrossRef]
- Radom, M.; Rybarczyk, A.; Szawulak, B.; Andrzejewski, H.; Chabelski, P.; Kozak, A.; Formanowicz, P. Holmes: A graphical tool for development, simulation and analysis of Petri net based models of complex biological systems. Bioinformatics 2017, 33, 3822–3823. [Google Scholar] [CrossRef] [PubMed]
- Einloft, J.; Ackermann, J.; Nöthen, J.; Koch, I. MonaLisa—Visualization and analysis of functional modules in biochemical networks. Bioinformatics 2013, 29, 1469–1470. [Google Scholar] [CrossRef] [PubMed]
- Formanowicz, D.; Radom, M.; Rybarczyk, A.; Formanowicz, P. The role of Fenton reaction in ROS-induced toxicity underlying atherosclerosis—Modeled and analyzed using a Petri net-based approach. Biosystems 2018, 165, 71–87. [Google Scholar] [CrossRef]
- Gillespie, D. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Mossa, J.; Ramji, D. Cytokines: Roles in atherosclerosis disease progression and potential therapeutic targets. Future Med. Chem. 2016, 8, 1317–1330. [Google Scholar] [CrossRef] [PubMed]
- Moss, J.; Ramji, D. Interferon-γ: Promising therapeutic target in atherosclerosis. World J. Exp. Med. 2015, 5, 154–159. [Google Scholar] [CrossRef] [PubMed]
- Wullaert, A.; Bonnet, M.; Pasparakis, M. NF-κB in the regulation of epithelial homeostasis and inflammation. Cell Res. 2011, 21, 146–158. [Google Scholar] [CrossRef] [PubMed]
- Bhat, O.; Dhawan, V. Role of IL-18 and its signaling in atherosclerosis. Inflamm. Cell Signal. 2015, 2, e707. [Google Scholar] [CrossRef]
- Kanters, E.; Pasparakis, M.; Gijbels, M.; Vergouwe, M.; Partouns-Hendriks, I.; Fijneman, R.; Clausen, B.; Förster, I.; Kockx, M.; Rajewsky, K.; et al. Inhibition of NF-κB activation in macrophages increases atherosclerosis in LDL receptor-deficient mice. J. Clin. Investig. 2003, 112, 1176–1185. [Google Scholar] [CrossRef] [PubMed]
- Blankenberg, S.; Barbaux, S.; Tiret, L. Adhesion molecules and atherosclerosis. Atherosclerosis 2003, 170, 191–203. [Google Scholar] [CrossRef]
- Parka, J.G.; Ryuc, S.; Junga, I.H.; Lee, Y.H.; Kanga, K.; Lee, M.R.; Lee, M.N.; Sonn, S.; Lee, J.; Lee, H.; et al. Evaluation of VCAM-1 antibodies as therapeutic agent for atherosclerosis in apolipoprotein E-deficient mice. Atherosclerosis 2013, 226, 356–363. [Google Scholar] [CrossRef]
| Place | Biological Meaning | References | Place | Biological Meaning | References |
|---|---|---|---|---|---|
| active IL-18-IL-18Rs and ) complex | [3,23] | MyD88 | [24] | ||
| INF- synthesized by T and NK cells | [3,23,25] | Receptors MyD88 complex | [24] | ||
| IL-18R | [3,23] | TLR-MyD88-IRAK4 complex | [24] | ||
| activated macrophages | [3,23,26] | TLR-MyD88-IRAK4 -IRAK1P complex | [24] | ||
| pro IL-18 | [3] | TLR-MyD88-IRAK4-IRAK1P-TRAF6 complex | [24] | ||
| TNF | [3,26,27,28,29] | IRAK1P-TRAF6-TAB2-TAB1-TAK1 complex at plasma membrane | [24] | ||
| ICE | [3] | IRAK1 degraded | [24] | ||
| IL-18 | [3] | UBC13-UEV1A-TRAF6-TAK1P-TAB2P-TAB1 complex | [24] | ||
| iNOS activated | [28,30] | TAK1 activated | [24] | ||
| NO | [30] | MAP kinase phosphorylation activation | [28] | ||
| contractility failure | [30] | IKK complex phosphorylated activated | [24,28] | ||
| foamy cells | [26,30] | RIP1 ubiquitinated | [29] | ||
| high shear stress | [30,31] | TRAF2 autoubiquitinated | [29] | ||
| IFR1 | [25] | FLIP | [28,29] | ||
| JAK-STAT pathway activated | [23,25] | TRAF2-TRADD-RIP1-TRAF5-TNFR complex | [29] | ||
| INF--IFNRs complex | [23,25] | active TNFR1 signalling complex | [29] | ||
| peroxynitrite | [30,31] | SODD | [27] | ||
| modified oxidized LDL | [26,30] | TNFR1 stable with SODD | [27] | ||
| FASL and FAS | [3,29] | TNFR1 endocytosed | [29] | ||
| VCAM1 | [3,26,28,30] | FADD recruited | [29] | ||
| ICAM1 | [3,26,28,30] | pro caspase 8 recruited | [29] | ||
| MCP1 | [26,28] | DISC | [29] | ||
| monocytes | [26] | IB phosphorylated | [28] | ||
| macrophages | [26] | p50–p65-IB phosporylated complex | [28] | ||
| LPS binding protein LBP | [32] | p50–p65 dimer-NFB (early phase) | [28] | ||
| microbial infection LPS | [32] | p50–p65 dimer in the nucleus | [28] | ||
| LPS-LPB complex | [32] | caspase 8 active | [29] | ||
| TL4 activated | [32] | caspase 3 active | [29,31] |
| Transition | Biological Meaning | References | Transition | Biological Meaning | References |
|---|---|---|---|---|---|
| induction cell-mediated immunity | [23] | IRAK4 recruitment | [24] | ||
| INF- synthesis influencing | [23] | connection with IRAK1 and its phosphorylation | [24] | ||
| infection modulation | [23] | TRAF6 recruitment and binding to IRAK1 | [24] | ||
| classical macrophages activation by INF- | [3,23] | IRAK1P-TRAF6 dissociation | [24] | ||
| pro IL-18 synthesis | [3] | TAK1-TAB2 phosphorylation | [24] | ||
| modulation by TNF | [3] | TRAF6-TAK1P-TAB2P-TAB1 complex translocation to cytosol | [24] | ||
| modulation by INF- | [3,23] | TRAF6 ubiquitination | [24] | ||
| pro IL-18 activation by caspase 1 enzymatic cleavage | [3] | IKK complex phosphorylation | [24,28,33] | ||
| IL-18 and IL-18Rs binding | [3] | p38 and MAPK signalling pathway | [28] | ||
| nitric oxide synthesis | [30] | RIP1 recruites TAK1 via TAB2 | [29] | ||
| cardiac contractile dysfunction | [30] | RIP1 ubiquitination | [29] | ||
| cardiovascular disease (CVD) | [30] | TRAF2 ubiquitination | [29] | ||
| IFR1 synthesis | [25] | forming TRAF2-TRADD- RIP1-TRAF5 complex | [29] | ||
| JAK and STAT pathway activation | [23,25] | TNFR1 trimerization | [27,29] | ||
| INF--IFNRs interaction | [23,25] | usage | [27] | ||
| reaction catalysed by NADPH oxydase | [26,30] | TNFR1 stabilization | [27] | ||
| lipids peroxydation | [26,30] | SODD expression | [27] | ||
| neighboring endothelial cells stimulation | [3,26] | TNFR1 endocytosis | [29] | ||
| neovascularization inhibition | [3] | FADD recruitment | [29] | ||
| FasL expression on inflammatory cells | [3] | pro caspase 8 recruitment | [29] | ||
| ICAM1 and VCAM1 up regulation | [3] | connection through DDs | [29] | ||
| ICAM1 increasing | [30] | ubiquitylation and degradation | [28,33] | ||
| VCAM1 decreasing | [30] | phosphorylation cascade initiation | [28,33] | ||
| hemodialysis (HD) | [31] | IB dissociation from the complex | [28,33] | ||
| attracting monocytes | [26] | p50–p65 translocation to the nucleus | [28,33] | ||
| transformation into macrophages | [26] | MCP1 gene transcription | [28] | ||
| activation | [26] | VCAM1 transcription | [26,28] | ||
| transformation into foamy cells | [26,30] | ICAM1 transcription | [28] | ||
| atherosclerotic plaque | [26] | TNF gene transcription | [28,29] | ||
| severe inflammation | [3,32] | iNOS gene transcription | [28,30] | ||
| LPS and LBP binding | [32] | proinflammatory response | [28,29,30] | ||
| LPS presentation to TLR4 and CD14 | [32] | no apoptosis | [28,29] | ||
| TLR4 and MyD88 connection | [24] | caspase 8 autocleavage and activation | [29] | ||
| MyD88 recruitment | [24] | caspase 3 activation | [29,31] | ||
| active IL-18-IL-18Rs ( and ) and MyD88 connection | [3] | apoptosis enhancement | [29,31] |
| Place | Initial Number of Tokens | Place | Initial Number of Tokens | Place | Initial Number of Tokens | Place | Initial Number of Tokens |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 100 | 0 | ||||
| 100 | 0 | 0 | 0 | ||||
| 100 | 0 | 0 | 1000 | ||||
| 0 | 0 | 0 | 0 | ||||
| 100 | 1000 | 0 | 100 | ||||
| 100 | 100 | 0 | 10 | ||||
| 1000 | 100 | 0 | 10 | ||||
| 10 | 100 | 0 | 100 | ||||
| 1000 | 100 | 0 | 0 | ||||
| 10 | 0 | 10 | 0 | ||||
| 0 | 10 | 0 | 0 | ||||
| 0 | 10 | 10 | 100 | ||||
| 0 | 0 | 0 | 100 | ||||
| 100 | 100 | 100 | 100 |
| Process | Duration | Time Information Coming from the Available Literature | Time Interval |
|---|---|---|---|
| binding of ligands and proteins, influence of molecules, activation of enzymes, proteins and processes | 1 | seconds [39] | Very Short |
| recruitment, connection, phosphorylation, stabilization of molecules, modulation of the activation of proteins and processes, ubiquitination | 40 | seconds to a minute [40] | Short |
| decrease in molecules availability, dissociation of protein complexes | 100 | about twice shorter than synthesis and expression [41] | Medium |
| synthesis of biomolecules (e.g., INF-, pro IL-18), increase in molecules availability/production, TNFR1 endocytosis, translocation of protein complexes from cytosol to nucleus and from nucleus to cytosol, lipids peroxidation | 200 | >minutes [40] | Long |
| severe inflammation, differentiation of monocytes into macrophages | 500 | >hours [37] | Very Long |
| atherosclerotic plaque development, CVD | 1000 | >days [37,41] | Very, Very Long |
| Transition | Kinetic Parameter c | Rate Function | Transition | Kinetic Parameter c | Rate Function |
|---|---|---|---|---|---|
| 1.0 | 0.025 | ||||
| 1.0 | 0.025 | ||||
| 0.01 | 0.025 | ||||
| 1.0 | 0.01 | ||||
| 0.005 | 0.025 | ||||
| 1.0 | 0.005 | ||||
| 1.0 | 0.025 | ||||
| 1.0 | 0.025 | ||||
| 1.0 | 0.005 | ||||
| 0.005 | 0.025 | ||||
| 0.002 | 0.025 | ||||
| 0.002 | 0.025 | ||||
| 0.005 | 0.005 | ||||
| 1.0 | 0.005 | ||||
| 0.005 | 0.002 | ||||
| 0.01 | 0.025 | ||||
| 0.005 | 0.005 | ||||
| 0.005 | 0.005 | ||||
| 0.005 | 0.025 | ||||
| 0.005 | 0.025 | ||||
| 0.025 | 0.025 | ||||
| 0.005 | 0.005 | ||||
| 0.01 | 1.0 | ||||
| 0.005 | 0.01 | ||||
| 0.025 | 0.005 | ||||
| 0.005 | 0.005 | ||||
| 1.0 | 0.005 | ||||
| 0.005 | 0.005 | ||||
| 0.002 | 0.005 | ||||
| 0.005 | 0.005 | ||||
| 1.0 | 0.025 | ||||
| 0.025 | 0.005 | ||||
| 0.025 | 0.025 | ||||
| 0.025 | 1.0 | ||||
| 0.025 | 0.002 |
| MCT-Set | Contained Transitions | Biological Interpretation |
|---|---|---|
| , , , , , , , , , , , , , , | MyD88-dependent signaling pathway | |
| , , , , , , | induction of apoptosis influenced by caspases 3 and 8 that are situated at pivotal junctions in apoptosis pathways | |
| , , , | JAK-STAT signaling pathway stimulated by INF- and its impact on the regulation of iNOS expression | |
| , , , | activation of the innate immune system through TLR signaling pathways regulated by TIR domain-containing adaptors, such as MyD88 | |
| , , | influence of nitric oxide on cardiovascular system | |
| , , | transformation of monocytes into activated macrophages | |
| , , | activation of a silencer of TNFR1 signaling pathway | |
| , , | formation of an active TNFR1 signaling complex | |
| , | activation of macrophages by the classical pathway | |
| , | pro IL-18 signaling pathway | |
| , | SODD signaling pathway |
| Cluster No. | Biological Interpretation | No. of t-Invariants | Contained Processes | |
|---|---|---|---|---|
| MCT-Sets | Single Transitions | |||
| SODD signaling pathway | 1 | |||
| The involvement of the IL-18 cytokine in the formation of the atherosclerotic plaque in patients suffering from CKD without influence of SODD signaling pathway | 216 | , , , , , , , , , | , , , , , , , , , , , , , , , , , , , , , | |
| pro IL-18 signaling pathway and activation of macrophages by the classical pathway | 1 | , | , | |
| IL-18 synthesis and IL-18- mediated INF- induction | 1 | , | , , , | |
| activation of macrophages by INF- leading to lipids peroxidation and atherosclerotic plaque development | 1 | , , , | ||
| influence of NO on cardiovascular system and activation of the innate immune system through TLR together with pro IL-18 signaling pathway leading to atherosclerosis development | 3 | , , , , , | , , , , , , , , | |
| MCT Set | Activity | Knockout Impact (Transitions) | Knockout Impact (t-Invariants) |
|---|---|---|---|
| activation of macrophages by the classical pathway | 95.71% | 99.55% | |
| pro-IL-18 signaling pathway | 85.71% | 99.10% | |
| IL-18 and IL-18Rs binding | 80.00% | 98.65% | |
| MyD88-dependent signaling pathway | 75.71% | 98.21% | |
| TNF gene transcription | 24.29% | 90.13% | |
| modulation by INF- | 0% | 73.54% | |
| hemodialysis (HD) | 7.14% | 73.54% | |
| activation of the innate immune system through TLR signaling pathways regulated by TIR domain-containing adaptors, such as MyD88 | 4.29% | 73.54% | |
| active IL-18-IL-18Rs ( and ) and MyD88 connection | 0% | 73.54% | |
| lipids peroxydation | 8.57% | 68.61% | |
| JAK-STAT signaling pathway stimulated by INF- and its impact on the regulation of iNOS expression | 14.29% | 68.16% | |
| proinflammatory response | 5.71% | 60.99% | |
| formation of an active TNFR1 signaling complex | 17.14% | 48.43% | |
| neighboring endothelial cells stimulation | 0% | 48.43% | |
| ICAM1 increasing | 0% | 43.05% | |
| VCAM1 decreasing | 0% | 43.05% | |
| MCP1 gene transcription | 0% | 43.05% | |
| transformation into foamy cells | 5.71% | 36.32% | |
| VCAM1 transcription | 0% | 32.29% | |
| ICAM1 transcription | 0% | 32.29% | |
| activation of a silencer of TNFR1 signaling pathway | 2.86% | 30.49% | |
| transformation of monocytes into activated macrophages | 2.86% | 30.49% | |
| no apoptosis | 0% | 30.49% | |
| modulation by TNF | 0% | 25.56% | |
| induction of apoptosis influenced by caspases 3 and 8 that are situated at pivotal junctions in apoptosis pathways | 8.57% | 25.11% | |
| infection modulation | 0% | 25.11% | |
| INF- synthesis influencing | 0% | 25.11% | |
| atherosclerotic plaque | 0% | 23.77% | |
| ICAM1 and VCAM1 up regulation | 0% | 21.52% | |
| influence of NO on cardiovascular system | 2.86% | 14.35% | |
| reaction catalysed by NADPH oxydase | 0% | 13.00% | |
| neovascularization inhibition | 0% | 0.90% | |
| SODD signaling pathway | 1.43% | 0.45% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Formanowicz, D.; Rybarczyk, A.; Radom, M.; Tanaś, K.; Formanowicz, P. A Stochastic Petri Net-Based Model of the Involvement of Interleukin 18 in Atherosclerosis. Int. J. Mol. Sci. 2020, 21, 8574. https://doi.org/10.3390/ijms21228574
Formanowicz D, Rybarczyk A, Radom M, Tanaś K, Formanowicz P. A Stochastic Petri Net-Based Model of the Involvement of Interleukin 18 in Atherosclerosis. International Journal of Molecular Sciences. 2020; 21(22):8574. https://doi.org/10.3390/ijms21228574
Chicago/Turabian StyleFormanowicz, Dorota, Agnieszka Rybarczyk, Marcin Radom, Krzysztof Tanaś, and Piotr Formanowicz. 2020. "A Stochastic Petri Net-Based Model of the Involvement of Interleukin 18 in Atherosclerosis" International Journal of Molecular Sciences 21, no. 22: 8574. https://doi.org/10.3390/ijms21228574
APA StyleFormanowicz, D., Rybarczyk, A., Radom, M., Tanaś, K., & Formanowicz, P. (2020). A Stochastic Petri Net-Based Model of the Involvement of Interleukin 18 in Atherosclerosis. International Journal of Molecular Sciences, 21(22), 8574. https://doi.org/10.3390/ijms21228574






