Rapid Cellular Perception of Gravitational Forces in Human Jurkat T Cells and Transduction into Gene Expression Regulation
Abstract
1. Introduction
2. Results
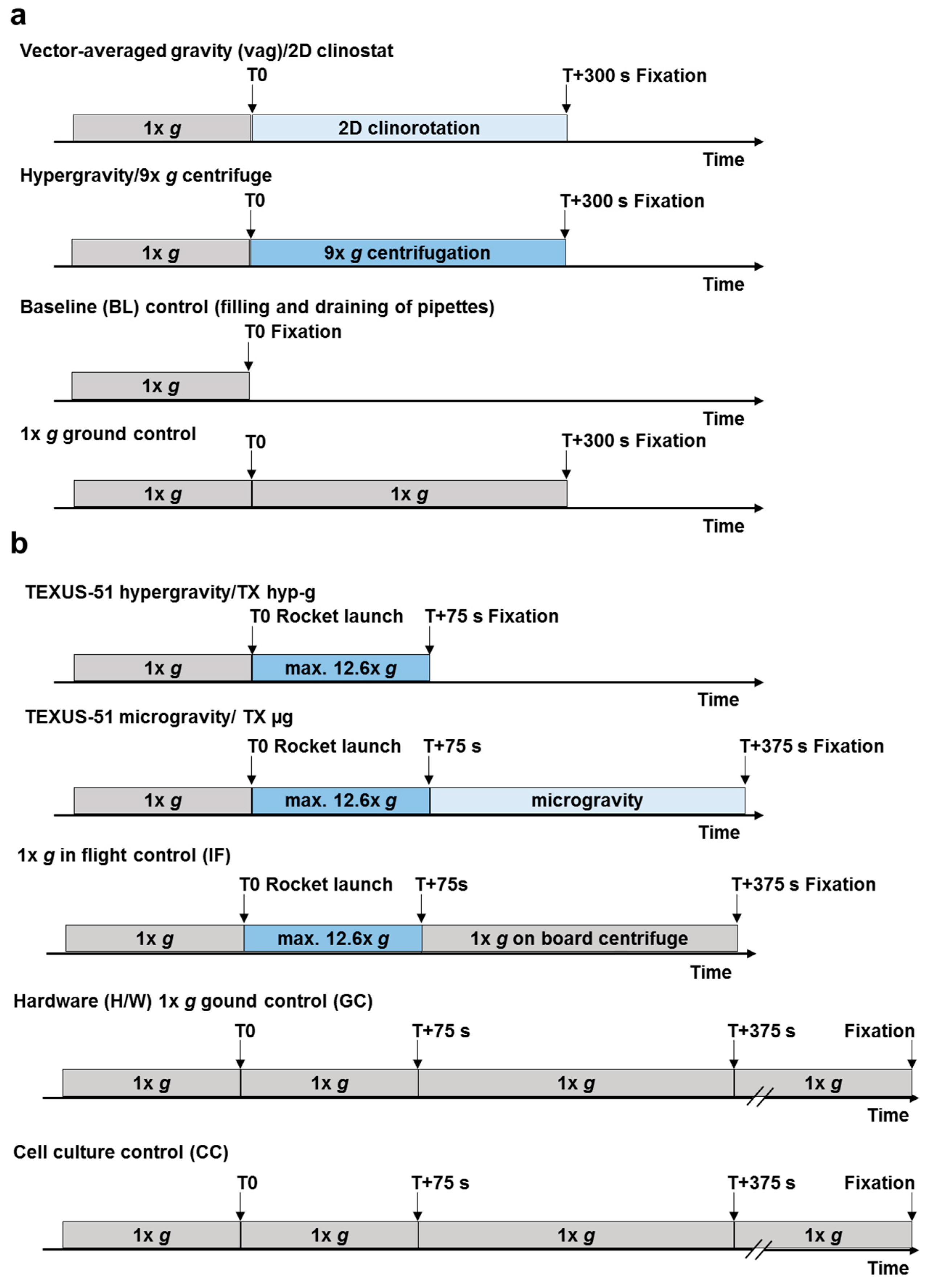
2.1. 2D Clinostat, Centrifuge and Suborbital Ballistic Rocket Experiments with Human Jurkat T Cells
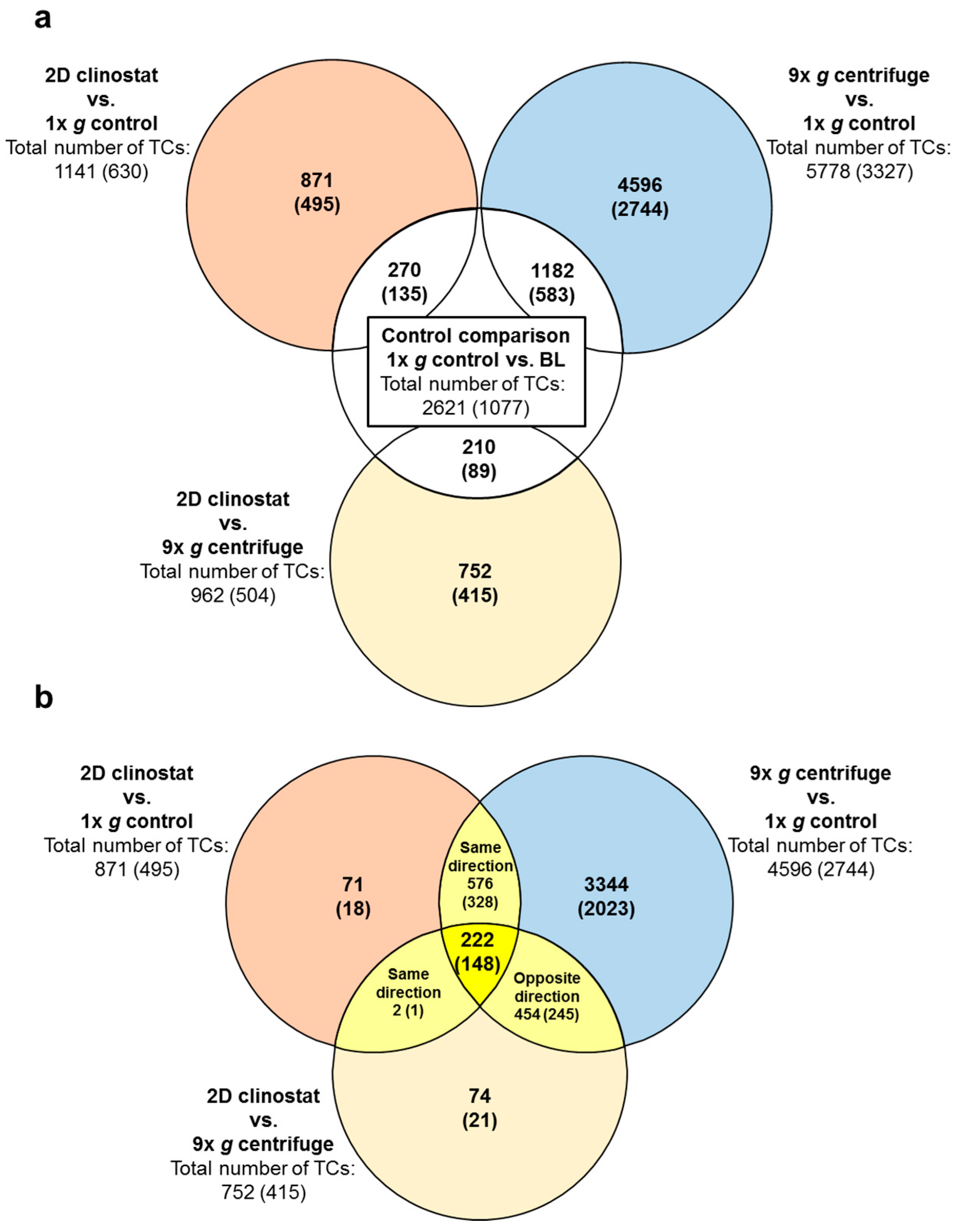
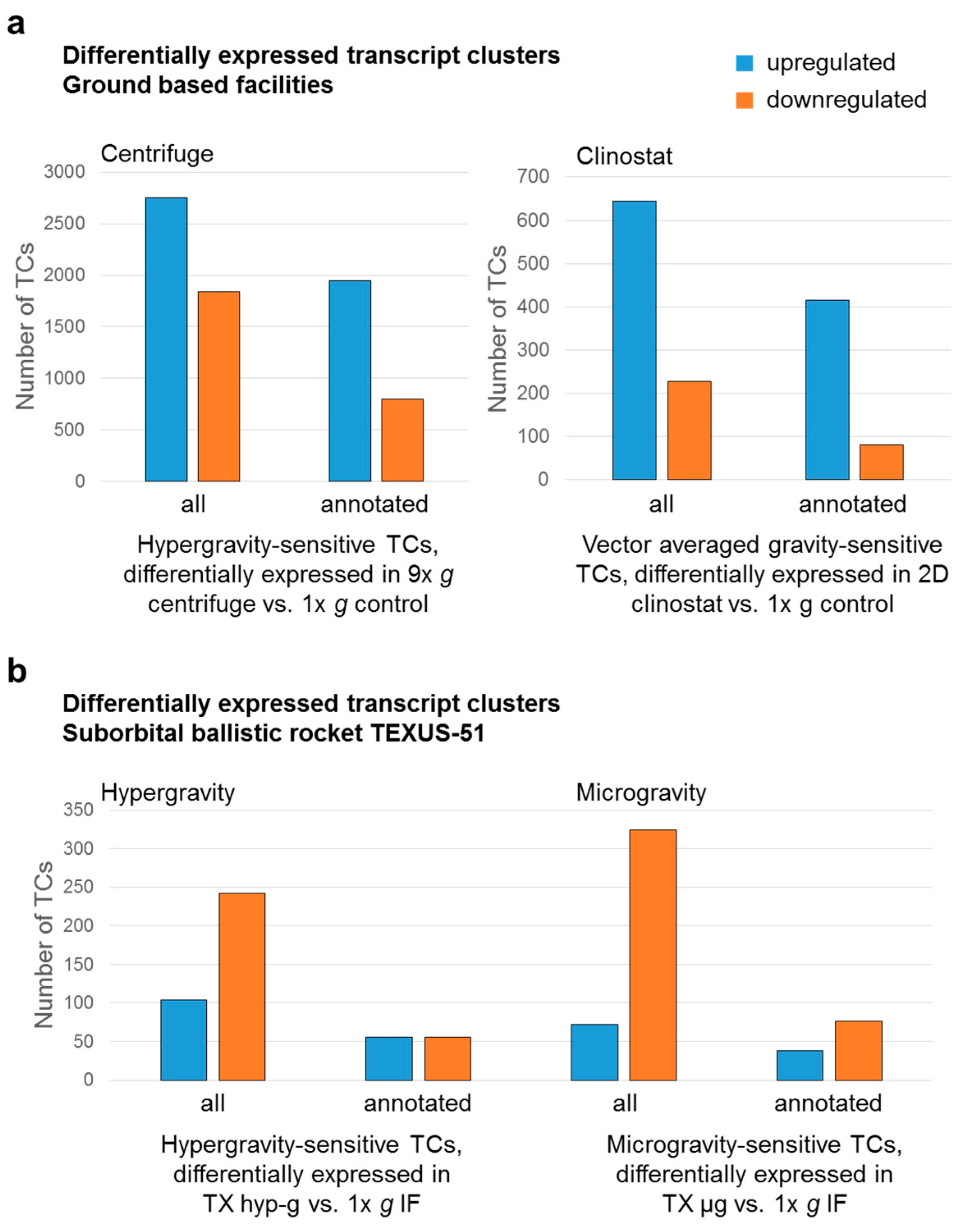
2.2. Identification of Differential Gene Expression in Ground Based Facilities Experiments
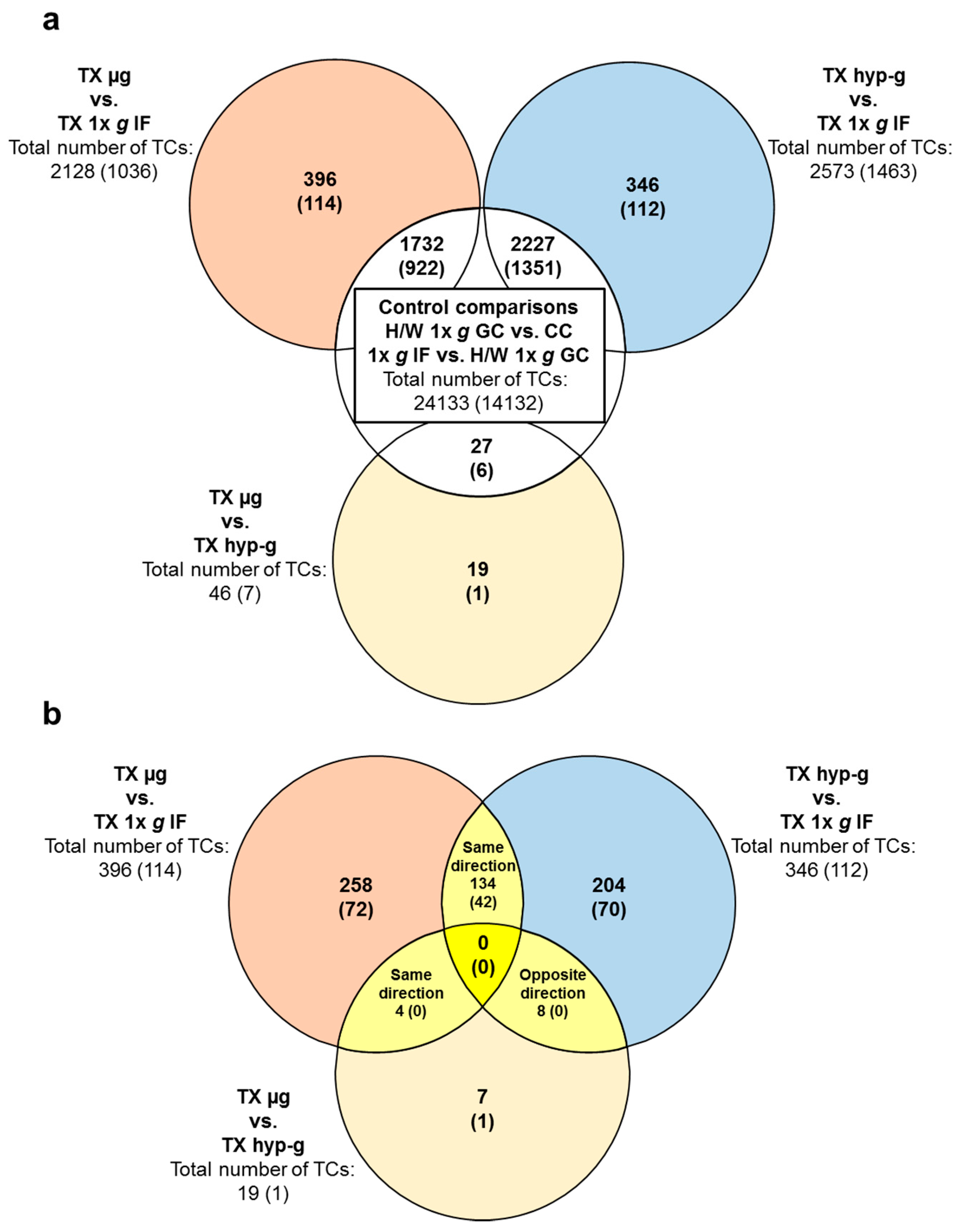
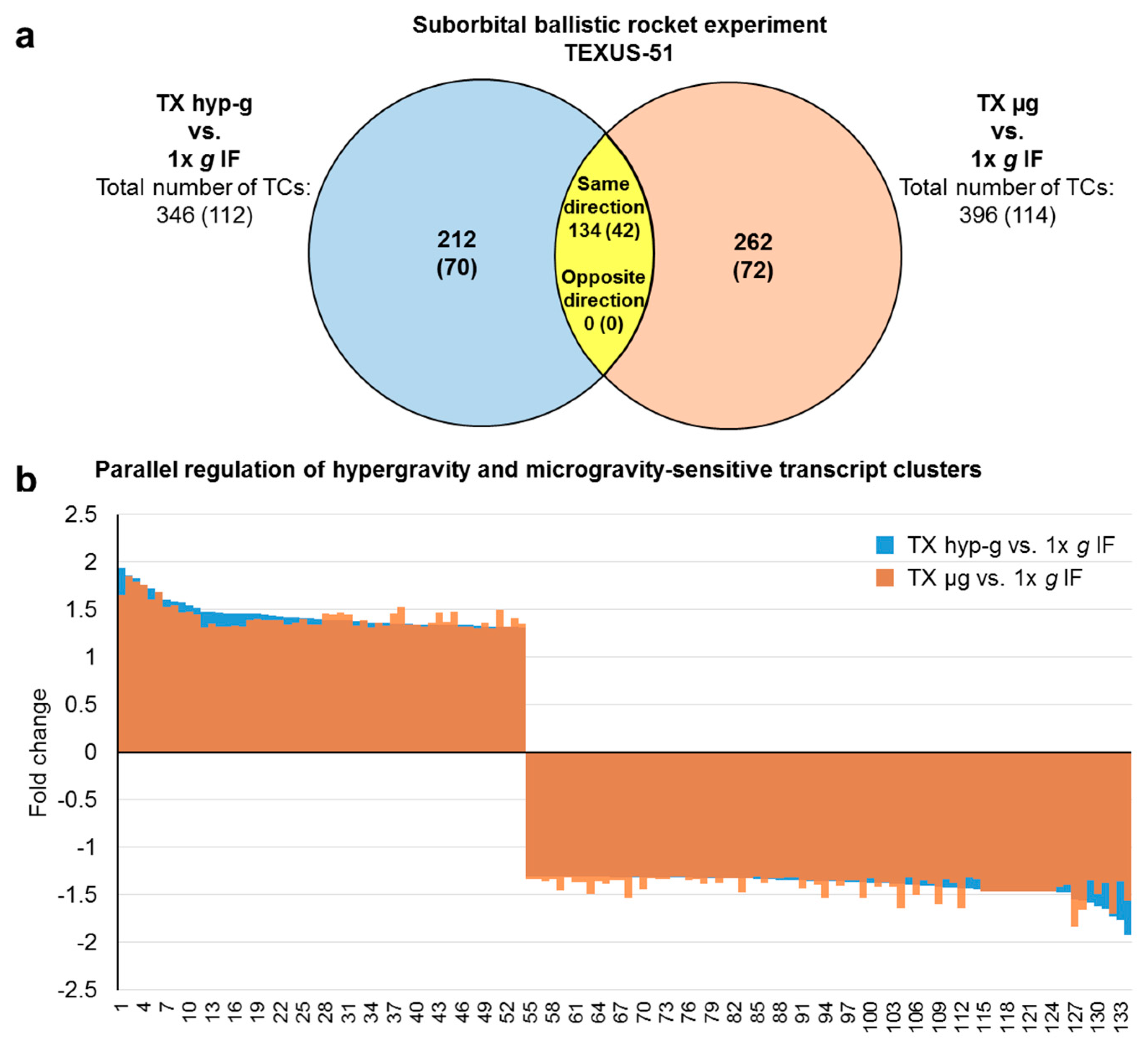
2.3. Comparison of GBFs with TEXUS-51 Gene Expression Results
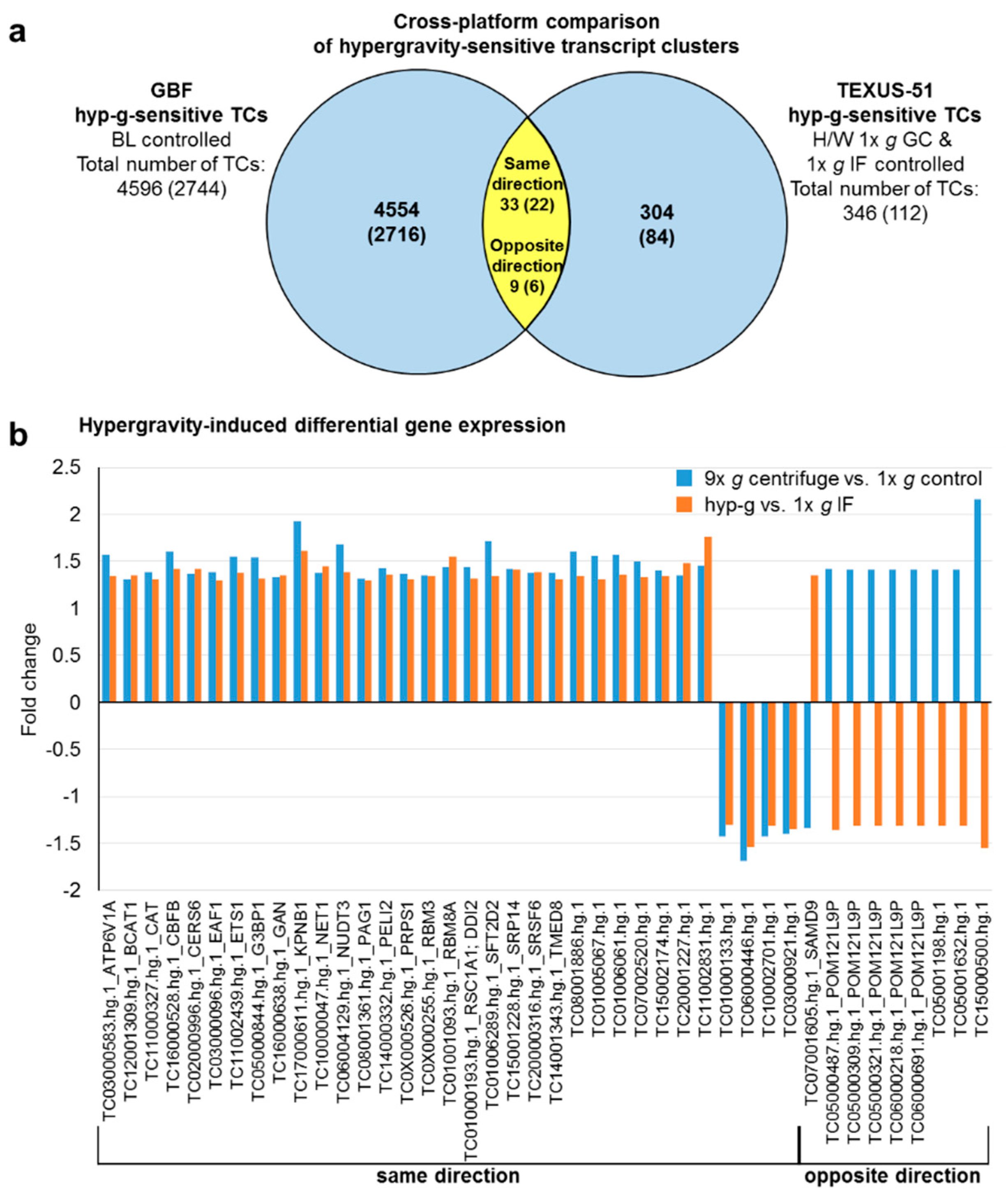
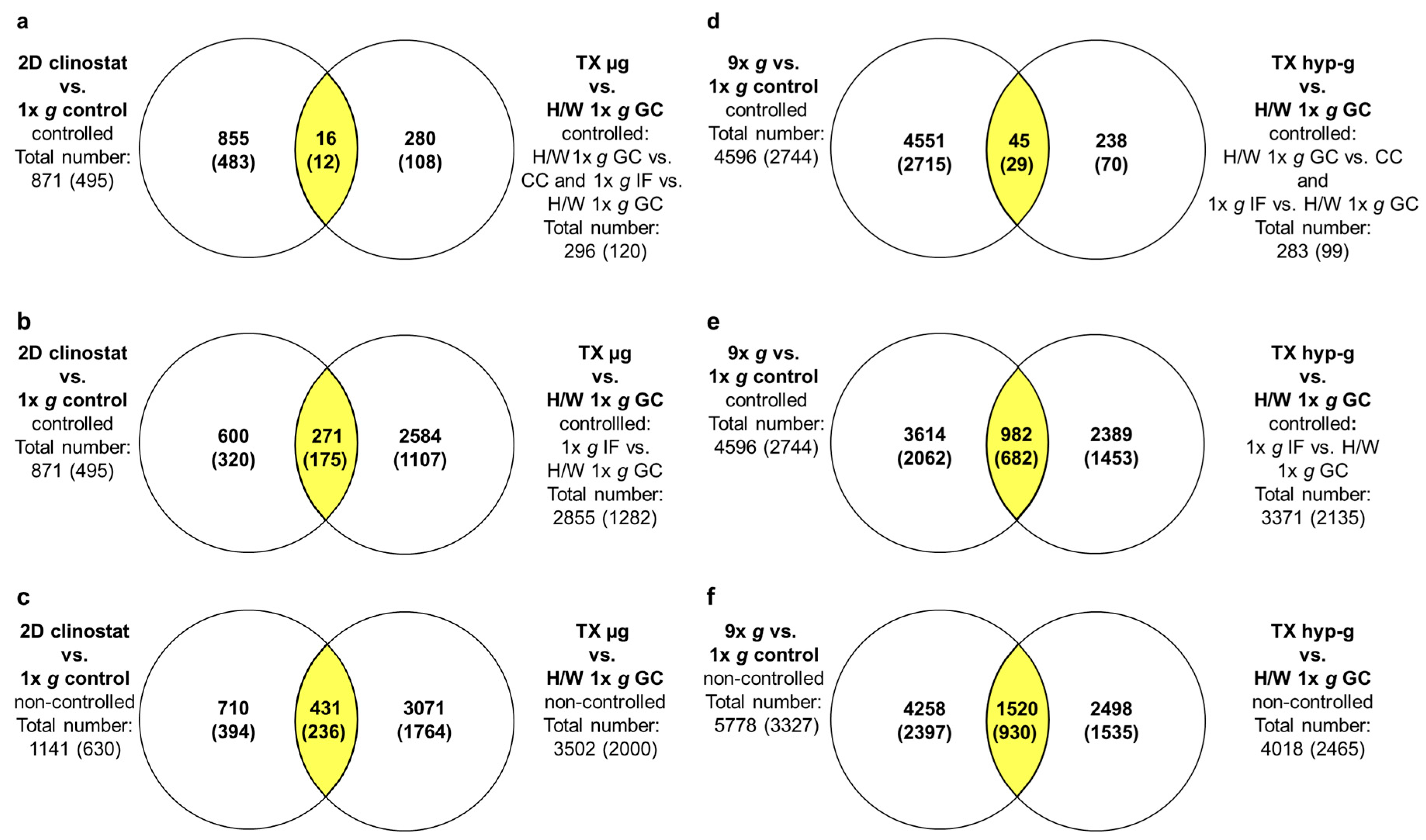
2.4. GBFs and TEXUS-51 Cross Platform Comparison of Hypergravity and Microgravity-Sensitive TCs
2.5. Maximally, Minimally and Non-Controlled Cross Platform Comparisons
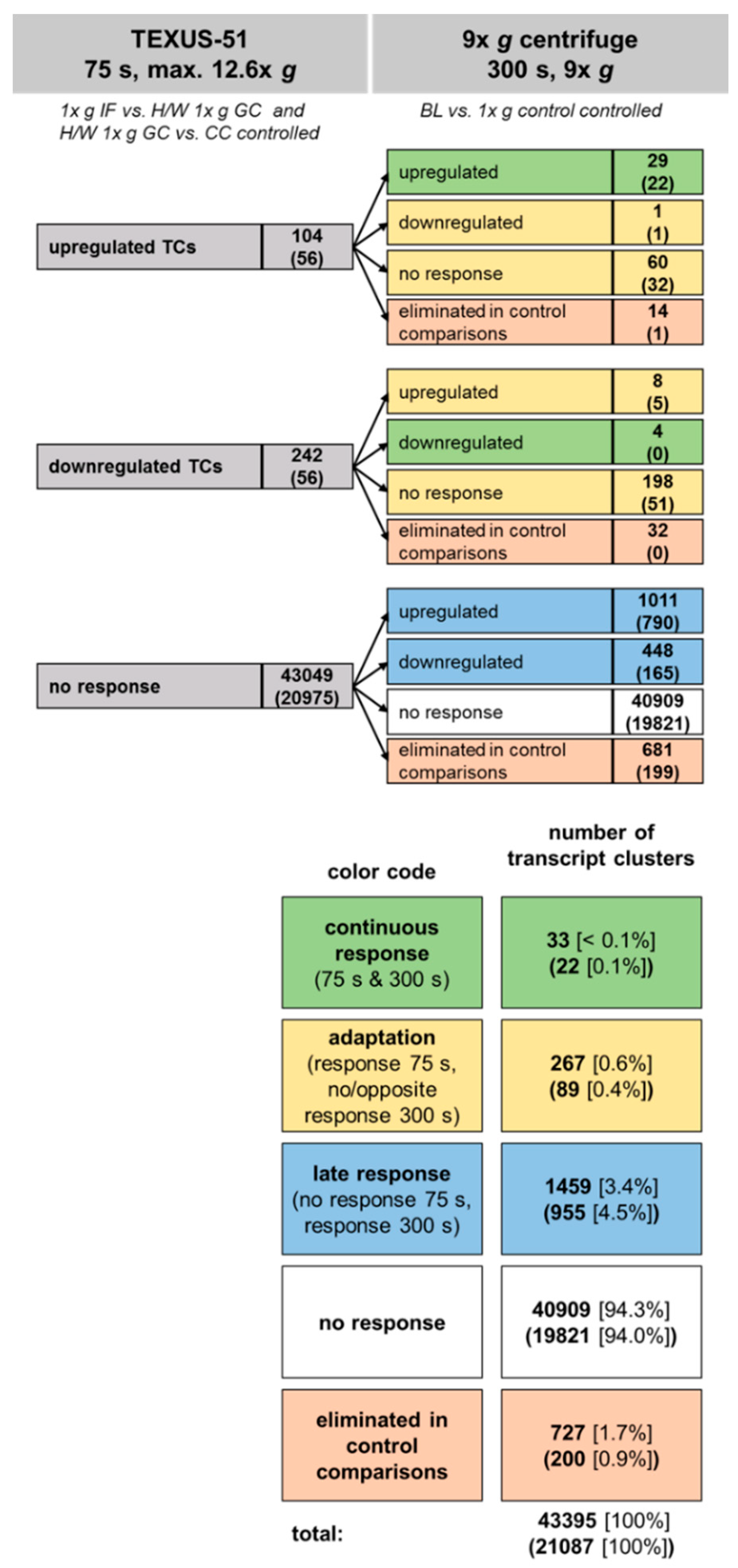
2.6. Development of Hypergravity-Sensitive TCs Over Time
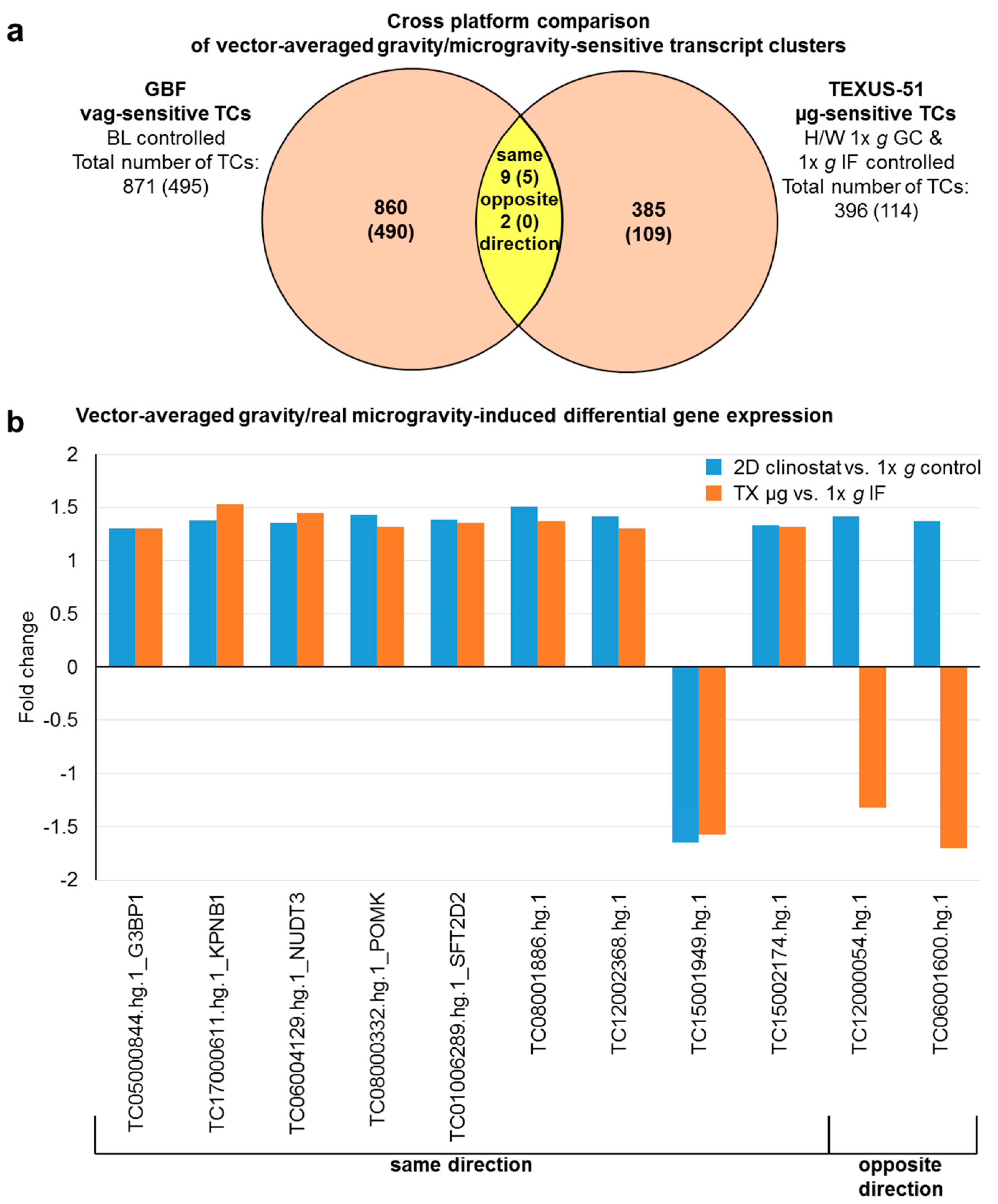
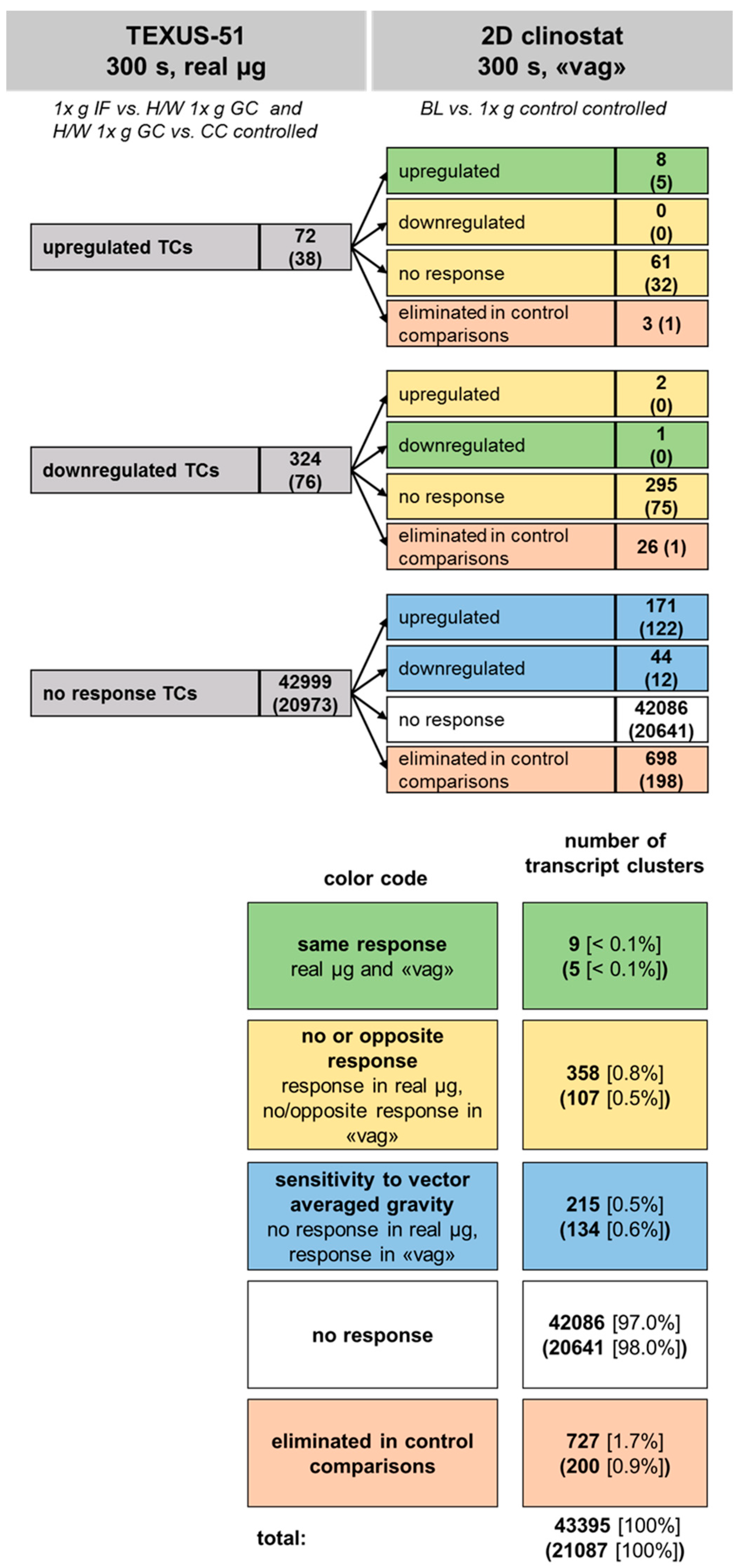
2.7. Comparison of Gene Regulation in Flight-Induced Microgravity and Vector-Averaged Gravity
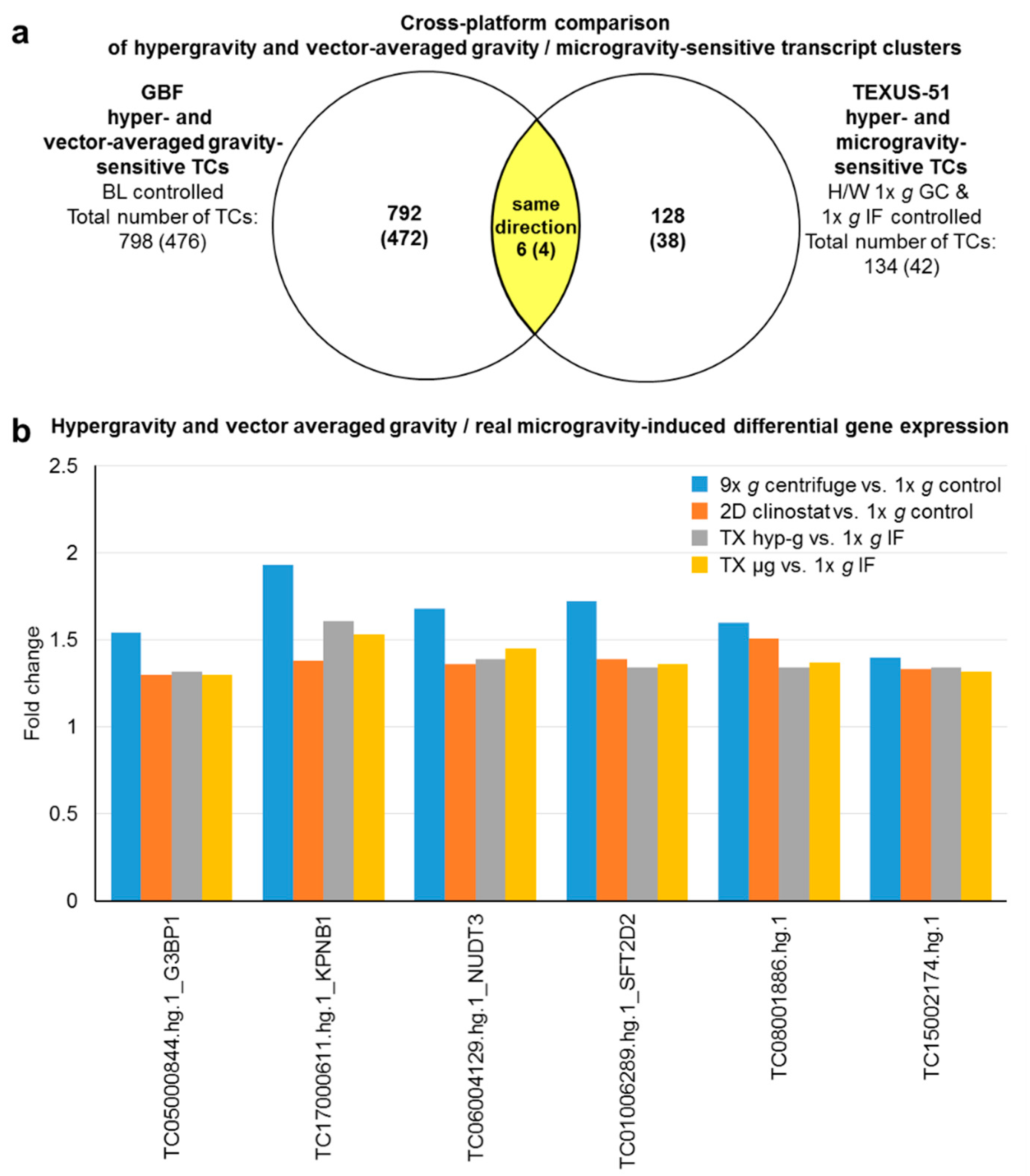
2.8. Cross Platform and Altered Gravity Condition Overlap Analysis of TC Regulation in Vector-Averaged Gravity, Flight-Induced Microgravity, and Hypergravity in GBF and TEXUS-51
3. Discussion
4. Materials and Methods
4.1. Cell Culture
4.2. TEXUS-51 Suborbital Ballistic Rocket Experiment
4.3. TEXUS-51 Mission Procedures
4.4. Experimental Preparation Procedures for TEXUS-51 Experiments
4.5. Ground Based Facilities (GBFs) Experiments
4.6. RNA Purification
4.7. RNA Sample Processing and Microarray Data Analysis
4.8. Applied Control Strategy for Revealing Microgravity and Hypergravity Sensitivity
4.9. Intra-Platform and Inter-Platform Comparisons
4.10. Functional Annotation Analysis
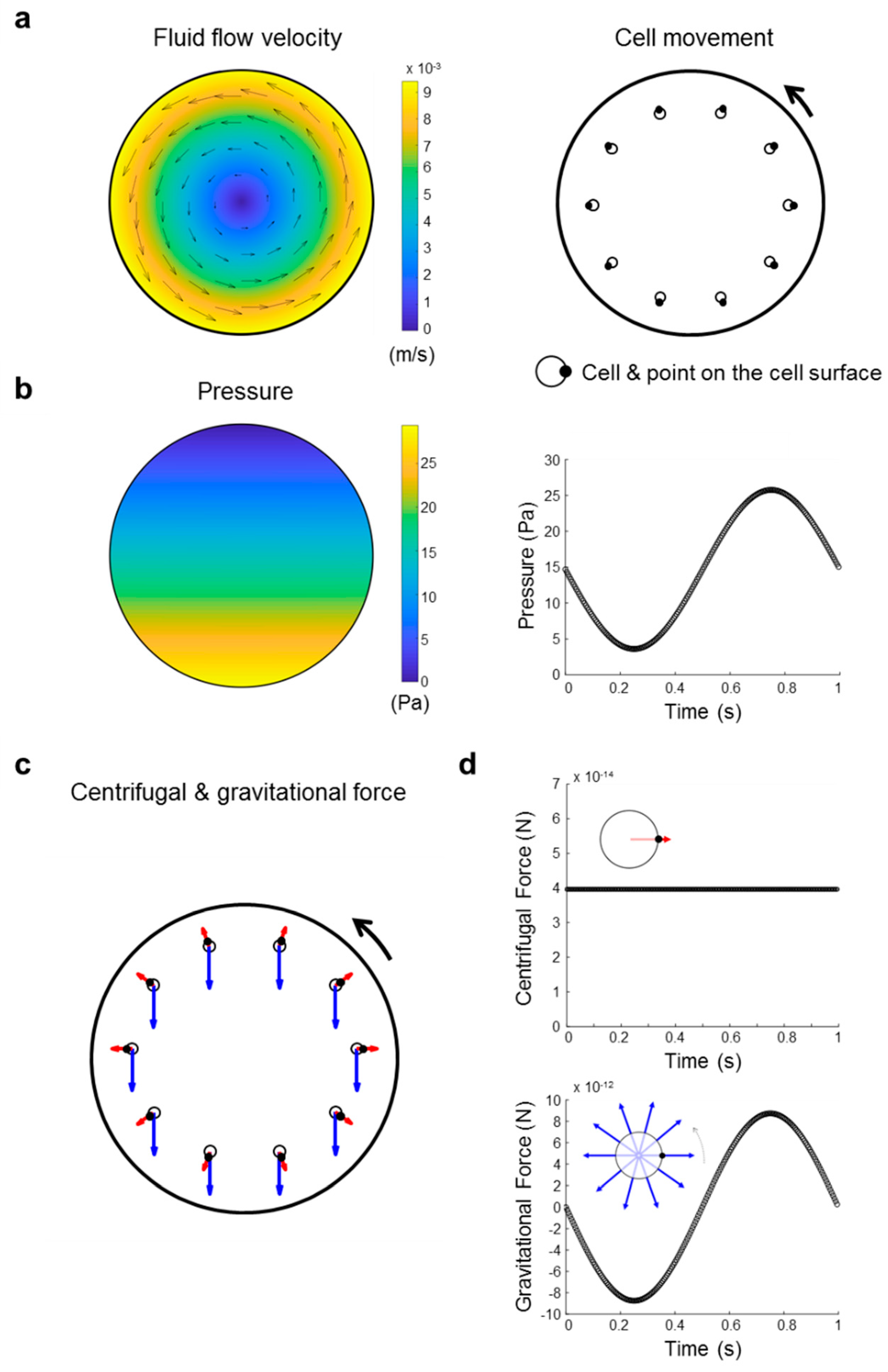
4.11. Investigation of Forces Present in a Clinostat
4.12. Data Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| % | percentage |
| °C | degree celsius |
| µg | microgravity |
| 1D | one dimensional |
| 1× g IF | 1g in flight |
| 2D | two dimensional |
| 3D | three dimensional |
| BL | baseline |
| CC | cell culture control |
| CO2 | carbon dioxide |
| DLR | German Aerospace Center |
| FC | fold change |
| g | gravity |
| GBF | ground based facility |
| GC | ground control |
| GEO | Gene Expression Omnibus |
| GO | gene ontology |
| h | hours |
| H/W | hardware |
| hyp-g | hypergravity |
| i.e. | that is |
| ID | identifier |
| ISS | International Space Station |
| km | kilometer |
| max. | maximum |
| min | minute |
| min. | minimum |
| mL | milliliter |
| mm | millimeter |
| mM | millimolar |
| mPa | millipascale |
| N | newton |
| n/a | not available |
| Pa | pascale |
| rcf | relative centrifugal force |
| RPM | random positioning machine |
| rpm | rounds per minute |
| RWV | rotating wall vessel |
| s | second |
| T | Time after launch |
| TC | transcript cluster |
| TEXUS/TX | German: Technologische Experimente unter Schwerelosigkeit |
| vag | vector-averaged gravity |
References
- Dubinin, N.P.; Vaulina, E.N. The evolutionary role of gravity. Life Sci. Space Res. 1976, 14, 47–55. [Google Scholar] [PubMed]
- Nicogossian, A.E.; Robbins, D. Space Physiology and Medicine, 3rd ed.; Lea & Febiger: Philadelphia, PA, USA, 1994. [Google Scholar]
- McCarthy, I.; Goodship, A.; Herzog, R.; Oganov, V.; Stussi, E.; Vahlensieck, M. Investigation of bone changes in microgravity during long and short duration space flight: Comparison of techniques. Eur. J. Clin. Investig. 2000, 30, 1044–1054. [Google Scholar] [CrossRef] [PubMed]
- Clement, G.; Moore, S.T.; Raphan, T.; Cohen, B. Perception of tilt (somatogravic illusion) in response to sustained linear acceleration during space flight. Exp. Brain Res. 2001, 138, 410–418. [Google Scholar] [CrossRef] [PubMed]
- Sonnenfeld, G. The immune system in space and microgravity. Med. Sci. Sports Exerc. 2002, 34, 2021–2027. [Google Scholar] [CrossRef] [PubMed]
- Crucian, B.E.; Chouker, A.; Simpson, R.J.; Mehta, S.; Marshall, G.; Smith, S.M.; Zwart, S.R.; Heer, M.; Ponomarev, S.; Whitmire, A.; et al. Immune System Dysregulation During Spaceflight: Potential Countermeasures for Deep Space Exploration Missions. Front. Immunol. 2018, 9, 1437. [Google Scholar] [CrossRef]
- Guilak, F.; Tedrow, J.R.; Burgkart, R. Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Commun. 2000, 269, 781–786. [Google Scholar] [CrossRef]
- Pajerowski, J.D.; Dahl, K.N.; Zhong, F.L.; Sammak, P.J.; Discher, D.E. Physical plasticity of the nucleus in stem cell differentiation. Proc. Natl. Acad. Sci. USA 2007, 104, 15619–15624. [Google Scholar] [CrossRef]
- Starr, D.A. A nuclear-envelope bridge positions nuclei and moves chromosomes. J. Cell Sci. 2009, 122, 577–586. [Google Scholar] [CrossRef]
- Thiel, C.S.; de Zelicourt, D.; Tauber, S.; Adrian, A.; Franz, M.; Simmet, D.M.; Schoppmann, K.; Hauschild, S.; Krammer, S.; Christen, M.; et al. Rapid adaptation to microgravity in mammalian macrophage cells. Sci. Rep. 2017, 7, 43. [Google Scholar] [CrossRef]
- Thiel, C.S.; Lauber, B.A.; Polzer, J.; Ullrich, O. Time course of cellular and molecular regulation in the immune system in altered gravity: Progressive damage or adaptation? Reach Rev. Hum. Space Explor. 2017, 5, 22–32. [Google Scholar] [CrossRef]
- Adrian, A.; Schoppmann, K.; Sromicki, J.; Brungs, S.; von der Wiesche, M.; Hock, B.; Kolanus, W.; Hemmersbach, R.; Ullrich, O. The oxidative burst reaction in mammalian cells depends on gravity. Cell Commun. Signal. CCS 2013, 11, 98. [Google Scholar] [CrossRef] [PubMed]
- Thiel, C.S.; Hauschild, S.; Huge, A.; Tauber, S.; Lauber, B.A.; Polzer, J.; Paulsen, K.; Lier, H.; Engelmann, F.; Schmitz, B.; et al. Dynamic gene expression response to altered gravity in human T cells. Sci. Rep. 2017, 7, 5204. [Google Scholar] [CrossRef] [PubMed]
- Thiel, C.S.; Huge, A.; Hauschild, S.; Tauber, S.; Lauber, B.A.; Polzer, J.; Paulsen, K.; Lier, H.; Engelmann, F.; Schmitz, B.; et al. Stability of gene expression in human T cells in different gravity environments is clustered in chromosomal region 11p15.4. NPJ Microgravity 2017, 3, 22. [Google Scholar] [CrossRef] [PubMed]
- Meloni, M.A.; Galleri, G.; Pippia, P.; Cogoli-Greuter, M. Cytoskeleton changes and impaired motility of monocytes at modelled low gravity. Protoplasma 2006, 229, 243–249. [Google Scholar] [CrossRef]
- Brown, A.H. From gravity and the organism to gravity and the cell. Gravit. Space Res. 1991, 4, 7–18. [Google Scholar]
- Van Loon, J.W.A. The Gravity Environment in Space Experiments in Biology in Space and Life on Earth. Effects of Spaceflight on Biological Systems; Wiley-VCH GmbH & Co KGaA: Hoboken, NJ, USA, 2007. [Google Scholar]
- Häder, D.-P.; Braun, M.; Grimm, D.; Hemmersbach, R. Gravireceptors in eukaryotes—A comparison of case studies on the cellular level. NPJ Microgravity 2017, 3, 1–8. [Google Scholar] [CrossRef]
- Labib, M.; Piontek, D.; Valsecchi, N.; Griffith, B.; Dejmek, M.; Jean, I.; Mailloux, M.; Palardy, R.; Michels, J.; Michalyna, C.; et al. The Fluid Science Laboratory’s Microgravity Vibration Isolation Subsystem Overview and Commissioning Update. In Proceedings of the SpaceOps 2010 Conference Delivering on the Dream Hosted by NASA Marshall Space Flight Center and Organized by AIAA, Huntsville, Alabama, 25–30 April 2010. [Google Scholar]
- Herranz, R.; Anken, R.; Boonstra, J.; Braun, M.; Christianen, P.C.; de Geest, M.; Hauslage, J.; Hilbig, R.; Hill, R.J.; Lebert, M.; et al. Ground-based facilities for simulation of microgravity: Organism-specific recommendations for their use, and recommended terminology. Astrobiology 2013, 13, 1–17. [Google Scholar] [CrossRef]
- Minster, O.; Innocenti, L.; Mesland, D. Looking at Science on Board Eureca; ESA Publiactions Division: Noordwijk, The Netherlands, 1993. [Google Scholar]
- Briegleb, W. Some qualitative and quantitative aspects of the fast-rotating clinostat as a research tool. ASGSB Bull. Publ. Am. Soc. Gravit. Space Biol. 1992, 5, 23–30. [Google Scholar]
- Sarkar, D.; Nagaya, T.; Koga, K.; Nomura, Y.; Gruener, R.; Seo, H. Culture in vector-averaged gravity under clinostat rotation results in apoptosis of osteoblastic ROS 17/2.8 cells. J. Bone Miner. Res. Off. J. Am. Soc. Bone Miner. Res. 2000, 15, 489–498. [Google Scholar] [CrossRef]
- Hasenstein, K.H.; van Loon, J.J.W.A.; Beysens, D.A. Clinostats and Other Rotating Systems-Design, Function and Limitations. In Generation and Applications of Extra-Terrestrial Environments on Earth; Deaniel, A., Beysens, J.J.W.A.v.L., Eds.; River Publishers: Gistrup, Denmark, 2015. [Google Scholar]
- Von Sachs, J.F. Ueber Ausschliessung Der Geotropischen und Heliotropischen Kruemmung Waehrend des Wachsthums. Würzburger Arbeiten 1879, 2, 209–225. [Google Scholar]
- Blancaflor, E.B.; Masson, P.H. Plant gravitropism. Unraveling the ups and downs of a complex process. Plant Physiol. 2003, 133, 1677–1690. [Google Scholar] [CrossRef] [PubMed]
- Hoson, T.; Kamisaka, S.; Masuda, Y.; Yamashita, M.; Buchen, B. Evaluation of the three-dimensional clinostat as a simulator of weightlessness. Planta 1997, 203, S187–S197. [Google Scholar] [CrossRef] [PubMed]
- Wuest, S.L.; Richard, S.; Kopp, S.; Grimm, D.; Egli, M. Simulated microgravity: Critical review on the use of random positioning machines for mammalian cell culture. BioMed Res. Int. 2015, 2015, 971474. [Google Scholar] [CrossRef] [PubMed]
- Borst, A.G.; van Loon, J.J.W.A. Technology and Developments for the Random Positioning Machine. Microgravity Sci. Technol. 2008, 21, 287. [Google Scholar] [CrossRef]
- Hauslage, J.; Cevik, V.; Hemmersbach, R. Pyrocystis noctiluca represents an excellent bioassay for shear forces induced in ground-based microgravity simulators (clinostat and random positioning machine). NPJ Microgravity 2017, 3, 12. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, R.P.; Goodwin, T.J.; Wolf, D.A. Cell culture for three-dimensional modeling in rotating-wall vessels: An application of simulated microgravity. J. Tissue Cult. Methods Tissue Cult. Assoc. Man. Celltissueand Organ Cult. Proced. 1992, 14, 51–57. [Google Scholar] [CrossRef]
- Liu, T.; Li, X.; Sun, X.; Ma, X.; Cui, Z. Analysis on forces and movement of cultivated particlesin a rotating wall vessel bioreactor. Biochem. Eng. J. 2003, 18, 97–104. [Google Scholar] [CrossRef]
- Berry, M.V.; Geim, A.K. Of flying frogs and levitrons. Eur. J. Phys. 1997, 18, 307. [Google Scholar] [CrossRef]
- Maret, G.; Dransfeld, K. Biomolecules and Polymers in High Steady Magnetic Fields. In Strong and Ultrastrong Magnetic Fields and Their Applications; Herlach, F., Ed.; Springer: Berlin, Germany, 1985; Volume 57, pp. 143–204. [Google Scholar]
- Schwarzenberg, M.; Pippia, P.; Meloni, M.A.; Cossu, G.; Cogoli-Greuter, M.; Cogoli, A. Signal transduction in T lymphocytes—A comparison of the data from space, the free fall machine and the random positioning machine. Adv. Space Res. 1999, 24, 793–800. [Google Scholar] [CrossRef]
- Mattok, C. Biorack on Spacelab IML-1; ESA Publications Division: Noordwijk, The Netherlands, 1995. [Google Scholar]
- Van Loon, J.J.; Folgering, E.H.; Bouten, C.V.; Veldhuijzen, J.P.; Smit, T.H. Inertial shear forces and the use of centrifuges in gravity research. What is the proper control? J. Biomech. Eng. 2003, 125, 342–346. [Google Scholar] [CrossRef]
- Ryskin, G. Brownian motion in a rotating fluid: Diffusivity is a function of the rotation rate. Phys. Rev. Lett. 1988, 61, 1442–1445. [Google Scholar] [CrossRef] [PubMed]
- Ingber, D. How cells (might) sense microgravity. FASEB J. 1999, 13, S3–S15. [Google Scholar] [CrossRef] [PubMed]
- Vorselen, D.; Roos, W.H.; MacKintosh, F.C.; Wuite, G.J.; van Loon, J.J. The role of the cytoskeleton in sensing changes in gravity by nonspecialized cells. FASEB J. 2014, 28, 536–547. [Google Scholar] [CrossRef] [PubMed]
- Comet, B. Limiting factors for human health and performance: Microgravity and reduced gravity. Study on the Survivability and Adaptation of Humans to Long-Duration Interplanetary and Planetary Environments. Technical Note. 2001. Available online: https://scholar.google.com/scholar?hl=de&as_sdt=0%2C5&q=41.%09Comet%2C+B.+Limiting+factors+for+human+health+and+performance%3A+Microgravity+and+reduced+gravity.&btnG=#d=gs_cit&u=%2Fscholar%3Fq%3Dinfo%3AUPctsa7Ug34J%3Ascholar.google.com%2F%26output%3Dcite%26scirp%3D0%26hl%3Dde (accessed on 13 January 2020).
- Frippiat, J.P.; Crucian, B.E.; De Quervain, D.J.; Grimm, D.; Montano, N.; Praun, S.; Roozendaal, B.; Schelling, G.; Thiel, M.; Ullrich, O. Towards human exploration of space: The THESEUS review series on immunology research priorities. NPJ Microgravity 2016, 2, 16040. [Google Scholar] [CrossRef] [PubMed]
- Choukèr, A.; Ullrich, O. The Immune System in Space: Are We Prepared? Conclusions, Outlook, and Recommendations. In The Immune System in Space: Are We Prepared; Springer Science & Business Media: Berlin, Germany, 2016; pp. 123–127. [Google Scholar]
- Clément, G. Fundamentals of Space Medicine; Springer Science & Business Media: Berlin, Germany, 2011; Volume 23. [Google Scholar]
- Board, S.S.; Council, N.R. Recapturing a Future for Space Exploration: Life and Physical Sciences Research for a New Era; National Academies Press: Washington, DC, USA, 2011. [Google Scholar]
- Thiel, C.S.; Tauber, S.; Christoffel, S.; Huge, A.; Lauber, B.A.; Polzer, J.; Paulsen, K.; Lier, H.; Engelmann, F.; Schmitz, B. Rapid coupling between gravitational forces and the transcriptome in human myelomonocytic U937 cells. Sci. Rep. 2018, 8, 13267. [Google Scholar] [CrossRef] [PubMed]
- Thiel, C.S.; Tauber, S.; Lauber, B.; Polzer, J.; Seebacher, C.; Uhl, R.; Neelam, S.; Zhang, Y.; Levine, H.; Ullrich, O. Rapid Morphological and Cytoskeletal Response to Microgravity in Human Primary Macrophages. Int. J. Mol. Sci. 2019, 20, 2402. [Google Scholar] [CrossRef]
- Lin, C.J.; Peery, J.H.; Schowalter, W. Simple shear flow round a rigid sphere: Inertial effects and suspension rheology. J. Fluid Mech. 1970, 44, 1–17. [Google Scholar] [CrossRef]
- Poe, G.; Acrivos, A. Closed-streamline flows past rotating single cylinders and spheres: Inertia effects. J. Fluid Mech. 1975, 72, 605–623. [Google Scholar] [CrossRef]
- Tajik, A.; Zhang, Y.; Wei, F.; Sun, J.; Jia, Q.; Zhou, W.; Singh, R.; Khanna, N.; Belmont, A.S.; Wang, N. Transcription upregulation via force-induced direct stretching of chromatin. Nat. Mater. 2016, 15, 1287. [Google Scholar] [CrossRef]
- Athirasala, A.; Hirsch, N.; Buxboim, A. Nuclear mechanotransduction: Sensing the force from within. Curr. Opin. Cell Biol. 2017, 46, 119–127. [Google Scholar] [CrossRef]
- Thorpe, S.D.; Lee, D.A. Dynamic regulation of nuclear architecture and mechanics—A rheostatic role for the nucleus in tailoring cellular mechanosensitivity. Nucleus 2017, 8, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Michaela Simmet, D.; Schwarzwalder, A.; Paulsen, K.; Tauber, S.; Engelmann, F.; Sandra Thiel, C.; Ullrich, O. Biotechnology for the investigation of the monocyte-macrophage-system in microgravity and space. Recent Pat. Space Technol. 2013, 3, 48–63. [Google Scholar] [CrossRef]
- Brungs, S.; Hauslage, J.; Hemmersbach, R. Validation of random positioning versus clinorotation using a macrophage model system. Microgravity Sci. Technol. 2019, 31, 223–230. [Google Scholar] [CrossRef]
- Tauber, S.; Christoffel, S.; Thiel, C.S.; Ullrich, O. Transcriptional Homeostasis of Oxidative Stress-Related Pathways in Altered Gravity. Int. J. Mol. Sci. 2018, 19, 2814. [Google Scholar] [CrossRef]
- Vogel, J.; Thiel, C.S.; Tauber, S.; Stockmann, C.; Gassmann, M.; Ullrich, O. Expression of Hypoxia-Inducible Factor 1alpha (HIF-1alpha) and Genes of Related Pathways in Altered Gravity. Int. J. Mol. Sci. 2019, 20, 436. [Google Scholar] [CrossRef]
- Bolstad, B.M.; Irizarry, R.A.; Astrand, M.; Speed, T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef]
- Rosenbluth, M.J.; Lam, W.A.; Fletcher, D.A. Force microscopy of nonadherent cells: A comparison of leukemia cell deformability. Biophys. J. 2006, 90, 2994–3003. [Google Scholar] [CrossRef]
- Semisch, A.; Ohle, J.; Witt, B.; Hartwig, A. Cytotoxicity and genotoxicity of nano-and microparticulate copper oxide: Role of solubility and intracellular bioavailability. Part. Fibre Toxicol. 2014, 11, 10. [Google Scholar] [CrossRef]


| GBF | TEXUS-51 | ||
|---|---|---|---|
| Gravity conditions and controls | Cell culture control | n/a | CC (cell culture control: cells kept under standard cell culture conditions in a cell culture incubator) |
| Hardware 1× g ground control | 1× g ground control [5 min] (sample exposure inside the pipettes used for centrifugation and 2D clinorotation experiments) | H/W 1× g GC (hardware 1× g ground control: ground control samples incubated in the hardware identical in construction to the flight hardware for identification of hardware-based effects) | |
| 1×gin-flight control | n/a | 1× g IF [5 min] (1× g in flight: sample exposure to 75s hypergravity max. 12.6× g plus 5 min 1× g centrifugation in the centrifuge on board the suborbital rocket during the flight) | |
| Baseline control | BL (filling and draining of pipettes for identification of pipetting effects) | n/a | |
| Hypergravity | 9× g centrifuge [5 min] (sample exposure to centrifugal forces of 9g) | TX hyp-g [75 s, max. 12.6× g] (sample exposure to hypergravity with a maximum of 12.6× g during the first 75 s of the rocket launch) | |
| Vector-averaged gravity (vag)/Microgravity (µg) | 2D clinostat [5 min] (sample exposure to vector averaged gravity) | TX µg [5 min] (sample exposure to 75 s, max. 12.6× g followed by 5 min microgravity during the suborbital rocket flight) |
| Significantly Differentially Expressed TCs in the GBF Experiments | |||||
|---|---|---|---|---|---|
| 1× g Control vs. BL | 9× g Centrifuge vs. 1× g Control | 2D Clinostat vs. 1× g Control | 2D Clinostat vs. 9× g Centrifuge | ||
| All differentially expressed transcript clusters | upregulated | 2125 | 3046 | 768 | 339 |
| downregulated | 496 | 2732 | 373 | 623 | |
| total number | 2621 | 5778 | 1141 | 962 | |
| Annotated differentially expressed transcript clusters | upregulated | 890 | 2089 | 475 | 149 |
| downregulated | 187 | 1238 | 155 | 355 | |
| total number | 1077 | 3327 | 630 | 504 | |
| Total Number of TCs | Up or Down-Regulated TCs * | Average FC of 9× g Centrifuge vs. 1× g Control | Min./Max. FC of 9× g Centrifuge vs. 1× g Control | Average FC of 2D Clinostat vs. 1× g Control | Min./Max. FC of 2D Clinostat vs. 1× g Control | Average FC of 2D Clinostat vs. 9× g Centrifuge | Min./Max. FC of 2D Clinostat vs. 9× g Centrifuge | |||
|---|---|---|---|---|---|---|---|---|---|---|
| hypergravity-sensitive transcript clusters Differentially expressed TCs in 9× g centrifuge vs. 1× g control | all (annotated) | 4596 (2744) | ↑ | 2753 (1945) | 1.52 (1.49) | 4.28 (2.60) | - | - | - | - |
| ↓ | 1843 (799) | −1.44 (−1.43) | −4.00 (−2.39) | - | - | - | - | |||
| vector-averaged gravity-sensitive transcript clusters Differentially expressed TCs in 2D clinostat vs. 1× g control | all (annotated) | 871 (495) | ↑ | 644 (415) | - | - | 1.39 (1.37) | 2.38 (1.74) | - | - |
| ↓ | 227 (80) | - | - | −1.38 (−1.37) | −2.22 (−1.78) | - | - | |||
| 2D clinostat vs. 9× g centrifuge-sensitive transcript clusters Differentially expressed TCs in 2D clinostat vs. 9× g centrifuge | all (annotated) | 752 (415) | ↑ | 231 (106) | - | - | - | - | 1.41 (1.39) | 2.43 (1.87) |
| ↓ | 521 (309) | - | - | - | - | −1.40 (−1.38) | −2.12 (−1.93) | |||
| hypergravity and vector-averaged gravity-sensitive transcript clusters Differentially expressed TCs in 9g centrifuge vs. 1× g control and in 2D clinostat vs. 1× g control | all (annotated) | 798 (476) | ↑ | 618 * (409 *) | 1.75 (1.71) | 4.28 (2.60) | 1.40 (1.37) | 2.38 (1.74) | - | - |
| ↓ | 180 * (67 *) | −1.64 (−1.70) | −2.39 (−2.39) | −1.39 (−1.38) | −2.22 (−1.78) | - | - | |||
| Intersecting set of all three gravity condition comparison groups Differentially expressed TCs in 2D clinostat vs. 1× g control and in 9× g centrifuge vs. 1× g control and in 2D clinostat vs. 9× g centrifuge. # | all (annotated) | 222 (148) | ↑ | 199 * (134 *) | 2.02 (1.94) | 4.28 (2.44) | 1.43 (1.4) | 2.38 (1.67) | −1.41 (−1.39) | −1.86 (−1.6) |
| ↓ | 23 * (14 *) | −2.03 (−2.12) | −2.22 (−2.22) | −1.42 (−1.46) | −1.63 (−1.63) | 1.43 (1.46) | 1.57 (1.75) |
| Significantly Differentially Expressed TCs in the TEXUS-51 Experiments | ||||||||
|---|---|---|---|---|---|---|---|---|
| H/W 1× g GC vs. CC | 1× g IF vs. H/W 1× g GC | TX hyp-g vs. H/W 1× g GC | TX hyp-g vs. 1× g IF | TX µg vs. H/W 1× g GC | TX µg vs. 1× g IF | TX µg vs. TX hyp-g | ||
| All differentially expressed transcript clusters | upregulated | 15,995 | 571 | 2874 | 1842 | 2295 | 1101 | 23 |
| downregulated | 7886 | 536 | 1144 | 731 | 1207 | 1027 | 23 | |
| total number | 23,881 | 1107 | 4018 | 2573 | 3502 | 2128 | 46 | |
| Annotated differentially expressed transcript clusters | upregulated | 9243 | 258 | 2039 | 1270 | 1575 | 721 | 5 |
| downregulated | 4828 | 282 | 426 | 193 | 425 | 315 | 2 | |
| total number | 14,071 | 540 | 2465 | 1463 | 2000 | 1036 | 7 | |
| Total Number of TCs | Up or Down-Regulated TCs * | Average FC of TX hyp-g vs. 1× g IF | Min./Max. FC of TX hyp-g vs. 1× g IF | Average FC of TX µg vs. 1× g IF | Min./Max. FC of TX µg vs. 1× g IF | Average FC of TX µg vs. TX hyp-g | Min./Max. FC of TX µg vs. TX hyp-g | |||
|---|---|---|---|---|---|---|---|---|---|---|
| hypergravity-sensitive transcript clusters Differentially expressed TCs in TX hyp-g vs. 1× g IF | all (annotated) | 346 (112) | ↑ | 104 (56) | 1.45 (1.40) | 1.94 (1.86) | - | - | - | - |
| ↓ | 242 (56) | −1.36 (−1.33) | −1.92 (−1.40) | - | - | - | - | |||
| microgravity-sensitive transcript clusters Differentially expressed TCs in TX µg vs. 1× g IF | all (annotated) | 396 (114) | ↑ | 72 (38) | - | - | 1.40 (1.39) | 1.85 (1.85) | - | - |
| ↓ | 324 (76) | - | - | −1.36 (−1.33) | −1.83 (−1.49) | - | - | |||
| TX µg vs. TX hyp-g-sensitive transcript clusters Differentially expressed TCs in TX µg vs. TX hyp-g | all (annotated) | 19 (1) | ↑ | 4 (0) | - | - | - | - | 1.37 (n/a) | 1.43 (n/a) |
| ↓ | 15 (1) | - | - | - | - | −1.39 (−1.33) | −1.68 (−1.33) | |||
| hypergravity and microgravity-sensitive transcript clusters Differentially expressed TCs in TX hyp-g vs. 1× g IF and in TX µg vs. 1× g IF | all (annotated) | 134 (42) | ↑ | 54 * (31 *) | 1.45 (1.44) | 1.94 (1.86) | 1.42 (1.41) | 1.85 (1.85) | - | - |
| ↓ | 80 * (11 *) | −1.39 (−1.34) | −1.92 (−1.40) | −1.40 (−1.34) | −1.83 (−1.41) | - | - |
| Ground Based Facilities Fold Changes | TEXUS-51 Fold Changes | ||||
|---|---|---|---|---|---|
| Gene Symbol | Transcript Cluster ID | 9× g Centrifuge vs. 1× g Control | 2D Clinostat vs. 1× g Control | TX hyp-g vs. 1× g IF | TX µg vs. 1× g IF |
| Hypergravity-sensitive transcript clusters | |||||
| ATP6V1A | TC03000583.hg.1 | 1.57 | 1.34 | ||
| BCAT1 | TC12001309.hg.1 | 1.31 | 1.35 | ||
| CAT | TC11000327.hg.1 | 1.39 | 1.31 | ||
| CBFB | TC16000528.hg.1 | 1.60 | 1.42 | ||
| CERS6 | TC02000996.hg.1 | 1.37 | 1.42 | ||
| EAF1 | TC03000096.hg.1 | 1.39 | 1.30 | ||
| ETS1 | TC11002439.hg.1 | 1.55 | 1.38 | ||
| G3BP1 | TC05000844.hg.1 | 1.54 | 1.32 | ||
| GAN | TC16000638.hg.1 | 1.33 | 1.35 | ||
| KPNB1 | TC17000611.hg.1 | 1.93 | 1.61 | ||
| NET1 | TC10000047.hg.1 | 1.38 | 1.45 | ||
| NUDT3 | TC06004129.hg.1 | 1.68 | 1.39 | ||
| PAG1 | TC08001361.hg.1 | 1.32 | 1.30 | ||
| PELI2 | TC14000332.hg.1 | 1.43 | 1.36 | ||
| POM121L9P | TC05000487.hg.1 | 1.42 | −1.36 | ||
| POM121L9P | TC05000309.hg.1 | 1.41 | −1.31 | ||
| POM121L9P | TC05000321.hg.1 | 1.41 | −1.31 | ||
| POM121L9P | TC06000218.hg.1 | 1.41 | −1.31 | ||
| POM121L9P | TC06000691.hg.1 | 1.41 | −1.31 | ||
| PRPS1 | TC0X000526.hg.1 | 1.37 | 1.31 | ||
| RBM3 | TC0X000255.hg.1 | 1.35 | 1.34 | ||
| RBM8A | TC01001093.hg.1 | 1.44 | 1.55 | ||
| RSC1A1; DDI2 | TC01000193.hg.1 | 1.44 | 1.32 | ||
| SAMD9 | TC07001605.hg.1 | −1.34 | 1.35 | ||
| SFT2D2 | TC01006289.hg.1 | 1.72 | 1.34 | ||
| SRP14 | TC15001228.hg.1 | 1.42 | 1.41 | ||
| SRSF6 | TC20000316.hg.1 | 1.38 | 1.39 | ||
| TMED8 | TC14001343.hg.1 | 1.38 | 1.31 | ||
| Vector-averaged gravity/flight-induced microgravity-sensitive transcript clusters | |||||
| G3BP1 | TC05000844.hg.1 | 1.30 | 1.30 | ||
| KPNB1 | TC17000611.hg.1 | 1.38 | 1.53 | ||
| NUDT3 | TC06004129.hg.1 | 1.36 | 1.45 | ||
| POMK; SGK196 | TC08000332.hg.1 | 1.43 | 1.32 | ||
| SFT2D2 | TC01006289.hg.1 | 1.39 | 1.36 | ||
| Hypergravity and vector-averaged gravity/flight-induced microgravity double-sensitive transcript clusters | |||||
| G3BP1 | TC05000844.hg.1 | 1.54 | 1.30 | 1.32 | 1.30 |
| KPNB1 | TC17000611.hg.1 | 1.93 | 1.38 | 1.61 | 1.53 |
| NUDT3 | TC06004129.hg.1 | 1.68 | 1.36 | 1.39 | 1.45 |
| SFT2D2 | TC01006289.hg.1 | 1.72 | 1.39 | 1.34 | 1.36 |
| Category | Enriched Term | Gene Count | % of Genes | Modified Fisher p-Value | Fold Enrichment |
|---|---|---|---|---|---|
| GOTERM_BP_DIRECT | Transport | 5 | 20 | 9.9 × 10−4 | 10.5 |
| GOTERM_CC_DIRECT | Cytosol | 11 | 44 | 4.4 × 10−3 | 2.5 |
| GOTERM_MF_DIRECT | Nucleotide binding | 4 | 16 | 8.8 × 10−3 | 8.8 |
| GOTERM_MF_DIRECT | Poly(A) RNA binding | 6 | 24 | 1.1 × 10−2 | 4.1 |
| GOTERM_CC_DIRECT | Nuclear speck | 3 | 12 | 2.6 × 10−2 | 11.3 |
| GOTERM_MF_DIRECT | RNA binding | 4 | 16 | 1.9 × 10−2 | 5.6 |
| GOTERM_CC_DIRECT | Intracellular membrane-bounded organelle | 4 | 16 | 3.2 × 10−2 | 5.4 |
| GOTERM_BP_DIRECT | Regulation of alternative mRNA splicing, via spliceosome | 2 | 8 | 4.9 × 10−2 | 38.4 |
| Sorted by regulation in 2D clinostat vs. 1× g control | 2D Clinostat vs. 1× g Control | TX µg vs. 1× g IF | 9× g Centrifuge vs. 1× g Control | TX hyp-g vs. 1× g IF | ||||||||||||||
| All | Annotated | All | Annotated | All | Annotated | All | Annotated | |||||||||||
| up-regulated | 181 | 0.42% | 127 | 0.61% | up-regulated | 8 | 4.4% | 5 | 3.9% | 171 | 94.5% | 125 | 98.4% | 8 | 4.4% | 5 | 3.9% | |
| down-regulated | 2 | 1.1% | 0 | 0.0% | 0 | 0.0% | 0 | 0.0% | 1 | 0.6% | 0 | 0.0% | ||||||
| non-responsive | 171 | 94.5% | 122 | 96.1% | 10 | 5.5% | 2 | 1.6% | 172 | 95.0% | 122 | 96.1% | ||||||
| down-regulated | 45 | 0.11% | 12 | 0.06% | up-regulated | 0 | 0.0% | 0 | 0.0% | 0 | 0.0% | 0 | 0.0% | 0 | 0.0% | 0 | 0.0% | |
| down-regulated | 1 | 2.2% | 0 | 0.0% | 31 | 68.9% | 7 | 58.3% | 0 | 0.0% | 0 | 0.0% | ||||||
| non-responsive | 44 | 97.8% | 12 | 100.0% | 14 | 31.1% | 5 | 41.7% | 45 | 100.0% | 12 | 100.0% | ||||||
| non-responsive | 42442 | 99.47% | 20748 | 99.33% | up-regulated | 61 | 0.1% | 32 | 0.2% | 877 | 2.1% | 692 | 3.3% | 82 | 0.2% | 50 | 0.2% | |
| down-regulated | 295 | 0.7% | 75 | 0.4% | 422 | 1.0% | 159 | 0.8% | 209 | 0.5% | 56 | 0.3% | ||||||
| non-responsive | 42086 | 99.2% | 20641 | 99.5% | 41143 | 96.9% | 19897 | 95.9% | 42151 | 99.3% | 20642 | 99.5% | ||||||
| Sorted by regulation in TX µg vs. 1× g IF | TX µg vs. 1× g IF | 2D Clinostat vs. 1× g Control | 9× g Centrifuge vs. 1× g Control | TX hyp-g vs. 1× g IF | ||||||||||||||
| All | Annotated | All | Annotated | All | Annotated | All | Annotated | |||||||||||
| up-regulated | 69 | 0.16% | 37 | 0.18% | up-regulated | 8 | 11.6% | 5 | 13.5% | 24 | 34.8% | 16 | 43.2% | 51 | 73.91% | 30 | 81.1% | |
| down-regulated | 0 | 0.0% | 0 | 0.0% | 0 | 0.0% | 0 | 0.0% | 0 | 0.00% | 0 | 0.0% | ||||||
| non-responsive | 61 | 88.4% | 32 | 86.5% | 45 | 65.2% | 21 | 56.8% | 18 | 26.09% | 7 | 18.9% | ||||||
| down-regulated | 298 | 0.70% | 75 | 0.36% | up-regulated | 2 | 0.7% | 0 | 0.0% | 3 | 1.0% | 0 | 0.0% | 0 | 0.00% | 0 | 0.0% | |
| down-regulated | 1 | 0.3% | 0 | 0.0% | 7 | 2.3% | 3 | 4.0% | 65 | 21.81% | 11 | 14.7% | ||||||
| non-responsive | 295 | 99.0% | 75 | 100.0% | 288 | 96.6% | 72 | 96.0% | 233 | 78.19% | 64 | 85.3% | ||||||
| non-responsive | 42301 | 99.14% | 20775 | 99.46% | up-regulated | 171 | 0.4% | 122 | 0.6% | 1021 | 2.4% | 801 | 3.9% | 39 | 0.09% | 25 | 0.1% | |
| down-regulated | 44 | 0.1% | 12 | 0.1% | 446 | 1.1% | 163 | 0.8% | 145 | 0.34% | 45 | 0.2% | ||||||
| non-responsive | 42086 | 99.5% | 20641 | 99.4% | 40834 | 96.5% | 19811 | 95.4% | 42117 | 99.57% | 20705 | 99.7% | ||||||
| Sorted by regulation in 9g centrifuge vs. 1× g control | 9× g Centrifuge vs. 1× g Control | 2D Clinostat vs. 1× g Control | TX hyp-g vs. 1× g IF | TX µg vs. 1× g IF | ||||||||||||||
| All | Annotated | All | Annotated | All | Annotated | All | Annotated | |||||||||||
| up-regulated | 1048 | 2.46% | 817 | 3.91% | up-regulated | 171 | 16.3% | 125 | 15.3% | 29 | 2.8% | 22 | 2.7% | 24 | 2.3% | 16 | 2.0% | |
| down-regulated | 0 | 0.0% | 0 | 0.0% | 8 | 0.8% | 5 | 0.6% | 3 | 0.3% | 0 | 0.0% | ||||||
| non-responsive | 877 | 83.7% | 692 | 84.7% | 1011 | 96.5% | 790 | 96.7% | 1021 | 97.4% | 801 | 98.0% | ||||||
| down-regulated | 453 | 1.06% | 166 | 0.79% | up-regulated | 0 | 0.0% | 0 | 0.0% | 1 | 0.2% | 1 | 0.6% | 0 | 0.0% | 0 | 0.0% | |
| down-regulated | 31 | 6.8% | 7 | 4.2% | 4 | 0.9% | 0 | 0.0% | 7 | 1.5% | 3 | 1.8% | ||||||
| non-responsive | 422 | 93.2% | 159 | 95.8% | 448 | 98.9% | 165 | 99.4% | 446 | 98.5% | 163 | 98.2% | ||||||
| non-responsive | 41167 | 96.48% | 19904 | 95.29% | up-regulated | 10 | 0.0% | 2 | 0.0% | 60 | 0.1% | 32 | 0.2% | 45 | 0.1% | 21 | 0.1% | |
| down-regulated | 14 | 0.0% | 5 | 0.0% | 198 | 0.5% | 51 | 0.3% | 288 | 0.7% | 72 | 0.4% | ||||||
| non-responsive | 41143 | 99.9% | 19897 | 100.0% | 40909 | 99.4% | 19821 | 99.6% | 40834 | 99.2% | 19811 | 99.5% | ||||||
| Sorted by regulation in TX hyp-g vs. 1× g IF | TX hyp-g vs. 1× g IF | 2D Clinostat vs. 1× g Control | 9× g Centrifuge vs. 1× g Control | TX µg vs. 1× g IF | ||||||||||||||
| All | Annotated | All | Annotated | All | Annotated | All | Annotated | |||||||||||
| up-regulated | 90 | 0.21% | 55 | 0.26% | up-regulated | 8 | 8.9% | 5 | 9.1% | 29 | 32.2% | 22 | 40.0% | 51 | 56.7% | 30 | 54.5% | |
| down-regulated | 0 | 0.0% | 0 | 0.0% | 1 | 1.1% | 1 | 1.8% | 0 | 0.0% | 0 | 0.0% | ||||||
| non-responsive | 82 | 91.1% | 50 | 90.9% | 60 | 66.7% | 32 | 58.2% | 39 | 43.3% | 25 | 45.5% | ||||||
| down-regulated | 210 | 0.49% | 56 | 0.27% | up-regulated | 1 | 0.5% | 0 | 0.0% | 8 | 3.8% | 5 | 8.9% | 0 | 0.0% | 0 | 0.0% | |
| down-regulated | 0 | 0.0% | 0 | 0.0% | 4 | 1.9% | 0 | 0.0% | 65 | 31.0% | 11 | 19.6% | ||||||
| non-responsive | 209 | 99.5% | 56 | 100.0% | 198 | 94.3% | 51 | 91.1% | 145 | 69.0% | 45 | 80.4% | ||||||
| non-responsive | 42368 | 99.30% | 20776 | 99.47% | up-regulated | 172 | 0.4% | 122 | 0.6% | 1011 | 2.4% | 790 | 3.8% | 18 | 0.0% | 7 | 0.0% | |
| down-regulated | 45 | 0.1% | 12 | 0.1% | 448 | 1.1% | 165 | 0.8% | 233 | 0.5% | 64 | 0.3% | ||||||
| non-responsive | 42151 | 99.5% | 20642 | 99.4% | 40909 | 96.6% | 19821 | 95.4% | 42117 | 99.4% | 20705 | 99.7% | ||||||
| Condition | Gene ID | ENSEMBL Gene Name | UniProt Protein Name | Shortened Description (UniProt) |
|---|---|---|---|---|
| Hyp-g | G3BP1 | G3BP stress granule assembly factor 1 | Ras GTPase-activating protein-binding protein 1 | ATP- and magnesium-dependent helicase that plays an essential role in innate immunity. |
| Hyp-g & µg | KPNB1 | karyopherin subunit beta 1 | Importin subunit beta-1 | Functions in nuclear protein import, either in association with an adapter protein, like an importin-alpha subunit, which binds to nuclear localization signals (NLS) in cargo substrates, or by acting as autonomous nuclear transport receptor. |
| Hyp-g | NUDT3 | nudix hydrolase 3 | Diphosphoinositol polyphosphate phosphohydrolase 1 | Cleaves a beta-phosphate from the diphosphate groups in PP-InsP5 (diphosphoinositol pentakisphosphate) and [PP]2-InsP4 (bisdiphosphoinositol tetrakisphosphate), suggesting that it may play a role in signal transduction. |
| Hyp-g | POMK | protein O-mannose kinase | protein O-mannose kinase | Generates phosphorylated O-mannosyl trisaccharide which is a carbohydrate structure present in alpha-dystroglycan (DAG1), which is required for binding laminin G-like domain-containing extracellular proteins with high affinity. |
| Hyp-g | SFT2D2 | SFT2 domain containing 2 | vesicle transport protein SFT2B | May be involved in fusion of retrograde transport vesicles derived from an endocytic compartment with the Golgi complex. |
| µg | CBFB | core-binding factor subunit beta | core-binding factor subunit beta | Forms the heterodimeric complex core-binding factor (CBF) with RUNX family proteins. RUNX members modulate the transcription of their target genes, within their regulatory regions via their runt domain, while CBFB is a non-DNA-binding regulatory subunit that allosterically enhances the sequence-specific DNA-binding capacity of RUNX. |
| µg | SAMD9 | sterile alpha motif domain containing 9 | sterile alpha motif domain-containing protein 9 | May play a role in the inflammatory response to tissue injury and the control of extra-osseous calcification, acting as a downstream target of TNF-alpha signaling. |
| µg | SRSF6 | serine and arginine rich splicing factor 6 | serine/arginine-rich splicing factor 6 | Plays a role in constitutive splicing and modulates the selection of alternative splice sites. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiel, C.S.; Christoffel, S.; Tauber, S.; Vahlensieck, C.; de Zélicourt, D.; Layer, L.E.; Lauber, B.; Polzer, J.; Ullrich, O. Rapid Cellular Perception of Gravitational Forces in Human Jurkat T Cells and Transduction into Gene Expression Regulation. Int. J. Mol. Sci. 2020, 21, 514. https://doi.org/10.3390/ijms21020514
Thiel CS, Christoffel S, Tauber S, Vahlensieck C, de Zélicourt D, Layer LE, Lauber B, Polzer J, Ullrich O. Rapid Cellular Perception of Gravitational Forces in Human Jurkat T Cells and Transduction into Gene Expression Regulation. International Journal of Molecular Sciences. 2020; 21(2):514. https://doi.org/10.3390/ijms21020514
Chicago/Turabian StyleThiel, Cora Sandra, Swantje Christoffel, Svantje Tauber, Christian Vahlensieck, Diane de Zélicourt, Liliana E. Layer, Beatrice Lauber, Jennifer Polzer, and Oliver Ullrich. 2020. "Rapid Cellular Perception of Gravitational Forces in Human Jurkat T Cells and Transduction into Gene Expression Regulation" International Journal of Molecular Sciences 21, no. 2: 514. https://doi.org/10.3390/ijms21020514
APA StyleThiel, C. S., Christoffel, S., Tauber, S., Vahlensieck, C., de Zélicourt, D., Layer, L. E., Lauber, B., Polzer, J., & Ullrich, O. (2020). Rapid Cellular Perception of Gravitational Forces in Human Jurkat T Cells and Transduction into Gene Expression Regulation. International Journal of Molecular Sciences, 21(2), 514. https://doi.org/10.3390/ijms21020514







