Small-Angle Scattering and Multifractal Analysis of DNA Sequences
Abstract
1. Introduction
2. Theoretical Background
2.1. Iterated Function Systems and Chaos Game Representation of DNA Sequences
2.2. Fractals and Multifractals
2.3. Small-Angle Scattering
3. Results and Discussion
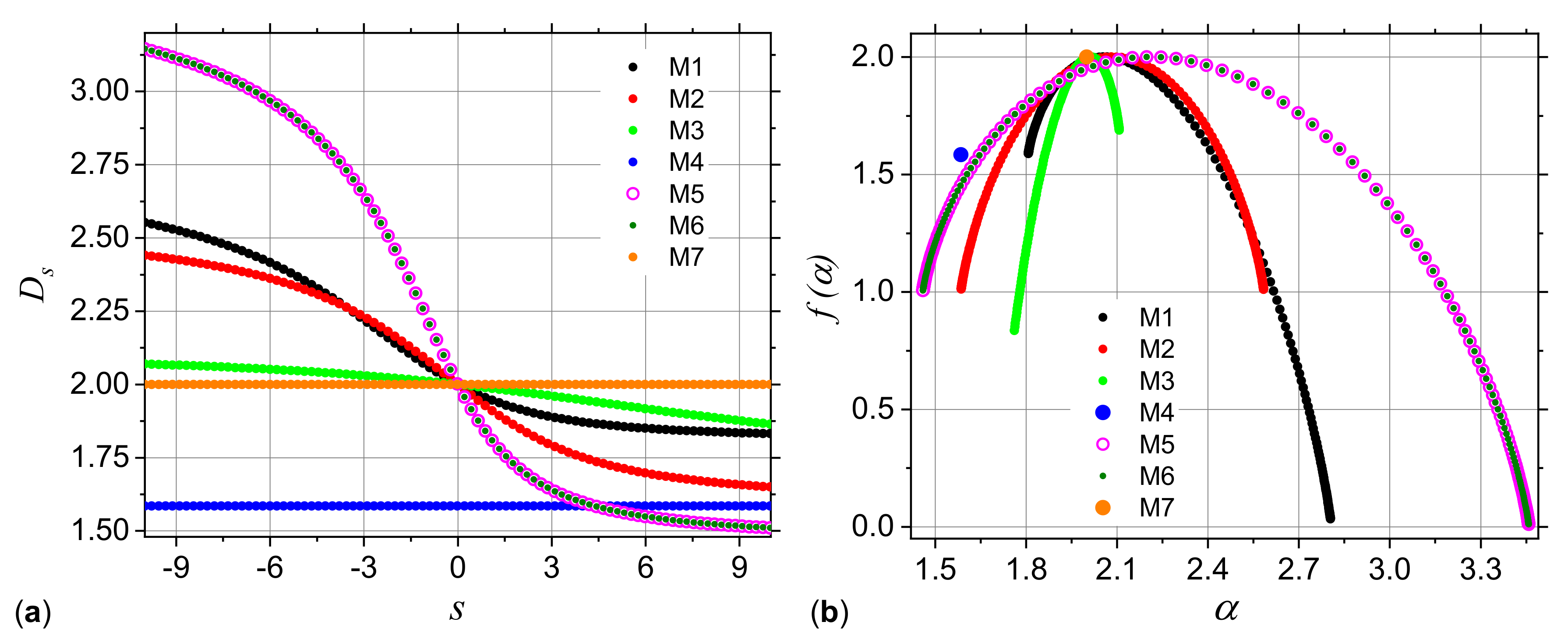
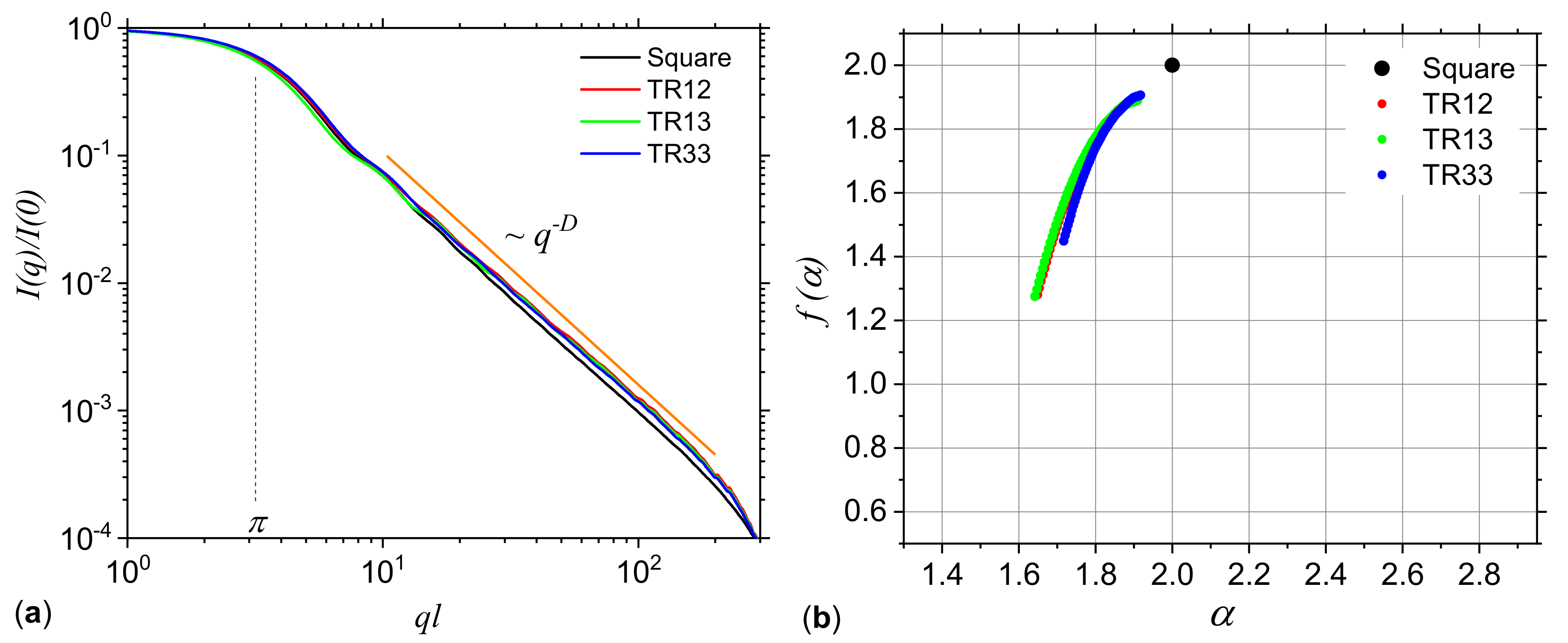
3.1. Analysis of Theoretical Models
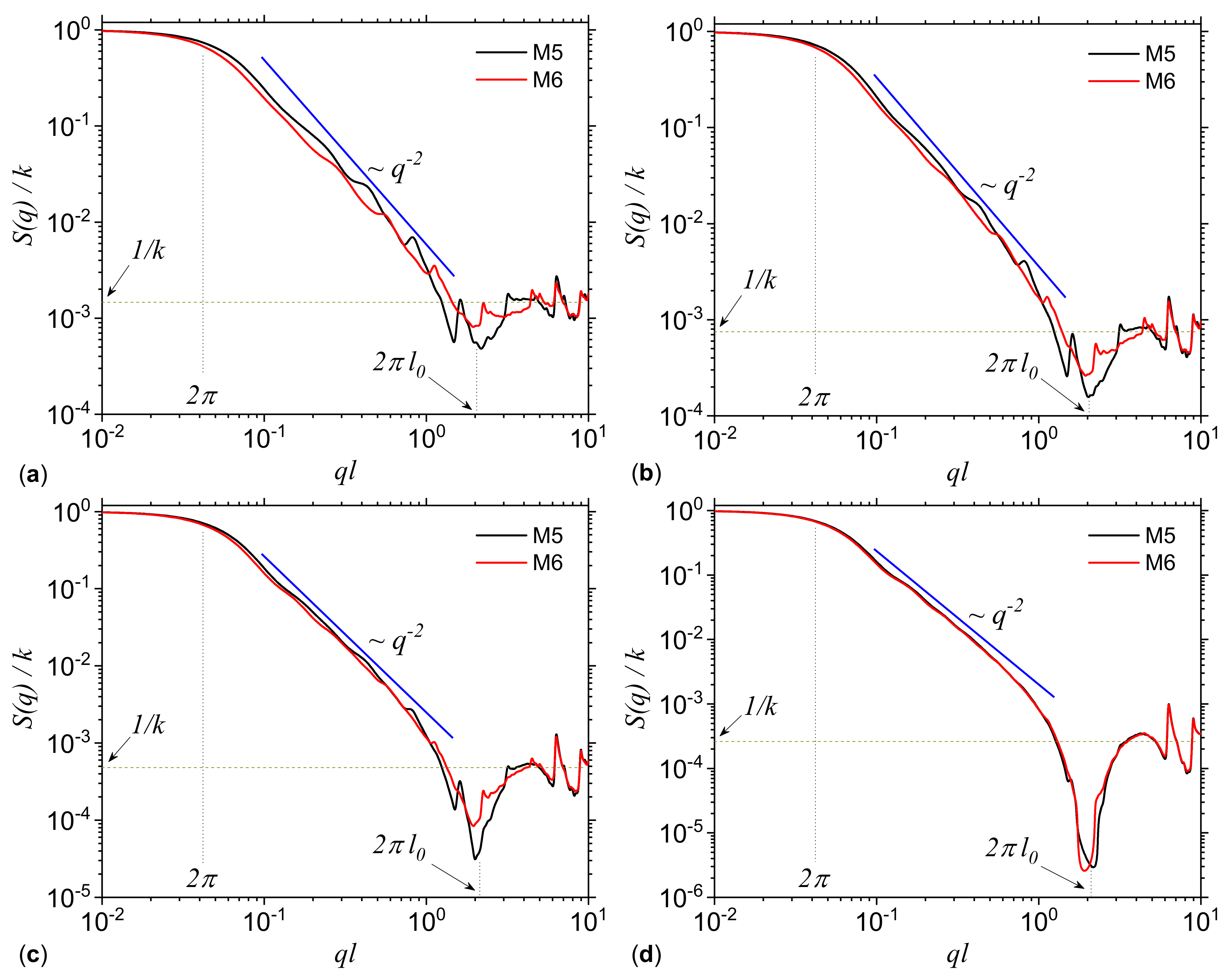
3.1.1. Multiplicative Deterministic Cascades
3.1.2. Missing Sequences Models
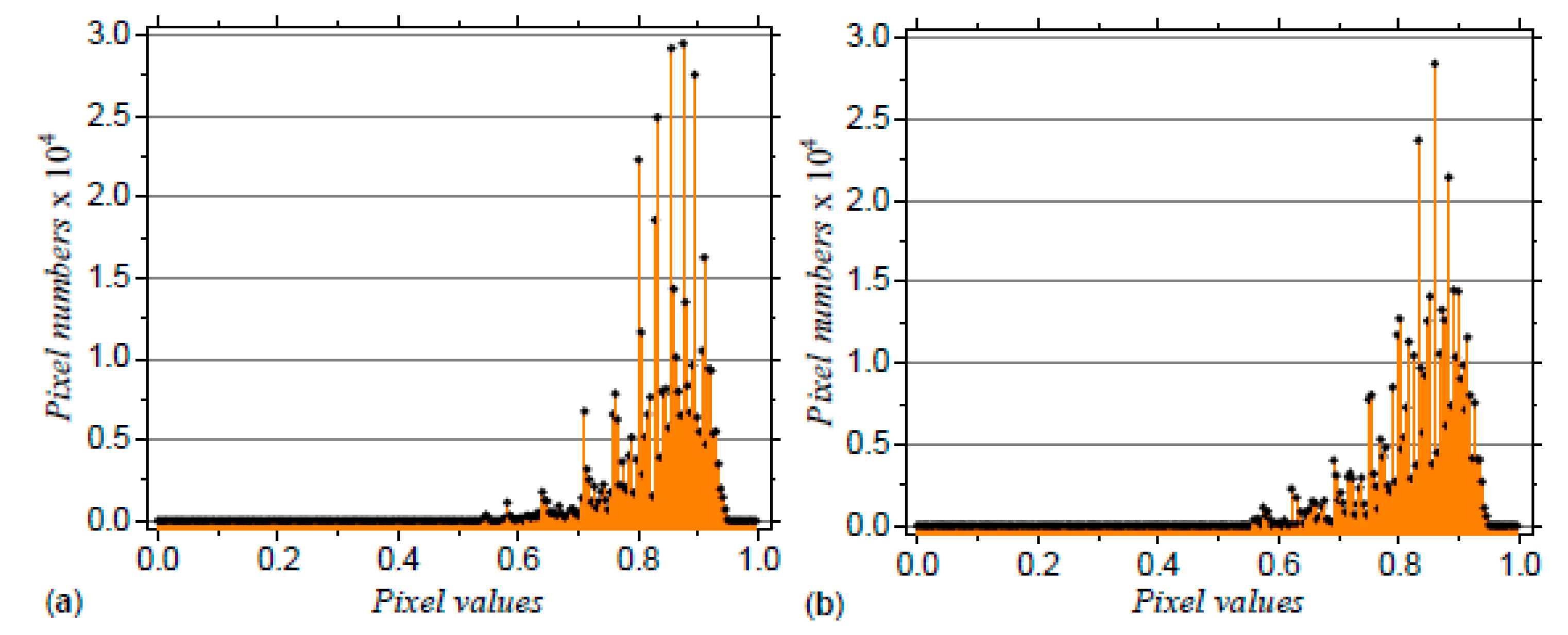
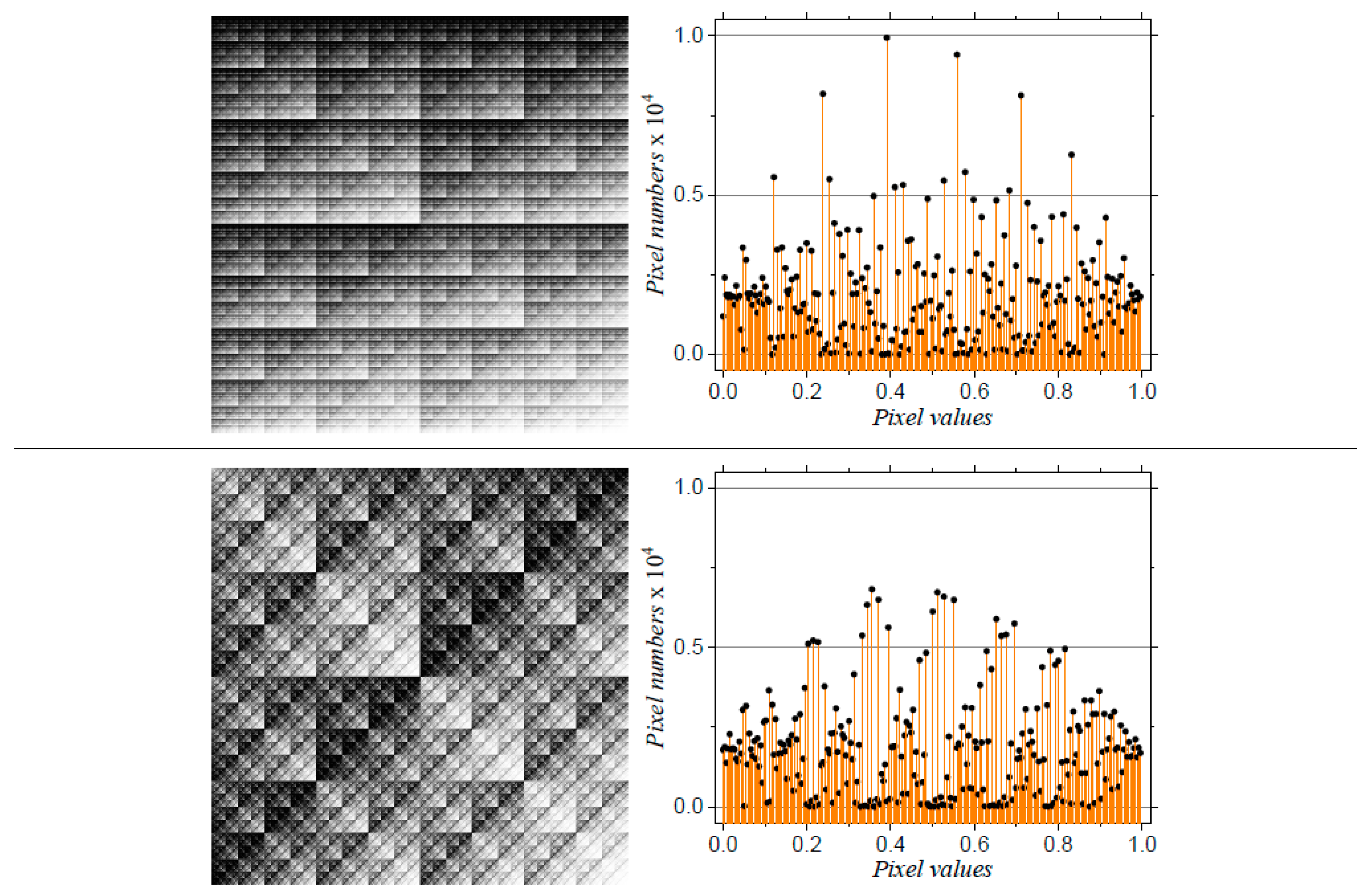
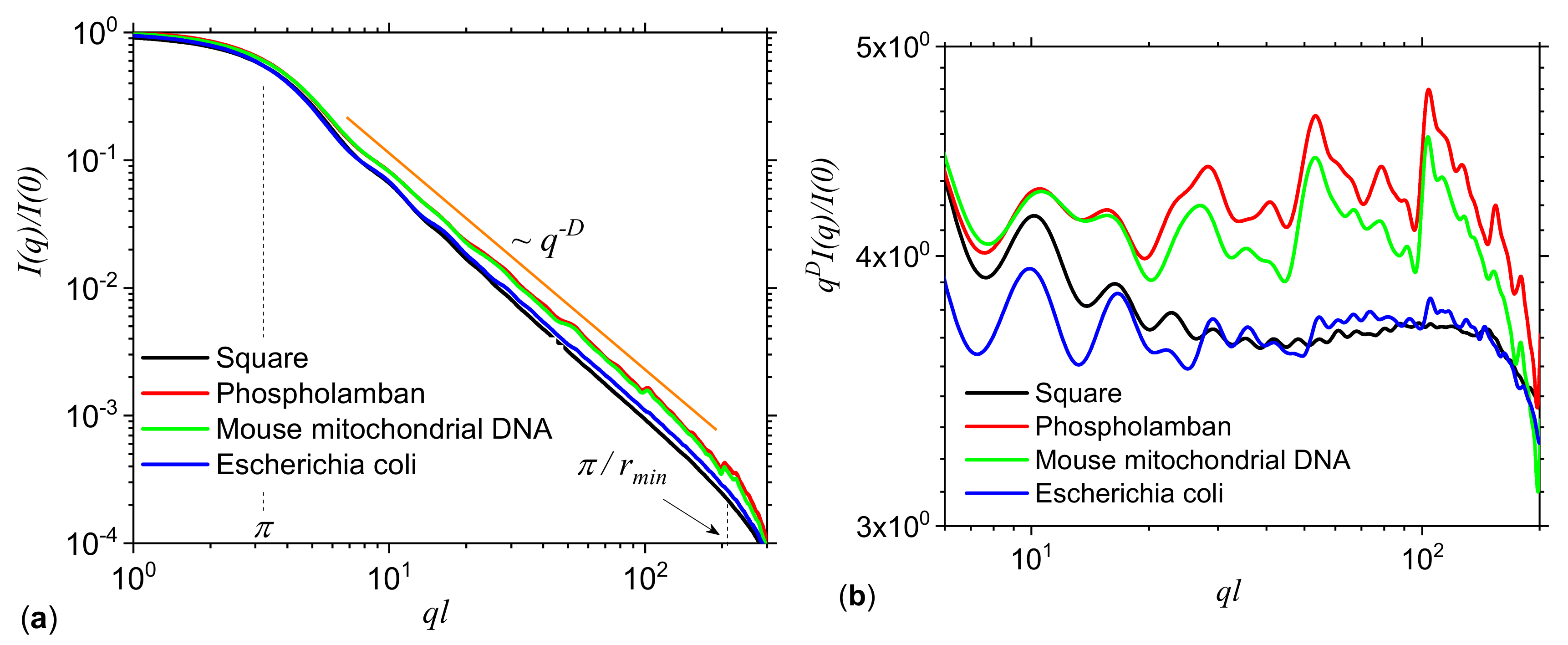
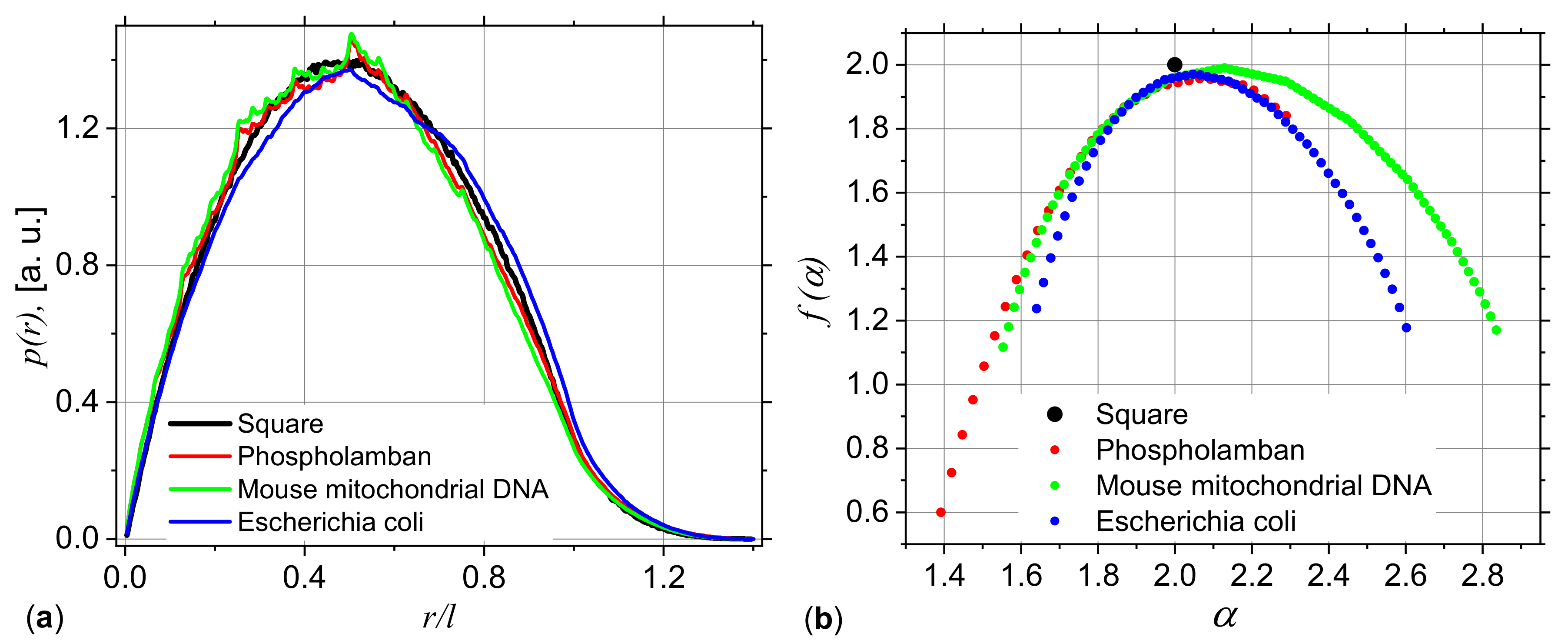
3.2. Application to DNA Sequences: Phospholamban, Mouse mitochondrion and Escherichia coli
4. Conclusions
Funding
Conflicts of Interest
References
- Arneodo, A.; Vaillant, C.; Audit, B.; Argoul, F.; d’Aubenton Carafa, Y.; Thermes, C. Multi-scale coding of genomic information: From DNA sequence to genome structure and function. Phys. Rep. 2011, 498, 45–188. [Google Scholar] [CrossRef]
- Felsenfeld, G.; Groudine, M. Controlling the double helix. Nature 2003, 421, 448–453. [Google Scholar] [CrossRef] [PubMed]
- Albrecht-Buehler, G. Fractal genome sequences. Gene 2012, 498, 20–27. [Google Scholar] [CrossRef] [PubMed]
- Albuquerque, E.L.; Fulco, U.L.; Freire, V.N.; Caetano, E.W.S.; Lyra, M.L.; de Moura, F.A.B.F. DNA-based nanobiostructured devices: The role of quasiperiodicity and correlation effects. Phys. Rep. 2014, 535, 139–209. [Google Scholar] [CrossRef]
- Niu, X.H.; Hu, X.H.; Shi, F.; Xia, J.B. Predicting DNA binding proteins using support vector machine with hybrid fractal features. J. Theor. Biol. 2014, 343, 186–192. [Google Scholar] [CrossRef]
- Lennon, F.E.; Cianci, G.C.; Cipriai, N.A.; Hensing, T.A.; Zhang, H.J.; Chen, C.T.; Murgu, S.T.; Vokes, E.E.; Vannier, M.W.; Salgia, R. Lung cancer—A fractal viewpoint. Nat. Rev. Clin. Oncol. 2015, 12, 664–675. [Google Scholar] [CrossRef]
- Babic, M.; Mihelic, J.; Calì, M. Complex Network Characterization Using Graph Theory and Fractal Geometry: The Case Study of Lung Cancer DNA Sequences. Appl. Sci. 2020, 10, 3037. [Google Scholar] [CrossRef]
- Li, W. Mutual information functions versus correlation functions. J. Stat. Phys. 1990, 60, 823–837. [Google Scholar] [CrossRef]
- Voss, R.F. Evolution of long-range fractal correlations and 1/f noise in DNA base sequences. Phys. Rev. Lett. 1992, 68, 3805–3808. [Google Scholar] [CrossRef]
- Havlin, S.; Buldyrev, S.V.; Goldberger, A.L.; Mantegna, R.N.; Peng, C.K.; Simons, M.; Stanley, H.E. Statistical and linguistic features of DNA sequences. Fractals 1995, 3, 269–284. [Google Scholar] [CrossRef]
- Herzel, H.; Große, I. Measuring correlations in symbol sequences. Phys. A Stat. Mech. Appl. 1995, 216, 518–542. [Google Scholar] [CrossRef]
- Bernaola-Galván, P.; Román-Roldán, R.; Oliver, J.L. Compositional segmentation and long-range fractal correlations in DNA sequences. Phys. Rev. E 1996, 53, 5181–5189. [Google Scholar] [CrossRef] [PubMed]
- Arneodo, A.; d’Aubenton Carafa, Y.; Bacry, E.; Graves, P.V.; Muzy, J.F.; Thermes, C. Wavelet based fractal analysis of DNA sequences. Phys. D Nonlinear Phenom. 1996, 96, 291–320. [Google Scholar] [CrossRef]
- Jeffrey, H.J. Chaos game representation of gene structure. Nucleic Acids Res. 1990, 18, 2163–2170. [Google Scholar] [CrossRef]
- Hoang, T.; Yin, C.; Yau, S.S.T. Numerical encoding of DNA sequences by chaos game representation with application in similarity comparison. Genomics 2016, 108, 134–142. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, J.M.; Rodriguez, M.A.; Abramson, G. Multifractal analysis of DNA sequences using a novel chaos-game representation. Phys. A Stat. Mech. Appl. 2001, 300, 271–284. [Google Scholar] [CrossRef]
- Han, J.-J.; Fu, W.-J. Wavelet-based multifractal analysis of DNA sequences by using chaos-game representation. Chin. Phys. B 2010, 19, 010205. [Google Scholar] [CrossRef]
- Yu, Z.G.; Anh, V.; Lau, K.S. Chaos game representation of protein sequences based on the detailed HP model and their multifractal and correlation analyses. J. Theor. Biol. 2004, 226, 341–348. [Google Scholar] [CrossRef]
- Zu-Guo, Y.; Qian-Jun, X.; Long, S.; Jun-Wu, Y.; Anh, V. Chaos game representation of functional protein sequences, and simulation and multifractal analysis of induced measures. Chin. Phys. B 2010, 19, 068701. [Google Scholar] [CrossRef]
- Pal, M.; Kiran, V.S.; Rao, P.M.; Manimaran, P. Multifractal detrended cross-correlation analysis of genome sequences using chaos-game representation. Phys. A Stat. Mech. Appl. 2016, 456, 288–293. [Google Scholar] [CrossRef]
- Zaia, A.; Maponi, P.; Zannotti, M.; Casoli, T. Biocomplexity and Fractality in the Search of Biomarkers of Aging and Pathology: Mitochondrial DNA Profiling of Parkinson’s Disease. Int. J. Mol. Sci. 2020, 21, 1758. [Google Scholar] [CrossRef] [PubMed]
- Feigin, L.A.; Svergun, D.I. Structure Analysis by Small-Angle X-Ray and Neutron Scattering; Springer: Boston, MA, USA, 1987; p. 335. [Google Scholar] [CrossRef]
- Martin, J.E.; Hurd, A.J. Scattering from fractals. J. Appl. Cryst. 1987, 20, 61–78. [Google Scholar] [CrossRef]
- Schmidt, P.W. Small-angle scattering studies of disordered, porous and fractal systems. J. Appl. Cryst. 1991, 24, 414–435. [Google Scholar] [CrossRef]
- Cherny, A.Y.; Anitas, E.M.; Osipov, V.A.; Kuklin, A.I. Deterministic fractals: Extracting additional information from small-angle scattering data. Phys. Rev. E 2011, 84, 036203. [Google Scholar] [CrossRef]
- Anitas, E.M.; Slyamov, A. Structural characterization of chaos game fractals using small-angle scattering analysis. PLoS ONE 2017, 12, 1–16. [Google Scholar] [CrossRef]
- Debye, P. Zerstreuung von Röntgenstrahlen. Ann. Phys. 1915, 351, 809–823. [Google Scholar] [CrossRef]
- Provata, A.; Almirantis, Y. Fractal Cantor Patterns in the Sequence Structure of DNA. Fractals 2000, 8, 15–27. [Google Scholar] [CrossRef]
- Barnsley, M.F. Fractals Everywhere, 2nd ed.; Morgan Kaufmann: Burlington, MA, USA, 2000. [Google Scholar]
- Rogers, C.A. Hausdorff Measures; Cambridge University Press: Cambridge, UK, 1970; p. 179. [Google Scholar]
- Dimension und äußeres Maß. Mathematische Annalen 1918, 79, 157–179. [CrossRef]
- Gouyet, J.F. Physics and Fractal Structures; Masson: Paris, France, 1996; p. 234. [Google Scholar]
- Arneodo, A.; Decoster, N.; Roux, S. A wavelet-based method for multifractal image analysis. I. Methodology and test applications on isotropic and anisotropic random rough surfaces. Eur. Phys. J. B 2000, 15, 567–600. [Google Scholar] [CrossRef]
- Decoster, N.; Roux, S.; Arnéodo, A. A wavelet-based method for multifractal image analysis. II. Applications to synthetic multifractal rough surfaces. Eur. Phys. J. B 2000, 15, 739–764. [Google Scholar] [CrossRef]
- Muzy, J.F.; Bacry, E.; Arneodo, A. Multifractal formalism for fractal signals: The structure-function approach versus the wavelet-transform modulus-maxima method. Phys. Rev. E 1993, 47, 875–884. [Google Scholar] [CrossRef]
- Chhabra, A.; Jensen, R.V. Direct Determination of the f (alpha) Singularity Spectrum. Phys. Rev. Lett. 1989, 62, 1327. [Google Scholar] [CrossRef] [PubMed]
- Pantos, E.; van Garderen, H.F.; Hilbers, P.A.J.; Beelen, T.P.M.; van Santen, R.A. Simulation of small-angle scattering from large assemblies of multi-type scatterer particle. J. Mol. Struct. 1996, 383, 303. [Google Scholar] [CrossRef][Green Version]
- Meakin, P. Diffusion-limited aggregation on multifractal lattices: A model for fluid-fluid displacement in porous media. Phys. Rev. A 1987, 36, 2833–2837. [Google Scholar] [CrossRef] [PubMed]
- Martinez, V.J.; Jones, B.J.T.; Dominguez-Tenreiro, R.; van de Weygaert, R. Clustering Paradigms and Multifractal Measures. Astrophys. J. 1990, 357. [Google Scholar] [CrossRef]
- Tarquis, A.M.; Losada, J.C.; Benito, R.M.; Borondo, F. Multifractal analysis of tori destruction in a molecular Hamiltonian system. Phys. Rev. E 2001, 65, 016213. [Google Scholar] [CrossRef]
- Hao, B.; Xie, H.; Yu, Z.; Chen, G. Avoided Strings in Bacterial Complete Genomes and a Related Combinatorial Problem. Annals of Combinatorics. Ann. Comb. 2000, 4, 247–255. [Google Scholar] [CrossRef]
- Hao, B.L.; Lee, H.; Zhang, S.Y. Fractals related to long DNA sequences and complete genomes. Chaos Solitons Fract. 2000, 11, 825–836. [Google Scholar] [CrossRef]
- Hao, B.; Xie, H.; Yu, Z.; Chen, G.Y. Factorizable language: from dynamics to bacterial complete genomes. Physica A 2000, 288, 10–20. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, P. DNA Sequences with Forbidden Words and the Generalized Cantor Set. J. Appl. Math. Phys. 2019, 7, 1687–1696. [Google Scholar] [CrossRef]
- Cherny, A.Y.; Anitas, E.M.; Kuklin, A.I.; Balasoiu, M.; Osipov, V.A. Scattering from generalized Cantor fractals. J. Appl. Cryst. 2010, 43, 790–797. [Google Scholar] [CrossRef]
- Anitas, E.M. Small-Angle Scattering from Fractals: Differentiating between Various Types of Structures. Symmetry 2020, 12, 65. [Google Scholar] [CrossRef]
- NCBI. PLN Phospholamban [Homo Sapiens (Human)]. Available online: https://www.ncbi.nlm.nih.gov/gene/5350 (accessed on 29 June 2020).
- Bibb, M.J.; Van Etten, R.A.; Wright, C.T.; Walberg, M.W.; Clayton, D.A. Sequence and gene organization of mouse mitochondrial DNA. Cell 1981, 26, 167–180. [Google Scholar] [CrossRef]
- Brooks, J.T.; Sowers, E.G.; Wells, J.G.; Green, K.D.; Griffin, P.M.; Hoekstra, P.M.; Strockbine, N.A. Non-O157 Shiga toxin-producing Escherichia coli infections in the United States. J. Infect. Dis. 2005, 192, 1422–1429. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Murase, K.; Sato, M.P.; Toyoda, A.; Itoh, T.; Mainil, J.G.; Piérard, D.; Yoshino, S.; Kimata, K.; Isobe, J.; et al. Differential dynamics and impacts of prophages and plasmids on the pangenome and virulence factor repertoires of Shiga toxin-producing Escherichia coli O145:H28. Microb. Genom. 2020, 6, 1–13. [Google Scholar] [CrossRef]
- Feng, J.; Wang, T.-M. A 3D graphical representation of RNA secondary structures based on chaos game representation. Chem. Phys. Lett. 2008, 454, 355–361. [Google Scholar] [CrossRef]
- Anitas, E.M.; Marcelli, G.; Szakacs, Z.; Todoran, R.; Todoran, D. Structural Properties of Vicsek-like Deterministic Multifractals. Symmetry 2019, 11, 806. [Google Scholar] [CrossRef]
- Berthelsen, C.L.; Glazier, J.A.; Skolnick, M.H. Global fractal dimension of human DNA sequences treated as pseudorandom walks. Phys. Rev. A 1992, 45, 8902–8913. [Google Scholar] [CrossRef]
- Yu, Z.G.; Anh, V.; Lau, K.S. Measure representation and multifractal analysis of complete genomes. Phys. Rev. E 2001, 64, 031903. [Google Scholar] [CrossRef]
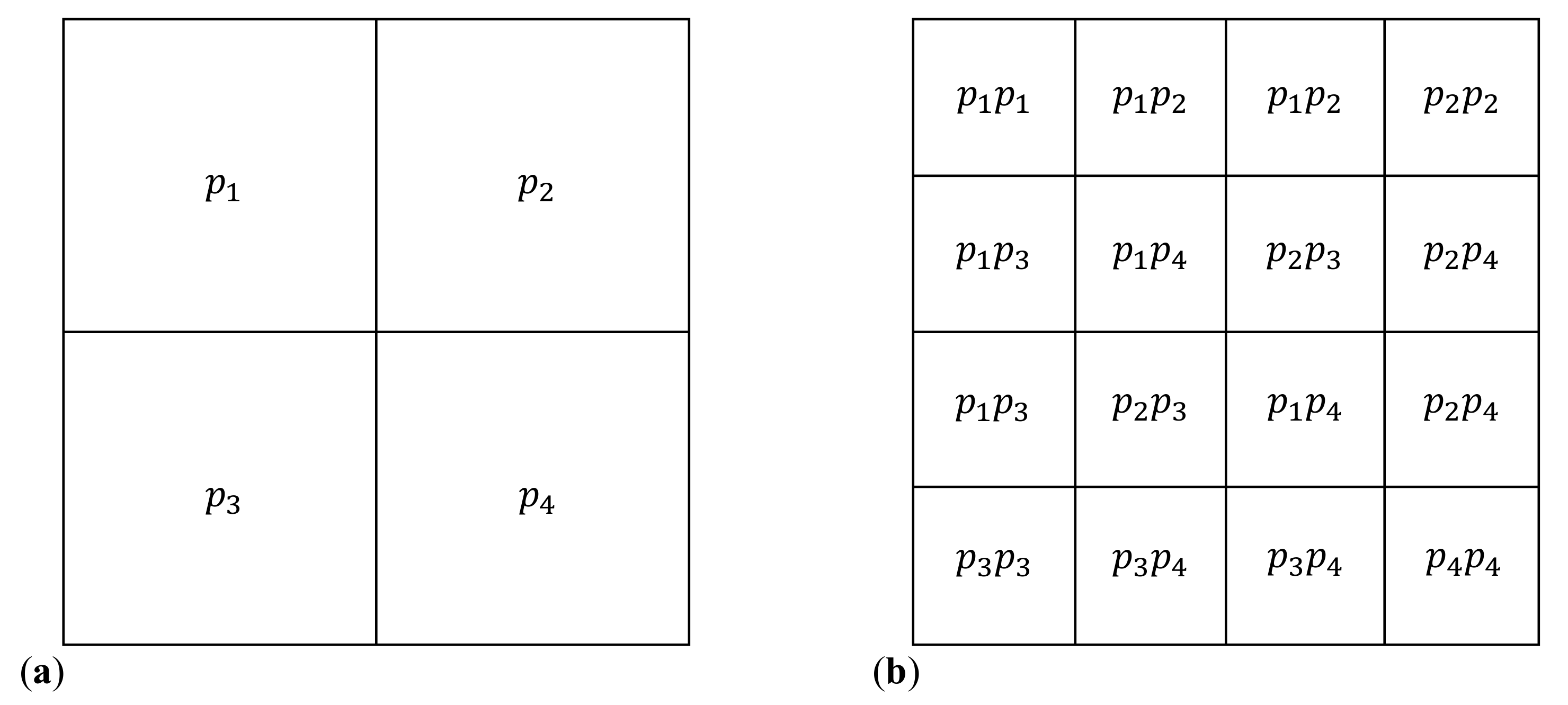




| w | a | b | c | d | e | f | p |
|---|---|---|---|---|---|---|---|
| 1 | 1/2 | 0 | 0 | 1/2 | 0 | 0 | 1/4 |
| 2 | 1/2 | 0 | 0 | 1/2 | 0 | 1/2 | 1/4 |
| 3 | 1/2 | 0 | 0 | 1/2 | 1/2 | 0 | 1/4 |
| 4 | 1/2 | 0 | 0 | 1/2 | 1/2 | 1/2 | 1/4 |
| Model | ||||
|---|---|---|---|---|
| M1 | 1 | 1 | 1 | 0.5 |
| M2 | 1 | 1 | 0.5 | 0.5 |
| M3 | 1 | 0.75 | 0.75 | 0.75 |
| M4 | 1 | 1 | 1 | 0 |
| M5 | 1 | 1 | 0.5 | 0.25 |
| M6 | 0.5 | 1 | 1 | 0.25 |
| M7 | 1 | 1 | 1 | 1 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anitas, E.M. Small-Angle Scattering and Multifractal Analysis of DNA Sequences. Int. J. Mol. Sci. 2020, 21, 4651. https://doi.org/10.3390/ijms21134651
Anitas EM. Small-Angle Scattering and Multifractal Analysis of DNA Sequences. International Journal of Molecular Sciences. 2020; 21(13):4651. https://doi.org/10.3390/ijms21134651
Chicago/Turabian StyleAnitas, Eugen Mircea. 2020. "Small-Angle Scattering and Multifractal Analysis of DNA Sequences" International Journal of Molecular Sciences 21, no. 13: 4651. https://doi.org/10.3390/ijms21134651
APA StyleAnitas, E. M. (2020). Small-Angle Scattering and Multifractal Analysis of DNA Sequences. International Journal of Molecular Sciences, 21(13), 4651. https://doi.org/10.3390/ijms21134651





