Predicting Apoptosis Protein Subcellular Locations based on the Protein Overlapping Property Matrix and Tri-Gram Encoding
Abstract
1. Introduction
2. Results and Discussion
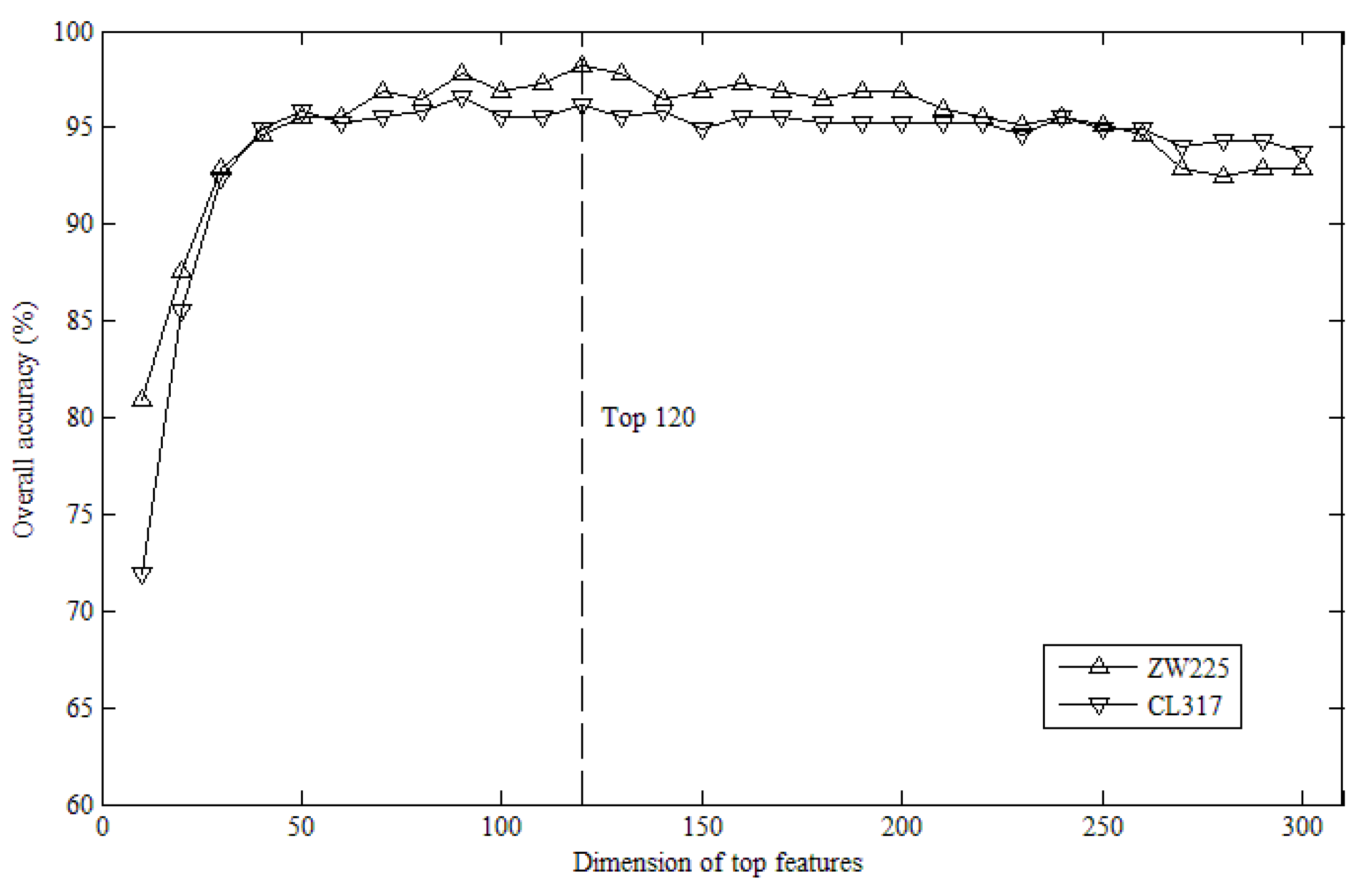
2.1. Effects of Top K Features
2.2. Performance Comparison with Existing Methods
3. Materials and Methods
3.1. Datasets
3.2. Feature Extraction from POPM
3.3. Support Vector Machine
3.4. Feature Selection by SVM-RFE
3.5. Performance Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Steller, H. Mechanisms and genes of cellular suicide. Science 1995, 267, 1445–1449. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.P.; Doctor, K. Subcellular location prediction of apoptosis proteins. Proteins 2003, 50, 44–48. [Google Scholar] [CrossRef]
- Ding, Y.S.; Zhang, T.L. Using Chou’s pseudo amino acid composition to predict subcellular localization of apoptosis proteins: An approach with immune genetic algorithm-based ensemble classifier. Pattern Recogn. Lett. 2008, 29, 1887–1892. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, R.; Zhang, T.; Gu, Q. Using the concept of Chou’s pseudo amino acid composition to predict apoptosis proteins subcellular location: An approach by approximate entropy. Protein Pept. Lett. 2008, 15, 392–396. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liao, B.; Li, D.; Zhu, W. A novel representation for apoptosis protein subcellular localization prediction using support vector machine. J. Theor. Biol. 2009, 259, 361–365. [Google Scholar] [CrossRef]
- Qiu, J.D.; Luo, S.H.; Huang, J.H.; Sun, X.Y.; Liang, R.P. Predicting subcellular location of apoptosis proteins based on wavelet transform and support vector machine. Amino Acids 2010, 38, 1201–1208. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Shi, F. Support vector machines for predicting apoptosis proteins types. Acta Biotheor. 2005, 53, 39–47. [Google Scholar] [CrossRef][Green Version]
- Liu, T.; Zheng, X.; Wang, C.; Wang, J. Prediction of subcellular location of apoptosis proteins using pseudo amino acid composition: An approach from auto covariance transformation. Protein Pept. Lett. 2010, 17, 1263–1269. [Google Scholar] [CrossRef]
- Gu, Q.; Ding, Y.S.; Jiang, X.Y.; Zhang, T.L. Prediction of subcellular location apoptosis proteins with ensemble classifier and feature selection. Amino Acids 2010, 38, 975–983. [Google Scholar] [CrossRef]
- Saravanan, V.; Lakshmi, P.T. APSLAP: An adaptive boosting technique for predicting subcellular localization of apoptosis protein. Acta Biotheor. 2013, 61, 481–497. [Google Scholar] [CrossRef]
- Zhou, X.B.; Chen, C.; Li, Z.C.; Zou, X.Y. Improved prediction of subcellular location for apoptosis proteins by the dual-layer support vector machine. Amino Acids 2008, 35, 383–388. [Google Scholar] [CrossRef]
- Yu, X.; Zheng, X.; Liu, T.; Dou, Y.; Wang, J. Predicting subcellular location of apoptosis proteins with pseudo amino acid composition: Approach from amino acid substitution matrix and auto covariance transformation. Amino Acids 2012, 42, 1619–1625. [Google Scholar] [CrossRef]
- Lin, H.; Wang, H.; Ding, H.; Chen, Y.L.; Li, Q.Z. Prediction of subcellular localization of apoptosis protein using Chou’s pseudo amino acid composition. Acta Biotheor. 2009, 57, 321–330. [Google Scholar] [CrossRef]
- Chen, Y.L.; Li, Q.Z. Prediction of the subcellular location of apoptosis proteins. J. Theor. Biol. 2007, 245, 775–783. [Google Scholar] [CrossRef]
- Chen, Y.L.; Li, Q.Z. Prediction of apoptosis protein subcellular location using improved hybrid approach and pseudo-amino acid composition. J. Theor. Biol. 2007, 248, 377–381. [Google Scholar] [CrossRef] [PubMed]
- Liao, B.; Jiang, J.B.; Zeng, Q.G.; Zhu, W. Predicting apoptosis protein subcellular location with PseAAC by incorporating tripeptide composition. Protein Pept. Lett. 2011, 18, 1086–1092. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Wang, Z.H.; Zhang, Z.R.; Wang, Y.X. A novel method for apoptosis protein subcellular localization prediction combining encoding based on grouped weight and support vector machine. FEBS Lett. 2006, 580, 6169–6174. [Google Scholar] [CrossRef]
- Liu, T.; Tao, P.; Li, X.; Qin, Y.; Wang, C. Prediction of subcellular location of apoptosis proteins combining tri-gram encoding based on PSSM and recursive feature elimination. J. Theor. Biol. 2015, 366, 8–12. [Google Scholar] [CrossRef]
- Zhang, S.; Liang, Y. Predicting apoptosis protein subcellular localization by integrating auto-cross correlation and PSSM into Chou’s PseAAC. J. Theor. Biol. 2018, 457, 163–169. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Li, S.; Qiu, W.Y.; Chen, C.; Chen, R.X.; Wang, L.; Wang, M.H.; Zhang, Y. Accurate prediction of subcellular location of apoptosis proteins combining Chou’s PseAAC and PsePSSM based on wavelet denoising. Oncotarget 2017, 8, 107640–107665. [Google Scholar] [CrossRef]
- Xiang, Q.; Liao, B.; Li, X.; Xu, H.; Chen, J.; Shi, Z.; Dai, Q.; Yao, Y. Subcellular localization prediction of apoptosis proteins based on evolutionary information and support vector machine. Artif. Intell. Med. 2017, 78, 41–46. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Liu, S.; Zhang, S. Detrended cross-correlation coefficient: Application to predict apoptosis protein subcellular localization. Math. Biosci. 2016, 282, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, T.; Liu, C. Prediction of apoptosis protein subcellular localization via heterogeneous features and hierarchical extreme learning machine. SAR QSAR Environ. Res. 2019, 30, 209–228. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Cai, L.; Liao, B.; Fu, X.; Bing, P.; Yang, J. Prediction of Protein Subcellular Localization Based on Fusion of Multi-view Features. Molecules 2019, 24, 919. [Google Scholar] [CrossRef]
- Yu, B.; Li, S.; Qiu, W.; Wang, M.; Du, J.; Zhang, Y.; Chen, X. Prediction of subcellular location of apoptosis proteins by incorporating PsePSSM and DCCA coefficient based on LFDA dimensionality reduction. BMC Genom. 2018, 19, 478. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, S. Prediction of Apoptosis Protein’s Subcellular Localization by Fusing Two Different Descriptors Based on Evolutionary Information. Acta Biotheor. 2018, 66, 61–78. [Google Scholar] [CrossRef]
- Altschul, S.F.; Madden, T.L.; Schaffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef]
- Zielezinski, A.; Vinga, S.; Almeida, J.; Karlowski, W.M. Alignment-free sequence comparison: Benefits, applications, and tools. Genome Biol. 2017, 18, 186. [Google Scholar] [CrossRef] [PubMed]
- Dou, Y.; Zheng, X.; Yang, J.; Wang, J. Prediction of catalytic residues based on an overlapping amino acid classification. Amino Acids 2010, 39, 1353–1361. [Google Scholar] [CrossRef] [PubMed]
- Dou, Y.; Yao, B.; Zhang, C. PhosphoSVM: Prediction of phosphorylation sites by integrating various protein sequence attributes with a support vector machine. Amino Acids 2014, 46, 1459–1469. [Google Scholar] [CrossRef]
- Taylor, W.R. The classification of amino acid conservation. J. Theor. Biol. 1986, 119, 205–218. [Google Scholar] [CrossRef]
- Manavalan, B.; Basith, S.; Shin, T.H.; Wei, L.; Lee, G. mAHTPred: A sequence-based meta-predictor for improving the prediction of anti-hypertensive peptides using effective feature representation. Bioinformatics 2018. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Luan, S.; Nagai, L.A.E.; Su, R.; Zou, Q. Exploring sequence-based features for the improved prediction of DNA N4-methylcytosine sites in multiple species. Bioinformatics 2018. [Google Scholar] [CrossRef] [PubMed]
- Manavalan, B.; Basith, S.; Shin, T.H.; Choi, S.; Kim, M.O.; Lee, G. MLACP: Machine-learning-based prediction of anticancer peptides. Oncotarget 2017, 8, 77121–77136. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Chen, H.; Su, R. M6APred-EL: A Sequence-Based Predictor for Identifying N6-methyladenosine Sites Using Ensemble Learning. Mol. Ther. Nucleic Acids 2018, 12, 635–644. [Google Scholar] [CrossRef] [PubMed]
- Manavalan, B.; Shin, T.H.; Lee, G. DHSpred: Support-vector-machine-based human DNase I hypersensitive sites prediction using the optimal features selected by random forest. Oncotarget 2018, 9, 1944–1956. [Google Scholar] [CrossRef]
- Wei, L.; Zhou, C.; Chen, H.; Song, J.; Su, R. ACPred-FL: A sequence-based predictor using effective feature representation to improve the prediction of anti-cancer peptides. Bioinformatics 2018, 34, 4007–4016. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Li, L.; Yu, S.; Xiao, W.; Li, Y.; Huang, L.; Zheng, X.; Zhou, S.; Yang, H. Sequence-based identification of recombination spots using pseudo nucleic acid representation and recursive feature extraction by linear kernel SVM. BMC Bioinform. 2014, 15, 340. [Google Scholar] [CrossRef]
- Li, L.; Yu, S.; Xiao, W.; Li, Y.; Hu, W.; Huang, L.; Zheng, X.; Zhou, S.; Yang, H. Protein submitochondrial localization from integrated sequence representation and SVM-based backward feature extraction. Mol. Biosyst. 2015, 11, 170–177. [Google Scholar] [CrossRef] [PubMed]
- Su, R.; Hu, J.; Zou, Q.; Manavalan, B.; Wei, L. Empirical comparison and analysis of web-based cell-penetrating peptide prediction tools. Brief. Bioinform. 2019. [Google Scholar] [CrossRef] [PubMed]
- Basith, S.; Manavalan, B.; Shin, T.H.; Lee, G. iGHBP: Computational identification of growth hormone binding proteins from sequences using extremely randomised tree. Comput. Struct. Biotechnol. J. 2018, 16, 412–420. [Google Scholar] [CrossRef]
- Qu, K.; Han, K.; Wu, S.; Wang, G.; Wei, L. Identification of DNA-Binding Proteins Using Mixed Feature Representation Methods. Molecules 2017, 22, 1602. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Xing, P.; Su, R.; Shi, G.; Ma, Z.S.; Zou, Q. CPPred-RF: A Sequence-based Predictor for Identifying Cell-Penetrating Peptides and Their Uptake Efficiency. J. Proteome Res. 2017, 16, 2044–2053. [Google Scholar] [CrossRef]
| Dataset | Location 1 | Sens (%) | Spec (%) | MCC | OA (%) |
|---|---|---|---|---|---|
| ZW225 | Cyto | 100 | 98.1 | 0.970 | 98.2 |
| Memb | 96.6 | 100 | 0.972 | ||
| Mito | 96.0 | 100 | 0.977 | ||
| Nucl | 100 | 99.5 | 0.985 | ||
| CL317 | Cyto | 99.1 | 98.5 | 0.973 | 96.2 |
| Memb | 92.7 | 98.9 | 0.923 | ||
| Mito | 97.1 | 99.3 | 0.951 | ||
| Secr | 88.2 | 100 | 0.936 | ||
| Nucl | 96.2 | 99.2 | 0.954 | ||
| Endo | 95.7 | 99.3 | 0.950 |
| Method | Sens for Each Class (%) | OA (%) | |||
|---|---|---|---|---|---|
| Cyto | Memb | Mito | Nucl | ||
| EBGW_SVM [17] | 90.0 | 93.3 | 60.0 | 63.4 | 83.1 |
| DF_SVM [5] | 87.1 | 92.1 | 64.0 | 73.2 | 84.0 |
| PSSM_AC [8] | 82.9 | 92.1 | 68.0 | 78.0 | 84.0 |
| ID_SVM [15] | 92.9 | 91.0 | 68.0 | 73.2 | 85.8 |
| Auto_Cova [12] | 81.3 | 93.3 | 85.7 | 84.6 | 87.1 |
| EN_FKNN [9] | 94.3 | 94.4 | 60.0 | 80.5 | 88.0 |
| Tri-gram PSSM [18] | 97.1 | 98.9 | 96.0 | 97.6 | 97.8 |
| PsePSSM-DCCA-LFDA [25] | 100 | 98.9 | 100 | 100 | 99.6 |
| Our method | 100 | 96.6 | 96.0 | 100 | 98.2 |
| Method | Sens for Each Class (%) | OA (%) | |||||
|---|---|---|---|---|---|---|---|
| Cyto | Memb | Mito | Secr | Nucl | Endo | ||
| ID [14] | 81.3 | 81.8 | 85.3 | 88.2 | 82.7 | 83.0 | 82.7 |
| ID_SVM [15] | 91.1 | 89.1 | 79.4 | 58.8 | 73.1 | 87.2 | 84.2 |
| DF_SVM [5] | 92.9 | 85.5 | 76.5 | 76.5 | 93.6 | 86.5 | 88.0 |
| PseAAC_SVM [13] | 93.8 | 90.9 | 85.3 | 76.5 | 90.4 | 95.7 | 91.1 |
| PSSM-AC [8] | 93.8 | 90.9 | 91.2 | 82.4 | 86.5 | 95.7 | 91.5 |
| APSLAP [10] | 99.1 | 89.1 | 85.3 | 88.2 | 84.3 | 95.8 | 92.4 |
| Tri-gram PSSM [18] | 98.2 | 96.4 | 94.1 | 82.4 | 96.2 | 95.7 | 95.9 |
| PsePSSM-DCCA-LFDA [25] | 99.1 | 100 | 100 | 100 | 100 | 100 | 99.7 |
| Our method | 99.1 | 92.7 | 97.1 | 88.2 | 96.2 | 95.7 | 96.2 |
| Physicochemical Properties | Amino Acid Residues |
|---|---|
| Polar | N, Q, S, D, E, C, T, K, R, H, Y, W |
| Positive | K, H, R |
| Negative | D, E |
| Charged | K, H, R, D, E |
| Hydrophobic | A, G, C, T, I, V, L, K, H, F, Y, W, M |
| Aliphatic | I, V, L |
| Aromatic | F, Y, W, H |
| Small | P, N, D, T, C, A, G, S, V |
| Tiny | A, S, G, C |
| Proline | P |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zheng, H.; Wang, C.; Xiao, W.; Liu, T. Predicting Apoptosis Protein Subcellular Locations based on the Protein Overlapping Property Matrix and Tri-Gram Encoding. Int. J. Mol. Sci. 2019, 20, 2344. https://doi.org/10.3390/ijms20092344
Yang Y, Zheng H, Wang C, Xiao W, Liu T. Predicting Apoptosis Protein Subcellular Locations based on the Protein Overlapping Property Matrix and Tri-Gram Encoding. International Journal of Molecular Sciences. 2019; 20(9):2344. https://doi.org/10.3390/ijms20092344
Chicago/Turabian StyleYang, Yang, Huiwen Zheng, Chunhua Wang, Wanyue Xiao, and Taigang Liu. 2019. "Predicting Apoptosis Protein Subcellular Locations based on the Protein Overlapping Property Matrix and Tri-Gram Encoding" International Journal of Molecular Sciences 20, no. 9: 2344. https://doi.org/10.3390/ijms20092344
APA StyleYang, Y., Zheng, H., Wang, C., Xiao, W., & Liu, T. (2019). Predicting Apoptosis Protein Subcellular Locations based on the Protein Overlapping Property Matrix and Tri-Gram Encoding. International Journal of Molecular Sciences, 20(9), 2344. https://doi.org/10.3390/ijms20092344





