Intrinsically Disordered Linkers Impart Processivity on Enzymes by Spatial Confinement of Binding Domains
Abstract
1. Introduction
2. Results
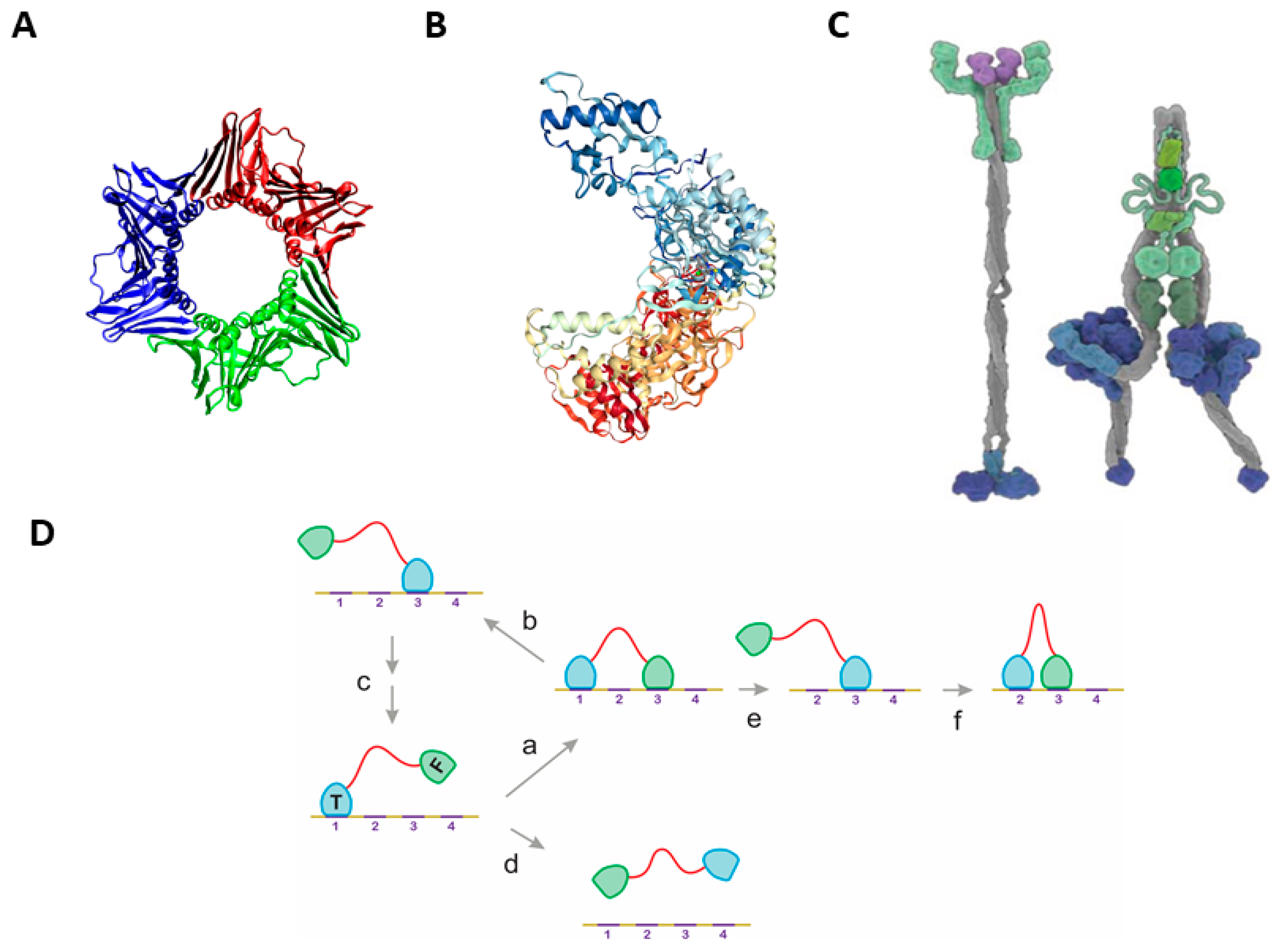
2.1. The Classical Mechanisms of Processivity
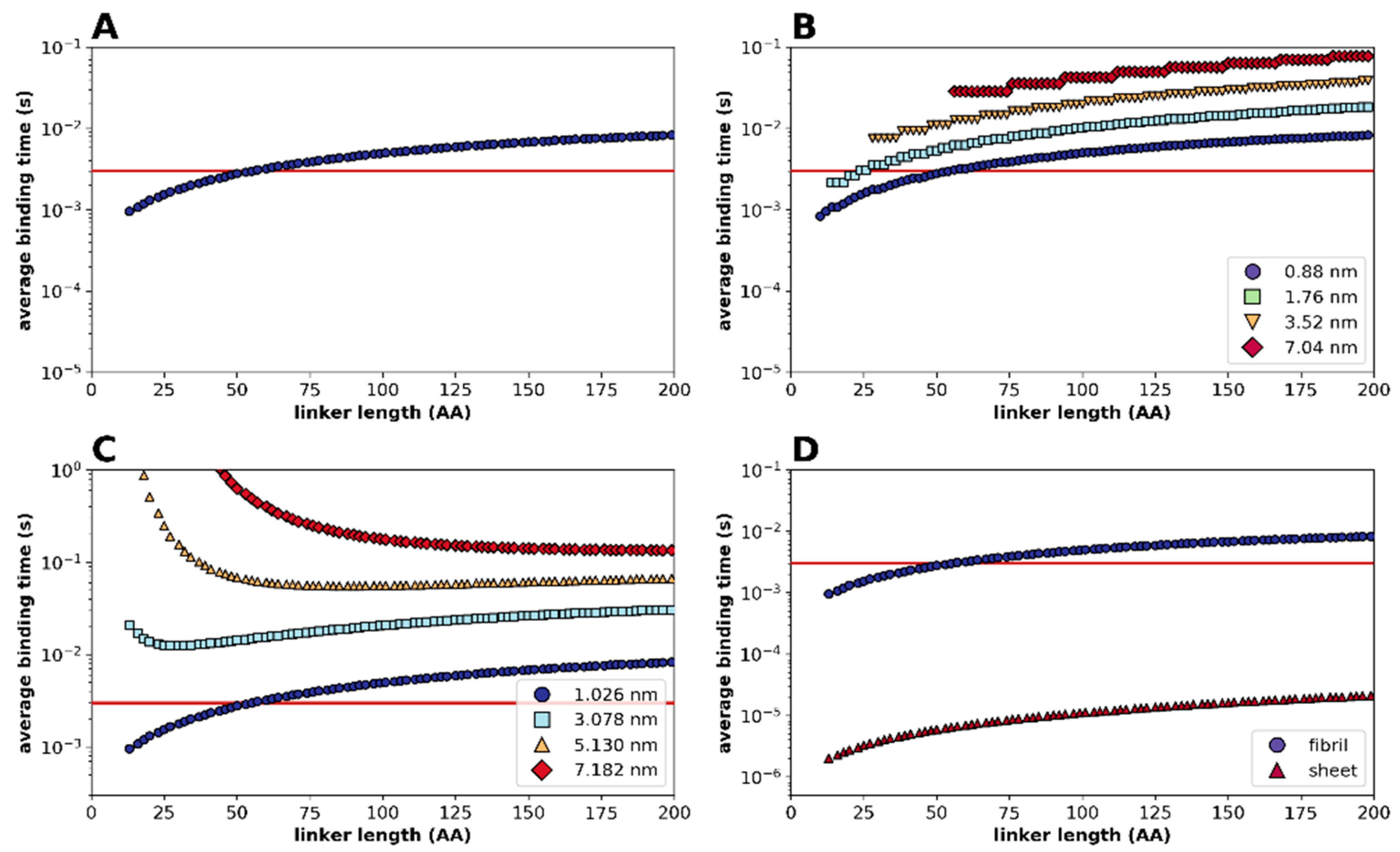
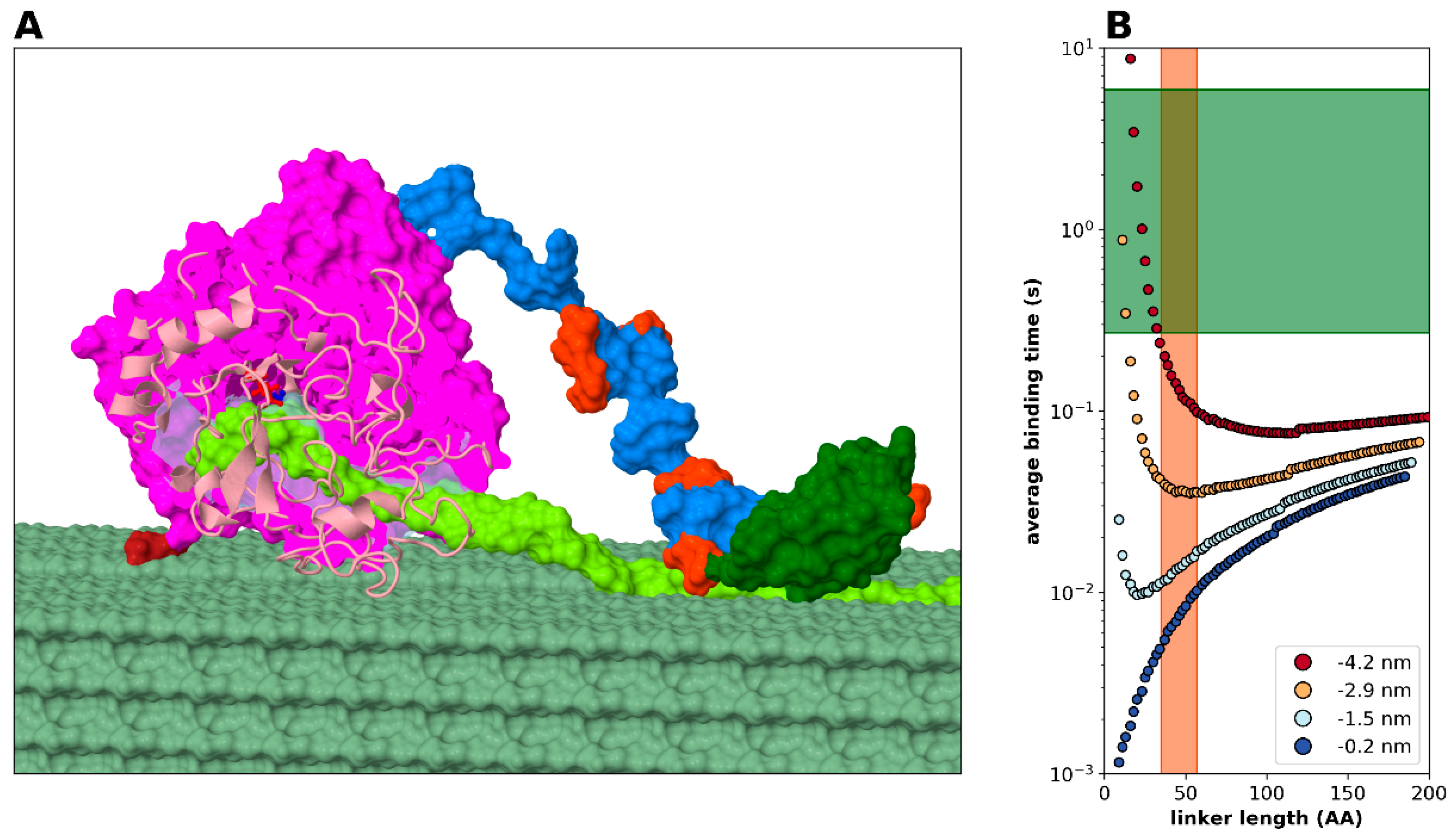
2.2. Statistical Physical Modelling of Domain-Linker-Domain Enzymes
2.3. Multiple Examples of DLD-Type Processive Enzymes
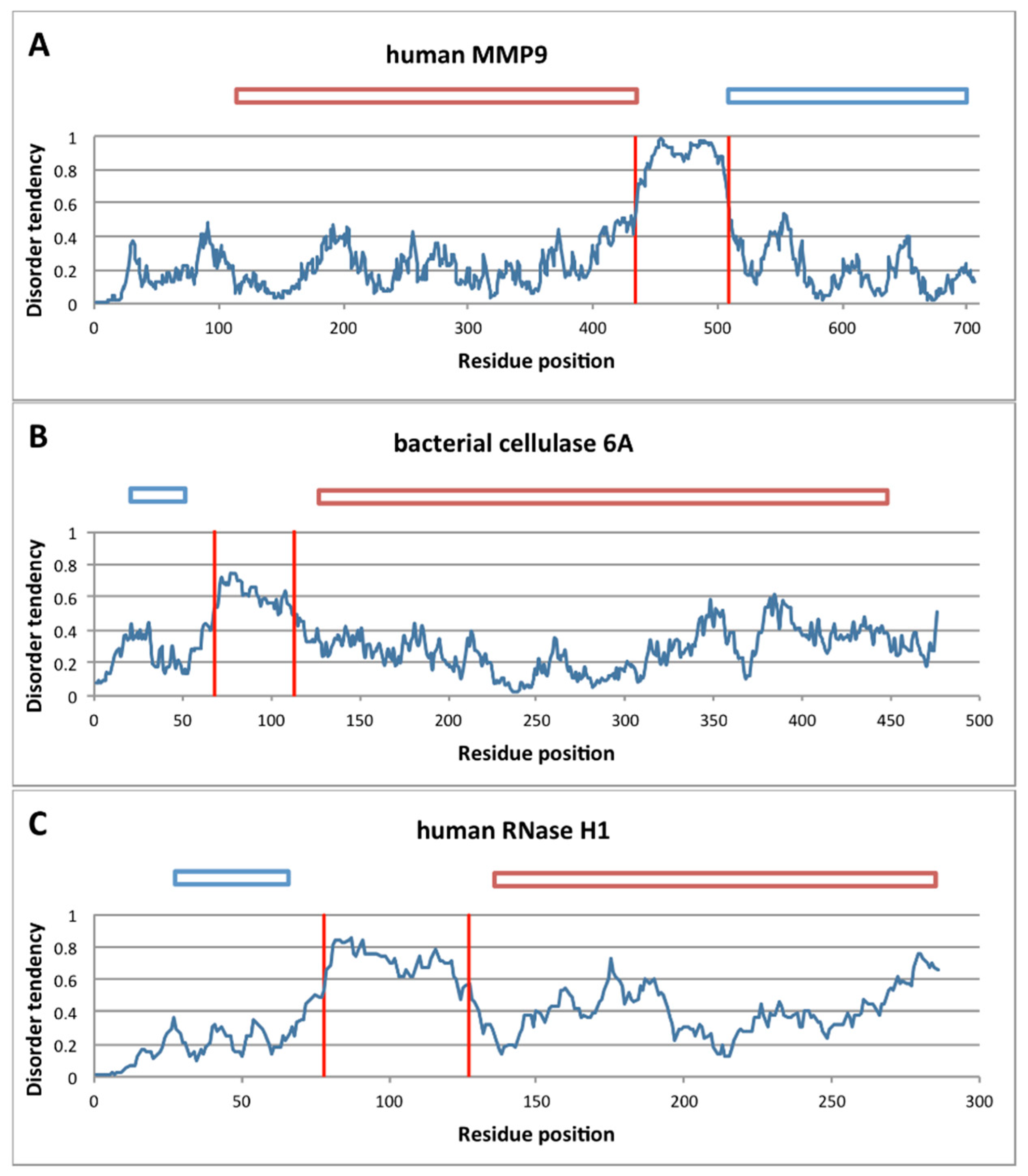
2.3.1. Structural Disorder of Linkers in Monomeric Processive Enzymes
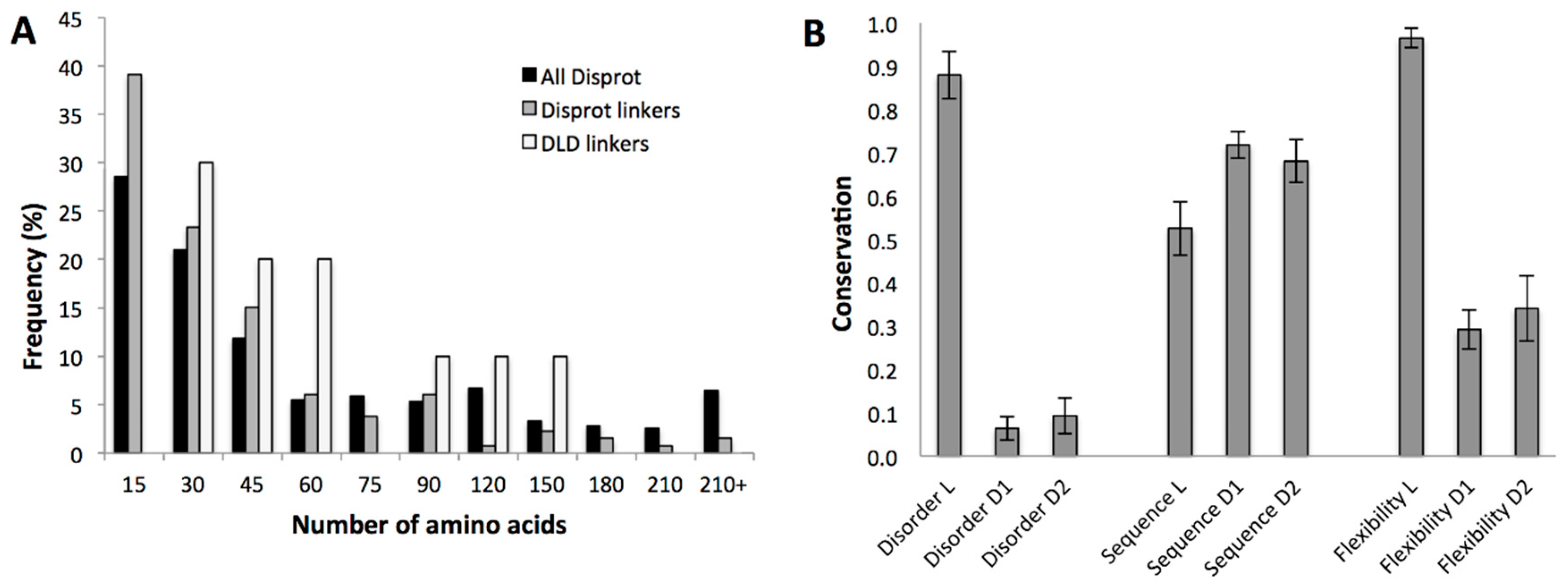
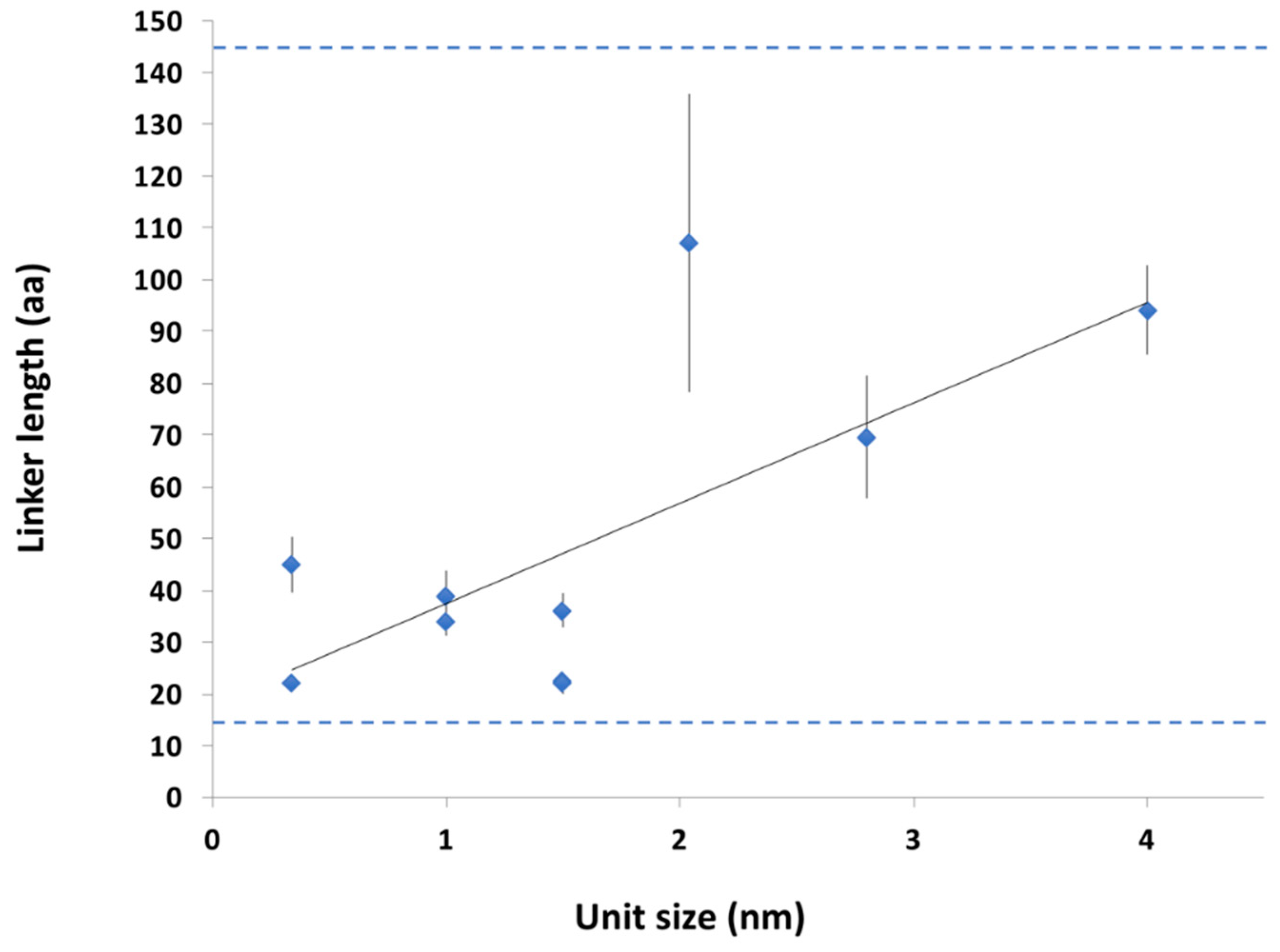
2.3.2. Conservation of Sequence, Length and Dynamics of Linkers
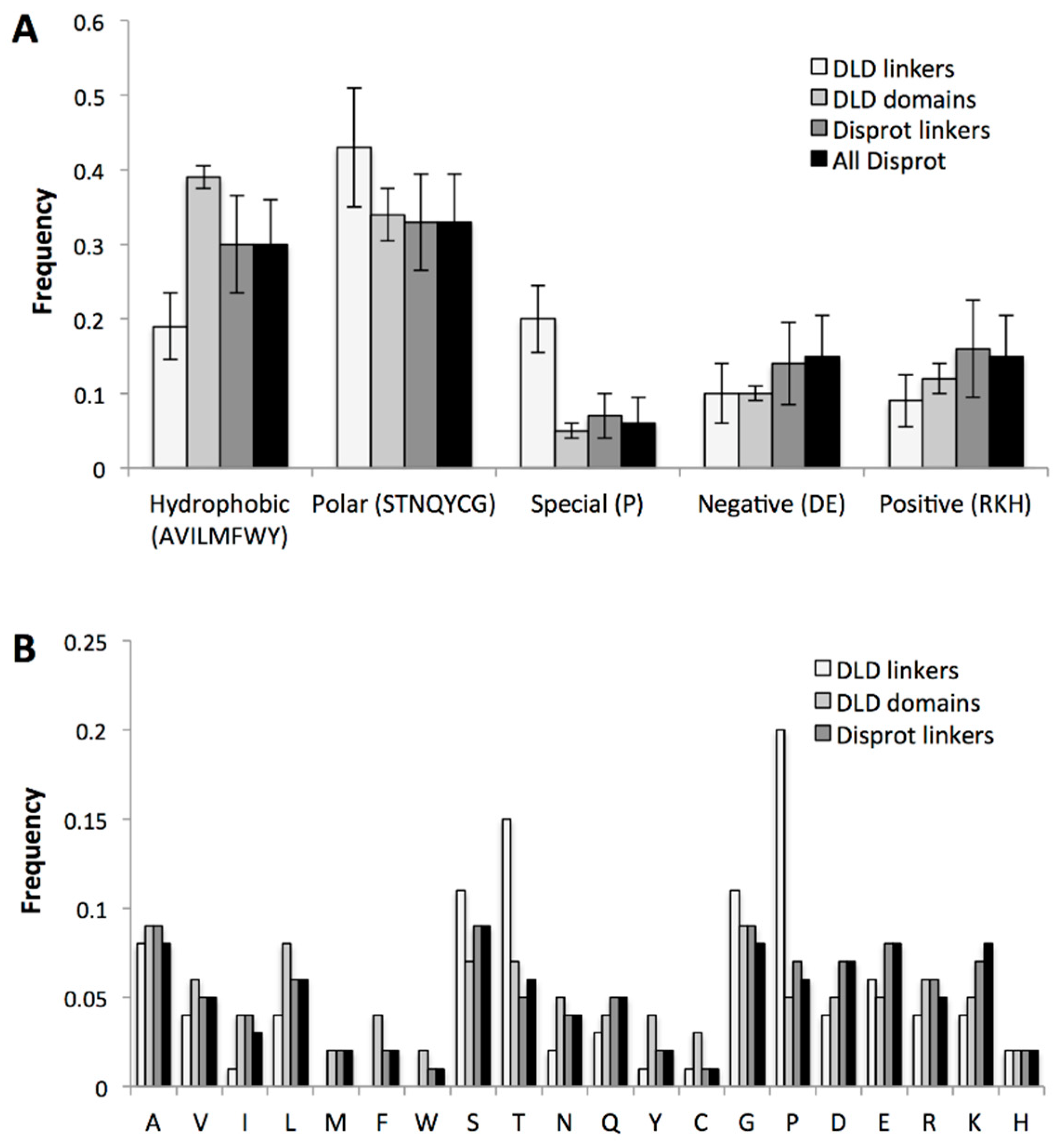
2.3.3. Specific Sequence Features of Processive Linkers
2.3.4. Modelling Cellulase, a Processive Enzyme
3. Discussion
4. Data and Methods
4.1. Collection of Processive Enzymes and Intrinsically Disordered Proteins
4.2. Statistical Kinetic Modelling of Linker Regions
4.3. Assessing Structural Disorder of Linkers
4.4. Flexibility of Linker Regions
4.5. Charge State and Kappa Value Calculation of Linkers
4.6. Amino-Acid Composition and Length Distribution of Linkers
4.7. Variability and Conservation of Linker Regions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AFM | atomic-force microscopy |
| DLD | domain-linker-domain |
| FJC | freely jointed chain |
| ID | intrinsically disordered |
| IDP | intrinsically disordered protein |
| IDR | intrinsically disordered region |
| MMP-9 | matrix metalloproteinase-9 |
| PTM | post-translational modification |
| RNAse-H1 | ribonuclease H1 |
| SAXS | small-angle X-ray scattering |
References
- Breyer, W.A.; Matthews, B.W. A structural basis for processivity. Protein Sci. 2001, 10, 1699–1711. [Google Scholar] [CrossRef]
- Bambara, R.A.; Uyemura, D.; Choi, T. On the processive mechanism of Escherichia coli DNA polymerase I. Quantitative assessment of processivity. J. Biol. Chem. 1978, 253, 413–423. [Google Scholar]
- Bonderoff, J.M.; Lloyd, R.E. Time-dependent increase in ribosome processivity. Nucleic Acids Res. 2010, 38, 7054–7067. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Breyer, W.A.; Matthews, B.W. Structure of Escherichia coli exonuclease I suggests how processivity is achieved. Nat. Struct. Biol. 2000, 7, 1125–1128. [Google Scholar] [PubMed]
- Gaidamakov, S.A.; Gorshkova, I.I.; Schuck, P.; Steinbach, P.J.; Yamada, H.; Crouch, R.J.; Cerritelli, S.M. Eukaryotic RNases H1 act processively by interactions through the duplex RNA-binding domain. Nucleic Acids Res. 2005, 33, 2166–2175. [Google Scholar] [CrossRef]
- Boraston, A.B.; Bolam, D.N.; Gilbert, H.J.; Davies, G.J. Carbohydrate-binding modules: fine-tuning polysaccharide recognition Carbohydrate-binding modules: Fine-tuning polysaccharide recognition. Biochem. J. 2004, 382, 769–781. [Google Scholar] [CrossRef]
- Akopian, T.N.; Kisselev, A.F.; Goldberg, A.L. Processive degradation of proteins and other catalytic properties of the proteasome from Thermoplasma acidophilum. J. Biol. Chem. 1997, 272, 1791–1798. [Google Scholar] [CrossRef][Green Version]
- Schrader, E.K.; Harstad, K.G.; Matouschek, A. Targeting proteins for degradation. Nat. Chem. Biol. 2009, 5, 815–822. [Google Scholar] [CrossRef]
- Gyimesi, M.; Sarlos, K.; Kovacs, M. Processive translocation mechanism of the human Bloom’s syndrome helicase along single-stranded DNA. Nucleic Acids Res. 2010, 38, 4404–4414. [Google Scholar] [CrossRef] [PubMed]
- Hochstrasser, M. Lingering mysteries of ubiquitin-chain assembly. Cell 2006, 124, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Sowa, M.E.; Harper, J.W. From loops to chains: Unraveling the mysteries of polyubiquitin chain specificity and processivity. ACS Chem. Biol. 2006, 1, 20–24. [Google Scholar] [CrossRef] [PubMed]
- Gyimesi, M.; Sarlós, K.; Derényi, I.; Kovács, M. Streamlined determination of processive run length and mechanochemical coupling of nucleic acid motor activities. Nucleic Acids Res. 2010, 38, e102. [Google Scholar] [CrossRef] [PubMed]
- Kolomeisky, A.B.; Fisher, M.E. Molecular motors: A theorist’s perspective. Annu. Rev. Phys. Chem. 2007, 58, 675–695. [Google Scholar] [CrossRef] [PubMed]
- Rock, R.S.; Ramamurthy, B.; Dunn, A.R.; Beccafico, S.; Rami, B.R.; Morris, C.; Spink, B.J.; Franzini-Armstrong, C.; Spudich, J.A.; Sweeney, H. A flexible domain is essential for the large step size and processivity of myosin VI. Mol. Cell 2005, 17, 603–609. [Google Scholar] [CrossRef] [PubMed]
- Shastry, S.; Hancock, W.O. Neck linker length determines the degree of processivity in kinesin-1 and kinesin-2 motors. Curr. Biol. 2010, 20, 939–943. [Google Scholar] [CrossRef] [PubMed]
- Krishna, T.S.; Fenyö, D.; Kong, X.-P.; Gary, S.; Chait, B.T.; Burgers, P.; Kuriyan, J. Crystallization of proliferating cell nuclear antigen (PCNA) from Saccharomyces cerevisiae. J. Mol. Biol. 1994, 241, 265–268. [Google Scholar] [CrossRef]
- Krishna, T.S.; Kong, X.-P.; Gary, S.; Burgers, P.M.; Kuriyan, J. Crystal structure of the eukaryotic DNA polymerase processivity factor PCNA. Cell 1994, 79, 1233–1243. [Google Scholar] [CrossRef]
- Huang, H.; Chopra, R.; Verdine, G.L.; Harrison, S.C. Structure of a covalently trapped catalytic complex of HIV-1 reverse transcriptase: Implications for drug resistance. Science 1998, 282, 1669–1675. [Google Scholar] [CrossRef]
- Asenjo, A.B.; Weinberg, Y.; Sosa, H. Nucleotide binding and hydrolysis induces a disorder-order transition in the kinesin neck-linker region. Nat. Struct. Mol. Biol. 2006, 13, 648–654. [Google Scholar] [CrossRef] [PubMed]
- Carter, A.P. Crystal clear insights into how the dynein motor moves. J. Cell Sci. 2013, 126, 705–713. [Google Scholar] [CrossRef]
- Tompa, P. Unstructural biology coming of age. Curr. Opin. Struct. Biol. 2011, 21, 419–425. [Google Scholar] [CrossRef]
- Varadi, M.; Guharoy, M.; Zsolyomi, F.; Tompa, P. DisCons: A novel tool to quantify and classify evolutionary conservation of intrinsic protein disorder. BMC Bioinform. 2015, 16, 153. [Google Scholar] [CrossRef][Green Version]
- Tompa, P.; Fuxreiter, M.; Oldfield, C.J.; Simon, I.; Dunker, A.K.; Uversky, V.N. Close encounters of the third kind: Disordered domains and the interactions of proteins. Bioessays 2009, 31, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Wright, P.E.; Dyson, H.J. Linking folding and binding. Curr. Opin. Struct. Biol. 2009, 19, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P. The interplay between structure and function in intrinsically unstructured proteins. FEBS Lett. 2005, 579, 3346–3354. [Google Scholar] [CrossRef]
- Tompa, P.; Fuxreiter, M. Fuzzy complexes: Polymorphism and structural disorder in protein-protein interactions. Trends Biochem. Sci. 2008, 33, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, B.A.; Portman, J.J.; Wolynes, P.G. Speeding molecular recognition by using the folding funnel: The fly-casting mechanism. Proc. Natl. Acad. Sci. USA 2000, 97, 8868–8873. [Google Scholar] [CrossRef]
- Vuzman, D.; Azia, A.; Levy, Y. Searching DNA via a “Monkey Bar” mechanism: The significance of disordered tails. J. Mol. Biol. 2010, 396, 674–684. [Google Scholar] [CrossRef]
- Mittag, T.; Orlicky, S.; Choy, W.-Y.; Tang, X.; Lin, H.; Sicheri, F.; Kay, L.E.; Tyers, M.; Forman-Kay, J.D. Dynamic equilibrium engagement of a polyvalent ligand with a single-site receptor. Proc. Natl. Acad. Sci. USA 2008, 105, 17772–17777. [Google Scholar] [CrossRef]
- Song, J.; Ng, S.C.; Tompa, P.; Lee, K.A.; Chan, H.S. Polycation-pi interactions are a driving force for molecular recognition by an intrinsically disordered oncoprotein family. PLoS Comput. Biol. 2013, 9, e1003239. [Google Scholar] [CrossRef]
- Carrard, G.; Koivula, A.; Söderlund, H.; Béguin, P. Cellulose-binding domains promote hydrolysis of different sites on crystalline cellulose. Proc. Natl. Acad. Sci. USA 2000, 97, 10342–10347. [Google Scholar] [CrossRef] [PubMed]
- Srisodsuk, M.; Reinikainen, T.; Penttilä, M.; Teeri, T.T. Role of the interdomain linker peptide of Trichoderma reesei cellobiohydrolase I in its interaction with crystalline cellulose. J. Biol. Chem. 1993, 268, 20756–20761. [Google Scholar]
- Rosenblum, G.; Steen, P.E.V.D.; Cohen, S.R.; Grossmann, J.G.; Frenkel, J.; Sertchook, R.; Slack, N.; Strange, R.W.; Opdenakker, G.; Sagi, I. Insights into the structure and domain flexibility of full-length pro-matrix metalloproteinase-9/gelatinase B. Structure 2007, 15, 1227–1236. [Google Scholar] [CrossRef]
- Tompa, P. Intrinsically unstructured proteins. Trends Biochem. Sci. 2002, 27, 527–533. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, T.; Mao, A.; Xu, J. Esophageal cancer stem cells express PLGF to increase cancer invasion through MMP9 activation. Tumour Biol. 2014, 35, 12749–12755. [Google Scholar] [CrossRef]
- Gao, D.; Chundawat, S.P.S.; Sethi, A.; Balan, V.; Gnanakaran, S.; Dale, B.E. Increased enzyme binding to substrate is not necessary for more efficient cellulose hydrolysis. Proc. Natl. Acad. Sci. USA 2013, 110, 10922–10927. [Google Scholar] [CrossRef]
- Rosenblum, G.; Meroueh, S.; Toth, M.; Fisher, J.F.; Fridman, R.; Mobashery, S.; Sagi, I. Molecular structures and dynamics of the stepwise activation mechanism of a matrix metalloproteinase zymogen: Challenging the cysteine switch dogma. J. Am. Chem. Soc. 2007, 129, 13566–13574. [Google Scholar] [CrossRef]
- Tilbeurgh, H.V.; Tomme, P.; Claeyssens, M.; Bhikhabhai, R.; Pettersson, G. Limited proteolysis of the cellobiohydrolase I from Trichoderma reesei. Separation of functional domains. FEBS Lett. 1986, 204, 223–227. [Google Scholar] [CrossRef]
- Von Ossowski, I.; Eaton, J.T.; Czjzek, M.; Perkins, S.J.; Frandsen, T.P.; Schülein, M.; Panine, P.; Henrissat, B.; Receveur-Bréchot, V. Protein disorder: Conformational distribution of the flexible linker in a chimeric double cellulase. Biophys. J. 2005, 88, 2823–2832. [Google Scholar] [CrossRef]
- Pell, G.; Szabo, L.; Charnock, S.J.; Xie, H.; Gloster, T.M.; Davies, G.J.; Gilbert, H.J. Structural and biochemical analysis of Cellvibrio japonicus xylanase 10C: How variation in substrate-binding cleft influences the catalytic profile of family GH-10 xylanases. J. Biol. Chem. 2004, 279, 11777–11788. [Google Scholar] [CrossRef]
- Dosztanyi, Z.; Csizmok, V.; Tompa, P.; Simon, I. IUPred: Web server for the prediction of intrinsically unstructured regions of proteins based on estimated energy content. Bioinformatics 2005, 21, 3433–3434. [Google Scholar] [CrossRef]
- Noivirt-Brik, O.; Prilusky, J.; Sussman, J.L. Assessment of disorder predictions in CASP8. Proteins 2009, 77 (Suppl. S9), 210–216. [Google Scholar] [CrossRef]
- Bellay, J.; Han, S.; Michaut, M.; Kim, T.; Costanzo, M.; Andrews, B.J.; Boone, C.; Bader, G.D.; Myers, C.L.; Kim, P.M. Bringing order to protein disorder through comparative genomics and genetic interactions. Genome Biol. 2011, 12, R14. [Google Scholar] [CrossRef] [PubMed]
- Piovesan, D.; Tabaro, F.; Mičetić, I.; Necci, M.; Quaglia, F.; Oldfield, C.J.; Aspromonte, M.C.; Davey, N.E.; Davidović, R.; Dosztányi, Z.; et al. DisProt 7.0: A major update of the database of disordered proteins. Nucleic Acids Res. 2017, 45, D219–D227. [Google Scholar] [CrossRef] [PubMed]
- Cilia, E.; Pancsa, R.; Tompa, P.; Lenaerts, T. From protein sequence to dynamics and disorder with DynaMine. Nat. Commun. 2013, 4, 2741. [Google Scholar] [CrossRef] [PubMed]
- Daughdrill, G.W.; Narayanaswami, P.; Gilmore, S.H.; Belczyk, A.; Brown, C.J. Dynamic behavior of an intrinsically unstructured linker domain is conserved in the face of negligible amino acid sequence conservation. J. Mol. Evol. 2007, 65, 277–288. [Google Scholar] [CrossRef] [PubMed]
- Mao, A.H.; Crick, S.L.; Vitalis, A.; Chicoine, C.L.; Pappu, R.V. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 8183–8188. [Google Scholar] [CrossRef]
- Das, R.K.; Pappu, R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA 2013, 110, 13392–13397. [Google Scholar] [CrossRef] [PubMed]
- George, R.A.; Heringa, J. An analysis of protein domain linkers: Their classification and role in protein folding. Protein Eng. 2002, 15, 871–879. [Google Scholar] [CrossRef]
- Fuxreiter, M.; Tompa, P.; Simon, I. Local structural disorder imparts plasticity on linear motifs. Bioinformatics 2007, 23, 950–956. [Google Scholar] [CrossRef] [PubMed]
- The UniProt Consortium. UniProt: The universal protein knowledgebase. Nucleic Acids Res. 2017, 45, D158–D169. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Olsen, J.V.; Daub, H.; Mann, M. Global effects of kinase inhibitors on signaling networks revealed by quantitative phosphoproteomics. Mol. Cell. Proteom. 2009, 8, 2796–2808. [Google Scholar] [CrossRef] [PubMed]
- Harrison, M.J.; Nouwens, A.S.; Jardine, D.R.; Zachara, N.E.; Gooley, A.A.; Nevalainen, H.; Packer, N.H. Modified glycosylation of cellobiohydrolase I from a high cellulase-producing mutant strain of Trichoderma reesei. Eur. J. Biochem. 1998, 256, 119–127. [Google Scholar] [CrossRef]
- Chung, J.; Khadka, P.; Chung, I.K. Nuclear import of hTERT requires a bipartite nuclear localization signal and Akt-mediated phosphorylation. J. Cell Sci. 2012, 125, 2684–2697. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.A.; Kim, K.; Lee, J.H.; Cha, J.S.; Khadka, P.; Cho, H.S.; Chung, I.K. Akt-mediated phosphorylation increases the binding affinity of hTERT for importin alpha to promote nuclear translocation. J. Cell Sci. 2015, 128, 2287–2301. [Google Scholar] [CrossRef]
- Kang, S.S.; Kwon, T.; Kwon, D.Y.; Do, S.I. Akt protein kinase enhances human telomerase activity through phosphorylation of telomerase reverse transcriptase subunit. J. Biol. Chem. 1999, 274, 13085–13090. [Google Scholar] [CrossRef]
- Overall, C.M.; Butler, G.S. Protease yoga: Extreme flexibility of a matrix metalloproteinase. Structure 2007, 15, 1159–1161. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Zhu, J.; Ragauskas, A.; Deng, Y.; Ragauskas, A. Enhanced enzymatic hydrolysis of spruce by alkaline pretreatment at low temperature. Biotechnol. Bioeng. 2008, 99, 1320–1328. [Google Scholar] [CrossRef]
- Igarashi, K.; Koivula, A.; Wada, M.; Kimura, S.; Penttilä, M.; Samejima, M. High speed atomic force microscopy visualizes processive movement of Trichoderma reesei cellobiohydrolase I on crystalline cellulose. J. Biol. Chem. 2009, 284, 36186–36190. [Google Scholar] [CrossRef]
- Seidl, V. Chitinases of filamentous fungi: A large group of diverse proteins with multiple physiological functions. Fungal Biol. Rev. 2008, 22, 36–42. [Google Scholar] [CrossRef]
- Van der Lee, R.; Buljan, M.; Lang, B.; Weatheritt, R.J.; Daughdrill, G.W.; Dunker, A.K.; Fuxreiter, M.; Gough, J.; Gsponer, J.; Jones, D.T.; et al. Classification of intrinsically disordered regions and proteins. Chem. Rev. 2014, 114, 6589–6631. [Google Scholar] [CrossRef] [PubMed]
- Czovek, A.; Szollosi, G.J.; Derenyi, I. The relevance of neck linker docking in the motility of kinesin. Biosystems 2008, 93, 29–33. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Czovek, A.; Szollosi, G.J.; Derenyi, I. Neck-linker docking coordinates the kinetics of kinesin’s heads. Biophys. J. 2011, 100, 1729–1736. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Katoh, K. MAFFT: A novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002, 30, 3059–3066. [Google Scholar] [CrossRef] [PubMed]
- Capra, J.A.; Singh, M. Predicting functionally important residues from sequence conservation. Bioinformatics 2007, 23, 1875–1882. [Google Scholar] [CrossRef] [PubMed]
| Protein Name | UniProt ID | ATP | Partner | Linker Length | Kappa Value (Plot Region) | Processivity | |
|---|---|---|---|---|---|---|---|
| 1 | H. sapiensRNAse H1 | O60930 | - | RNA | 50 aa (78–127) | 0.254 (2) | |
| 2 | H. sapiensXPF | Q92889 | - | DNA | 22 aa (821–842) | 0.187 (1) | 60 nucleotides |
| 3 | T. reeseiCel7A | P62694 | - | cellulose | 33 aa (445–477) | 0.503 (1) | 21 catalytic steps |
| 4 | H. insolensCel6A | Q9C1S9 | - | cellulose | 46 aa (68–113) | 0.288 (1) | |
| 5 | C. cellulolyticumCel48F * | P37698 | - | cellulose | 28 aa (106–133) | 0.069 (2) | |
| 6 | C. thermocellum1,4-beta-glucanase * | Q5TIQ4 | - | cellulose | 103 aa (688–790) | 0.238 (1) | |
| 7 | H. sapiensTelomerase | O14746 | - | DNA | 94 aa (231–324) | 0.252 (1) | |
| 8 | X. laevisXMAP215 | Q9PT63 | - | tubulin | 121 aa (1079–1199) | 0.189 (1) | 25 tubulin dimers |
| 9 | H. sapiensChitotriosidase-1 | Q13231 | - | chitooligosaccharides | 31 aa (387–417) | 0.263 (1) | 8.6 cleavage steps |
| 10 | B. circulansChitinase A1 | P20533 | - | crystalline-chitin | 23 aa (444–466) | 0.353 (1) | |
| 11 | O. sativa subsp. JaponicaChitinase 2 | Q7DNA1 | - | chitin | 17 aa (74–90) | 0.848 (1) | |
| 12 | H. sapiensMMP-9 | P14780 | - | gelatine | 76 aa (434–509) | 0.112 (1) |
| Enzyme | UniProt ID | PTMs | Domain Binding | Ref. |
|---|---|---|---|---|
| H. sapiens RNASEH1 | O60930 | Phosphorylation: S74, S76 | [52] | |
| T. reesei Cel7A | P62694 | Glycosylation: T461, T462, T463, T462, T469, T470, T471, S473, S474 | + | [53] |
| H. sapiens Telomerase | O14746 | Phosphorylation: S227 | [54,55,56] | |
| H. sapiens Nedd4-1 | P46934 | Phosphorylation: S670, S742, S743, S747, Y785, S884, S888. Ubiqutination: K882 | ||
| H. sapiens MMP-9 | P14780 | + |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabo, B.; Horvath, T.; Schad, E.; Murvai, N.; Tantos, A.; Kalmar, L.; Chemes, L.B.; Han, K.-H.; Tompa, P. Intrinsically Disordered Linkers Impart Processivity on Enzymes by Spatial Confinement of Binding Domains. Int. J. Mol. Sci. 2019, 20, 2119. https://doi.org/10.3390/ijms20092119
Szabo B, Horvath T, Schad E, Murvai N, Tantos A, Kalmar L, Chemes LB, Han K-H, Tompa P. Intrinsically Disordered Linkers Impart Processivity on Enzymes by Spatial Confinement of Binding Domains. International Journal of Molecular Sciences. 2019; 20(9):2119. https://doi.org/10.3390/ijms20092119
Chicago/Turabian StyleSzabo, Beata, Tamas Horvath, Eva Schad, Nikoletta Murvai, Agnes Tantos, Lajos Kalmar, Lucía Beatriz Chemes, Kyou-Hoon Han, and Peter Tompa. 2019. "Intrinsically Disordered Linkers Impart Processivity on Enzymes by Spatial Confinement of Binding Domains" International Journal of Molecular Sciences 20, no. 9: 2119. https://doi.org/10.3390/ijms20092119
APA StyleSzabo, B., Horvath, T., Schad, E., Murvai, N., Tantos, A., Kalmar, L., Chemes, L. B., Han, K.-H., & Tompa, P. (2019). Intrinsically Disordered Linkers Impart Processivity on Enzymes by Spatial Confinement of Binding Domains. International Journal of Molecular Sciences, 20(9), 2119. https://doi.org/10.3390/ijms20092119






