The Monetite Structure Probed by Advanced Solid-State NMR Experimentation at Fast Magic-Angle Spinning
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Solid-State NMR
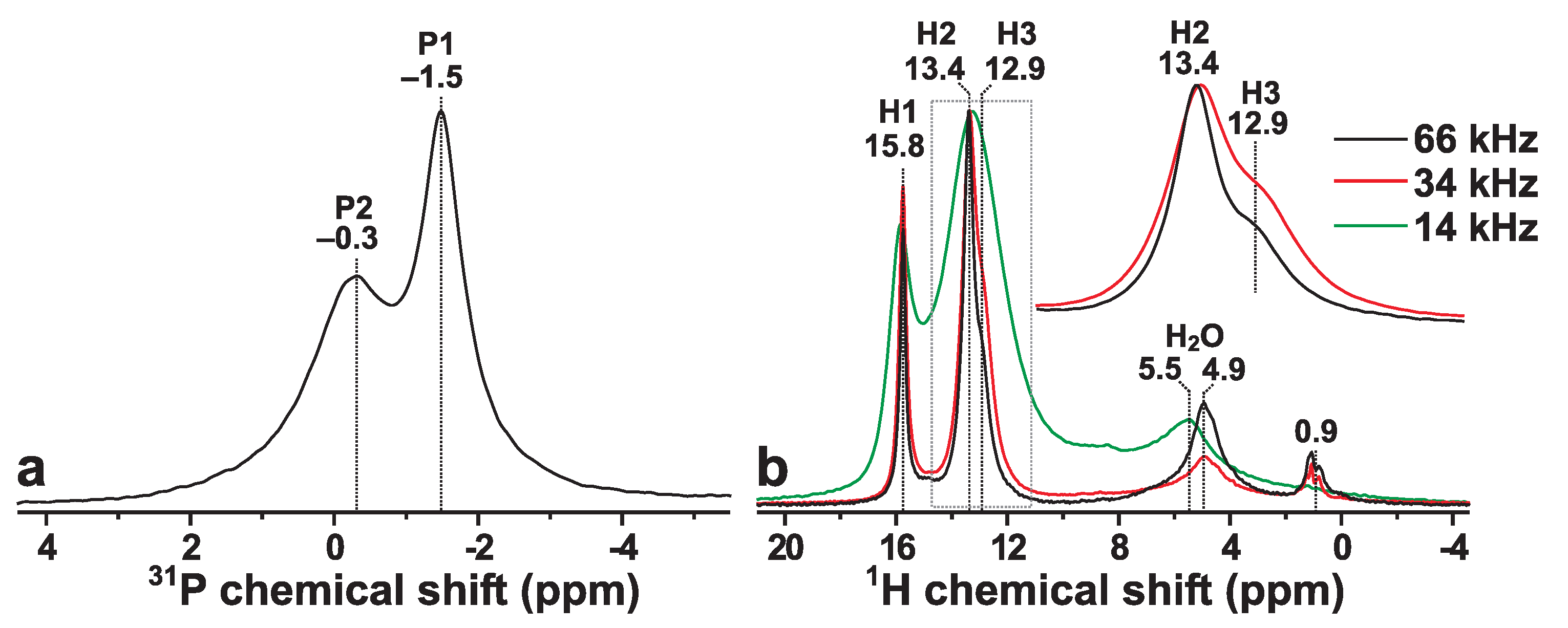
2.2.1. Single-Pulse NMR Experiments
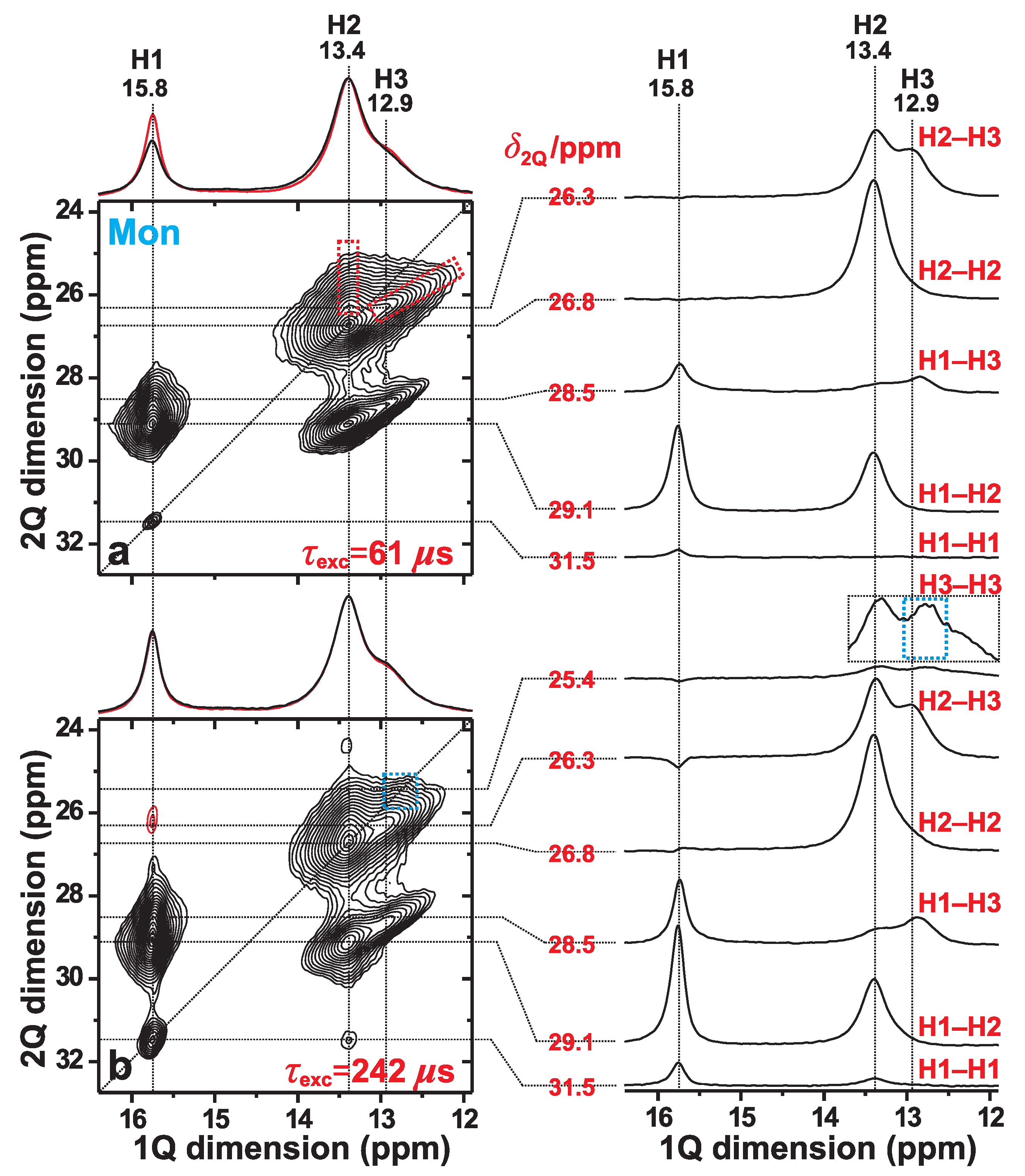
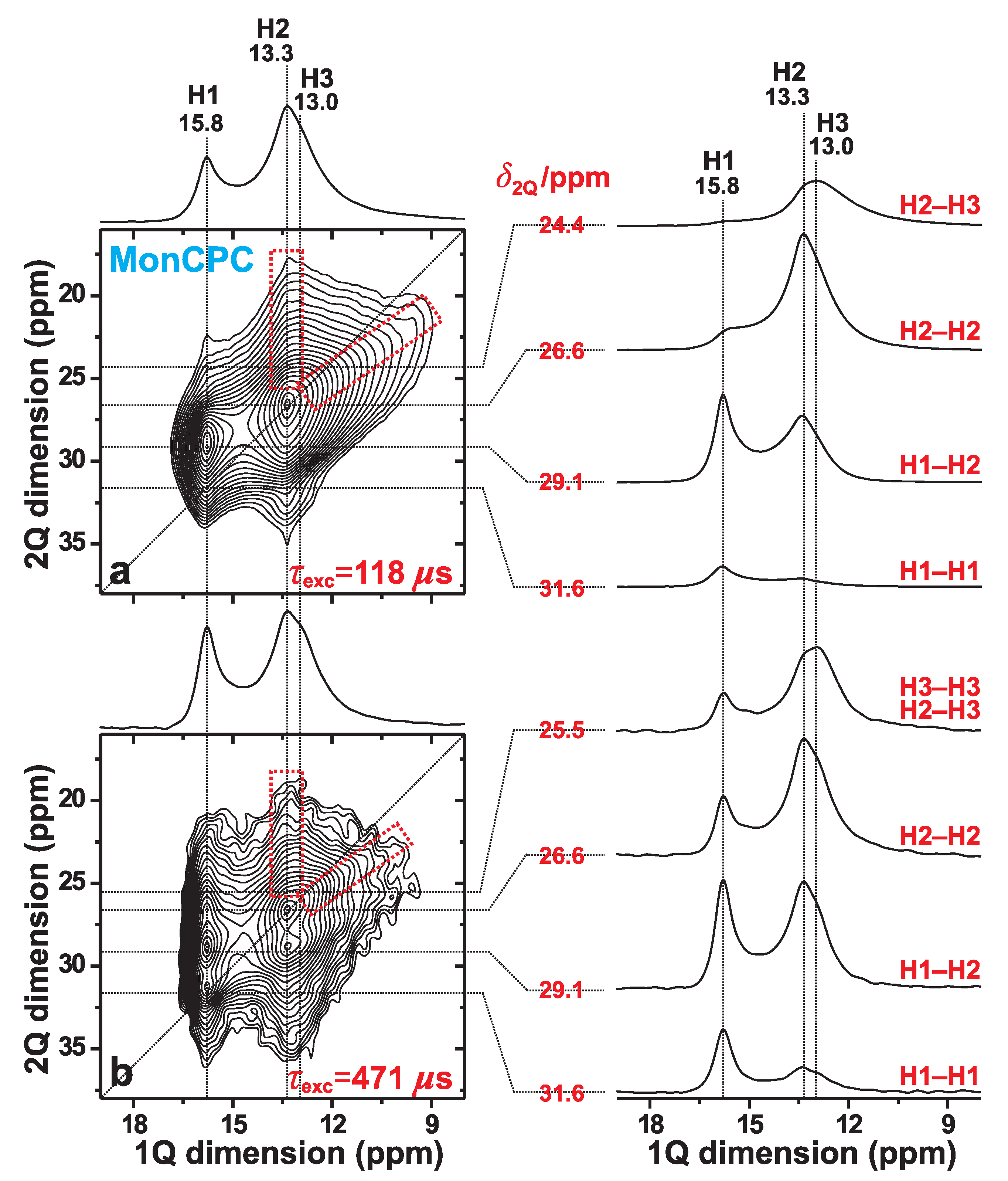
2.2.2. 2Q–1Q H NMR Experiments
2.2.3. P{H} HETCOR NMR Experiments
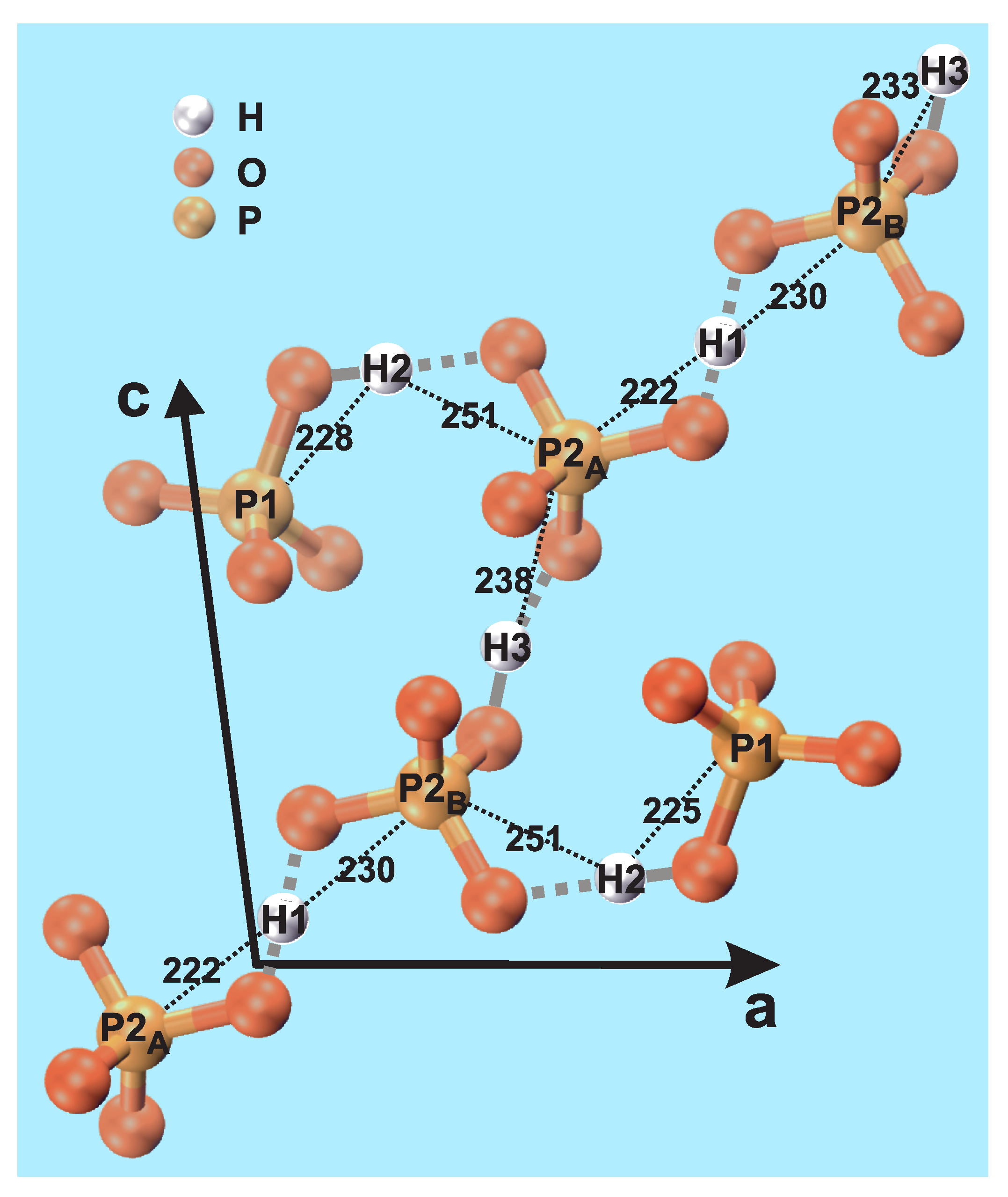
3. Results and Discussion
3.1. Local P and H Environments: MAS NMR Results
3.2. H–H Proximities in Monetite: 2Q–1Q Correlation NMR
3.3. H–H Proximities in the Monetite-Based Cement
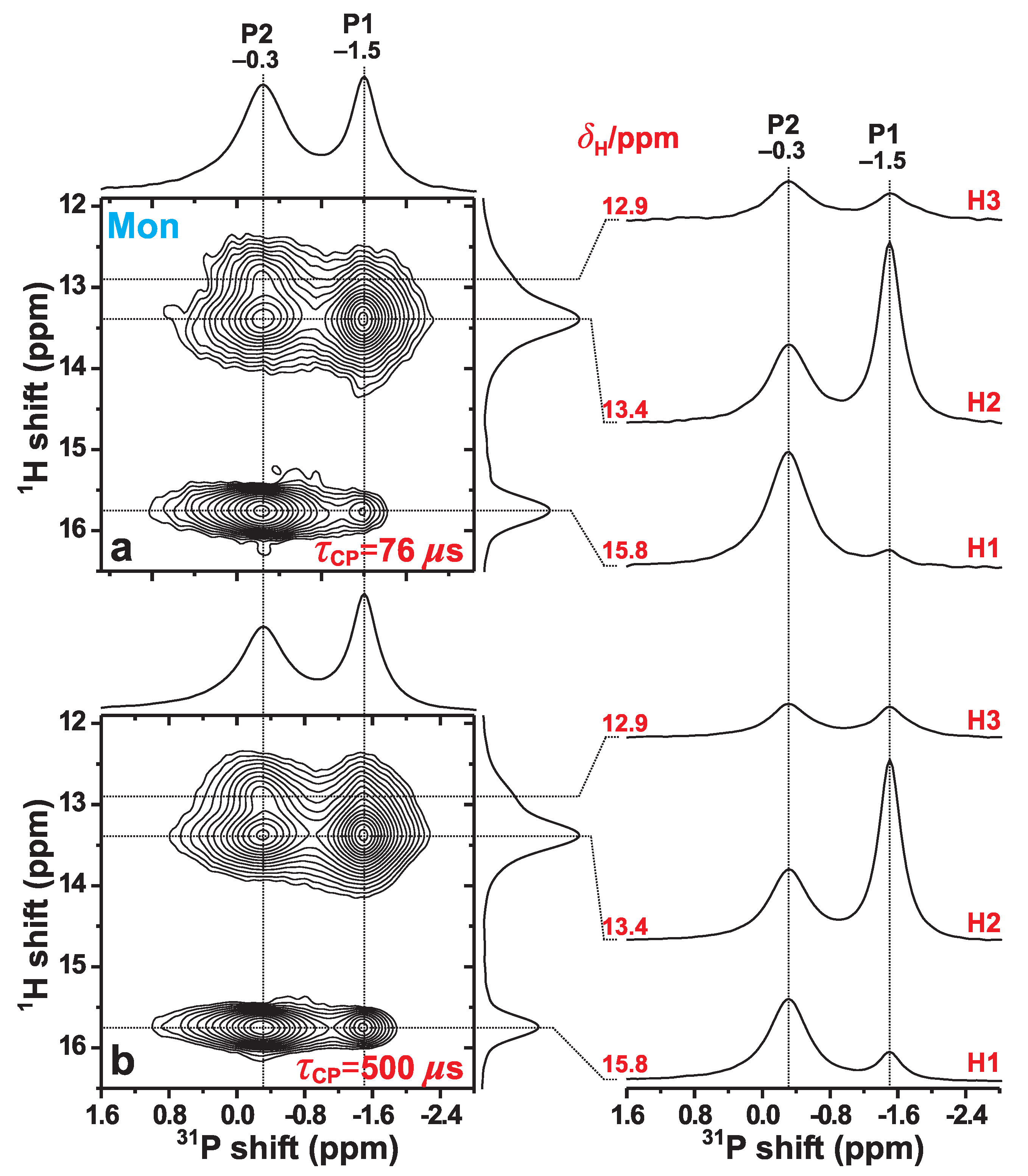
3.4. H–P Proximities in Monetite: P{H} HETCOR NMR
3.4.1. Relative H–P Contacts
3.4.2. Effective H–P Distances
3.4.3. Discussion on the H–P Contacts in Monetite and MonCPC
3.5. Interatomic-Distance Determination Procedure
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Johnsson, M.S.A.; Nancollas, G.H. The Role of Brushite and Octacalcium Phosphate in Apatite Formation. Crit. Rev. Oral Biol. Med. 1992, 3, 61–82. [Google Scholar] [CrossRef]
- Pak, C.Y.C.; Poindexter, J.R.; Adams-Huet, B.; Pearle, M.S. Predictive Value of Kidney Stone Composition in the Detection of Metabolic Abnormalities. Am. J. Med. 2003, 115, 26–32. [Google Scholar] [CrossRef]
- Grover, L.M.; Knowles, J.C.; Flemming, G.J.P.; Barralet, J.E. In vitro ageing of brushite calcium phosphate cement. Biomaterials 2003, 24, 4133–4141. [Google Scholar] [CrossRef]
- Dorozhkin, S.V. Amorphous Calcium (Ortho)Phosphates. Acta Biomater. 2010, 6, 4457–4475. [Google Scholar] [CrossRef] [PubMed]
- Tamimi, F.; Sheikh, Z.; Barralet, J. Dicalcium Phosphate Cements: Brushite and Monetite. Acta Biomater. 2012, 8, 474–487. [Google Scholar] [CrossRef]
- Catti, M.; Ferraris, G.; Filhol, A. Hydrogen Bonding in the Crystalline State. CaHPO4 (Monetite), P1¯ or P1? A Novel Neutron Diffraction Study. Acta Cryst. 1977, B33, 1223–1229. [Google Scholar] [CrossRef]
- MacLennan, G.; Beevers, C.A. The Crystal Structure of Dicalcium Phosphate, CaHPO4. Acta Cryst. 1955, 8, 579–583. [Google Scholar] [CrossRef]
- Jones, D.W.; Cruickshank, D.W.J. The Crystal Structures of Two Calcium Orthophosphates: CaHPO4 and Ca(H2PO4)2·H2O. Z. Kristallogr. 1961, 116, 101–125. [Google Scholar] [CrossRef]
- Denne, W.A.; Jones, D.W. Neutron Diffraction Investigation of the Hydrogen Positions in the Crystal Structure of Monetite, CaHPO4. J. Cryst. Mol. Struct. 1971, 1, 347–354. [Google Scholar] [CrossRef]
- Dickens, B.; Bowen, J.S.; Brown, W.E. A Refinement of the Crystal Structure of CaHPO4 (Synthetic Monetite). Acta Cryst. 1972, B28, 797–806. [Google Scholar] [CrossRef]
- Catti, M.; Ferraris, G.; Mason, S.A. Low-Temperature Ordering of Hydrogen Atoms in CaHPO4 (Monetite): X-ray and Neutron Diffraction Study at 145 K. Acta Cryst. 1980, B36, 254–259. [Google Scholar] [CrossRef]
- Rothwell, W.P.; Waugh, J.S.; Yesinowski, J.P. High-Resolution Variable-Temperature 31P NMR of Solid Calcium Phosphates. J. Am. Chem. Soc. 1980, 102, 2637–2643. [Google Scholar] [CrossRef]
- Aue, W.P.; Roufosse, A.H.; Glimcher, M.J.; Griffin, R.G. Solid-State Phosphorus-31 Nuclear Magnetic Resonance Studies of Synthetic Solid Phases of Calcium Phosphate: Potential Models of Bone Mineral. Biochemistry 1984, 23, 6110–6114. [Google Scholar] [CrossRef] [PubMed]
- Yesinowski, J.P.; Eckert, H. Hydrogen Environments in Calcium Phosphates: 1H MAS NMR at High Spinning Speeds. J. Am. Chem. Soc. 1987, 109, 6274–6282. [Google Scholar] [CrossRef]
- Miquel, J.L.; Facchini, L.; Legrand, A.P.; Rey, C.; Lemaitre, J. Solid State NMR to Study Calcium Phosphate Ceramics. Colloids Surf. 1990, 45, 427–433. [Google Scholar] [CrossRef]
- Bak, M.; Thomsen, J.K.; Jakobsen, H.J.; Petersen, S.E.; Petersen, T.E.; Nielsen, N.C. Solid-State 13C and 31P NMR Analysis of Urinary Stones. J. Urol. 2000, 164, 856–863. [Google Scholar] [CrossRef]
- Hlel, F.; Kamoun, S.; Guidara, K. Investigation of Phosphorus Site Condensation in CaHPO4 by Analysis of 31P MAS-NMR Tensor and X-Ray Powder Patterns. Z. Naturforsch. A 2006, 61, 375–382. [Google Scholar] [CrossRef]
- Legrand, A.P.; Sfihi, H.; Lequeux, N.; Lemaître, J. 31P Solid-State NMR Study of the Chemical Setting Process of a Dual-Paste Injectable Brushite Cements. J. Biomed. Mater. Res. 2009, 91B, 46–54. [Google Scholar] [CrossRef]
- Xue, X.; Kanzaki, M. Proton Distributions and Hydrogen Bonding in Crystalline and Glassy Hydrous Silicates and Related Inorganic Materials: Insights from High-Resolution Solid-State Nuclear Magnetic Resonance Spectroscopy. J. Am. Ceram. Soc. 2009, 92, 2803–2830. [Google Scholar] [CrossRef]
- Pourpoint, F.; Diogo, C.C.; Gervais, C.; Bonhomme, C.; Fayon, F.; Dalicieux, S.L.; Gennero, I.; Salles, J.P.; Howes, A.P.; Dupree, R.; et al. High-Resolution Solid State NMR Experiments for the Characterization of Calcium Phosphate Biomaterials and Biominerals. J. Mater. Res. 2011, 26, 2355–2368. [Google Scholar] [CrossRef]
- Schnell, I.; Spiess, H.W. High-Resolution 1H NMR Spectroscopy in the Solid State: Very Fast Sample Rotation and Multiple-Quantum Coherences. J. Magn. Reson. 2001, 151, 153–227. [Google Scholar] [CrossRef] [PubMed]
- Baldus, M. Correlation Experiments for Assignment and Structure Elucidation of Immobilized Polypeptides under Magic Angle Spinning. Prog. Nucl. Magn. Reson. Spectrosc. 2002, 41, 1–47. [Google Scholar] [CrossRef]
- De Paëpe, G. Dipolar Recoupling in Magic Angle Spinning Solid-State Nuclear Magnetic Resonance. Annu. Rev. Phys. Chem. 2012, 63, 661–684. [Google Scholar] [CrossRef] [PubMed]
- Edén, M. Advances in Symmetry-Based Pulse Sequences in Magic-Angle Spinning Solid-State NMR. eMagRes 2013, 2, 351–364. [Google Scholar] [CrossRef]
- Saalwächter, K. Robust NMR Approaches for the Determination of Homonuclear Dipole-Dipole Coupling Constants in Studies of Solid Materials and Biomolecules. ChemPhysChem 2013, 14, 3000–3014. [Google Scholar] [CrossRef]
- Edén, M.; Zhou, D.; Yu, J. Improved Double-Quantum NMR Correlation Spectroscopy of Dipolar-Coupled Quadrupolar Spins. Chem. Phys. Lett. 2006, 431, 397–403. [Google Scholar] [CrossRef]
- Lo, A.Y.H.; Edén, M. Efficient Symmetry-Based Homonuclear Dipolar Recoupling of Quadrupolar Spins: Double-Quantum NMR Correlations in Amorphous Solids. Phys. Chem. Chem. Phys. 2008, 10, 6635–6644. [Google Scholar] [CrossRef]
- Teymoori, G.; Pahari, B.; Stevensson, B.; Edén, M. Low-Power Broadband Homonuclear Dipolar Recoupling Without Decoupling: Double-Quantum 13C NMR Correlations at Very Fast Magic-Angle Spinning. Chem. Phys. Lett. 2012, 547, 103–109. [Google Scholar] [CrossRef]
- Teymoori, G.; Pahari, B.; Edén, M. Low-Power Broadband Homonuclear Dipolar Recoupling in MAS NMR by Two-Fold Symmetry Pulse Schemes for Magnetization Transfers and Double-Quantum Excitation. J. Magn. Reson. 2015, 261, 205–220. [Google Scholar] [CrossRef]
- Edén, M. Homonuclear Dipolar Recoupling of Half-Integer Spin Quadrupolar Nuclei: Techniques and Applications. Solid State Nucl. Magn. Reson. 2009, 36, 1–10. [Google Scholar] [CrossRef]
- Mathew, R.; Turdean-Ionescu, C.; Yu, Y.; Stevensson, B.; Izquierdo-Barba, I.; García, A.; Arcos, D.; Vallet-Regí, M.; Edén, M. Proton Environments in Biomimetic Calcium Phosphates Formed from Mesoporous Bioactive CaO–SiO2–P2O5 Glasses In Vitro: Insights from Solid-State NMR. J. Phys. Chem. C 2017, 121, 13223–13238. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Guo, H.; Pujari-Palmer, M.; Stevensson, B.; Grins, J.; Engqvist, H.; Edén, M. Advanced Solid-State 1H/31P NMR Characterization of Pyrophosphate-Doped Calcium Phosphate Cements for Biomedical Applications: The Structural Role of Pyrophosphate. Ceram. Int. 2019, 45, 20642–20655. [Google Scholar] [CrossRef]
- Grover, L.M.; Wright, A.J.; Gbureck, U.; Bolarinwa, A.; Song, J.; Liu, Y.; Farrar, D.F.; Howling, G.; Rose, J.; Barralet, J.E. The Effect of Amorphous Pyrophosphate on Calcium Phosphate Cement Resorption and Bone Generation. Biomaterials 2013, 34, 6631–6637. [Google Scholar] [CrossRef] [PubMed]
- Roberts, J.E.; Vega, S.; Griffin, R.G. Two-Dimensional Heteronuclear Chemical Shift Correlation Spectroscopy in Rotating Solids. J. Am. Chem. Soc. 1984, 106, 2506–2512. [Google Scholar] [CrossRef]
- Marion, D.; Ikura, M.; Tschudin, R.; Bax, A. Rapid Recording of 2D NMR Spectra without phase cycling. Application to the Study of Hydrogen Exchange in Proteins. J. Magn. Reson. 1989, 85, 393–399. [Google Scholar] [CrossRef]
- Fung, B.M.; Khitrin, A.K.; Ermolaev, K. An Improved Broadband Decoupling Sequence for Liquid Crystals and Solids. J. Magn. Reson. 2000, 142, 97–101. [Google Scholar] [CrossRef]
- Leonova, E.; Hakeem, A.S.; Jansson, K.; Stevensson, B.; Shen, Z.; Grins, J.; Esmaeilzadeh, S.; Edén, M. Nitrogen-Rich La–Si–Al–O–N Oxynitride Glass Structures Probed by Solid State NMR. J. Non-Cryst. Solids 2008, 354, 49–60. [Google Scholar] [CrossRef]
- Matlab; The Mathworks, Inc.: Natick, MA, USA, 2013.
- Guo, H.; Pujari-Palmer, M.; Yu, Y.; Stevensson, B.; Engqvist, H.; Edén, M. Quantitative Phase Analyses of Pyrophosphate-Bearing Monetite and Brushite Biocements by Solid-State NMR and Powder XRD. Ceram. Int. 2019. submitted. [Google Scholar]
- Pourpoint, F.; Gervais, C.; Bonhomme-Coury, L.; Azaïs, T.; Coelho, C.; Mauri, F.; Alonso, B.; Babonneau, F.; Bonhomme, C. Calcium Phosphates and Hydroxyapatite: Solid-State NMR Experiments and First-Principles Calculations. Appl. Magn. Reson. 2007, 32, 435–457. [Google Scholar] [CrossRef]
- Brinkmann, A.; Edén, M.; Levitt, M.H. Synchronous Helical Pulse Sequences in Magic-Angle-Spinning Nuclear Magnetic Resonance. Double Quantum Spectroscopy of Recoupled Multiple-Spin Systems. J. Chem. Phys. 2000, 112, 8539–8554. [Google Scholar] [CrossRef]
- Kolodziejski, W.; Klinowski, J. Kinetics of Cross-Polarization in Solid State NMR: A Guide for Chemists. Chem. Rev. 2002, 102, 613–628. [Google Scholar] [CrossRef] [PubMed]
- Massiot, D.; Fayon, F.; Capron, M.; King, I.; Le Calvé, S.; Alonso, B.; Durand, J.O.; Bujoli, B.; Gan, Z.; Hoatson, G. Modelling One- and Two-Dimensional Solid-State NMR Spectra. Magn. Reson. Chem. 2002, 40, 70–76. [Google Scholar] [CrossRef]
- Baldus, M.; Meier, B.H.; Ernst, R.R.; Kentgens, A.P.; Altenschildesche, H.M.Z.; Nesper, R. Structure Investigation on Anhydrous Disodium Hydrogen Phosphate using Solid-State NMR and X-ray Techniques. J. Am. Chem. Soc. 1995, 117, 5141–5147. [Google Scholar] [CrossRef]
- Lupulescu, A.; Brown, S.P.; Spiess, H.W. Rotor-Encoded Heteronuclear MQ MAS NMR Spectroscopy of Half-Integer Quadrupolar and Spin I=1/2 Nuclei. J. Magn. Reson. 2002, 154, 101–129. [Google Scholar] [CrossRef]
- Edén, M. Quadrupolar Coupling Selective Cross-Polarization in Solid-State NMR. Phys. Chem. Chem. Phys. 2006, 8, 1994–1999. [Google Scholar] [CrossRef]
- Langer, B.; Schnell, I.; Spiess, H.W.; Grimmer, A.R. Temperature Calibration under Ultrafast MAS Conditions. J. Magn. Reson. 1999, 138, 182–186. [Google Scholar] [CrossRef]
- Grimmer, A.R.; Kretschmer, A.; Cajipe, V.B. Influence of Magic Angle Spinning on Sample Temperature. Magn. Reson. Chem. 1997, 35, 86–90. [Google Scholar] [CrossRef]
- Aluas, M.; Tripon, C.; Griffin, J.M.; Filip, X.; Ladizhansky, V.; Griffin, R.G.; Brown, S.P.; Filip, C. CHHC and 1H–1H Magnetization Exchange: Analysis by Experimental Solid-State NMR and 11-Spin Density-Matrix Simulations. J. Magn. Reson. 2009, 199, 173–187. [Google Scholar] [CrossRef][Green Version]
- Bradley, J.P.; Tripon, C.; Filip, C.; Brown, S.P. Determining Relative Proton–Proton Proximities from the Build-Up of Two-Dimensional Correlation Peaks in 1H Double-Quantum MAS NMR: Insight from Multi-Spin Density-Matrix Simulations. Phys. Chem. Chem. Phys. 2009, 11, 6941–6952. [Google Scholar] [CrossRef]
| Site | H1 | H2 | H3 |
|---|---|---|---|
| H1 | 663 | 376;377;399 | 435;440 |
| H2 | 323;357 | 356;363;374 | |
| H3 | 663 |
| Site | H1 | H2 | H3 |
|---|---|---|---|
| P1 | 382;389 | 225;228 | 347;396 |
| P2 | 222;230 | 251;251 | 233;238 |
| Site | H1 | H2 | H3 | |||
|---|---|---|---|---|---|---|
| P1 | 0.016(0.012) | 367(385) | 0.312(0.290) | 224(226) | 0.061(0.016) | 294(366) |
| P2 | 0.246(0.296) | 233(226) | 0.176(0.156) | 246(251) | 0.189(0.230) | 243(235) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Stevensson, B.; Pujari-Palmer, M.; Guo, H.; Engqvist, H.; Edén, M. The Monetite Structure Probed by Advanced Solid-State NMR Experimentation at Fast Magic-Angle Spinning. Int. J. Mol. Sci. 2019, 20, 6356. https://doi.org/10.3390/ijms20246356
Yu Y, Stevensson B, Pujari-Palmer M, Guo H, Engqvist H, Edén M. The Monetite Structure Probed by Advanced Solid-State NMR Experimentation at Fast Magic-Angle Spinning. International Journal of Molecular Sciences. 2019; 20(24):6356. https://doi.org/10.3390/ijms20246356
Chicago/Turabian StyleYu, Yang, Baltzar Stevensson, Michael Pujari-Palmer, Hua Guo, Håkan Engqvist, and Mattias Edén. 2019. "The Monetite Structure Probed by Advanced Solid-State NMR Experimentation at Fast Magic-Angle Spinning" International Journal of Molecular Sciences 20, no. 24: 6356. https://doi.org/10.3390/ijms20246356
APA StyleYu, Y., Stevensson, B., Pujari-Palmer, M., Guo, H., Engqvist, H., & Edén, M. (2019). The Monetite Structure Probed by Advanced Solid-State NMR Experimentation at Fast Magic-Angle Spinning. International Journal of Molecular Sciences, 20(24), 6356. https://doi.org/10.3390/ijms20246356







