Nitropyridine-1-Oxides as Excellent π-Hole Donors: Interplay between σ-Hole (Halogen, Hydrogen, Triel, and Coordination Bonds) and π-Hole Interactions
Abstract
1. Introduction
2. Results and Discussion
2.1. CSD Search
2.2. MEP Study
2.3. Two Component Complexes
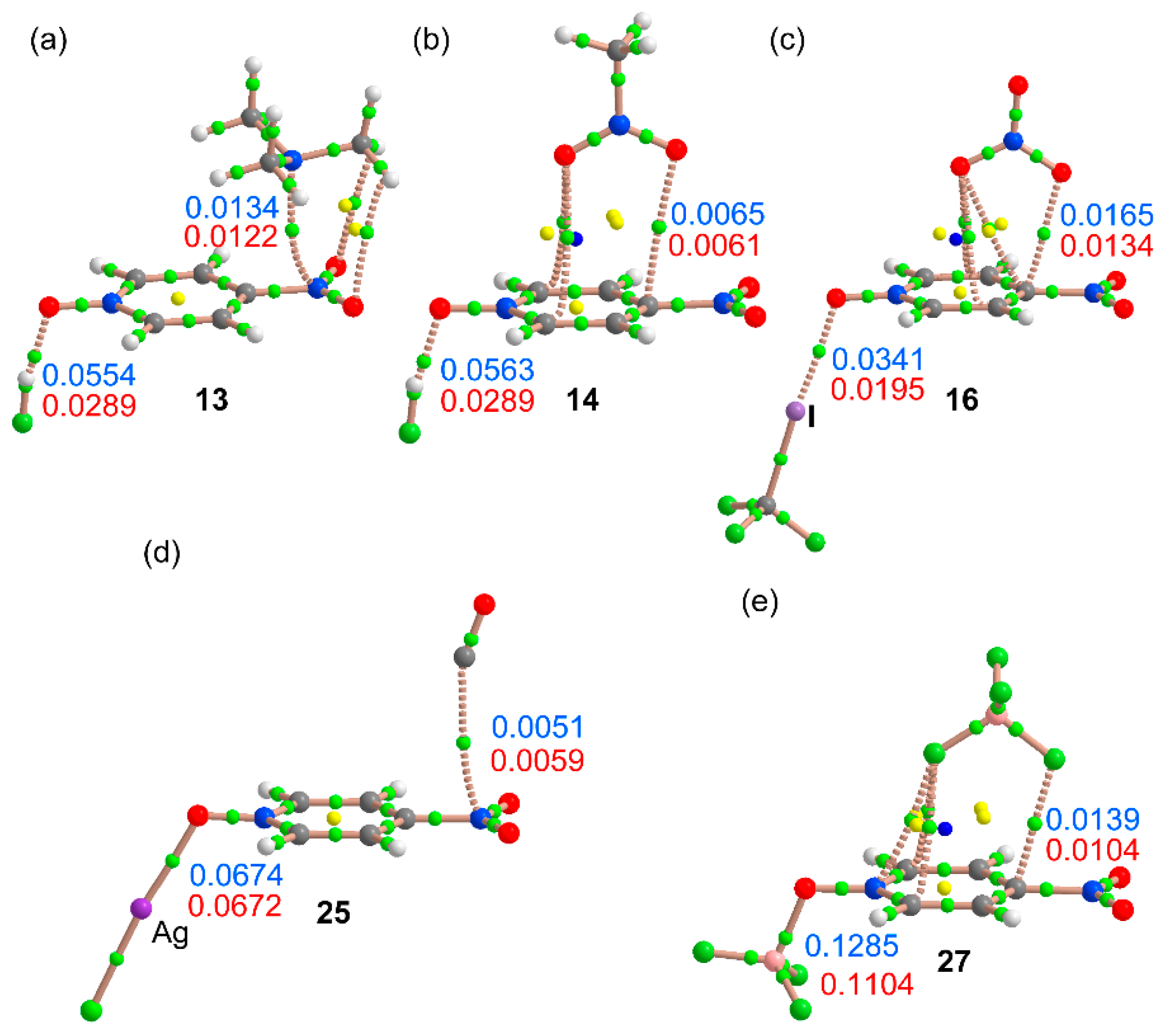
2.4. Three Component Systems
2.5. QTAIM Results
3. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schneider, H.J. Binding mechanisms in supramolecular complexes. Angew. Chem. Int. Ed. 2009, 48, 3924–3977. [Google Scholar] [CrossRef] [PubMed]
- Lehn, J.M. Supramolecular Chemistry Concepts and Perspectives; Wiley-VCH: Weinheim, Germany, 1995. [Google Scholar]
- Steed, J.W.; Atwood, J.L. Supramolecular Chemistry; Wiley: Chichester, UK, 2000. [Google Scholar]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond in Structural Chemistry and Biology; International Union of Crystal: Oxford, UK; New York, NY, USA, 1999. [Google Scholar]
- Scheiner, S. Hydrogen Bonding: A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Grabowski, S.J. Grabowski in Hydrogen Bonding—New Insights; Springer: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Roselló, Y.; Benito, M.; Molins, E.; Barceló-Oliver, M.; Frontera, A. Adenine as a Halogen Bond Acceptor: A Combined Experimental and DFT Study. Crystals 2019, 9, 224. [Google Scholar] [CrossRef]
- Carreras, L.; Benet-Buchholz, J.; Franconetti, A.; Frontera, A.; van Leeuwen, P.W.N.M.; Vidal-Ferran, A. Halogen bonding effects on the outcome of reactions at metal centres. Chem. Commun. 2019, 55, 2380–2383. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Rozas, S.; Elguero, J. Charge-Transfer Complexes between Dihalogen Compounds and Electron Donors. J. Phys. Chem. A 1998, 102, 9278–9285. [Google Scholar] [CrossRef]
- Karpfen, A. Charge-Transfer Complexes between NH3 and the Halogens F2, ClF, and Cl2: An ab Initio Study on the Intermolecular Interaction. J. Phys. Chem. A 2000, 104, 6871–6875. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Wieczorek, R.; Hobza, P.; Michalska, D. Halogen bonded complexes between volatile anaesthetics (chloroform, halothane, enflurane, isoflurane) and formaldehyde: A theoretical study. Phys. Chem. Chem. Phys. 2011, 13, 5105–5113. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Ford, C.L., Jr.; Demouchet, K. Comparison of hydrogen bonds, halogen bonds, C–H⋯π interactions, and C–X⋯π interactions using high-level ab initio methods. Chem. Phys. Lett. 2015, 621, 165–170. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. A Unified View of Halogen Bonding, Hydrogen Bonding and Other σ-Hole Interactions; Scheiner, S., Ed.; Springer: Dordrecht, Germany, 2015; Volume 19, p. 357. [Google Scholar]
- Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. Σ-holes, π-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Effects of Multiple Substitution upon the P∙∙∙N Noncovalent Interaction. Chem. Phys. 2011, 387, 79–84. [Google Scholar] [CrossRef]
- Adhikari, U.; Scheiner, S. Effects of Charge and Substituent on the S···N Chalcogen Bond. J. Phys. Chem. A 2014, 118, 3183–3192. [Google Scholar] [CrossRef] [PubMed]
- Zierkiewicz, W.; Bienko, D.C.; Michalska, D.; Zeegers-Huyskens, T. Theoretical investigation of the halogen bonded complexes between carbonyl bases and molecular chlorine. J. Comput. Chem. 2015, 36, 821–832. [Google Scholar] [CrossRef] [PubMed]
- Southern, S.A.; Bryce, D.L. NMR Investigations of Noncovalent Carbon Tetrel Bonds. Computational Assessment and Initial Experimental Observation. J. Phys. Chem. A 2015, 119, 11891–11899. [Google Scholar] [CrossRef] [PubMed]
- Southern, S.A.; Errulat, D.; Frost, J.M.; Gabidullin, B.; Bryce, D.L. Faraday Discuss. 2017, 203, 165–186. [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. Aerogen Bonding Interaction: A New Supramolecular Force? Angew. Chem. Int. Ed. 2015, 54, 7340–7343. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. π-Hole aerogen bonding interactions. Phys. Chem. Chem. Phys. 2015, 17, 24748–24753. [Google Scholar] [CrossRef] [PubMed]
- Frontera, A.; Bauzá, A. S⋅⋅⋅ Sn Tetrel Bonds in the Activation of Peroxisome Proliferator-Activated Receptors (PPARs) by Organotin Molecules. Chem. Eur. J. 2018, 24, 16582–16587. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudi, G.; Seth, S.K.; Bauza, A.; Zubkov, F.I.; Gurbanov, A.V.; White, J.; Stilinovic, V.; Doert, T.; Frontera, A. Pb⋯X (X = N, S, I) tetrel bonding interactions in Pb(II) complexes: X-ray characterization, Hirshfeld surfaces and DFT calculations. CrystEngComm 2018, 20, 2812–2821. [Google Scholar] [CrossRef]
- Del Bene, J.E.; Alkorta, I.; Elguero, J. The Pnicogen Bond in Review: Structures, Energies, Bonding Properties, and Spin-Spin Coupling Constants of Complexes Stabilized by Pnicogen Bonds; Scheiner, S., Ed.; Springer: Dordrecht, Germany, 2015; Volume 19, p. 191. [Google Scholar]
- Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Modulating intramolecular P⋯N pnictogen interactions. Phys. Chem. Chem. Phys. 2016, 18, 9148–9160. [Google Scholar] [CrossRef]
- Bauza, A.; Seth, S.K.; Frontera, A. Tetrel bonding interactions at work: Impact on tin and lead coordination compounds. Coord. Chem. Rev. 2019, 384, 107–125. [Google Scholar] [CrossRef]
- Grabowski, S.J. Tetrel bond–σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Rozas, I.; Elguero, J. Molecular Complexes between Silicon Derivatives and Electron-Rich Groups. J. Phys. Chem. A 2001, 105, 743–749. [Google Scholar] [CrossRef]
- Franconetti, A.; Frontera, A. Theoretical and Crystallographic Study of Lead(IV) Tetrel Bonding Interactions. Chem. Eur. J. 2019, 25, 6007–6013. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Sensitivity of noncovalent bonds to intermolecular separation: Hydrogen, halogen, chalcogen, and pnicogen bonds. CrystEngComm 2013, 15, 3119–3124. [Google Scholar] [CrossRef]
- Marín-Luna, M.; Alkorta, I.; Elguero, J. A theoretical study of the HnF4−nSi:N-base (n = 1–4) tetrel-bonded complexes. Theor. Chem. Acc. 2017, 136, 41. [Google Scholar] [CrossRef]
- Liu, M.; Li, Q.; Scheiner, S. Comparison of tetrel bonds in neutral and protonated complexes of pyridineTF3 and furanTF3 (T = C, Si, and Ge) with NH3. Phys. Chem. Chem. Phys. 2017, 19, 5550–5559. [Google Scholar] [CrossRef]
- Benz, S.; Macchione, M.; Verolet, Q.; Mareda, J.; Sakai, N.; Matile, S. Anion Transport with Chalcogen Bonds. J. Am. Chem. Soc. 2016, 138, 9093–9096. [Google Scholar] [CrossRef]
- Birman, V.B.; Li, X. Benzotetramisole: A Remarkably Enantioselective Acyl Transfer Catalyst. Org. Lett. 2006, 8, 1351–1354. [Google Scholar] [CrossRef]
- Fukumoto, S.; Nakashima, T.; Kawai, T. Photon-Quantitative Reaction of a Dithiazolylarylene in Solution. Angew. Chem. Int. Ed. 2011, 50, 1565–1568. [Google Scholar] [CrossRef]
- Leverett, C.A.; Purohit, V.C.; Romo, D. Enantioselective, Organocatalyzed, Intramolecular Aldol Lactonizations with Keto Acids Leading to Bi- and Tricyclic β-Lactones and Topology-Morphing Transformations. Angew. Chem. Int. Ed. 2010, 49, 9479–9483. [Google Scholar] [CrossRef] [PubMed]
- Robinson, E.R.T.; Walden, D.M.; Fallan, C.; Greenhalgh, M.D.; Cheong, P.H.-Y.; Smith, A.D. Non-bonding 1,5-S⋯O interactions govern chemo-and enantioselectivity in isothiourea-catalyzed annulations of benzazoles. Chem. Sci. 2016, 7, 6919–6927. [Google Scholar] [CrossRef] [PubMed]
- Cinar, M.E.; Ozturk, T. Thienothiophenes, Dithienothiophenes, and Thienoacenes: Syntheses, Oligomers, Polymers, and Properties. Chem. Rev. 2015, 115, 3036–3140. [Google Scholar] [CrossRef] [PubMed]
- Barbarella, G.; Di Maria, F. Supramolecular Oligothiophene Microfibers Spontaneously Assembled on Surfaces or Coassembled with Proteins inside Live Cells. Acc. Chem. Res. 2015, 48, 2230–2241. [Google Scholar] [CrossRef] [PubMed]
- Kremer, A.; Fermi, A.; Biot, N.; Wouters, J.; Bonifazi, D. Supramolecular Wiring of Benzo-1,3-chalcogenazoles through Programmed Chalcogen Bonding Interactions. Chem. Eur. J. 2016, 22, 5665–5675. [Google Scholar] [CrossRef] [PubMed]
- Wonner, P.; Vogel, L.; Düser, M.; Gomes, L.; Kniep, F.; Mallick, B.; Werz, D.B.; Huber, S.M. Carbon-Halogen Bond Activation by Selenium-Based Chalcogen Bonding. Angew. Chem. Int. Ed. 2017, 56, 12009–12012. [Google Scholar] [CrossRef]
- Benz, S.; Mareda, J.; Besnard, C.; Sakai, N.; Matile, S. Catalysis with chalcogen bonds: Neutral benzodiselenazole scaffolds with high-precision selenium donors of variable strength. Chem. Sci. 2017, 8, 8164–8169. [Google Scholar] [CrossRef]
- Benz, S.; Besnard, C.; Matile, S. Chalcogen-Bonding Catalysis: From Neutral to Cationic Benzodiselenazole Scaffolds. Helv. Chim. Acta 2018, 101, e1800075. [Google Scholar] [CrossRef]
- Benz, S.; Poblador-Bahamonde, A.I.; Low-Ders, N.; Matile, S. Catalysis with Pnictogen, Chalcogen, and Halogen Bonds. Angew. Chem. Int. Ed. 2018, 57, 5408–5412. [Google Scholar] [CrossRef]
- Grabowski, S.J. Triel Bonds, π-Hole-π-Electrons Interactions in Complexes of Boron and Aluminium Trihalides and Trihydrides with Acetylene and Ethylene. Molecules 2015, 20, 11297–11316. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Directionality of π-holes in nitro compounds. Chem. Commun. 2015, 51, 1491–1493. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A.; Mooibroek, T.J. π-Hole Interactions Involving Nitro Compounds: Directionality of Nitrate Esters. Cryst. Growth Des. 2016, 16, 5520–5524. [Google Scholar] [CrossRef]
- Saha, U.; Dutta, D.; Nath, H.; Franconetti, A.; Frontera, A.; Bhattacharyya, M.K. Supramolecular association in Cu(II) coordination complexes involving energetically significant NO⋯NO π–hole interaction and cooperative π-stacked ternary assembly: Experimental and theoretical studies. Inorg. Chim. Acta 2019, 488, 159–169. [Google Scholar] [CrossRef]
- Nashre-ul-Islam, S.M.; Dutta, D.; Frontera, A.; Bhattacharyya, M.K. Supramolecular association involving nitrile–nitrile interactions in polymeric Mn(II) coordination complexes: A combined experimental and theoretical study. Inorg. Chim. Acta 2019, 487, 424–432. [Google Scholar] [CrossRef]
- Dutta, D.; Nath, H.; Frontera, A.; Bhattacharyya, M.K. A novel oxalato bridged supramolecular ternary complex of Cu(II) involving energetically significant π-hole interaction: Experimental and theoretical studies. Inorg. Chim. Acta 2019, 487, 354–361. [Google Scholar] [CrossRef]
- Prohens, R.; de Sande, D.; Font-Bardia, M.; Franconetti, A.; González, F.J.; Frontera, A. Gallic Acid Dimer as a Double π–Hole Donor: Evidence from X-ray, Theoretical Calculations, and Generalization from the Cambridge Structural Database. Cryst. Growth Des. 2019, 19, 3989–3997. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. 2016, B72, 171–179. [Google Scholar] [CrossRef]
- Li, W.; Spada, L.; Tasinato, N.; Rampino, S.; Evangelisti, L.; Gualandi, A.; Cozzi, P.G.; Melandri, S.; Barone, V.; Puzzarini, C. Theory Meets Experiment for Noncovalent Complexes: The Puzzling Case of Pnicogen Interactions. Angew. Chem. Int. Ed. 2018, 57, 13853–13857. [Google Scholar] [CrossRef]
- Bauzá, A.; Sharko, A.V.; Senchyk, G.A.; Rusanov, E.B.; Frontera, A.; Domasevitch, K.V. π–hole interactions at work: Crystal engineering with nitro-derivatives. CrystEngComm 2017, 19, 1933–1937. [Google Scholar] [CrossRef]
- Salonen, L.M.; Ellermann, M.; Diederich, F. Aromatic rings in chemical and biological recognition: Energetics and structures. Angew. Chem. Int. Ed. 2011, 50, 4808–4842. [Google Scholar] [CrossRef]
- Meyer, E.A.; Castellano, R.K.; Diederich, F. Interactions with aromatic rings in chemical and biological recognition. Angew. Chem. Int. Ed. 2003, 42, 1210–1250. [Google Scholar] [CrossRef] [PubMed]
- Allen, F.H.; Motherwell, W.D.S. Applications of the Cambridge Structural Database in organic chemistry and crystal chemistry. Acta Cryst. 2002, B58, 407–422. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R. Life-science applications of the Cambridge Structural Database. Acta Cryst. 2002, D58, 879–888. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.-J.; Yatsimirski, A. Principles and Methods in Supramolecular Chemistry; Wiley: Chichester, UK, 2000. [Google Scholar]
- Quiñonero, D.; Frontera, A.; Garau, C.; Ballester, P.; Costa, A.; Deya, P.M. Interplay Between Cation–π, Anion–π and π–π Interactions. ChemPhysChem 2006, 7, 2487–2491. [Google Scholar] [CrossRef] [PubMed]
- Frontera, A.; Quiñonero, D.; Costa, A.; Ballester, P.; Deya, P.M. MP2 study of cooperative effects between cation–π, anion–π and π–π interactions. New J. Chem. 2007, 31, 556–560. [Google Scholar] [CrossRef]
- Lucas, X.; Estarellas, C.; Escudero, D.; Frontera, A.; Quiñonero, D.; Deya, P.M. Very long-range effects: Cooperativity between anion-π and hydrogen-bonding interactions. ChemPhysChem 2009, 10, 2256–2264. [Google Scholar] [CrossRef]
- Escudero, D.; Frontera, A.; Quiñonero, D.; Deya, P.M. Interplay between anion-π and hydrogen bonding interactions. J. Comput. Chem. 2009, 30, 75–82. [Google Scholar] [CrossRef]
- Estarellas, C.; Frontera, A.; Quiñonero, D.; Deya, P.M. Theoretical study on cooperativity effects between anion-π and halogen-bonding interactions. ChemPhysChem 2011, 12, 2742–7250. [Google Scholar] [CrossRef]
- Alkorta, I.; Blanco, F.; Deyà, P.M.; Elguero, J.; Estarellas, C.; Frontera, A.; Quiñonero, D. Cooperativity of hydrogen and halogen bond interactions. Theor. Chem. Acc. 2010, 126, 1–14. [Google Scholar] [CrossRef]
- Galmés, B.; Martínez, D.; Infante-Carrió, M.F.; Franconetti, A.; Frontera, A. Theoretical ab Initio Study on Cooperativity Effects between Nitro π-hole and Halogen Bonding Interactions. ChemPhysChem 2019, 20, 1135–1144. [Google Scholar] [CrossRef]
- Bader, R.W.F. Atoms in Molecules: A Quantum Theory; Clarendon: Oxford, UK, 1990. [Google Scholar]
- Cheeseman, J.R.; Carrol, M.T.; Bader, R.F.W. The mechanics of hydrogen bond formation in conjugated systems. Chem. Phys. Lett. 1988, 143, 450–458. [Google Scholar]
- Williams, R.J.; Cromer, D.T.; Watson, W.H. The crystal and molecular structure of a 4-nitropyridine N-oxide adduct of trans-dichlorodiaquocopper(II), CuCl2(H2O)2·2(C5H4N2O3). Acta Cryst. 1971, B27, 1619–1624. [Google Scholar] [CrossRef]
- Nizhnik, Y.P.; Lu, J.; Rosokha, S.V.; Kochi, J.K. Lewis acid effects on donor–acceptor associations and redox reactions: Ternary complexes of heteroaromatic N-oxides with boron trifluoride and organic donors. New J. Chem. 2009, 33, 2317–2325. [Google Scholar] [CrossRef]
- Ban-Oganowska, H.; Hanuza, J.; Maczka, M.; Waskowska, A.; van der Maas, J.H.; Oganowski, W.; Talik, Z. Vibrational properties and X-ray crystal structure of 3-iodo-2,6-dimethyl-4-nitropyridine N-oxide. Vib. Spect. 2001, 26, 83–97. [Google Scholar] [CrossRef]
- Moreno Fuquen, R.; de Almeida Santos, R.H.; Lechat, J.R. Crystal structure of the 1:1 complex formed by 4-nitropyridine N-oxide and 4-nitrophenol. J. Cryst. Spect. Res. 1992, 22, 201–204. [Google Scholar] [CrossRef]
- TURBOMOLE V7.0 2015, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, Since 2007. Available online: http://www.turbomole.com (accessed on 12 July 2019).
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Perdew, J.P. Generalized gradient approximation to the angle- and system-averaged exchange hole. J. Chem. Phys. 1998, 109, 3313–3320. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Hättig, C.; Schmitz, G.; Koßmann, J. Auxiliary basis sets for density-fitted correlated wavefunction calculations: Weighted core-valence and ECP basis sets for post-d elements. Phys. Chem. Chem. Phys. 2012, 14, 6549–6552. [Google Scholar] [CrossRef]
- Bergner, A.; Dolg, M.; Küchle, W.; Stoll, H.; Preuss, H. Ab initio energy adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
- Weigend, F. Segmented contracted basis sets for one- and two-component Dirac-Fock effective core potentials. J. Chem. Phys. 2010, 133, 174102. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H.P.; et al. Gaussian 09; Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll; Version 17.11.14; TK Gristmill Software: Overland Park, KS, USA, 2013; Available online: aim.tkgristmill.com (accessed on 12 July 2019).
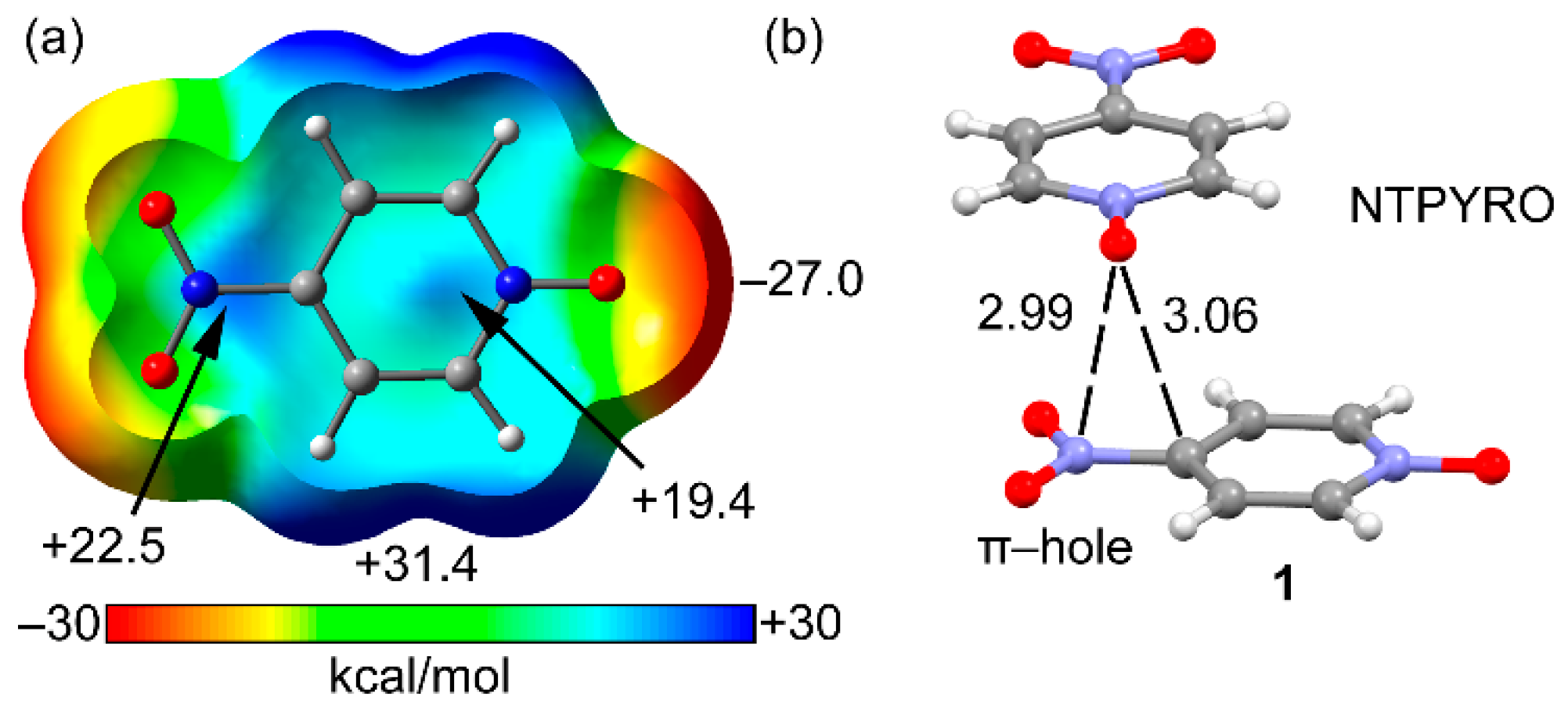

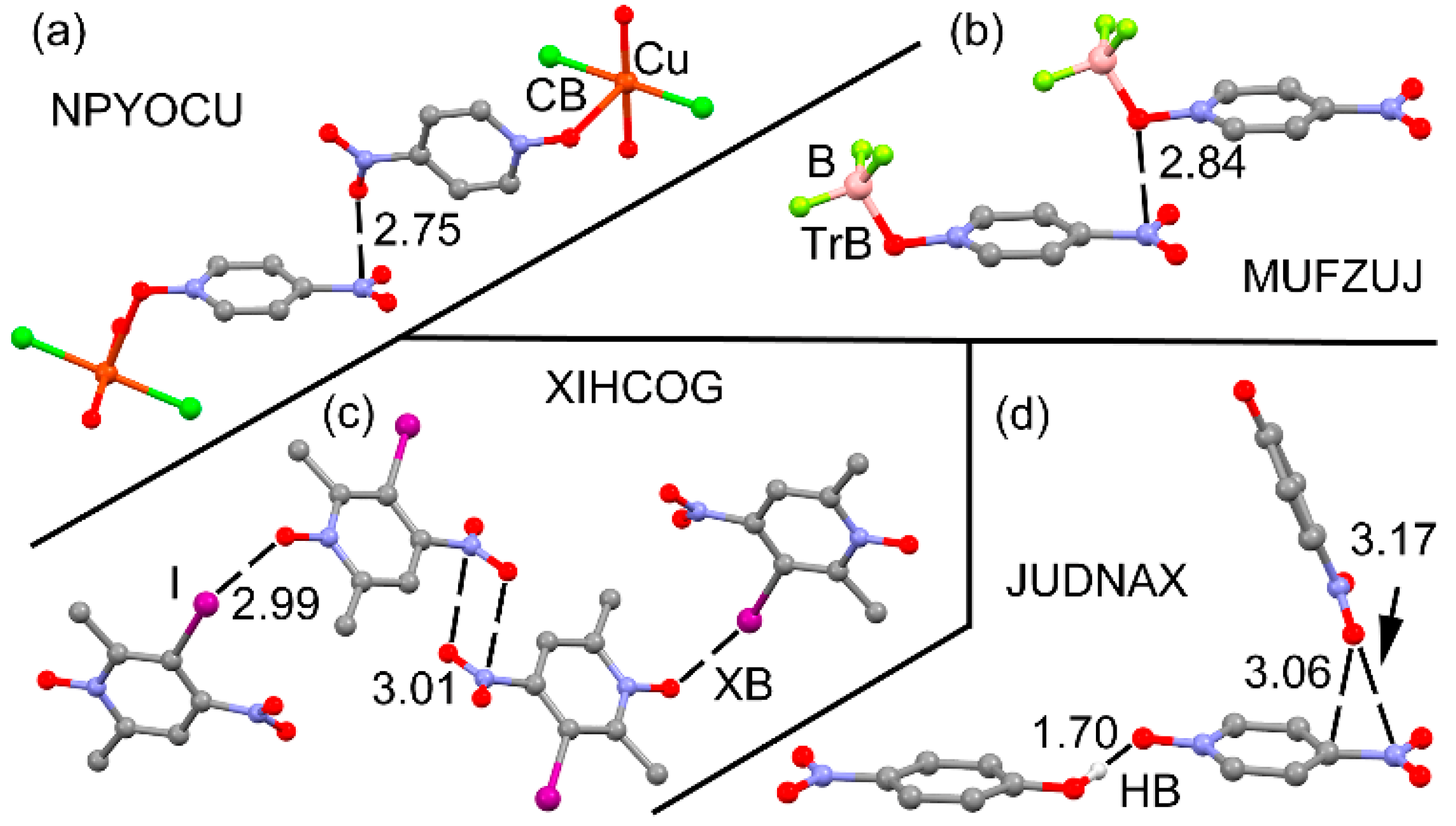
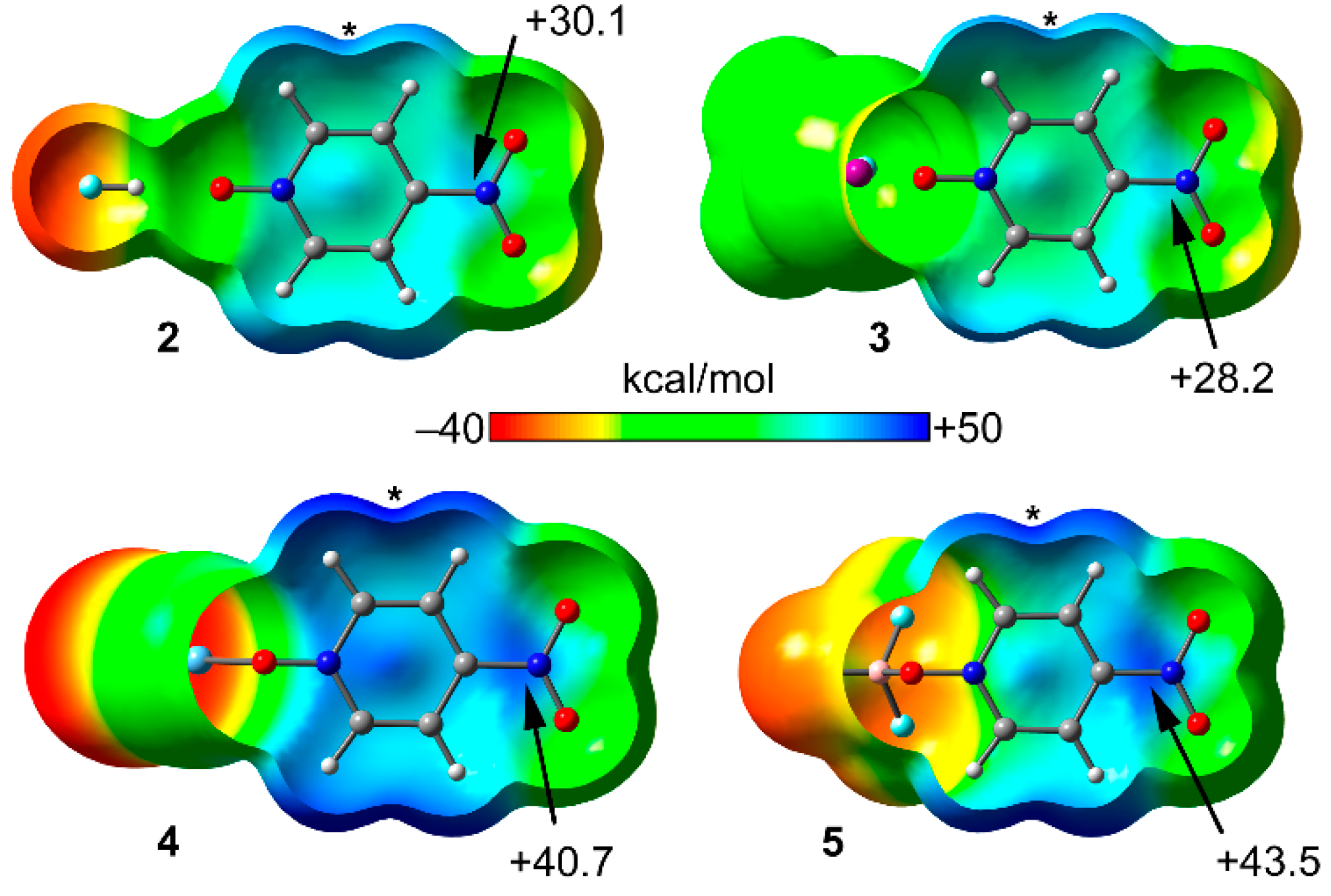
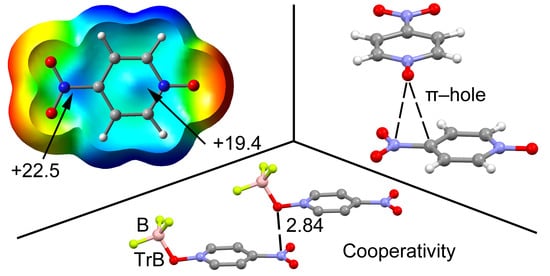
| Compound | Vs,πh | Vs,centroid | Vs,max |
|---|---|---|---|
| 1 | 22.5 | 19.4 | 31.7 |
| 2 (1 + HF) | 30.1 | 27.6 | 38.1 |
| 3 (1 + CF3I) | 28.2 | 25.1 | 34.4 |
| 4 (1 + AgCl) | 40.7 | 39.5 | 47.1 |
| 5 (1 +BF3) | 43.1 | 41.2 | 45.3 |
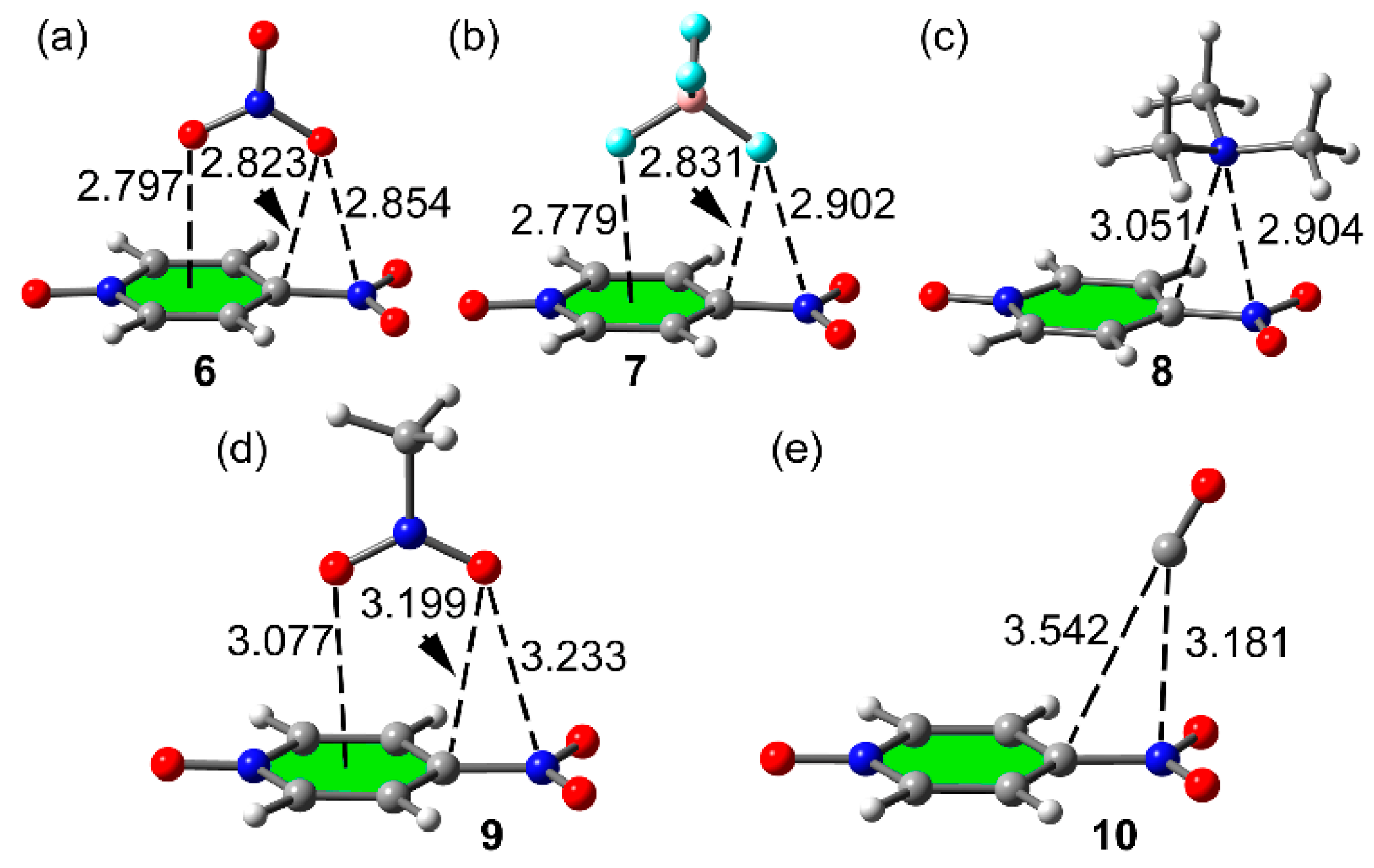
| Complex | ΔE | d | ρ(r) | ∇2ρ(r) |
|---|---|---|---|---|
| 2 (1 + HF) | −7.2 | 1.760 | 0.0289 | 0.1193 |
| 3 (1 + CF3I) | −5.0 | 2.883 | 0.0195 | 0.0651 |
| 4 (1 + AgCl) | −21.2 | 2.166 | 0.0672 | 0.3429 |
| 5 (1 +BF3) | −73.1 | 1.611 | 0.1104 | 0.2615 |
| 6 (1 + NO3−) | −15.2 | 2.854 | 0.0134 a | 0.0476 |
| 7 (1 + BF4−) | −12.4 | 2.901 | 0.0104 a | 0.0403 |
| 8 (1 + Me3N) | −7.0 | 2.903 | 0.0122 b | 0.0418 |
| 9 (1 + MeNO2) | −4.2 | 3.233 | 0.0061 a | 0.0223 |
| 10 (1 + CO) | −1.9 | 3.181 | 0.0059 a | 0.0242 |
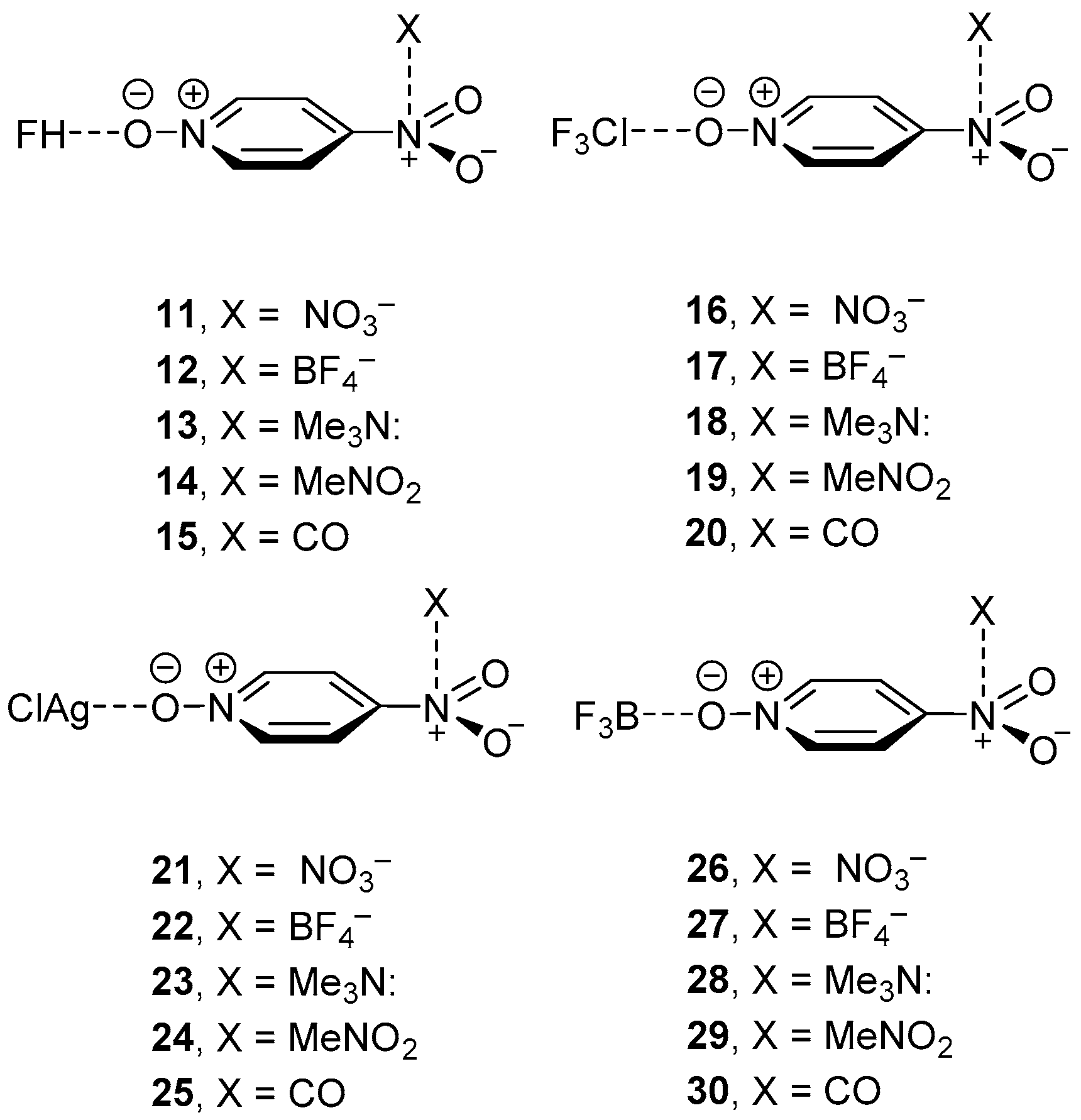
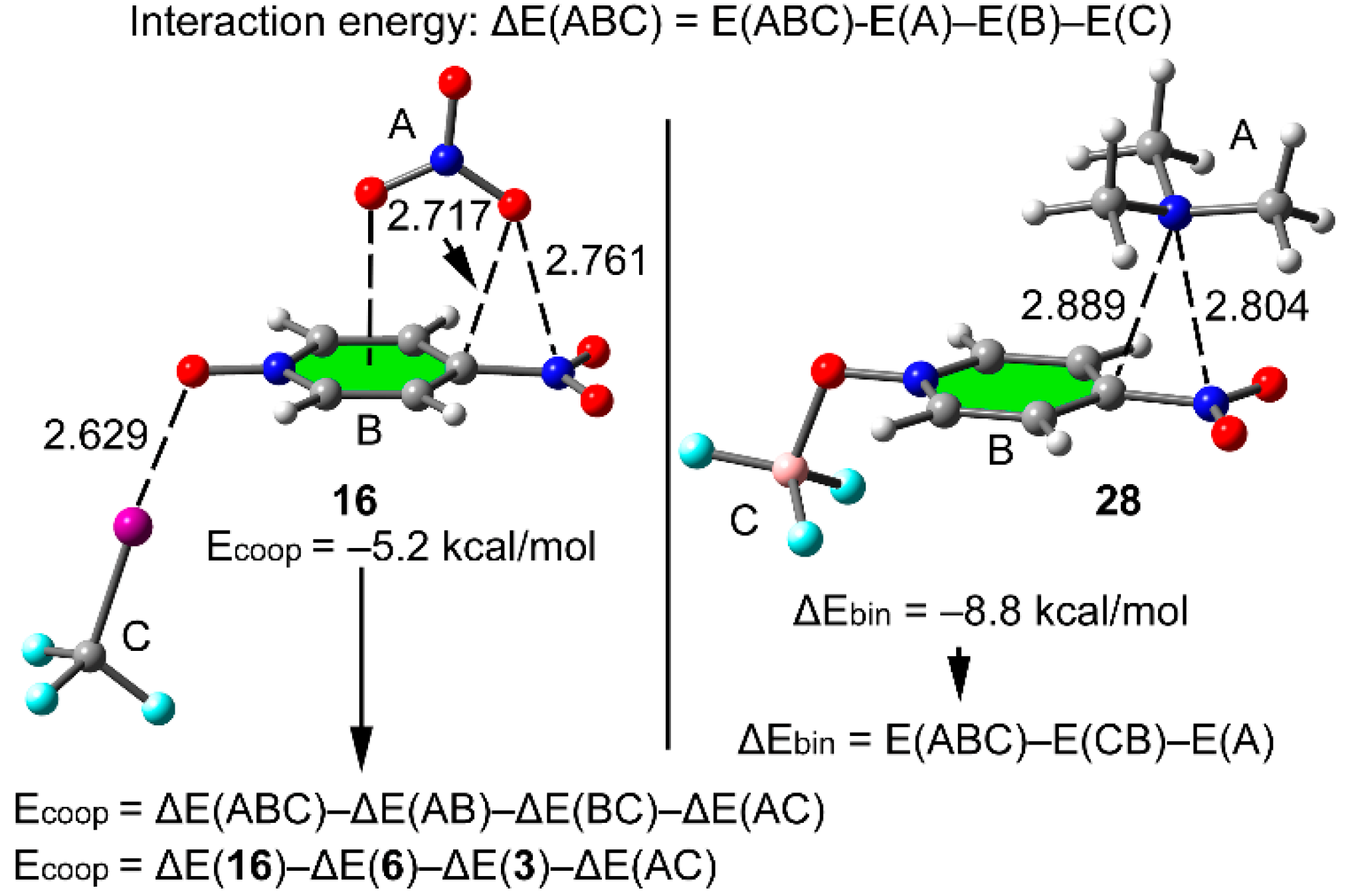
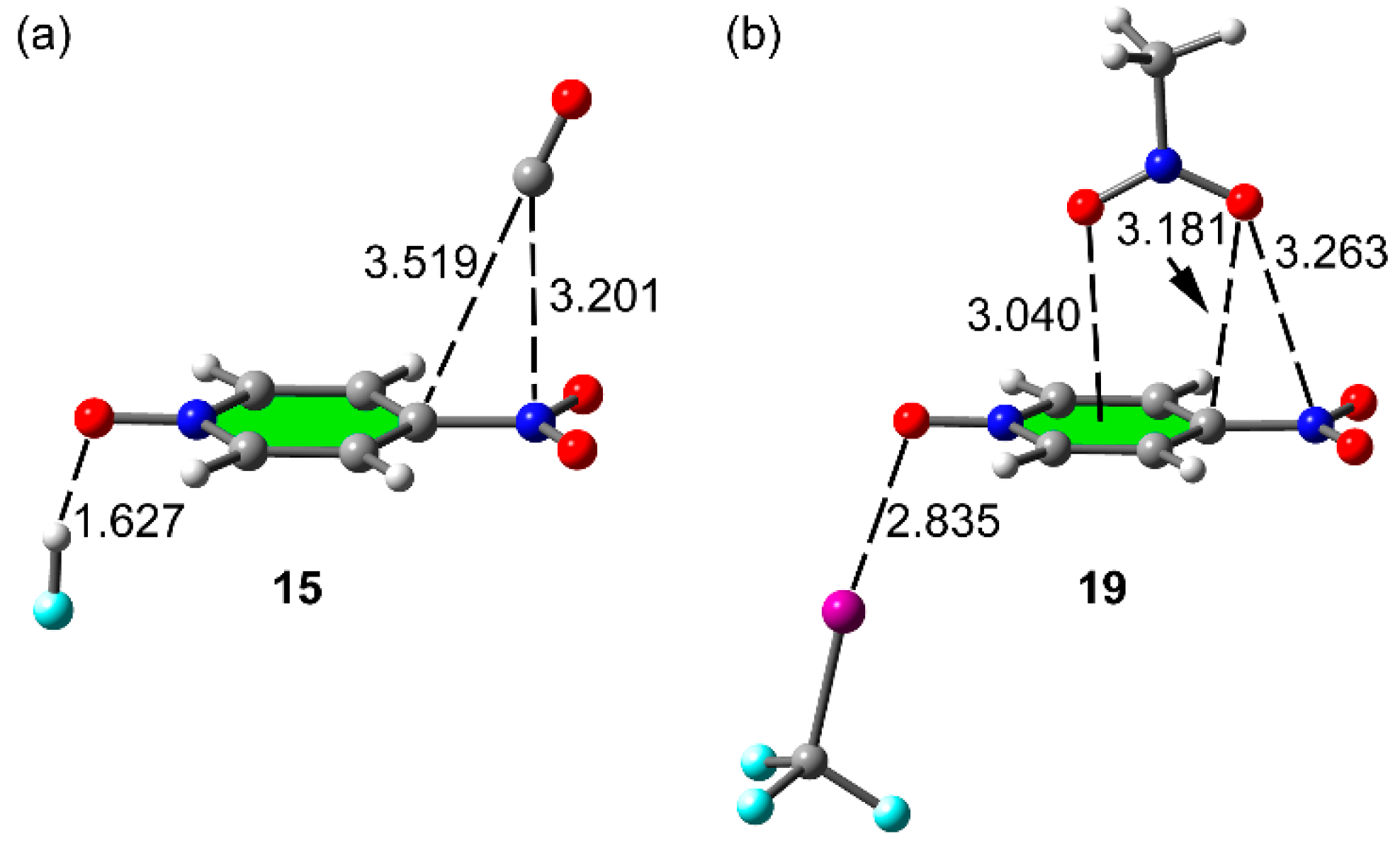
| Cmpnd | ΔE | Ecoop or ΔEbin | dπh | dσB | Δdπh | ΔdσB | ρ(r)πh × 100 | ρ(r)σB × 100 | Δρ(r)πh × 100 | Δρ(r)σB × 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | −32.9 | −9.1 | 2.764 | 1.512 | −0.090 | −0.248 | 1.63 | 7.24 | 0.29 | 4.35 |
| 12 | −29.0 | −7.9 | 2.815 | 1.530 | −0.086 | −0.230 | 1.21 | 6.88 | 0.17 | 3.99 |
| 13 | −18.2 | −4.7 | 2.868 | 1.610 | −0.035 | −0.150 | 1.34 | 5.54 | 0.12 | 2.65 |
| 14 | −15.7 | −4.5 | 3.211 | 1.603 | −0.022 | −0.157 | 0.65 | 5.63 | 0.04 | 2.74 |
| 15 | −12.5 | −3.8 | 3.201 | 1.627 | 0.020 | −0.133 | 0.57 | 5.28 | −0.02 | 2.39 |
| 16 | −26.5 | −5.2 | 2.761 | 2.629 | −0.093 | −0.254 | 1.65 | 3.41 | 0.31 | 1.46 |
| 17 | −22.7 | −4.2 | 2.846 | 2.666 | −0.055 | −0.217 | 1.18 | 3.15 | 0.14 | 1.20 |
| 18 | −12.5 | −0.6 | 2.892 | 2.831 | −0.011 | −0.052 | 1.29 | 2.19 | 0.07 | 0.24 |
| 19 | −10.0 | −0.6 | 3.263 | 2.835 | 0.030 | −0.048 | 0.63 | 2.19 | 0.02 | 0.24 |
| 20 | −7.1 | −0.2 | 3.153 | 2.915 | −0.028 | 0.032 | 0.61 | 1.86 | 0.02 | −0.09 |
| 21 | −51.8 | −31.5 | 2.716 | 2.132 | −0.138 | −0.034 | 1.88 | 7.49 | 0.54 | 0.77 |
| 22 | −47.0 | −26.0 | 2.795 | 2.136 | −0.106 | −0.030 | 1.32 | 7.39 | 0.28 | 0.67 |
| 23 | −29.9 | −9.4 | 2.838 | 2.164 | −0.065 | −0.002 | 1.47 | 6.87 | 0.25 | 0.15 |
| 24 | −27.7 | −6.9 | 3.128 | 2.158 | −0.105 | −0.008 | 0.68 | 6.89 | 0.07 | 0.17 |
| 25 | −23.4 | −2.3 | 3.264 | 2.165 | 0.083 | −0.001 | 0.51 | 6.74 | −0.08 | 0.02 |
| 26 | −104.6 | −30.7 | 2.656 | 1.547 | −0.198 | −0.064 | 2.13 | 13.17 | 0.79 | 2.13 |
| 27 | −99.1 | −25.8 | 2.748 | 1.555 | −0.153 | −0.056 | 1.39 | 12.85 | 0.35 | 1.81 |
| 28 | −82.6 | −8.8 | 2.804 | 1.596 | −0.099 | −0.015 | 1.59 | 11.51 | 0.37 | 0.47 |
| 29 | −80.0 | −6.6 | 3.232 | 1.594 | −0.001 | −0.017 | 0.67 | 11.53 | 0.06 | 0.49 |
| 30 | −75.4 | −2.2 | 3.175 | 1.608 | −0.006 | −0.003 | 0.59 | 11.14 | 0.00 | 0.10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galmés, B.; Franconetti, A.; Frontera, A. Nitropyridine-1-Oxides as Excellent π-Hole Donors: Interplay between σ-Hole (Halogen, Hydrogen, Triel, and Coordination Bonds) and π-Hole Interactions. Int. J. Mol. Sci. 2019, 20, 3440. https://doi.org/10.3390/ijms20143440
Galmés B, Franconetti A, Frontera A. Nitropyridine-1-Oxides as Excellent π-Hole Donors: Interplay between σ-Hole (Halogen, Hydrogen, Triel, and Coordination Bonds) and π-Hole Interactions. International Journal of Molecular Sciences. 2019; 20(14):3440. https://doi.org/10.3390/ijms20143440
Chicago/Turabian StyleGalmés, Bartomeu, Antonio Franconetti, and Antonio Frontera. 2019. "Nitropyridine-1-Oxides as Excellent π-Hole Donors: Interplay between σ-Hole (Halogen, Hydrogen, Triel, and Coordination Bonds) and π-Hole Interactions" International Journal of Molecular Sciences 20, no. 14: 3440. https://doi.org/10.3390/ijms20143440
APA StyleGalmés, B., Franconetti, A., & Frontera, A. (2019). Nitropyridine-1-Oxides as Excellent π-Hole Donors: Interplay between σ-Hole (Halogen, Hydrogen, Triel, and Coordination Bonds) and π-Hole Interactions. International Journal of Molecular Sciences, 20(14), 3440. https://doi.org/10.3390/ijms20143440