Study on Structural Evolution, Thermochemistry and Electron Affinity of Neutral, Mono- and Di-Anionic Zirconium-Doped Silicon Clusters ZrSin0/-/2- (n = 6–16)
Abstract
1. Introduction
2. Results and Discussion
2.1. Evolution of the Ground State Structure
2.2. PES of Mono-Anionic Species
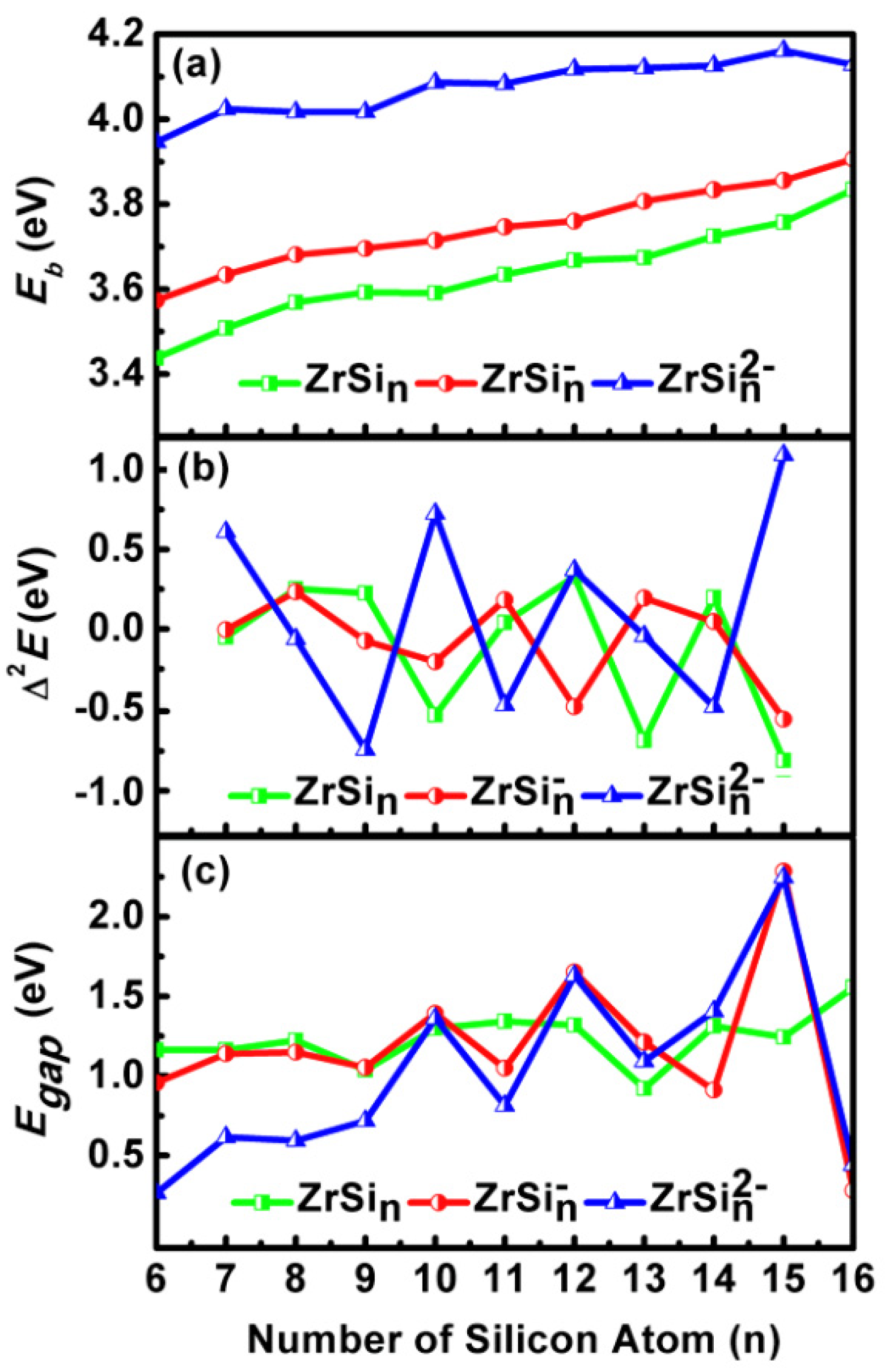
2.3. Stability
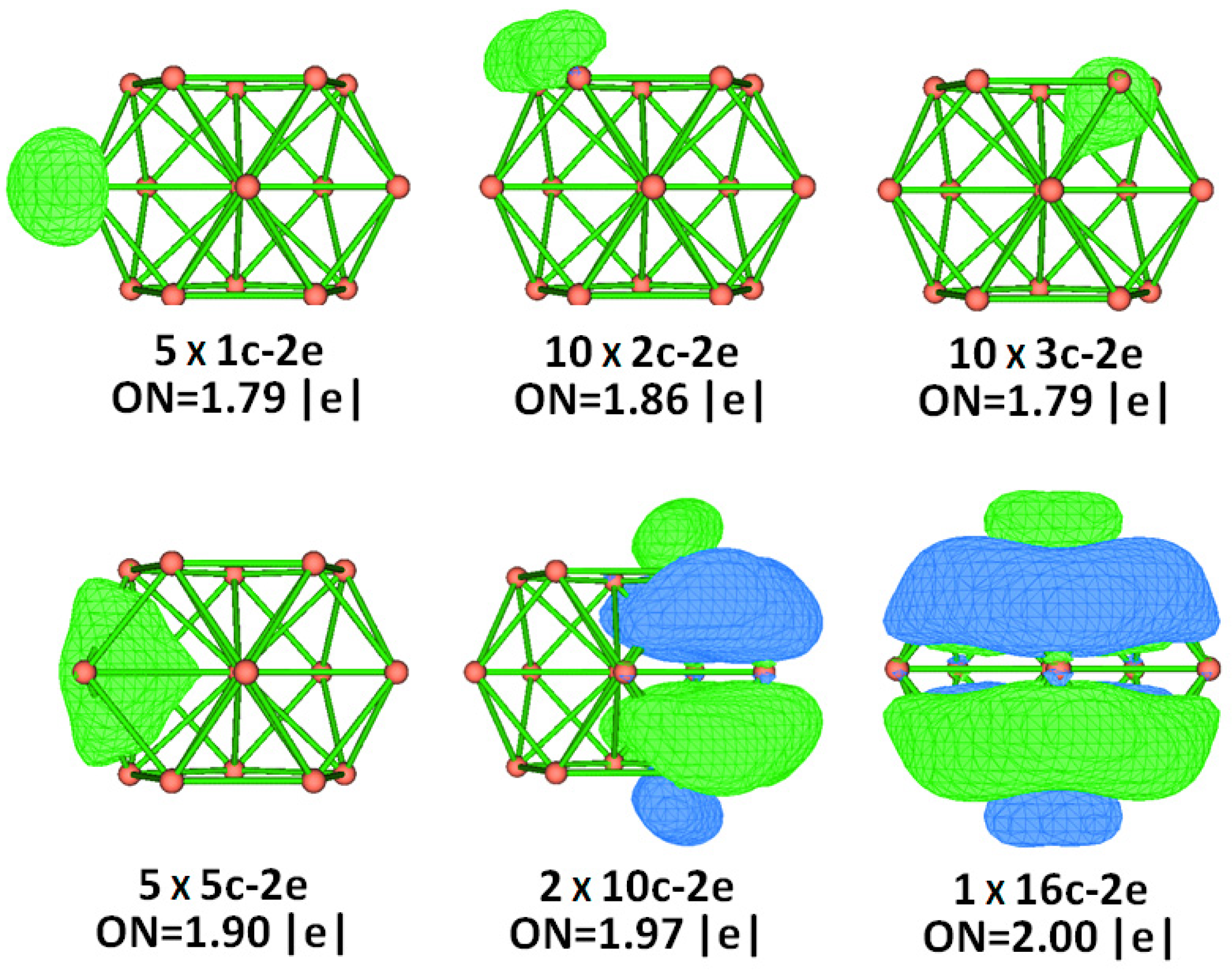
2.4. Chemical Bonding Analysis
3. Conclusions
4. Theoretical Methods
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gunaratne, K.D.D.; Berkemir, C.; Harmon, C.L.; Castleman, A.W., Jr. Probing the valence orbitals of transition metal-silicon diatomic anions: ZrSi, NbSi, MoSi, PdSi and WSi. Phys. Chem. Chem. Phys. 2013, 15, 6068–6079. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.L.; östling, M. Metal Silicides in CMOS Technology: Past, Present, and Future Trends. Crit. Rev. Solid State 2003, 28, 1–129. [Google Scholar] [CrossRef]
- Kahng, D.; Lepselter, M.P. Planar Epitaxial Silicon Schottky Barrier Diodes. Bell Syst. Tech. J. 1965, 1525–1527. [Google Scholar] [CrossRef]
- Chen, X.; Jin, J.H.; Sha, G.Y.; Li, C.; Zhang, B.S.; Su, D.S.; Williams, C.T.; Liang, C.H. Silicon-nickel intermetallic compounds supported on silica as a highly efficient catalyst for CO methanation. Catal. Sci. Technol. 2014, 4, 53–61. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Zhao, J.; Li, J.H.; Lei, J.; Cheng, X.K. Effect of hot-dip siliconizing time on phase composition and microstructure of Mo-MoSi2 high temperature structural materials. Ceram. Int. 2019, 45, 5588–5593. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, H.Y.; Baik, H.K.; Lee, S.M. Si-Zr alloy thin-film anodes for microbatteries. J. Power. Sources 2003, 119–121, 113–116. [Google Scholar] [CrossRef]
- Yeom, H.; Jo, H.; Maier, B.; Corradini, M.; Sridharan, K. Multi-Functional Zirconium-Silicide Coatings on Zirconium-alloy for Improved Accident Tolerance. Trans. Am. Nucl. Soc. 2017, 116, 399–402. [Google Scholar]
- Okabayashi, J.; Toyoda, S.; Kumigashira, H.; Oshima, M. Chemical reaction and metallic cluster formation by annealing-temperature control in ZrO2 gate dielectrics on Si. Appl. Phys. Lett. 2004, 85, 5959–5961. [Google Scholar] [CrossRef]
- Beck, S.M. Studies of silicon cluster-metal atom compound formation in a supersonic molecular beam. J. Chem. Phys. 1987, 87, 4233–4234. [Google Scholar] [CrossRef]
- Kumar, V.; Kawazoe, Y. Metal-Encapsulated Fullerenelike and Cubic Caged Clusters of Silicon. Phys. Rev. Lett. 2001, 87, 045503. [Google Scholar] [CrossRef]
- Kumar, V.; Kawazoe, Y. Magic behavior of Si15M and Si16M (M=Cr, Mo, and W) clusters. Phys. Rev. B 2002, 65, 073404. [Google Scholar] [CrossRef]
- Kumar, V.; Briere, T.M.; Kawazoe, Y. Ab initio calculations of electronic structures, polarizabilities, Raman and infrared spectra, optical gaps, and absorption spectra of M@Si16 (M=Ti and Zr) clusters. Phys. Rev. B 2003, 68, 155412. [Google Scholar] [CrossRef]
- Kumar, V.; Majumder, C.; Kawazoe, Y. M@Si16, M = Ti, Zr, Hf: ∏ conjugation, ionization potentials and electron affinities. Chem. Phys. Lett. 2002, 363, 319–322. [Google Scholar] [CrossRef]
- Kawamura, H.; Kumar, V.; Kawazoe, Y. Growth behavior of metal-doped silicon clusters SinM (M=Ti,Zr,Hf; n=8-16). Phys. Rev. B 2005, 71, 075423. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Kumar, M. The electronic structures and properties of transition metal-doped silicon nanoclusters: A density functional investigation. Chem. Phys. 2008, 353, 170–176. [Google Scholar] [CrossRef]
- Sen, P.; Mitas, L. Electronic structure and ground states of transition metals encapsulated in a Si12 hexagonal prism cage. Phys. Rev. B 2003, 68, 155404. [Google Scholar] [CrossRef]
- Lu, J.; Nagase, S. Structural and Electronic Properties of Metal-Encapsulated Silicon Clusters in a Large Size Range. Phys. Rev. Lett. 2003, 90, 115506. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Han, J.G. Geometries, stabilities, and electronic properties of different-sized ZrSin(n = 1–16) clusters: A density-functional investigation. J. Chem. Phys. 2005, 123, 064306. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.J.; Su, Z.M. Electronic structures and chemical bonding in transition metal monosilicides MSi (M=3d, 4d, 5d elements). J. Chem. Phys. 2006, 124, 184306. [Google Scholar] [CrossRef]
- Wu, J.H.; Liu, C.X.; Wang, P.; Zhang, S.; Yang, G.; Lu, C. Structures, Stabilities, and Electronic Properties of Small-Sized Zr2Sin (n = 1–11) Clusters: A Density Functional Study. Z. Naturforsch. 2015, 70, 805–814. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.H. Investigation of Size-Selective Zr2@Sin (n = 16-24) Caged Clusters. J. Phys. Chem. A 2008, 114, 4562–4567. [Google Scholar] [CrossRef] [PubMed]
- Koyasu, K.; Atobe, J.; Akutsu, M.; Mitsui, M.; Nakajima, A. Electronic and Geometric Stabilities of Clusters with Transition Metal Encapsulated by Silicon. J. Phys. Chem. A 2007, 111, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Koyasu, K.; Atobe, J.; Furuse, S.; Nakajima, A. Anion photoelectron spectroscopy of transition metal- and lanthanide metal-silicon clusters: MSin- (n = 6–20). J. Chem. Phys. 2008, 129, 214301. [Google Scholar] [CrossRef] [PubMed]
- Gunaratne, K.D.D.; Hazra, A.; Castleman, A.W., Jr. Photoelectron imaging spectroscopy and theoretical investigation of ZrSi. J. Chem. Phys. 2011, 134, 204303. [Google Scholar] [CrossRef] [PubMed]
- Sevy, A.; Sorensen, J.J.; Persinger, T.D.; Franchina, J.A. Bond dissociation energies of TiSi, ZrSi, HfSi, VSi, NbSi, and TaSi. J. Chem. Phys. 2017, 147, 084301. [Google Scholar] [CrossRef] [PubMed]
- Maroulis, G.; Begué, D.; Pouchan, C. Accurate dipole polarizabilities of small silicon clusters from ab initio and density functional theory calculations. J. Chem. Phys. 2003, 119, 794–797. [Google Scholar] [CrossRef]
- Maroulis, G. Quantifying the Performance of Conventional DFT Methods on a Class of Difficult Problems: The Interaction (Hyper)Polarizability of Two Water Molecules as a Test Case. Int. J. Quantum Chem. 2012, 112, 2231–2241. [Google Scholar] [CrossRef]
- Jiang, W.Y.; Laury, M.L.; Powell, M.; Wilson, A.K. Comparative Study of Single and Double Hybrid Density Functionals for the Prediction of 3d Transition Metal Thermochemistry. J. Chem. Theory Comput. 2012, 8, 4102–4111. [Google Scholar] [CrossRef]
- Liu, Y.M.; Yang, J.C.; Cheng, L. Structural Stability and Evolution of Scandium-Doped Silicon Clusters: Evolution of Linked to Encapsulated Structures and Its Influence on the Prediction of Electron Affinities for ScSin (n = 4−16) Clusters. Inorg. Chem. 2018, 57, 12934–12940. [Google Scholar] [CrossRef]
- Chen, B.L.; Sun, W.G.; Kuang, X.Y.; Lu, C.; Xia, X.X.; Shi, H.X.; Maroulis, G. Structural Stability and Evolution of Medium-Sized Tantalum-Doped Boron Clusters: A Half-Sandwich-Structured TaB12- Cluster. Inorg. Chem. 2018, 57, 343–350. [Google Scholar] [CrossRef]
- Xing, X.D.; Hermann, A.; Kuang, X.Y.; Ju, M.; Lu, C.; Jin, Y.Y.; Xia, X.X.; Maroulis, G. Insights into the geometries, electronic and magnetic properties of neutral and charged palladium clusters. Sci. Rep. 2016, 6, 19656. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.Y.; Maroulis, G.; Kuang, X.Y.; Ding, L.P.; Lu, C.; Wang, J.J.; Lv, J.; Zhang, C.Z.; Ju, M. Geometries, stabilities and fragmental channels of neutral and charged sulfur clusters: SnQ (n = 3–20, Q = 0, ±1). Phys. Chem. Chem. Phys. 2015, 17, 13590–13597. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Zhou, S.; Huang, X.M.; Chen, M.; King, R.B.; Zhao, J.J. Revisit of Large-Gap Si16 Clusters Encapsulating Group-IV Metal Atoms (Ti, Zr, Hf). J. Comput. Chem. 2018, 39, 2268–2272. [Google Scholar] [CrossRef] [PubMed]
- Baerends, E.J.; Gritsenko, O.V.; Meer, R.V. The Kohn-Sham gap, the fundamental gap and the optical gap: the physical meaning of occupied and virtual Kohn-Sham orbital energies. Phys. Chem. Chem. Phys. 2013, 15, 16408–16425. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Dolg, M. ABCluster: the artificial bee colony algorithm for cluster global optimization. Phys. Chem. Chem. Phys. 2015, 17, 24173–24181. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09, Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Peterson, K.A.; Figgen, D.; Dolg, M.; Stoll, H. Energy-consistent relativistic pseudopotentials and correlation consistent basis sets for the 4d elements Y-Pd. J. Chem. Phys. 2007, 126, 124101. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Towards chemical accuracy for the thermodynamics of large molecules: new hybrid density functionals including non-local correlation effects. Phys. Chem. Chem. Phys. 2006, 8, 4398–4401. [Google Scholar] [CrossRef]
- Akola, J.; Manninen, M.; Häkkinen, H.; Landman, U.; Li, X.; Wang, L.S. Photoelectron spectra of aluminum cluster anions: Temperature effects and ab initio simulations. Phys. Rev. B 1999, 60, R11297–R11300. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.W. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
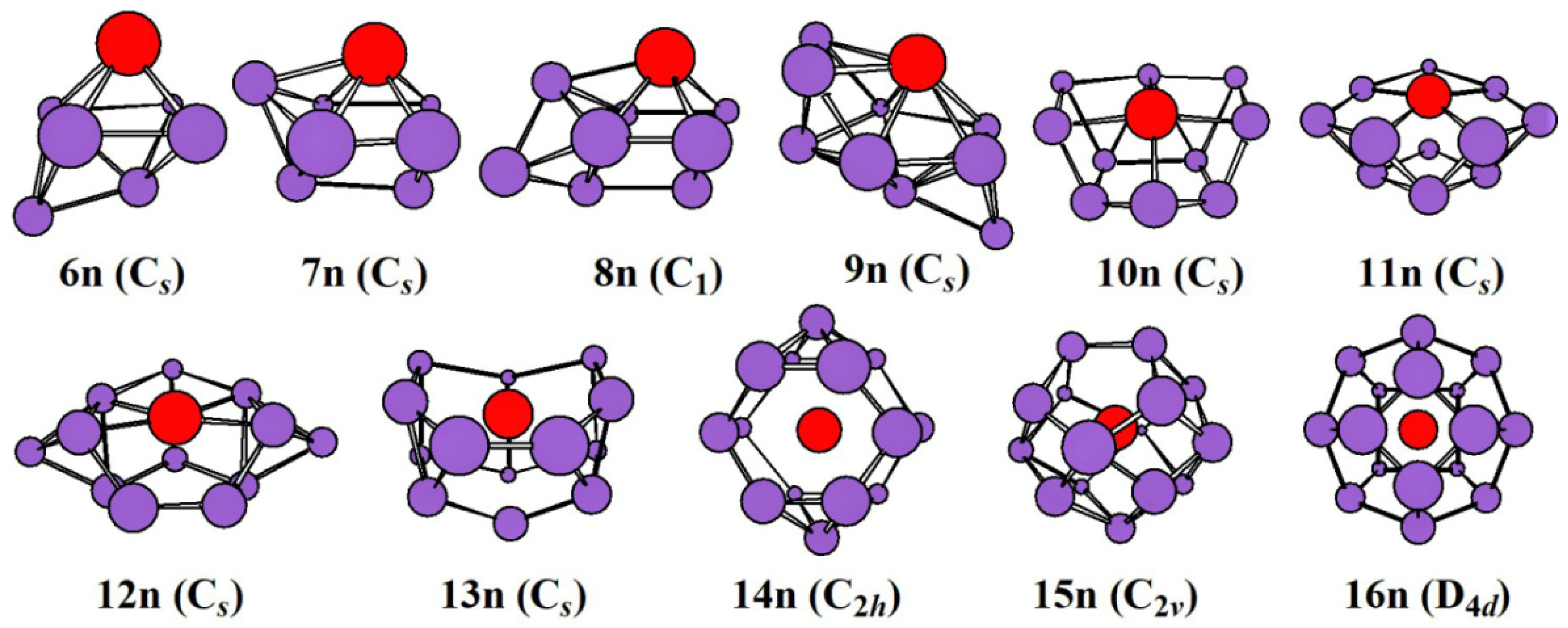
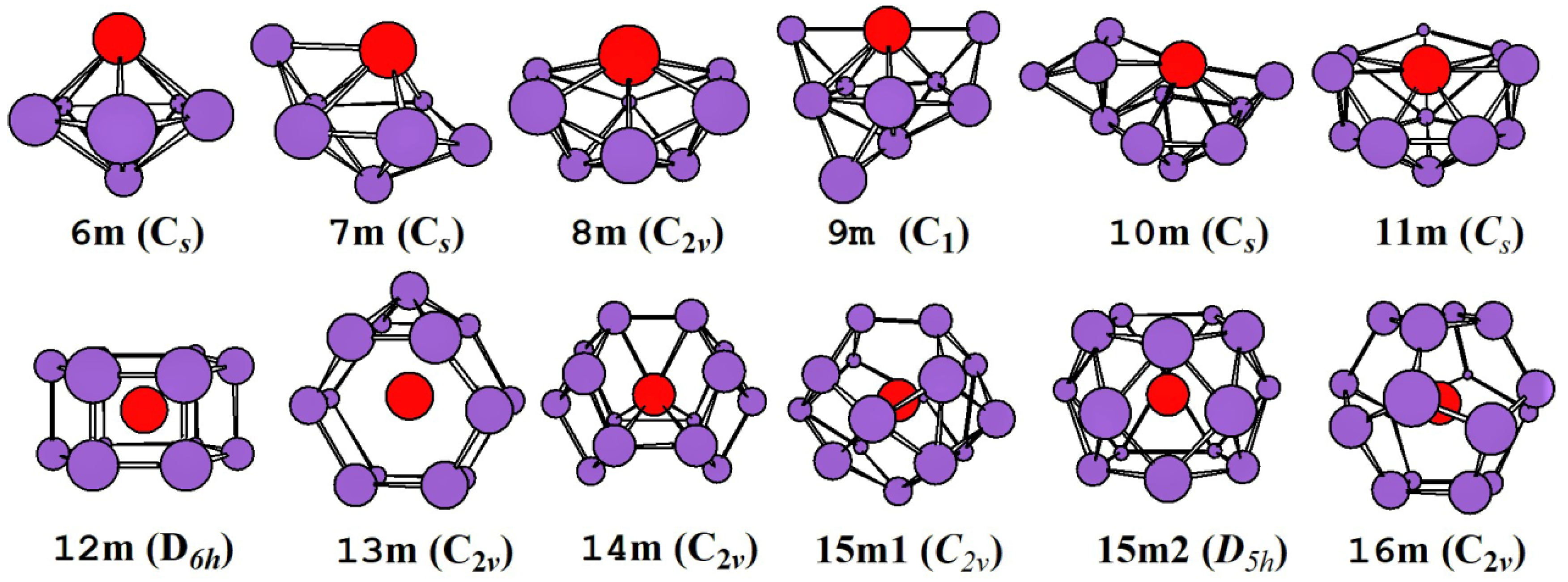
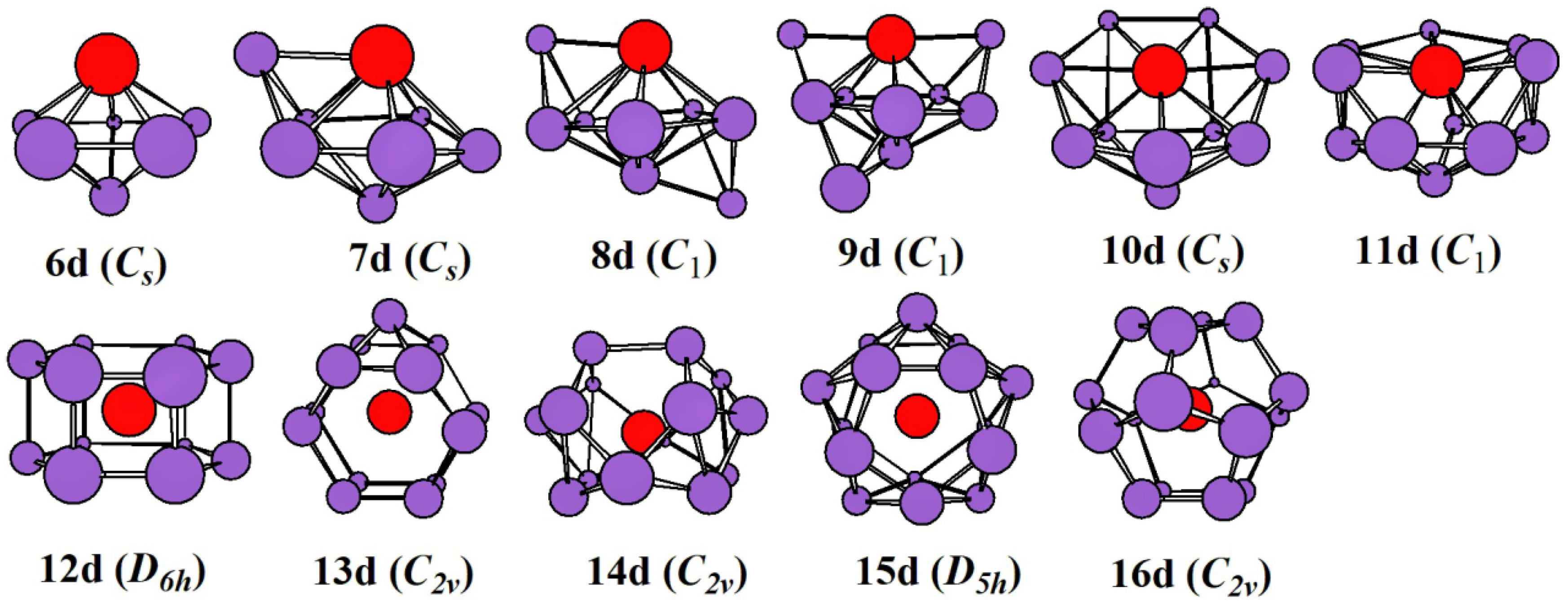
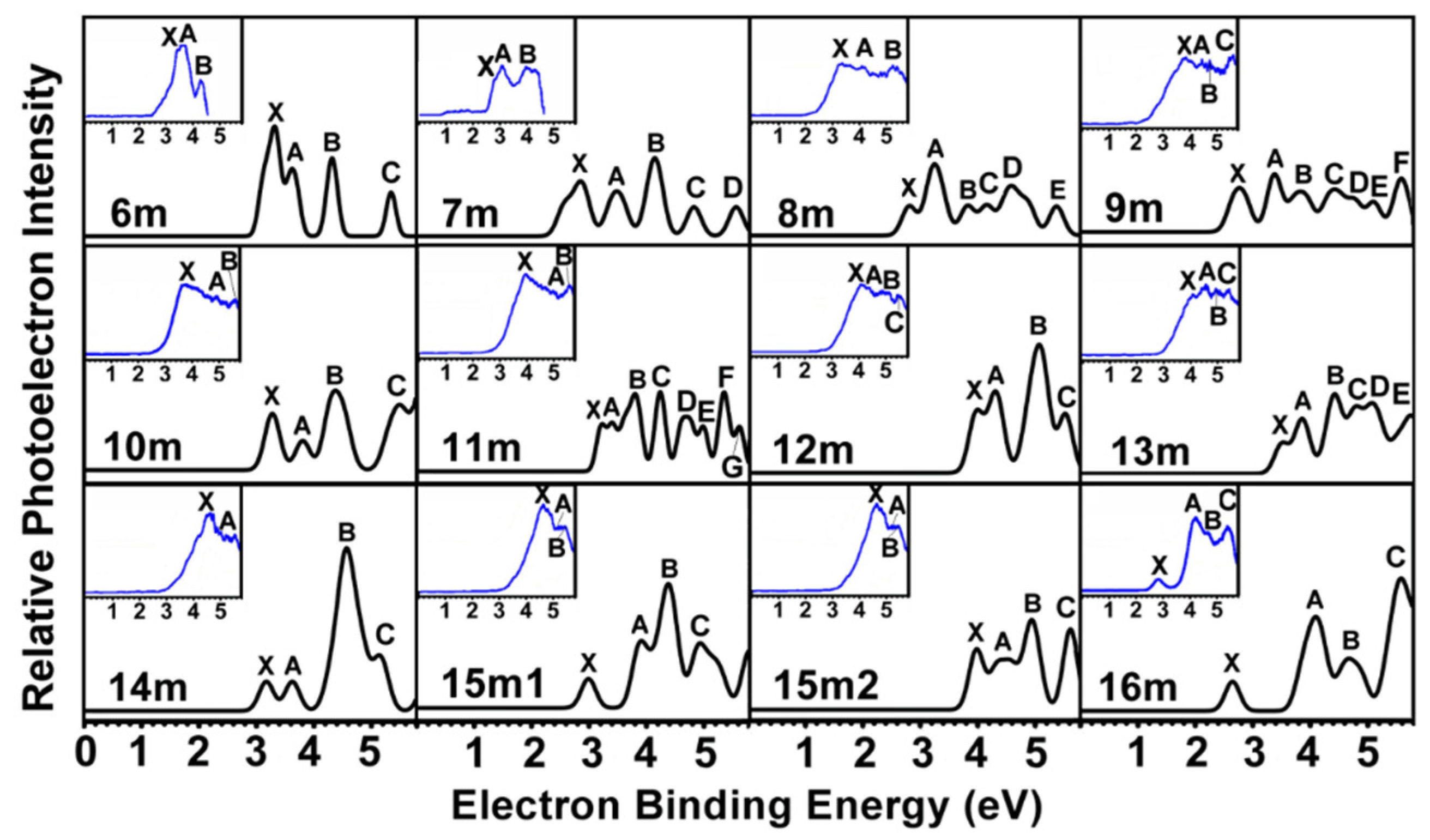
| ZrSin | ZrSin- | ZrSin2- | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n | State | Eb | Q(Zr) | State | Eb | Q(Zr) | State | Eb | Q(Zr) |
| 6 | 1A1 | 3.44 | −0.13 | 2A’’ | 3.57 | 0.25 | 1A′ | 3.95 | −0.49 |
| 7 | 1A′ | 3.51 | −0.34 | 2A’ | 3.63 | 0.04 | 1A′ | 4.02 | −0.58 |
| 8 | 1A | 3.57 | −0.16 | 2B2 | 3.68 | −0.40 | 1A | 4.02 | −0.31 |
| 9 | 1A1 | 3.59 | −0.50 | 2A | 3.7 | −0.20 | 2A | 4.02 | −0.70 |
| 10 | 1A′ | 3.59 | −0.53 | 2A′ | 3.71 | −0.40 | 1A′ | 4.09 | −0.90 |
| 11 | 1A′ | 3.63 | −0.98 | 2A’’ | 3.75 | −0.60 | 1A | 4.08 | −0.76 |
| 12 | 1A′ | 3.67 | −0.87 | 2A2u | 3.76 | −1.20 | 1A1g | 4.12 | −1.33 |
| 13 | 1A′ | 3.67 | −1.87 | 2A1 | 3.81 | −1.20 | 1A1 | 4.12 | −1.24 |
| 14 | 1Ag | 3.72 | −2.66 | 2B1 | 3.83 | −1.20 | 1A1 | 4.13 | −1.45 |
| 15 | 1A1 | 3.76 | −3.31 | 2A1′ | 3.85 | −1.29 | 1A1′ | 4.16 | −2.90 |
| 16 | 1A1 | 3.83 | −1.89 | 2B1 | 3.91 | −0.90 | 1A1 | 4.13 | −0.77 |
| AEA | VDE | |||
|---|---|---|---|---|
| Species | Theor | Exptl | Theor | Exptl |
| 6n←6m | 2.24 | 2.30 ± 0.0043 a | 3.32 | 3.4 ± 0.1 a |
| 7n←7m | 2.29 | 2.40 ± 0.0043 a | 2.86 | 2.8 ± 0.1 a |
| 8n←8m | 2.31 | 2.30 ± 0.0043 a | 2.81 | 3.3 ± 0.1 a |
| 9n←9m | 2.29 | 2.20 ± 0.0043 a | 2.76 | 3.9 ± 0.1 a |
| 10n←10m | 2.64 | 2.70 ± 0.0043 a | 3.35 | 3.8 ± 0.1 a |
| 11n←11m | 2.65 | 2.90 ± 0.0043 a | 3.25 | 4.0 ± 0.1 a |
| 12n←12m | 2.50 | 2.90 ± 0.0043 a | 3.99 | 4.1 ± 0.1 a |
| 13n←13m | 3.11 | 3.00 ± 0.0043 a | 3.53 | 4.1 ± 0.1 a |
| 14n←14m | 2.90 | 3.00 ± 0.0043 a | 3.18 | 4.5 ± 0.1 a |
| 15n←15m1 | 2.87 | 3.20 ± 0.0043 a | 3.00 | 4.7 ± 0.1 a |
| 15n←15m2 | 2.86 | 3.20 ± 0.0043 a | 3.97 | 4.7 ± 0.1 a |
| 16n←16m | 2.52 | 2.46 ± 0.080 b | 2.65 | 2.9 ± 0.1 a |
| Spin Multiplicity | Property | |||||
|---|---|---|---|---|---|---|
| Method | 1 | 3 | 5 | AEA | VDE | D0 |
| mPW2PLYP/LARGE// mPW2PLYP/MIDDLE | 0.00 | 0.26 | 0.17 | 1.44 | 1.45 | 2.74 |
| CCSD(T)/LARGE// mPW2PLYP/MIDDLE | 0.00 | 0.26 | 0.18 | 1.55 | 1.56 | 2.64 |
| B3LYP/LANL2DZ b | 0.13 | 0.13 | 0.00 | 1.58 | 1.61 | 2.51 c |
| B3LYP/mixed basis Set b | 0.12 | 0.08 | 0.00 | 1.55 | 1.59 | |
| CCSD(T)/mixed basis set b | 0.00 | 0.13 | 0.10 | |||
| Exp. | 1.46 d | 1.58 d | 2.95 c | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, C.; Han, L.; Yang, J.; Cheng, L. Study on Structural Evolution, Thermochemistry and Electron Affinity of Neutral, Mono- and Di-Anionic Zirconium-Doped Silicon Clusters ZrSin0/-/2- (n = 6–16). Int. J. Mol. Sci. 2019, 20, 2933. https://doi.org/10.3390/ijms20122933
Dong C, Han L, Yang J, Cheng L. Study on Structural Evolution, Thermochemistry and Electron Affinity of Neutral, Mono- and Di-Anionic Zirconium-Doped Silicon Clusters ZrSin0/-/2- (n = 6–16). International Journal of Molecular Sciences. 2019; 20(12):2933. https://doi.org/10.3390/ijms20122933
Chicago/Turabian StyleDong, Caixia, Limin Han, Jucai Yang, and Lin Cheng. 2019. "Study on Structural Evolution, Thermochemistry and Electron Affinity of Neutral, Mono- and Di-Anionic Zirconium-Doped Silicon Clusters ZrSin0/-/2- (n = 6–16)" International Journal of Molecular Sciences 20, no. 12: 2933. https://doi.org/10.3390/ijms20122933
APA StyleDong, C., Han, L., Yang, J., & Cheng, L. (2019). Study on Structural Evolution, Thermochemistry and Electron Affinity of Neutral, Mono- and Di-Anionic Zirconium-Doped Silicon Clusters ZrSin0/-/2- (n = 6–16). International Journal of Molecular Sciences, 20(12), 2933. https://doi.org/10.3390/ijms20122933





