Phosphatidylcholine Membrane Fusion Is pH-Dependent
Abstract
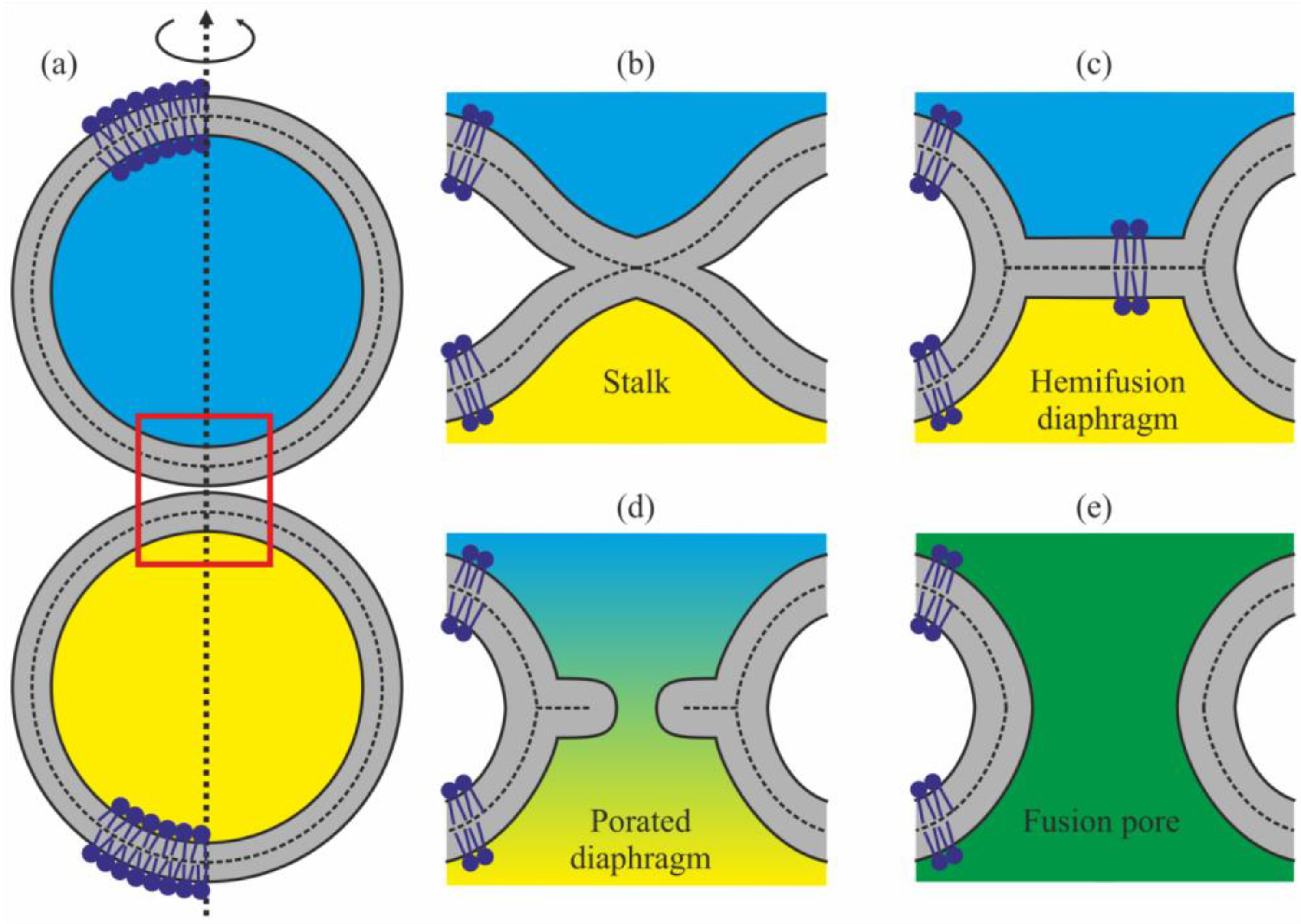
:1. Introduction
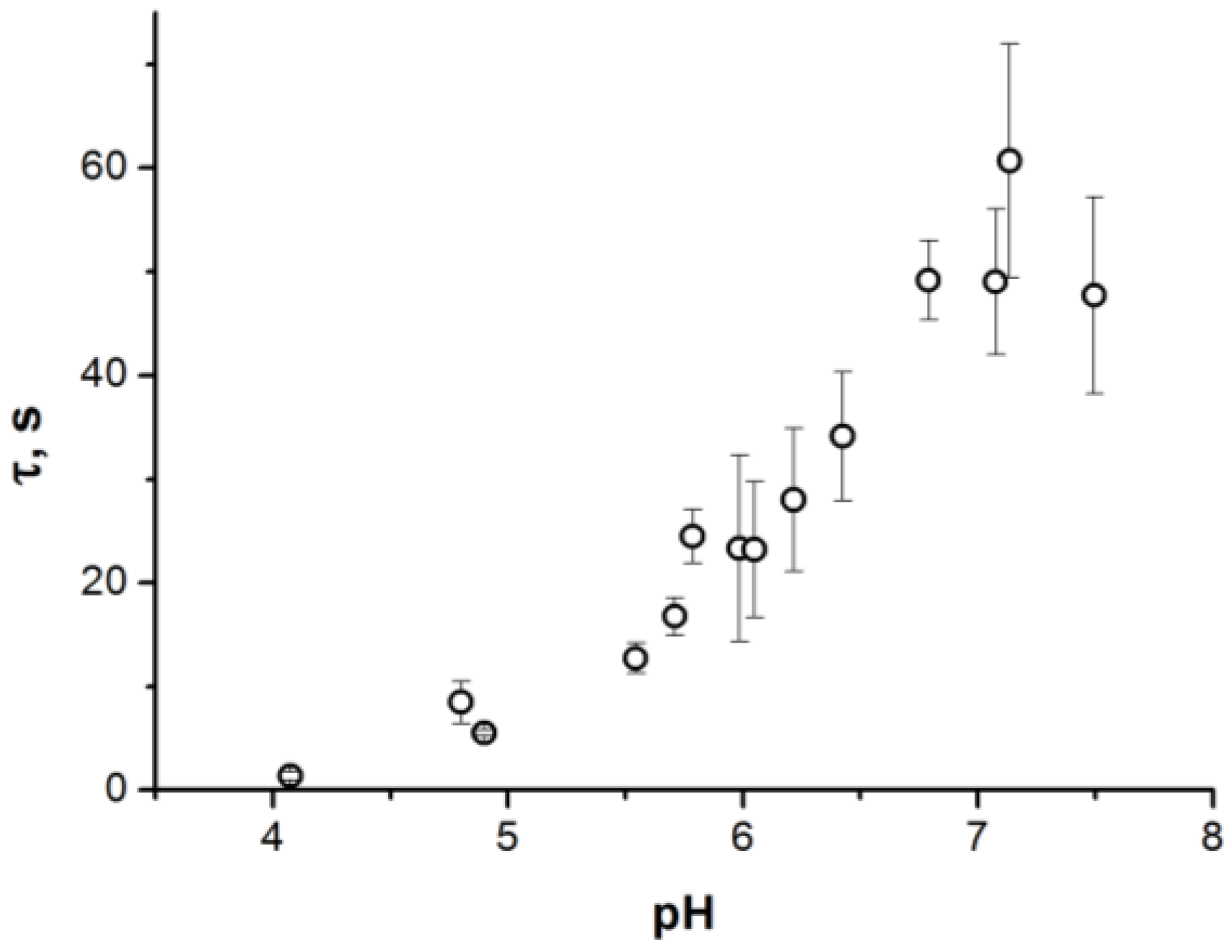
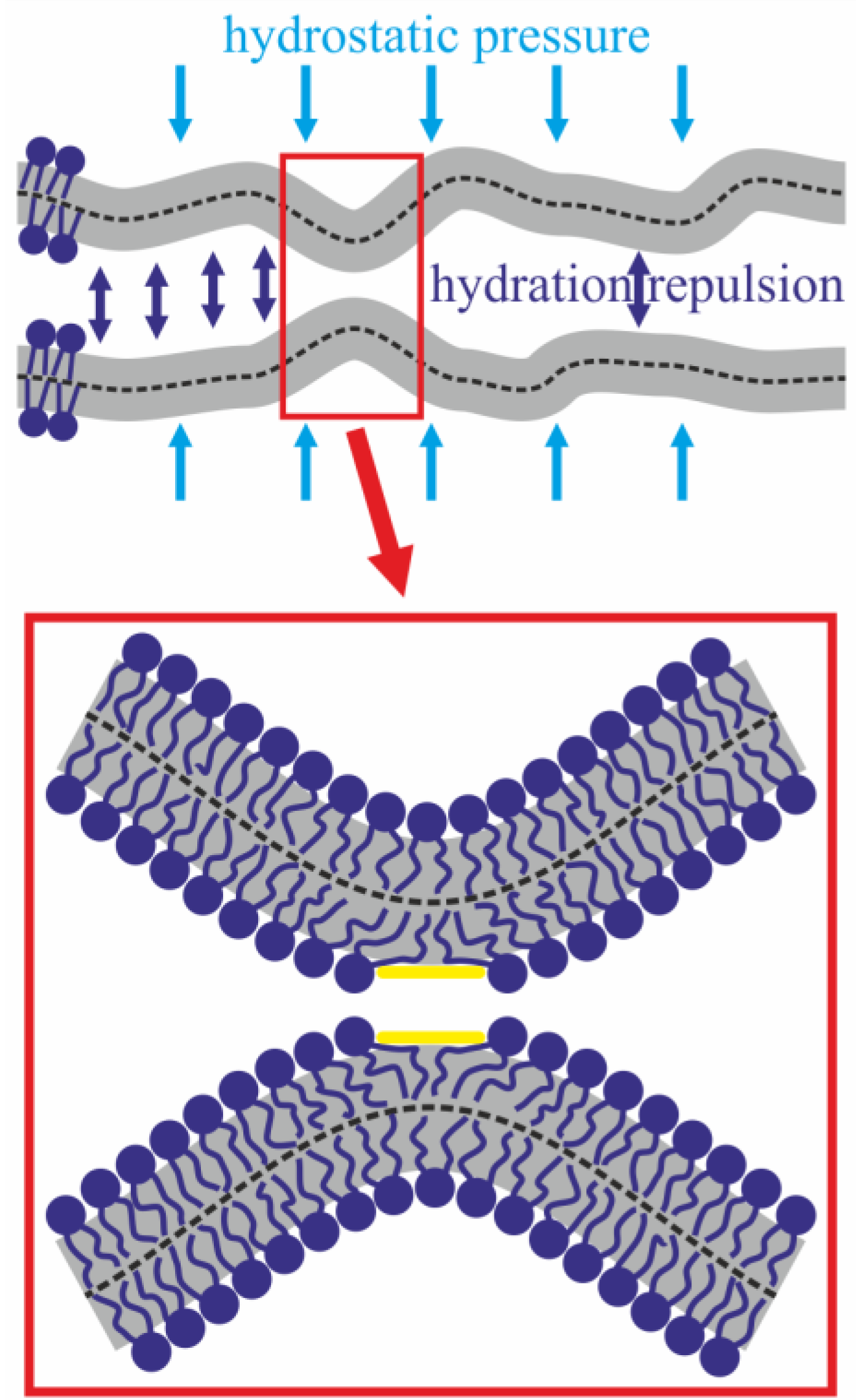
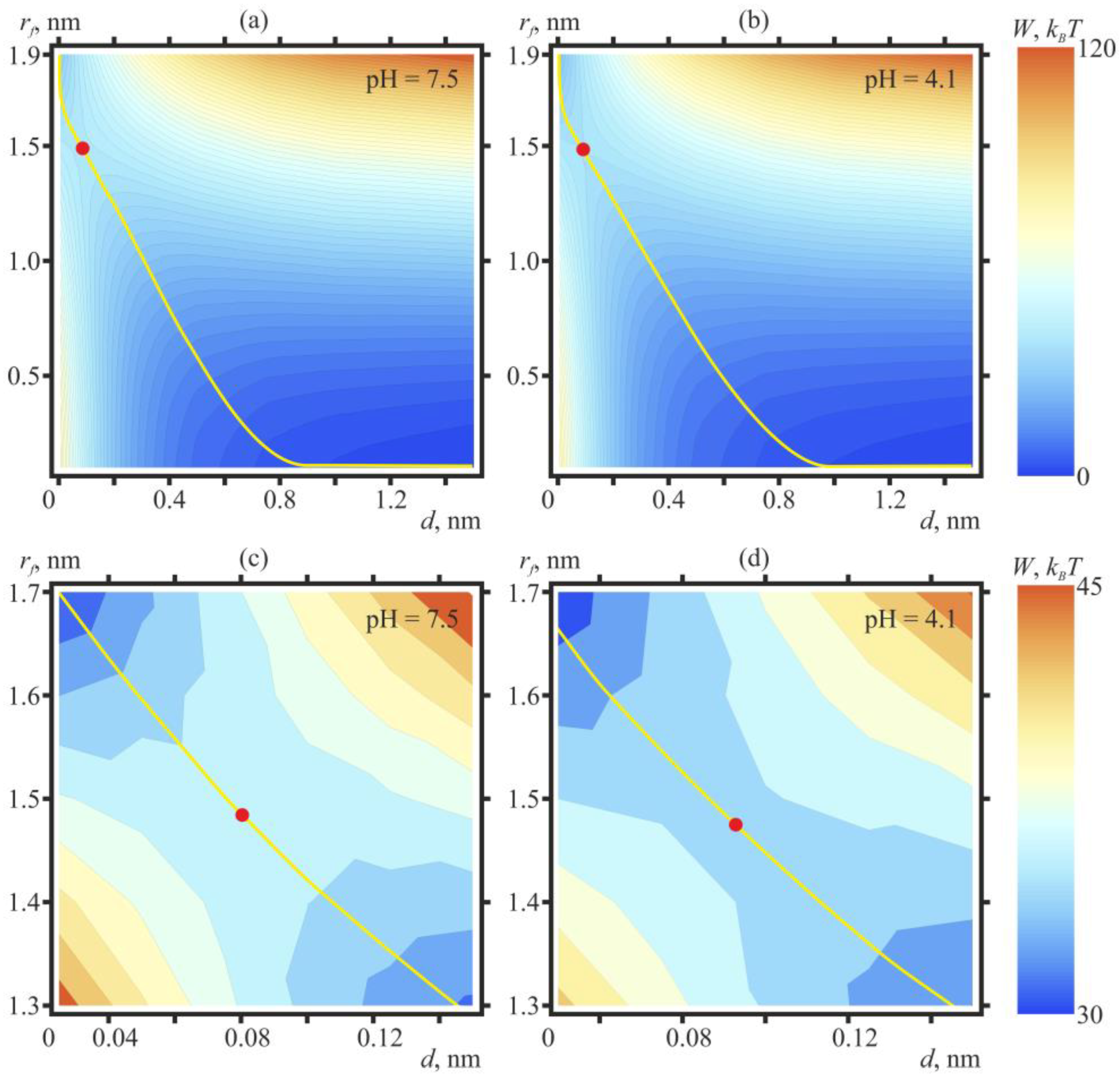
2. Results
3. Discussion
4. Materials and Methods
4.1. Experimental Section
4.2. Theoretical Section
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| BLM | Bilayer Lipid Membrane |
| DOPC | Dioleoylphosphatidylcholine |
| DOPE | Dioleoylphosphatidylethanolamine |
References
- Chernomordik, L.V.; Kozlov, M.M. Mechanics of membrane fusion. Nat. Struct. Mol. Biol. 2008, 15, 675–683. [Google Scholar] [CrossRef] [PubMed]
- McNeil, P.L.; Steinhardt, R.A. Plasma membrane disruption: repair, prevention, adaptation. Annu. Rev. Cell Dev. Biol. 2003, 19, 697–731. [Google Scholar] [CrossRef] [PubMed]
- Wassarman, P.M. Mammalian fertilization. Cell 1999, 96, 175–183. [Google Scholar] [CrossRef]
- Chen, E.H.; Grote, E.; Mohler, W.; Vignery, A. Cell-cell fusion. FEBS Lett. 2007, 581, 2181–2193. [Google Scholar] [CrossRef] [PubMed]
- Mohler, W.A.; Shemer, G.; del Campo, J.J.; Valansi, C.; Opoku-Serebuoh, E.; Scranton, V.; Assaf, N.; White, J.G.; Podbilewicz, B. The type I membrane protein EFF-1 is essential for developmental cell fusion. Dev. Cell 2002, 2, 355–362. [Google Scholar] [CrossRef]
- Sapir, A.; Avinoam, O.; Podbilewicz, B.; Chernomordik, L.V. Viral and developmental cell fusion mechanisms: conservation and divergence. Dev. Cell 2008, 14, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Jahn, R.; Südhof, T.C. Membrane fusion and exocytosis. Annu. Rev. Biochem. 1999, 68, 863–911. [Google Scholar] [CrossRef] [PubMed]
- Jackson, M.B.; Chapman, E.R. The fusion pores of Ca2+-triggered exocytosis. Nat. Struct. Mol. Biol. 2008, 15, 684–689. [Google Scholar] [CrossRef] [PubMed]
- Jahn, R.; Scheller, R.H. SNAREs—Engines for membrane fusion. Nat. Rev. Mol. Cell Biol. 2006, 7, 631. [Google Scholar] [CrossRef] [PubMed]
- Hoppins, S.; Lackner, L.; Nunnari, J. The machines that divide and fuse mitochondria. Annu. Rev. Biochem. 2007, 76, 751–780. [Google Scholar] [CrossRef] [PubMed]
- Wickner, W.; Schekman, R. Membrane fusion. Nat. Struct. Mol. Biol. 2008, 15, 658–664. [Google Scholar] [CrossRef] [PubMed]
- Luzio, J.P.; Pryor, P.R.; Bright, N.A. Lysosomes: Fusion and function. Nat. Rev. Mol. Cell Biol. 2007, 8, 622–632. [Google Scholar] [CrossRef] [PubMed]
- Rizo, J.; Rosenmund, C. Synaptic vesicle fusion. Nat. Struct. Mol. Biol. 2008, 15, 665–674. [Google Scholar] [CrossRef] [PubMed]
- Harrison, S.C. Viral membrane fusion. Virology 2015, 479, 498–507. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, M.M.; Markin, V.S. Possible mechanism of membrane fusion. Biofizika 1983, 28, 242–247. [Google Scholar] [PubMed]
- Chernomordik, L.V.; Kozlov, M.M.; Melikyan, G.B.; Abidor, I.G.; Markin, V.S.; Chizmadzhev, Y.A. The shape of lipid molecules and monolayer membrane fusion. Biochim. Biophys. Acta 1985, 812, 643–655. [Google Scholar] [CrossRef]
- Kuzmin, P.I.; Zimmerberg, J.; Chizmadzhev, Y.A.; Cohen, F.S. A quantitative model for membrane fusion based on low-energy intermediates. Proc. Natl. Acad. Sci. USA 2001, 98, 7235–7240. [Google Scholar] [CrossRef] [PubMed]
- Chernomordik, L.V.; Melikyan, G.B.; Chizmadzhev, Y.A. Biomembrane fusion: A new concept derived from model studies using two interacting planar lipid bilayers. Biochim. Biophys. Acta 1987, 906, 309–352. [Google Scholar] [CrossRef]
- Zimmerberg, J.; Cohen, F.S.; Finkelstein, A. Fusion of phospholipid vesicles with planar phospholipid bilayer membranes. I. Discharge of vesicular contents across the planar membrane. J. Gen. Physiol. 1980, 75, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Cohen, F.S.; Zimmerberg, J.; Finkelstein, A. Fusion of phospholipid vesicles with planar phospholipid bilayer membranes. II. Incorporation of a vesicular membrane marker into the planar membrane. J. Gen. Physiol. 1980, 75, 251–270. [Google Scholar] [CrossRef] [PubMed]
- Chernomordik, L.V.; Kozlov, M.M. Protein-lipid interplay in fusion and fission of biological membranes. Annu. Rev. Biochem. 2003, 72, 175–207. [Google Scholar] [CrossRef] [PubMed]
- Lentz, B.R.; Malinin, V.; Haque, M.E.; Evans, K. Protein machines and lipid assemblies: Current views of cell membrane fusion. Curr. Opin. Struct. Biol. 2000, 10, 607–615. [Google Scholar] [CrossRef]
- Martens, S.; Kozlov, M.M.; McMahon, H.T. How synaptotagmin promotes membrane fusion. Science 2007, 316, 1205–1208. [Google Scholar] [CrossRef] [PubMed]
- Chernomordik, L.V.; Zimmerberg, J.; Kozlov, M.M. Membranes of the world unite! J. Cell Biol. 2006, 175, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Schwenen, L.L.; Hubrich, R.; Milovanovic, D.; Geil, B.; Yang, J.; Kros, A.; Jahn, R.; Steinem, C. Resolving single membrane fusion events on planar pore-spanning membranes. Sci. Rep. 2015, 5, 12006. [Google Scholar] [CrossRef] [PubMed]
- Katsov, K.; Müller, M.; Schick, M. Field theoretic study of bilayer membrane fusion: II. Mechanism of a stalk-hole complex. Biophys. J. 2006, 90, 915–926. [Google Scholar] [CrossRef] [PubMed]
- Molotkovsky, R.J.; Galimzyanov, T.R.; Jiménez-Munguía, I.; Pavlov, K.V.; Batishchev, O.V.; Akimov, S.A. Switching between successful and dead-end intermediates in membrane fusion. Int. J. Mol. Sci. 2017, 18, 2598. [Google Scholar] [CrossRef] [PubMed]
- Akimov, S.A.; Molotkovsky, R.J.; Galimzyanov, T.R.; Radaev, A.V.; Shilova, L.A.; Kuzmin, P.I.; Batishchev, O.V.; Voronina, G.F.; Chizmadzhev, Y.A. Model of membrane fusion: Continuous transition to fusion pore with regard of hydrophobic and hydration interactions. Biol. Membr. 2014, 31, 14–24. [Google Scholar] [CrossRef]
- Chernomordik, L.V.; Frolov, V.A.; Leikina, E.; Bronk, P.; Zimmerberg, J. The pathway of membrane fusion catalyzed by influenza hemagglutinin: restriction of lipids, hemifusion, and lipidic fusion pore formation. J. Cell Biol. 1998, 140, 1369–1382. [Google Scholar] [CrossRef] [PubMed]
- Boonstra, S.; Blijleven, J.S.; Roos, W.H.; Onck, P.R.; van der Giessen, E.; van Oijen, A.M. Hemagglutinin-mediated membrane fusion: A biophysical perspective. Annu. Rev. Biophys. 2018, 47. [Google Scholar] [CrossRef] [PubMed]
- Lamb, R.A.; Choppin, P.W. The gene structure and replication of influenza virus. Annu. Rev. Biochem. 1983, 52, 467–506. [Google Scholar] [CrossRef] [PubMed]
- Lakadamyali, M.; Rust, M.J.; Babcock, H.P.; Zhuang, X. Visualizing infection of individual influenza viruses. Proc. Natl. Acad. Sci. USA 2003, 100, 9280–9285. [Google Scholar] [CrossRef] [PubMed]
- Skehel, J.J.; Wiley, D.C. Receptor binding and membrane fusion in virus entry: The influenza hemagglutinin. Annu. Rev. Biochem. 2000, 69, 531–569. [Google Scholar] [CrossRef] [PubMed]
- Chlanda, P.; Mekhedov, E.; Waters, H.; Schwartz, C.L.; Fischer, E.R.; Ryham, R.J.; Cohen, F.S.; Blank, P.S.; Zimmerberg, J. The hemifusion structure induced by influenza virus haemagglutinin is determined by physical properties of the target membranes. Nat. Microbiol. 2016, 1, 16050. [Google Scholar] [CrossRef] [PubMed]
- Zawada, K.E.; Wrona, D.; Rawle, R.J.; Kasson, P.M. Influenza viral membrane fusion is sensitive to sterol concentration but surprisingly robust to sterol chemical identity. Sci. Rep. 2016, 6, 29842. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Raphael, R.M. Solution pH alters mechanical and electrical properties of phosphatidylcholine membranes: relation between interfacial electrostatics, intramembrane potential, and bending elasticity. Biophys. J. 2007, 92, 2451–2462. [Google Scholar] [CrossRef] [PubMed]
- Mitkova, D.; Vitkova, V. The aqueous surroundings alter the bending rigidity of lipid membranes. Russ. J. Electrochem. 2016, 52, 1172–1178. [Google Scholar] [CrossRef]
- Batishchev, O.V.; Indenbom, A.V. Effect of acidity on the formation of solvent-free lipid bilayers. Russ. J. Electrochem. 2006, 42, 1107–1112. [Google Scholar] [CrossRef]
- Melikyan, G.B.; Abidor, I.G.; Chernomordik, L.V.; Chailakhyan, L.M. Electrostimulated fusion and fission of bilayer lipid membranes. Biochim. Biophys. Acta 1983, 730, 395–398. [Google Scholar] [CrossRef]
- Zimmermann, R.; Küttner, D.; Renner, L.; Kaufmann, M.; Zitzmann, J.; Müller, M.; Werner, C. Charging and structure of zwitterionic supported bilayer lipid membranes studied by streaming current measurements, fluorescence microscopy, and attenuated total reflection Fourier transform infrared spectroscopy. Biointerphases 2009, 4, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Leikin, S.L.; Kozlov, M.M.; Chernomordik, L.V.; Markin, V.S.; Chizmadzhev, Y.A. Membrane fusion: Overcoming of the hydration barrier and local restructuring. J. Theor. Biol. 1987, 129, 411–425. [Google Scholar] [CrossRef]
- Pinot, M.; Vanni, S.; Pagnotta, S.; Lacas-Gervais, S.; Payet, L.A.; Ferreira, T.; Gautier, R.; Goud, B.; Antonny, B.; Barelli, H. Polyunsaturated phospholipids facilitate membrane deformation and fission by endocytic proteins. Science 2014, 345, 693–697. [Google Scholar] [CrossRef] [PubMed]
- Rawicz, W.; Olbrich, K.C.; McIntosh, T.; Needham, D.; Evans, E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000, 79, 328–339. [Google Scholar] [CrossRef]
- Ermakov, Y.A. The determination of binding site density and assocition constants for monovalent cation adsorption onto liposomes made from mixtures of zwitterionic and charged lipids. Biochim. Biophys. Acta 1990, 1023, 91–97. [Google Scholar] [CrossRef]
- Tocanne, J.F.; Teissie, J. Ionization of phospholipids and phospholipid-supported interfacial lateral diffusion of protons in membrane model systems. Biochim. Biophys. Acta 1990, 1031, 111–142. [Google Scholar] [CrossRef]
- Mueller, P.; Rudin, D.O.; Tien, H.T.; Wescott, W.C. Methods for the formation of single bimolecular lipid membranes in aqueous solution. J. Phys. Chem. 1963, 67, 534–535. [Google Scholar] [CrossRef]
- Hamm, M.; Kozlov, M.M. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. E 2000, 3, 323–335. [Google Scholar] [CrossRef]
- Leikin, S.; Kozlov, M.M.; Fuller, N.L.; Rand, R.P. Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes. Biophys. J. 1996, 71, 2623–2632. [Google Scholar] [CrossRef]
- Nagle, J.F.; Wilkinson, D.A. Lecithin bilayers. Density measurement and molecular interactions. Biophys. J. 1978, 23, 159–175. [Google Scholar] [CrossRef]
- Galimzyanov, T.R.; Molotkovsky, R.J.; Kuzmin, P.I.; Akimov, S.A. Stabilization of bilayer structure of raft due to elastic deformations of membrane. Biol. Membr. 2011, 28, 307–314. [Google Scholar] [CrossRef]
- Israelachvili, J.; Pashley, R. The hydrophobic interaction is long range, decaying exponentially with distance. Nature 1982, 300, 341–342. [Google Scholar] [CrossRef] [PubMed]
- Rand, R.P.; Parsegian, V.A. Hydration forces between phospholipid bilayers. Biochim. Biophys. Acta 1989, 988, 351–376. [Google Scholar] [CrossRef]
- Lipowsky, R. Generic interactions of flexible membranes. In Structure and Dynamics of Membranes from Cells to Vesicles; Lipowsky, R., Sackmann, E., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 1995; Volume 1, pp. 537–539. ISBN 978-0-444-81975-8. [Google Scholar]
- Hamm, M.; Kozlov, M.M. Tilt model of inverted amphiphilic mesophase. Eur. Phys. J. B 1998, 6, 519–528. [Google Scholar] [CrossRef]
- Templer, R.H.; Khoo, B.J.; Seddon, J.M. Gaussian curvature modulus of an amphiphilic monolayer. Langmuir 1998, 14, 7427–7434. [Google Scholar] [CrossRef]
- Sodt, A.J.; Venable, R.M.; Lyman, E.; Pastor, R.W. Nonadditive compositional curvature energetics of lipid bilayers. Phys. Rev. Lett. 2016, 117, 138104. [Google Scholar] [CrossRef] [PubMed]
- Kollmitzer, B.; Heftberger, P.; Rappolt, M.; Pabst, G. Monolayer spontaneous curvature of raft-forming membrane lipids. Soft Matter 2013, 9, 10877–10884. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akimov, S.A.; Polynkin, M.A.; Jiménez-Munguía, I.; Pavlov, K.V.; Batishchev, O.V. Phosphatidylcholine Membrane Fusion Is pH-Dependent. Int. J. Mol. Sci. 2018, 19, 1358. https://doi.org/10.3390/ijms19051358
Akimov SA, Polynkin MA, Jiménez-Munguía I, Pavlov KV, Batishchev OV. Phosphatidylcholine Membrane Fusion Is pH-Dependent. International Journal of Molecular Sciences. 2018; 19(5):1358. https://doi.org/10.3390/ijms19051358
Chicago/Turabian StyleAkimov, Sergey A., Michael A. Polynkin, Irene Jiménez-Munguía, Konstantin V. Pavlov, and Oleg V. Batishchev. 2018. "Phosphatidylcholine Membrane Fusion Is pH-Dependent" International Journal of Molecular Sciences 19, no. 5: 1358. https://doi.org/10.3390/ijms19051358
APA StyleAkimov, S. A., Polynkin, M. A., Jiménez-Munguía, I., Pavlov, K. V., & Batishchev, O. V. (2018). Phosphatidylcholine Membrane Fusion Is pH-Dependent. International Journal of Molecular Sciences, 19(5), 1358. https://doi.org/10.3390/ijms19051358






