Exploring Configuration Space and Path Space of Biomolecules Using Enhanced Sampling Techniques—Searching for Mechanism and Kinetics of Biomolecular Functions
Abstract
1. Introduction
2. Multiscale Enhanced Sampling (MSES)
2.1. Overview of MSES
2.2. MSES Extension Using Adiabatic Separation
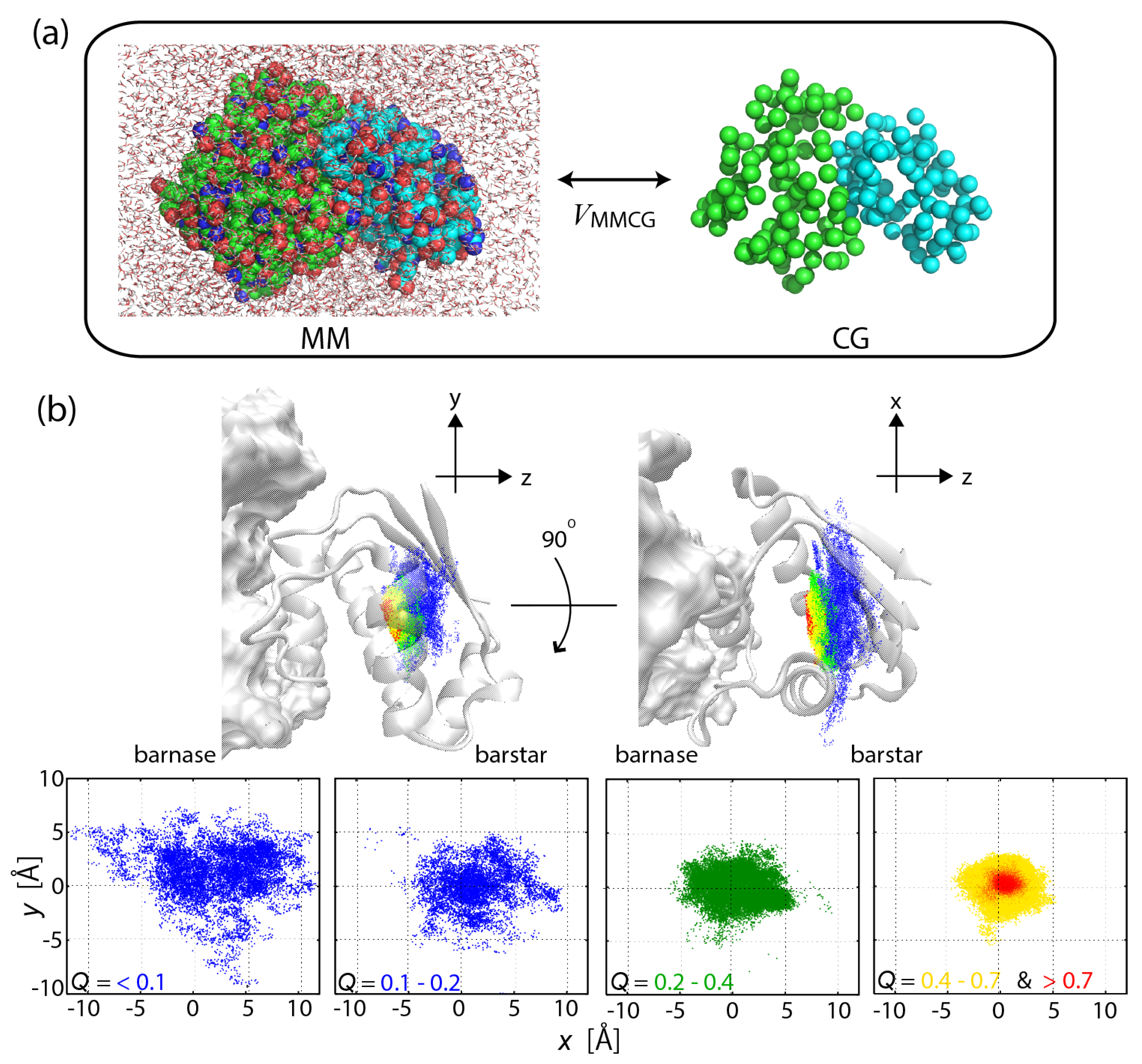
2.3. MSES Applications to Biomolecular Systems
3. String Method
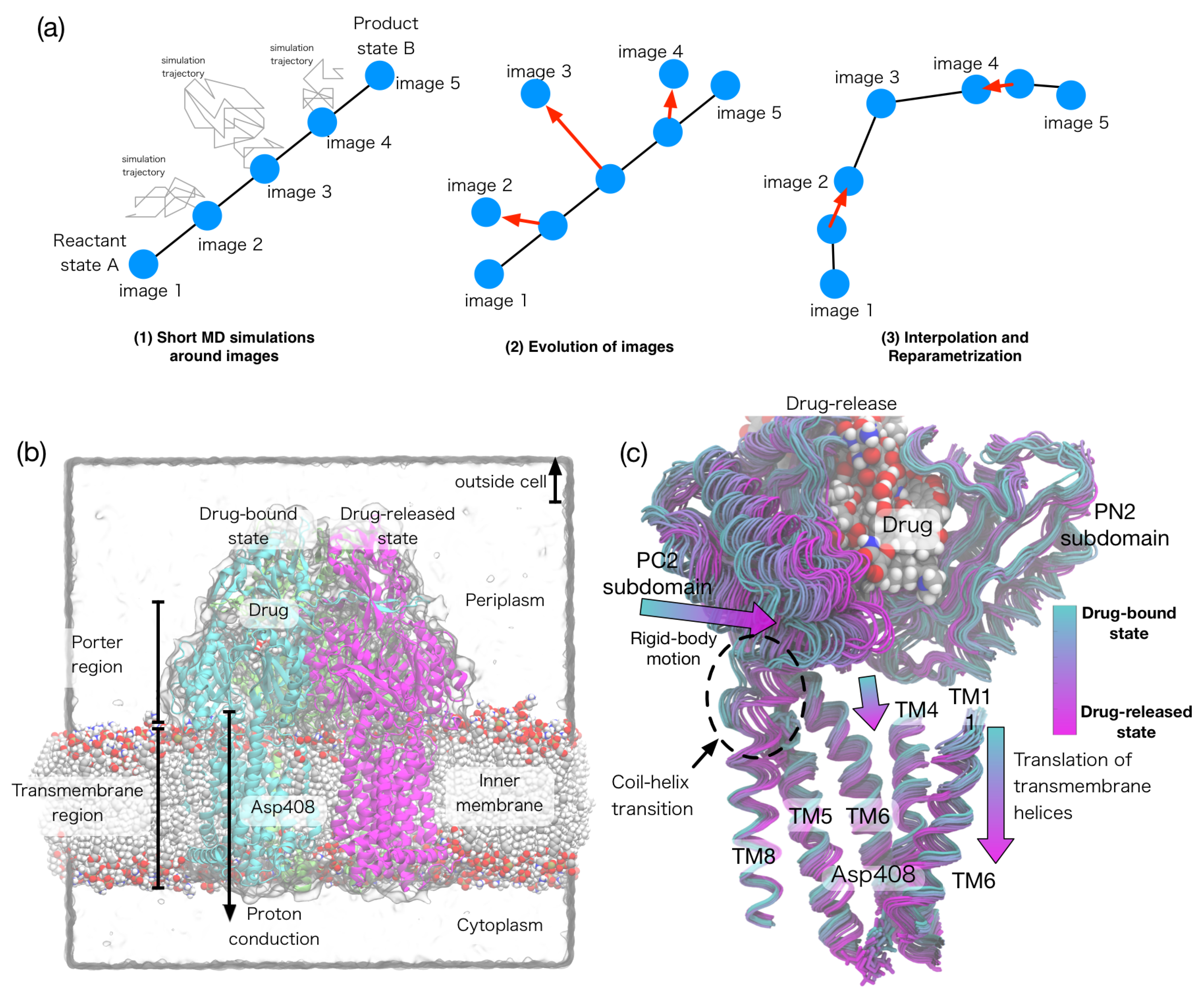
3.1. Overview of String Method
3.2. Impact of the CV Choice on the Accuracy of Pathways
3.3. String Method Applications to Biomolecular Systems
4. Calculation of Kinetics for Biomolecules
4.1. Onsager–Machlup Action Method
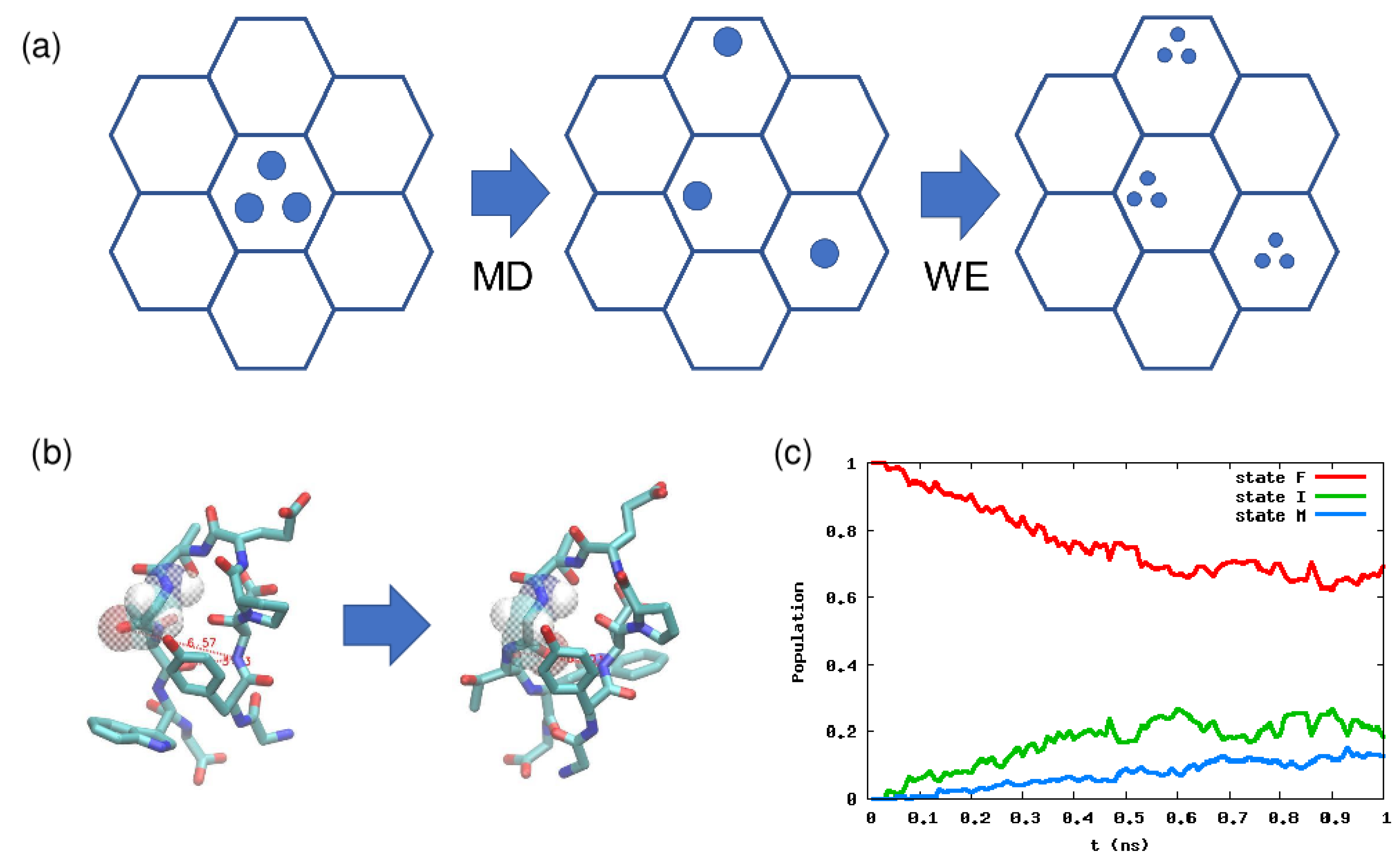
4.2. Weighted Ensemble Method
5. Concluding Remarks
- (a)
- Larger molecular systems: Obviously, these enhanced sampling techniques will be used for much larger systems; recent foci in computational studies include on protein–protein, protein–DNA, and protein–RNA complexes, proteins in membranes, and proteins in crowded environments. The signaling pathways in a cell is a future target [103] and has already been studied in [32,36]. Though there have been several attempts to model atomistic details in a cell [104], multiscale-type methods such as MSES would be quite useful here. A signaling pathway represents sequential molecular processes, including proteins associations, dissociations, and associated chemical reactions, and sampling all molecular processes is not feasible, so the path sampling ideas such as the string method and the OM method should play a role. Multicellular dynamics could be another target [105]. It is quite unrealistic to model all atomistic details, so a CG model for multiple cells such as cellular Potts models might be combined with MD simulations to represent the associated molecular processes.
- (b)
- More efficient methods: Recent advances in computational resources such as GPGPU and Anton [8] have been very promising, but it is still necessary to devise efficient numerical algorithms. In particular, for sampling dynamics or kinetics, we need to combine path sampling algorithms with conventional MD simulations, so the slowness of the latter would be a bottleneck. In materials science, hyperdynamics [106] is usually used to accelerate the barrier crossing processes, but it assumes the transition state theory (TST), which works best if the barrier height is much larger than . It is, however, not always the case for protein dynamics, and we need to use path sampling ideas to accelerate dynamics. It would also be promising to accelerate MD simulations using novel ideas of machine learning [107,108,109,110].
- (c)
- Right CVs or reaction coordinates: Determining how to choose “right” CVs is always an issue, and the quality of the calculations heavily relies on this choice. We usually use intuitive and chemically “reasonable” variables, such as hydrogen bond distances, or geometrical measures, such as root mean square displacement (RMSD) from a reference structure and the radius of gyration (). As mentioned above (Section 3.2), the committor function is the best reaction coordinate, and for its calculation we must know the transition states in advance, but it is not always the case. The string method can extract an importance multidimensional curve, connecting a reactant and product, but for diffusive pathways, the application of the string method encounters some difficulties. Hence, it has been a trend to borrow ideas from recently developed statistics methods to this field of protein dynamics. Principal component analysis (PCA) [17] has been used for extracting “large” functional motions of biomolecules as principal modes, but it is a linear and static analysis, and recently several other methods have been developed. Relaxation mode analysis (RMA) [111] or time-structure-based independent component analysis (tICA) [112] are such methods, and these methods can extract the slowest motions of biomolecules. Manifold learning techniques such as ISOMAP [113,114] and diffusion map [101,115,116] have been applied to a CG model or atomistic protein systems. Other machine learning techniques are also promising and await further application to biomolecular systems [107,108,109,110].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MM | Molecular mechanics |
| CG | Coarse grained |
| CV | Collective variable |
| MSES | Multiscale enhanced sampling |
| MFEP | Minimum free energy path |
| OM | Onsager–Machlup |
| WE | Weighted ensemble |
References
- Petsko, G.A.; Ringe, D. Protein Structure and Function (Primers in Biology); New Science Press Ltd.: London, UK, 2008. [Google Scholar]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Murata, K.; Wolf, M. Cryo-electron microscopy for structural analysis of dynamic biological macromolecules. Biochim. Biophys. Acta Gen. Subj. 2018, 1862, 324–334. [Google Scholar] [CrossRef] [PubMed]
- Srajer, V.; Schmidt, M. Watching proteins function with time-resolved X-ray crystallography. J. Phys. D Appl. Phys. 2017, 50, 373001. [Google Scholar] [CrossRef] [PubMed]
- Vos, M.H.; Liebl, U. Time-resolved infrared spectroscopic studies of ligand dynamics in the active site from cytochrome c oxidase. Biochim. Biophys. Acta (BBA)-Bioenerget. 2015, 1847, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Balakrishnan, G.; Weeks, C.L.; Ibrahim, M.; Soldatova, A.V.; Spiro, T.G. Protein Dynamics from Time-Resolved UV Raman Spectroscopy. Curr. Opin. Struct. Biol. 2008, 18, 623–629. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y.; et al. Atomic-Level Characterization of the Structural Dynamics of Proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E. Principles of Multiscale Modeling; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Peters, B. Reaction Rate Theory and Rare Events; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Takada, S. Coarse-grained molecular simulations of large biomolecules. Curr. Opin. Struct. Biol. 2012, 22, 130. [Google Scholar] [CrossRef] [PubMed]
- Ingólfsson, H.I.; Lopez, C.A.; Uusitalo, J.J.; de Jong, D.H.; Gopal, S.M.; Periole, X.; Marrink, S.J. The power of coarse graining in biomolecular simulations. WIREs Comput. Mol. Sci. 2014, 4, 225–248. [Google Scholar] [CrossRef] [PubMed]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Pietrucci, F. Strateties for the explorarion of free energy landscapes: Unity in diversity and challenges ahead. Rev. Phys. 2017, 2, 32–45. [Google Scholar] [CrossRef]
- Maragliano, L.; Vanden-Eijnden, E. A Temperature Accelerated Method for Sampling Free Energy and Determining Reaction Pathways in Rare Events Simulations. Chem. Phys. Lett. 2006, 426, 168–175. [Google Scholar] [CrossRef]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef] [PubMed]
- Kitao, A.; Takemura, K. High anisotropy and frustration: the keys to regulating protein function efficiently in crowded environments. Curr. Opin. Struct. Biol. 2017, 42, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Fuchigami, S.; Matsunaga, Y.; Fujisaki, H.; Kidera, A. Protein Functional Motion: Basic Concepts and Computational Methodologies. Adv. Chem. Phys. 2011, 145, 35–82. [Google Scholar]
- Grubmüller, H. Predicting slow structural transitions in macromolecular systems: Conformational flooding. Phys. Rev. E 1995, 52, 2893–2906. [Google Scholar] [CrossRef]
- Nakajima, N.; Nakamura, H.; Kidera, A. Multicanonical Ensemble Generated by Molecular Dynamics Simulation for Enhanced Conformational Sampling of Peptides. J. Phys. Chem. B 1997, 101, 817–824. [Google Scholar] [CrossRef]
- Marinelli, F.; Faraldo-Gómez, J.D. Ensemble-Biased Metadynamics: A Molecular Simulation Method to Sample Experimental Distributions. Biophys. J. 2015, 108, 2779–2782. [Google Scholar] [CrossRef] [PubMed]
- Comer, J.; Gumbart, J.C.; Hénin, J.; Lelièvre, T.; Pohorille, A.; Chipot, C. The Adaptive Biasing Force Method: Everything You Always Wanted To Know but Were Afraid To Ask. J. Phys. Chem. B 2015, 119, 1129–1151. [Google Scholar] [CrossRef] [PubMed]
- Harada, R.; Kitao, A. Parallel Cascade Selection Molecular Dynamics (PaCS-MD) to generate conformational transition pathway. J. Chem. Phys. 2013, 139, 035103. [Google Scholar] [CrossRef] [PubMed]
- Hukushima, K.; Nemoto, K. Exchange Monte Carlo Method and Application to Spin Glass Simulations. J. Phys. Soc. Jpn. 1996, 65, 1604–1608. [Google Scholar] [CrossRef]
- Hansmann, U.H.E. Parallel Tempering Algorithm for Conformational Studies of Biological Molecules. Chem. Phys. Lett. 1997, 281, 140–150. [Google Scholar] [CrossRef]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Sugita, Y.; Kitao, A.; Okamoto, Y. Multidimensional replica-exchange method for free-energy calculations. J. Chem. Phys. 2000, 113, 6042–6051. [Google Scholar] [CrossRef]
- Fukunishi, H.; Watanabe, O.; Takada, S. On the Hamiltonian Replica Exchange Method for Efficient Sampling of Biomolecular Systems: Application to Protein Structure Prediction. J. Chem. Phys. 2002, 116, 9058–9067. [Google Scholar] [CrossRef]
- Moritsugu, K.; Terada, T.; Kidera, A. Scalable Free Energy Calculation of Proteins via Multiscale Essential Sampling. J. Chem. Phys. 2010, 133, 224105. [Google Scholar] [CrossRef] [PubMed]
- Moritsugu, K.; Terada, T.; Kidera, A. Disorder-to-order Transition of an Intrinsically Disordered Region of Sortase Revealed by Multiscale Enhanced Sampling. J. Am. Chem. Soc. 2012, 134, 7094–7101. [Google Scholar] [CrossRef] [PubMed]
- Moritsugu, K.; Terada, T.; Kidera, A. Multiscale Enhanced Sampling Driven by Multiple Coarse-grained Models. Chem. Phys. Lett. 2014, 616–617, 20–24. [Google Scholar] [CrossRef]
- Moritsugu, K.; Terada, T.; Kidera, A. Energy Landscape of All-Atom Protein-Protein Interactions Revealed by Multiscale Enhanced Sampling. PLoS Comput. Biol. 2014, 10, e1003901. [Google Scholar] [CrossRef] [PubMed]
- Moritsugu, K.; Terada, T.; Kidera, A. Multiscale Enhanced Sampling for Protein Systems: An Extension via Adiabatic Separation. Chem. Phys. Lett. 2016, 661, 279–283. [Google Scholar] [CrossRef]
- Moritsugu, K.; Terada, T.; Kidera, A. Free Energy Landscape of Protein-Ligand Interactions Coupled with Protein Structural Changes. J. Phys. Chem. B 2017, 121, 731–740. [Google Scholar] [CrossRef] [PubMed]
- Moritsugu, K.; Terada, T.; Kokubo, H.; Endo, S.; Tanaka, T.; Kidera, A. Multiscale enhanced sampling of glucokinase: Regulation of the enzymatic reaction via a large scale domain motion. J. Chem. Phys. 2018, 149, 072314. [Google Scholar] [CrossRef] [PubMed]
- Moritsugu, K.; Nishi, H.; Inariyama, K.; Kobayashi, M.; Kidera, A. Dynamic recognition and linkage specificity in K63 di-ubiquitin and TAB2 NZF domain complex. Sci. Rep. in press.
- Fujisaki, H.; Shiga, M.; Moritsugu, K.; Kidera, A. Multiscale enhanced path sampling based on the Onsager–Machlup action: Application to a model polymer. J. Chem. Phys. 2013, 139, 054117. [Google Scholar] [CrossRef] [PubMed]
- Zuckerman, D.M. Statistical Physics of Biomolecules: An Introduction; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Pearlman, D.A.; Kollman, P.A. The lag between the Hamiltonian and the system configuration in free energy perturbation calculations. J. Chem. Phys. 1989, 91, 7831–7839. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, M.; Yang, W. Random walk in orthogonal space to achieve efficient free-energy simulation of complex systems. Proc. Natl. Acad. Sci. USA 2008, 105, 20227–20232. [Google Scholar] [CrossRef] [PubMed]
- Maragliano, L.; Fischer, A.; Vanden-Eijnden, E.; Ciccotti, G. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J. Chem. Phys. 2006, 125, 024106. [Google Scholar] [CrossRef] [PubMed]
- Maragliano, L.; Vanden-Eijnden, E. On-the-fly string method for minimum free energy paths calculation. Chem. Phys. Lett. 2007, 446, 182–190. [Google Scholar] [CrossRef]
- Pan, A.C.; Sezer, D.; Roux, B. Finding transition pathways using the string method with swarms of trajectories. J. Phys. Chem. B 2008, 112, 3432–3440. [Google Scholar] [CrossRef] [PubMed]
- Kramers, H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica (Urecht) 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Szabo, A.; Schulten, K.; Schulten, Z. First passage time approach to diffusion controlled reactions. J. Chem. Phys. 1979, 72, 4350–45357. [Google Scholar] [CrossRef]
- Peters, B. Recent advances in transition path sampling: accurate reaction coordinates, likelihood maximisation and diffusive barrier-crossing dynamics. Mol. Simul. 2010, 36, 1265–1281. [Google Scholar] [CrossRef]
- Nakamura, T. Diffeomorphism invariance requirement on free-energy landscape to describe reaction phenomena. arXiv, 2018; arXiv:1803.09034. [Google Scholar]
- Bowman, G.R.; Pande, V.S.; Noé, F. (Eds.) An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Chodera, J.D.; Noé, F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Cao, S.; Zhu, L.; Huang, X. Constructing Markov State Models to elucidate the functional conformational changes of complex biomolecules. WIREs Comput. Mol. Sci. 2017, 8, e1343. [Google Scholar] [CrossRef]
- Thayer, K.M.; Lakhani, B.; Beveridge, D.L. Molecular Dynamics-Markov State Model of Protein Ligand Binding and Allostery in CRIB-PDZ: Conformational Selection and Induced Fit. J. Phys. Chem. B 2017, 121, 5509–5514. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C.; Noé, F.; Lu, J.; Sarich, M.; Vanden-Eijnden, E. Markov state models based on milestoning. J. Chem. Phys. 2011, 134, 204105. [Google Scholar] [CrossRef] [PubMed]
- Fujisaki, H.; Shiga, M.; Kidera, A. Onsager—Machlup action-based path sampling and its combination with replica exchange for diffusive and multiple pathways. J. Chem. Phys. 2010, 132, 134101. [Google Scholar] [CrossRef] [PubMed]
- Zuckerman, D.M.; Chong, L.T. Weighted Ensemble Simulation: Review of Methodology, Applications, and Software. Annu. Rev. Biophys. 2017, 46, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Shirts, M.R. Replica Exchange and Expanded Ensemble Simulations as Gibbs Sampling: Simple Improvements for Enhanced Mixing. J. Chem. Phys. 2011, 135, 194110. [Google Scholar] [CrossRef] [PubMed]
- Rosso, L.; Tuckerman, M.E. An Adiabatic Molecular Dynamics Method for the Calculation of Free Energy Profiles. Mol. Simul. 2002, 28, 91–112. [Google Scholar] [CrossRef]
- Morishita, T.; Itoh, S.G.; Okumura, H.; Mikami, M. Free-energy Calculation via Mean-force Dynamics Using a Logarithmic Energy Landscape. Phys. Rev. E 2012, 85, 066702. [Google Scholar] [CrossRef] [PubMed]
- Tirion, M.M. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Brooks, B.R.; Hummer, G. Protein Conformational Transitions Explored by Mixed Elastic Network Models. Proteins 2007, 69, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Yasar, F.; Bernhardt, N.A.; Hansmann, U.H.E. Replica-Exchange-with-Tunneling for Fast Exploration of Protein Landscapes. J. Chem. Phys. 2015, 143, 224102. [Google Scholar] [CrossRef] [PubMed]
- Bernhardt, N.A.; Xi, W.; Wang, W.; Hansmann, U.H.E. Simulating Protein Fold Switching by Replica-Exchange-with-Tunneling. J. Chem. Theory Comput. 2016, 12, 5656–5666. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Xi, W.; Hansmann, U.H.E.; Wei, Y. Fibril-Barrel Transitions in Cylindrin Amyloids. J. Chem. Theory Comput. 2017, 13, 3936–3944. [Google Scholar] [CrossRef] [PubMed]
- Xi, W.; Hansmann, U.H.E. Conversion between parallel and antiparallel β-sheets in wild type and Iowa mutant Aβ40 fibrils. J. Chem. Phys. 2018, 148, 045103. [Google Scholar] [CrossRef] [PubMed]
- Xi, W.; Vanderford, E.K.; Hansmann, U.H.E. Out-of-Register Aβ42 Assemblies as Models for Neurotoxic Oligomers and Fibrils. J. Chem. Theory Comput. 2018, 14, 1099–1110. [Google Scholar] [CrossRef] [PubMed]
- Bernhardt, N.A.; Hansmann, U.H.E. Simulating Protein Fold Switching by Replica Exchange with Tunneling. J. Phys. Chem. B 2018, 122, 1600–1607. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Chen, J.H. Multiscale enhanced sampling of intrinsically disordered protein conformations. J. Comput. Chem. 2016, 37, 550–557. [Google Scholar] [CrossRef] [PubMed]
- Vanden-Eijnden, E. Transition Path Theory. In Computer Simulations in Condensed Matter Systems: From Materials to CHemical Biology; Ferrario, M., Ciccotti, G., Binder, K., Eds.; Springer: Berlin, Germany, 2007; Volume 1, pp. 453–493. [Google Scholar]
- Jiang, W.; Phillips, J.C.; Huang, L.; Fajer, M.; Meng, Y.; Gumbart, J.C.; Luo, Y.; Schulten, K.; Roux, B. Generalized scalable multiple copy algorithms for molecular dynamics simulations in NAMD. Comput. Phys. Commun. 2014, 185, 908–916. [Google Scholar] [CrossRef] [PubMed]
- Pronk, S.; Lindahl, E.; Larsson, P.; Pouya, I.; Bowman, G.R.; Haque, I.S.; Beauchamp, K.; Hess, B.; Pande, V.S.; Kasson, P.M. Copernicus: A new paradigm for parallel adaptive molecular dynamics. In Proceedings of the 2011 International Conference for High Performance Computing, Networking, Storage and Analysis (SC’11), ACM, New York, NY, USA, 12–18 November 2011; pp. 60:1–60:10. [Google Scholar]
- Jung, J.; Mori, T.; Kobayashi, C.; Matsunaga, Y.; Yoda, T.; Feig, M.; Sugita, Y. GENESIS: A hybrid-parallel and multi-scale molecular dynamics simulator with enhanced sampling algorithms for biomolecular and cellular simulations. WIREs Comput. Mol. Sci. 2015, 5, 310–323. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, C.; Jung, J.; Matsunaga, Y.; Mori, T.; Ando, T.; Tamura, K.; Kamiya, M.; Sugita, Y. GENESIS 1.1: A hybrid-parallel molecular dynamics simulator with enhanced sampling algorithms on multiple computational platforms. J. Comput. Chem. 2017, 38, 2193–2206. [Google Scholar] [CrossRef] [PubMed]
- Shiga, M.; Fujisaki, H. A quantum generalization of intrinsic reaction coordinate using path integral centroid coordinate. J. Chem. Phys. 2012, 136, 184103. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Barragan, S.; Ishimura, K.; Shiga, M. On the hierarchical parallelization of ab initio simulations. Chem. Phys. Lett. 2016, 646, 130–135. [Google Scholar] [CrossRef]
- Abrams, C.F.; Vanden-Eijnden, E. Large-scale conformational sampling of proteins using temperature-accelerated molecular dynamics. Proc. Natl. Acad. Sci. USA 2010, 107, 4961–4966. [Google Scholar] [CrossRef] [PubMed]
- Vashisth, H.; Brooks, C.L., III. Conformational Sampling of Maltose-Transporter Components in Cartesian Collective Variables Is Governed by the Low-Frequency Normal Modes. J. Phys. Chem. Lett. 2012, 3, 3379–3384. [Google Scholar] [CrossRef] [PubMed]
- Pan, A.C.; Weinreich, T.M.; Shan, Y.; Scarpazza, D.P.; Shaw, D.E. Assessing the Accuracy of Two Enhanced Sampling Methods Using EGFR Kinase Transition Pathways: The Influence of Collective Variable Choice. J. Chem. Theory Comput. 2014, 10, 2860–2865. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, Y.; Komuro, Y.; Kobayashi, C.; Jung, J.; Mori, T.; Sugita, Y. Dimensionality of Collective Variables for Describing Conformational Changes of a Multi-Domain Protein. J. Phys. Chem. Lett. 2016, 7, 1446–1451. [Google Scholar] [CrossRef] [PubMed]
- Schlitter, J.; Engels, M.; Krüger, P.; Jacoby, E.; Wollmer, A. Targeted Molecular Dynamics Simulation of Conformational Change-Application to the T ↔ R Transition in Insulin. Mol. Simul. 1993, 10, 291–308. [Google Scholar] [CrossRef]
- Ovchinnikov, V.; Karplus, M.; Vanden-Eijnden, E. Free energy of conformational transition paths in biomolecules: the string method and its application to myosin VI. J. Chem. Phys. 2011, 134, 085103. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Tajkhorshid, E. Computational Recipe for Efficient Description of Large-Scale Conformational Changes in Biomolecular Systems. J. Chem. Theory Comput. 2014, 10, 2866–2880. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Enkavi, G.; Tajkhorshid, E. Atomic-level characterization of transport cycle thermodynamics in the glycerol-3-phosphate:phosphate antiporter. Nat. Commun. 2015, 6, 8393. [Google Scholar] [CrossRef] [PubMed]
- Izrailev, S.; Stepaniants, S.; Balsera, M.; Oono, Y.; Schulten, K. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 1997, 72, 1568–1581. [Google Scholar] [CrossRef]
- Gan, W.; Yang, S.; Roux, B. Atomistic view of the conformational activation of Src kinase using the string method with swarms-of-trajectories. Biophys. J. 2009, 97, L8–L10. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Hummer, G. Pore opening and closing of a pentameric ligand-gated ion channel. Proc. Natl. Acad. Sci. USA 2010, 107, 19814–19819. [Google Scholar] [CrossRef] [PubMed]
- Lev, B.; Murail, S.; Poitevin, F.; Cromer, B.A.; Baaden, M.; Delarue, M.; Allen, T.W. String method solution of the gating pathways for a pentameric ligand-gated ion channel. Proc. Natl. Acad. Sci. USA 2017, 114, E4158–E4167. [Google Scholar] [CrossRef] [PubMed]
- Stober, S.T.; Abrams, C.F. Energetics and mechanism of the normal-to-amyloidogenic isomerization of beta2-microglobulin: on-the-fly string method calculations. J. Phys. Chem. B 2012, 116, 9371–9375. [Google Scholar] [CrossRef] [PubMed]
- Singharoy, A.; Chipot, C.; Moradi, M.; Schulten, K. Chemomechanical Coupling in Hexameric Protein—Protein Interfaces Harnesses Energy within V-Type ATPases. J. Am. Chem. Soc. 2017, 139, 293–310. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Rui, H.; Roux, B. Conformational Transitions and Alternating-Access Mechanism in the Sarcoplasmic Reticulum Calcium Pump. J. Mol. Biol. 2017, 429, 647–666. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, Y.; Fujisaki, H.; Terada, T.; Furuta, T.; Moritsugu, K.; Kidera, A. Minimum Free Energy Path of Ligand-Induced Transition in Adenylate Kinase. PLoS Comput. Biol. 2012, 8, e1002555. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, Y.; Yamane, T.; Terada, T.; Moritsugu, K.; Fujisaki, H.; Murakami, S.; Ikeguchi, M.; Kidera, A. Energetics and conformational pathways of functional rotation in the multidrug transporter AcrB. eLife 2018, 7, 243. [Google Scholar] [CrossRef] [PubMed]
- Wolf-Watz, M.; Thai, V.; Henzler-Wildman, K.; Hadjipavlou, G.; Eisenmesser, E.Z.; Kern, D. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat. Struct. Mol. Biol. 2004, 11, 945–949. [Google Scholar] [CrossRef] [PubMed]
- Du, D.; van Veen, H.W.; Murakami, S.; Pos, K.M.; Luisi, B.F. Structure, mechanism and cooperation of bacterial multidrug transporters. Curr. Opin. Struct. Biol. 2015, 33, 76–91. [Google Scholar] [CrossRef] [PubMed]
- Grazioli, G.; Andricioaei, I. Advances in milestoning. I. Enhanced sampling via wind-assisted reweighted milestoning (WARM). J. Chem. Phys. 2018, 149, 084103. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Swope, W.C.; Noe, F.; Prinz, J.-H.; Shirts, M.R.; Pande, V.S. Dynamical reweighting: Improved estimates of dynamical properties from simulations at multiple temperatures. J. Chem. Phys. 2011, 134, 244107. [Google Scholar] [CrossRef] [PubMed]
- Zuckerman, D.M.; Woolf, T.B. Efficient dynamic importance sampling of rare events in one dimension. Phys. Rev. E 2001, 63, 016702. [Google Scholar] [CrossRef] [PubMed]
- Takayanagi, S.; Iba, Y. Backward Simulation of Stochastic Process using a Time Reverse Monte Carlo method. arXiv, 2018; arXiv:1708.08045. [Google Scholar]
- Donati, L.; Hartmann, C.; Keller, B.G. Girsanov reweighting for path ensembles and Markov state models. J. Chem. Phys. 2017, 146, 244112. [Google Scholar] [CrossRef] [PubMed]
- Beccara, S.; Škrbić, T.; Covino, R.; Faccioli, P. Dominant folding pathways of a WW domain. Proc. Natl. Acad. Sci. USA 2012, 109, 2330–2335. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Lee, I.-H.; Joung, I.; Lee, J.; Brooks, B.R. Finding multiple reaction pathways via global optimization of action. Nat. Commun. 2017, 8, 15443. [Google Scholar] [CrossRef] [PubMed]
- Huber, G.A.; Kim, S. Weighted-ensemble Brownian dynamics simulations for protein association reactions. Biophys. J. 1996, 70, 97–110. [Google Scholar] [CrossRef]
- Fujisaki, H.; Moritsugu, K.; Mitsutake, A.; Suetani, H. Conformational change of a biomolecule studied by the weighted ensemble method: Use of the diffusion map method to extract reaction coordinates. J. Chem. Phys. 2018, 149, 134112. [Google Scholar] [CrossRef] [PubMed]
- Fujisaki, H.; Mitsutake, A.; Maragliano, L. Numerical investigation of kinetic properties of a small peptide using non-Markov type analysis and milestoning. unpublished.
- Marks, F.; Klingmüller, U.; Müller-Decker, K. Cellular Signal Processing: An Introduction to the Molecular Mechanisms of Signal Transduction, 2nd ed.; Garland Science: New York, NY, USA; London, UK, 2017. [Google Scholar]
- Trovato, F.; Fumagalli, G. Molecular simulations of cellular processes. Biophys. Rev. 2017, 9, 941–958. [Google Scholar] [CrossRef] [PubMed]
- Mak, M.; Kim, T.; Zaman, M.H.; Kamm, R.D. Multiscale mechanobiology: Computational models for integrating molecules to multicellular systems. Integr. Biol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Chena, L.Y.; Horing, N.J.M. An exact formulation of hyperdynamics simulations. J. Chem. Phys. 2007, 126, 224103. [Google Scholar] [CrossRef] [PubMed]
- Sultan, M.M.; Wayment-Steele, H.K.; Pande, V.S. Transferable Neural Networks for Enhanced Sampling of Protein Dynamics. J. Chem. Theory Comput. 2018, 14, 1887–1894. [Google Scholar] [CrossRef] [PubMed]
- Sultan, M.M.; Pande, V.S. Automated design of collective variables using supervised machine learning. J. Chem. Phys. 2018, 149, 094106. [Google Scholar] [CrossRef] [PubMed]
- Endo, K.; Tomobe, K.; Yasuoka, K. Multi-Step Time Series Generator for Molecular Dynamics. In The Thirty-Second AAAI Conference on Artificial Intelligence; AAAI Publications: Palo Alto, CA, USA, 2018. [Google Scholar]
- Brandt, S.; Sittel, F.; Ernst, M.; Stock, G. Machine Learning of Biomolecular Reaction Coordinates. J. Phys. Chem. Lett. 2018, 9, 2144–2150. [Google Scholar] [CrossRef] [PubMed]
- Mitsutake, A.; Takano, H. Relaxation mode analysis and Markov state relaxation mode analysis for chignolin in aqueous solution near a transition temperature. J. Chem. Phys. 2015, 143, 124111. [Google Scholar] [CrossRef] [PubMed]
- Naritomi, Y.; Fuchigami, S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: The case of domain motions. J. Chem. Phys. 2011, 134, 065101. [Google Scholar] [CrossRef] [PubMed]
- Suetani, H.; Soejima, K.; Matsuoka, R.; Parlitz, U.; Hata, H. Manifold learning approach for chaos in the dripping faucet. Phys. Rev. E 2012, 86, 036209. [Google Scholar] [CrossRef] [PubMed]
- Ito, R.; Yoshidome, T. An Accurate Computation of an Order Parameter with a Markov State Model Constructed using a Manifold-Learning Technique. Chem. Phys. Lett. 2018, 691, 22–27. [Google Scholar] [CrossRef]
- Rohrdanz, M.A.; Zheng, W.; Maggioni, M.; Clementi, C. Determination of reaction coordinates via locally scaled diffusion map. J. Chem. Phys. 2011, 134, 124116. [Google Scholar] [CrossRef] [PubMed]
- Nedialkova, L.V.; Amat, M.A.; Kevrekidis, I.G.; Hummer, G. Diffusion maps, clustering and fuzzy Markov modeling in peptide folding transitions. J. Chem. Phys. 2014, 141, 114102. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujisaki, H.; Moritsugu, K.; Matsunaga, Y. Exploring Configuration Space and Path Space of Biomolecules Using Enhanced Sampling Techniques—Searching for Mechanism and Kinetics of Biomolecular Functions. Int. J. Mol. Sci. 2018, 19, 3177. https://doi.org/10.3390/ijms19103177
Fujisaki H, Moritsugu K, Matsunaga Y. Exploring Configuration Space and Path Space of Biomolecules Using Enhanced Sampling Techniques—Searching for Mechanism and Kinetics of Biomolecular Functions. International Journal of Molecular Sciences. 2018; 19(10):3177. https://doi.org/10.3390/ijms19103177
Chicago/Turabian StyleFujisaki, Hiroshi, Kei Moritsugu, and Yasuhiro Matsunaga. 2018. "Exploring Configuration Space and Path Space of Biomolecules Using Enhanced Sampling Techniques—Searching for Mechanism and Kinetics of Biomolecular Functions" International Journal of Molecular Sciences 19, no. 10: 3177. https://doi.org/10.3390/ijms19103177
APA StyleFujisaki, H., Moritsugu, K., & Matsunaga, Y. (2018). Exploring Configuration Space and Path Space of Biomolecules Using Enhanced Sampling Techniques—Searching for Mechanism and Kinetics of Biomolecular Functions. International Journal of Molecular Sciences, 19(10), 3177. https://doi.org/10.3390/ijms19103177





