Using MOEA with Redistribution and Consensus Branches to Infer Phylogenies
Abstract
:1. Introduction
2. Materials and Methods
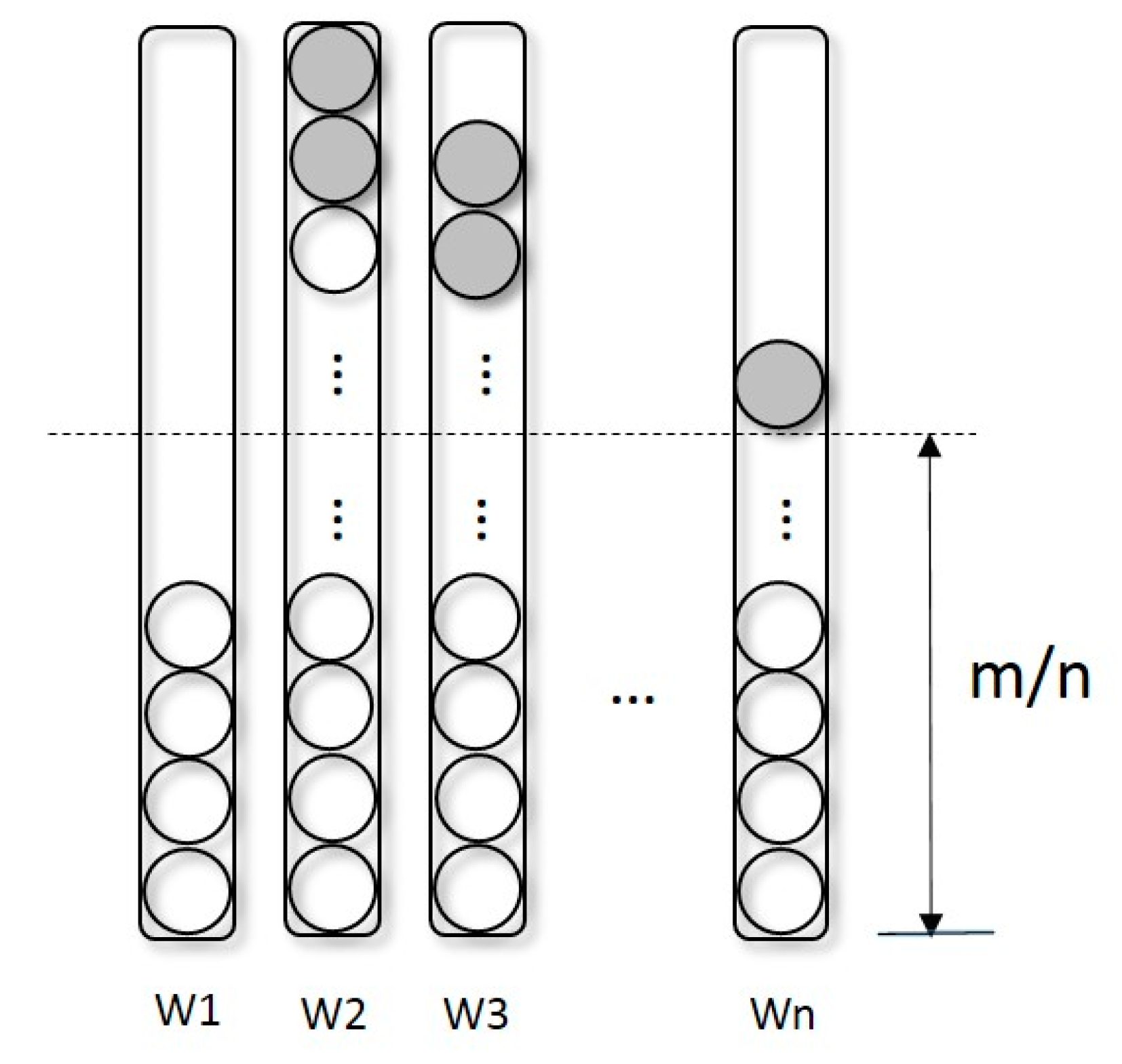
2.1. Selection Operator-Redistribution
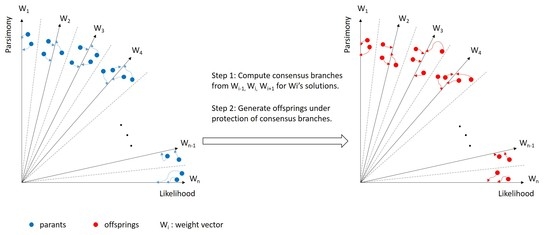
2.2. Consensus
2.3. MOEA-RC
- Step 1.
- Population initiation: Two options can be chosen to initialize population: (1) using molecular sequences, which have been pre-processed, such as alignment, to randomly build N phylogenetic trees; and (2) using user given trees.
- Step 2.
- Evaluation: Evaluate trees by MP and ML and update reference point at the same time.
- Step 3.
- Redistribution: As described in Section 2.1, separate the population into several sub-populations according to Equation (2) and Sort trees in each sub-population by their fitness computed by Equation (3).
- Step 4.
- Computation of consensus: Generate consensus branches for each sub-population as described above.
- Step 5.
- Generation of offspring: Randomly select two individuals from the current population and do a crossover operation to generate two new solutions. Many crossover operators are available in the literature (Lewis 1998 [13]; Congdon 2002 [34]). We chose Prune–Delete–Graft (PDG), which is described by Lewis (1998) [13], because it has been successfully applied under different criteria. Then, use the nearest neighbor interchange (NNI) [35] to mutate the two new solutions. Repeat this step until N new solutions have been generated.
- Step 6.
- Merging: Merge the offspring with the current population.
- Step 7.
- Repeat: Return to Step 2 and repeat until the stop condition is reached. The stop condition in this paper is the maximum number of evaluation times set by the user. The stop condition in this paper is a given specific number of generations.
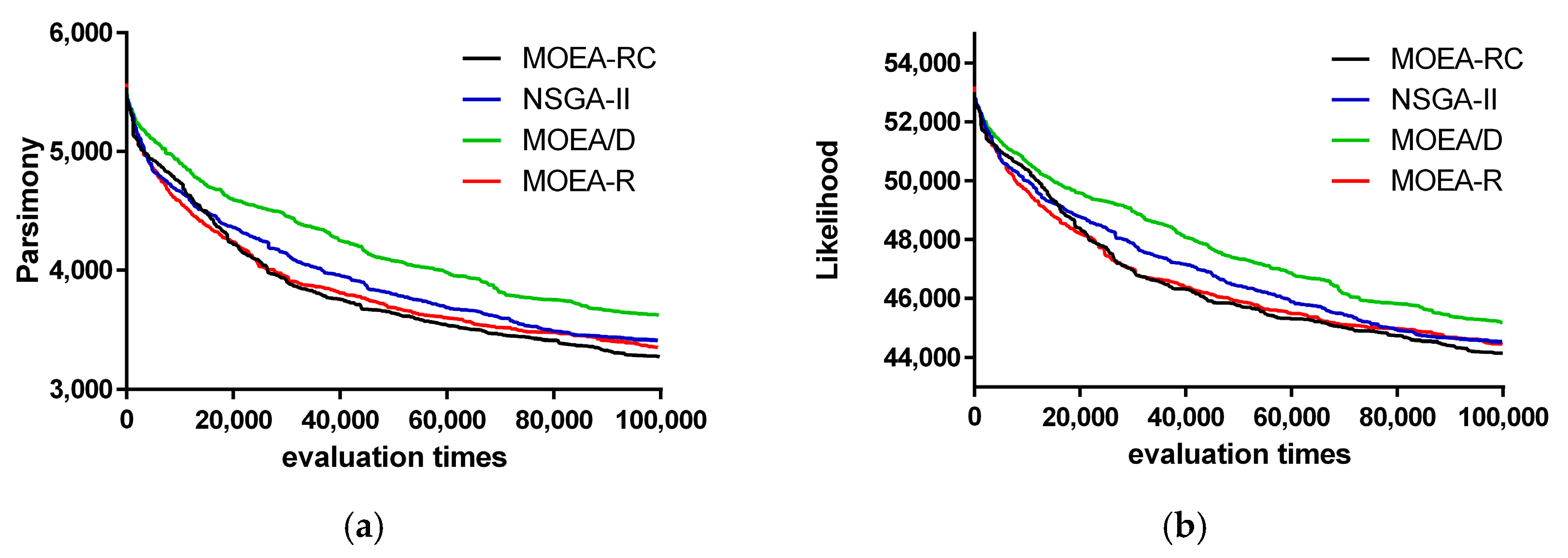
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Saitou, N.; Nei, M. The neighbor-joining method: A new method for reconstructing phylogenetic trees. Mol. Biol. Evol. 1987, 4, 406–425. [Google Scholar] [PubMed]
- Gascuel, O. BIONJ: An improved version of the NJ algorithm based on a simple model of sequence data. Mol. Biol. Evol. 1997, 14, 685–695. [Google Scholar] [CrossRef] [PubMed]
- Felsenstein, J. Inferring Phylogenies; Sinauer Associates: Sunderland, MA, USA, 2004; Volume 2. [Google Scholar]
- Jukes, T.H.; Cantor, C.R.; Munro, H. Evolution of protein molecules. In Mammalian Protein Metabolism; Elsevier: New York, NY, USA, 1969; pp. 21–132. [Google Scholar]
- Hasegawa, M.; Kishino, H.; Yano, T.-A. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 1985, 22, 160–174. [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Nei, M. Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees. Mol. Biol. Evol. 1993, 10, 512–526. [Google Scholar] [PubMed]
- Tavaré, S. Some probabilistic and statistical problems in the analysis of DNA sequences. Lect. Math. Life Sci. 1986, 17, 57–86. [Google Scholar]
- Cancino, W.; Delbem, A. A multi-criterion evolutionary approach applied to phylogenetic reconstruction. In New Achievements in Evolutionary Computation; InTech: Rijeka, Croatia, 2010. [Google Scholar]
- Lemmon, A.R.; Milinkovitch, M.C. The metapopulation genetic algorithm: An efficient solution for the problem of large phylogeny estimation. Proc. Natl. Acad. Sci. USA 2002, 99, 10516–10521. [Google Scholar] [CrossRef] [PubMed]
- Chor, B.; Tuller, T. Maximum likelihood of evolutionary trees: Hardness and approximation. Bioinformatics 2005, 21, i97–i106. [Google Scholar] [CrossRef] [PubMed]
- Felsenstein, J. PHYLIP: Phylogeny Inference Package. Cladistics 1989, 5, 164–166. [Google Scholar]
- Strimmer, K.; Von Haeseler, A. Quartet puzzling: A quartet maximum-likelihood method for reconstructing tree topologies. Mol. Biol. Evol. 1996, 13, 964–969. [Google Scholar] [CrossRef]
- Lewis, P.O. A genetic algorithm for maximum-likelihood phylogeny inference using nucleotide sequence data. Mol. Biol. Evol. 1998, 15, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, H. Construction of phylogenetic trees from amino acid sequences using a genetic algorithm. Genome Inform. 1995, 6, 19–28. [Google Scholar]
- Moilanen, A. Searching for most parsimonious trees with simulated evolutionary optimization. Cladistics 1999, 15, 39–50. [Google Scholar] [CrossRef]
- Santander-Jiménez, S.; Vega-Rodríguez, M.A. On the design of shared memory approaches to parallelize a multiobjective bee-inspired proposal for phylogenetic reconstruction. Inf. Sci. 2015, 324, 163–185. [Google Scholar] [CrossRef]
- Goloboff, P.A.; Farris, J.S.; Nixon, K.C. TNT, a free program for phylogenetic analysis. Cladistics 2008, 24, 774–786. [Google Scholar] [CrossRef]
- Stamatakis, A. RAxML version 8: A tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 2014, 30, 1312–1313. [Google Scholar] [CrossRef] [PubMed]
- Minh, B.Q.; Vinh, L.S.; Von Haeseler, A.; Schmidt, H.A. pIQPNNI: Parallel reconstruction of large maximum likelihood phylogenies. Bioinformatics 2005, 21, 3794–3796. [Google Scholar] [CrossRef] [PubMed]
- Ronquist, F.; Teslenko, M.; Van Der Mark, P.; Ayres, D.L.; Darling, A.; Höhna, S.; Larget, B.; Liu, L.; Suchard, M.A.; Huelsenbeck, J.P. MrBayes 3.2: Efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 2012, 61, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Zwickl, D.J. Genetic Algorithm Approaches for the Phylogenetic Analysis of Large Biological Sequence Datasets under the Maximum Likelihood Criterion; University of Texas at Austin: Austin, TX, USA, 2006. [Google Scholar]
- Helaers, R.; Milinkovitch, M.C. MetaPIGA v2.0: Maximum likelihood large phylogeny estimation using the metapopulation genetic algorithm and other stochastic heuristics. BMC Bioinform. 2010, 11, 379. [Google Scholar] [CrossRef] [PubMed]
- Macey, J.R. Plethodontid salamander mitochondrial genomics: A parsimony evaluation of character conflict and implications for historical biogeography. Cladistics 2005, 21, 194–202. [Google Scholar] [CrossRef]
- Burleigh, J.G.; Mathews, S. Assessing systematic error in the inference of seed plant phylogeny. Int. J. Plant Sci. 2007, 168, 125–135. [Google Scholar] [CrossRef]
- Schmidt, O.; Drake, H.L.; Horn, M.A. Hitherto unknown [Fe-Fe]-hydrogenase gene diversity in anaerobes and anoxic enrichments from a moderately acidic fen. Appl. Environ. Microbiol. 2010, 76, 2027–2031. [Google Scholar] [CrossRef] [PubMed]
- Poladian, L.; Jermiin, L. Multi-objective evolutionary algorithms and phylogenetic inference with multiple data sets. Soft Comput. 2006, 10, 359–368. [Google Scholar] [CrossRef]
- Coello, C.C.; Dhaenens, C.; Jourdan, L. Advances in Multi-Objective Nature Inspired Computing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 272. [Google Scholar]
- Ishibuchi, H.; Nojima, Y.; Doi, T. Comparison between single-objective and multi-objective genetic algorithms: Performance comparison and performance measures. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1143–1150. [Google Scholar]
- Deb, K. A fast elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2000, 6, 182–197. [Google Scholar] [CrossRef]
- Santander-Jiménez, S.; Vega-Rodríguez, M.A. A hybrid approach to parallelize a fast non-dominated sorting genetic algorithm for phylogenetic inference. Concurr. Comput. 2015, 27, 702–734. [Google Scholar] [CrossRef]
- Santander-Jiménez, S.; Vega-Rodríguez, M.A. Parallel multiobjective metaheuristics for inferring phylogenies on multicore clusters. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 1678–1692. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Jansson, J.; Shen, C.; Sung, W.-K. Improved algorithms for constructing consensus trees. JACM 2016, 63, 28. [Google Scholar] [CrossRef]
- Congdon, C.B. Gaphyl: An evolutionary algorithms approach for the study of natural evolution. In Proceedings of the 4th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 9–13 July 2002; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2002; pp. 1057–1064. [Google Scholar]
- Waterman, M.S.; Smith, T.F. On the similarity of dendrograms. J. Theor. Biol. 1978, 73, 789–800. [Google Scholar] [CrossRef]
- Ingman, M.; Gyllensten, U. mtDB: Human Mitochondrial Genome Database, a resource for population genetics and medical sciences. Nucleic Acids Res. 2004, 34, 749–751. [Google Scholar] [CrossRef] [PubMed]
- Chase, M.W.; Soltis, D.E.; Olmstead, R.G.; Morgan, D.; Les, D.H.; Mishler, B.D.; Duvall, M.R.; Price, R.A.; Hills, H.G.; Qiu, Y.-L. Phylogenetics of seed plants: An analysis of nucleotide sequences from the plastid gene rbcL. Ann. Mo. Bot. Gard. 1993, 80, 528–580. [Google Scholar] [CrossRef]
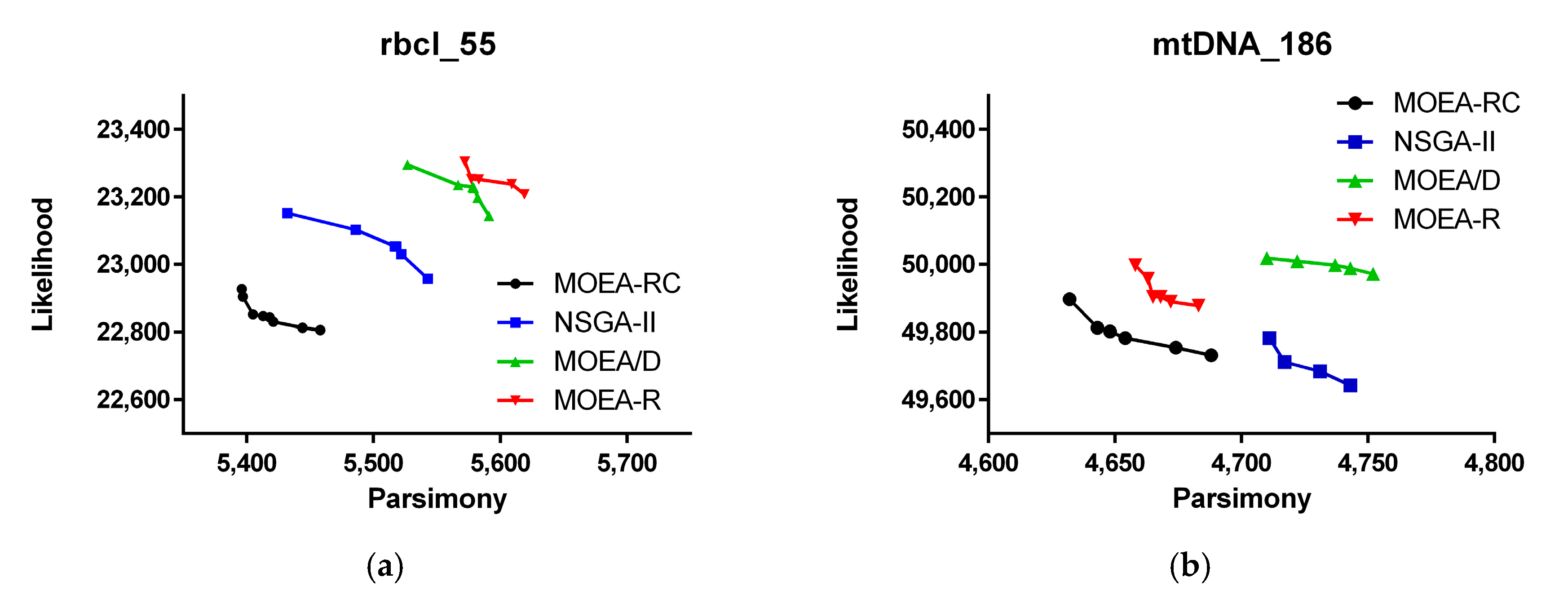
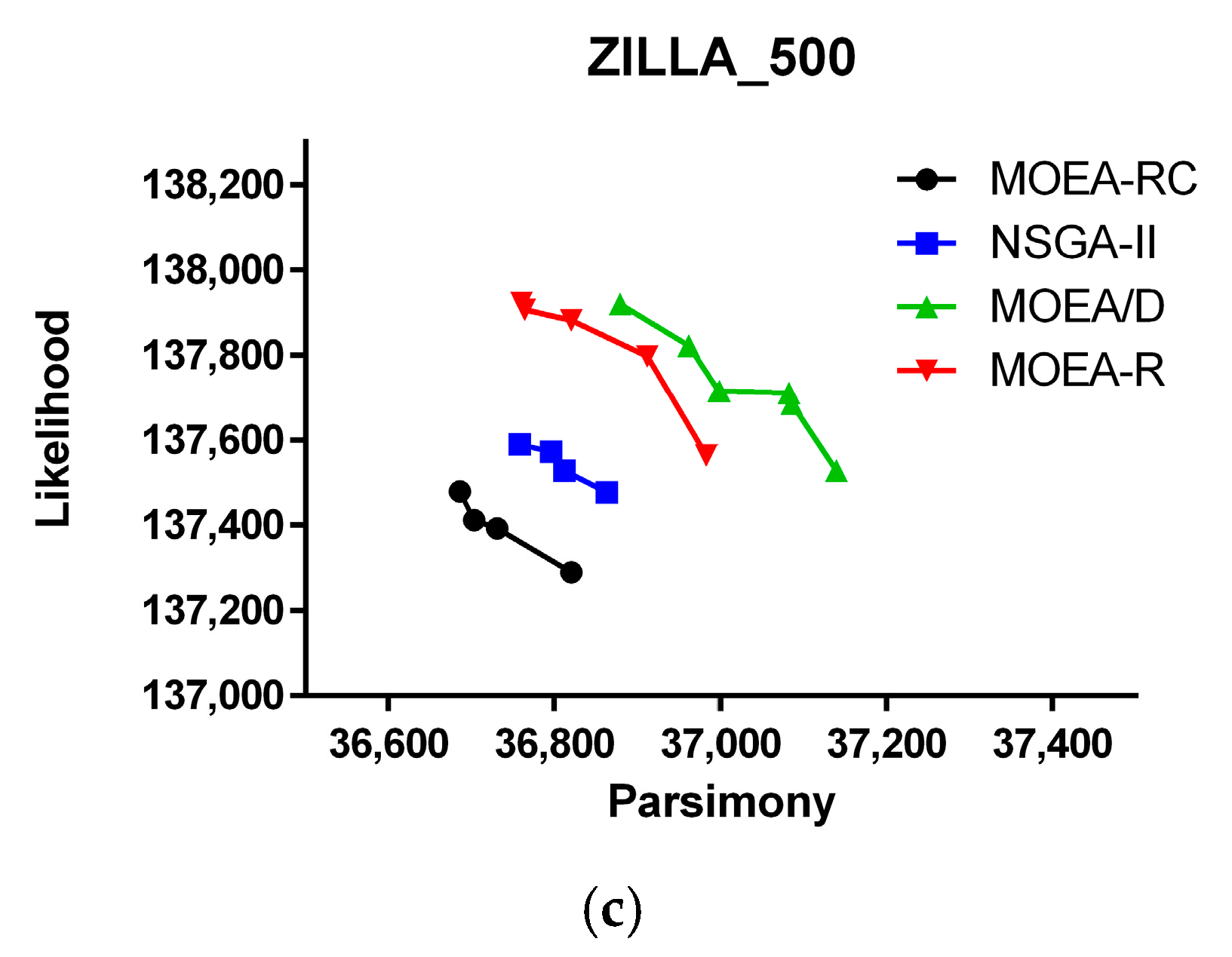

| Dataset | Number of Sequence | Nucleotides per Sequence | Data Description |
|---|---|---|---|
| rbcl_55 | 55 | 1314 | rbcl plastid gene [13] |
| mtDNA_186 | 186 | 16,608 | Human mitochondrial DNA [36] |
| ZILLA_500 | 500 | 759 | 500 rbcL sequences from plant plastids [37] |
| Parameter | Value |
|---|---|
| Population size | 100 |
| Generations | 100 |
| Selection method | Binary tournament [9] |
| Crossover method | Prune-Delete-Graft [13] |
| Crossover probability | 0.8 |
| Mutation method | NNI [35] |
| Mutation probability | 0.2 |
| Substitution model | GTR [7] |
| Algorithm | Metrics | Dataset | ||
|---|---|---|---|---|
| rbcl_55 | mtDNA_186 | ZILLA_500 | ||
| MOEA-RC | ML | −22,156.4 (+) | −39,927.6 (+) | −84,633.1 (+) |
| MP | 4977 (+) | 2460 (+) | 17,186 (+) | |
| Run time | 1059.80 | 66,215.13 | 13,016.22 | |
| MOEA/D | ML | −22,169.6 | −39,937.5 | −84,715.9 |
| MP | 4979 | 2461 | 17,194 | |
| Run time | 1302.64 | 65,620.20 | 13,082.54 | |
| NSGA-II | ML | −22,193.3 | −39,942.5 | −84,719.4 |
| MP | 4979 | 2463 | 17,192 | |
| Run time | 1287.07 | 66,010.94 | 12,812.62 | |
| PhyloMOEA | ML | −2200.1 | −39,938.2 | −84,704.6 |
| MP | 4982 | 2461 | 17,191 | |
| Run time | 2163.4 | >24 h | >24 h | |
| MOEA-R | ML | −22,244.7 | −39,984.6 | −84,714.6 |
| MP | 4979 | 2464 | 17,196 | |
| Run time | 1061.13 | 65,174.37 | 12,442.53 | |
| Metrics | Algorithm | Dataset | ||
|---|---|---|---|---|
| rbcl_55 | mtDNA_186 | ZILLA_500 | ||
| MP | MOEA-RC | 4977 (+) | 2460 | 17,186 |
| DNAPARS | 4984 | 2438 (+) | 17,055 (+) | |
| MEGA 7 | 4978 | 2457 | 17,077 | |
| ML | MOEA-RC | −22,156.4 (+) | −39,927.6 (+) | −84,633.1 (+) |
| Raxml | −22,188.2 | −40,921.0 | −95,577.0 | |
| MEGA 7 | −22,205.2 | −40,957.0 | −95,834.0 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, X.; Zhang, M.; Yuan, S.; Ge, S.; Liu, X.; Zeng, X.; Xia, N. Using MOEA with Redistribution and Consensus Branches to Infer Phylogenies. Int. J. Mol. Sci. 2018, 19, 62. https://doi.org/10.3390/ijms19010062
Min X, Zhang M, Yuan S, Ge S, Liu X, Zeng X, Xia N. Using MOEA with Redistribution and Consensus Branches to Infer Phylogenies. International Journal of Molecular Sciences. 2018; 19(1):62. https://doi.org/10.3390/ijms19010062
Chicago/Turabian StyleMin, Xiaoping, Mouzhao Zhang, Sisi Yuan, Shengxiang Ge, Xiangrong Liu, Xiangxiang Zeng, and Ningshao Xia. 2018. "Using MOEA with Redistribution and Consensus Branches to Infer Phylogenies" International Journal of Molecular Sciences 19, no. 1: 62. https://doi.org/10.3390/ijms19010062
APA StyleMin, X., Zhang, M., Yuan, S., Ge, S., Liu, X., Zeng, X., & Xia, N. (2018). Using MOEA with Redistribution and Consensus Branches to Infer Phylogenies. International Journal of Molecular Sciences, 19(1), 62. https://doi.org/10.3390/ijms19010062