Protein-Protein Interactions Prediction Using a Novel Local Conjoint Triad Descriptor of Amino Acid Sequences
Abstract
:1. Introduction
2. Results and Discussion
2.1. Evaluation Metrics
2.2. Experimental Setup
2.3. Results on PPIs of S. cerevisiae
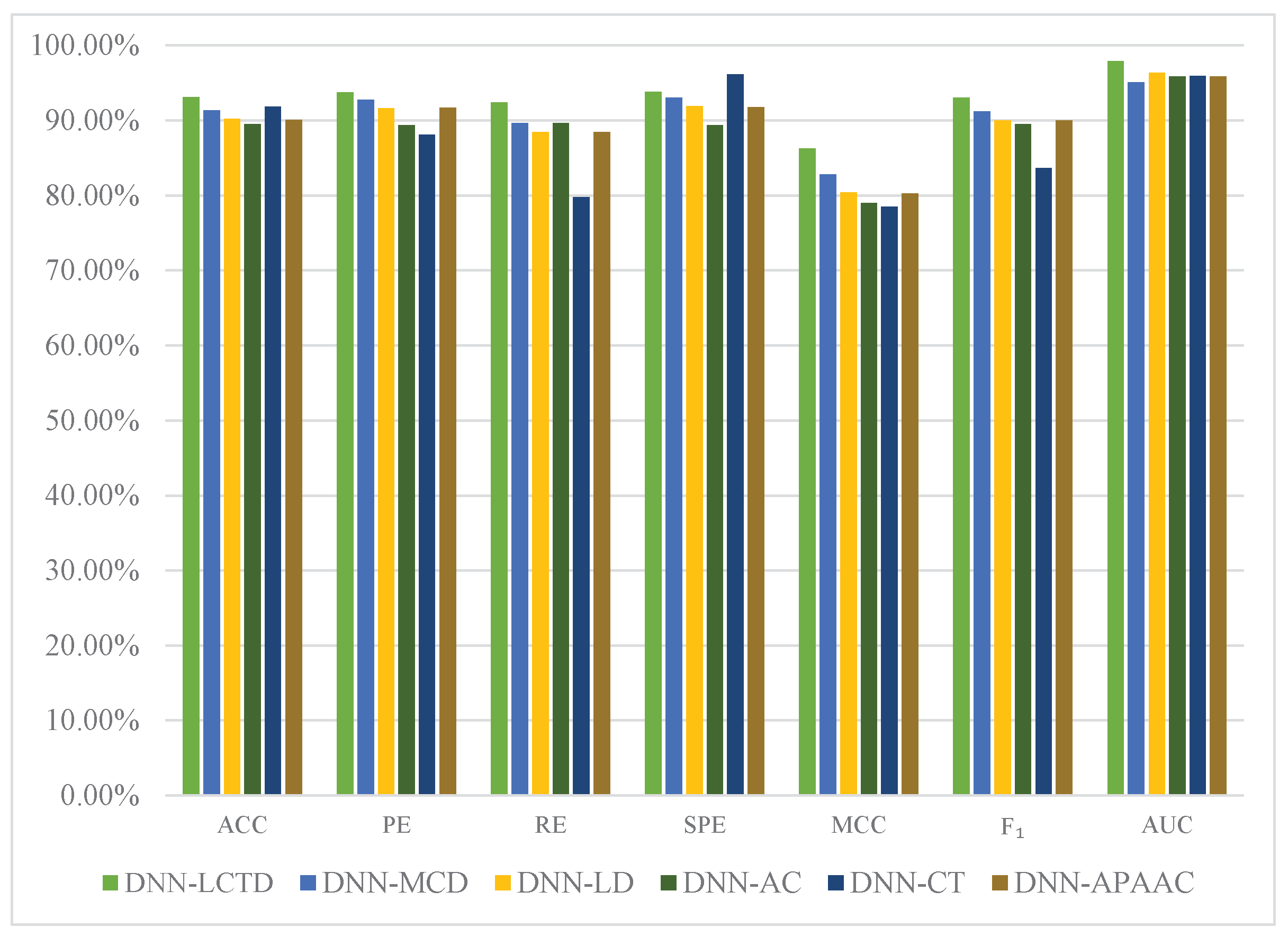
2.4. Comparison with Different Descriptors
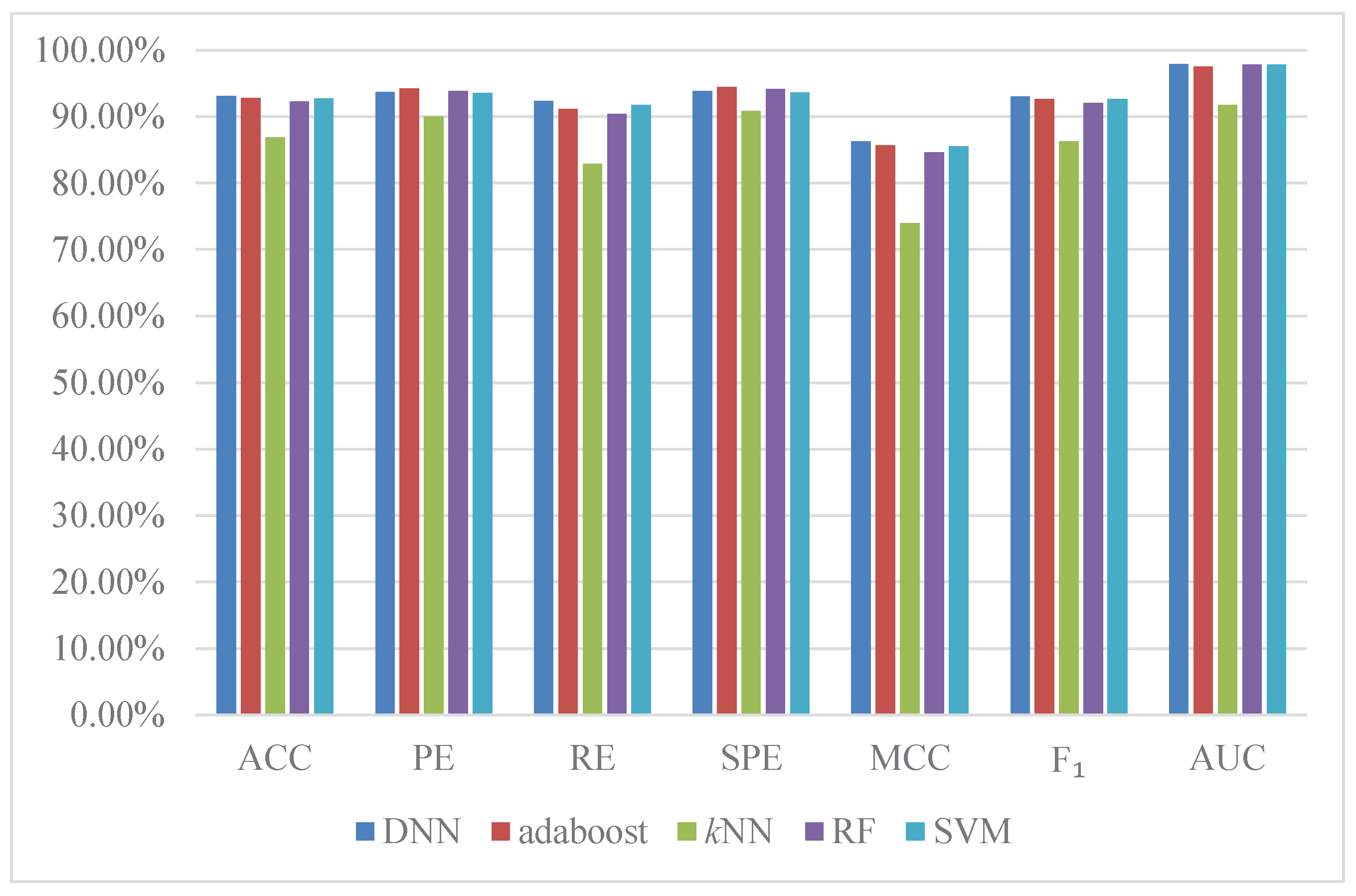
2.5. Comparison with Existing Methods
2.6. Results on Independent Datasets
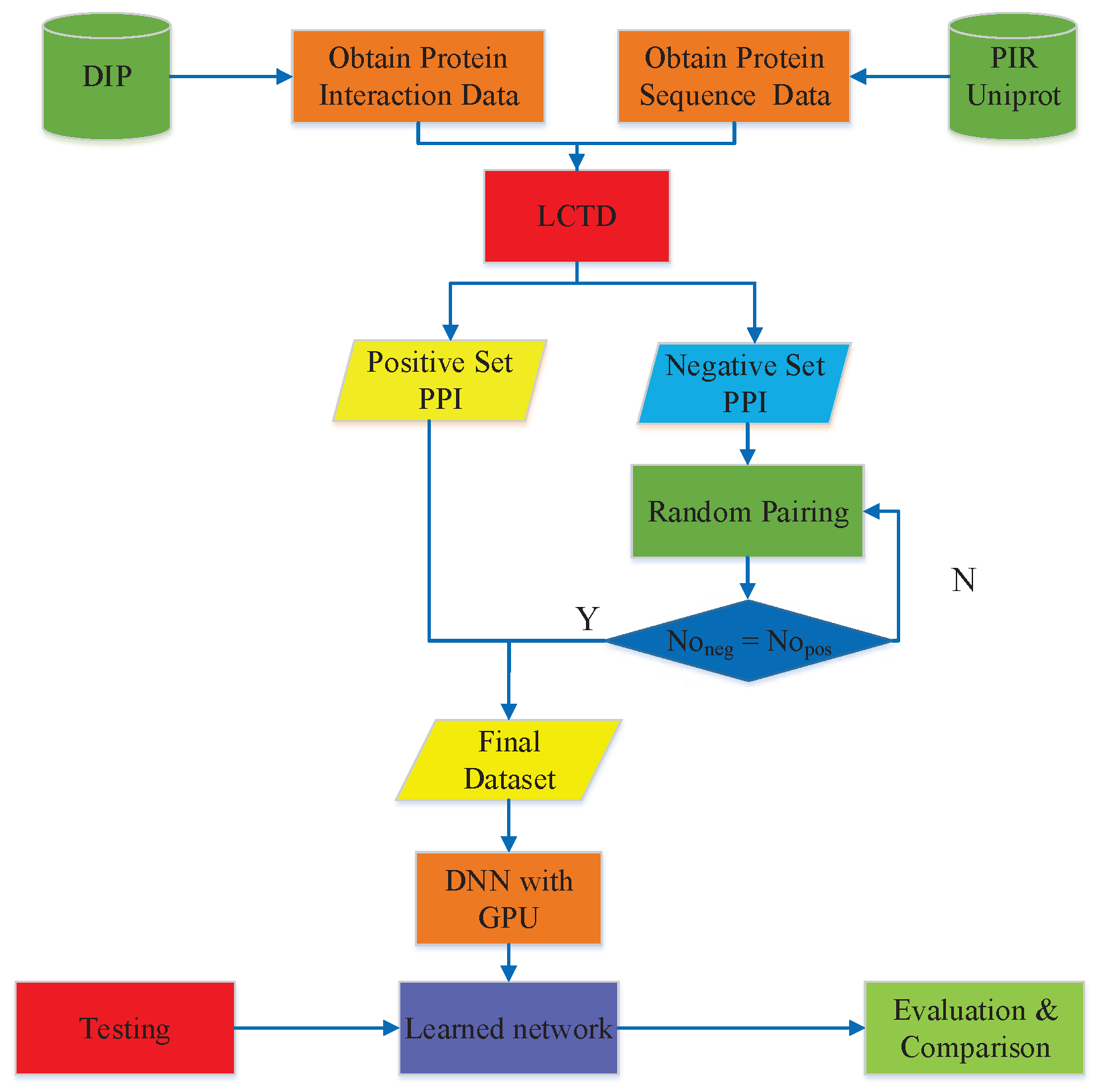
3. Materials and Methods
3.1. PPIs Datasets
3.2. Feature Vector Extraction
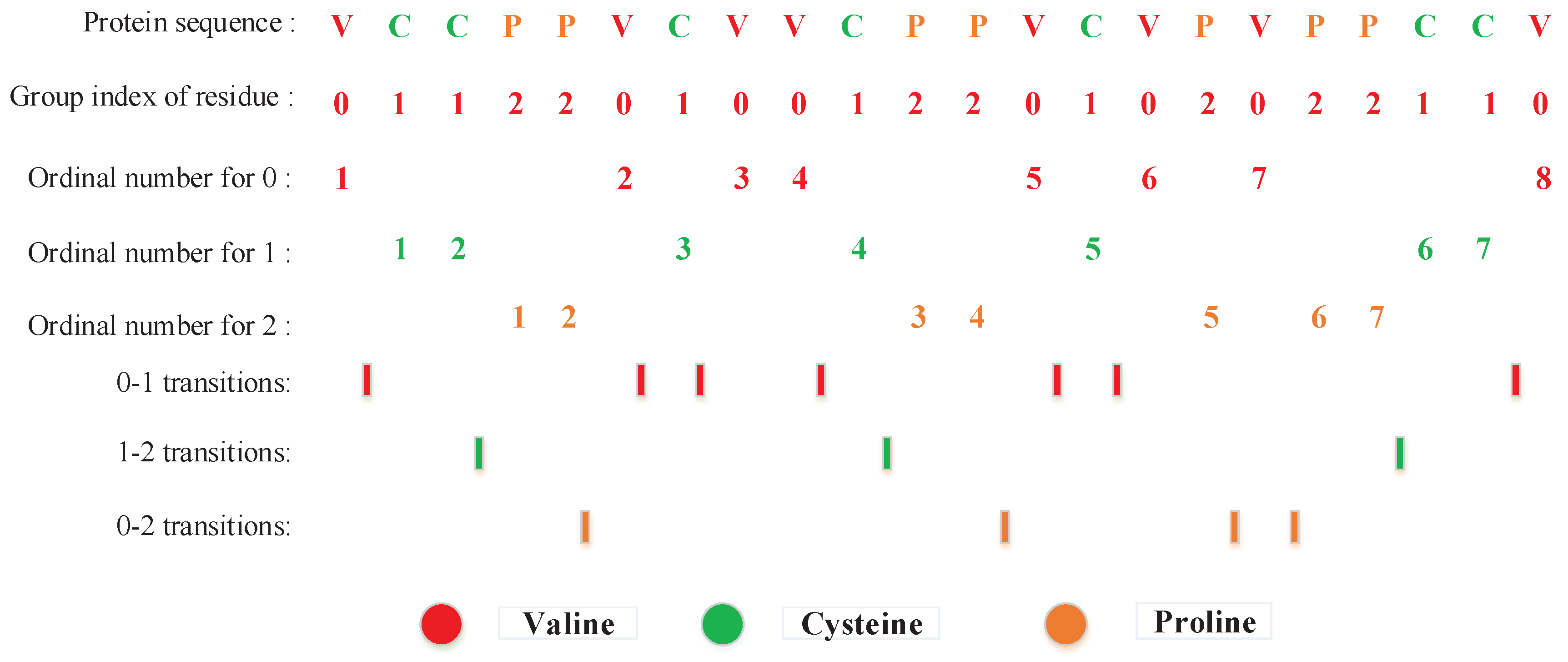
3.2.1. Conjoint Triad (CT) Method
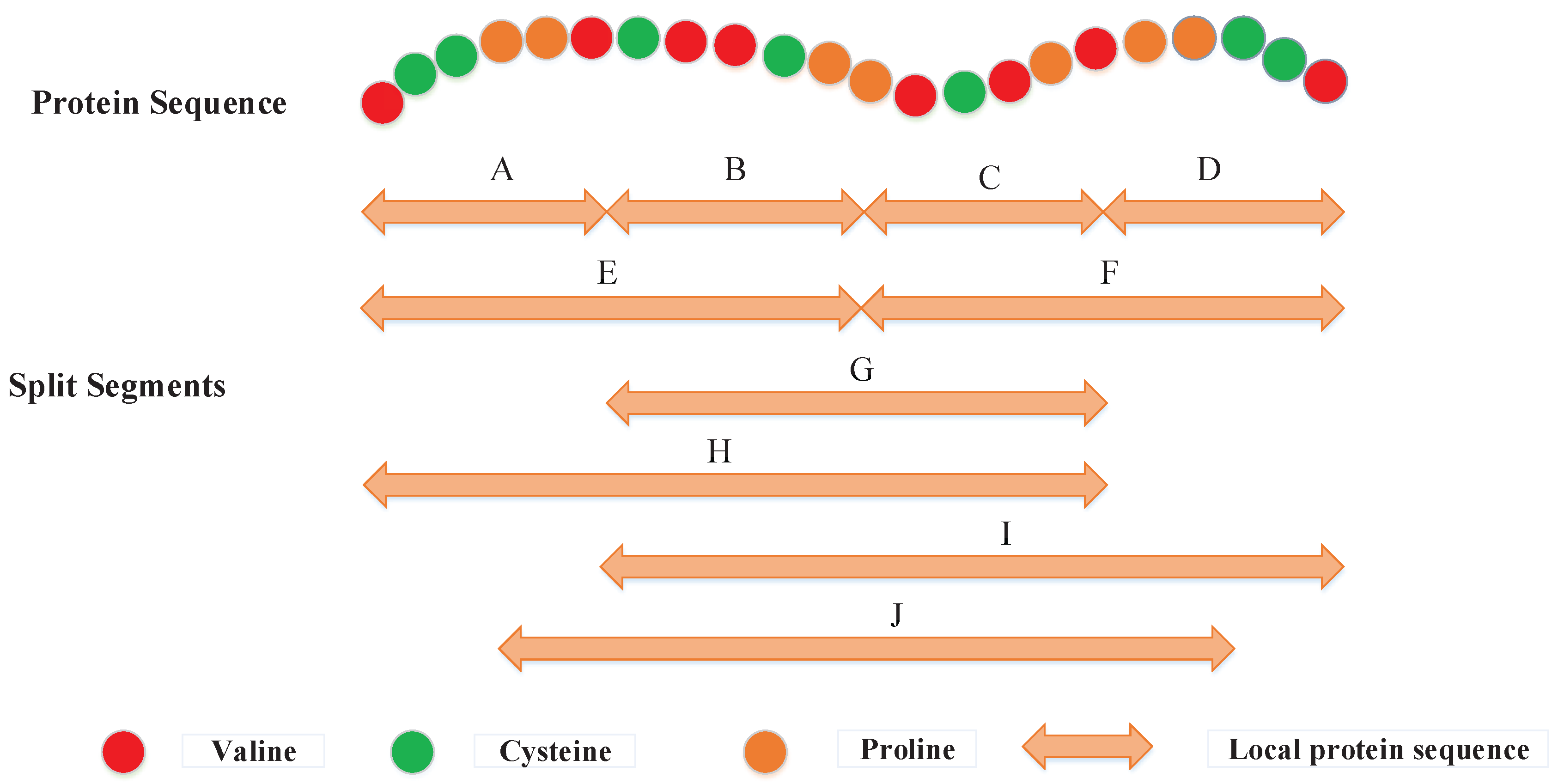
3.2.2. Local Descriptor (LD)
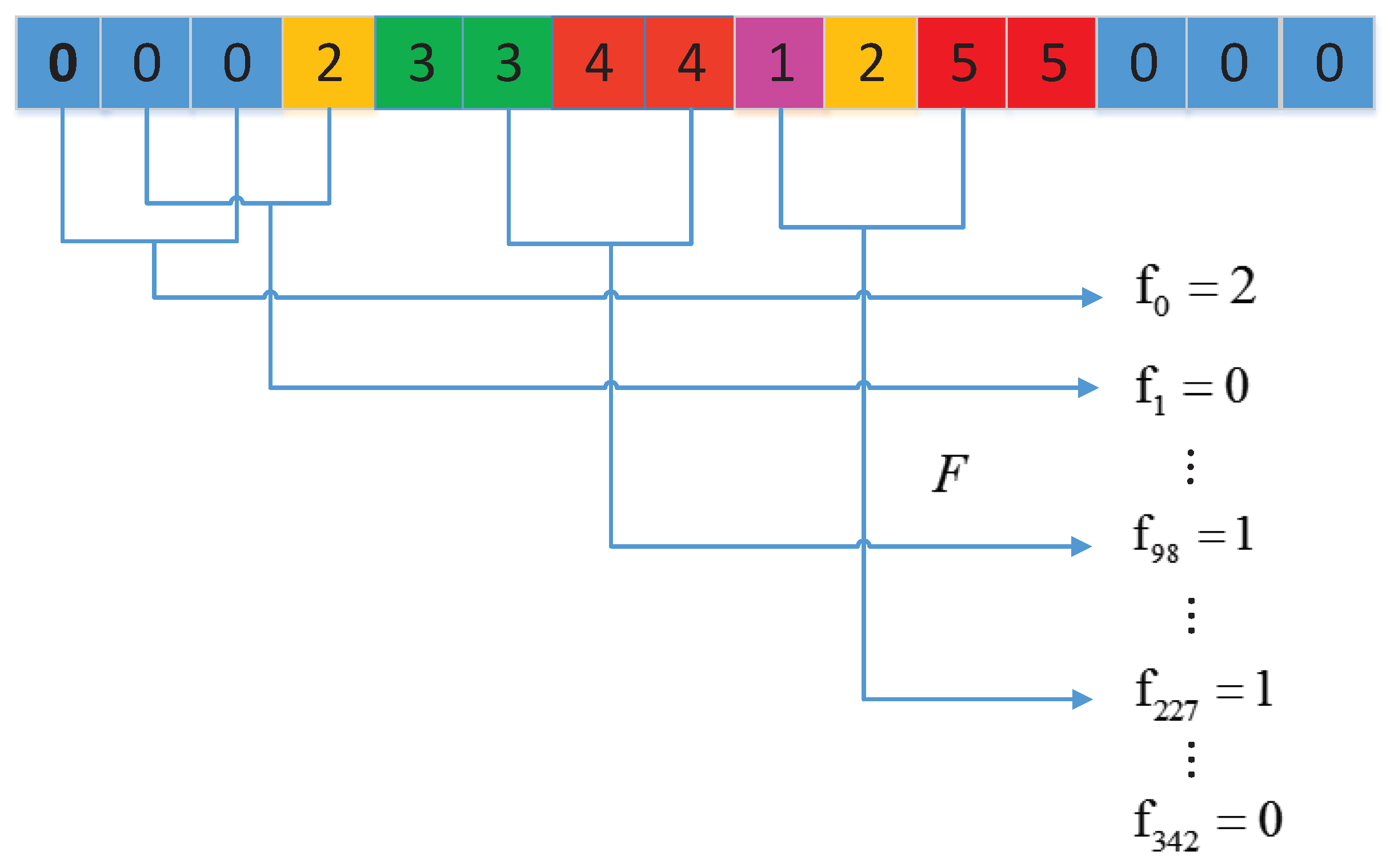
3.2.3. Local Conjoint Triad Descriptor (LCTD)
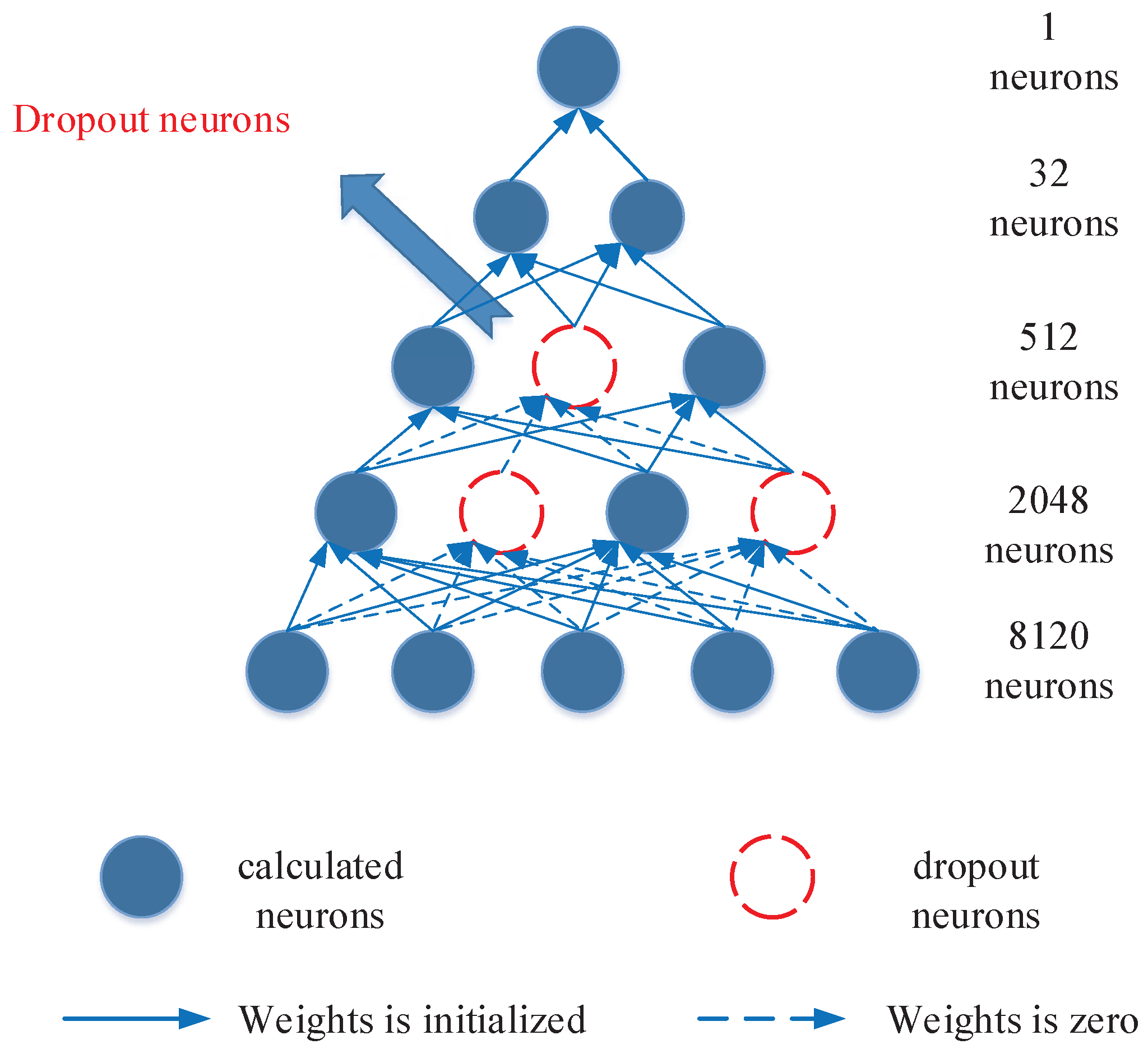
3.3. Deep Neural Network
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Williams, N.E. Immunoprecipitation procedures. Methods Cell Biol. 2000, 62, 449–453. [Google Scholar] [PubMed]
- Santoro, C.; Mermod, N.; Andrews, P.C.; Tjian, R. A family of human CCAAT-box-binding proteins active in transcription and DNA replication: Cloning and expression of multiple cDNAs. Nature 1988, 334, 218–224. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.M.; Wang, R.S.; Chen, L.; Aihara, K. Uncovering signal transduction networks from high-throughput data by integer linear programming. Nucleic Acids Res. 2008, 36, e48. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, J.; Fan, C.; Tang, Y.; Deng, L. KATZLGO: Large-scale Prediction of LncRNA Functions by Using the KATZ Measure Based on Multiple Networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, Z.; Chen, Z.; Deng, L. Integrating Multiple Heterogeneous Networks for Novel LncRNA-disease Association Inference. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Fu, G.; Wang, J.; Zhao, Y. NewGOA: Predicting new GO annotations of proteins by bi-random walks on a hybrid graph. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Alvarez, S.; Nusinow, D.A. Data on the identification of protein interactors with the Evening Complex and PCH1 in Arabidopsis using tandem affinity purification and mass spectrometry (TAP–MS). Data Brief 2016, 8, 56–60. [Google Scholar] [CrossRef] [PubMed]
- Mehla, J.; Caufield, J.H.; Uetz, P. Mapping protein-protein interactions using yeast two-hybrid assays. Cold Spring Harb. Protoc. 2015, 2015, 442–452. [Google Scholar] [CrossRef] [PubMed]
- Gavin, A.C.; Bösche, M.; Krause, R.; Grandi, P.; Marzioch, M.; Bauer, A.; Schultz, J.; Rick, J.M.; Michon, A.M.; Cruciat, C.M.; et al. Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature 2002, 415, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Skrabanek, L.; Saini, H.K.; Bader, G.D.; Enright, A.J. Computational prediction of protein-protein interactions. Mol. Biotechnol. 2008, 38, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Deng, M.; Sun, F.; Chen, T. An integrated approach to the prediction of domain-domain interactions. BMC Bioinform. 2006, 7, 1–15. [Google Scholar]
- Enright, A.J.; Iliopoulos, I.; Kyrpides, N.C.; Ouzounis, C.A. Protein interaction maps for complete genomes based on gene fusion events. Nature 1999, 402, 86–90. [Google Scholar] [PubMed]
- Aloy, P.; Russell, R.B. Interrogating protein interaction networks through structural biology. Proc. Natl. Acad. Sci. USA 2002, 99, 5896–5901. [Google Scholar] [CrossRef] [PubMed]
- Aloy, P.; Russell, R.B. InterPreTS: Protein Inter action Pre diction through T ertiary S tructure. Bioinformatics 2003, 19, 161–162. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.W.; Tien, A.C.; Huang, W.S.; Lee, Y.C.G.; Peng, C.L.; Tseng, H.H.; Kao, C.Y.; Huang, C.Y.F. POINT: A database for the prediction of protein-protein interactions based on the orthologous interactome. Bioinformatics 2004, 20, 3273–3276. [Google Scholar] [CrossRef] [PubMed]
- Du, T. Predicting Protein-Protein Interactions, Interaction Sites and Residue-Residue Contact Matrices with Machine Learning Techniques; University of Delaware: Newark, DE, USA, 2015. [Google Scholar]
- Bock, J.R.; Gough, D.A. Predicting protein-protein interactions from primary structure. Bioinformatics 2001, 17, 455–460. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Zhang, J.; Luo, X.; Zhu, W.; Yu, K.; Chen, K.; Li, Y.; Jiang, H. Predicting protein-protein interactions based only on sequences information. Proc. Natl. Acad. Sci. USA 2007, 104, 4337–4341. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Yu, L.; Wen, Z.; Li, M. Using support vector machine combined with auto covariance to predict protein-protein interactions from protein sequences. Nucleic Acids Res. 2008, 36, 3025–3030. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Xia, J.F.; Gui, J. Prediction of protein-protein interactions from protein sequence using local descriptors. Protein Pept. Lett. 2010, 17, 1085–1090. [Google Scholar] [CrossRef] [PubMed]
- You, Z.H.; Zhu, L.; Zheng, C.H.; Yu, H.J.; Deng, S.P.; Ji, Z. Prediction of protein-protein interactions from amino acid sequences using a novel multi-scale continuous and discontinuous feature set. BMC Bioinform. 2014, 15, S9. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Sun, S.; Hu, C.; Yao, Y.; Yan, Y.; Zhang, Y. DeepPPI: Boosting Prediction of Protein-Protein Interactions with Deep Neural Networks. J. Chem. Inform. Model. 2017, 57, 1499–1510. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; You, Z.; Li, X.; Chen, X.; Jiang, T.; Zhang, J. PCVMZM: Using the Probabilistic Classification Vector Machines Model Combined with a Zernike Moments Descriptor to Predict Protein-Protein Interactions from Protein Sequences. Int. J. Mol. Sci. 2017, 18, 1029. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Li, D.; Wu, Y.; Zou, Q.; Liu, X. An empirical study of features fusion techniques for protein-protein interaction prediction. Curr. Bioinform. 2016, 27, 899–901. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes. Bioinformatics 2004, 21, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef] [PubMed]
- Asgari, E.; Mofrad, M.R.K. Continuous Distributed Representation of Biological Sequences for Deep Proteomics and Genomics. PLoS ONE 2015, 10, e0141287. [Google Scholar] [CrossRef] [PubMed]
- Browne, M.W. Cross-validation methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef] [PubMed]
- Bewick, V.; Cheek, L.; Ball, J. Statistics review 13: Receiver operating characteristic curves. Crit. Care 2004, 8, 508–512. [Google Scholar] [CrossRef] [PubMed]
- Akobeng, A.K. Understanding diagnostic tests 3: Receiver operating characteristic curves. Acta Paediatr. 2007, 96, 644–647. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. In Neural Networks: Tricks of The Trade; Springer: Berlin, Germany, 2012; pp. 437–478. [Google Scholar]
- Zhou, Y.Z.; Gao, Y.; Zheng, Y.Y. Prediction of protein-protein interactions using local description of amino acid sequence. Adv. Comput. Sci. Edu. Appl. 2011, 202, 254–262. [Google Scholar]
- Ben-Hur, A.; Noble, W.S. Choosing negative examples for the prediction of protein-protein interactions. BMC Bioinform. 2006, 7, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Collins, M.; Schapire, R.E.; Singer, Y. Logistic Regression, AdaBoost and Bregman Distances. Mach. Learn. 2002, 48, 253–285. [Google Scholar] [CrossRef]
- Xenarios, I.; Rice, D.W.; Salwinski, L.; Baron, M.K.; Marcotte, E.M.; Eisenberg, D. DIP: The database of interacting proteins. Nucleic Acids Res. 2000, 28, 289–291. [Google Scholar] [CrossRef] [PubMed]
- Shin, C.J.; Wong, S.; Davis, M.J.; Ragan, M.A. Protein-protein interaction as a predictor of subcellular location. BMC Syst. Biol. 2009, 3, 28. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Ding, Y.; Su, R.; Tang, J.; Zou, Q. Prediction of human protein subcellular localization using deep learning. J. Parallel Distrib. Comput. 2017. [Google Scholar] [CrossRef]
- Davies, M.N.; Secker, A.; Freitas, A.A.; Clark, E.; Timmis, J.; Flower, D.R. Optimizing amino acid groupings for GPCR classification. Bioinformatics 2008, 24, 1980–1986. [Google Scholar] [CrossRef] [PubMed]
- Tong, J.C.; Tammi, M.T. Prediction of protein allergenicity using local description of amino acid sequence. Front. Biosci. 2007, 13, 6072–6078. [Google Scholar] [CrossRef]
- Dubchak, I.; Muchnik, I.; Holbrook, S.R.; Kim, S.H. Prediction of protein folding class using global description of amino acid sequence. Proc. Natl. Acad. Sci. USA 1995, 92, 8700–8704. [Google Scholar] [CrossRef] [PubMed]
- Min, S.; Lee, B.; Yoon, S. Deep learning in bioinformatics. Brief. Bioinform. 2016, 18, 851–869. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Cotter, A.; Shamir, O.; Srebro, N.; Sridharan, K. Better mini-batch algorithms via accelerated gradient methods. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; pp. 1647–1655. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. Comput. Sci. 2015, 14, 38–39. [Google Scholar]
| Name | Range | Recommendation |
|---|---|---|
| Learning rate | ||
| Batch size | ||
| Weight initialization | uniform, normal, lecun_uniform, glorot_normal, glorot_uniform | glorot_normal |
| Per-parameter adaptive learning rate | SGD, RMSprop, Adagrad, Adadelta, Adam, Adamax, Nadam | Adam |
| Activation function | relu, tanh, sigmoid, softmax, softplus | relu, sigmoid |
| Dropout rate | 0.5, 0.6, 0.7 | 0.6 |
| Depth | 2, 3, 4, 5, 6, 7, 8, 9 | 3 |
| Width | 16, 32, 64, 128, 256, 1024, 2048, 4096 | 2048, 512, 32 |
| GPU | Yes, No | Yes |
| Method | Name | Parameters | |||
|---|---|---|---|---|---|
| Guo’s work [19] | SVM + AC | C | kernel | ||
| 32768.0 | 0.074325444687670064 | poly | |||
| Yang’s work [20] | kNN + LD | n_neighbors | weights | algorithm | p |
| 3 | distance | auto | 1 | ||
| Zhou’s work [33] | SVM + LD | C | kernel | ||
| 3.1748021 | 0.07432544468767006 | rbf | |||
| You’s work [21] | RF + MCD | n_estimators | max_features | criterion | bootstrap |
| 5000 | auto | gini | True | ||
| Method | ACC | PE | RE | SPE | MCC | AUC | ||
|---|---|---|---|---|---|---|---|---|
| DNN-LCTD | fold 1 | |||||||
| fold 2 | ||||||||
| fold 3 | ||||||||
| fold 4 | ||||||||
| fold 5 | ||||||||
| Average | ||||||||
| Du’s work [22] | DNN + APAAC | 94.21% ± 0.45% | ||||||
| You’s work [21] | RF + MCD | |||||||
| Zhou’s work [33] | SVM + LD | |||||||
| Yang’s work [20] | kNN + LD | |||||||
| Guo’s work [19] | SVM + AC |
| ACC | PE | RE | SPE | MCC | AUC | ||
|---|---|---|---|---|---|---|---|
| fold 1 | 82.53% | 92.24% | 71.01% | 94.04% | 66.85% | 80.24% | 92.47% |
| fold 2 | 82.89% | 93.57% | 70.71% | 95.12% | 67.86% | 80.55% | 93.52% |
| fold 3 | 82.56% | 93.25% | 70.30% | 94.89% | 67.22% | 80.16% | 92.52% |
| fold 4 | 82.09% | 94.02% | 68.95% | 95.52% | 66.74% | 79.56% | 93.08% |
| fold 5 | 82.24% | 91.74% | 70.26% | 93.86% | 66.14% | 79.58% | 92.85% |
| Average |
| ACC (%) | PE (%) | RE (%) | SPE (%) | MCC (%) | (%) | AUC (%) | |
|---|---|---|---|---|---|---|---|
| DNN-LCTD | |||||||
| DNN-MCD | |||||||
| DNN-LD | |||||||
| DNN-AC | |||||||
| DNN-CT | |||||||
| DNN-APAAC |
| Method | DNN-LCTD (GPU) | DNN-LCTD (CPU) | SVM | kNN | Random Forest | Adaboost |
|---|---|---|---|---|---|---|
| Times (s) | 718 | 2680 | 106,347 | 2814 | 6906 | 70,026 |
| Species | Test Pairs | ACC | ||
|---|---|---|---|---|
| DNN-LCTD | Du’s Work [22] | Zhou’s Work [33] | ||
| C. elegans | 4013 | 93.17% | 94.84% | 75.73% |
| E. coli | 6984 | 94.62% | 92.19% | 71.24% |
| H. sapiens | 1412 | 94.18% | 93.77% | 76.27% |
| H. pylori | 1420 | 87.38% | 93.66% | 75.87% |
| M. musculus | 313 | 92.65% | 91.37% | 76.68% |
| Group 0 | Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 |
|---|---|---|---|---|---|---|
| A, G, V | C | F, I, L, P | M, S, T, Y | H, N, Q, W | K, R | D, E |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, L.; Jia, L.; Ren, Y.; Yu, G. Protein-Protein Interactions Prediction Using a Novel Local Conjoint Triad Descriptor of Amino Acid Sequences. Int. J. Mol. Sci. 2017, 18, 2373. https://doi.org/10.3390/ijms18112373
Wang J, Zhang L, Jia L, Ren Y, Yu G. Protein-Protein Interactions Prediction Using a Novel Local Conjoint Triad Descriptor of Amino Acid Sequences. International Journal of Molecular Sciences. 2017; 18(11):2373. https://doi.org/10.3390/ijms18112373
Chicago/Turabian StyleWang, Jun, Long Zhang, Lianyin Jia, Yazhou Ren, and Guoxian Yu. 2017. "Protein-Protein Interactions Prediction Using a Novel Local Conjoint Triad Descriptor of Amino Acid Sequences" International Journal of Molecular Sciences 18, no. 11: 2373. https://doi.org/10.3390/ijms18112373
APA StyleWang, J., Zhang, L., Jia, L., Ren, Y., & Yu, G. (2017). Protein-Protein Interactions Prediction Using a Novel Local Conjoint Triad Descriptor of Amino Acid Sequences. International Journal of Molecular Sciences, 18(11), 2373. https://doi.org/10.3390/ijms18112373





