The Compositional HJ-Biplot—A New Approach to Identifying the Links among Bioactive Compounds of Tomatoes
Abstract
:1. Introduction
2. Results and Discussion
2.1. General Description of the Tomato Samples
2.2. Differences in Bioactive Compounds by Cultivar and Cultivation System
3. Materials and Methods
3.1. Tomato Sampling
3.2. Sample Preparation
3.3. Analytical Methods
3.4. Statistical Methods
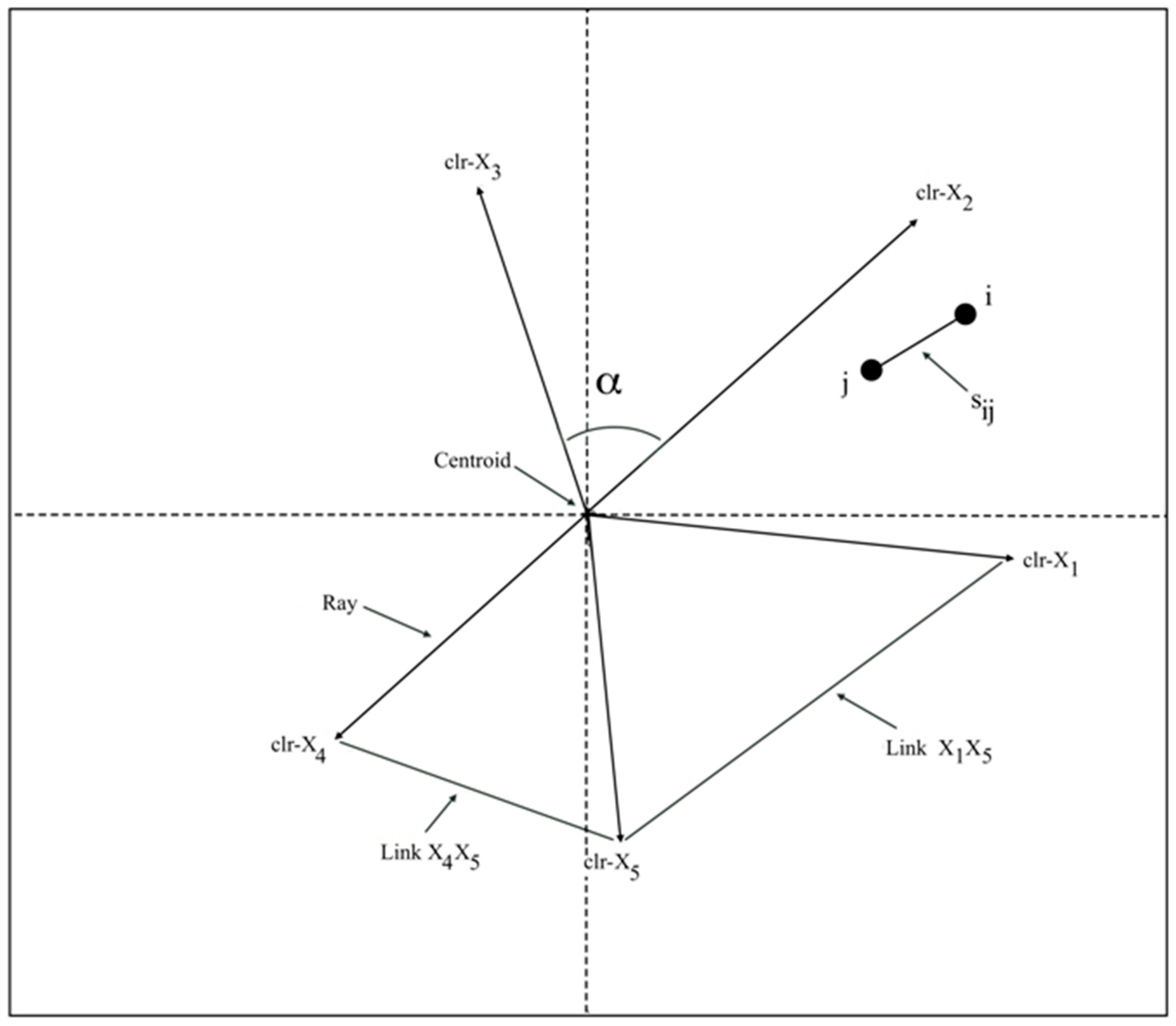
- The similarity (Sij) between two samples or individuals is taken to be an inverse function of their distance, in such a way that closer samples are more similar.
- The centroid represents the center-of-gravity formed by the geometric mean of the compositional parts used in the clr-transformation.
- ray provides information on the variance of the corresponding log-ratio with respect to the geometric mean (gm):
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hernández Suárez, M.; Rodríguez Rodríguez, E.M.; Díaz Romero, C. Chemical composition and nutritional value of tomatoes. In Tomatoes: Cultivation, Varieties and Nutrition; Higashide, T., Ed.; Nova Science Publishers: New York, NY, USA, 2013; pp. 191–222. [Google Scholar]
- ISTAC. Instituto Canario de Estadística. Available online: http://www.gobiernodecanarias.org/istac (accessed on 13 January 2016).
- Aitchison, J. The Statistical Analysis of Compositional Data; Chapman and Hall: London, UK, 1986; p. 416. [Google Scholar]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modeling and Analysis of Compositional Data; John Wiley and Sons, Ltd.: Chichester, UK, 2015; p. 272. [Google Scholar]
- Aitchison, J.; Greenacre, M. Biplots for compositional data. Appl. Stat. 2002, 51, 375–382. [Google Scholar] [CrossRef]
- Gabriel, K.R. The biplot graphic display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Guil, J.L.; Torija, M.E.; Giménez, J.J.; Rodríguez-García, I.; Giménez, A. Oxalic acid and calcium determination in wild edible plants. J. Agric. Food Chem. 1996, 44, 1821–1823. [Google Scholar] [CrossRef]
- Montañés, L.; Heras, L.; Abadía, J.; Sanz, M. Plant analysis interpretation based on a new index: Deviation from optimum percentage (DOP). J. Plant Nutr. 1993, 16, 1289–1308. [Google Scholar] [CrossRef]
- Galindo-Villardón, M. Una alternativa de representación simultánea: HJ-Biplot. Qüestiió 1986, 10, 13–23. [Google Scholar]
- Frutos, E.; Galindo, P.; Leiva, V. An interactive biplot implementation in R for modeling genotype-by-environment interaction. Stoch. Environ. Res. Risk Assess. 2014, 28, 1629–1641. [Google Scholar] [CrossRef]
- Hernández, M.; Espinosa, F.; Galindo, P. Tomato fruit quality as influenced by interactions in agricultural techniques and harvest period. J. Plant Nutr. Soil Sci. 2014, 177, 443–448. [Google Scholar] [CrossRef]
- Valdivia-Mares, L.E.; Rodríguez, F.A.; Sánchez, J.J.; Vargas-Ponce, O. Phenology, agronomic and nutritional potential of three wild husk tomato species (Physalis, Solanaceae) from Mexico. Sci. Hortic. (Amsterdam) 2016, 200, 83–94. [Google Scholar] [CrossRef]
- Figàs, M.R.; Prohens, J.; Raigón, M.D.; Fita, A.; García-Martínez, M.D.; Casanova, C.; Borràs, D.; Plazas, M.; Andújar, I.; Soler, S. Characterization of composition traits related to organoleptic and functional quality for the differentiation, selection and enhancement of local varieties of tomato from different cultivar groups. Food Chem. 2015, 187, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Lahoz, I.; Pérez-de-Castro, A.; Valcárcel, M.; Macua, J.I.; Beltrán, J.; Roselló, S.; Cebolla-Cornejo, J. Effect of water deficit on the agronomical performance and quality of processing tomato. Sci. Hortic. 2016, 200, 55–65. [Google Scholar] [CrossRef]
- Hernández Suárez, M.; Rodríguez Rodríguez, E.M.; Díaz Romero, C. Mineral and trace element concentrations in cultivars of tomatoes. Food Chem. 2007, 104, 489–499. [Google Scholar] [CrossRef]
- Erba, D.; Casiraghi, M.C.; Ribas-Agustí, A.; Cáceres, R.; Marfà, O.; Castellari, M. Nutritional value of tomatoes (Solanum lycopersicum L.) grown in greenhouse by different agronomic techniques. J. Food Compos. Anal. 2013, 31, 245–251. [Google Scholar] [CrossRef]
- Bramley, P.M. Is lycopene beneficial to human health? Phytochemistry 2000, 54, 233–236. [Google Scholar] [CrossRef]
- Willcox, J.K.; Catignani, G.L.; Lazarus, S. Tomatoes and cardiovascular health. Crit. Rev. Food Sci. Nutr. 2003, 43, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Mitjavila, S. Sustanciasnaturalesnocivas en los alimentos. In Toxicología y Seguridad de los Alimentos; Derache, J., Ed.; Omega: Barcelona, Spain, 1990. [Google Scholar]
- Danesi, F.; Bordoni, A. Effect of home freezing and Italian style of cooking on antioxidant activity of edible vegetables. J. Food Sci. 2008, 73, H109–H112. [Google Scholar] [CrossRef] [PubMed]
- Omoni, A.O.; Aluko, R.E. The anti-carcinogenic and anti-atherogenic effects of lycopene: A review. Trends Food Sci. Technol. 2005, 16, 344–350. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barceló-Vidal, C. Isometric logratio transformations for compositional data analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Fanasca, S.; Colla, G.; Maiani, G.; Venneria, E.; Rouphael, Y.; Azzini, E.; Saccardo, F. Changes in antioxidant content of tomato fruits in response to cultivar and nutrient solution composition. J. Agric. Food Chem. 2006, 54, 4319–4325. [Google Scholar] [CrossRef] [PubMed]
- Flueret, A.; Macheix, J.J. Quinyl esters and glucose derivatives of hydroxycinnamics during growth and ripening of tomato fruit. Phytochemistry 1981, 20, 667–671. [Google Scholar] [CrossRef]
- Clé, C.; Hill, L.M.; Niggeweg, R.; Martin, C.R.; Guisez, Y.; Prinsen, E.; Jansen, M.A. Modulation of chlorogenic acid biosynthesis in Solanumlycopersicum; consequences for phenolic accumulation and UV-tolerance. Phytochemistry 2008, 69, 2149–2156. [Google Scholar] [CrossRef] [PubMed]
- AOAC (Association Official of Analytical Chemists). Official Methods of Analysis of AOAC International, 18th ed.; Horwitz, W., Latimer, G.W., Jr., Eds.; AOAC International: Gaithersburg, MD, USA, 2006. [Google Scholar]
- Kujala, T.S.; Loponen, J.M.; Klika, K.D.; Pihlaja, K. Phenolic and betacyanins in red beetroot (Beta vulgaris) root: Distribution and effect of cold storage on the content of total phenolic and three individual compounds. J. Agric. Food Chem. 2000, 48, 5338–5342. [Google Scholar] [CrossRef] [PubMed]
- Fish, W.; Perkins-Veazie, P.; Collins, J. A quantitative assay for lycopene that utilizes reduced volumes of organic solvents. J. Food Comp. Anal. 2002, 15, 309–317. [Google Scholar] [CrossRef]
- Rodríguez Galdón, B.; Tascón Rodríguez, C.; Rodríguez Rodríguez, E.M.; Díaz Romero, C. Fructans and major compounds in onion cultivars (Allium cepa). J. Food Compos. Anal. 2009, 22, 25–32. [Google Scholar] [CrossRef]
- Hernández Suárez, M.; Rodríguez Rodríguez, E.; Díaz Romero, C. Analysis of organic acid content in cultivars of tomato harvested in Tenerife. Eur. Food Res. Technol. 2008, 226, 423–435. [Google Scholar] [CrossRef]
- Hernández, M.; Rodríguez, E.; Díaz, C. Free hydroxycinnamic acids, lycopene, and color parameters in tomato cultivars. J. Agric. Food Chem. 2007, 55, 8604–8615. [Google Scholar]
- Comas-Cufí, M.; Thió-Henestrosa, S. CoDaPack 2.0. A stand-alone, multi-platform compositional software. In Proceedings of the 4th International Workshop on Compositional Data Analysis, CoDaWork'11, Sant Feliu de Guíxols, Spain, 9–13 May 2011.
- Vicente Villardón, J.L. MULTBIPLOT: A Package for Multivariate Analysis Using Biplots; Departamento de Estadística, Universidad de Salamanca: Salamanca, Spain, 2015. [Google Scholar]
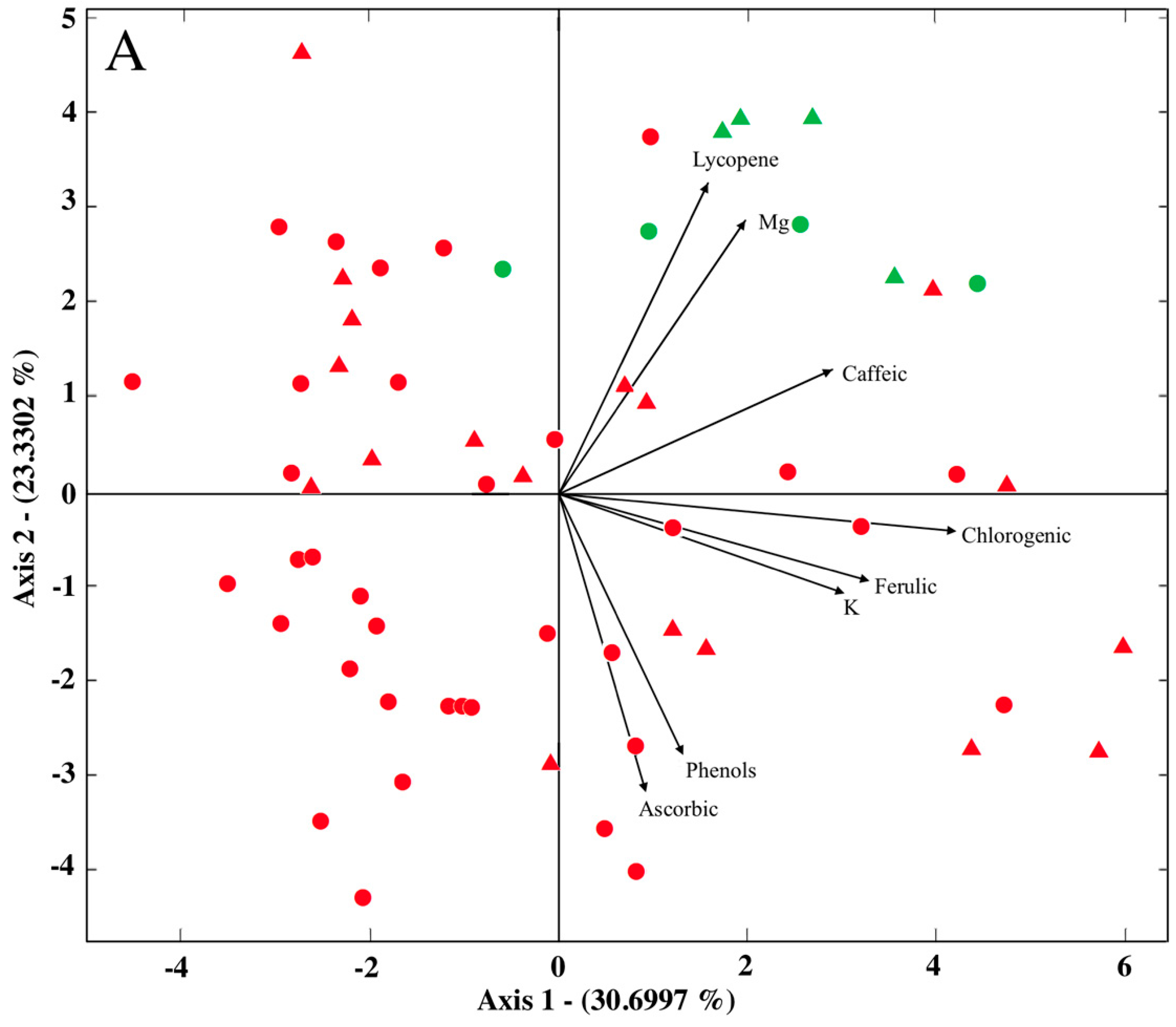
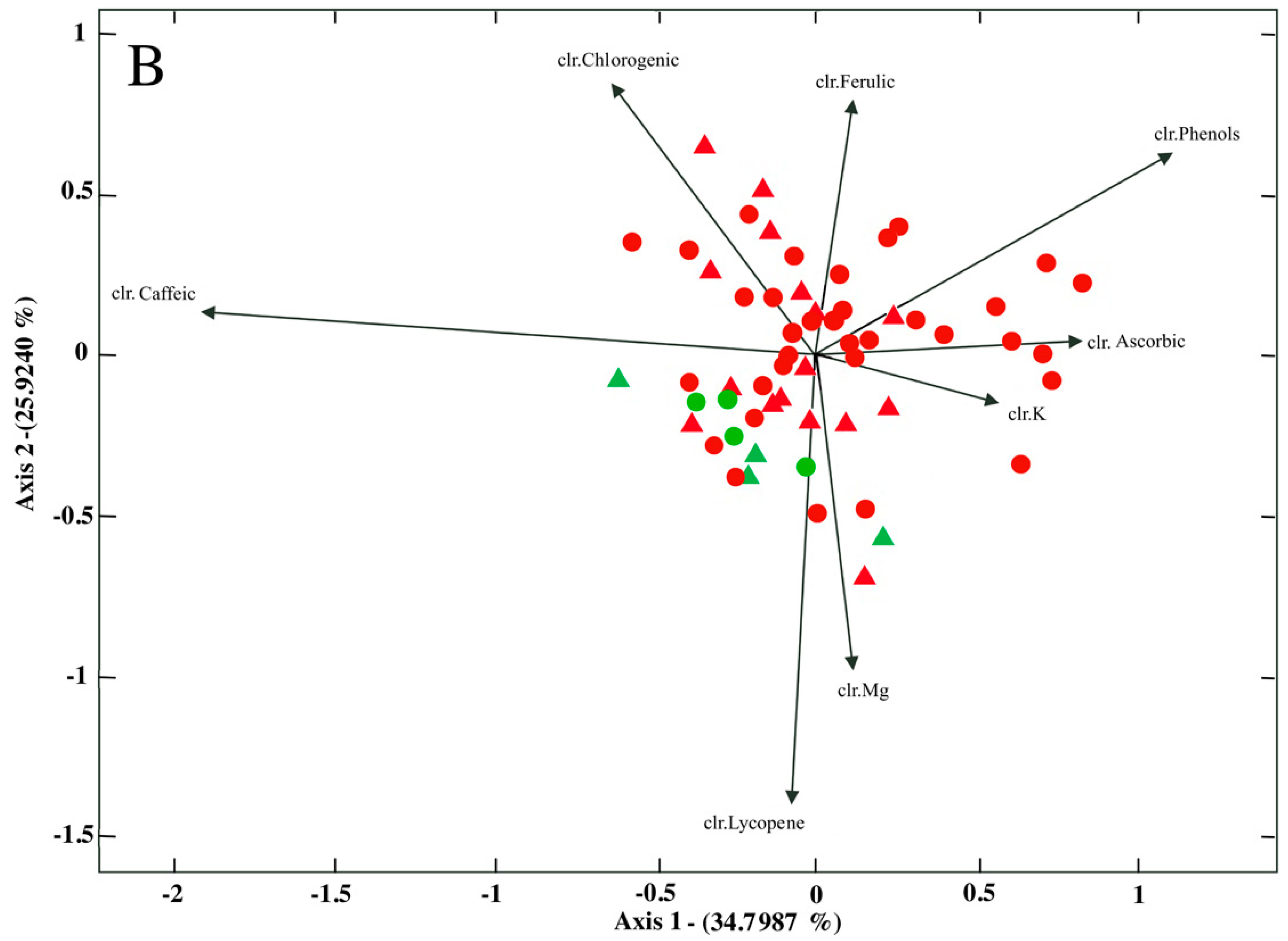
| Compound | Cultivar | Cultivation System | p-Value | |
|---|---|---|---|---|
| Soil | No-Soil | |||
| Proximate Composition (% FW) | ||||
| Moisture | Dunkan | 93.78 ± 0.55 | 94.11 ± 0.51 | 0.061 1 |
| Mariana | 94.28 ± 0.47 | 93.88 ± 0.58 | ||
| p-Value | 0.129 2 | |||
| Ash | Dunkan | 0.75 ± 0.09 | 0.73 ± 0.04 | 0.159 |
| Mariana | 0.69 ± 0.07 | 0.74 ± 0.07 | ||
| p-Value | 0.952 | |||
| Protein | Dunkan | 0.68 ± 0.05 | 0.75 ± 0.13 | 0.049 |
| Mariana | 0.70 ± 0.07 | 0.77 ± 0.07 | ||
| p-Value | 0.015 | |||
| Fructose | Dunkan | 1.41 ± 0.09 | 1.38 ± 0.24 | 0.765 |
| Mariana | 1.24 ± 0.22 | 1.39 ± 0.17 | ||
| p-Value | 0.145 | |||
| Glucose | Dunkan | 1.40 ± 0.09 | 1.37 ± 0.24 | 0.798 |
| Mariana | 1.23 ± 0.22 | 1.38 ± 0.17 | ||
| p-Value | 0.137 | |||
| Mineral Elements (mg/kg FW) | ||||
| P | Dunkan | 255 ± 26.0 | 280 ± 36.3 | 0.455 |
| Mariana | 242 ± 20.8 | 276 ± 32.3 | ||
| p-Value | 0.014 | |||
| Na | Dunkan | 42.29 ± 5.31 | 46.23 ± 2.67 | 0.405 |
| Mariana | 40.66 ± 9.63 | 53.00 ± 12.7 | ||
| p-Value | 0.001 | |||
| K | Dunkan | 2654 ± 340 | 2844 ± 332 | 0.165 |
| Mariana | 2570 ± 275 | 2859 ± 214 | ||
| p-Value | 0.093 | |||
| Ca | Dunkan | 88.76 ± 8.53 | 83.00 ± 5.74 | 0.295 |
| Mariana | 85.65 ± 14.4 | 82.00 ± 7.67 | ||
| p-Value | 0.046 | |||
| Mg | Dunkan | 159 ± 13 | 167 ± 18 | 3.05 × 10−4 |
| Mariana | 115 ± 16 | 133 ± 13 | ||
| p-Value | 0.009 | |||
| Fe | Dunkan | 3.36 ± 0.65 | 3.14 ± 0.48 | 0.109 |
| Mariana | 2.66 ± 0.32 | 2.98 ± 0.48 | ||
| p-Value | 0.176 | |||
| Cu | Dunkan | 0.35 ± 0.18 | 0.47 ± 0.20 | 0.623 |
| Mariana | 0.32 ± 0.08 | 0.33 ± 0.04 | ||
| p-Value | 0.260 | |||
| Zn | Dunkan | 0.80 ± 0.18 | 0.99 ± 0.29 | 0.146 |
| Mariana | 0.98 ± 0.31 | 0.96 ± 0.12 | ||
| p-Value | 0.718 | |||
| Mn | Dunkan | 1.04 ± 0.12 | 0.99 ± 0.12 | 0.053 |
| Mariana | 1.04 ± 0.11 | 1.02 ± 0.13 | ||
| p-Value | 0.009 | |||
| Compound | Cultivar | Cultivation System | p-Value | |
|---|---|---|---|---|
| Soil | No-Soil | |||
| Organic Acids (mg 100 g−1 FW) | ||||
| Citric acid | Dunkan | 422 ± 64.7 | 443 ± 93.4 | 0.001 1 |
| Mariana | 541 ± 138 | 561 ± 131 | ||
| p-Value | 0.999 2 | |||
| Malic acid | Dunkan | 25.7 ± 9.87 | 22.1 ± 4.16 | 0.732 |
| Mariana | 25.5 ± 9.14 | 19.9 ± 5.95 | ||
| p-Value | 0.001 | |||
| Ascorbic acid | Dunkan | 14.8 ± 0.61 | 14.4 ± 1.38 | 0.009 |
| Mariana | 15.2 ± 2.04 | 15.0 ± 1.67 | ||
| p-Value | 0.087 | |||
| Oxalic acid | Dunkan | 16.9 ± 6.13 | 17.3 ± 4.06 | 0.104 |
| Mariana | 13.2 ± 2.93 | 14.1 ± 4.43 | ||
| p-Value | 0.798 | |||
| Fumaric acid | Dunkan | 5.69 ± 1.437 | 5.62 ± 1.37 | 0.026 |
| Mariana | 4.33 ± 1.37 | 4.08 ± 1.09 | ||
| p-Value | 0.499 | |||
| Pyruvic acid | Dunkan | 1.40 ± 0.44 | 1.87 ± 0.71 | 0.608 |
| Mariana | 1.80 ± 0.89 | 1.40 ± 0.74 | ||
| p-Value | 0.079 | |||
| Antioxidant Compounds (mg 100 g−1 FW) | ||||
| Total phenols | Dunkan | 24.3 ± 3.00 | 23.5 ± 1.07 | 0.091 |
| Mariana | 26.3 ± 6.77 | 23.6 ± 6.81 | ||
| p-Value | 0.016 | |||
| Lycopene | Dunkan | 2.34 ± 0.12 | 2.63 ± 0.36 | 0.001 |
| Mariana | 1.73 ± 0.36 | 1.76 ± 0.40 | ||
| p-Value | 0.741 | |||
| Chlorogenic acid | Dunkan | 1.08 ± 0.24 | 1.09 ± 0.13 | 0.814 |
| Mariana | 0.996 ± 0.26 | 1.15 ± 0.42 | ||
| p-Value | 0.344 | |||
| Ferulic acid | Dunkan | 0.124 ± 0.03 | 0.125 ± 0.02 | 0.685 |
| Mariana | 0.121 ± 0.03 | 0.130 ± 0.02 | ||
| p-Value | 0.548 | |||
| Caffeic acid | Dunkan | 0.115 ± 0.02 | 0.115 ± 0.05 | 0.010 |
| Mariana | 0.083 ± 0.03 | 0.093 ± 0.02 | ||
| p-Value | 0.674 | |||
| Xi/Xj | Variance ln(Xi/Xj) | clr-Variances | |||||||
|---|---|---|---|---|---|---|---|---|---|
| K | Mg | Ascorbic | Lycopene | Phenols | Chlorogenic | Caffeic | Ferulic | ||
| K | 0.026 | 0.018 | 0.063 | 0.057 | 0.061 | 0.121 | 0.047 | 0.012 | |
| Mg | −30.59 | 0.045 | 0.043 | 0.104 | 0.087 | 0.111 | 0.081 | 0.025 | |
| Ascorbic | −28.77 | 0.182 | 0.084 | 0.051 | 0.080 | 0.138 | 0.057 | 0.022 | |
| Lycopene | −50.01 | −19.42 | −21.24 | 0.126 | 0.105 | 0.129 | 0.099 | 0.044 | |
| Phenols | −23.87 | 0.672 | 0.490 | 26.14 | 0.112 | 0.164 | 0.092 | 0.052 | |
| Chlorogenic | −55.68 | −25.09 | −26.90 | −0.567 | −31.81 | 0.089 | 0.038 | 0.035 | |
| Caffeic | −80.43 | −49.84 | −51.66 | −30.42 | −56.56 | −24.76 | 0.130 | 0.073 | |
| Ferulic | −77.02 | −46.43 | −48.25 | −27.01 | −53.15 | −21.34 | 0.341 | 0.031 | |
| Mean ln(Xi/Xj) | 0.294 | ||||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández Suárez, M.; Molina Pérez, D.; Rodríguez-Rodríguez, E.M.; Díaz Romero, C.; Espinosa Borreguero, F.; Galindo-Villardón, P. The Compositional HJ-Biplot—A New Approach to Identifying the Links among Bioactive Compounds of Tomatoes. Int. J. Mol. Sci. 2016, 17, 1828. https://doi.org/10.3390/ijms17111828
Hernández Suárez M, Molina Pérez D, Rodríguez-Rodríguez EM, Díaz Romero C, Espinosa Borreguero F, Galindo-Villardón P. The Compositional HJ-Biplot—A New Approach to Identifying the Links among Bioactive Compounds of Tomatoes. International Journal of Molecular Sciences. 2016; 17(11):1828. https://doi.org/10.3390/ijms17111828
Chicago/Turabian StyleHernández Suárez, Marcos, Daniel Molina Pérez, Elena M. Rodríguez-Rodríguez, Carlos Díaz Romero, Francisco Espinosa Borreguero, and Purificación Galindo-Villardón. 2016. "The Compositional HJ-Biplot—A New Approach to Identifying the Links among Bioactive Compounds of Tomatoes" International Journal of Molecular Sciences 17, no. 11: 1828. https://doi.org/10.3390/ijms17111828
APA StyleHernández Suárez, M., Molina Pérez, D., Rodríguez-Rodríguez, E. M., Díaz Romero, C., Espinosa Borreguero, F., & Galindo-Villardón, P. (2016). The Compositional HJ-Biplot—A New Approach to Identifying the Links among Bioactive Compounds of Tomatoes. International Journal of Molecular Sciences, 17(11), 1828. https://doi.org/10.3390/ijms17111828








