DeepCNF-D: Predicting Protein Order/Disorder Regions by Weighted Deep Convolutional Neural Fields
Abstract
:1. Introduction
2. Results
2.1. Dataset, Programs to Be Compared, and Evaluation Measures
2.1.1. Training, Validation, and Evaluation Dataset
| Datasets | Length of Disordered Regions | Number of Fragments of Disordered Regions | ||||||
|---|---|---|---|---|---|---|---|---|
| 1–5 | 6–15 | 16–25 | >25 | 1–5 | 6–15 | 16–25 | >25 | |
| Disorder723 | 964 | 2083 | 883 | 852 | 492 | 226 | 45 | 19 |
| UniProt90 | 12,804 | 37,420 | 16,646 | 22,655 | 4133 | 4093 | 852 | 514 |
| CASP9 | 272 | 494 | 215 | 119 | 118 | 52 | 11 | 3 |
| CASP10 | 163 | 261 | 113 | 55 | 73 | 31 | 6 | 2 |
2.1.2. Programs for Comparison
2.1.3. Evaluation Measurement
2.2. Determining the Best Model Parameters on Disorder723 Dataset
2.2.1. Contributions of Number of Layers
| Number of Hidden Layers | AUC Value of 10 cross Validation Batch Datasets | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Mean | |
| 1 | 0.878 | 0.925 | 0.842 | 0.853 | 0.882 | 0.835 | 0.871 | 0.868 | 0.898 | 0.842 | 0.869 |
| 2 | 0.904 | 0.947 | 0.875 | 0.886 | 0.917 | 0.861 | 0.903 | 0.909 | 0.939 | 0.868 | 0.901 |
| 3 | 0.887 | 0.936 | 0.863 | 0.873 | 0.902 | 0.852 | 0.887 | 0.908 | 0.923 | 0.857 | 0.889 |
2.2.2. Contributions of Different Weight Ratios
| Weight Ratio | AUC Value of 10 cross Validation Batch Datasets | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Mean | |
| 5:5 | 0.884 | 0.932 | 0.857 | 0.871 | 0.902 | 0.842 | 0.884 | 0.895 | 0.921 | 0.850 | 0.884 |
| 2:8 | 0.892 | 0.938 | 0.863 | 0.882 | 0.911 | 0.853 | 0.891 | 0.902 | 0.928 | 0.857 | 0.892 |
| 1:9 | 0.899 | 0.943 | 0.869 | 0.887 | 0.915 | 0.858 | 0.897 | 0.911 | 0.933 | 0.862 | 0.897 |
| 0.7:9.3 | 0.904 | 0.947 | 0.875 | 0.886 | 0.917 | 0.861 | 0.903 | 0.909 | 0.939 | 0.868 | 0.901 |
| 0.5:9.5 | 0.901 | 0.948 | 0.872 | 0.884 | 0.919 | 0.857 | 0.902 | 0.903 | 0.942 | 0.864 | 0.899 |
2.2.3. Contributions of Different Combinations of Feature Classes
| Feature Class | AUC Value of 10 cross Validation Batch Datasets | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Mean | |
| Amino acid | 0.843 | 0.877 | 0.793 | 0.832 | 0.845 | 0.784 | 0.852 | 0.834 | 0.865 | 0.803 | 0.833 |
| Structural | 0.864 | 0.904 | 0.830 | 0.841 | 0.858 | 0.826 | 0.863 | 0.858 | 0.882 | 0.819 | 0.855 |
| Evolution | 0.874 | 0.920 | 0.836 | 0.857 | 0.879 | 0.832 | 0.876 | 0.880 | 0.908 | 0.834 | 0.870 |
| Amino acid + Evolution | 0.883 | 0.928 | 0.845 | 0.866 | 0.887 | 0.843 | 0.884 | 0.885 | 0.917 | 0.847 | 0.879 |
| Structural + Evolution | 0.895 | 0.935 | 0.868 | 0.873 | 0.901 | 0.850 | 0.897 | 0.896 | 0.924 | 0.859 | 0.889 |
| All features | 0.904 | 0.947 | 0.875 | 0.886 | 0.917 | 0.861 | 0.903 | 0.909 | 0.939 | 0.868 | 0.901 |
2.3. Comparison with Other Methods on Disorder723 and CASP Datasets
2.3.1. Performance on Disorder723 Dataset
| Methods | AUC Value of 10 cross Validation Batch Datasets | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Mean | |
| Iupred (long) | 0.747 | 0.764 | 0.645 | 0.758 | 0.727 | 0.702 | 0.732 | 0.694 | 0.747 | 0.689 | 0.721 |
| Iupred (short) | 0.821 | 0.857 | 0.756 | 0.826 | 0.823 | 0.752 | 0.840 | 0.787 | 0.839 | 0.795 | 0.810 |
| SPINE-D | 0.885 | 0.929 | 0.885 | 0.888 | 0.897 | 0.848 | 0.877 | 0.906 | 0.914 | 0.838 | 0.887 |
| DisoPred3 | 0.894 | 0.932 | 0.892 | 0.920 | 0.910 | 0.846 | 0.879 | 0.896 | 0.917 | 0.840 | 0.893 |
| DeepCNF-D | 0.904 | 0.947 | 0.875 | 0.886 | 0.917 | 0.861 | 0.903 | 0.909 | 0.939 | 0.868 | 0.901 |
2.3.2. Performance on CASP Dataset
| Predictor | Precision | Bacc | MCC | AUC |
|---|---|---|---|---|
| Iupred (long) | 0.238 | 0.546 | 0.118 | 0.567 |
| Iupred (short) | 0.433 | 0.698 | 0.342 | 0.657 |
| SPINE-D | 0.382 | 0.769 | 0.391 | 0.832 |
| DisoPred3 | 0.665 | 0.704 | 0.464 | 0.842 |
| DeepCNF-D | 0.598 | 0.752 | 0.486 | 0.855 |
| DeepCNF-D (ami_only) | 0.549 | 0.707 | 0.400 | 0.700 |
| Predictor | Precision | Bacc | MCC | AUC |
|---|---|---|---|---|
| Iupred (long) | 0.231 | 0.575 | 0.145 | 0.621 |
| Iupred (short) | 0.413 | 0.729 | 0.374 | 0.712 |
| SPINE-D | 0.307 | 0.779 | 0.366 | 0.876 |
| DisoPred3 | 0.607 | 0.719 | 0.467 | 0.883 |
| DeepCNF-D | 0.529 | 0.764 | 0.474 | 0.898 |
| DeepCNF-D (ami_only) | 0.504 | 0.737 | 0.433 | 0.772 |
3. Conclusions and Discussions
4. Method
4.1. Order/Disorder Definition
4.2. DeepCNF Model
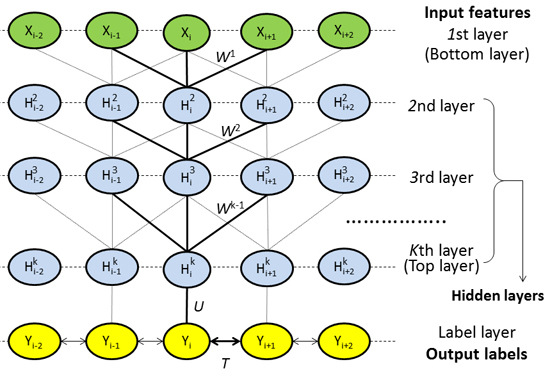
4.2.1. Model Architecture
4.2.2. Deep Convolutional Neural Network
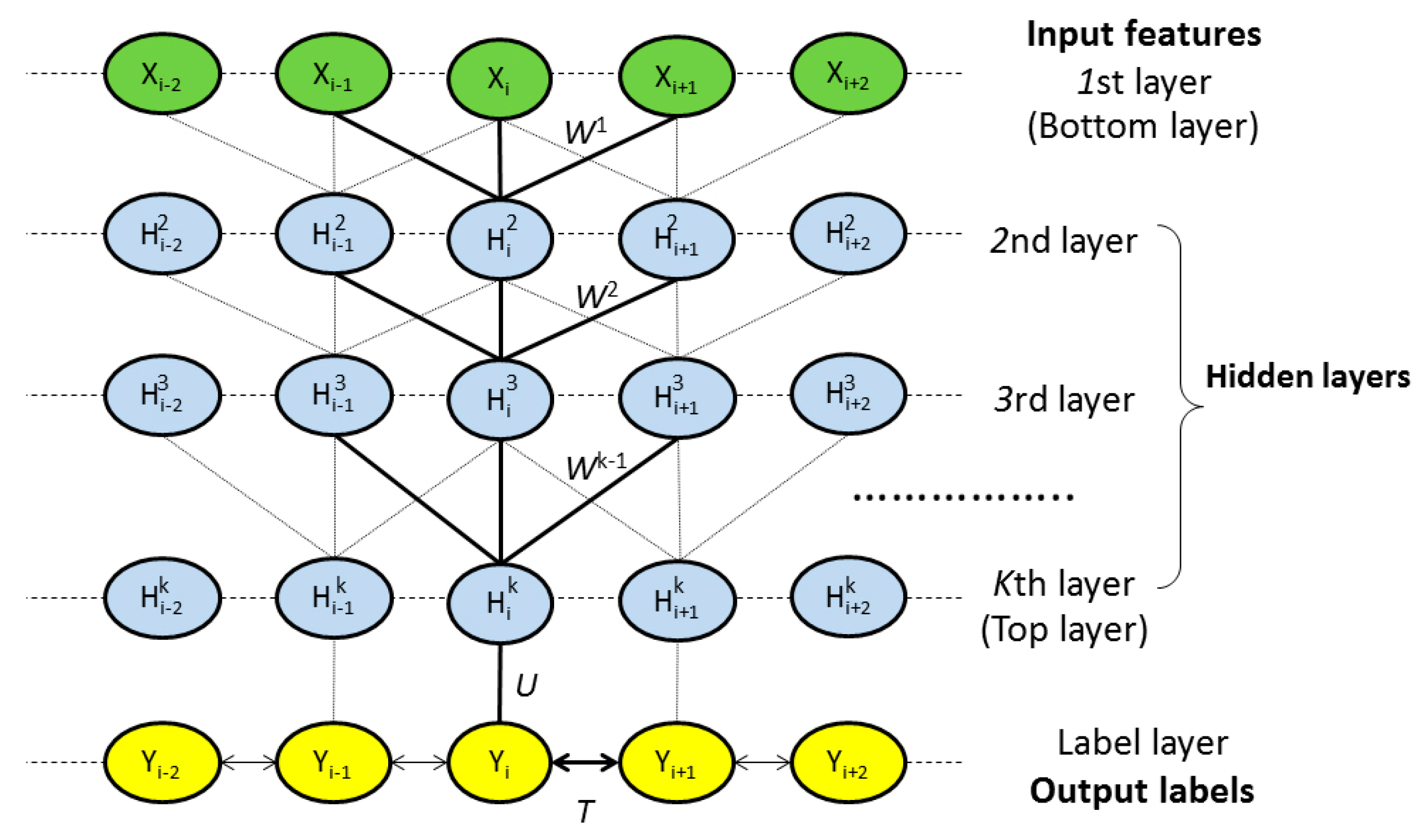
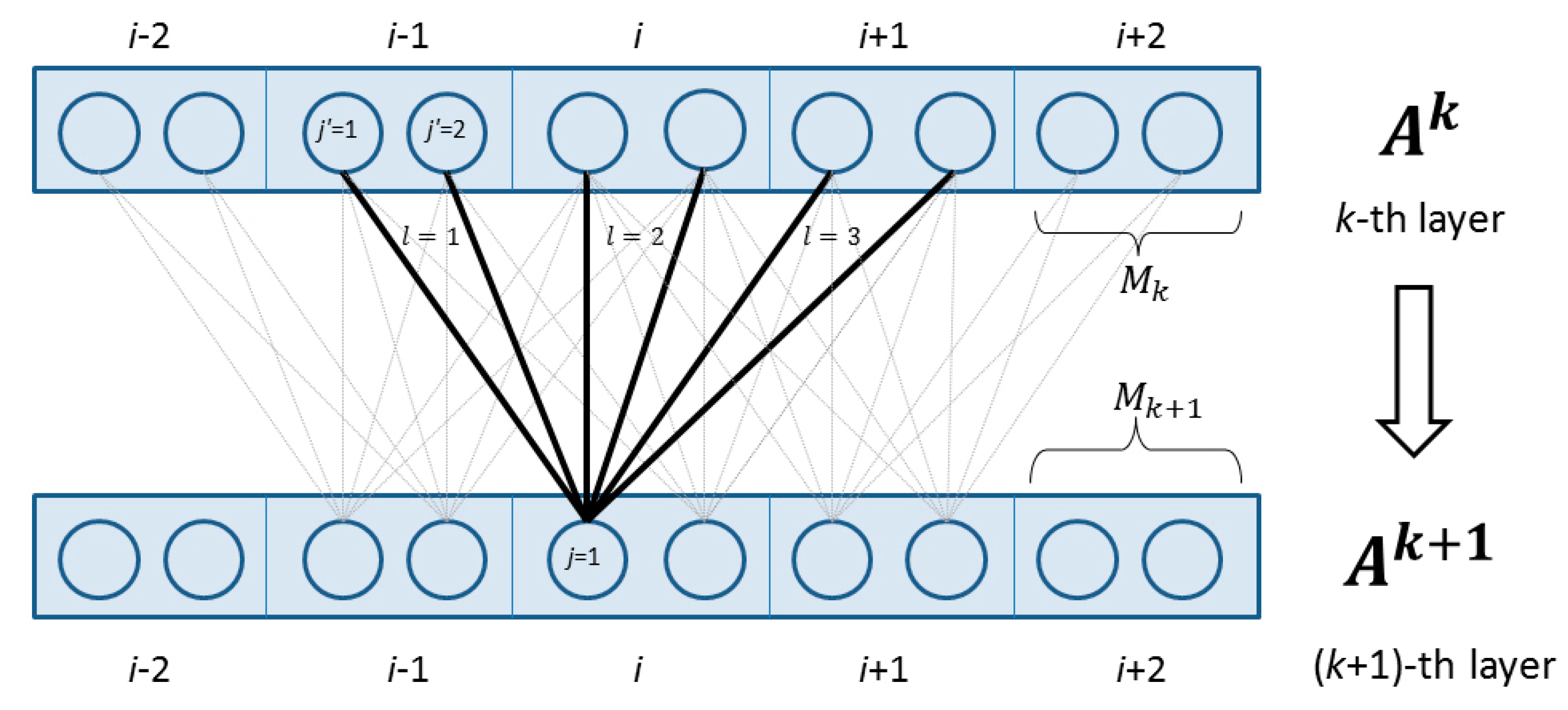
4.2.3. Weighted DeepCNFs
4.2.4. Training Method, Regularization, and Time Complexity
4.3. Protein Features
4.3.1. Amino Acid Related Features
4.3.2. Evolution Related Features
4.3.3. Structure Related Features
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jirgensons, B. Optical rotation and viscosity of native and denatured proteins. X. Further studies on optical rotatory dispersion. Arch. Biochem. Biophys. 1958, 74, 57–69. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Dunker, A.K. Intrinsically disordered proteins and intrinsically disordered protein regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef] [PubMed]
- Dunker, A.K.; Oldfield, C.J.; Meng, J.; Romero, P.; Yang, J.Y.; Chen, J.W.; Vacic, V.; Obradovic, Z.; Uversky, V.N. The unfoldomics decade: An update on intrinsically disordered proteins. BMC Genom. 2008, 9, S1. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.R.; Ruigrok, R.W.; Blackledge, M. Describing intrinsically disordered proteins at atomic resolution by NMR. Curr. Opin. Struct. Biol. 2013, 23, 426–435. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Wang, K.; Liu, Y.; Xue, B.; Uversky, V.N.; Dunker, A.K. Predicting intrinsic disorder in proteins: An overview. Cell Res. 2009, 19, 929–949. [Google Scholar] [CrossRef] [PubMed]
- Dosztányi, Z.; Csizmok, V.; Tompa, P.; Simon, I. IUPred: Web server for the prediction of intrinsically unstructured regions of proteins based on estimated energy content. Bioinformatics 2005, 21, 3433–3434. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.T.; Cozzetto, D. DISOPRED3: Precise disordered region predictions with annotated protein-binding activity. Bioinformatics 2015, 31, 857–863. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Faraggi, E.; Xue, B.; Dunker, A.K.; Uversky, V.N.; Zhou, Y. SPINE-D: Accurate prediction of short and long disordered regions by a single neural-network based method. J. Biomol. Struct. Dyn. 2012, 29, 799–813. [Google Scholar] [CrossRef] [PubMed]
- Eickholt, J.; Cheng, J. DNdisorder: Predicting protein disorder using boosting and deep networks. BMC Bioinform. 2013, 14, 88. [Google Scholar] [CrossRef] [PubMed]
- Ishida, T.; Kinoshita, K. PrDOS: Prediction of disordered protein regions from amino acid sequence. Nucleic Acids Res. 2007, 35, W460–W464. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Dunbrack, R.L.; Williams, R.W.; Dunker, A.K.; Uversky, V.N. PONDR-FIT: A meta-predictor of intrinsically disordered amino acids. Biochim. Biophys. Acta 2010, 1804, 996–1010. [Google Scholar] [CrossRef] [PubMed]
- Hirose, S.; Shimizu, K.; Kanai, S.; Kuroda, Y.; Noguchi, T. POODLE-L: A two-level SVM prediction system for reliably predicting long disordered regions. Bioinformatics 2007, 23, 2046–2053. [Google Scholar] [CrossRef] [PubMed]
- Kozlowski, L.P.; Bujnicki, J.M. MetaDisorder: A meta-server for the prediction of intrinsic disorder in proteins. BMC Bioinform. 2012, 13, 111. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Eickholt, J.; Cheng, J. A comprehensive overview of computational protein disorder prediction methods. Mol. BioSyst. 2012, 8, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Monastyrskyy, B.; Kryshtafovych, A.; Moult, J.; Tramontano, A.; Fidelis, K. Assessment of protein disorder region predictions in CASP10. Proteins Struct. Funct. Bioinform. 2014, 82, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Sauer, U.H. OnD-CRF: Predicting order and disorder in proteins conditional random fields. Bioinformatics 2008, 24, 1401–1402. [Google Scholar] [CrossRef] [PubMed]
- Lafferty, J.; McCallum, A.; Pereira, F.C. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the 18th International Conference on Machine Learning (ICML-2001), Williamstown, MA, USA, 28 June–1 July 2001.
- Becker, J.; Maes, F.; Wehenkel, L. On the encoding of proteins for disordered regions prediction. PLoS ONE 2013, 8, e82252. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Bo, L.; Xu, J. Conditional neural fields. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 1419–1427.
- Lee, H.; Grosse, R.; Ranganath, R.; Ng, A.Y. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In Proceedings of the 26th Annual International Conference on Machine Learning, 2009, ACM, Montreal, QC, Canada, 14–18 June 2009; pp. 609–616.
- Wang, Z.; Zhao, F.; Peng, J.; Xu, J. Protein 8-class secondary structure prediction using conditional neural fields. Proteomics 2011, 11, 3786–3792. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wang, S. AcconPred: Predicting solvent accessibility and contact number simultaneously by a multitask learning framework under the conditional neural fields model. BioMed Res. Int. 2015. [Google Scholar] [CrossRef]
- Cheng, J.; Sweredoski, M.J.; Baldi, P. Accurate prediction of protein disordered regions by mining protein structure data. Data Min. Knowl. Discov. 2005, 11, 213–222. [Google Scholar] [CrossRef]
- Di Domenico, T.; Walsh, I.; Martin, A.J.; Tosatto, S.C. MobiDB: A comprehensive database of intrinsic protein disorder annotations. Bioinformatics 2012, 28, 2080–2081. [Google Scholar] [CrossRef] [PubMed]
- Monastyrskyy, B.; Fidelis, K.; Moult, J.; Tramontano, A.; Kryshtafovych, A. Evaluation of disorder predictions in CASP9. Proteins Struct. Funct. Bioinform. 2011, 79, 107–118. [Google Scholar] [CrossRef] [PubMed]
- Faraggi, E.; Zhang, T.; Yang, Y.; Kurgan, L.; Zhou, Y. SPINE X: Improving protein secondary structure prediction by multistep learning coupled with prediction of solvent accessible surface area and backbone torsion angles. J. Comput. Chem. 2012, 33, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. ROC graphs: Notes and practical considerations for researchers. Mach. Learn. 2004, 31, 1–38. [Google Scholar]
- De Lannoy, G.; François, D.; Delbeke, J.; Verleysen, M. Weighted conditional random fields for supervised interpatient heartbeat classification. IEEE Trans. Biomed. Eng. 2012, 59, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Dunbrack, R.L. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar] [CrossRef] [PubMed]
- The Source Code of Method DeepCNF-D. Available online: http://ttic.uchicago.edu/~wangsheng/DeepCNF_D_package_v1.00.tar.gz (accessed on 25 March 2015).
- Ward, J.J.; Sodhi, J.S.; McGuffin, L.J.; Buxton, B.F.; Jones, D.T. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004, 337, 635–645. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zheng, W.-M. CLePAPS: Fast pair alignment of protein structures based on conformational letters. J. Bioinform. Computat. Biol. 2008, 6, 347–366. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, W.-M. Fast multiple alignment of protein structures using conformational letter blocks. Open Bioinform. J. 2009, 3, 69–83. [Google Scholar] [CrossRef]
- Wang, S.; Peng, J.; Xu, J. Alignment of distantly related protein structures: Algorithm, bound and implications to homology modeling. Bioinformatics 2011, 27, 2537–2545. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Ma, J.; Peng, J.; Xu, J. Protein structure alignment beyond spatial proximity. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wang, S. Algorithms, applications, and challenges of protein structure alignment. Adv. Protein Chem. Struct. Biol. 2014, 94, 121–175. [Google Scholar] [PubMed]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Neyshabur, B.; Panigrahy, R. Sparse matrix factorization. 2013; arXiv:13113315. [Google Scholar]
- Martens, J. Deep learning via Hessian-free optimization. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 735–742.
- Schlessinger, A.; Punta, M.; Rost, B. Natively unstructured regions in proteins identified from contact predictions. Bioinformatics 2007, 23, 2376–2384. [Google Scholar] [CrossRef] [PubMed]
- Gross, S.S.; Russakovsky, O.; Do, C.B.; Batzoglou, S. Training conditional random fields for maximum labelwise accuracy. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; pp. 529–536.
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Meiler, J.; Müller, M.; Zeidler, A.; Schmäschke, F. Generation and evaluation of dimension-reduced amino acid parameter representations by artificial neural networks. Mol. Model. Ann. 2001, 7, 360–369. [Google Scholar] [CrossRef]
- Duan, M.; Huang, M.; Ma, C.; Li, L.; Zhou, Y. Position-Specific residue preference features around the ends of helices and strands and a novel strategy for the prediction of secondary structures. Protein Sci. 2008, 17, 1505–1512. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.H.; Huang, H.; Kihara, D. Statistical potential-based amino acid similarity matrices for aligning distantly related protein sequences. Proteins Struct. Funct. Bioinform. 2006, 64, 587–600. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wang, S.; Zhao, F.; Xu, J. Protein threading using context-specific alignment potential. Bioinformatics 2013, 29, i257–i265. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Peng, J.; Wang, S.; Xu, J. A conditional neural fields model for protein threading. Bioinformatics 2012, 28, i59–i66. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wang, S.; Wang, Z.; Xu, J. MRFalign: Protein homology detection through alignment of markov random fields. PLoS Comput. Biol. 2014, 10, e1003500. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed]
- Söding, J.; Biegert, A.; Lupas, A.N. The HHpred interactive server for protein homology detection and structure prediction. Nucleic Acids Res. 2005, 33 (Suppl. 2), W244–W248. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Weng, S.; Ma, J.; Tang, Q. DeepCNF-D: Predicting Protein Order/Disorder Regions by Weighted Deep Convolutional Neural Fields. Int. J. Mol. Sci. 2015, 16, 17315-17330. https://doi.org/10.3390/ijms160817315
Wang S, Weng S, Ma J, Tang Q. DeepCNF-D: Predicting Protein Order/Disorder Regions by Weighted Deep Convolutional Neural Fields. International Journal of Molecular Sciences. 2015; 16(8):17315-17330. https://doi.org/10.3390/ijms160817315
Chicago/Turabian StyleWang, Sheng, Shunyan Weng, Jianzhu Ma, and Qingming Tang. 2015. "DeepCNF-D: Predicting Protein Order/Disorder Regions by Weighted Deep Convolutional Neural Fields" International Journal of Molecular Sciences 16, no. 8: 17315-17330. https://doi.org/10.3390/ijms160817315
APA StyleWang, S., Weng, S., Ma, J., & Tang, Q. (2015). DeepCNF-D: Predicting Protein Order/Disorder Regions by Weighted Deep Convolutional Neural Fields. International Journal of Molecular Sciences, 16(8), 17315-17330. https://doi.org/10.3390/ijms160817315