Active Transport Can Greatly Enhance Cdc20:Mad2 Formation
Abstract
:1. Introduction
2. The Model
2.1. Mad2 Template Model
2.1.1. Mad2-Activation and Its Function in Sequestering Cdc20
2.1.2. Autocatalytic Amplification of Cdc20:C-Mad2 Formation
| Parameter | Human | Budding Yeast | Remarks | |
|---|---|---|---|---|
| Rate constants: | k1 | 1.00 × 10−3 µM−1s−1 | 4.83 × 10−5 µM−1s−1 | [34]/[32] |
| k2 | 2.00 × 10−1 µM−1s−1 | 3.00 × 10−1 µM−1s−1 | [35]/[32] | |
| k3 | 1.00 × 102 µM−1s−1 | 3.00 × 10−3 µM−1s−1 | [28]/[32] | |
| k4 | 1.00 × 10−2 µM−1s−1 | NA | [28] | |
| k5 | 1.00 × 102 µM−1 s−1 | NA | [28] | |
| k−1 | 1.00 × 10−2 s−1 | 4.83 × 10−6 s−1 | [28]/[32] | |
| k−2 | 2.00 × 10−1s−1 | 4.50 × 10−1 s−1 | [35]/[32] | |
| k−3 | 0.00 s−1 | 2.00 × 10−1 µM−1s−1 | [28]/[32] | |
| k−4 | 3.00 × 10−2 s−1 | NA | [28] | |
| k−5 | 0.00 s−1 | NA | [28] | |
| Initial amount: | ||||
| Cdc20 | 0.22 µM | 0.1 µM | [36,37]/[32] | |
| O-Mad2 | 0.15 µM | 0.2 µM | [35]/[32] | |
| Cdc20:C-Mad2 | 0 µM | 0 µM | [29]/[33] | |
| Mad1:C-Mad2 | 0.05 µM | 0.00616 µM | [31]/[32] | |
| Mad1:C-Mad2:Mad2* | 0 µM | 0 µM | [31]/[32] | |
| Cdc20:C-Mad2:Mad2* | 0 µM | NA | [31] | |
| Diffusion constants: | ||||
| Cdc20 | 19.5 µm2s−1 | 19.5 µm2s−1 | [38] | |
| O-Mad2 | 0.0 − 50.0 µm2s−1 | 0.0 − 50.0 µm2s−1 | ||
| Cdc20:C-Mad2 | 0.0 − 14.0 µm2s−1 | 0.0 − 14.0 µm2s−1 | ||
| Mad1:C-Mad2 | 0 | 0 | ||
| Mad1:C-Mad2:Mad2* | 0 | 0 | ||
| Cdc20:C-Mad2:Mad2* | 0.0 − 11.0 µm2s−1 | NA | ||
| Environment: | ||||
| radius of the kinetochore | 0.1 µm | 0.015 µm | [39]/[40,41] | |
| radius of the cell | 10 µm | 2 µm | [42]/[43] |
2.1.3. APC Inhibition
2.2. Mathematical Treatment and Simulation
2.2.1. Reaction-Diffusion-Convection System
2.2.2. Model Assumptions
2.2.3. Numerical Simulation
3. Results and Discussion
3.1. Quantitative Analysis of the SAC Model
3.2. Reaction-Diffusion System of the “Mad2 Template” Model
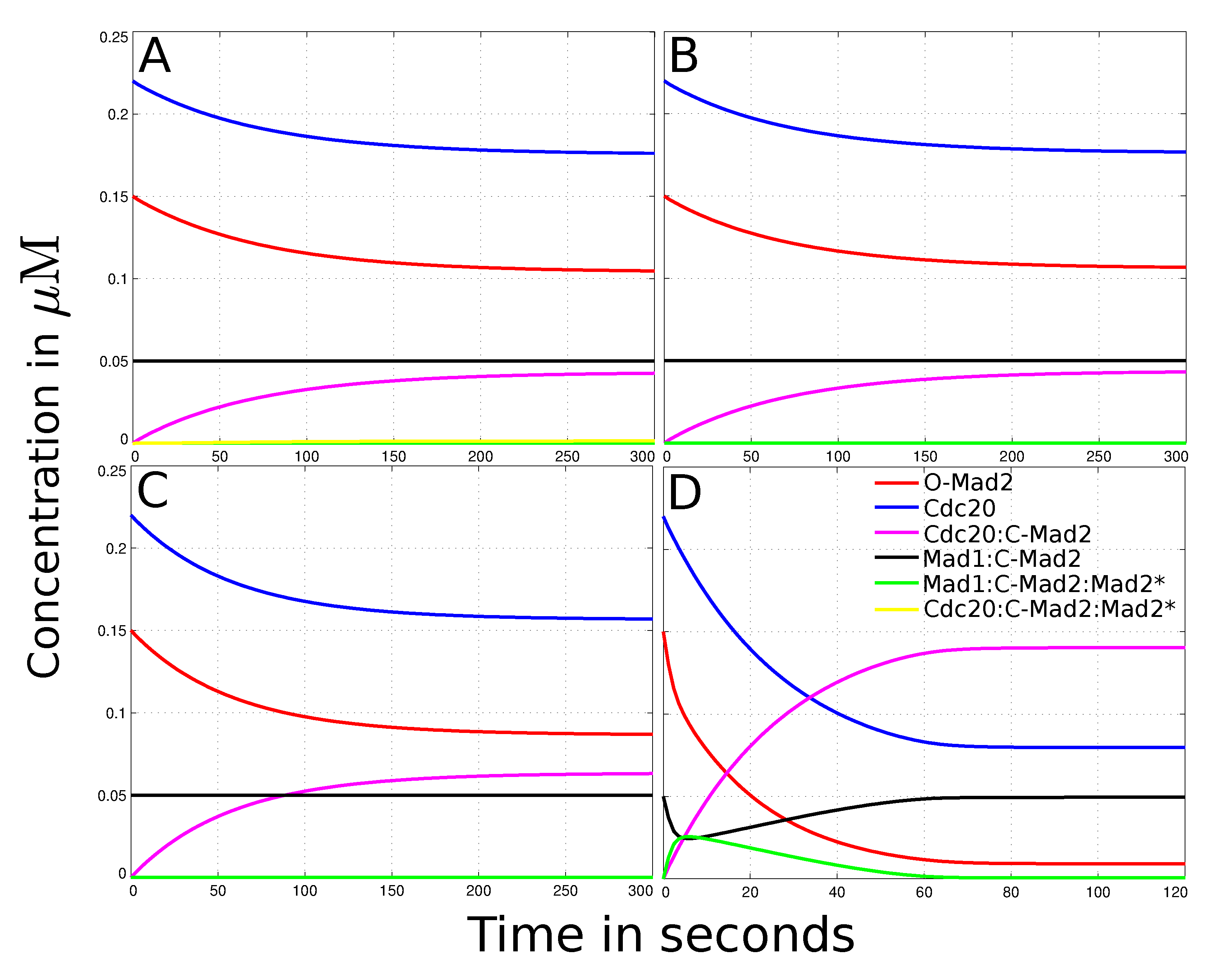
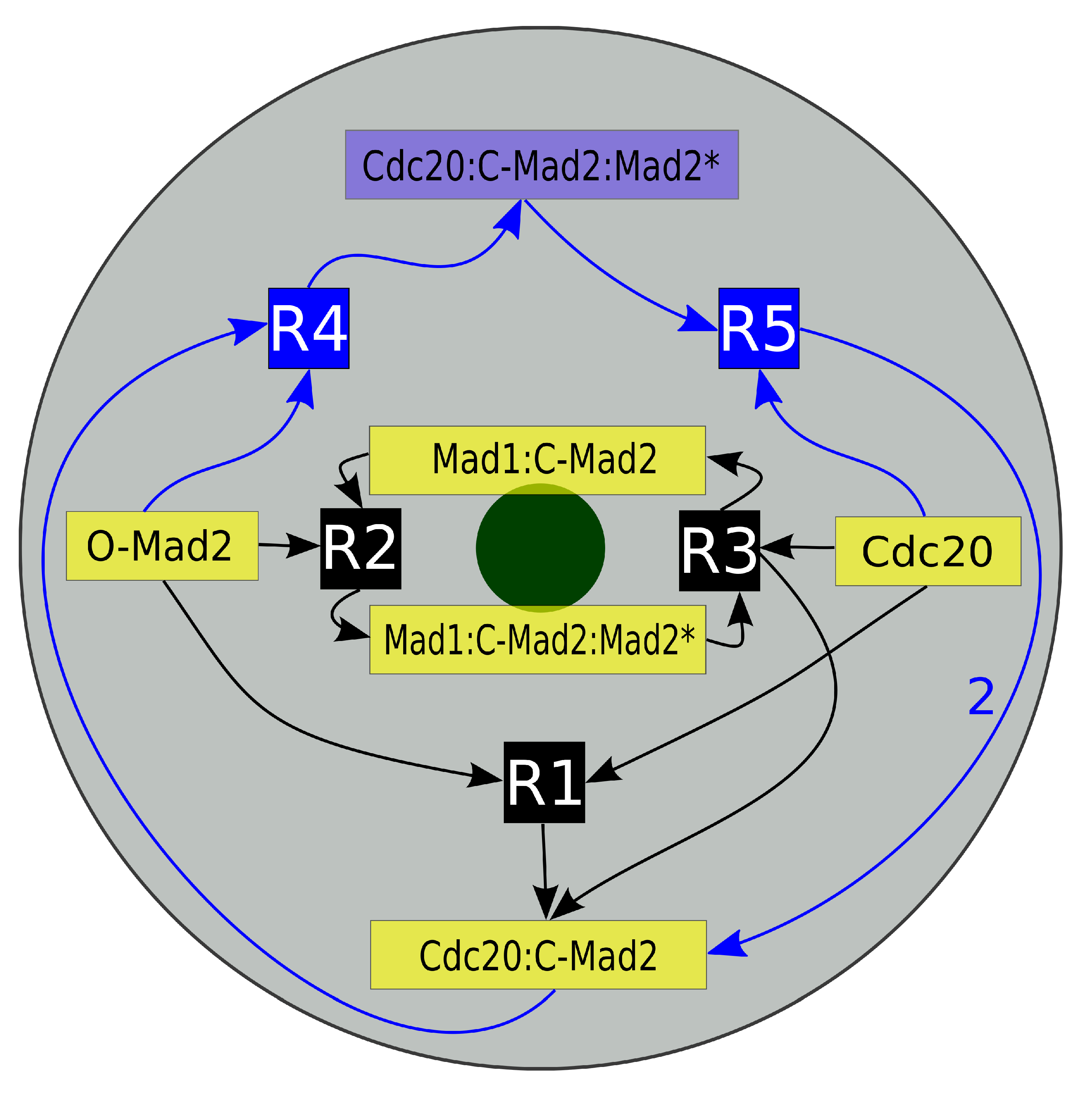
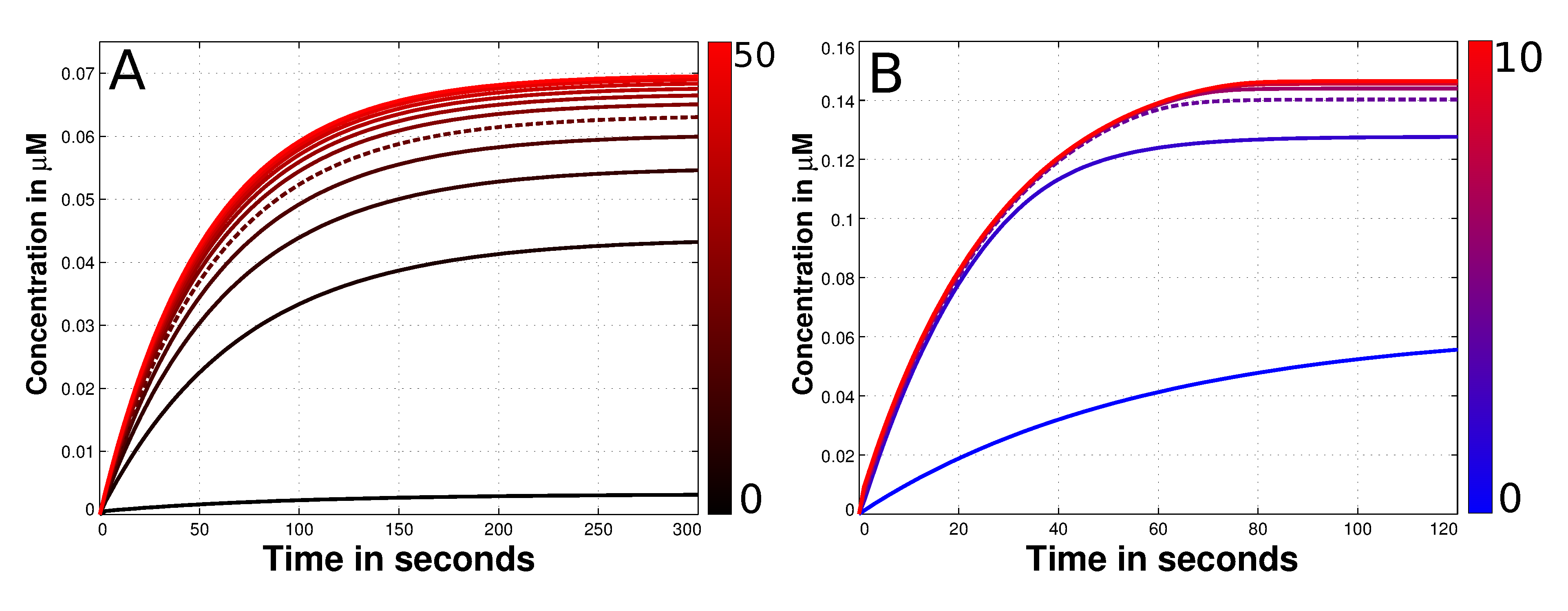
3.3. Mad2 Active Transport towards Spindle Mid-Zone
4. Conclusions
Supplementary Materials
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Minshull, J.; Sun, H.; Tonks, N.K.; Murray, A.W. A MAP kinase-dependent spindle assembly checkpoint in Xenopus egg extracts. Cell 1994, 79, 475–486. [Google Scholar] [CrossRef] [PubMed]
- Hartwell, L.H.; Culotti, J.; Reid, B. Genetic control of the cell-division cycle in yeast. I. Detection of mutants. Proc. Natl. Acad. Sci. USA 1970, 66, 352–359. [Google Scholar] [CrossRef] [PubMed]
- King, R.W.; Peters, J.M.; Tugendreich, S.; Rolfe, M.; Hieter, P.; Kirschner, M.W. A 20S complex containing CDC27 and CDC16 catalyzes the mitosis-specific conjugation of ubiquitin to cyclin B. Cell 1995, 81, 279–288. [Google Scholar] [CrossRef] [PubMed]
- Sethi, N.; Monteagudo, M.C.; Koshland, D.; Hogan, E.; Burke, D.J. The CDC20 gene product of Saccharomyces cerevisiae, a beta-transducin homolog, is required for a subset of microtubule-dependent cellular processes. Mol. Cell. Biol. 1991, 11, 5592–5602. [Google Scholar] [PubMed]
- Shirayama, M.; Zachariae, W.; Ciosk, R.; Nasmyth, K. The Polo-like kinase Cdc5p and the WD-repeat protein Cdc20p/fizzy are regulators and substrates of the anaphase promoting complex in Saccharomyces cerevisiae. EMBO J. 1998, 17, 1336–1349. [Google Scholar] [CrossRef] [PubMed]
- Sudakin, V.; Ganoth, D.; Dahan, A.; Heller, H.; Hershko, J.; Luca, F.C.; Ruderman, J.V.; Hershko, A. The cyclosome, a large complex containing cyclin-selective ubiquitin ligase activity, targets cyclins for destruction at the end of mitosis. Mol. Biol. Cell 1995, 6, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Robbins, J.A.; Cross, F.R. Regulated degradation of the APC coactivator Cdc20. Cell Div. 2010, 5, 23. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D.; Degrassi, F. Aneuploidy: A matter of bad connections. Trends Cell Biol. 2005, 15, 442–451. [Google Scholar] [PubMed]
- Suijkerbuijk, S.J.; Kops, G.J. Preventing aneuploidy: The contribution of mitotic checkpoint proteins. Biochim. Biophys. Acta 2008, 1786, 24–31. [Google Scholar] [PubMed]
- Morais da Silva, S.; Moutinho-Santos, T.; Sunkel, C.E. A tumor suppressor role of the Bub3 spindle checkpoint protein after apoptosis inhibition. J. Cell Biol. 2013, 201, 385–393. [Google Scholar] [PubMed]
- Holland, A.J.; Cleveland, D.W. Boveri revisited: Chromosomal instability, aneuploidy and tumorigenesis. Nat. Rev. Mol. Cell Biol. 2009, 10, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Fang, X.; Wei, Z.; York, J.P.; Zhang, P. Loss of spindle assembly checkpoint-mediated inhibition of CDC20 promotes tumorigenesis in mice. J. Cell Biol. 2009, 185, 983–994. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Murray, A.W. Feedback control of mitosis in budding yeast. Cell 1991, 66, 519–531. [Google Scholar] [CrossRef] [PubMed]
- Hoyt, M.A.; Totis, L.; Roberts, B.T. S. cerevisiae genes required for cell cycle arrest in response to loss of microtubule function. Cell 1991, 66, 507–517. [Google Scholar] [CrossRef] [PubMed]
- Vagnarelli, P.; Earnshaw, W.C. Chromosomal passengers: The four-dimensional regulation of mitotic events. Chromosoma 2004, 113, 211–222. [Google Scholar] [CrossRef] [PubMed]
- Fisk, H.A.; Mattison, C.P.; Winey, M. A field guide to the Mps1 family of protein kinases. Cell Cycle 2004, 3, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Karess, R. Rod-Zw10-Zwilch: A key player in the spindle checkpoint. Trends Cell Biol. 2005, 15, 386–392. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wang, Z.; Ge, L.; Chen, N.; Liu, H. The RZZ complex and the spindle assembly checkpoint. Cell Struct. Funct. 2009, 34, 31–45. [Google Scholar] [CrossRef] [PubMed]
- Buffin, E.; Emre, D.; Karess, R.E. Flies without a spindle checkpoint. Nat. Cell Biol. 2007, 9, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Raff, J.W.; Jeffers, K.; Huang, J.Y. The roles of Fzy/Cdc20 and Fzr/Cdh1 in regulating the destruction of cyclin B in space and time. J. Cell Biol. 2002, 157, 1139–1149. [Google Scholar] [CrossRef] [PubMed]
- Saffery, R.; Irvine, D.V.; Griffiths, B.; Kalitsis, P.; Choo, K.H. Components of the human spindle checkpoint control mechanism localize specifically to the active centromere on dicentric chromosomes. Hum. Genet. 2000, 107, 376–384. [Google Scholar] [CrossRef] [PubMed]
- Saffery, R.; Irvine, D.V.; Griffiths, B.; Kalitsis, P.; Wordeman, L.; Choo, K.H. Human centromeres and neocentromeres show identical distribution patterns of >20 functionally important kinetochore-associated proteins. Hum. Mol. Genet. 2000, 9, 175–185. [Google Scholar] [CrossRef] [PubMed]
- Williams, B.C.; Li, Z.; Liu, S.; Williams, E.V.; Leung, G.; Yen, T.J.; Goldberg, M.L. Zwilch, a new component of the ZW10/ROD complex required for kinetochore functions. Mol. Biol. Cell 2003, 14, 1379–1391. [Google Scholar] [CrossRef] [PubMed]
- Kops, G.J.P.L.; Weaver, B.A.A.; Cleveland, D.W. On the road to cancer: Aneuploidy and the mitotic checkpoint. Nat. Rev. Cancer 2005, 5, 773–785. [Google Scholar] [CrossRef] [PubMed]
- Fang, G.; Yu, H.; Kirschner, M.W. The checkpoint protein MAD2 and the mitotic regulator CDC20 form a ternary complex with the anaphase-promoting complex to control anaphase initiation. Genes Dev. 1998, 12, 1871–1883. [Google Scholar] [CrossRef] [PubMed]
- Doncic, A.; Ben-Jacob, E.; Barkai, N. Evaluating putative mechanisms of the mitotic spindle checkpoint. Proc. Natl. Acad. Sci. USA 2005, 102, 6332–6337. [Google Scholar] [CrossRef] [PubMed]
- Sear, R.P.; Howard, M. Modeling dual pathways for the metazoan spindle assembly checkpoint. Proc. Natl. Acad. Sci. USA 2006, 103, 16758–16763. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Dittrich, P.; Diekmann, S.; Schmitt, E. Mad2 binding is not sufficient for complete Cdc20 sequestering in mitotic transition control (an in silico study). Biophys. Chem. 2008, 134, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Diekmann, S.; Schmitt, E.; Dittrich, P. In-silico modeling of the mitotic spindle assembly checkpoint. PLoS One 2008, 3, e1555. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Schmitt, E.; Dittrich, P.; Diekmann, S. In silico study of kinetochore control, amplification, and inhibition effects in MCC assembly. BioSystems 2009, 95, 35–50. [Google Scholar] [CrossRef] [PubMed]
- De Antoni, A.; Pearson, C.G.; Cimini, D.; Canman, J.C.; Sala, V.; Nezi, L.; Mapelli, M.; Sironi, L.; Faretta, M.; Salmon, E.D.; Musacchio, A. The Mad1/Mad2 complex as a template for Mad2 activation in the spindle assembly checkpoint. Curr. Biol. 2005, 15, 214–225. [Google Scholar] [CrossRef] [PubMed]
- Simonetta, M.; Manzoni, R.; Mosca, R.; Mapelli, M.; Massimiliano, L.; Vink, M.; Novak, B.; Musacchio, A.; Ciliberto, A. The influence of catalysis on mad2 activation dynamics. PLoS Biol. 2009, 7, e10. [Google Scholar] [CrossRef] [PubMed]
- Lohel, M.; Ibrahim, B.; Diekmann, S.; Dittrich, P. The role of localization in the operation of the mitotic spindle assembly checkpoint. Cell Cycle 2009, 8, 2650–2660. [Google Scholar] [CrossRef] [PubMed]
- Musacchio, A.; Salmon, E.D. The spindle-assembly checkpoint in space and time. Nat. Rev. Mol. Cell Biol. 2007, 8, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Howell, B.J.; Hoffman, D.B.; Fang, G.; Murray, A.W.; Salmon, E.D. Visualization of Mad2 dynamics at kinetochores, along spindle fibers, and at spindle poles in living cells. J. Cell Biol. 2000, 150, 1233–1250. [Google Scholar] [CrossRef] [PubMed]
- Fang, G. Checkpoint protein BubR1 acts synergistically with Mad2 to inhibit anaphase-promoting complex. Mol. Biol. Cell 2002, 13, 755–766. [Google Scholar] [CrossRef] [PubMed]
- Stegmeier, F.; Rape, M.; Draviam, V.M.; Nalepa, G.; Sowa, M.E.; Ang, X.L.; McDonald, E.R.; Li, M.Z.; Hannon, G.J.; Sorger, P.K.; et al. Anaphase initiation is regulated by antagonistic ubiquitination and deubiquitination activities. Nature 2007, 446, 876–881. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Shah, J.V.; Berns, M.W.; Cleveland, D.W. In vivo quantitative studies of dynamic intracellular processes using fluorescence correlation spectroscopy. Biophys. J. 2006, 91, 343–351. [Google Scholar] [CrossRef] [PubMed]
- Cherry, L.M.; Faulkner, A.J.; Grossberg, L.A.; Balczon, R. Kinetochore size variation in mammalian chromosomes: An image analysis study with evolutionary implications. J. Cell Sci. 1989, 92, 281–289. [Google Scholar] [PubMed]
- Joglekar, A.P.; Bloom, K.; Salmon, E.D. In vivo protein architecture of the eukaryotic kinetochore with nanometer scale accuracy. Curr. Biol. 2009, 19, 694–699. [Google Scholar] [CrossRef] [PubMed]
- Haase, J.; Mishra, P.K.; Stephens, A.; Haggerty, R.; Quammen, C.; Taylor, R.M.; Yeh, E.; Basrai, M.A.; Bloom, K. A 3D map of the yeast kinetochore reveals the presence of core and accessory centromere-specific histone. Curr. Biol. 2013, 23, 1939–1944. [Google Scholar] [CrossRef] [PubMed]
- Morgan, D. The Cell Cycle: Principles of Control; Sinauer Associates, Inc.: Sunderland, MA, USA, 2007. [Google Scholar]
- Yamaguchi, M.; Namiki, Y.; Okada, H.; Mori, Y.; Furukawa, H.; Wang, J.; Ohkusu, M.; Kawamoto, S. Structome of Saccharomyces cerevisiae determined by freeze-substitution and serial ultrathin-sectioning electron microscopy. J. Electron. Microsc. 2011, 60, 321–335. [Google Scholar]
- Sudakin, V.; Chan, G.K.; Yen, T.J. Checkpoint inhibition of the APC/C in HeLa cells is mediated by a complex of BUBR1, BUB3, CDC20, and MAD2. J. Cell Biol. 2001, 154, 925–936. [Google Scholar] [CrossRef] [PubMed]
- Malureanu, L.A.; Jeganathan, K.B.; Hamada, M.; Wasilewski, L.; Davenport, J.; van Deursen, J.M. BubR1 N terminus acts as a soluble inhibitor of cyclin B degradation by APC/C(Cdc20) in interphase. Dev. Cell 2009, 16, 118–131. [Google Scholar]
- Kulukian, A.; Han, J.S.; Cleveland, D.W. Unattached kinetochores catalyze production of an anaphase inhibitor that requires a Mad2 template to prime Cdc20 for BubR1 binding. Dev. Cell 2009, 16, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Medema, R.H. Relaying the checkpoint signal from kinetochore to APC/C. Dev. Cell 2009, 16, 6–8. [Google Scholar] [CrossRef] [PubMed]
- Herzog, F.; Primorac, I.; Dube, P.; Lenart, P.; Sander, B.; Mechtler, K.; Stark, H.; Peters, J.M. Structure of the anaphase-promoting complex/cyclosome interacting with a mitotic checkpoint complex. Science 2009, 323, 1477–1481. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, I.; Miniowitz, S.; Moshe, Y.; Hershko, A. Inhibitory factors associated with anaphase-promoting complex/cylosome in mitotic checkpoint. Proc. Natl. Acad. Sci. USA 2007, 104, 4870–4875. [Google Scholar] [CrossRef] [PubMed]
- Eytan, E.; Braunstein, I.; Ganoth, D.; Teichner, A.; Hittle, J.C.; Yen, T.J.; Hershko, A. Two different mitotic checkpoint inhibitors of the anaphase-promoting complex/cyclosome antagonize the action of the activator Cdc20. Proc. Natl. Acad. Sci. USA 2008, 105, 9181–9185. [Google Scholar] [PubMed]
- Loew, L.M.; Schaff, J.C. The virtual cell: A software environment for computational cell biology. Trends Biotechnol. 2001, 19, 401–406. [Google Scholar] [CrossRef] [PubMed]
- MATLAB. version 8.3.0.532 (R2014a); The MathWorks Inc.: Natick, MA, USA, 2014.
- Lince-Faria, M.; Maffini, S.; Orr, B.; Ding, Y.; Florindo, C.; Sunkel, C.; Tavares, A.; Johansen, J.; Johansen, K.; Maiato, H. Spatiotemporal control of mitosis by the conserved spindle matrix protein megator. J. Cell Biol. 2009, 184, 647–657. [Google Scholar] [CrossRef] [PubMed]
- Reimann, J.D.; Freed, E.; Hsu, J.Y.; Kramer, E.R.; Peters, J.M.; Jackson, P.K. Emi1 is a mitotic regulator that interacts with Cdc20 and inhibits the anaphase promoting complex. Cell 2001, 105, 645–655. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Kirschner, M.W. Emi1 preferentially inhibits ubiquitin chain elongation by the anaphase-promoting complex. Nat. Cell Biol. 2013, 15, 797–806. [Google Scholar] [CrossRef] [PubMed]
- Marzo, I.; Naval, J. Antimitotic drugs in cancer chemotherapy: Promises and pitfalls. Biochem. Pharmacol. 2013, 86, 703–710. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Dittrich, P.; Diekmann, S.; Schmitt, E. Stochastic effects in a compartmental model for mitotic checkpoint regulation. J. Integr. Bioinform. 2007, 4, 66. [Google Scholar]
- Mistry, H.B.; MacCallum, D.E.; Jackson, R.C.; Chaplain, M.A.; Davidson, F.A. Modeling the temporal evolution of the spindle assembly checkpoint and role of Aurora B kinase. Proc. Natl. Acad. Sci. USA 2008, 105, 20215–20220. [Google Scholar] [CrossRef] [PubMed]
- Kreyssig, P.; Escuela, G.; Reynaert, B.; Veloz, T.; Ibrahim, B.; Dittrich, P. Cycles and the Qualitative Evolution of Chemical Systems. PLoS One 2012, 7, e45772. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, B.; Henze, R.; Gruenert, G.; Egbert, M.M.; Huwald, J.; Dittrich, P. Rule-based modeling in space for linking heterogeneous interaction data to large-scale dynamical molecular complexes. Cells 2013, 2, 506–544. [Google Scholar] [PubMed]
- Tschernyschkow, S.; Herda, S.; Gruenert, G.; Doring, V.; Gorlich, D.; Hofmeister, A.; Hoischen, C.; Dittrich, P.; Diekmann, S.; Ibrahim, B. Rule-based modeling and simulations of the inner kinetochore structure. Prog. Biophys. Mol. Biol. 2013, 113, 33–45. [Google Scholar]
- Kreyssig, P.; Wozar, C.; Peter, S.; Veloz, T.; Ibrahim, B.; Dittrich, P. Effects of small particle numbers on long-term behaviour in discrete biochemical systems. Bioinformatics 2014, 30, i475–i481. [Google Scholar] [CrossRef] [PubMed]
- Caydasi, A.K.; Lohel, M.; Grunert, G.; Dittrich, P.; Pereira, G.; Ibrahim, B. A dynamical model of the spindle position checkpoint. Mol. Syst. Biol. 2012, 8, 582. [Google Scholar] [CrossRef] [PubMed]
- Caydasi, A.; Ibrahim, B.; Pereira, G. Monitoring spindle orientation: Spindle position checkpoint in charge. Cell Div. 2010, 5, 28. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ibrahim, B.; Henze, R. Active Transport Can Greatly Enhance Cdc20:Mad2 Formation. Int. J. Mol. Sci. 2014, 15, 19074-19091. https://doi.org/10.3390/ijms151019074
Ibrahim B, Henze R. Active Transport Can Greatly Enhance Cdc20:Mad2 Formation. International Journal of Molecular Sciences. 2014; 15(10):19074-19091. https://doi.org/10.3390/ijms151019074
Chicago/Turabian StyleIbrahim, Bashar, and Richard Henze. 2014. "Active Transport Can Greatly Enhance Cdc20:Mad2 Formation" International Journal of Molecular Sciences 15, no. 10: 19074-19091. https://doi.org/10.3390/ijms151019074
APA StyleIbrahim, B., & Henze, R. (2014). Active Transport Can Greatly Enhance Cdc20:Mad2 Formation. International Journal of Molecular Sciences, 15(10), 19074-19091. https://doi.org/10.3390/ijms151019074






