Identification of Different Donor-Acceptor Structures via Förster Resonance Energy Transfer (FRET) in Quantum-Dot-Perylene Bisimide Assemblies
Abstract
:Preface
1. Introduction
- The attachment of dye molecules has been accomplished via chemical bonds to a polymer shell covering the QD surface [21]. This results in timely and spatially fixed donor acceptor complexes, which are well defined [7] but with a relatively low FRET efficiency [22] since donor-acceptor distances are relatively large. Thus more than one dye per QD is needed to achieve high FRET efficiencies. Since QD-dye assemblies are possible candidates to monitor e.g., biological processes [24], such systems might not be optimal sensors to detect processes on the base of a single event.
- The third approach is related to self-organized QD-dye assemblies via suitable functional groups of the dyes, which can anchor via “ligand-type” bonds to surface atoms of the QD. This approach is related to a dynamic process [3,4,25], which takes place as a competition between ligand bonding (e.g., of TOPO) and dye bonding This implies that QD-dye assemblies are not permanent in time, but might be nevertheless effective FRET systems on a single dye/single QD level. Such a dynamic approach, however, is often accompanied by NON-FRET photoluminescence (PL) quenching [5], which might be even larger than the influence of FRET itself [3]. This process is related to the excitonic wave function outside of the QD. The wavefunction will be disturbed by the dye attachment finally resulting in (self-) localization of the electron close to the surface or in modification of surface states giving rise to non-radiative decay [4]. On the other hand, this Non-FRET quenching mechanism might also be used as a monitor for dye related properties, like their functional group specific complexation constants. As an example, ortho-pyridyl free base porphyrins did not result in QD PL quenching while para- and meta-pyridyl freebase porphyrins have been shown to be strong quenchers. However, in case of properly selected ligands (class (iii)), rather stable QD-dye assemblies are formed [3].
2. Results and Discussion
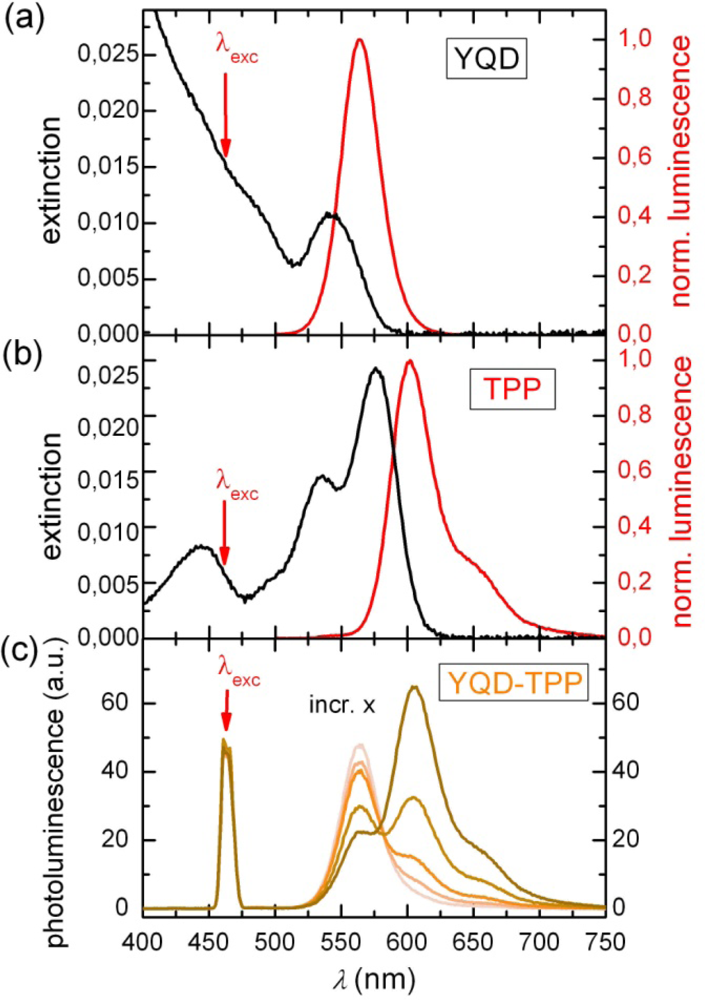
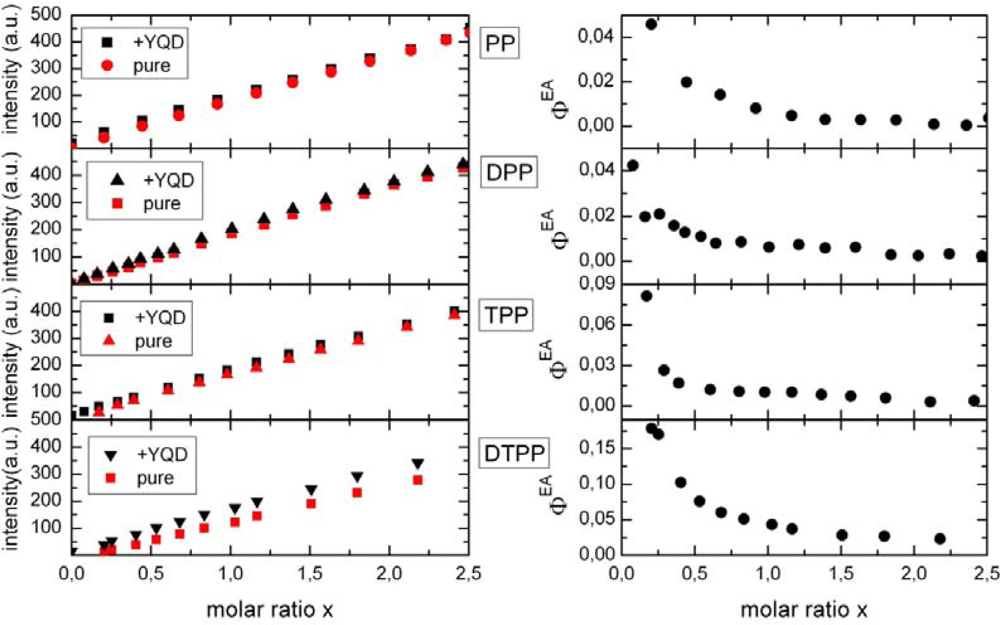
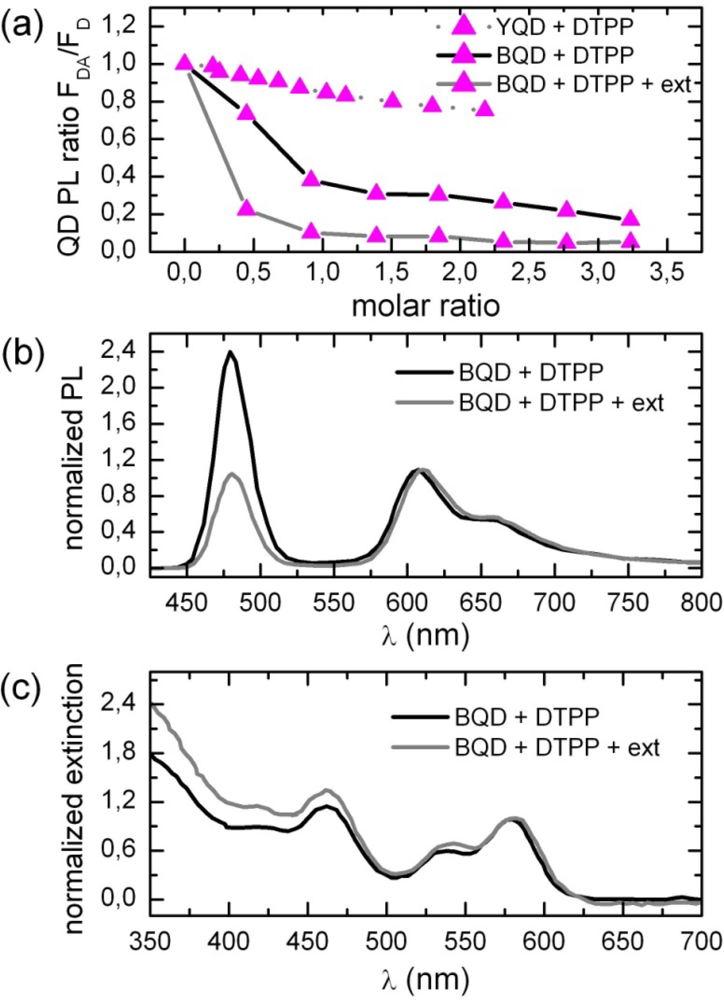
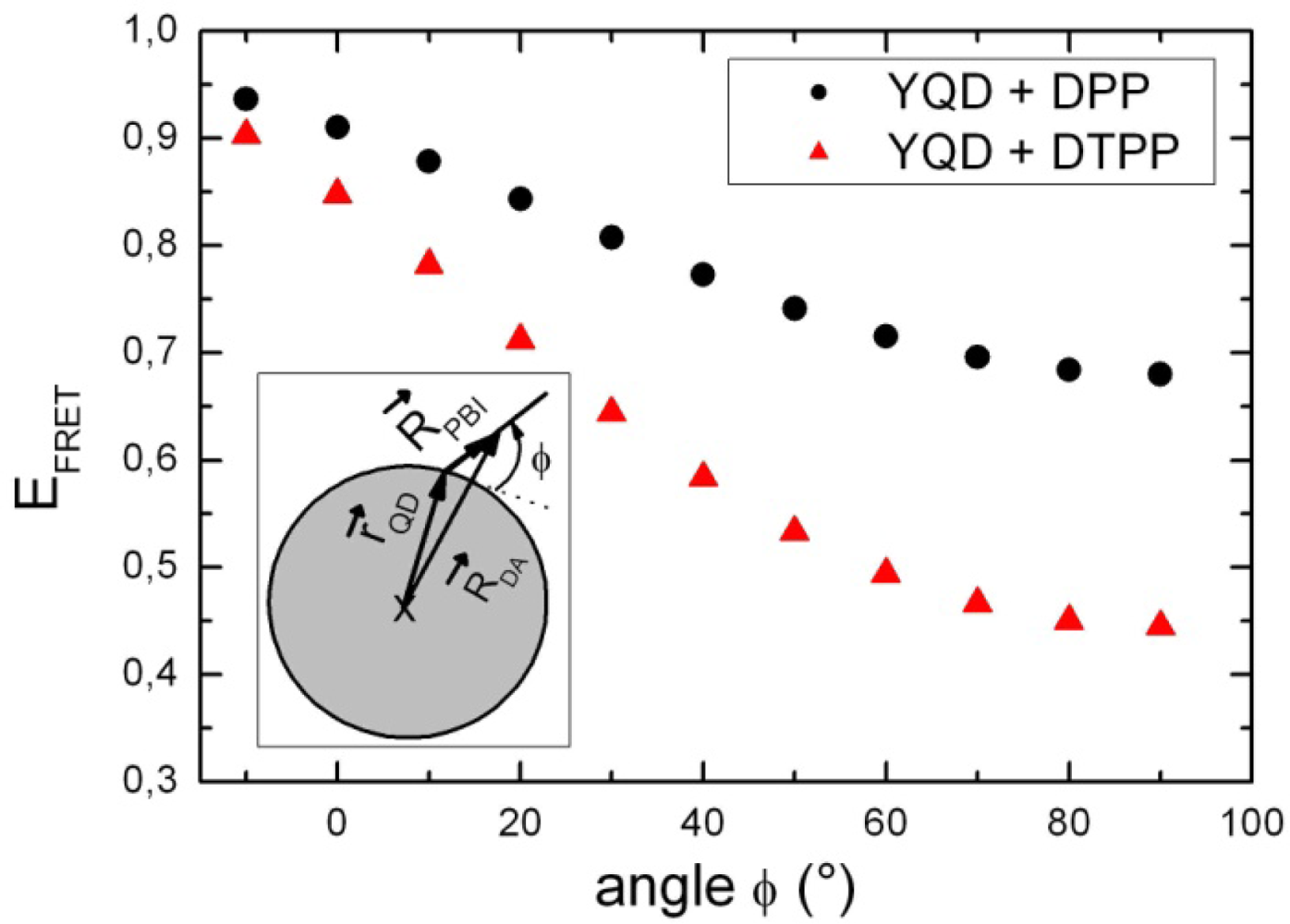
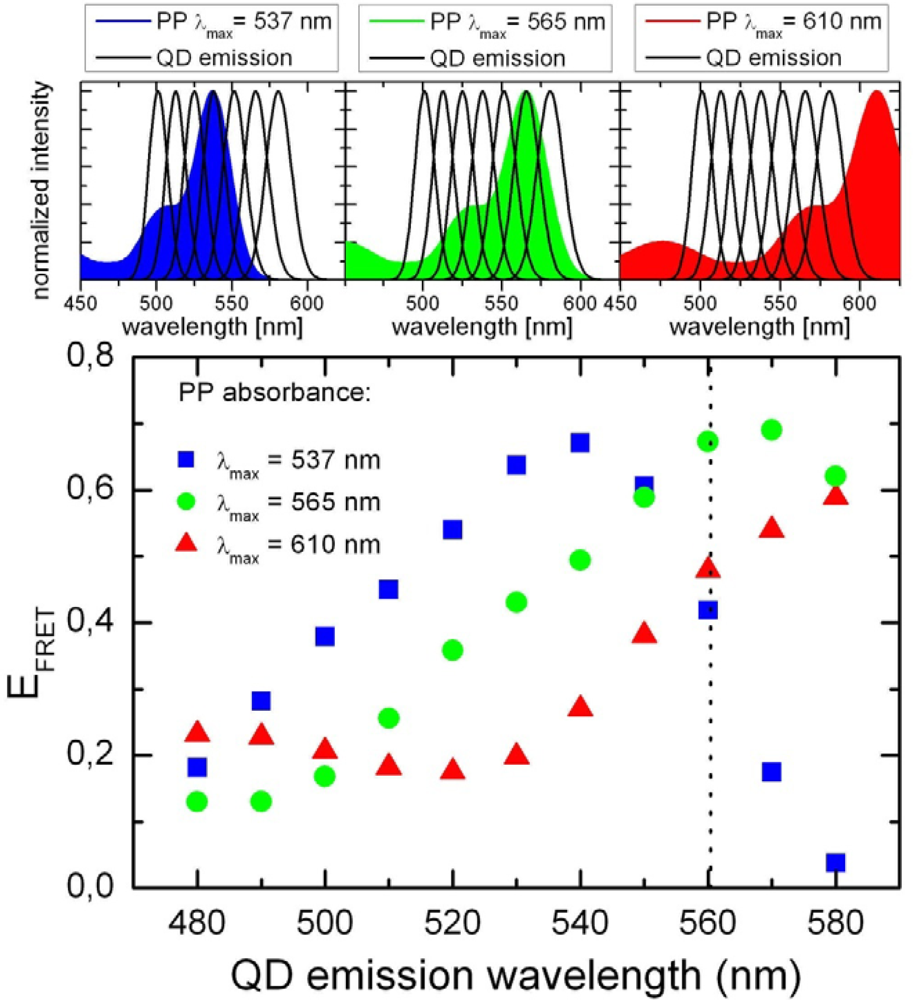
2.1. Ensemble Experiments
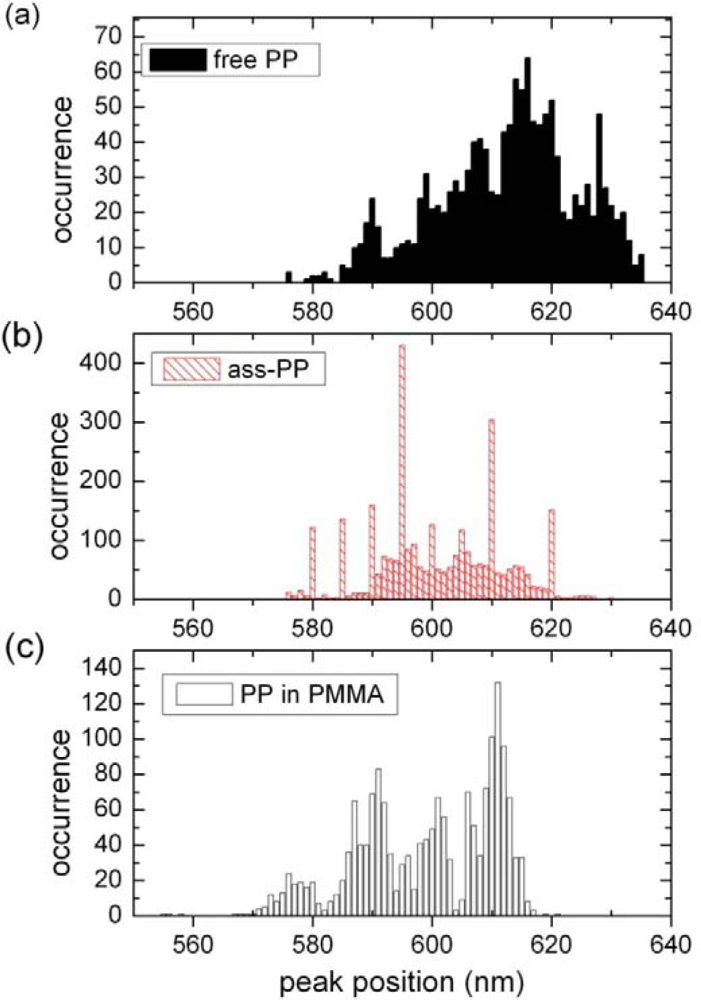
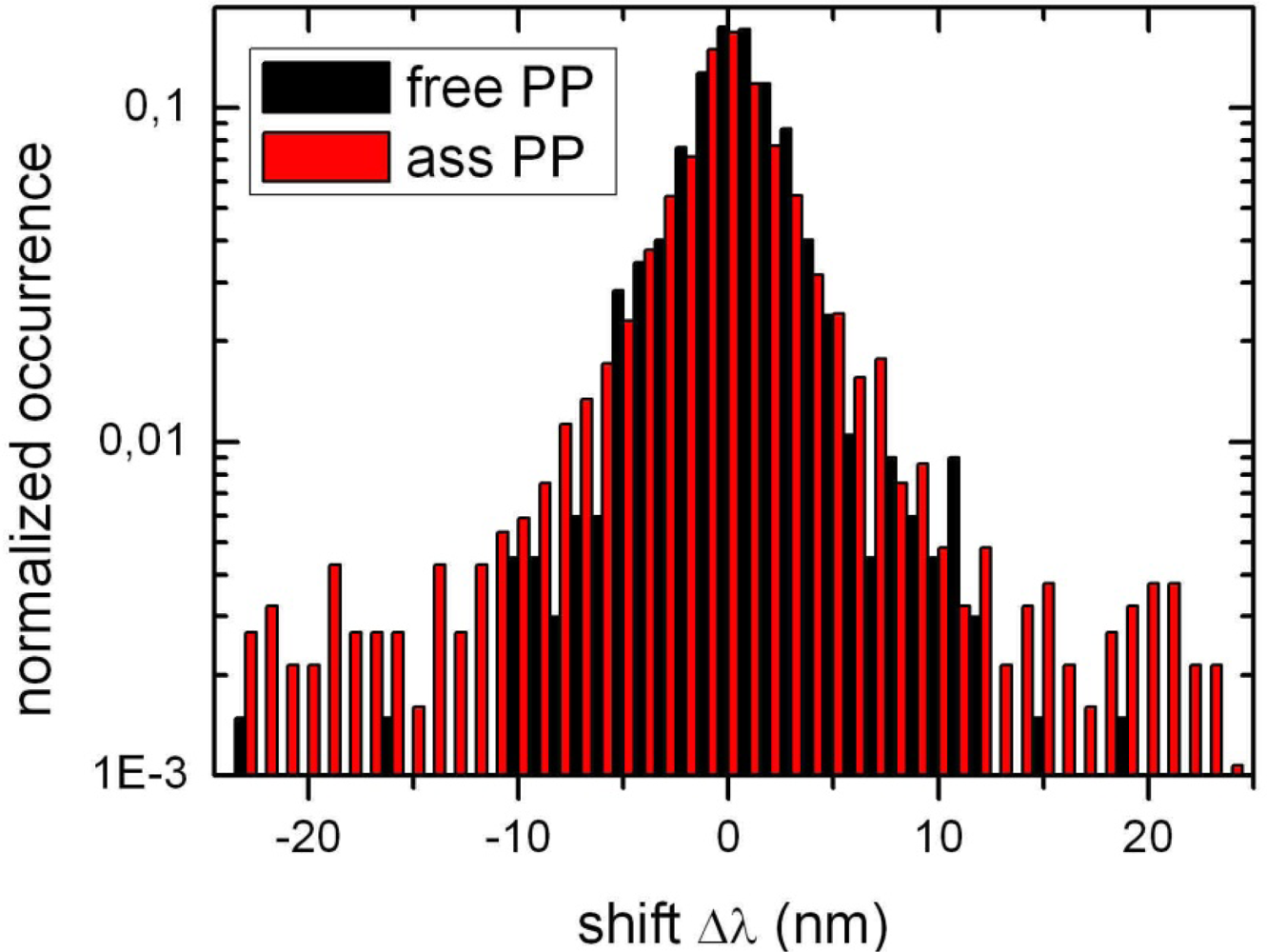
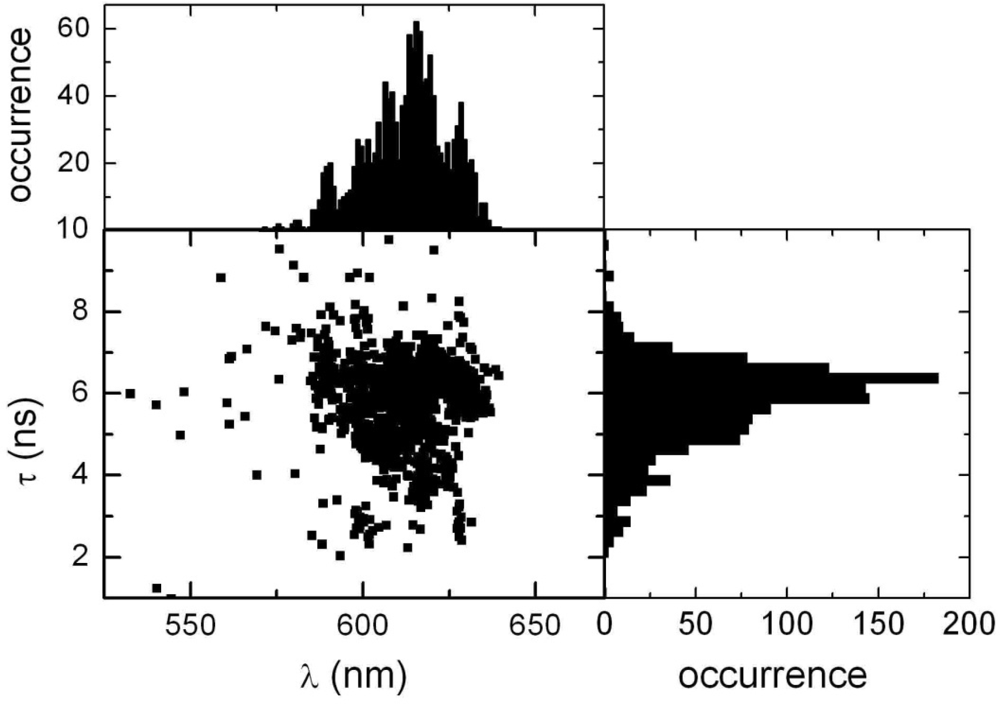
2.2. Single Particle/Single Molecule Experiments
3. Discussion
3. Experimental Section
4. Conclusions
Acknowledgments
References and Notes
- Täuber, D; Schuster, J; Heidernätsch, M; Bauer, M; Radons, G; von Borczyskowski, C. Discrimination between Static and Dynamic Heterogeneities in Single Dye Diffusion in Ultrathin Liquid Films. Diffus. Fundam. J 2009, 11, 452–453. [Google Scholar]
- Cichos, F; von Borczyskowski, C; Orrit, M. Power-law Intermittency of Single Emitters. Curr. Opin. Colloid Interface Sci 2007, 12, 272–284. [Google Scholar]
- Zenkevich, E; Shulga, A; Cichos, F; Petrov, E; Blaudeck, T; von Borczyskowski, C. Nanoassemblies Designed from Semiconductor Quantum Dots and Molecular Arrays. J. Phys. Chem. B 2005, 109, 8679–8692. [Google Scholar]
- Blaudeck, T; Zenkevich, EI; Cichos, F; von Borczyskowski, C. Probing Wave Functions at Semiconductor Quantum-Dot Surfaces by Non-FRET Photoluminescence Quenching. J. Phys Chem. C 2008, 112, 20251–20257. [Google Scholar]
- Kowerko, D; Schuster, J; Amecke, N; Abdel-Mottaleb, M; Dobrawa, R; Würthner, F; von Borczyskowski, C. FRET and NON-FRET Processes in Single Self-aggregated Quantum Dot Perylene Bisimide Assemblies. Phys. Chem. Chem. Phys 2009, in press.. [Google Scholar]
- Kowerko, D; Schuster, J; von Borczyskowski, C. Restricted Conformation Dynamics of Single Functionalized Perylene Bisimide Molecules on SiO2 Surfaces and in Thin Polymer Films. Mol. Phys 2009, 107, 1911–1921. [Google Scholar]
- Clapp, AR; Medintz, IL; Mattoussi, H. Förster Resonance Energy Transfer Investigations Using Quantum-Dot Fluorophores. Chem. Phys. Chem 2006, 7, 47–57. [Google Scholar]
- Jin, R. Super Robust Nanoparticles for Biology and Biomedicine. Angew. Chem. Int. Ed 2008, 47, 6750–6753. [Google Scholar]
- De, M; Ghosh, PS; Rotello, VM. Applications of Nanoparticles in Biology. Adv. Mat 2008, 20, 4225–4217. [Google Scholar]
- Scholes, GD; Rumbles, G. Excitons in Nanoscale Systems. Nat. Mat 2006, 5, 683–696. [Google Scholar]
- Beek, WJE; Janssen, RAJ. Photoinduced Electron Transfer in Heterosupramolecular Assemblies of TiO2 Nanoparticles and Terthiophene Carboxylic Acid in Apolar Solvents. Adv. Funct. Mater 2002, 12, 519–525. [Google Scholar]
- Huynh, WU; Dittmer, JJ; Alivisatos, AP. Hybrid Nanorod-Polymer Solar Cells. Science 2002, 295, 2425–2427. [Google Scholar]
- Gur, I; Fromer, NA; Chen, CP; Kanaras, AG; Alivisatos, AP. Hybrid Solar Cells with Prescribed Nanoscale Morphologies Based on Hyperbranched Semiconductor Nanocrystals. Nano Lett 2007, 7, 409–414. [Google Scholar]
- Clapp, AR; Mednitz, IL; Fisher, BR; Anderson, GP; Mattoussi, H. Can Luminescent Quantum Dots Be Efficient Energy Acceptors with Organic Dye Donors? J. Am. Chem. Soc 2005, 127, 1242–1250. [Google Scholar]
- Dayal, S; Lou, Y; Samia, ACS; Berlin, JC; Kenney, ME; Burda, C. Observation of Non-Förster-Type Energy-Transfer Behavior in Quantum Dot-Phthalocyanine Conjugates. J. Am. Chem. Soc 2006, 128, 13974–13975. [Google Scholar]
- Lim, TC; Bailey, VJ; Ho, Y-P; Wang, T-H. Intercalating Dyes as an Acceptor in Quantum-Dot-Mediated FRET. Nanotechnology 2008, 19, 75701. [Google Scholar]
- Hohng, S; Ha, T. Single-Molecule Quantum-Dot Fluorescence Resonance Energy Transfer. Chem. Phys. Chem 2005, 6, 956–960. [Google Scholar]
- Roy, R; Hohng, S; Ha, T. A Practical Guide to Single-Molecule FRET. Nat. Meth 2008, 5, 507–516. [Google Scholar]
- Anni, M; Manna, L; Cigolani, R; Valerini, D; Creti, A; Lomascolo, M. Förster Energy Transfer from Blue-emitting Polymers to Colloidal CdSe/ZnS Core Shell Quantum Dots. Appl. Phys. Lett 2004, 85, 4169–4171. [Google Scholar]
- Ginger, DS; Greenham, NC. Photoinduced Electron Transfer from Conjugated Polymers to CdSe Nanocrystals. Phys. Rev. B 1999, 59, 10622–10629. [Google Scholar]
- Potapova, I; Mruk, R; Hübner, C; Zentel, R; Basché, T; Mews, A. CdSe/ZnS Nanocrystals with Dye-Functionalized Polymer Ligands Containing Many Anchor goups. Angew. Chem 2005, 117, 2490–2493. [Google Scholar]
- Clapp, AR; Medintz, IL; Mauro, JM; Fisher, BR; Bawendi, MG; Mattoussi, H. Fluorescence Resonance Energy Transfer Between Quantum Dot Donors and Dye-Labeled Protein Acceptors. J. Am. Chem. Soc 2004, 126, 301–310. [Google Scholar]
- Pons, T; Medintz, IL; Sykora, M; Matoussi, H. Spectrally Resolved Energy Transfer using Quantum Dot Donors: Ensemble and Single-Molecule Photoluminescence Studies. Phys Rev B 2006, 73, 245302:1–245302:7. [Google Scholar]
- Medintz, IL; Clapp, AR; Mattoussi, H; Goldman, ER; Fisher, B; Mauro, M. Self-assembled Nanoscale Biosensors Based on Quantum Dot FRET Donors. Nat Mat 2003, 630–638.
- Ji, X; Copenhaver, D; Sichmeller, C; Peng, X. Ligand Bonding and Dynamics on Colloidal Nanocrystals at Room Temperature: The Case of Alkylamines on CdSe Nanocrystals. J. Am. Chem. Soc 2008, 130, 5726–5735. [Google Scholar]
- Ren, T; Mandal, PK; Erker, W; Liu, Z; Avlasevich, Y; Puhl, L; Müllen, K; Basché, T. A Simple and Versatile Route to Stable Quantum Dot-Dye Hybrids in Nonaqueous and Aqueous Solutions. J. Am. Chem. Soc 2008, 130, 17240–17241. [Google Scholar]
- Hofkens, J; Vosch, T; Maus, M; Köhn, F; Cotlet, M; Weil, T; Herrmann, A; Müllen, K; De Schryver, FC. Conformational Rearrangements in and Twisting of a Single Molecule. Chem. Phys. Lett 2001, 333, 255–263. [Google Scholar]
- Landes, C; Burda, C; Braun, M; El-Sayed, MA. Electron Shuttling Across the Interface of CdSe Nanoparticles Monitored by Femtosecond Laser Spectroscopy. J. Phys. Chem. B 2001, 105, 2981–2986. [Google Scholar]
- Boulebaa, A; Issac, A; Stockwell, D; Huang, Z; Huang, J; Gao, J; Lian, T. Photoinduced Ultrafast Electron Transfer from CdSe Quantum Dots to Re-bipyridyl Complexes. J. Am. Chem. Soc 2007, 129, 1532–15133. [Google Scholar]
- Issac, A; Jin, S; Lian, T. Intermittent Electron Transfer Activity from Single CdSe/ZnS Quantum Dots. J. Am. Chem. Soc 2008, 130, 11280–11281. [Google Scholar]
- Petrov, EP; Cichos, F; von Borczyskowski, C. Intrinsic Photophysics of Semiconductor Nanocrystals in Dielectric Media: Formation of Surface States. J Luminesc 2006, 119–120, 412–417. [Google Scholar]
- Zenkevich, EI; Blaudeck, T; Shulga, A; Cichos, F; von Borczyskowski, C. Identification and Assignment of Porphyrin–CdSe Hetero-Nanoassemblies. J. Luminesc 2007, 122, 784–788. [Google Scholar]
- Lakowicz, J. Principles of Fluorescence Spectroscopy; Springer: New York, NY, USA, 2006. [Google Scholar]
- von Borczyskowski, C; Cichos, F; Martin, J; Schuster, J; Issac, A; Brabandt, J. Common Luminescence Intensity Fluctuations of Single Particle and Single Molecules in Non-conducing Matrices. Eur. Phys. J. 2007, 144, 13–25. [Google Scholar]
- Xu, CS; Kim, H; Yang, H; Hayden, CC. Multiparameter Fluorescence Spectroscopy of Single Quantum Dot-Dye FRET Hybrids. J. Am. Chem. Soc 2007, 129, 11008. [Google Scholar]
- van Sark, W; Frederix, P; Bol, A; Gerritsen, H; Meijerink, A. Blueing, Bleaching, and Blinking of Single CdSe/ZnS Quantum Dots. ChemPhysChem 2002, 3, 871–879. [Google Scholar]
- Bae, WK; Nam, MK; Char, K; Lee, S. Gram-Scale One-Pot Synthesis of Highly Luminescent Blue Emitting Cd1-xZnxS/ZnS Nanocrystals. Chem. Mater 2008, 20, 5307–5313. [Google Scholar]
- Lu, H; Schops, O; Woggon, U; Niemeyer, CM. Self-Assembled Donor Comprising Quantum Dots and Fluorescent Proteins for Long-Range Fluorescence Resonance Energy Transfer. J. Am. Chem. Soc 2008, 130, 4815–4827. [Google Scholar]
- Valeur, B. Molecular Fluorescence – Prinicples and Applications; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Fron, E; Schweitzer, G; Osswald, P; Würthner, F; Marsal, P; Beljonne, D; Müllen, K; De Schryver, FC; Van der Auweraer, M. Photophysical Study of Bay substituted Perylenediimides. Photochem. Photobiol. Sci 2008, 7, 1509–1521. [Google Scholar]
- Lang, E; Würthner, F; Köhler, J. Photophysical Properties of a Tetraphenoxy-Substituted Perylene Bisimide Derivative Characterized by Single-Molecule Spectroscopy. ChemPhysChem 2005, 6, 935–941. [Google Scholar]
- Würthner, F; Sautter, A; Schmid, D; Weber, PJA. Fluorescent and Electroactive Cyclic Assemblies from Perylene Tetracarboxylic Acid Bisimide Ligands and Metal Phosphane Triflates. Chem. Eur. J. 2001, 7, 894–902. [Google Scholar]
- Zenkevich, EI; Shulga, AM; Blaudeck, T; von Borczyskowski, C. Physics, Chemistry and Application of Nanostructures; Borisenko, VI, Gaponenko, SV, Gurin, VS, Eds.; World Scientific Publishing: Singapore, 2007; pp. 133–136. [Google Scholar]

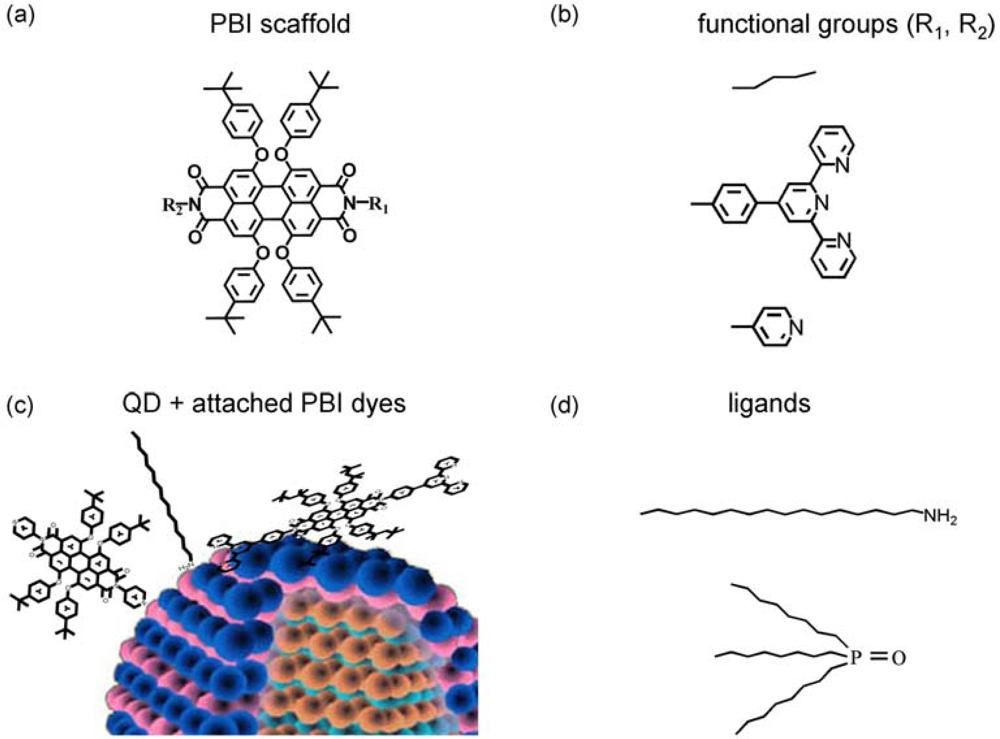
| Abbreviation | R1 | R2 |
|---|---|---|
| PP | pyr | alk |
| DPP | pyr | pyr |
| TPP | tpy | alk |
| DTPP | tpy | tpy |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kowerko, D.; Krause, S.; Amecke, N.; Abdel-Mottaleb, M.; Schuster, J.; Von Borczyskowski, C. Identification of Different Donor-Acceptor Structures via Förster Resonance Energy Transfer (FRET) in Quantum-Dot-Perylene Bisimide Assemblies. Int. J. Mol. Sci. 2009, 10, 5239-5256. https://doi.org/10.3390/ijms10125239
Kowerko D, Krause S, Amecke N, Abdel-Mottaleb M, Schuster J, Von Borczyskowski C. Identification of Different Donor-Acceptor Structures via Förster Resonance Energy Transfer (FRET) in Quantum-Dot-Perylene Bisimide Assemblies. International Journal of Molecular Sciences. 2009; 10(12):5239-5256. https://doi.org/10.3390/ijms10125239
Chicago/Turabian StyleKowerko, Danny, Stefan Krause, Nicole Amecke, Mohamed Abdel-Mottaleb, Jörg Schuster, and Christian Von Borczyskowski. 2009. "Identification of Different Donor-Acceptor Structures via Förster Resonance Energy Transfer (FRET) in Quantum-Dot-Perylene Bisimide Assemblies" International Journal of Molecular Sciences 10, no. 12: 5239-5256. https://doi.org/10.3390/ijms10125239
APA StyleKowerko, D., Krause, S., Amecke, N., Abdel-Mottaleb, M., Schuster, J., & Von Borczyskowski, C. (2009). Identification of Different Donor-Acceptor Structures via Förster Resonance Energy Transfer (FRET) in Quantum-Dot-Perylene Bisimide Assemblies. International Journal of Molecular Sciences, 10(12), 5239-5256. https://doi.org/10.3390/ijms10125239




