Excess Properties, FT-IR Spectral Analysis, and CO2 Absorption Performance of Monoethanolamine with Diethylene Glycol Monoethyl Ether or Methyldiethanolamine Binary Solutions
Abstract
1. Introduction
2. Results and Discussion
2.1. Density and Viscosity
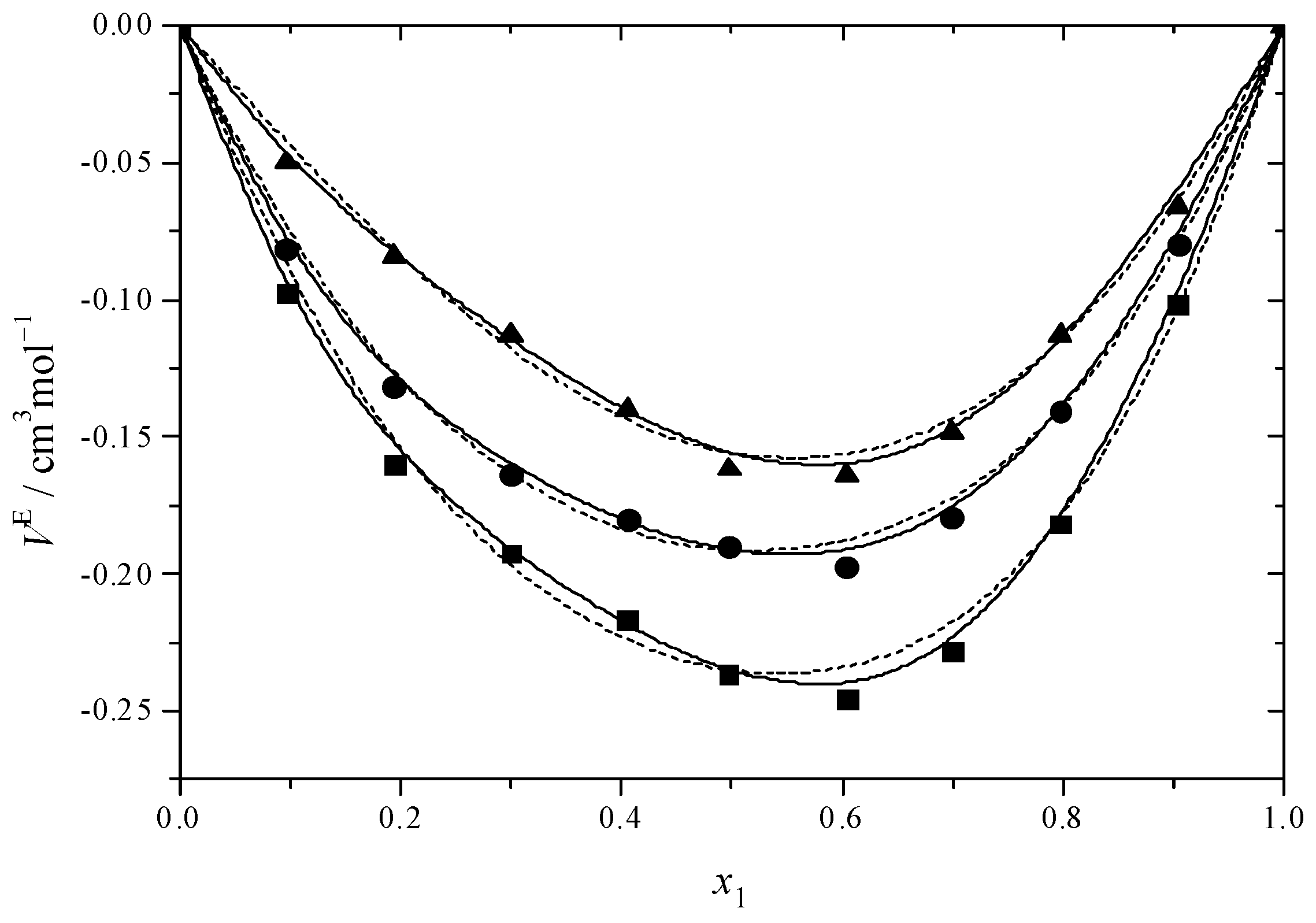
2.2. Excess Properties
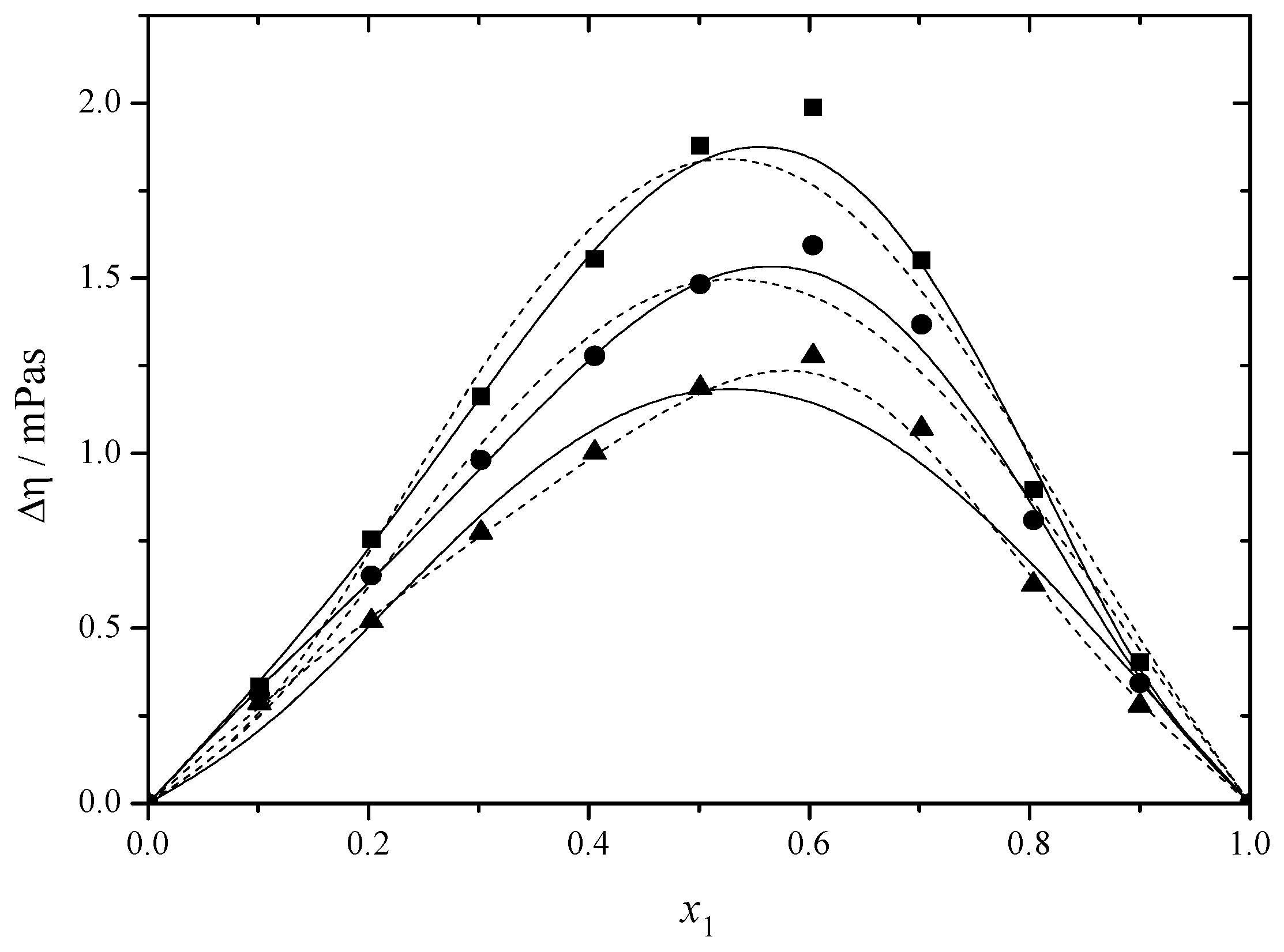
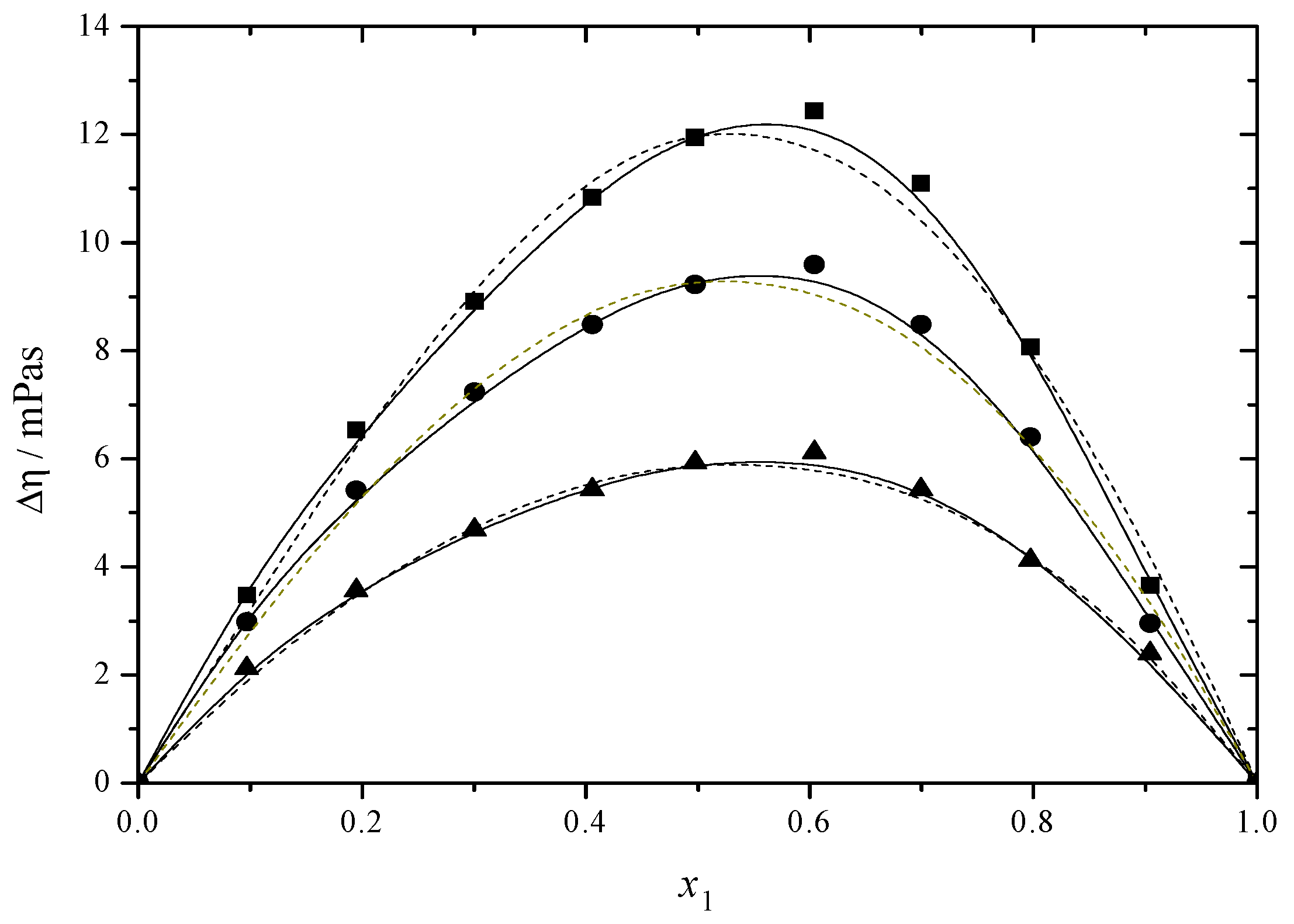
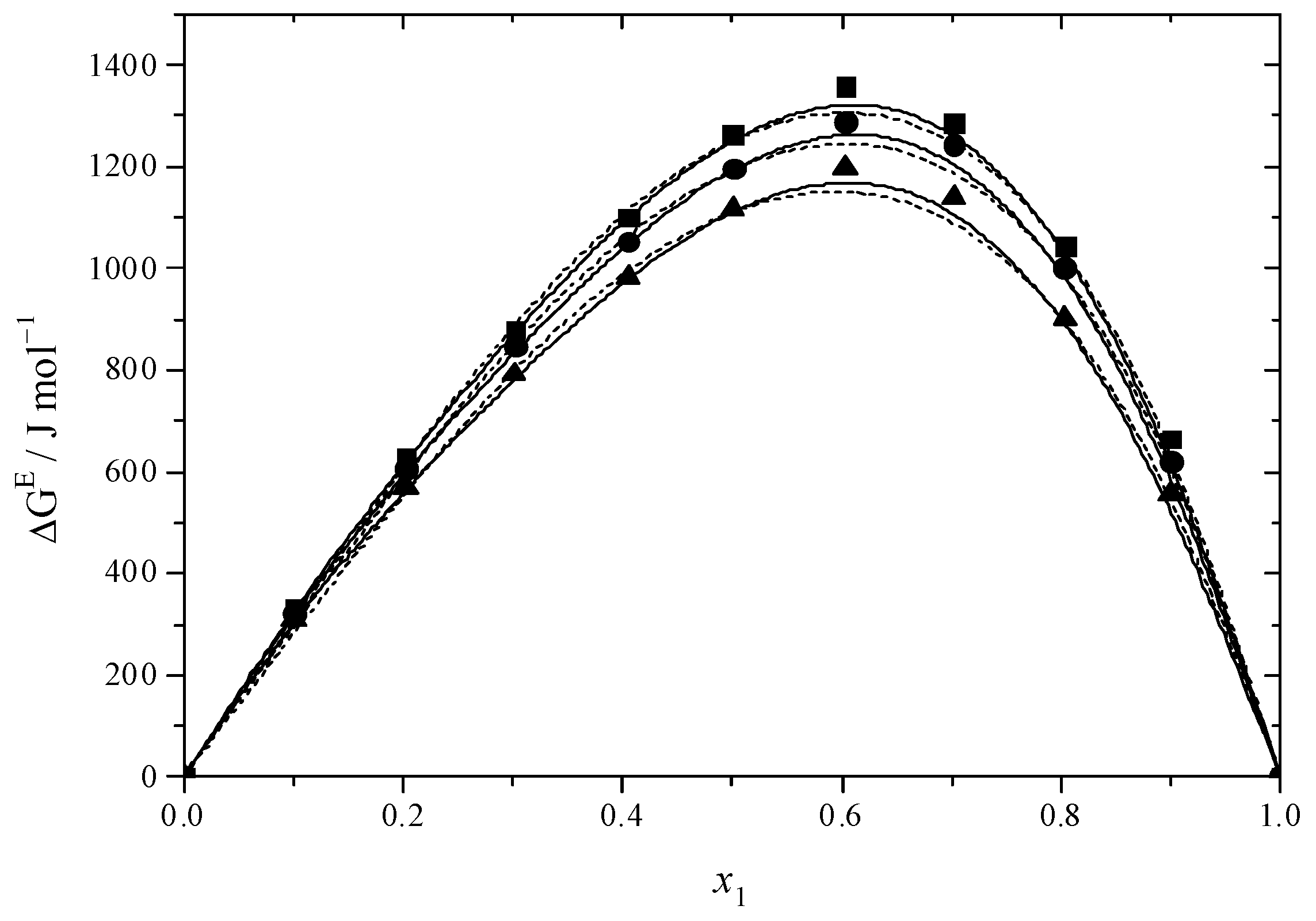
2.3. Thermodynamic Functions of Activation
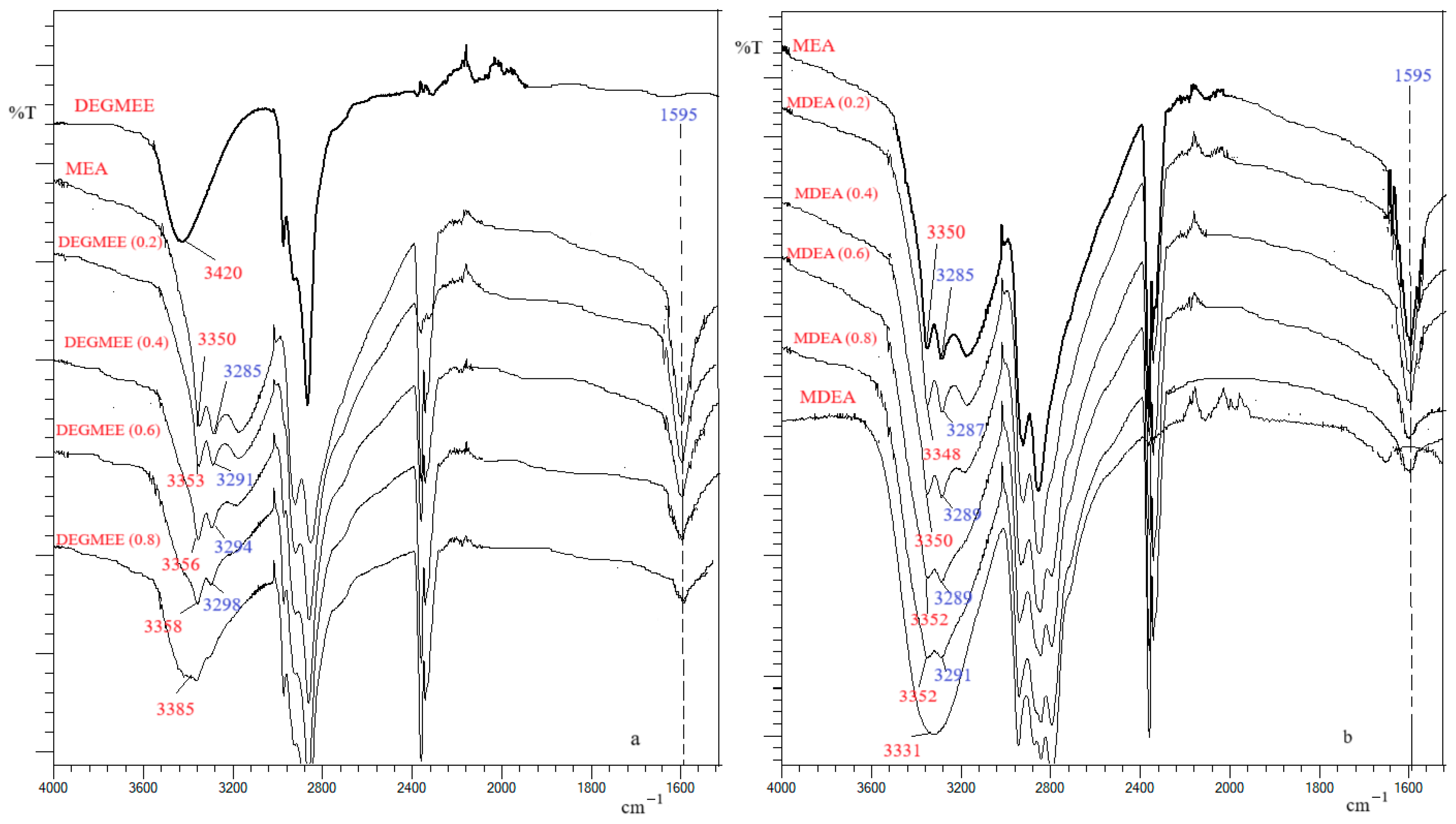
2.4. FT-IR Spectra
2.5. CO2 Absorption
3. Materials and Methods
3.1. Materials
3.2. Experimental Analysis
3.3. Spectral Analyses
3.4. CO2 Absorption
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, K.; Dong, X.; Jiang, Q.; Zhao, J. Assessing energy resilience and its greenhouse effect: A global perspective. Energy Econ. 2021, 104, 105659. [Google Scholar] [CrossRef]
- Wang, L.; Liu, S.; Wang, R.; Li, Q.; Zhang, S. Regulating phase separation behavior of a DEEA-TETA biphasic solvent using sulfolane for energy-saving CO2 capture. Environ. Sci. Technol. 2019, 53, 12873–12881. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Shi, H.; Lee, J.Y. CO2 absorption mechanism in amine solvents and enhancement of CO2 capture capability in blended amine solvent. Int. J. Greenh. Gas Control 2016, 45, 181–188. [Google Scholar] [CrossRef]
- Yu, K.M.K.; Curcic, I.; Gabriel, J.; Tsang, S.C.E. Recent advances in CO2 capture and utilization. ChemSusChem 2008, 1, 893–899. [Google Scholar] [CrossRef]
- Richner, G. Promoting CO2 absorption in aqueous amines with benzylamine. Energy Procedia 2013, 37, 423–430. [Google Scholar] [CrossRef]
- Yang, H.; Xu, Z.; Fan, M.; Gupta, R.; Slimane, R.B.; Bland, A.E.; Wright, I. Progress in carbon dioxide separation and capture: A review. J. Environ. Sci. 2008, 20, 14–27. [Google Scholar] [CrossRef]
- Shekhah, O.; Belmabkhout, Y.; Chen, Z.; Guillerm, V.; Cairns, A.; Adil, K.; Eddaoudi, M. Made-to-order metal-organic frameworks for trace carbon dioxide removal and air capture. Nat. Commun. 2014, 5, 4228. [Google Scholar] [CrossRef] [PubMed]
- Wilmer, C.E.; Farha, O.K.; Bae, Y.-S.; Hupp, J.T.; Snurr, R.Q. Structure-property relationships of porous materials for carbon dioxide separation and capture. Energy Environ. Sci. 2012, 5, 9849–9856. [Google Scholar] [CrossRef]
- Razzak, S.A.; Ali, S.A.M.; Hossain, M.M.; deLasa, H. Biological CO2 fixation with production of microalgae in wastewater-a review. Renew. Sustain. Energy Rev. 2017, 76, 379–390. [Google Scholar] [CrossRef]
- Zhu, Q. Developments on CO2-utilization technologies. Clean Energy 2019, 3, 85–100. [Google Scholar] [CrossRef]
- Wang, M.; Lawal, A.; Stephenson, P.; Sidders, J.; Ramshaw, C. Post-combustion CO2 capture with chemical absorption: A state-of-the-art review. Chem. Eng. Res. Des. 2011, 89, 1609–1624. [Google Scholar] [CrossRef]
- Freeman, S.A.; Dugas, R.; Van Wagener, D.H.; Nguyen, T.; Rochelle, G.T. Carbon dioxide capture with concentrated, aqueous piperazine. Int. J. Greenh. Gas Control 2010, 4, 119–124. [Google Scholar] [CrossRef]
- Ghosh, U.K.; Kentish, S.E.; Stevens, G.W. Absorption of carbon dioxide into aqueous potassium carbonate promoted by boric acid. Energy Procedia 2009, 1, 1075–1081. [Google Scholar] [CrossRef][Green Version]
- Mumford, K.A.; Wu, Y.; Smith, K.H.; Stevens, G.W. Review of solvent based carbon-dioxide capture technologies. Front. Chem. Sci. Eng. 2015, 9, 125–141. [Google Scholar] [CrossRef]
- Vitillo, J.C.; Smit, B.; Gagliardi, L. Introduction: Carbon capture and separation. Chem. Rev. 2017, 117, 9521–9523. [Google Scholar] [CrossRef] [PubMed]
- Budzianowski, W.M. Explorative analysis of advanced solvent processes for energy efficient carbon dioxide capture by gas-liquid absorption. Int. J. Greenh. Gas Control 2016, 49, 108–120. [Google Scholar] [CrossRef]
- Guo, H.; Dong, Y.; Ping, T.; Shi, X.; Shen, S. Density, viscosity and excess properties of binary mixtures of monoethanolamine and 2-alkoxyethanols as temperatures from (293.15 to 353.15) K. J. Mol. Liq. 2020, 299, 112191. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, Y.; Cao, R.; Zang, J.; Ma, K.; Zhang, J. Fundamental physicochemical properties, intermolecular interactions and CO2 absorption properties of binary mixed solutions of monoethanolamine + diethylenetriamine. J. Mol. Liq. 2024, 413, 125974. [Google Scholar] [CrossRef]
- Tan, J.; Shao, H.; Xu, J.; Du, L.; Lu, G. Mixture absorption system of monoethanolamine triethylene glycol for CO2 capture. Ind. Eng. Chem. Res. 2011, 50, 3966–3976. [Google Scholar] [CrossRef]
- Zhang, J.; Zhai, W.; Wang, Y.; Zhang, B.; Ma, X.; Ma, K.; Zhang, J. Excess properties, intermolecular interaction, and CO2 capture performance of diethylene glycol monomethyl ether + ethylenediamine binary mixed solutions. J. Mol. Liq. 2025, 417, 126561. [Google Scholar] [CrossRef]
- Chai, L.; Wang, Y.; Wang, X.; Wang, E.; Zhai, W.; Ma, K.; Zhang, J. Basic physicochemical properties, excess properties, and intermolecular interactions of n-propanol/isopropanol and ethylenediamine binary mixtures. J. Mol. Liq. 2023, 389, 122868. [Google Scholar] [CrossRef]
- Cao, R.; Wang, X.; Zhai, W.; Chai, L.; Wang, E.; Wang, Y.; Ma, K.; Zhang, J. Excess properties and intermolecular interactions of 2-methoxyethanol + ethylenediamine binary system: Density, viscosity, spectral analyses, computational chemistry, and CO2 absorption property. J. Chem. Thermodyn. 2024, 195, 107313. [Google Scholar] [CrossRef]
- Feng, M.; Wang, X.; Chai, L.; Wang, E.; Wang, Y.; Wei, F.; Zhang, J. Density, viscosity, excess properties, and intermolecular interaction of propylene glycol methyl ether+1,2-propylenediamine binary system. J. Mol. Liq. 2024, 400, 124554. [Google Scholar] [CrossRef]
- Zhai, W.; Chai, L.; Wang, E.; Wang, X.; Zang, J.; Ma, K.; Zhang, J. Excess properties, intermolecular interactions, and CO2 absorption property of ethylene glycol + diethylenetriamine binary solutions. J. Mol. Liq. 2024, 395, 123954. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chai, L.; Wang, E.; Wei, X.; Wu, Z.; Zhang, J. Excess properties, spectral analyses, and CO2 capture performance of N-methyldiethanolamine + polyethylene glycol 300 binary system. J. Mol. Liq. 2023, 390 (Pt B), 123165. [Google Scholar] [CrossRef]
- Chai, L.; Xing, G.; Wang, W.; Zhao, Z.; Zhang, J.; Cao, J. Excess properties, computational chemistry and spectroscopic analyses of 1,2-propanediamine+n-propanol/isopropanol binary mixtures. J. Mol. Liq. 2023, 382, 121896. [Google Scholar] [CrossRef]
- Versteeg, G.F.; Van Swaaij, W.P.M. Solubility and diffusivity of acid gases (carbon dioxide, nitrous oxide) in aqueous alkanolamine solutions. J. Chem. Eng. Data 1988, 33, 29–34. [Google Scholar] [CrossRef]
- Aronu, U.E.; Hartono, A.; Svendsen, H.F. Density, viscosity, and N2O solubility of aqueous amino acid salt and amine amino acid salt solutions. J. Chem. Thermodyn. 2012, 45, 90–99. [Google Scholar] [CrossRef]
- Cleeton, C.; Kvam, O.; Rea, R.; Sarkisov, L.; De Angelis, M.G. Competitive H2S-CO2 absorption in reactive aqueous methyldiethanolamine solution: Prediction with ePC-SAFT. Fluid Phase Equilibria 2020, 511, 112453. [Google Scholar] [CrossRef]
- Li, M.; Liu, X.; Zhu, C.; Fu, T.; Gao, X.; Ma, Y. Volumetric and viscometric properties of monoethanolamine (MEA) + 3-dimethylamino-1-propanol (3DMA1P) + H2O at T = (293.15 to 333.15) K. J. Chem. Thermodyn. 2023, 180, 107018. [Google Scholar] [CrossRef]
- Geng, Y.; Chen, S.; Wang, T.; Yu, D.; Peng, C.; Liu, H.; Hu, Y. Density, viscosity and electrical conductivity of 1-butyl-3-methylimidazolium hexafluorophosphate + monoethanolamine and + N, N-dimethylethanolamine. J. Mol. Liq. 2008, 143, 100–108. [Google Scholar] [CrossRef]
- Valtz, A.; Coquelet, C.; Richon, D. Volumetric properties of the monoethanolamine methanol mixture at atmospheric pressure from 283.15 to 353.15 K. Termochimica Acta 2005, 428, 185–191. [Google Scholar] [CrossRef]
- Moosavi, M.; Sisco, C.J.; Rostami, A.A.; Vargas, F.M. Thermodynamic properties and CO2 solubility of monoethanolamine + diethylenetriamine/aminoethylethanolamine mixtures: Experimental measurements and thermodynamic modelling. Fluid Phase Equilibria 2017, 449, 175–185. [Google Scholar] [CrossRef]
- Hernandez-Mendoza, M.; Zuniga-Moreno, A.; Manriquez-Ramirez, M.E.; Elizalde-Solis, O. Densities and excess molar volumes of binary systems N,N-Dimethylformamide + Ethanolamine or N,N-Diethylethanolamine. J. Solut. Chem. 2014, 43, 1981–1996. [Google Scholar] [CrossRef]
- Song, J.-H.; Park, S.-B.; Yoon, J.-H.; Lee, H. Densities and viscosities of monoethanolamine + ethylene glycol + water. J. Chem. Eng. Data 1996, 41, 1152–1154. [Google Scholar] [CrossRef]
- Li, X.; Xu, G.; Wang, Y.; Hu, Y. Density, Viscosity, and Excess Properties for Binary Mixture of Diethylene Glycol Monoethyl Ether + Water from 293.15 to 333.15 K at Atmospheric Pressure. Chin. J. Chem. Eng. 2009, 17, 1009–1013. [Google Scholar] [CrossRef]
- Tseng, Y.-M.; Thompson, A.R. Communication. Densities and refractive indices of diethylene glycol ether—Water solutions. J. Chem. Eng. Data 1962, 7, 483. [Google Scholar] [CrossRef]
- Dhondge, S.S.; Pandhurnekar, C.P.; Parwate, D.V. Thermodynamic and optical studies of some ethylene glycol ethers in aqueous solutions at T = 298.15 K. J. Chem. Thermodyn. 2009, 41, 577–585. [Google Scholar] [CrossRef]
- Suneetha, P.; Srinivasa Krishna, T.; Gowrisankar, M.; Ramachandran, D. Volumetric, acoustic and spectroscopic study of 1-butyl-3-methylimidazolium trifluoromethanesulfonate with alkoxyalkanols at different temperatures. J. Mol. Liq. 2017, 238, 170–183. [Google Scholar] [CrossRef]
- Haghtalab, A.; Shojaeian, A. Volumetric and viscometric behaviour of the binary systems of N-methyldiethanolamine and diethanolamine with 1-butyl-3-methylimidazolium acetate at various temperatures. J. Chem. Thermodyn. 2014, 68, 128–137. [Google Scholar] [CrossRef]
- Yin, Y.; Fu, T.; Zhu, C.; Ma, Y. Volumetric and viscometric study and FT-IR analysis of binary and ternary mixtures of 1-butyl-3-methylimidazolium tetrafluoroborate, methyldiethanolamine and water. J. Mol. Liq. 2017, 243, 664–676. [Google Scholar] [CrossRef]
- DiGuilio, R.M.; Lee, R.j.; Schaffer, S.T.; Brasher, L.L.; Teja, A.S. Densities and viscosities of the ethanolamines. J. Chem. Eng. Data 1992, 37, 239–242. [Google Scholar] [CrossRef]
- Bernal-Garcia, J.M.; Ramos-Estrada, M.; Iglesias-Silva, A.; Hall, K.R. Densities and excess molar volumes of aqueous solutions of n-Methyldiethanolamine (MDEA) at temperatures from (283.15 to 363.15) K. J. Chem. Eng. Data 2003, 48, 1442–1445. [Google Scholar] [CrossRef]
- Yin, Y.; Zhu, C.; Ma, Y. Volumetric and viscometric properties of binary and ternary mixtures of 1-butyl-3-methylimidazolium tetrafluoroborate, monoethanolamine and water. J. Chem. Thermodyn. 2016, 102, 413–428. [Google Scholar] [CrossRef]
- Alvarez, E.; Cerdeira, F.; Gomez-Diaz, D.; Navaza, J.M. Density, speed of sound, isentropic compressibility, and excess volume of (monoethanolamine + 2-amino-2-methyl-1-propanol), (monoethanolamine + triethanolamine), and (monoethanolamine + n-methyldiethanolamine) at temperatures from (293.15 to 323.15) K. J. Chem. Eng. Data 2010, 55, 994–999. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, S.; Zhang, W.; Lan, Y.; Zhang, X. Density, viscosity, conductivity, refractive index and interaction study of binary mixtures of the ionic liquid 1-ethyl-3-methylimidazolium acetate with methyldiethanolamine. J. Mol. Liq. 2017, 233, 471–478. [Google Scholar] [CrossRef]
- Karunarathne, S.S.; Eimer, D.A.; Oi, L.E. Density, Viscosity, and Excess Properties of MDEA + H2O, DMEA + H2O, and DEEA + H2O Mixtures. Appl. Sci. 2020, 10, 3196. [Google Scholar] [CrossRef]
- Al-Ghawas, H.A.; Hagewiesche, D.P.; Ruiz-Ibanez, G.; Sandall, O.C. Physicochemical properties important for carbon dioxide absorption in aqueous methyldiethanolamine. J. Chem. Eng. Data 1989, 34, 385–391. [Google Scholar] [CrossRef]
- Belda, R. A proposed equation of correlation for the study of thermodynamic properties (density, viscosity, surface tension and refractive index) of liquid binary mixtures. Fluid Phase Equilibria 2009, 282, 88–99. [Google Scholar] [CrossRef]
- Herraez, J.V.; Belda, R.; Diez, O.; Herraez, M. An equation for the correlation of viscosities of binary mixtures. J. Sol. Chem. 2008, 37, 233–248. [Google Scholar] [CrossRef]
- Emmerling, U.; Figurski, G.; Rasmussen, P. Densities and kinematic viscosities for the systems benzene + methyl formate, benzene + ethyl formate, benzene + propyl formate, and benzene + butyl formate. J. Chem. Eng. Data 1998, 43, 289–292. [Google Scholar] [CrossRef]
- Gonzales-Olmos, R.; Iglesias, M. Influence of temperature on thermodynamics of ethers + xylenes. Fluid Phase Equilibria 2008, 267, 133–139. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Indust. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Grunberg, L.; Nissan, A.H. Mixture law for viscosity. Nature 1949, 164, 799–800. [Google Scholar] [CrossRef]
- Heric, E.L.; Brewer, J.G. Viscosity of some binary liquid nonelectrolyte mixtures. J. Chem. Eng. Data 1967, 12, 574–583. [Google Scholar] [CrossRef]
- McAllister, R.A. The viscosity of liquid mixtures. Am. Inst. Chem. Eng. 1960, 6, 427–431. [Google Scholar] [CrossRef]
- Jouyban, A.; Khoubnasabjafari, M.; Vaez-Gharamaleki, Z.; Fekari, Z.; Acree, W.E., Jr. Calculation of the viscosity of binary liquids at various temperatures using Jouyban-Acree model. Chem. Pharm. Bull. 2005, 53, 519–523. [Google Scholar] [CrossRef]
- Jouyban, A.; Azarbayiani, A.F.; Khoubnasabjafari, M.; Acree, W. Mathematical representation of the density of liquid mixtures at various temperatures using Jouyban-Acree model. Indian J. Chem. 2005, 44, 1553–1560. [Google Scholar]
- Redlich, O.; Kister, A.T. Algebraic Representation of Thermodynamic Properties and the Classification of Solutions. Ing. Eng. Chem. 1948, 40, 345–348. [Google Scholar] [CrossRef]
- Hwang, C.A.; Holste, J.C.; Hall, K.R.; Mansoori, G.A. A simple relation to predict or to correlate the excess functions of multicomponent mixtures. Fluid Phase Equilibria 1991, 62, 173–189. [Google Scholar] [CrossRef]
- Sharma, V.K.; Bhagour, S.; Sharma, D. Thermodynamic properties of ternary mixtures of 1-ethyl-3-methylimidazolium tetrafluoroborate with 1-methyl pyrrolidin-2-one or pyrrolidin-2-one + water. Thermochim. Acta 2013, 563, 72–81. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J.B. Intermolecular interaction of diamine-diol binary system: A mini-review. Adv. Colloid. Interfac. 2024, 304, 102662. [Google Scholar] [CrossRef]
- Bhagat, P.; Maken, S. Modeling of transport and volumetric properties of tributylamine based absorbents for CO2 capture. J. Mol. Liq. 2021, 326, 115240. [Google Scholar] [CrossRef]
- DeLuca, P.P.; Rebagay, T.V.; Casteel, J.F. The dielectric constant and dipole moment of N,N,N′, N′-tetramethylpimelamide at 25.degree.C. J. Chem. Eng. Data 1976, 21, 262–264. [Google Scholar] [CrossRef]
- Ouaar, F.; Negadi, A.; Bahadur, I.; Phadagi, R.; Feddal-Benabed, B.; Negadi, L. Volumetric, acoustic and transport properties of mixtures containing dimethyl sulfoxide and some amines or alkanolamines: Measurement and correlation. J. Chem. Thermodyn. 2018, 121, 197–198. [Google Scholar] [CrossRef]
- Rafiee, H.R.; Ranjbar, S.; Poursalman, F. Densities and viscosities of binary and ternary mixtures of cyclohexanone, 1,4-dioxane and isooctane from T=(288.15 to 313.15)K. J. Chem. Thermodyn. 2012, 54, 266–271. [Google Scholar] [CrossRef]
- Dominquez, M.; Pardo, J.I. Viscosities of the ternary mixture (2-butanol+n-hexane+1-butylamine) at 298.15 and 313.15 K. Fluid Phase Equilibria 2000, 169, 277–292. [Google Scholar] [CrossRef]
- Dubey, G.P.; Sharma, M.; Dubey, N. Study of densities, viscosities, and speeds of sound of binary liquid mixtures of butan-1-ol with n-alkanes (C6, C8, and C10) at T = (298.15, 303.15, and 308.15)K. J. Chem. Thermodyn. 2008, 40, 309–320. [Google Scholar] [CrossRef]
- Altun, A.; Sara, O.N. Density, viscosity and excess properties of binary mixtures of ethylene glycol and 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl) imide. J. Mol. Liq. 2022, 358, 119221. [Google Scholar] [CrossRef]
- Eyring, H.; Jhon, M.S. Significant Liquid Structures; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Avram, M.; Mateescu, G.D. Spectroscopia in Infrarosu. Aplicatii in Chimia Organica; Ed. Tehnica: Bucuresti, Romania, 1966. [Google Scholar]
- Darde, V.; Thomsen, K.; van Well, W.J.M.; Stenby, E.H. Chilled ammonia process for CO2 capture. Int. J. Greenh. Gas Control 2010, 4, 131–136. [Google Scholar] [CrossRef]



| Component | T/(K) | ρ/(g·cm−3) | η/(mPas) | ||
|---|---|---|---|---|---|
| This Work | Lit. Value | This Work | Lit. Value | ||
| MEA | 293.15 298.15 303.15 | 1.0162 1.0125 1.0095 | 1.0158 [30] 1.0156 [31] 1.0161 [32] 1.0120 [31] 1.0124 [33] 1.0125 [34] 1.0091 [35] 1.0082 [31] 1.0084 [33] | 23.77 18.65 14.79 | 23.54 [30] 23.66 [31] 23.65 [44] 18.64 [31] 18.88 [45] 14.60 [30] 15.04 [31] 14.75 [44] |
| DEGMEE | 293.15 298.15 303.15 | 0.9890 0.9848 0.9805 | 0.9887 [36] 0.9885 [37] 0.9842 [36] 0.9846 [38] 0.9794 [36] 0.9791 [39] | 4.59 3.89 3.41 | 4.551 [36] 3.861 [36] 3.368 [36] |
| MDEA | 293.15 298.15 303.15 | 1.0402 1.0362 1.0325 | 1.0406 [40] 1.03966 [41] 1.03556 [42] 1.037863 [43] 1.0367 [25] 1.03213 [41] 1.0328 [40] 1.0329 [25] | 102.92 74.93 57.58 | 102.7 [42] 103.3 [40] 74.81 [46] 75.90 [47] 57.57 [48] 57.615 [41] 57.3 [40] |
| T/(K) | ||||||
|---|---|---|---|---|---|---|
| x1 | ρ/(g·cm−3) | η/(mPa·s) | ||||
| 293.15 | 298.15 | 303.15 | 293.15 | 298.15 | 303.15 | |
| DEGMEE (1) + MEA (2) | ||||||
| 0.1013 0.2028 0.3022 0.4052 0.5011 0.6033 0.7020 0.8035 0.9000 | 1.0112 1.0072 1.0040 1.0011 0.9988 0.9966 0.9947 0.9928 0.9909 | 1.0076 1.0034 1.0001 0.9972 0.9948 0.9926 0.9906 0.9887 0.9868 | 1.0044 1.0002 0.9967 0.9936 0.9910 0.9886 0.9865 0.9846 0.9828 | 22.162 20.636 19.136 17.553 16.037 14.185 11.855 9.253 6.909 | 17.467 16.309 15.171 13.949 12.739 11.341 9.660 7.603 5.714 | 13.926 13.004 12.125 11.181 10.274 9.203 7.871 6.270 4.828 |
| MDEA (1) + MEA (2) | ||||||
| 0.0970 0.1949 0.3006 0.4059 0.4978 0.6044 0.6995 0.7972 0.9041 | 1.0218 1.0261 1.0296 1.0325 1.0347 1.0368 1.0382 1.0392 1.0399 | 1.0178 1.0219 1.0254 1.0282 1.0303 1.0324 1.0338 1.0349 1.0358 | 1.0142 1.0180 1.0214 1.0243 1.0265 1.0285 1.0299 1.0310 1.0320 | 34.926 45.730 56.475 66.733 75.117 84.051 90.236 94.933 98.981 | 27.093 35.036 42.804 49.975 55.890 62.256 66.504 69.914 72.488 | 21.066 26.690 32.338 37.598 42.022 46.775 50.157 53.023 55.878 |
| x1 | (kJ/mol) | (J/mol·K) | (kJ/mol) T (K) | ||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | |||
| DEGMEE (1) + MEA (2) | |||||
| 0.0000 0.1013 0.2028 0.3022 0.4052 0.5011 0.6033 0.7020 0.8035 0.9000 1.0000 | 34.57 33.83 33.60 33.17 32.76 32.32 31.38 29.65 28.14 25.88 21.32 | 49.90 46.97 45.89 44.27 42.83 41.45 38.64 33.65 30.01 24.26 11.63 | 19.94 20.06 20.15 20.20 20.21 20.17 20.05 19.79 19.34 18.77 17.91 | 19.69 19.83 19.92 19.97 19.99 19.96 19.86 19.62 19.19 18.65 17.85 | 19.44 19.59 19.69 19.75 19.78 19.75 19.67 19.45 19.04 18.53 17.79 |
| MDEA (1) + MEA (2) | |||||
| 0.0000 0.0970 0.1949 0.3006 0.4059 0.4978 0.6044 0.6995 0.7972 0.9041 1.0000 | 34.57 36.81 39.20 40.60 41.80 42.33 42.71 42.80 42.45 41.69 42.38 | 49.90 53.63 58.88 61.27 63.39 63.72 63.55 62.83 60.80 57.43 59.06 | 19.94 21.09 21.93 22.64 23.22 23.65 24.08 24.38 24.63 24.86 25.07 | 19.69 20.82 21.64 22.33 22.90 23.33 23.76 24.07 24.33 24.57 24.77 | 19.44 20.55 21.35 22.03 22.58 23.01 23.44 23.75 24.02 24.29 24.48 |
| Chemical Name | Molecular Formula | Source | CAS | Mass Fraction Purity | Purification |
|---|---|---|---|---|---|
| MEA DEGMEE MDEA | C2H7NO C6H14O3 C5H13NO2 | Sigma Aldrich Merck Darmstadt, Germany | 141-43-5 111-90-0 105-59-9 | ≥99.0% ≥98.0% ≥98.0% | None None None |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naum, M.M.; Neagu, M.; Dumitrescu, V. Excess Properties, FT-IR Spectral Analysis, and CO2 Absorption Performance of Monoethanolamine with Diethylene Glycol Monoethyl Ether or Methyldiethanolamine Binary Solutions. Molecules 2025, 30, 1523. https://doi.org/10.3390/molecules30071523
Naum MM, Neagu M, Dumitrescu V. Excess Properties, FT-IR Spectral Analysis, and CO2 Absorption Performance of Monoethanolamine with Diethylene Glycol Monoethyl Ether or Methyldiethanolamine Binary Solutions. Molecules. 2025; 30(7):1523. https://doi.org/10.3390/molecules30071523
Chicago/Turabian StyleNaum, Maria Magdalena, Mihaela Neagu, and Vasile Dumitrescu. 2025. "Excess Properties, FT-IR Spectral Analysis, and CO2 Absorption Performance of Monoethanolamine with Diethylene Glycol Monoethyl Ether or Methyldiethanolamine Binary Solutions" Molecules 30, no. 7: 1523. https://doi.org/10.3390/molecules30071523
APA StyleNaum, M. M., Neagu, M., & Dumitrescu, V. (2025). Excess Properties, FT-IR Spectral Analysis, and CO2 Absorption Performance of Monoethanolamine with Diethylene Glycol Monoethyl Ether or Methyldiethanolamine Binary Solutions. Molecules, 30(7), 1523. https://doi.org/10.3390/molecules30071523






