The Role of Chalcogen in the ROS Scavenging Mechanism of Model Phenyl Compounds
Abstract
1. Introduction
2. Results
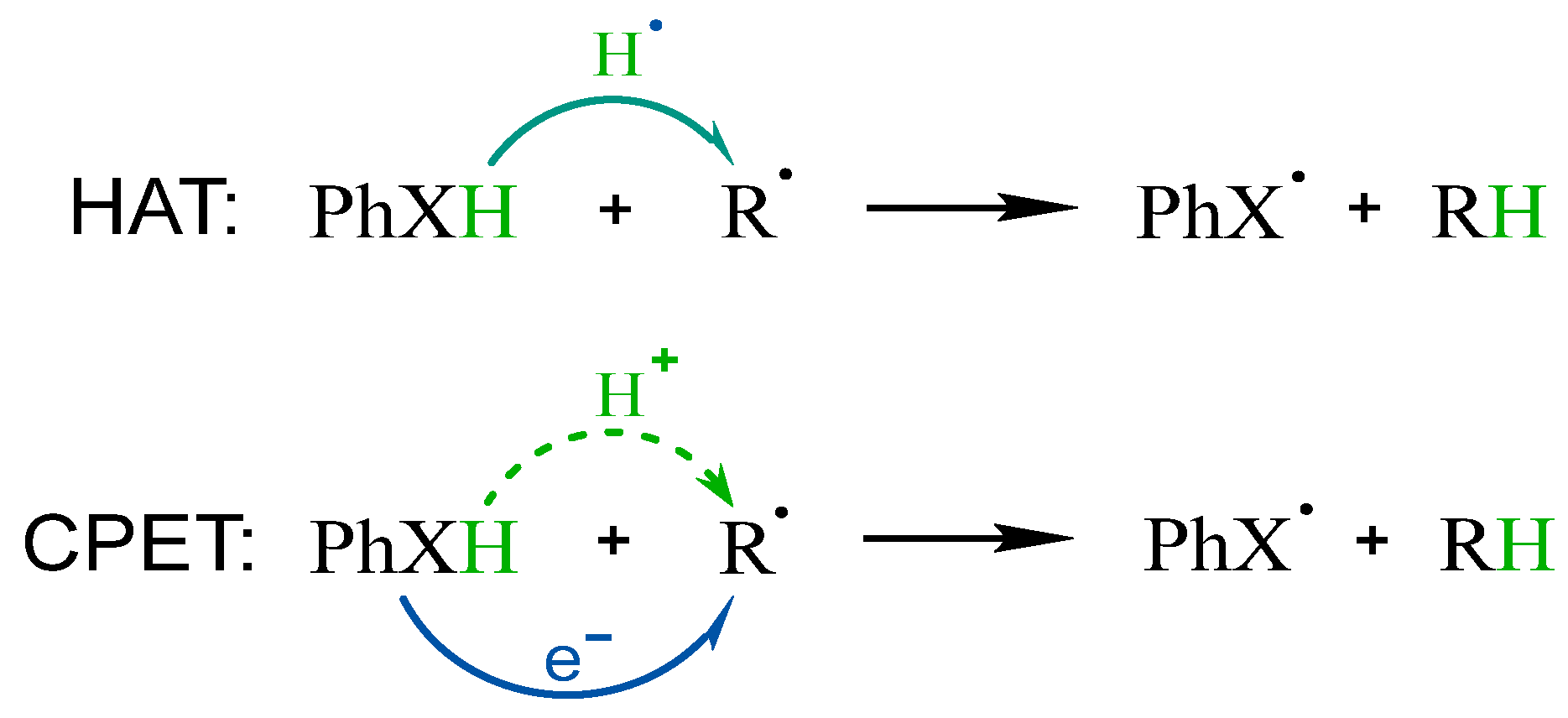
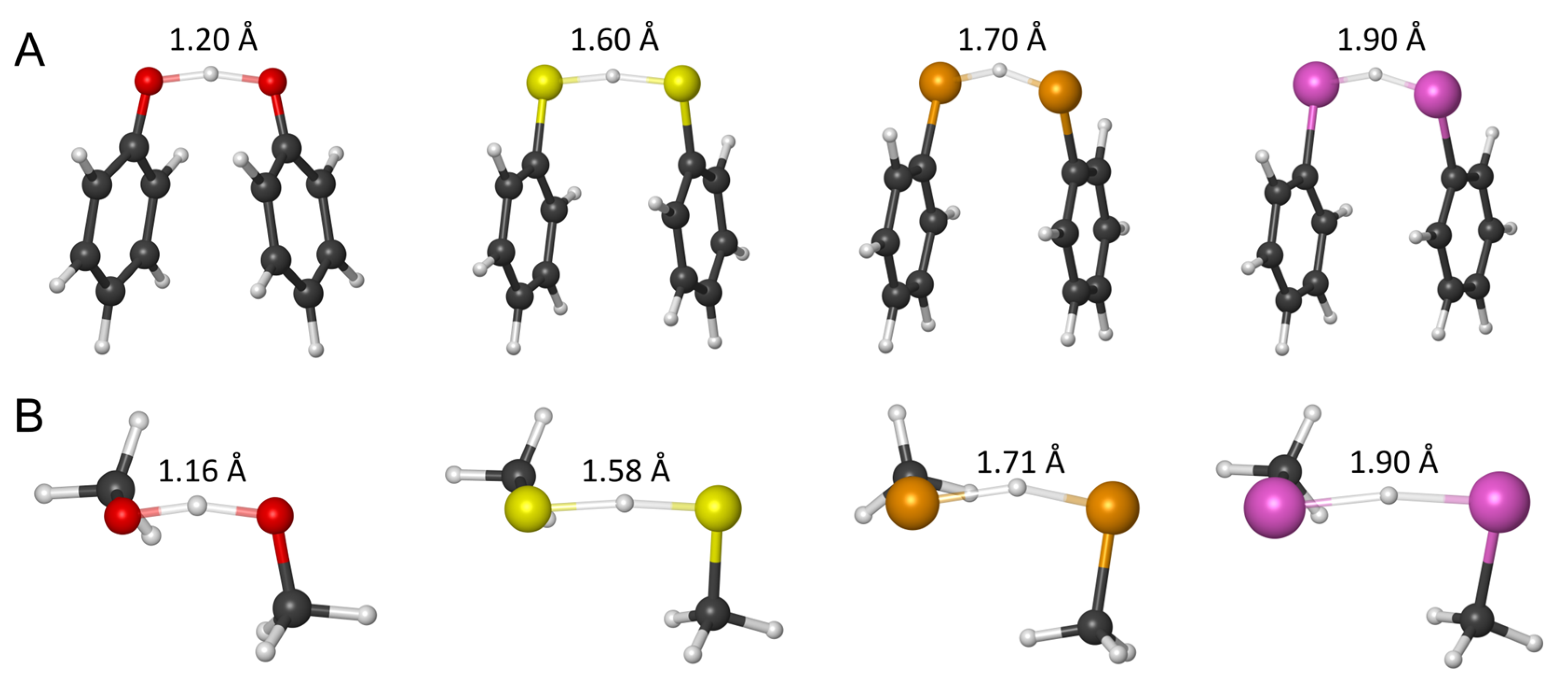
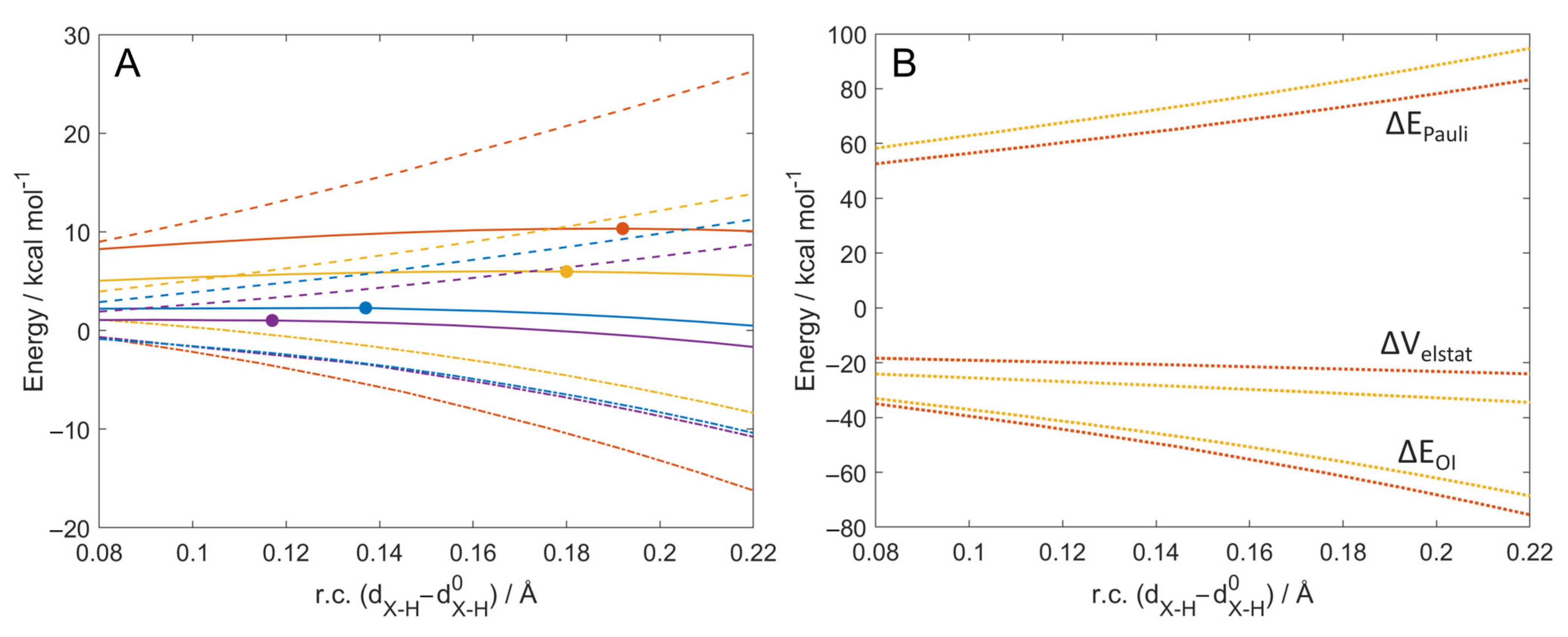
2.1. ROS Scavenging Activity and Mechanism of PhXH (X = O, S, Se, Te)
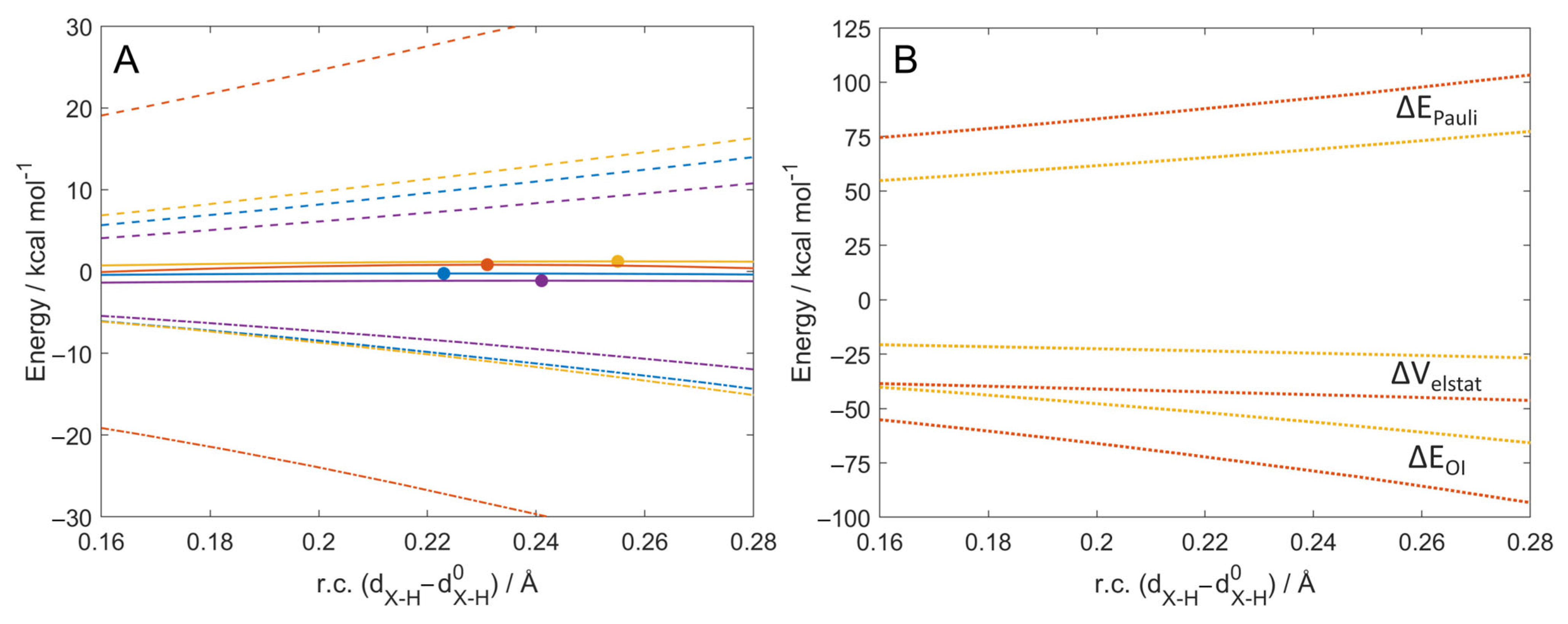
2.2. Aromaticity Role in ROS Scavenging Activity and Mechanism of Chalcogenols
3. Discussion
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADF | Amsterdam Density Functional |
| ASA | Activation Strain Analysis |
| BDE | Bond Dissociation Enthalpy |
| COSMO | COnductor-like Screening MOdel |
| CPET | Concerted Proton Electron Transfer |
| DFT | Density Functional Theory |
| EDA | Energy Decomposition Analysis |
| GPx | Glutathione Peroxidases |
| HAT | Hydrogen Atom Transfer |
| IBO | Intrinsic Bond Orbital |
| IRC | Intrinsic Reaction Coordinate |
| SOD | SuperOxide Dismutase |
| SPLET | Sequential Proton Loss Electron Transfer |
| ZORA | Zeroth Order Regular Approximation |
References
- Sies, H. Oxidative Stress: A Concept in Redox Biology and Medicine. Redox Biol. 2015, 4, 180–183. [Google Scholar] [CrossRef] [PubMed]
- Sies, H.; Berndt, C.; Jones, D.P. Oxidative Stress. Annu. Rev. Biochem. 2017, 86, 715–748. [Google Scholar] [CrossRef] [PubMed]
- Barnham, K.J.; Masters, C.L.; Bush, A.I. Neurodegenerative Diseases and Oxidative Stress. Nat. Rev. Drug. Discov. 2004, 3, 205–214. [Google Scholar] [CrossRef]
- Dubois-Deruy, E.; Peugnet, V.; Turkieh, A.; Pinet, F. Oxidative Stress in Cardiovascular Diseases. Antioxidants 2020, 9, 864. [Google Scholar] [CrossRef]
- Klaunig, J.E. Oxidative Stress and Cancer. Curr. Pharm. Des. 2019, 24, 4771–4778. [Google Scholar] [CrossRef]
- Tobe, E. Mitochondrial Dysfunction, Oxidative Stress, and Major Depressive Disorder. Neuropsychiatr. Dis. Treat. 2013, 9, 567. [Google Scholar] [CrossRef]
- Emiliani, F.E.; Sedlak, T.W.; Sawa, A. Oxidative Stress and Schizophrenia. Curr. Opin. Psychiatry 2014, 27, 185–190. [Google Scholar] [CrossRef]
- Umeno, A.; Biju, V.; Yoshida, Y. In Vivo ROS Production and Use of Oxidative Stress-Derived Biomarkers to Detect the Onset of Diseases Such as Alzheimer’s Disease, Parkinson’s Disease, and Diabetes. Free Radic. Res. 2017, 51, 413–427. [Google Scholar] [CrossRef]
- Kundu, S.; Ghosh, P.; Datta, S.; Ghosh, A.; Chattopadhyay, S.; Chatterjee, M. Oxidative Stress as a Potential Biomarker for Determining Disease Activity in Patients with Rheumatoid Arthritis. Free Radic. Res. 2012, 46, 1482–1489. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Kamrava, S.K.; Joghataei, M.T.; Darabi, R.; Shakeri-Zadeh, A.; Shahriari, M.; Reiter, R.J.; Ghaznavi, H.; Mehrzadi, S. Apoptosis Signaling Pathways in Osteoarthritis and Possible Protective Role of Melatonin. J. Pineal Res. 2016, 61, 411–425. [Google Scholar] [CrossRef]
- Gerber, P.A.; Rutter, G.A. The Role of Oxidative Stress and Hypoxia in Pancreatic Beta-Cell Dysfunction in Diabetes Mellitus. Antioxid. Redox Signal. 2017, 26, 501–518. [Google Scholar] [CrossRef] [PubMed]
- Juan, C.A.; Pérez de la Lastra, J.M.; Plou, F.J.; Pérez-Lebeña, E. The Chemistry of Reactive Oxygen Species (ROS) Revisited: Outlining Their Role in Biological Macromolecules (DNA, Lipids and Proteins) and Induced Pathologies. Int. J. Mol. Sci. 2021, 22, 4642. [Google Scholar] [CrossRef] [PubMed]
- Pryor, W.A. Why Is the Hydroxyl Radical the Only Radical That Commonly Adds to DNA? Hypothesis: It Has a Rare Combination of High Electrophilicity, High Thermochemical Reactivity, and a Mode of Production That Can Occur near DNA. Free Radic. Biol. Med. 1988, 4, 219–223. [Google Scholar] [CrossRef] [PubMed]
- Galano, A.; Raúl Alvarez-Idaboy, J. Computational Strategies for Predicting Free Radical Scavengers’ Protection against Oxidative Stress: Where Are We and What Might Follow? Int. J. Quantum Chem. 2019, 119, 1–23. [Google Scholar] [CrossRef]
- Pryor, W.A. Oxy-Radicals and Related Species: Their Formation, Lifetimes, and Reactions. Annu. Rev. Physiol. 1986, 48, 657–667. [Google Scholar] [CrossRef]
- Marnett, L.J. Peroxyl Free Radicals: Potential Mediators of Tumor Initiation and Promotion. Carcinogenesis 1987, 8, 1365–1373. [Google Scholar] [CrossRef]
- Michiels, C.; Raes, M.; Toussaint, O.; Remacle, J. Importance of SE-Glutathione Peroxidase, Catalase, and CU/ZN-SOD for Cell Survival against Oxidative Stress. Free Radic. Biol. Med. 1994, 17, 235–248. [Google Scholar] [CrossRef]
- Flohé, L. Glutathione Peroxidase: Fact and Fiction. Ciba Found. Symp. 1978, 65, 95–122. [Google Scholar]
- Orian, L.; Flohé, L. Selenium-Catalyzed Reduction of Hydroperoxides in Chemistry and Biology. Antioxidants 2021, 10, 1560. [Google Scholar] [CrossRef]
- Flohé, L.; Toppo, S.; Orian, L. The Glutathione Peroxidase Family: Discoveries and Mechanism. Free Radic. Biol. Med. 2022, 187, 113–122. [Google Scholar] [CrossRef]
- Eleutherio, E.C.A.; Silva Magalhães, R.S.; de Araújo Brasil, A.; Monteiro Neto, J.R.; de Holanda Paranhos, L. SOD1, More than Just an Antioxidant. Arch. Biochem. Biophys. 2021, 697, 108701. [Google Scholar] [CrossRef]
- Narayanaperumal, S.; Alberto, E.E.; de Andrade, F.M.; Lenardão, E.J.; Taube, P.S.; Braga, A.L. Ionic Liquid: An Efficient and Recyclable Medium for Synthesis of Unsymmetrical Diorganyl Selenides Promoted by InI. Org. Biomol. Chem. 2009, 7, 4647. [Google Scholar] [CrossRef]
- Galano, A.; Reiter, R.J. Melatonin and Its Metabolites vs. Oxidative Stress: From Individual Actions to Collective Protection. J. Pineal Res. 2018, 65, e12514. [Google Scholar] [CrossRef] [PubMed]
- Galano, A.; Tan, D.X.; Reiter, R.J. Melatonin as a Natural Ally against Oxidative Stress: A Physicochemical Examination. J. Pineal Res. 2011, 51, 1–16. [Google Scholar] [CrossRef]
- Galano, A.; Medina, M.E.; Tan, D.X.; Reiter, R.J. Melatonin and Its Metabolites as Copper Chelating Agents and Their Role in Inhibiting Oxidative Stress: A Physicochemical Analysis. J. Pineal Res. 2015, 58, 107–116. [Google Scholar] [CrossRef]
- Rahaman, M.M.; Hossain, R.; Herrera-Bravo, J.; Islam, M.T.; Atolani, O.; Adeyemi, O.S.; Owolodun, O.A.; Kambizi, L.; Daştan, S.D.; Calina, D.; et al. Natural Antioxidants from Some Fruits, Seeds, Foods, Natural Products, and Associated Health Benefits: An Update. Food Sci. Nutr. 2023, 11, 1657–1670. [Google Scholar] [CrossRef]
- Poli, G.; Leonarduzzi, G.; Biasi, F.; Chiarpotto, E. Oxidative Stress and Cell Signalling. Curr. Med. Chem. 2004, 11, 1163–1182. [Google Scholar] [CrossRef]
- Vogt, T. Phenylpropanoid Biosynthesis. Mol. Plant 2010, 3, 2–20. [Google Scholar] [CrossRef]
- Spiegel, M.; Cel, K.; Sroka, Z. The Mechanistic Insights into the Role of PH and Solvent on Antiradical and Prooxidant Properties of Polyphenols—Nine Compounds Case Study. Food Chem. 2023, 407, 134677. [Google Scholar] [CrossRef]
- Foti, M.C. Antioxidant Properties of Phenols. J. Pharm. Pharmacol. 2007, 59, 1673–1685. [Google Scholar] [CrossRef]
- Eghbaliferiz, S.; Iranshahi, M. Prooxidant Activity of Polyphenols, Flavonoids, Anthocyanins and Carotenoids: Updated Review of Mechanisms and Catalyzing Metals. Phytother. Res. 2016, 30, 1379–1391. [Google Scholar] [CrossRef] [PubMed]
- Biela, M.; Rimarčík, J.; Senajová, E.; Kleinová, A.; Klein, E. Antioxidant Action of Deprotonated Flavonoids: Thermodynamics of Sequential Proton-Loss Electron-Transfer. Phytochemistry 2020, 180, 112528. [Google Scholar] [CrossRef] [PubMed]
- Amić, A.; Marković, Z.; Dimitrić Marković, J.M.; Lučić, B.; Stepanić, V.; Amić, D. The 2H+/2e− Free Radical Scavenging Mechanisms of Uric Acid: Thermodynamics of NH Bond Cleavage. Comput. Theor. Chem. 2016, 1077, 2–10. [Google Scholar] [CrossRef]
- Klein, J.E.M.N.; Knizia, G. CPCET versus HAT: A Direct Theoretical Method for Distinguishing X–H Bond-Activation Mechanisms. Angew. Chem. Int. Ed. 2018, 57, 11913–11917. [Google Scholar] [CrossRef]
- Usharani, D.; Lacy, D.C.; Borovik, A.S.; Shaik, S. Dichotomous Hydrogen Atom Transfer vs. Proton-Coupled Electron Transfer During Activation of X–H Bonds (X = C, N, O) by Nonheme Iron–Oxo Complexes of Variable Basicity. J. Am. Chem. Soc. 2013, 135, 17090–17104. [Google Scholar] [CrossRef]
- Mayer, J.M. Proton-Coupled Electron Transfer: A Reaction Chemist’s View. Annu. Rev. Phys. Chem. 2004, 55, 363–390. [Google Scholar] [CrossRef]
- Maiorino, M.; Conrad, M.; Ursini, F. GPx4, Lipid Peroxidation, and Cell Death: Discoveries, Rediscoveries, and Open Issues. Antioxid. Redox Signal. 2018, 29, 61–74. [Google Scholar] [CrossRef]
- Narayanankutty, A.; Job, J.T.; Narayanankutty, V. Glutathione, an Antioxidant Tripeptide: Dual Roles in Carcinogenesis and Chemoprevention. Curr. Protein Pept. Sci. 2019, 20, 907–917. [Google Scholar] [CrossRef]
- Prabhakar, R.; Vreven, T.; Morokuma, K.; Musaev, D.G. Elucidation of the Mechanism of Selenoprotein Glutathione Peroxidase (GPx)-Catalyzed Hydrogen Peroxide Reduction by Two Glutathione Molecules: A Density Functional Study. Biochemistry 2005, 44, 11864–11871. [Google Scholar] [CrossRef]
- Ursini, F.; Bosello Travain, V.; Cozza, G.; Miotto, G.; Roveri, A.; Toppo, S.; Maiorino, M. A White Paper on Phospholipid Hydroperoxide Glutathione Peroxidase (GPx4) Forty Years Later. Free Radic. Biol. Med. 2022, 188, 117–133. [Google Scholar] [CrossRef]
- Antony, S.; Bayse, C.A. Modeling the Mechanism of the Glutathione Peroxidase Mimic Ebselen. Inorg. Chem. 2011, 50, 12075–12084. [Google Scholar] [CrossRef] [PubMed]
- Bayse, C.A.; Ortwine, K.N. Modeling the Glutathione Peroxidase-Like Activity of a Cyclic Seleninate by DFT and Solvent-Assisted Proton Exchange. Eur. J. Inorg. Chem. 2013, 2013, 3680–3688. [Google Scholar] [CrossRef]
- Madabeni, A.; Bortoli, M.; Nogara, P.A.; Ribaudo, G.; Dalla Tiezza, M.; Flohé, L.; Rocha, J.B.T.; Orian, L. 50 Years of Organoselenium Chemistry, Biochemistry and Reactivity: Mechanistic Understanding, Successful and Controversial Stories. Chem. Eur. J. 2024, 30, e202403003. [Google Scholar] [CrossRef]
- Nogara, P.A.; Oliveira, C.S.; Pereira, M.E.; Bortoli, M.; Orian, L.; Aschner, M.; Rocha, J.B.T. Therapeutic Applications of Low-Molecular-Weight Thiols and Selenocompounds. In Redox Chemistry and Biology of Thiols; Alvarez, B., Comini, M.A., Salinas, G., Trujillo, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 643–665. [Google Scholar]
- Zeppilli, D.; Madabeni, A.; Sancineto, L.; Bagnoli, L.; Santi, C.; Orian, L. Role of Group 12 Metals in the Reduction of H2O2 by Santi’s Reagent: A Computational Mechanistic Investigation. Inorg. Chem. 2023, 62, 17288–17298. [Google Scholar] [CrossRef]
- Ribaudo, G.; Bortoli, M.; Ongaro, A.; Oselladore, E.; Gianoncelli, A.; Zagotto, G.; Orian, L. Fluoxetine Scaffold to Design Tandem Molecular Antioxidants and Green Catalysts. RSC Adv. 2020, 10, 18583–18593. [Google Scholar] [CrossRef]
- Ribaudo, G.; Bortoli, M.; Witt, C.E.; Parke, B.; Mena, S.; Oselladore, E.; Zagotto, G.; Hashemi, P.; Orian, L. ROS-Scavenging Selenofluoxetine Derivatives Inhibit In Vivo Serotonin Reuptake. ACS Omega 2022, 7, 8314–8322. [Google Scholar] [CrossRef]
- Zeppilli, D.; Aldinio-Colbachini, A.; Ribaudo, G.; Tubaro, C.; Dalla Tiezza, M.; Bortoli, M.; Zagotto, G.; Orian, L. Antioxidant Chimeric Molecules: Are Chemical Motifs Additive? The Case of a Selenium-Based Ligand. Int. J. Mol. Sci. 2023, 24, 11797. [Google Scholar] [CrossRef]
- Dalla Tiezza, M.; Hamlin, T.A.; Bickelhaupt, F.M.; Orian, L. Radical Scavenging Potential of the Phenothiazine Scaffold: A Computational Analysis. ChemMedChem 2021, 16, 3763–3771. [Google Scholar] [CrossRef]
- Mangiavacchi, F.; Botwina, P.; Menichetti, E.; Bagnoli, L.; Rosati, O.; Marini, F.; Fonseca, S.F.; Abenante, L.; Alves, D.; Dabrowska, A.; et al. Seleno-Functionalization of Quercetin Improves the Non-Covalent Inhibition of Mpro and Its Antiviral Activity in Cells against SARS-CoV-2. Int. J. Mol. Sci. 2021, 22, 7048. [Google Scholar] [CrossRef]
- De Santi, C.; Pietrabissa, A.; Spisni, R.; Mosca, F.; Pacifici, G.M. Sulphation of Resveratrol, a Natural Compound Present in Wine, and Its Inhibition by Natural Flavonoids. Xenobiotica 2000, 30, 857–866. [Google Scholar] [CrossRef]
- Zeppilli, D.; Orian, L. Concerted Proton Electron Transfer or Hydrogen Atom Transfer? An Unequivocal Strategy to Discriminate These Mechanisms in Model Systems. Phys. Chem. Chem. Phys. 2025, 27, 6312–6324. [Google Scholar] [CrossRef] [PubMed]
- Bors, W.; Michel, C. Chemistry of the Antioxidant Effect of Polyphenols. Ann. N. Y. Acad. Sci. 2002, 957, 57–69. [Google Scholar] [CrossRef]
- Di Meo, F.; Lemaur, V.; Cornil, J.; Lazzaroni, R.; Duroux, J.-L.; Olivier, Y.; Trouillas, P. Free Radical Scavenging by Natural Polyphenols: Atom versus Electron Transfer. J. Phys. Chem. A 2013, 117, 2082–2092. [Google Scholar] [CrossRef] [PubMed]
- Al-Sehemi, A.G.; Irfan, A. Effect of Donor and Acceptor Groups on Radical Scavenging Activity of Phenol by Density Functional Theory. Arab. J. Chem. 2017, 10, S1703–S1710. [Google Scholar] [CrossRef]
- Platzer, M.; Kiese, S.; Tybussek, T.; Herfellner, T.; Schneider, F.; Schweiggert-Weisz, U.; Eisner, P. Radical Scavenging Mechanisms of Phenolic Compounds: A Quantitative Structure-Property Relationship (QSPR) Study. Front. Nutr. 2022, 9, 882458. [Google Scholar] [CrossRef]
- Marino, A.; Battaglini, M.; Moles, N.; Ciofani, G. Natural Antioxidant Compounds as Potential Pharmaceutical Tools against Neurodegenerative Diseases. ACS Omega 2022, 7, 25974–25990. [Google Scholar] [CrossRef]
- Brewer, M.S. Natural Antioxidants: Sources, Compounds, Mechanisms of Action, and Potential Applications. Compr. Rev. Food Sci. Food Saf. 2011, 10, 221–247. [Google Scholar] [CrossRef]
- Nimse, S.B.; Pal, D. Free Radicals, Natural Antioxidants, and Their Reaction Mechanisms. RSC Adv. 2015, 5, 27986–28006. [Google Scholar] [CrossRef]
- Škorňa, P.; Poliak, P.; Klein, E.; Lukeš, V. Theoretical Study of the Substituent Effect on the Hydrogen Atom Transfer Mechanism of Meta- and Para-Substituted Benzenetellurols. Comput. Theor. Chem. 2016, 1079, 64–69. [Google Scholar] [CrossRef]
- Hamlin, T.A.; Swart, M.; Bickelhaupt, F.M. Nucleophilic Substitution (SN2): Dependence on Nucleophile, Leaving Group, Central Atom, Substituents, and Solvent. ChemPhysChem 2018, 19, 1315–1330. [Google Scholar] [CrossRef]
- Mayer, J.M.; Hrovat, D.A.; Thomas, J.L.; Borden, W.T. Proton-Coupled Electron Transfer versus Hydrogen Atom Transfer in Benzyl/Toluene, Methoxyl/Methanol, and Phenoxyl/Phenol Self-Exchange Reactions. J. Am. Chem. Soc. 2002, 124, 11142–11147. [Google Scholar] [CrossRef] [PubMed]
- DiLabio, G.A.; Johnson, E.R. Lone Pair−π and Π−π Interactions Play an Important Role in Proton-Coupled Electron Transfer Reactions. J. Am. Chem. Soc. 2007, 129, 6199–6203. [Google Scholar] [CrossRef] [PubMed]
- Sirjoosingh, A.; Hammes-Schiffer, S. Proton-Coupled Electron Transfer versus Hydrogen Atom Transfer: Generation of Charge-Localized Diabatic States. J. Phys. Chem. A 2011, 115, 2367–2377. [Google Scholar] [CrossRef]
- Litwinienko, G.; Ingold, K.U. Solvent Effects on the Rates and Mechanisms of Reaction of Phenols with Free Radicals. Acc. Chem. Res. 2007, 40, 222–230. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Lim, I.S.; Schwerdtfeger, P.; Metz, B.; Stoll, H. All-Electron and Relativistic Pseudopotential Studies for the Group 1 Element Polarizabilities from K to Element 119. J. Chem. Phys. 2005, 122, 104103. [Google Scholar] [CrossRef]
- Zhang, Y.; Sayama, M.; Luo, M.; Lu, Y.; Tantillo, D.J. Not That DDT: A Databank of Dynamics Trajectories for Organic Reactions. J. Chem. Educ. 2022, 99, 2721–2725. [Google Scholar] [CrossRef]
- Knizia, G. Intrinsic Atomic Orbitals: An Unbiased Bridge between Quantum Theory and Chemical Concepts. J. Chem. Theory Comput. 2013, 9, 4834–4843. [Google Scholar] [CrossRef]
- Knizia, G.; Klein, J.E.M.N. Electron Flow in Reaction Mechanisms—Revealed from First Principles. Angew. Chem. Int. Ed. 2015, 54, 5518–5522. [Google Scholar] [CrossRef]
- Galano, A.; Alvarez-Idaboy, J.R. A Computational Methodology for Accurate Predictions of Rate Constants in Solution: Application to the Assessment of Primary Antioxidant Activity. J. Comput. Chem. 2013, 34, 2430–2445. [Google Scholar] [CrossRef]
- Wolters, L.P.; Bickelhaupt, F.M. The Activation Strain Model and Molecular Orbital Theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 324–343. [Google Scholar] [CrossRef] [PubMed]
- Bickelhaupt, F.M.; Houk, K.N. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem. Int. Ed. 2017, 56, 10070–10086. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Baerends, E.J. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; Wiley: Indianapolis, IN, USA, 2000; Volume 15, pp. 1–86. [Google Scholar]
- Vermeeren, P.; van der Lubbe, S.C.C.; Fonseca Guerra, C.; Bickelhaupt, F.M.; Hamlin, T.A. Understanding Chemical Reactivity Using the Activation Strain Model. Nat. Protoc. 2020, 15, 649–667. [Google Scholar] [CrossRef] [PubMed]
- van Zeist, W.-J.; Guerra, C.F.; Bickelhaupt, F.M. PyFrag—Streamlining Your Reaction Path Analysis. J. Comput. Chem. 2008, 29, 312–315. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- ADF2019, AMS2020, SCM. Theoretical Chemistry. Vrije Universiteit: Amsterdam, The Netherlands. Available online: https://www.scm.com/ (accessed on 10 January 2025).
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Total Energy Using Regular Approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Zaccaria, F.; Wolters, L.P.; Fonseca Guerra, C.; Orian, L. Insights on Selenium and Tellurium Diaryldichalcogenides: A Benchmark DFT Study. J. Comput. Chem. 2016, 37, 1672–1680. [Google Scholar] [CrossRef]
- Hordijk, Y.; Dalla Tiezza, M.; Rodrigues Silva, D.; Hamlin, T.A. Radical Addition Reactions: Hierarchical Ab Initio Benchmark and DFT Performance Study. ChemPhysChem 2025, 26, e202400728. [Google Scholar] [CrossRef]
- Nieuwland, C.; Fonseca Guerra, C. How the Chalcogen Atom Size Dictates the Hydrogen-Bond Donor Capability of Carboxamides, Thioamides, and Selenoamides. Chem. Eur. J. 2022, 28, e202200755. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Spiegel, M. Current Trends in Computational Quantum Chemistry Studies on Antioxidant Radical Scavenging Activity. J. Chem. Inf. Model. 2022, 62, 2639–2658. [Google Scholar] [CrossRef]
- Zeppilli, D.; Grolla, G.; Di Marco, V.; Ribaudo, G.; Orian, L. Radical Scavenging and Anti-Ferroptotic Molecular Mechanism of Olanzapine: Insight from a Computational Analysis. Inorg. Chem. 2024, 63, 21856–21867. [Google Scholar] [CrossRef]
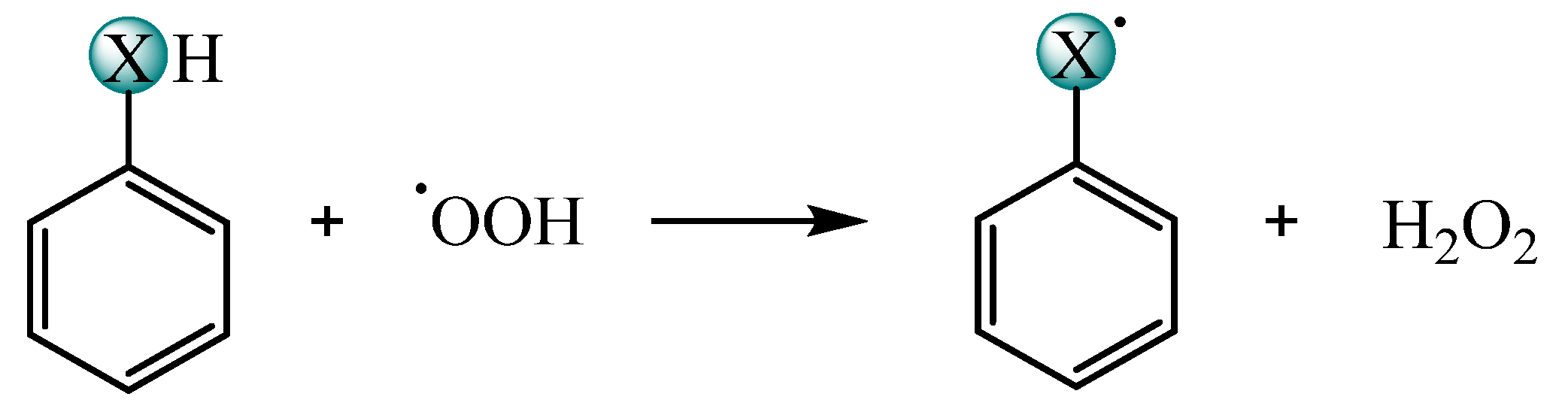

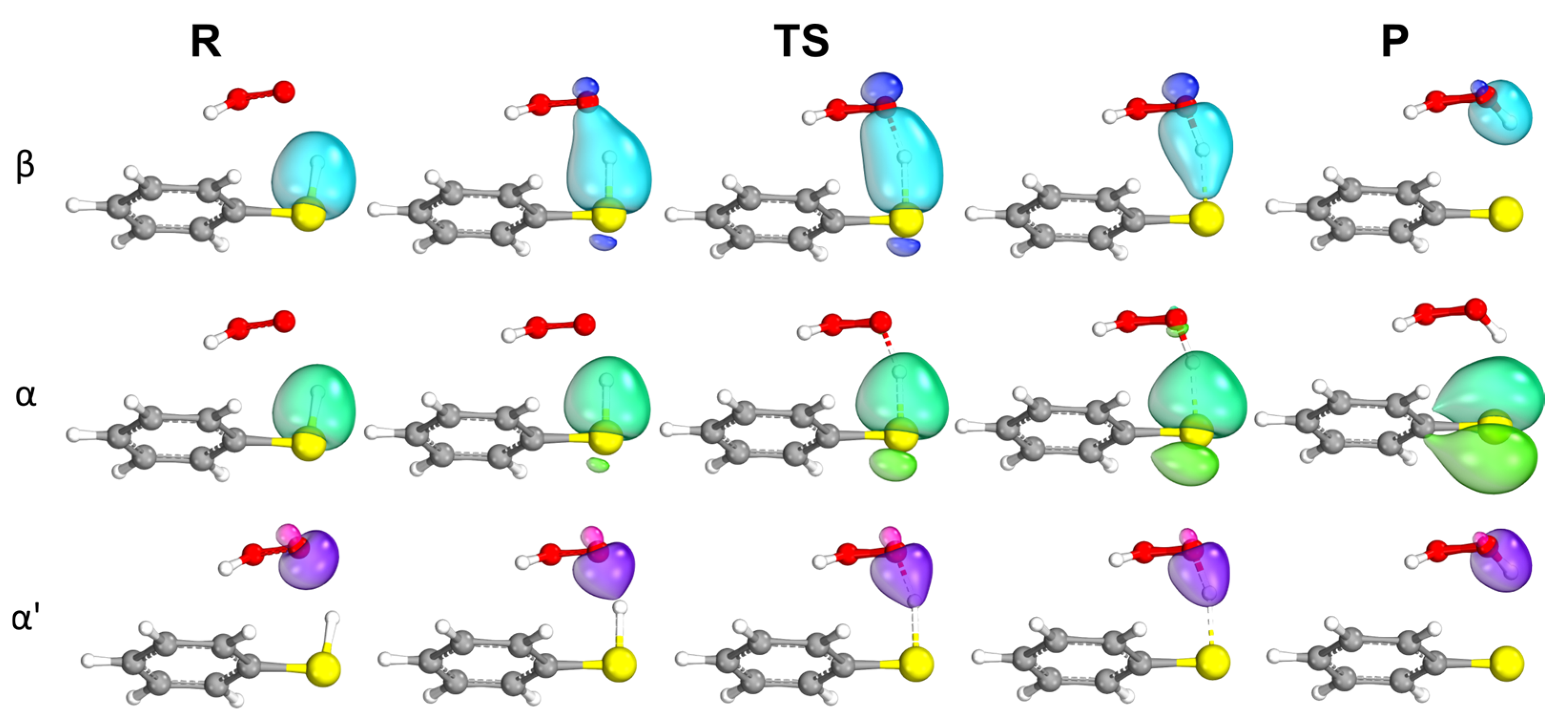
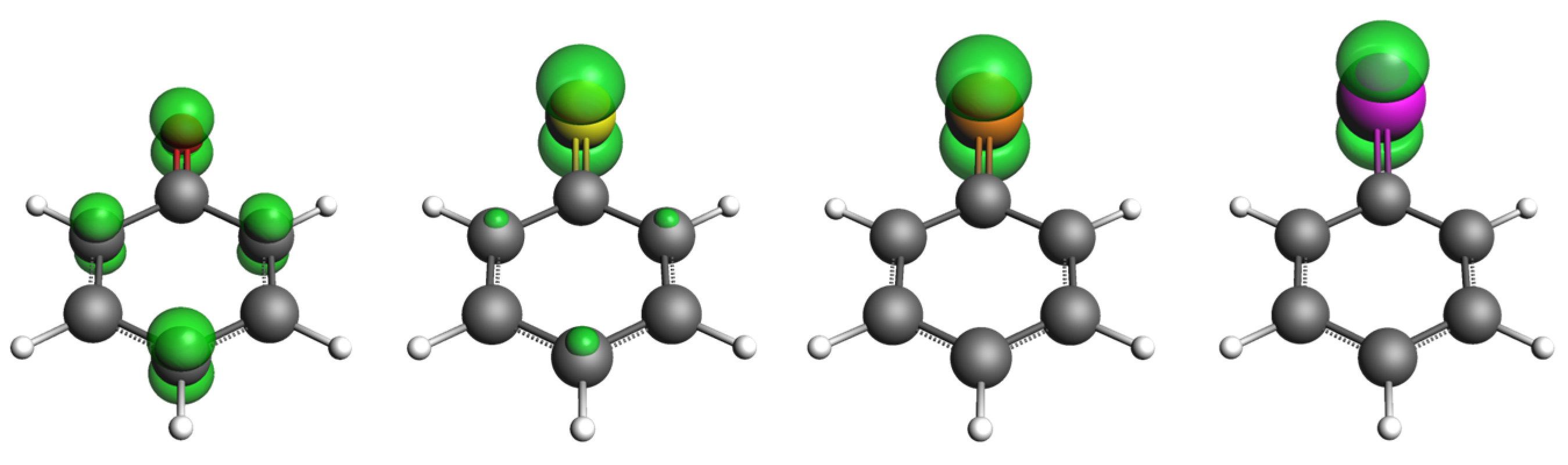
| X | ΔE | ΔG° | ||||
|---|---|---|---|---|---|---|
| Gas | Water | Benzene | Gas | Water | Benzene | |
| O | 4.5 | 0.8 | 2.9 | 3.9 | 1.6 | 2.3 |
| S | −7.5 | −8.6 | −8.1 | −5.2 | −6.5 | −5.8 |
| Se | −18.4 | −19.9 | −19.2 | −15.6 | −17.1 | −16.4 |
| Te | −29.1 | −30.7 | −30.0 | −25.2 | −26.8 | −26.1 |
| X | ΔE‡ | ΔG‡ | ||||
|---|---|---|---|---|---|---|
| Gas | Water | Benzene | Gas | Water | Benzene | |
| O | 10.8 | 12.4 | 12.1 | 18.6 | 20.3 | 19.9 |
| S | 6.4 | 9.4 | 8.0 | 16.0 | 19.1 | 17.6 |
| Se | 2.7 | 5.3 | 4.1 | 12.9 | 15.5 | 14.3 |
| Te | 1.4 | 3.9 | 2.8 | 11.8 | 14.3 | 13.2 |
| X | ΔE‡ | ΔG‡ | ||||
|---|---|---|---|---|---|---|
| Gas | Water | Benzene | Gas | Water | Benzene | |
| O | 1.6 | 5.5 | 3.6 | 12.3 | 16.2 | 14.3 |
| S | 2.0 | 3.0 | 2.5 | 11.4 | 12.4 | 11.9 |
| Se | 0.4 | 0.9 | 0.7 | 10.7 | 11.2 | 11.0 |
| Te | −0.4 * | −0.2 * | −0.3 * | 9.6 | 9.8 | 9.7 |
| X | ΔE‡ | ΔG‡ | ||||
|---|---|---|---|---|---|---|
| Gas | Water | Benzene | Gas | Water | Benzene | |
| O | 7.7 | 11.7 | 9.7 | 15.9 | 19.9 | 17.9 |
| S | 3.9 | 3.0 | 6.5 | 11.7 | 10.9 | 14.4 |
| Se | 3.4 | 3.1 | 5.9 | 12.0 | 11.8 | 14.5 |
| Te | 1.6 | 0.6 | 3.6 | 9.7 | 8.6 | 11.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeppilli, D.; Pedergnana, V.; Filippi, M.; Orian, L. The Role of Chalcogen in the ROS Scavenging Mechanism of Model Phenyl Compounds. Molecules 2025, 30, 1408. https://doi.org/10.3390/molecules30071408
Zeppilli D, Pedergnana V, Filippi M, Orian L. The Role of Chalcogen in the ROS Scavenging Mechanism of Model Phenyl Compounds. Molecules. 2025; 30(7):1408. https://doi.org/10.3390/molecules30071408
Chicago/Turabian StyleZeppilli, Davide, Veronica Pedergnana, Matteo Filippi, and Laura Orian. 2025. "The Role of Chalcogen in the ROS Scavenging Mechanism of Model Phenyl Compounds" Molecules 30, no. 7: 1408. https://doi.org/10.3390/molecules30071408
APA StyleZeppilli, D., Pedergnana, V., Filippi, M., & Orian, L. (2025). The Role of Chalcogen in the ROS Scavenging Mechanism of Model Phenyl Compounds. Molecules, 30(7), 1408. https://doi.org/10.3390/molecules30071408







