Binding Free Energy Analysis of Colicin D, E3 and E8 to Their Respective Cognate Immunity Proteins Using Computational Simulations
Abstract
1. Introduction
1.1. Protein–Protein Interactions
1.2. Binding Free Energy
1.3. Molecular Mechanics Poisson-Boltzmann Surface Area (MM-PBSA)
1.4. Molecular Mechanics Generalized Born Surface Area (MM-GBSA)
2. Results
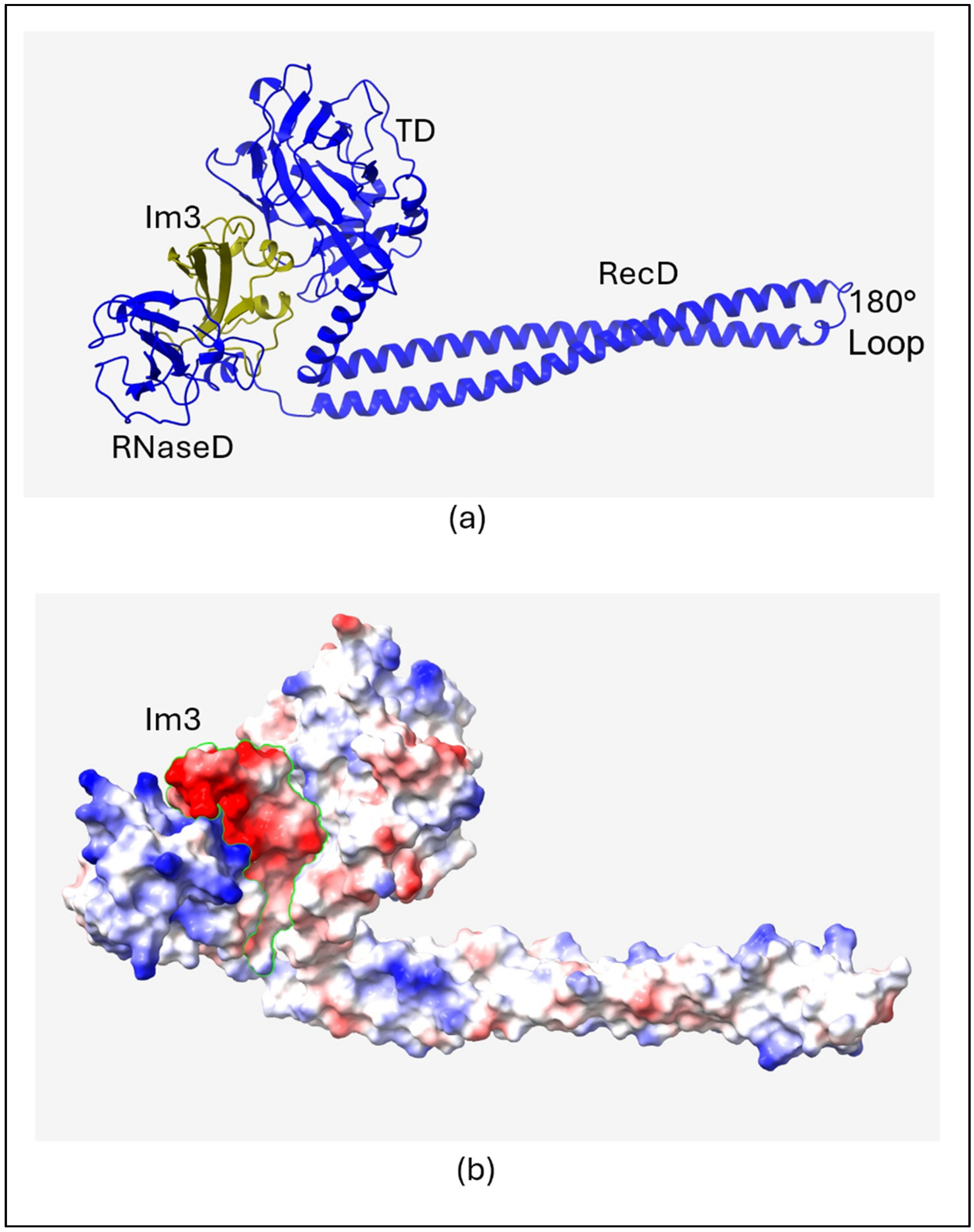
2.1. Structure of Colicin/Immunity Complexes
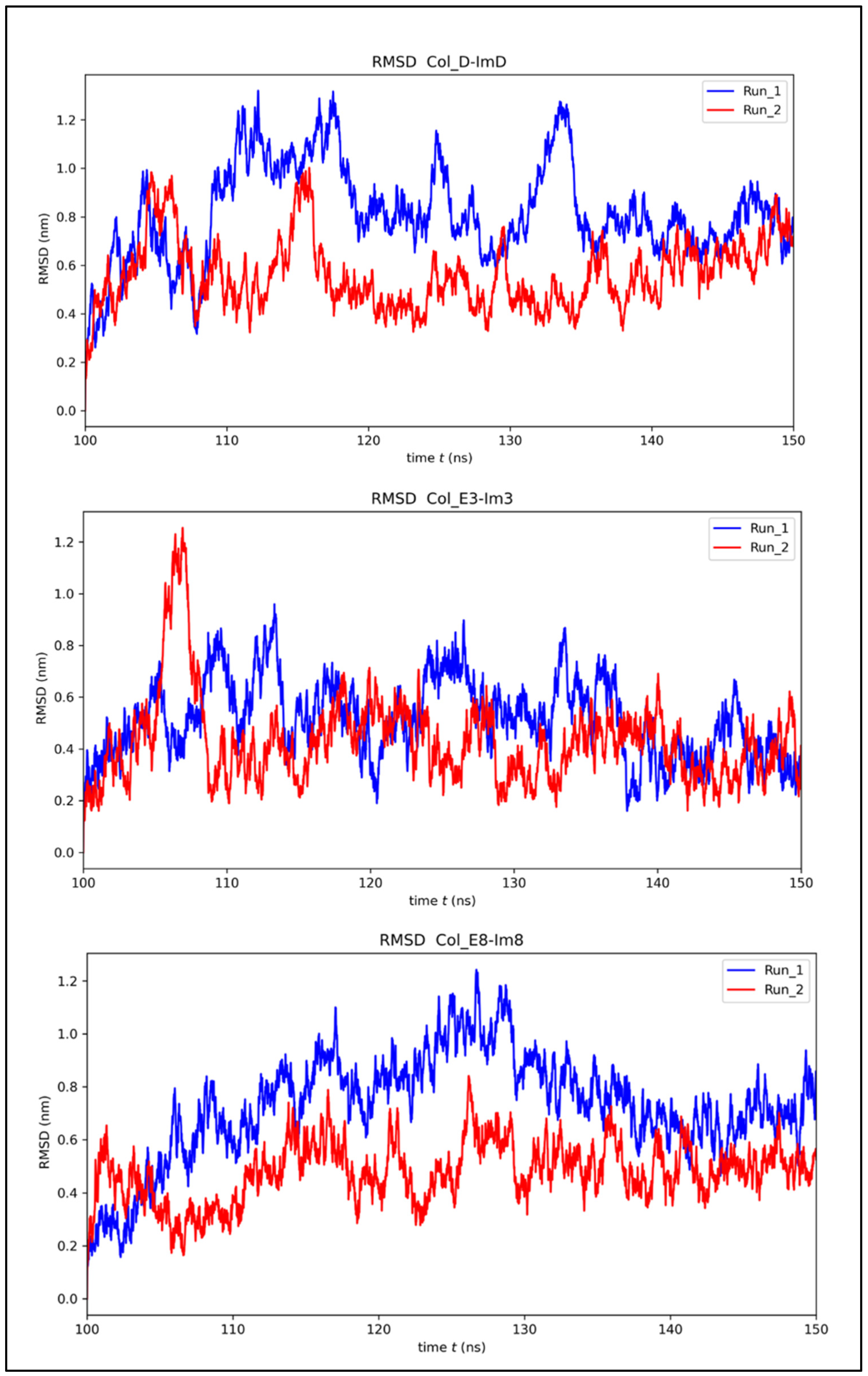
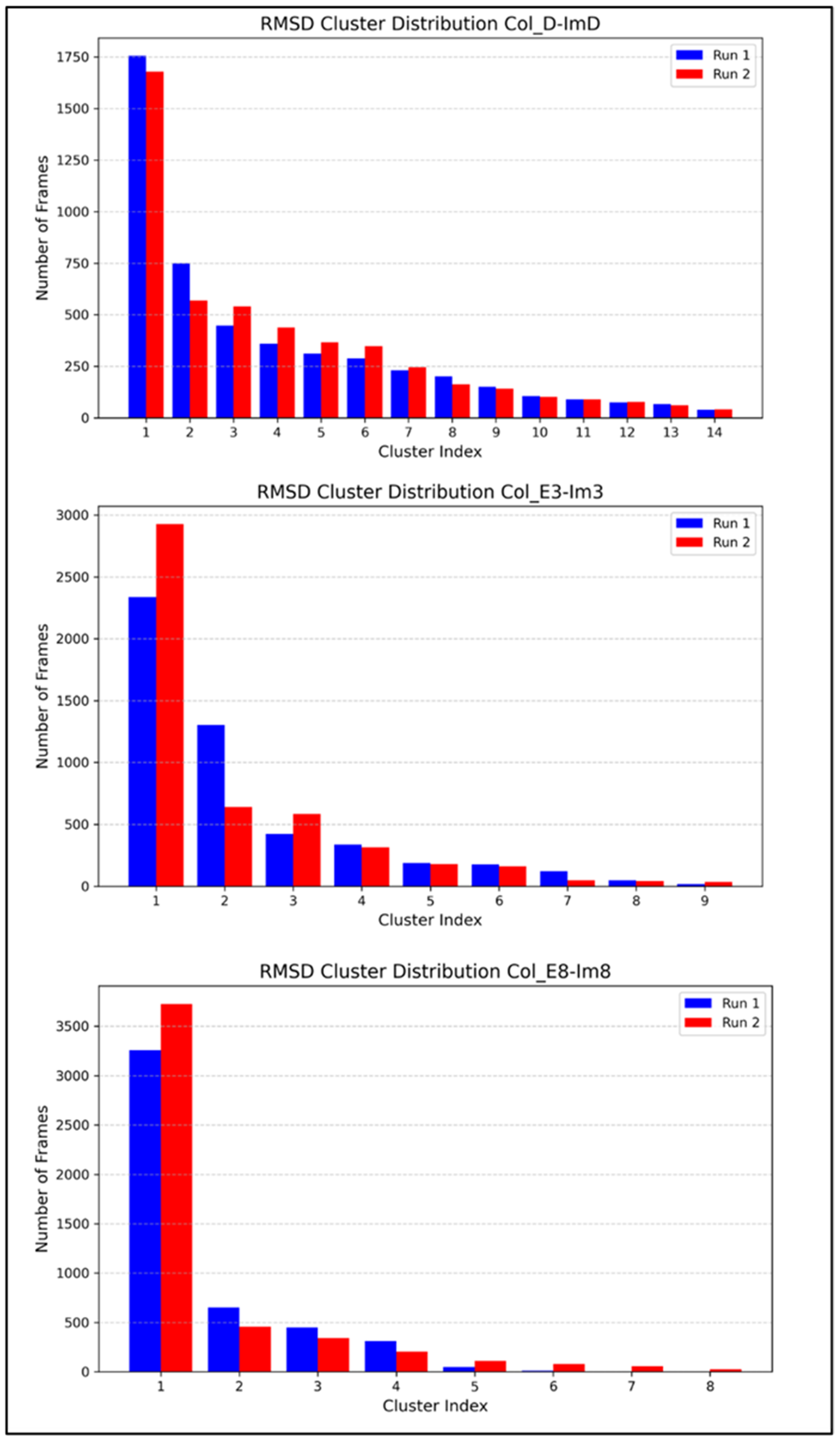
2.2. MD Simulations
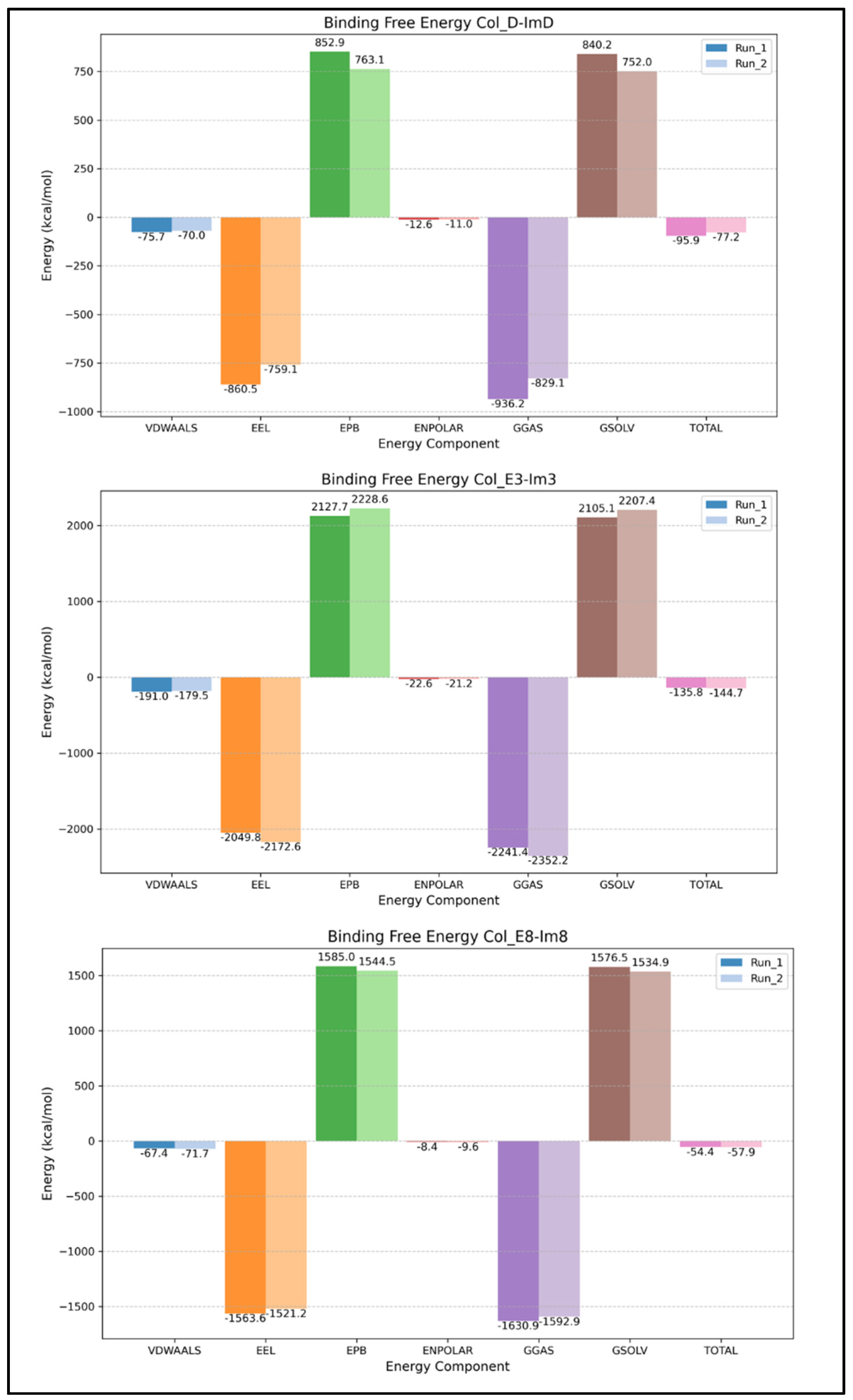
2.3. Binding Free Energy from gmx_MMPBSA
3. Discussion
3.1. Overestimation of Computational Binding Energies Compared to the Experiment
3.2. RMSF Maxima
3.3. Contribution of Interfacial Buried Water Molecules
4. Materials and Methods
4.1. Bacterial Strains and Plasmids
4.2. Structure Prediction with AlphaFold2
4.3. Molecular Dynamics Simulations with GROMACS
4.4. Binding Free Energy Calculations Using gmx_MMPBSA
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Cascales, E.; Buchanan, S.K.; Duché, D.; Kleanthous, C.; Lloubes, R.; Postle, K.; Riley, M.; Slatin, S.; Cavard, D. Colicin biology. Microbiol. Mol. Biol. Rev. 2007, 71, 158–229. [Google Scholar] [CrossRef] [PubMed]
- Soelaiman, S.; Jakes, K.; Wu, N.; Li, C.; Shoham, M. Crystal structure of colicin E3: Implications for cell entry and ribosome inactivation. Mol. Cell 2001, 8, 1053–1062. [Google Scholar] [CrossRef]
- Michel, B. After 30 years of study, the bacterial SOS response still surprises us. PLoS Biol. 2005, 3, e255. [Google Scholar] [CrossRef] [PubMed]
- Fagerquist, C.K.; Shi, Y.; Park, J. Unusual modifications of protein biomarkers expressed by plasmid, prophage, and bacterial host of pathogenic Escherichia coli identified using top-down proteomic analysis. Rapid Commun. Mass Spectrom. 2024, 38, e9667. [Google Scholar] [CrossRef]
- Parker, C.T.; Cooper, K.K.; Huynh, S.; Smith, T.P.; Bono, J.L.; Cooley, M. Genome sequences of eight shiga toxin-producing Escherichia coli strains isolated from a produce-growing region in California. Microbiol. Resour. Announc. 2018, 7, e00807-18. [Google Scholar] [CrossRef]
- Fagerquist, C.K.; Shi, Y.; Park, J. Plasmid-encoded colicin immunity proteins produced by pathogenic Escherichia coli identified by antibiotic induction, MALDI-TOF-TOF-MS/MS and top-down proteomic analysis. In Proceedings of the 72nd ASMS Conference on Mass Spectrometry and Allied Topics, Anaheim, CA, USA, 2–6 June 2024. [Google Scholar]
- Fagerquist, C.K.; Shi, Y.; Koirala, M. Plasmid-encoded gene expression of pathogenic bacteria by antibiotic induction as detected by MALDI-TOF-TOF mass spectrometry and top-down proteomic analysis. Int. J. Mass Spectrom. 2025, 551, 117430. [Google Scholar] [CrossRef]
- Safari-Alighiarloo, N.; Taghizadeh, M.; Rezaei-Tavirani, M.; Goliaei, B.; Peyvandi, A.A. Protein-protein interaction networks (PPI) and complex diseases. Gastroenterol. Hepatol. Bed Bench 2014, 7, 17–31. [Google Scholar]
- Alexov, E. Protein-protein interactions. Curr. Pharm. Biotechnol. 2008, 9, 55–56. [Google Scholar] [CrossRef]
- Arkin, M.R.; Tang, Y.; Wells, J.A. Small-molecule inhibitors of protein-protein interactions: Progressing toward the reality. Chem. Biol. 2014, 21, 1102–1114. [Google Scholar] [CrossRef]
- Lu, H.; Zhou, Q.; He, J.; Jiang, Z.; Peng, C.; Tong, R.; Shi, J. Recent advances in the development of protein–protein interactions modulators: Mechanisms and clinical trials. Signal Transduct. Target. Ther. 2020, 5, 213. [Google Scholar] [CrossRef]
- Koirala, M.; Alexov, E. Ab-initio binding of barnase–barstar with DelPhiForce steered Molecular Dynamics (DFMD) approach. J. Theor. Comput. Chem. 2020, 19, 2050016. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Aguilar, A.; Bernard, D.; Yang, C.Y. Targeting the MDM2-p53 Protein-Protein Interaction for New Cancer Therapy: Progress and Challenges. Cold Spring Harb. Perspect. Med. 2017, 7, a026245. [Google Scholar] [CrossRef]
- Koo, N.; Sharma, A.K.; Narayan, S. Therapeutics Targeting p53-MDM2 Interaction to Induce Cancer Cell Death. Int. J. Mol. Sci. 2022, 23, 5005. [Google Scholar] [CrossRef]
- Jha, K.; Karmakar, S.; Saha, S. Graph-BERT and language model-based framework for protein–protein interaction identification. Sci. Rep. 2023, 13, 5663. [Google Scholar] [CrossRef] [PubMed]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Bijak, V.; Szczygiel, M.; Lenkiewicz, J.; Gucwa, M.; Cooper, D.R.; Murzyn, K.; Minor, W. The current role and evolution of X-ray crystallography in drug discovery and development. Expert Opin. Drug Discov. 2023, 18, 1221–1230. [Google Scholar] [CrossRef] [PubMed]
- Bock, L.V.; Igaev, M.; Grubmüller, H. Single-particle Cryo-EM and molecular dynamics simulations: A perfect match. Curr. Opin. Struct. Biol. 2024, 86, 102825. [Google Scholar] [CrossRef]
- Koehler Leman, J.; Künze, G. Recent advances in NMR protein structure prediction with ROSETTA. Int. J. Mol. Sci. 2023, 24, 7835. [Google Scholar] [CrossRef]
- Saikusa, K. Advancing Native Mass Spectrometry Toward Cellular Biology. J. Mass Spectrom. 2024, 59, e5095. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W.; et al. Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.H.; Hou, T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef]
- Swanson, J.M.; Henchman, R.H.; McCammon, J.A. Revisiting free energy calculations: A theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 2004, 86, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Schlitter, J. Estimation of absolute and relative entropies of macromolecules using the covariance matrix. Chem. Phys. Lett. 1993, 215, 617–621. [Google Scholar] [CrossRef]
- Homeyer, N.; Gohlke, H. Free energy calculations by the molecular mechanics Poisson− Boltzmann surface area method. Mol. Inform. 2012, 31, 114–122. [Google Scholar] [CrossRef]
- Karplus, M.; Kushick, J.N. Method for estimating the configurational entropy of macromolecules. Macromolecules 1981, 14, 325–332. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Li, J.; He, X. Fragment-based quantum mechanical calculation of protein–protein binding affinities. J. Comput. Chem. 2018, 39, 1617–1628. [Google Scholar] [CrossRef]
- Wallis, R.; Moore, G.R.; James, R.; Kleanthous, C. Protein-protein interactions in colicin E9 DNase-immunity protein complexes. 1. Diffusion-controlled association and femtomolar binding for the cognate complex. Biochemistry 1995, 34, 13743–13750. [Google Scholar] [CrossRef]
- Walker, D.; Moore, G.R.; James, R.; Kleanthous, C. Thermodynamic consequences of bipartite immunity protein binding to the ribosomal ribonuclease colicin E3. Biochemistry 2003, 42, 4161–4171. [Google Scholar] [CrossRef]
- Keeble, A.H.; Kirkpatrick, N.; Shimizu, S.; Kleanthous, C. Calorimetric Dissection of Colicin Dnase—Immunity Protein Complex Specificity. Biochemistry 2006, 45, 3243–3254. [Google Scholar] [CrossRef]
- Shirts, M.R.; Mobley, D.L. An introduction to best practices in free energy calculations. Biomol. Simul. Methods Protoc. 2013, 924, 271–311. [Google Scholar]
- Lindorff-Larsen, K.; Maragakis, P.; Piana, S.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Systematic validation of protein force fields against experimental data. PLoS ONE 2012, 7, e32131. [Google Scholar] [CrossRef] [PubMed]
- Awoonor-Williams, E.; Rowley, C.N. Molecular simulation of nonfacilitated membrane permeation. Biochim. Biophys. Acta (BBA) Biomembr. 2016, 1858, 1672–1687. [Google Scholar] [CrossRef]
- Zhou, H.X. Association and dissociation kinetics of colicin E3 and immunity protein 3: Convergence of theory and experiment. Protein Sci. 2003, 12, 2379–2382. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.X. Disparate ionic-strength dependencies of on and off rates in protein–protein association. Biopolym. Orig. Res. Biomol. 2001, 59, 427–433. [Google Scholar] [CrossRef]
- Kleanthous, C.; Walker, D. Immunity proteins: Enzyme inhibitors that avoid the active site. Trends Biochem. Sci. 2001, 26, 624–631. [Google Scholar] [CrossRef]
- Li, C.; Jia, Z.; Chakravorty, A.; Pahari, S.; Peng, Y.; Basu, S.; Koirala, M.; Panday, S.K.; Petukh, M.; Li, L. DelPhi suite: New developments and review of functionalities. J. Comput. Chem. 2019, 40, 2502–2508. [Google Scholar] [CrossRef]
- Deng, Y.; Roux, B. Computations of standard binding free energies with molecular dynamics simulations. J. Phys. Chem. B 2009, 113, 2234–2246. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Abrams, C.; Bussi, G. Enhanced sampling in molecular dynamics using metadynamics, replica-exchange, and temperature-acceleration. Entropy 2013, 16, 163–199. [Google Scholar] [CrossRef]
- Kästner, J. Umbrella sampling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Straatsma, T.; Berendsen, H. Free energy of ionic hydration: Analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J. Chem. Phys. 1988, 89, 5876–5886. [Google Scholar] [CrossRef]
- Quiñones, B.; Yambao, J.C.; Lee, B.G. Draft genome sequences of Escherichia coli O113: H21 strains recovered from a major produce production region in California. Genome Announc. 2017, 5, e01203-17. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zeng, X.; Zhao, Y.; Chen, R. AlphaFold2 and its applications in the fields of biology and medicine. Signal Transduct. Target. Ther. 2023, 8, 115. [Google Scholar] [CrossRef]
- Chang, J.-W.; Sato, Y.; Ogawa, T.; Arakawa, T.; Fukai, S.; Fushinobu, S.; Masaki, H. Crystal structure of the central and the C-terminal RNase domains of colicin D implicated its translocation pathway through inner membrane of target cell. J. Biochem. 2018, 164, 329–339. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; MacKerell, A.D., Jr. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [CrossRef]
- Chong, S.-H.; Ham, S. Dynamics of Hydration Water Plays a Key Role in Determining the Binding Thermodynamics of Protein Complexes. Sci. Rep. 2017, 7, 8744. [Google Scholar] [CrossRef]
- Valdés-Tresanco, M.S.; Valdés-Tresanco, M.E.; Valiente, P.A.; Moreno, E. gmx_MMPBSA: A new tool to perform end-state free energy calculations with GROMACS. J. Chem. Theory Comput. 2021, 17, 6281–6291. [Google Scholar] [CrossRef]


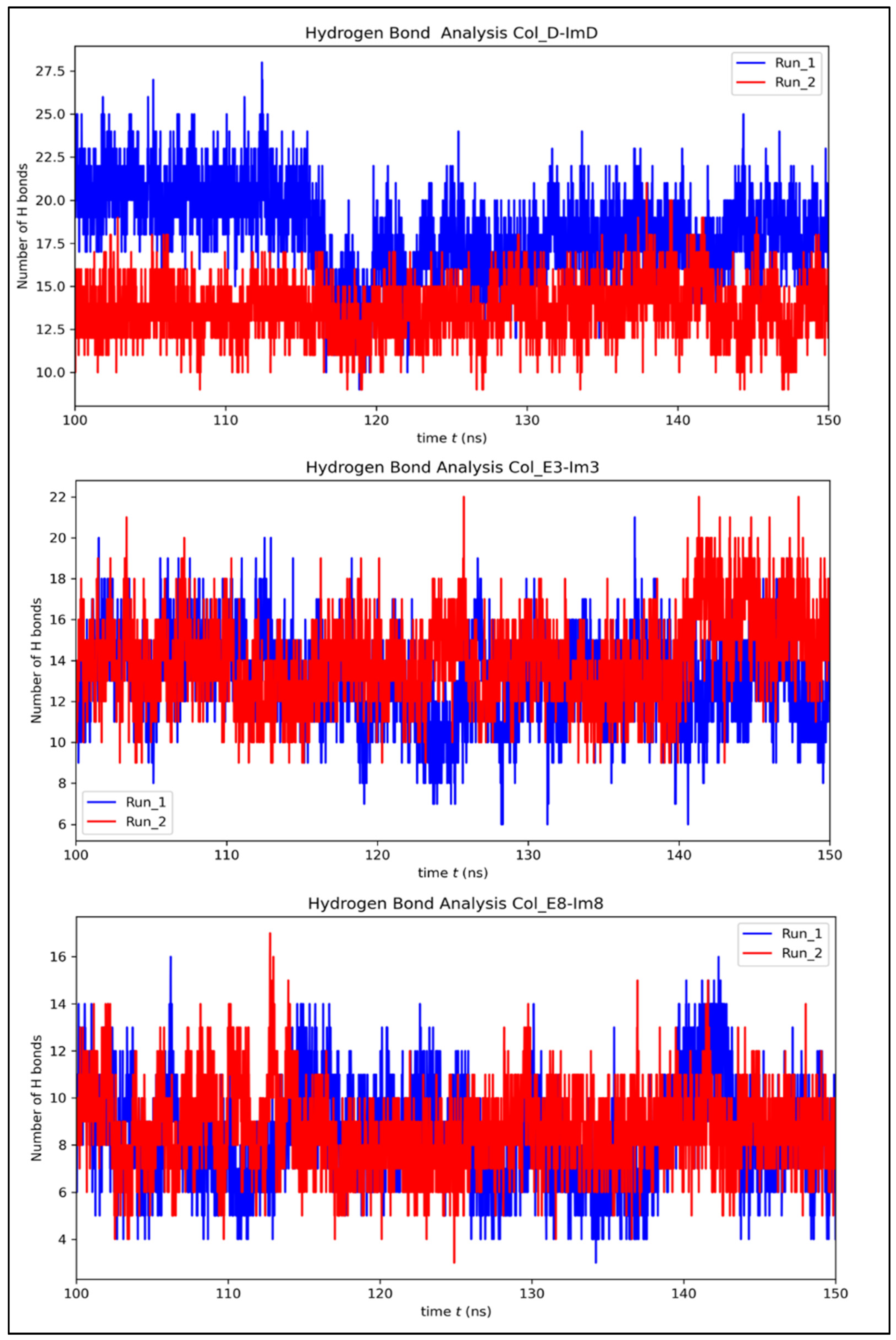
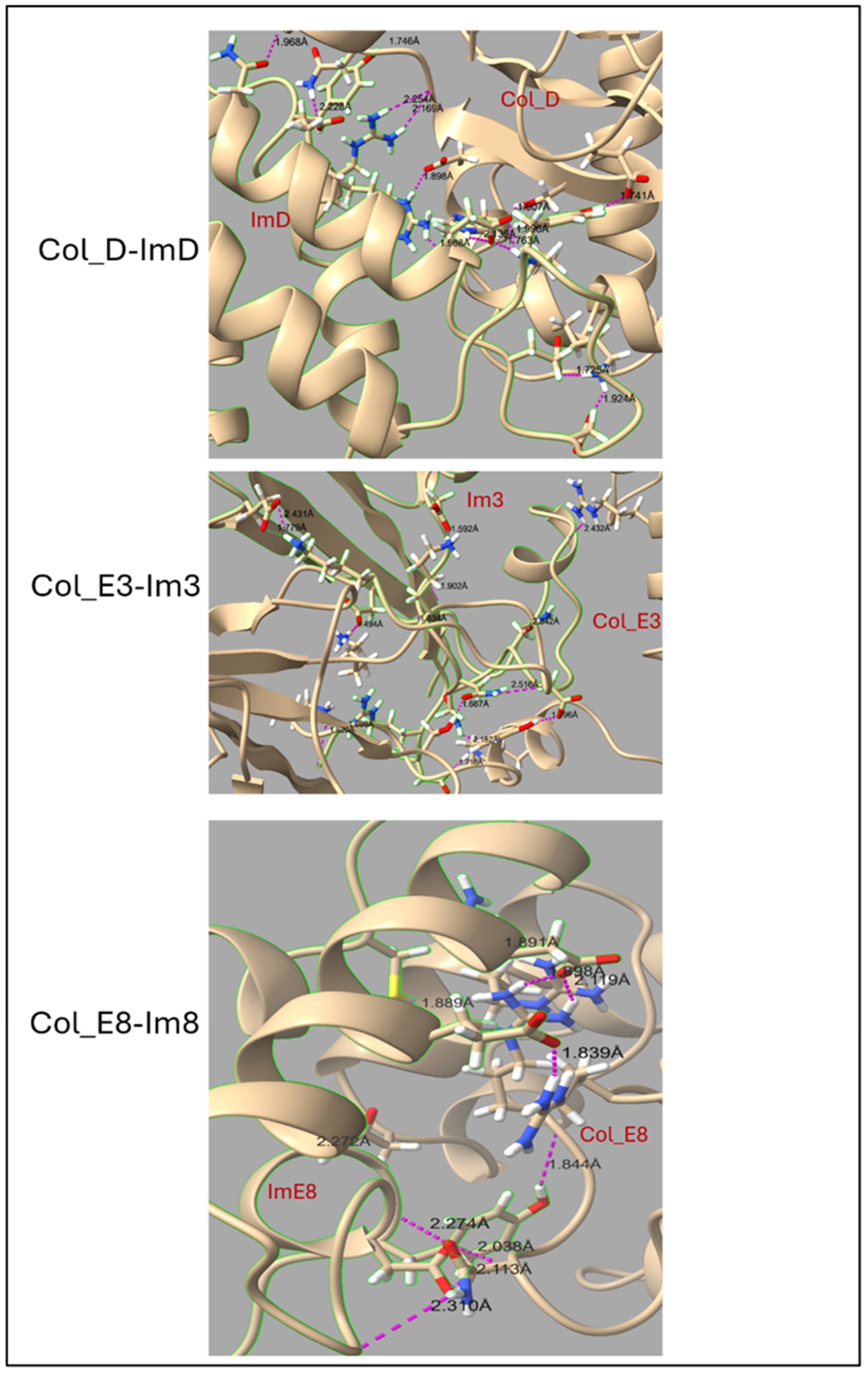
| Protein Complex | H-Bonds Before Simulation | Average H-Bonds After Simulation | Average Number of Buried Water Molecules |
|---|---|---|---|
| Col_D-ImD | 13 | 15.83 | 20.15 |
| Col_E3-Im3 | 11 | 13.56 | 23.55 |
| Col_E8-Im8 | 10 | 8.50 | 11.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koirala, M.; Fagerquist, C.K. Binding Free Energy Analysis of Colicin D, E3 and E8 to Their Respective Cognate Immunity Proteins Using Computational Simulations. Molecules 2025, 30, 1277. https://doi.org/10.3390/molecules30061277
Koirala M, Fagerquist CK. Binding Free Energy Analysis of Colicin D, E3 and E8 to Their Respective Cognate Immunity Proteins Using Computational Simulations. Molecules. 2025; 30(6):1277. https://doi.org/10.3390/molecules30061277
Chicago/Turabian StyleKoirala, Mahesh, and Clifton K. Fagerquist. 2025. "Binding Free Energy Analysis of Colicin D, E3 and E8 to Their Respective Cognate Immunity Proteins Using Computational Simulations" Molecules 30, no. 6: 1277. https://doi.org/10.3390/molecules30061277
APA StyleKoirala, M., & Fagerquist, C. K. (2025). Binding Free Energy Analysis of Colicin D, E3 and E8 to Their Respective Cognate Immunity Proteins Using Computational Simulations. Molecules, 30(6), 1277. https://doi.org/10.3390/molecules30061277







