The Stability of TiO2 Phases Studied Using r2SCAN in the Hubbard-Corrected Density Functional Theory
Abstract
1. Introduction
2. Results and Discussions
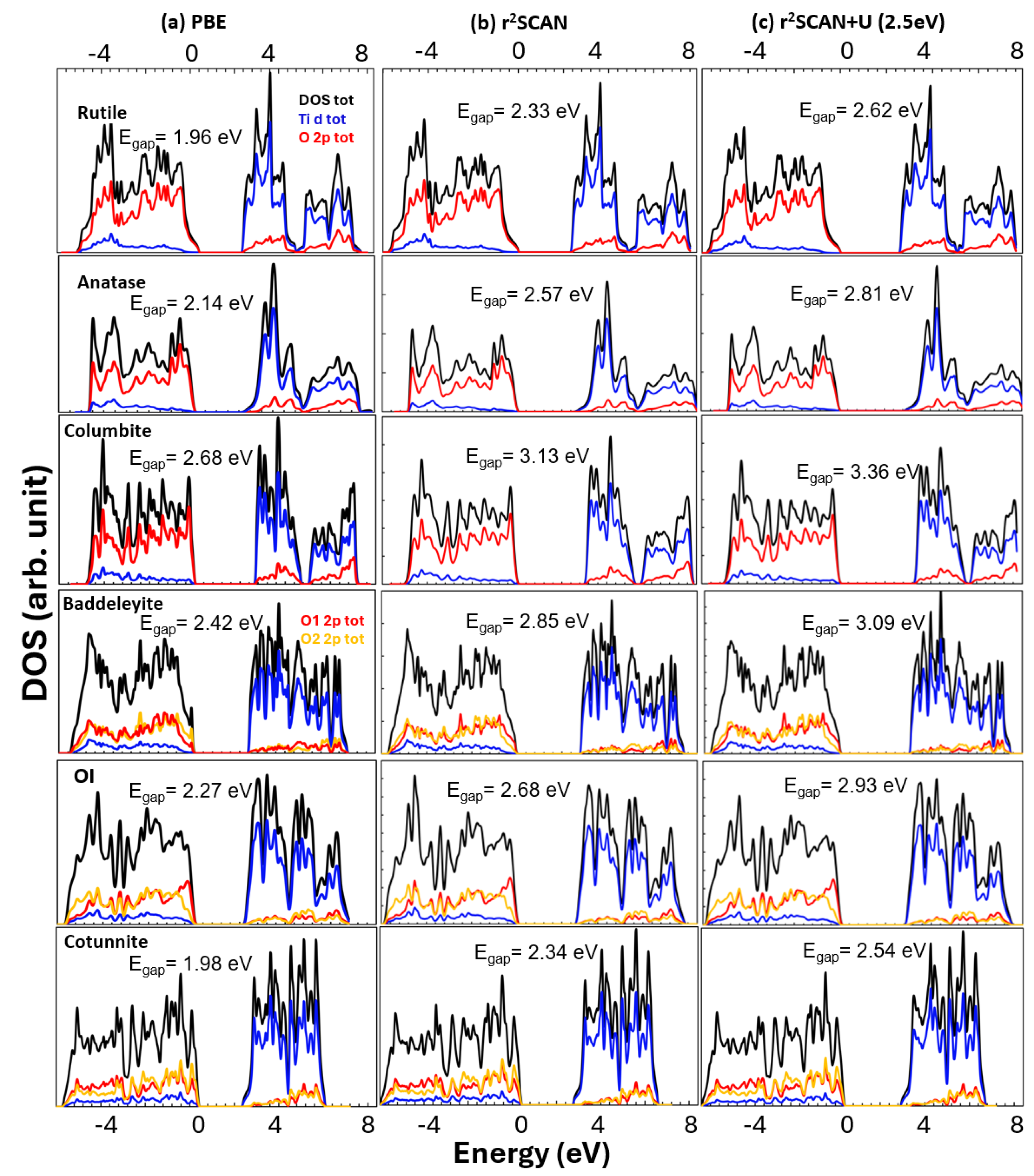
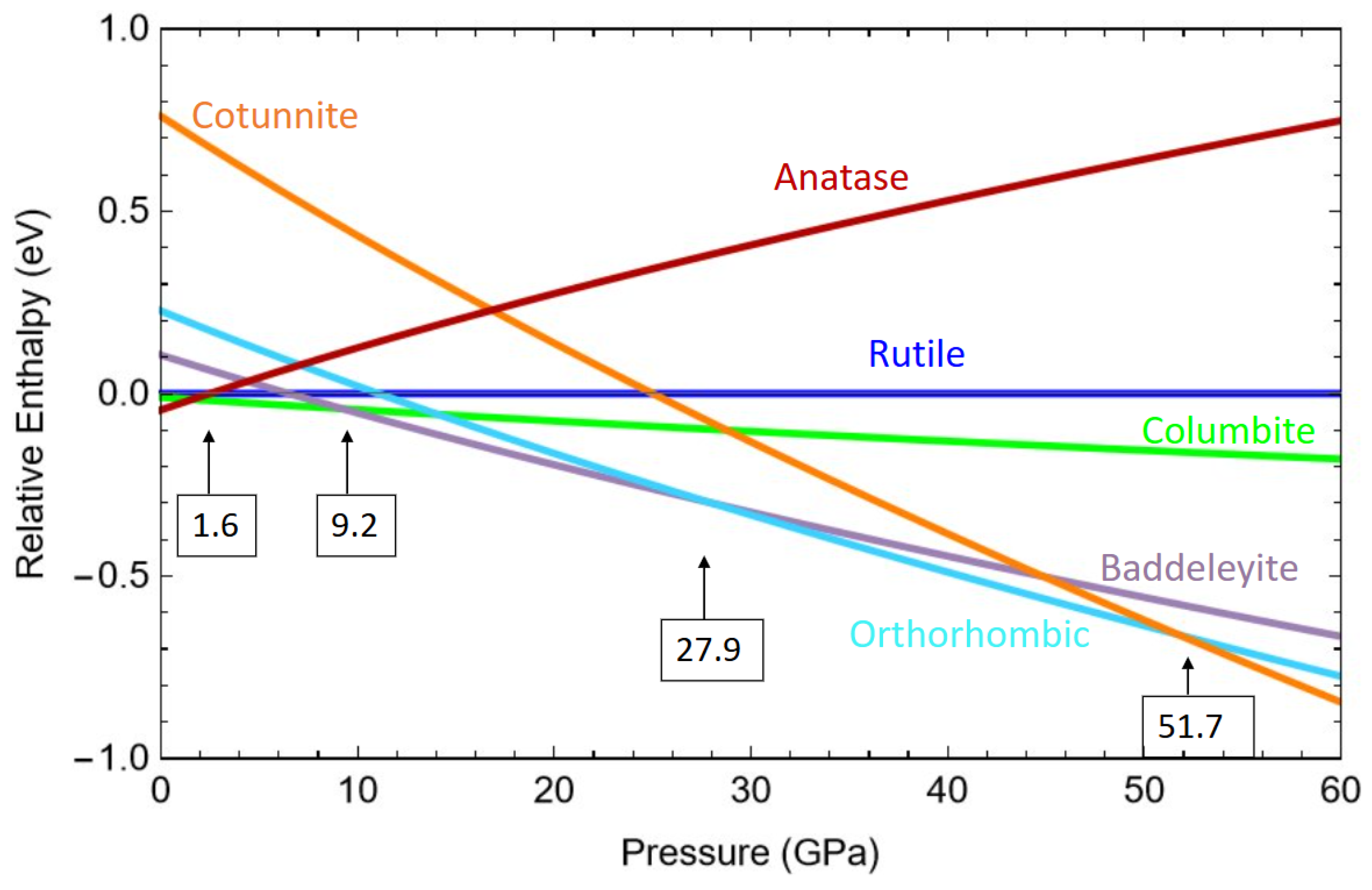
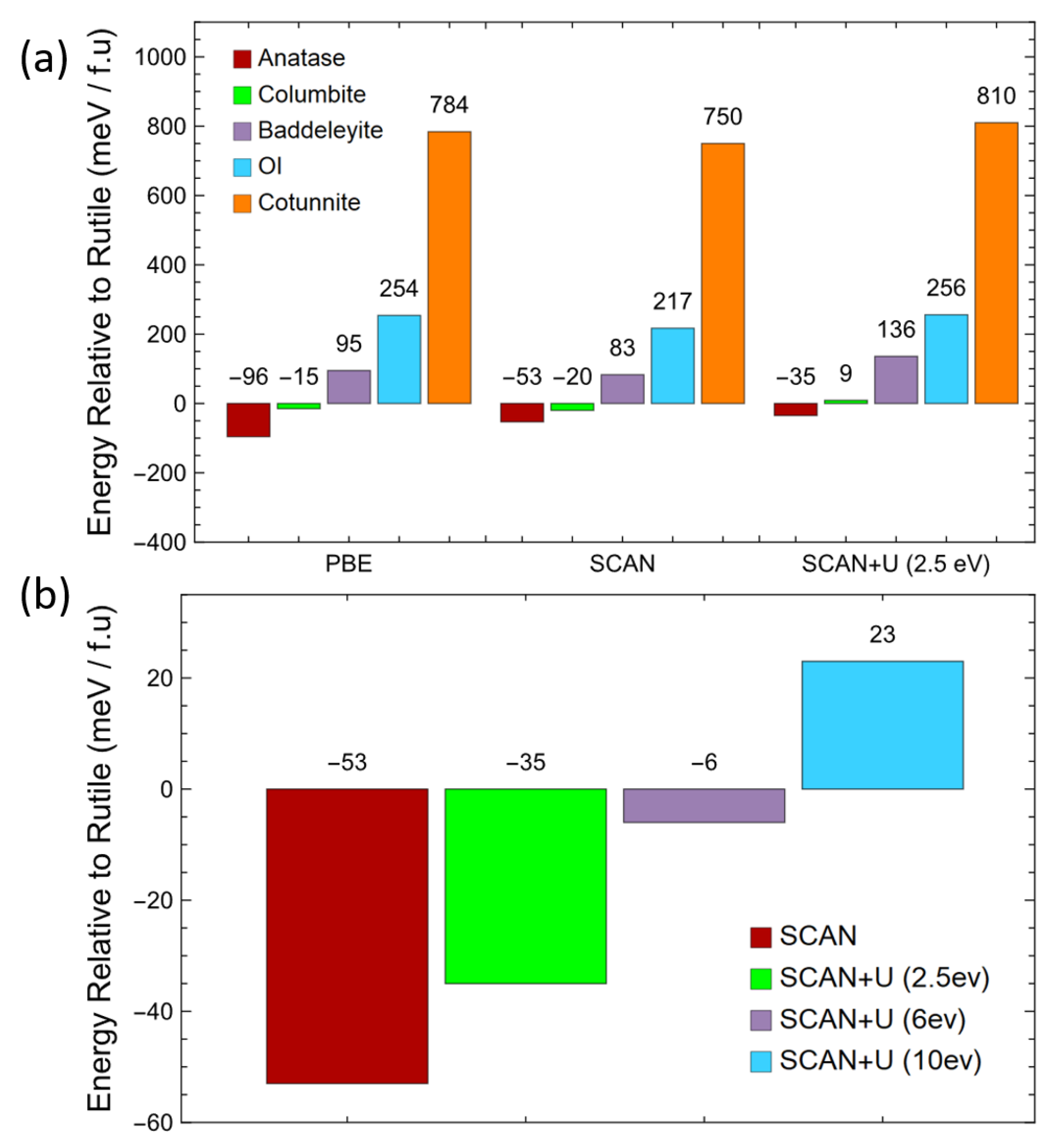
2.1. Equilibrium Structures and Phase Stability at 0 GPa
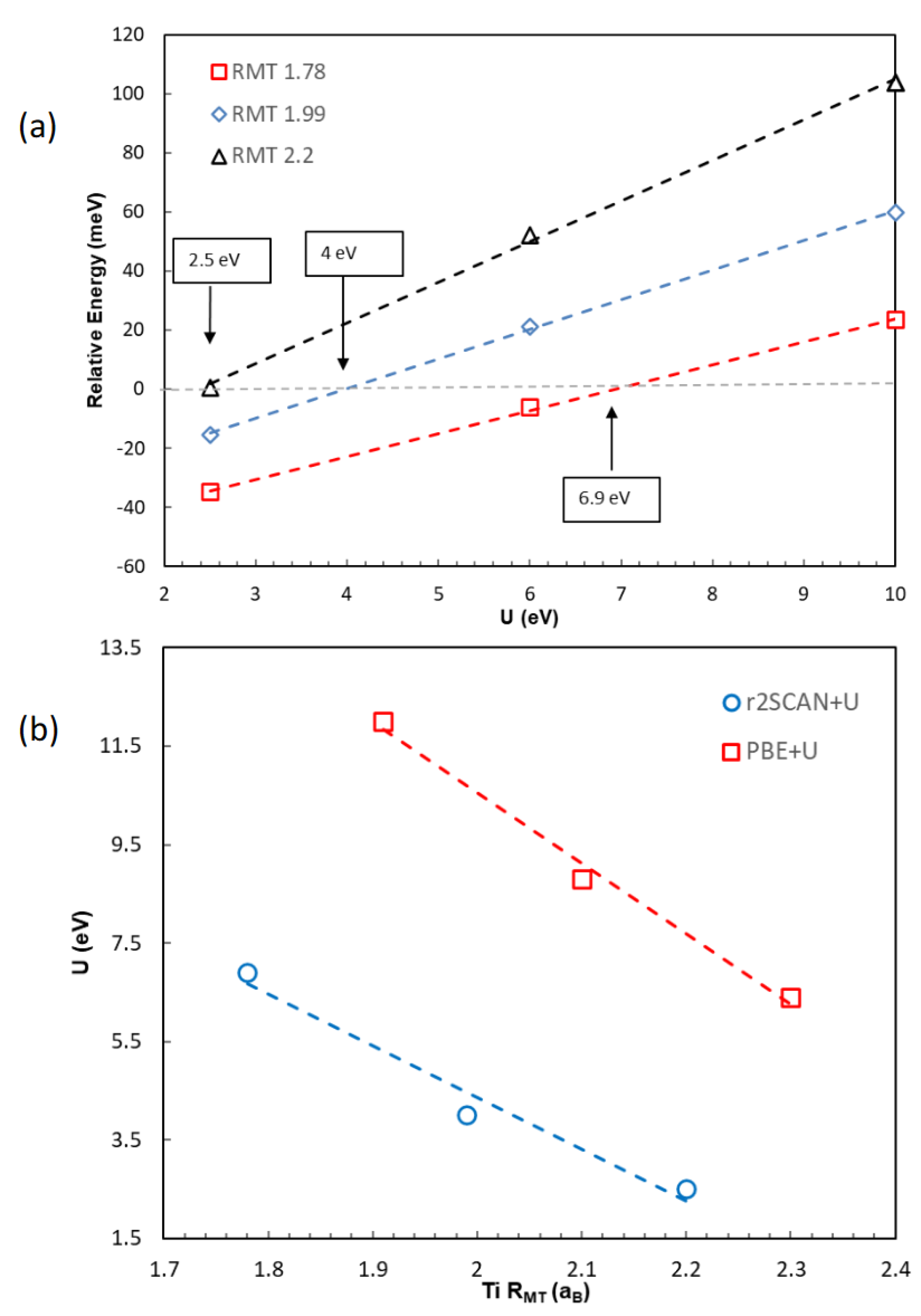
2.2. The Effect of the Hubbard Correction
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fujishima, A.; Honda, K. Electrochemical photolysis of water at a semiconductor electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef]
- Grätzel, M. Dye-sensitized solar cells. J. Photochem. Photobiol. C Photochem. Rev. 2003, 4, 145–153. [Google Scholar] [CrossRef]
- Chen, X.; Liu, L.; Yu, P.Y.; Mao, S.S. Increasing solar absorption for photocatalysis with black hydrogenated titanium dioxide nanocrystals. Science 2011, 331, 746–750. [Google Scholar] [CrossRef] [PubMed]
- Matsubu, J.C.; Zhang, S.; DeRita, L.; Marinkovic, N.S.; Chen, J.G.; Graham, G.W.; Pan, X.; Christopher, P. Adsorbate-mediated strong metal–support interactions in oxide-supported Rh catalysts. Nat. Chem. 2017, 9, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Chong, M.N.; Jin, B.; Chow, C.W.; Saint, C. Recent developments in photocatalytic water treatment technology: A review. Water Res. 2010, 44, 2997–3027. [Google Scholar] [CrossRef]
- Guo, Q.; Zhou, C.; Ma, Z.; Yang, X. Fundamentals of TiO2 photocatalysis: Concepts, mechanisms, and challenges. Adv. Mater. 2019, 31, 1901997. [Google Scholar] [CrossRef] [PubMed]
- Lang, R.; Du, X.; Huang, Y.; Jiang, X.; Zhang, Q.; Guo, Y.; Liu, K.; Qiao, B.; Wang, A.; Zhang, T. Single-atom catalysts based on the metal–oxide interaction. Chem. Rev. 2020, 120, 11986–12043. [Google Scholar] [CrossRef] [PubMed]
- O’regan, B.; Grätzel, M. A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 1991, 353, 737–740. [Google Scholar] [CrossRef]
- Lee, K.; Mazare, A.; Schmuki, P. One-dimensional titanium dioxide nanomaterials: Nanotubes. Chem. Rev. 2014, 114, 9385–9454. [Google Scholar] [CrossRef]
- Wen, J.; Li, X.; Liu, W.; Fang, Y.; Xie, J.; Xu, Y. Photocatalysis fundamentals and surface modification of TiO2 nanomaterials. Chin. J. Catal. 2015, 36, 2049–2070. [Google Scholar] [CrossRef]
- Matsubu, J.C.; Yang, V.N.; Christopher, P. Isolated metal active site concentration and stability control catalytic CO2 reduction selectivity. J. Am. Chem. Soc. 2015, 137, 3076–3084. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Sun, L.; Qi, X.; Wang, Z.; Fu, Q.; Pan, C. A novel strategy to enhance the multiple interface effect using amorphous carbon packaged hydrogenated TiO2 for stable and effective microwave absorption. J. Mater. Chem. C 2019, 7, 6152–6160. [Google Scholar] [CrossRef]
- Burdett, J.K.; Hughbanks, T.; Miller, G.J.; Richardson, J.W., Jr.; Smith, J.V. Structural-electronic relationships in inorganic solids: Powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K. J. Am. Chem. Soc. 1987, 109, 3639–3646. [Google Scholar] [CrossRef]
- Howard, C.; Sabine, T.; Dickson, F. Structural and thermal parameters for rutile and anatase. Acta Crystallogr. Sect. B Struct. Sci. 1991, 47, 462–468. [Google Scholar] [CrossRef]
- Abrahams, S.; Bernstein, J. Rutile: Normal probability plot analysis and accurate measurement of crystal structure. J. Chem. Phys. 1971, 55, 3206–3211. [Google Scholar] [CrossRef]
- Cromer, D.T.; Herrington, K. The structures of anatase and rutile. J. Am. Chem. Soc. 1955, 77, 4708–4709. [Google Scholar] [CrossRef]
- Arlt, T.; Bermejo, M.; Blanco, M.; Gerward, L.; Jiang, J.; Olsen, J.S.; Recio, J. High-pressure polymorphs of anatase TiO2. Phys. Rev. B 2000, 61, 14414. [Google Scholar] [CrossRef]
- Dubrovinskaia, N.A.; Dubrovinsky, L.S.; Ahuja, R.; Prokopenko, V.B.; Dmitriev, V.; Weber, H.P.; Osorio-Guillen, J.; Johansson, B. Experimental and theoretical identification of a new high-pressure TiO2 polymorph. Phys. Rev. Lett. 2001, 87, 275501. [Google Scholar] [CrossRef]
- Dubrovinsky, L.S.; Dubrovinskaia, N.A.; Swamy, V.; Muscat, J.; Harrison, N.M.; Ahuja, R.; Holm, B.; Johansson, B. The hardest known oxide. Nature 2001, 410, 653–654. [Google Scholar] [CrossRef] [PubMed]
- Gerward, L.; Staun Olsen, J. Post-rutile high-pressure phases in TiO2. J. Appl. Crystallogr. 1997, 30, 259–264. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zechetbauer, M.J.; Zhu, Y.T. Producing bulk ultrafine-grained materials by severe plastic deformation. JOM 2006, 58, 33–39. [Google Scholar] [CrossRef]
- Edalati, K.; Daio, T.; Ikoma, Y.; Arita, M.; Horita, Z. Graphite to diamond-like carbon phase transformation by high-pressure torsion. Appl. Phys. Lett. 2013, 103, 034108. [Google Scholar] [CrossRef]
- Edalati, K.; Daio, T.; Arita, M.; Lee, S.; Horita, Z.; Togo, A.; Tanaka, I. High-pressure torsion of titanium at cryogenic and room temperatures: Grain size effect on allotropic phase transformations. Acta Mater. 2014, 68, 207–213. [Google Scholar] [CrossRef]
- Edalati, K.; Arimura, M.; Ikoma, Y.; Daio, T.; Miyata, M.; Smith, D.J.; Horita, Z. Plastic deformation of BaTiO3 ceramics by high-pressure torsion and changes in phase transformations, optical and dielectric properties. Mater. Res. Lett. 2015, 3, 216–221. [Google Scholar] [CrossRef]
- Razavi-Khosroshahi, H.; Edalati, K.; Hirayama, M.; Emami, H.; Arita, M.; Yamauchi, M.; Hagiwara, H.; Ida, S.; Ishihara, T.; Akiba, E.; et al. Visible-light-driven photocatalytic hydrogen generation on nanosized TiO2-II stabilized by high-pressure torsion. ACS Catal. 2016, 6, 5103–5107. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Muscat, J.; Swamy, V.; Harrison, N.M. First-principles calculations of the phase stability of TiO2. Phys. Rev. B 2002, 65, 224112. [Google Scholar] [CrossRef]
- Al-Khatatbeh, Y.; Lee, K.K.; Kiefer, B. High-pressure behavior of TiO2 as determined by experiment and theory. Phys. Rev. B 2009, 79, 134114. [Google Scholar] [CrossRef]
- Ma, X.; Liang, P.; Miao, L.; Bie, S.; Zhang, C.; Xu, L.; Jiang, J. Pressure-induced phase transition and elastic properties of TiO2 polymorphs. Phys. Status Solidi (b) 2009, 246, 2132–2139. [Google Scholar] [CrossRef]
- Wu, X.; Holbig, E.; Steinle-Neumann, G. Structural stability of TiO2 at high pressure in density-functional theory based calculations. J. Phys. Condens. Matter 2010, 22, 295501. [Google Scholar] [CrossRef][Green Version]
- Dekura, H.; Tsuchiya, T.; Kuwayama, Y.; Tsuchiya, J. Theoretical and experimental evidence for a new post-cotunnite phase of titanium dioxide with significant optical absorption. Phys. Rev. Lett. 2011, 107, 045701. [Google Scholar] [CrossRef] [PubMed]
- Fu, Z.; Liang, Y.; Wang, S.; Zhong, Z. Structural phase transition and mechanical properties of TiO2 under high pressure. Phys. Status Solidi (b) 2013, 250, 2206–2214. [Google Scholar] [CrossRef]
- Swamy, V.; Wilson, N.C. First-principles calculations of the pressure stability and elasticity of dense TiO2 phases using the B3LYP hybrid functional. J. Phys. Chem. C 2014, 118, 8617–8625. [Google Scholar] [CrossRef]
- Liu, Q.J.; Ran, Z.; Liu, F.S.; Liu, Z.T. Phase transitions and mechanical stability of TiO2 polymorphs under high pressure. J. Alloys Compd. 2015, 631, 192–201. [Google Scholar] [CrossRef]
- Dong, H.K.; Li, M.B.; Qi, G.Q.; Xiu, X.M.; Shi, L.B. The structural phase transition and phase stability of TiO2 (P42/nmc) under high pressure from first-principles calculations. Phys. Scr. 2015, 91, 015701. [Google Scholar] [CrossRef]
- Basavaraj, K.; Nyayban, A.; Panda, S. Structural phase transitions and elastic properties of TiO2 polymorphs: Ab-initio study. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1248, 012064. [Google Scholar] [CrossRef]
- Arroyo-de Dompablo, M.; Morales-García, A.; Taravillo, M. DFT+U calculations of crystal lattice, electronic structure, and phase stability under pressure of TiO2 polymorphs. J. Chem. Phys. 2011, 135, 054503. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Perdew, burke, and ernzerhof reply. Phys. Rev. Lett. 1998, 80, 891. [Google Scholar] [CrossRef]
- Curnan, M.T.; Kitchin, J.R. Investigating the energetic ordering of stable and metastable TiO2 polymorphs using DFT+U and hybrid functionals. J. Phys. Chem. C 2015, 119, 21060–21071. [Google Scholar] [CrossRef]
- Park, K.; Raman, M.; Olatunbosun, A.J.; Pohlmann, J. Revisiting DFT+U calculations of TiO2 and the effect of the local-projection size. AIP Adv. 2024, 14, 065114. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Perdew, J.P.; Ruzsinszky, A. Semilocal density functional obeying a strongly tightened bound for exchange. Proc. Natl. Acad. Sci. USA 2015, 112, 685–689. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.H.; Kitchaev, D.A.; Ceder, G. Rationalizing accurate structure prediction in the meta-GGA SCAN functional. Phys. Rev. B 2019, 100, 035132. [Google Scholar] [CrossRef]
- Hinuma, Y.; Hayashi, H.; Kumagai, Y.; Tanaka, I.; Oba, F. Comparison of approximations in density functional theory calculations: Energetics and structure of binary oxides. Phys. Rev. B 2017, 96, 094102. [Google Scholar] [CrossRef]
- Zhang, Y.; Kitchaev, D.A.; Yang, J.; Chen, T.; Dacek, S.T.; Sarmiento-Pérez, R.A.; Marques, M.A.; Peng, H.; Ceder, G.; Perdew, J.P.; et al. Efficient first-principles prediction of solid stability: Towards chemical accuracy. NPJ Comput. Mater. 2018, 4, 1–6. [Google Scholar] [CrossRef]
- Shahi, C.; Sun, J.; Perdew, J.P. Accurate critical pressures for structural phase transitions of group IV, III-V, and II-VI compounds from the SCAN density functional. Phys. Rev. B 2018, 97, 094111. [Google Scholar] [CrossRef]
- Mazumder, J.T.; Mayengbam, R.; Tripathy, S. Theoretical investigation on structural, electronic, optical and elastic properties of TiO2, SnO2, ZrO2 and HfO2 using SCAN meta-GGA functional: A DFT study. Mater. Chem. Phys. 2020, 254, 123474. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Mori-Sánchez, P.; Cohen, A.J.; Yang, W. Many-electron self-interaction error in approximate density functionals. J. Chem. Phys. 2006, 125, 201102. [Google Scholar] [CrossRef]
- Furness, J.W.; Kaplan, A.D.; Ning, J.; Perdew, J.P.; Sun, J. Accurate and numerically efficient r2SCAN meta-generalized gradient approximation. J. Phys. Chem. Lett. 2020, 11, 8208–8215. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Furness, J.W.; Xiao, B.; Sun, J. Subtlety of TiO2 phase stability: Reliability of the density functional theory predictions and persistence of the self-interaction error. J. Chem. Phys. 2019, 150, 014105. [Google Scholar] [CrossRef] [PubMed]
- Niu, M.; Cheng, D.; Cao, D. Fluorite TiO2 (111) surface phase for enhanced visible-light solar energy conversion. J. Phys. Chem. C 2014, 118, 20107–20111. [Google Scholar] [CrossRef]
- Jovanovic, D.; Zagorac, D.; Matovic, B.; Zarubica, A.; Zagorac, J. Anion substitution and influence of sulfur on the crystal structures, phase transitions, and electronic properties of mixed TiO2/TiS2 compounds. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2021, 77, 833–847. [Google Scholar] [CrossRef]
- Simons, P.Y.; Dachille, F. The structure of TiO2 II, a high-pressure phase of TiO2. Acta Crystallogr. 1967, 23, 334–336. [Google Scholar] [CrossRef]
- Olsen, J.S.; Gerward, L.; Jiang, J. On the rutile/α-PbO2-type phase boundary of TiO2. J. Phys. Chem. Solids 1999, 60, 229–233. [Google Scholar] [CrossRef]
- Nishio-Hamane, D.; Shimizu, A.; Nakahira, R.; Niwa, K.; Sano-Furukawa, A.; Okada, T.; Yagi, T.; Kikegawa, T. The stability and equation of state for the cotunnite phase of TiO2 up to 70 GPa. Phys. Chem. Miner. 2010, 37, 129–136. [Google Scholar] [CrossRef]
- Sorantin, P.I.; Schwarz, K. Chemical bonding in rutile-type compounds. Inorg. Chem. 1992, 31, 567–576. [Google Scholar] [CrossRef]
- Cronemeyer, D.C. Electrical and optical properties of rutile single crystals. Phys. Rev. 1952, 87, 876. [Google Scholar] [CrossRef]
- Tang, H.; Berger, H.; Schmid, P.; Levy, F.; Burri, G. Photoluminescence in TiO2 anatase single crystals. Solid State Commun. 1993, 87, 847–850. [Google Scholar] [CrossRef]
- Zhu, T.; Gao, S.P. The stability, electronic structure, and optical property of TiO2 polymorphs. J. Phys. Chem. C 2014, 118, 11385–11396. [Google Scholar] [CrossRef]
- Mei, Z.G.; Wang, Y.; Shang, S.; Liu, Z.K. First-principles study of the mechanical properties and phase stability of TiO2. Comput. Mater. Sci. 2014, 83, 114–119. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite deformations of an elastic solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
- Dachille, F.; Simons, P.; Roy, R. Pressure-temperature studies of anatase, brookite, rutile and TiO2-II. Am. Mineral. J. Earth Planet. Mater. 1968, 53, 1929–1939. [Google Scholar]
- Himmetoglu, B.; Floris, A.; De Gironcoli, S.; Cococcioni, M. Hubbard-corrected DFT energy functionals: The LDA+U description of correlated systems. Int. J. Quantum Chem. 2014, 114, 14–49. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in molecules. Accounts Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Sofo, J.; Garcia, G. Implementation of Bader Theory in WIEN Package. Available online: http://www.wien2k.at/lapw/ (accessed on 15 December 2023).
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, B.; Fang, Y.; Haunschild, R.; Hao, P.; Ruzsinszky, A.; Csonka, G.I.; Scuseria, G.E.; Perdew, J.P. Density functionals that recognize covalent, metallic, and weak bonds. Phys. Rev. Lett. 2013, 111, 106401. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, B.; Ruzsinszky, A. Communication: Effect of the orbital-overlap dependence in the meta generalized gradient approximation. J. Chem. Phys. 2012, 137, 051101. [Google Scholar] [CrossRef] [PubMed]
- Zupan, A.; Burke, K.; Ernzerhof, M.; Perdew, J.P. Distributions and averages of electron density parameters: Explaining the effects of gradient corrections. J. Chem. Phys. 1997, 106, 10184–10193. [Google Scholar] [CrossRef]
- Zupan, A.; Perdew, J.P.; Burke, K.; Causà, M. Density-gradient analysis for density functional theory: Application to atoms. Int. J. Quantum Chem. 1997, 61, 835–845. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Sun, J.; Burke, K. Gedanken densities and exact constraints in density functional theory. J. Chem. Phys. 2014, 140, 18A533. [Google Scholar] [CrossRef]
- De Groot, F.; Grioni, M.; Fuggle, J.C.; Ghijsen, J.; Sawatzky, G.A.; Petersen, H. Oxygen 1s x-ray-absorption edges of transition-metal oxides. Phys. Rev. B 1989, 40, 5715. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.; Marks, L.D. WIEN2k: An APW+ lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- Blaha, P.; Schwarz, K.; Madsen, G.K.; Kvasnicka, D.; Luitz, J. WIEN2k; Vienna University Technology: Vienna, Austria, 2001. [Google Scholar]
- Doumont, J.; Tran, F.; Blaha, P. Implementation of self-consistent MGGA functionals in augmented plane wave based methods. Phys. Rev. B 2022, 105, 195138. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Solovyev, I.; Korotin, M.; Czyżyk, M.; Sawatzky, G. Density-functional theory and NiO photoemission spectra. Phys. Rev. B 1993, 48, 16929. [Google Scholar] [CrossRef]
- Liechtenstein, A.; Anisimov, V.I.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]


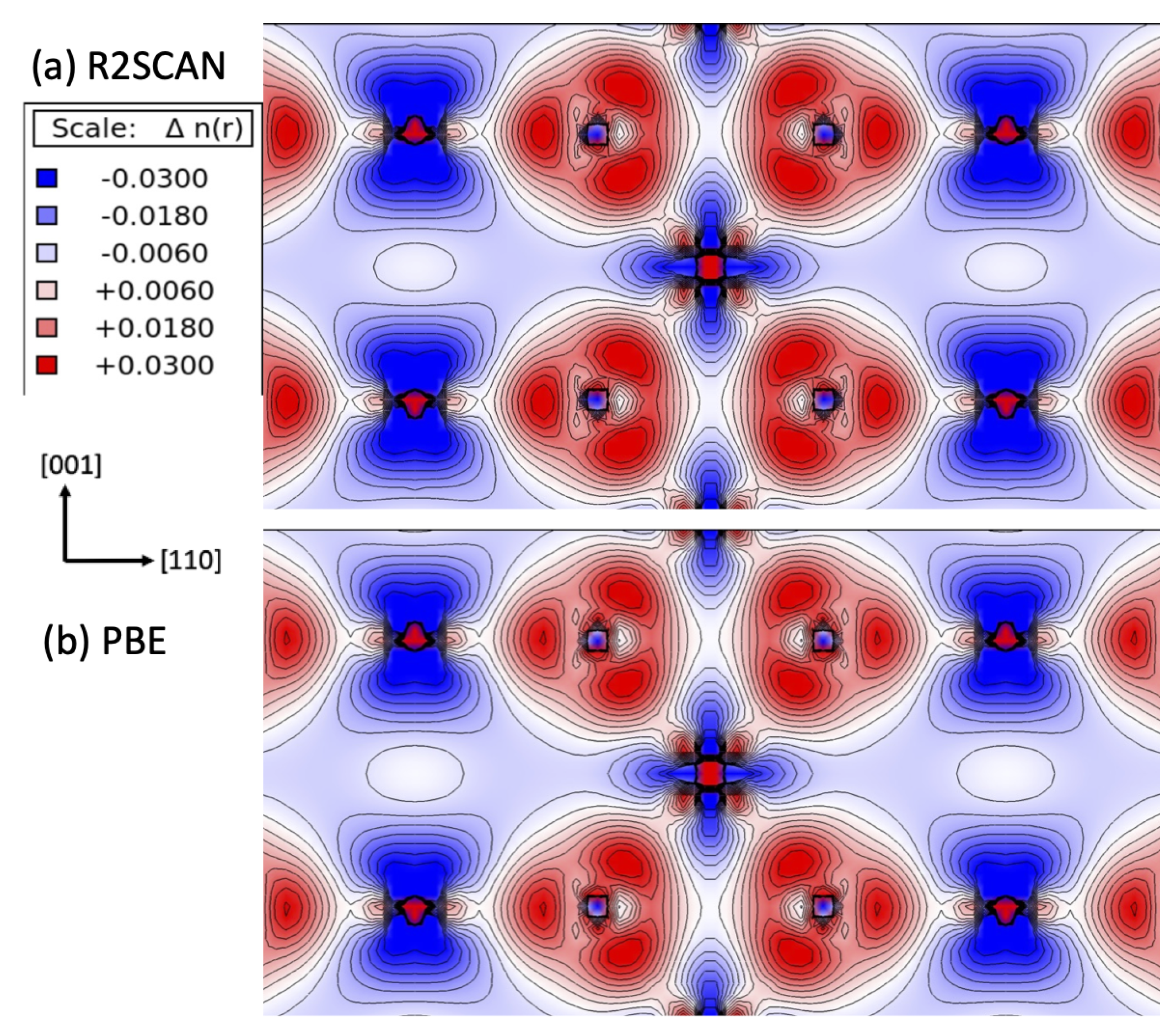
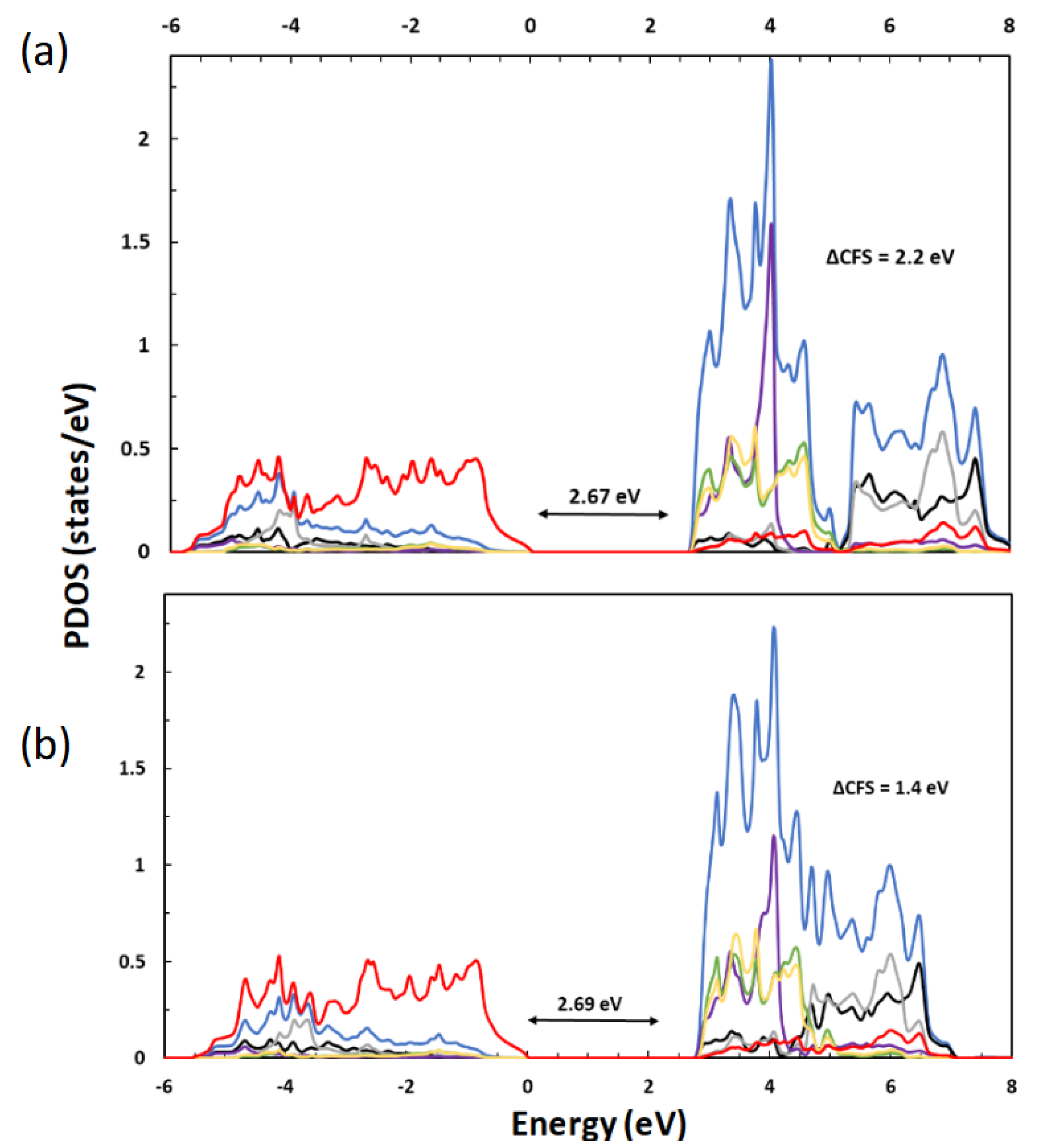
| Lattice Constants | |||||
|---|---|---|---|---|---|
| Phase | a | b (β) | c | (GPa) | Reference |
| rutile | 4.600 | 2.956 | 244 | this work (r2SCAN) | |
| 4.646 | 2.966 | 214 | this work (PBE) | ||
| 4.591 | 2.957 | other (SCAN) [53] | |||
| 4.655 | 2.970 | 210 | other (PBE) [32] | ||
| 4.593 a | 2.959 a | 235 b, 211 c, 210 d | expt. | ||
| anatase | 3.779 | 9.601 | 212 | this work (r2SCAN) | |
| 3.805 | 9.716 | 188 | this work (PBE) | ||
| 3.777 | 9.587 | other (SCAN) [53] | |||
| 3.806 | 9.737 | 170 | other (PBE) [32] | ||
| 3.785 a | 9.514 a | 179 c, 190 c | expt. | ||
| columbite | 4.549 | 5.521 | 4.897 | 254 | this work (r2SCAN) |
| 4.580 | 5.576 | 4.927 | 206 | this work (PBE) | |
| 4.537 | 5.504 | 4.905 | other (SCAN) [53] | ||
| 4.588 | 5.590 | 4.933 | 214 | other (PBE) [32] | |
| 4.541 c | 5.493 c | 4.906 c | 258 c,d, 253 b, 206 e | expt. | |
| baddeleyite | 4.836 | 4.857 | 5.059 | 273 | this work (r2SCAN) |
| (100.3) | |||||
| 4.861 | 4.906 | 5.111 | 171 | this work (PBE) | |
| (100.3) | |||||
| 4.800 | 4.867 | 5.026 | other (SCAN) [53] | ||
| (99.82) | |||||
| 4.866 | 4.920 | 5.108 | 149 | other (PBE) [32] | |
| (99.9) | |||||
| 4.662 c | 4.969 c | 4.911 c | 304 f, 298 b, 290 d, 175 e | expt. | |
| (99.4 c) | |||||
| OI | 9.358 | 4.950 | 4.801 | 280 | this work (r2SCAN) |
| 9.426 | 4.986 | 4.842 | 221 | this work (PBE) | |
| 9.428 | 4.985 | 4.837 | 247 | other (PBE) [32] | |
| 9.046 g,h | 4.834 g,h | 4.621 g,h | 318 g, 314 b, 222 e | expt. | |
| 9.037 h | 4.832 h | 4.629 h | 283 | this work (r2SCAN) | |
| 9.071 h | 4.864 h | 4.654 h | 229 | this work (PBE) | |
| 9.138 h | 4.853 h | 4.671 h | 252 | other (B3LYP) [33] | |
| cotunnite | 5.169 | 3.167 | 6.290 | 297 | this work (r2SCAN) |
| 5.217 | 3.185 | 6.329 | 184 | this work (PBE) | |
| 5.231 | 3.151 | 6.261 | 270 | other (PBE) [32] | |
| 5.240 | 3.163 | 6.297 | other (PBE) [54] | ||
| 5.18 | 3.191 | 6.328 | 213 | other (PW91) [29] | |
| 5.125 i | 2.914 i | 5.931 i | 255 | other (B3LYP) [33] | |
| 5.163 f,j | 2.989 f,j | 5.966 f,j | 431 f, 312 b, 294 e | expt. |
| Rutile | Bader Charge (e) | BCP (3, −1) (in Å) | |||
| XC Functional | U () | Ti | O | Ti; O(1) | Ti; O(2) |
| PBE | 0 | +2.28 | −1.14 | 1.002; 1.004 | 0.982; 0.977 |
| PBE+U | 6 | +2.46 | −1.23 | 1.003; 1.015 | 0.983; 0.985 |
| r2SCAN | 0 | +2.38 | −1.19 | 0.995; 0.996 | 0.976; 0.968 |
| r2SCAN+U | 2.5 | +2.46 | −1.23 | 0.993; 1.000 | 0.976; 0.974 |
| Anatase | Bader Charge (e) | BCP(in Å) | |||
| XC Functional | U (eV) | Ti | O | Ti; O(1) | Ti; O(2) |
| PBE | 0 | +2.26 | −1.13 | 0.997; 0.998 | 0.975; 0.974 |
| PBE+U | 6 | +2.44 | −1.22 | 1.001; 1.003 | 0.971; 0.978 |
| r2SCAN | 0 | +2.37 | −1.19 | 0.993; 0.994 | 0.965; 0.969 |
| r2SCAN+U | 2.5 | +2.44 | −1.22 | 0.991; 0.997 | 0.969; 0.971 |
| Rutile | Anatase | |||||
|---|---|---|---|---|---|---|
| Ti RMT: 1.78 aB | Ti-O(1) | Ti-O(2) | O-O a | Ti-O(1) | Ti-O(2) | O-O b |
| r2SCAN | 1.986 | 1.947 | 2.535 | 1.987 | 1.934 | 2.797 |
| PBE | 2.005 | 1.959 | 2.560 | 2.004 | 1.949 | 2.822 |
| r2SCAN+U (2.5 eV) | 1.986 | 1.952 | 2.536 | 1.988 | 1.940 | 2.805 |
| PBE+U (6 eV) | 2.007 | 1.973 | 2.563 | 2.005 | 1.962 | 2.839 |
| Ti RMT: 2.2 aB | ||||||
| r2SCAN | 1.982 | 1.944 | 2.531 | 1.987 | 1.939 | 2.803 |
| PBE | 2.006 | 1.956 | 2.556 | 2.007 | 1.949 | 2.822 |
| r2SCAN+U (2.5 eV) | 1.991 | 1.971 | 2.541 | 1.991 | 1.950 | 2.820 |
| PBE+U (7.7 eV) | 2.025 | 1.991 | 2.572 | 2.022 | 1.983 | 2.869 |
| Expt [14] | 1.980 | 1.949 | 2.537 | 1.969 | 1.936 | 2.799 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pohlmann, J.; Raman, M.; Bonds, L.; Park, K. The Stability of TiO2 Phases Studied Using r2SCAN in the Hubbard-Corrected Density Functional Theory. Molecules 2025, 30, 560. https://doi.org/10.3390/molecules30030560
Pohlmann J, Raman M, Bonds L, Park K. The Stability of TiO2 Phases Studied Using r2SCAN in the Hubbard-Corrected Density Functional Theory. Molecules. 2025; 30(3):560. https://doi.org/10.3390/molecules30030560
Chicago/Turabian StylePohlmann, Jared, Manjula Raman, Lily Bonds, and Kenneth Park. 2025. "The Stability of TiO2 Phases Studied Using r2SCAN in the Hubbard-Corrected Density Functional Theory" Molecules 30, no. 3: 560. https://doi.org/10.3390/molecules30030560
APA StylePohlmann, J., Raman, M., Bonds, L., & Park, K. (2025). The Stability of TiO2 Phases Studied Using r2SCAN in the Hubbard-Corrected Density Functional Theory. Molecules, 30(3), 560. https://doi.org/10.3390/molecules30030560






